中国海洋湖沼学会主办。
文章信息
- 王倩, 宋金宝, 曹海锦, 乔文丽. 2018.
- WANG Qian, SONG Jin-Bao, CAO Hai-Jin, QIAO Wen-Li. 2018.
- 波致应力的近似求解及其太平洋特征分析
- APPROXIMATE ESTIMATION OF WAVE-INDUCED STRESS AND ITS CHARACTERISTIC ANALYSIS IN THE PACIFIC
- 海洋与湖沼, 49(3): 524-534
- Oceanologia et Limnologia Sinica, 49(3): 524-534.
- http://dx.doi.org/10.11693/hyhz20170900242
-
文章历史
- 收稿日期:2017-09-26
- 收修改稿日期:2017-11-14
2. 河海大学海洋学院 南京 210098
2. College of Oceanography, Hohai University, Nanjing 210098, China
海气界面的动量通量即界面间动量的垂向输送, 反映了海洋与大气之间的摩擦拖曳作用, 直接控制和影响着海气边界层过程和海气边界层结构, 在海气相互作用、海洋-大气耦合模式、表面波与流的预报中起着重要的作用。目前在很多海洋环流的基础模式中, 风的作用对于海水的运动非常重要, 准确估算风应力是确定海气动量通量以及海浪与海洋环流模式驱动力的基础。如果利用涡相关法计算风应力, 需要观测不同时间和不同空间的湍流脉动情况, 观测存在较大的困难, 因此在实际应用中, 通常用块体公式来计算海面风应力, 利用海面拖曳系数或者海面空气动力学粗糙度对海面风应力参数化(邹仲水等, 2014)。
关于风应力的研究, 早期, 人们认为海气界面的动量通量只受到湍流剪切应力影响, 如今, 大量研究表明, 发生在海气界面的表面波对海气动量交换也有重要影响(Janssen, 1989; Belcher et al, 1993; Edson et al, 1998; Hristov et al, 1998, 2003; Sullivan et al, 2004; Veron et al, 2008)。现场观测(Davidson et al, 1973; Benilov et al, 1974; Smedman et al, 1994, 1999; Donelan et al, 1997; Rutgersson et al, 2001; , Semedo et al, 2009)和大涡模拟(Sullivan et al, 2008)表明, 通常情况海气界面动量通量有两个主要分量, 一是湍流剪切应力, 另一个是波致应力。当波浪传播速度小于风速时, 风为波浪提供能量, 但当波浪传播速度大于风速时, 波浪为风提供能量。在弱风条件下, 快速运动的波浪将诱导一个向上的动量通量, 这时波致应力将起主导作用, 总动量从水面指向大气, 这个由海洋到大气的向上动量输送将直接影响和修正海上大气边界层的流体动力学和湍流结构:如:近海面射流的生成(Miller et al, 1999), 平均风速随高度增加的减少(Rutgersson et al, 2001), 表面应力与风向的不一致(Grachev et al, 2003)等。事实上, 由于近表面气流的加速, 垂直风廓线不再满足对数廓线, 一个近表面波驱动风速最大值(a wind jet)将会产生。这种现象最早由Harris(1966)在实验室发现, 并称其为波驱动风(wave-driven wind)。前人研究表明, 对于涌浪, 部分波动量将以波驱动风的形式从海洋输运到大气中, 这时Monin-Obukhov相似理论不再适用, 涌浪对整个大气边界层将产生一定的影响, 这与通常人们认为的波边界层深度很浅(如: Makin et al, 1996)相矛盾。为了揭示涌浪对近海面风速廓线的影响, 人们提出了MABL海洋大气边界层模型(Makin, 2008; Hanley et al, 2008; Semedo et al, 2009)。Kudryavtsev等(2004)基于两层波边界层近似, 提出了一个涌浪与气流相互作用模型。他们利用该模型再现了Harris(1966)的实验室实验结果, 并解释了波驱动风的形成机制, 但是该模型只在波边界层范围内有效。基于波修正的Ekman模型, Makin(2008)通过推广混合长度的定义, 并在动量方程中考虑了科氏力的影响, 将Kudryavtsev等(2004)的模型推广到整个大气边界层。最近, Song等人(2015)基于Makin(2008)以及Hanley等人(2008)给出的波修正Ekman模型, 研究了表面波对稳定的海洋大气边界层(ABL)近海表风廓线的影响。他们比较分析了考虑波致应力与否模型解析解之间的差异, 并将解析解与波罗的海岛屿 stergarnsholm观测塔的资料进行了比较, 研究表明, 表面波不仅对近海面平均风廓线, 而且对海洋大气边界层的湍流结构均有重要的影响, 因为它们影响和改变了海洋大气边界层的结构。
虽然以上研究从不同角度揭示了波浪对海气界面动量通量以及海洋上方大气边界层的影响, 但仍有许多重要的科学问题不够清晰, 值得进一步探讨。总而言之, 如何准确计算拖曳系数(即风应力)一直是一个比较复杂的问题。本文的研究目的是比较波致应力的不同计算方法, 同时探讨波致应力在太平洋的季节性变化。波致应力的准确计算对反演拖曳系数具有重要的意义, 进而对风应力即海气界面动量通量交换的研究具有重要意义。
1 波致应力的计算方法海气界面的动量通量即海面风应力一般分为两部分, 湍流剪切应力和波致应力(徐德伦等, 2001):
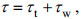 (1)
(1)式中, τ为风应力; τt为湍流剪切应力, 根据普朗特混合长假设的理论可以参数化表示, 本文不做详细介绍; τw为波致应力, 正值表示风产生的进入波浪的动量, 负值表示波浪诱导的进入风的动量, 波致应力定义为(Markin et al, 1995; Semedo et al, 2009; Song et al, 2015):
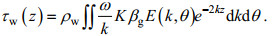 (2)
(2)式中, ρw是海水密度; z是距海平面的距离; ω是波浪的角频率; k是波数; K=(kx, ky)是水平方向的波数矢量; E(k, θ)是波浪波数方向谱; βg是波浪增长率。
根据波致应力的计算公式, 波致应力与波浪增长率βg和海浪谱E(k, θ)有关, 因此分别对波浪增长率公式和海浪谱计算公式进行敏感性分析, 并通过比较分析, 选择合适的波致应力计算方法。
1.1 波浪增长率公式的敏感性分析 1.1.1 不同的波浪增长率公式已知波浪的波数方向谱E(k, θ), 波浪增长率βg定义为:
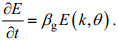 (3)
(3)不同的波浪增长率公式对波致应力的计算结果有重要影响, 这里给出4种常用的波浪增长率公式。
第一种, Komen等(1984)提到的波浪增长率公式:
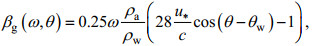 (4)
(4)式中, ρa、ρw分别是空气的密度和海水的密度; c是波浪的相速度; u*是摩擦速度; θ是波向; θw是风向。u*可以通过拖曳系数以及10m风速u10进行计算:
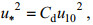 (5)
(5)Cd是在10米高度的拖曳系数, u10是10米高度风速, 该文采用Zijlema等(2012)给出拖曳系数计算公式:
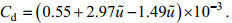 (6)
(6)式中, ũ=u10/uref,uref=31.5m/s。
第二种, Janssen(1991)提出的波浪增长率公式:
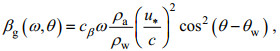 (7)
(7)cβ为Miles常数, 是无因次临界高度的函数:
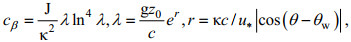 (8)
(8)式中, κ=0.41是冯卡曼常数, g是重力加速度, J=1.2是常数, z0是海表面空气动力粗糙度(Andrea, 2004):
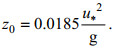 (9)
(9)第三种, Belcher等(1993)提到的波浪增长率公式:
 (10)
(10)Stewart(1974)提到波浪增长率系数cβ为:
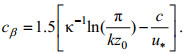 (11)
(11)式中, κ是冯卡曼常数, 取0.41; k是波浪的波数; z0是海表面空气动力粗糙度; c是波浪的相速度; u*是摩擦速度。
第四种, 波浪增长率βg的公式形式与式(10)相同, 但是波浪增长率系数cβ的计算公式不同, 选用的是Polnikov(2011)根据实验数据得到的经验公式:
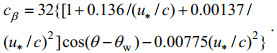 (12)
(12)式中, θw是风向; c是波浪的相速度; u*是摩擦速度。
1.1.2 敏感性分析首先作两点假设:一、风向沿着x轴正向, 波向与风向一致, 即θ=θw=0;二、只考虑深水情况, 有深水频散关系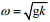
实验观测数据使用的是Plant(1982)用到的经典实验数据, 其中三角形表示Shemdin等(1967)的实验数据; 实心圆表示Larson(1975)的实验数据; “x”表示Wu等(1971、1979)的实验数据; 空心圆表示Snyder等(1981)利用固定传感器得到的实验数据; 方形表示Snyder等(1981)利用波跟踪传感器得到的实验数据。
计算波浪增长率时, 取定10m高度处的风速值, 作无因次波浪增长率βg/f随反波龄u*/c的变化曲线图。
图 1表明, 对于Komen(1984)的计算公式, 当波数较大, 即反波龄较大的时候, 误差较大, 使得总体计算结果有一定的误差; 对于Janssen(1991)的计算公式, 波数较大时与实验数据吻合较好, 但当波数较小的时候, 误差很大, 使得总体计算结果有一定的误差; 对于Polnikov(2011)的计算公式, 计算结果普遍高于测量值, 因此相对误差较大; 相比之下, Belcher等(1993)的计算公式虽然在反波龄较大时与实验观测数据的误差稍微较大, 但总体的吻合度较好。
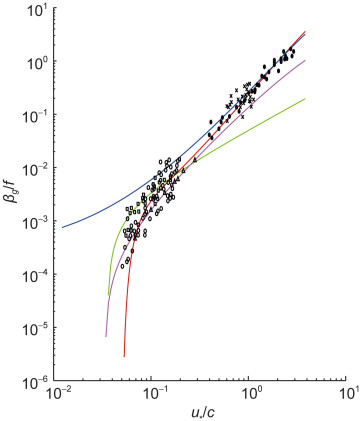 |
| 图 1 不同波浪增长率公式的计算结果比较 Fig. 1 Calculation results with formula of different wave growth rates 注:绿线: Komen(1984); 红线: Janssen(1991); 紫红线: Belcher等(1993); 蓝线: Polnikov(2011); 各点:实测实验数据 |
将4种公式的计算结果与经典实验观测数据进行对比, 考虑相对误差(RE)的平均值和最大值以及均方根误差(RMS):
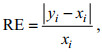 (13)
(13)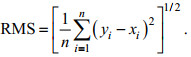 (14)
(14)式中, yi为公式的计算值, xi为实验的数据值。
表 1给出了风速分别为5m/s、10m/s、15m/s、20m/s情况下, 不同波浪增长率公式与实验观测数据的误差比较。可以看出, 改变给定风速的大小, 不同公式的计算结果与实验观测数据的相对误差和均方根误差都有所改变, 当风速较小时(< 15m/s左右)Belcher等的计算公式与实验观测数据吻合度较好, 而当风速较大时(> 20m/s左右)Janssen的计算公式与实验观测数据吻合度较好。
| 风速 | 波浪增长率公式 | RE均值 | RE最大值 | RMS |
| 5m/s | 1. Komen | 0.7617 | 4.2971 | 0.1957 |
| 2. Janssen | 0.8802 | 143.59 | 0.0486 | |
| 3. Belcher and Hunt | 0.4637 | 1.3564 | 0.1146 | |
| 4. Polnikov | 0.1955 | 13.7165 | 0.0616 | |
| 10m/s | 1.Komen | 0.8629 | 0.9827 | 0.8077 |
| 2. Janssen | 0.3449 | 78.6576 | 0.3360 | |
| 3. Belcher and Hunt | 0.5031 | 0.7567 | 0.4673 | |
| 4. Polnikov | 0.3747 | 8.3586 | 0.2683 | |
| 15m/s | 1. Komen | 0.8967 | 0.9683 | 1.7403 |
| 2. Janssen | 0.4462 | 0.8837 | 1.1093 | |
| 3. Belcher and Hunt | 0.5334 | 0.5737 | 1.0502 | |
| 4. Polnikov | 0.3820 | 3.5198 | 0.9144 | |
| 20m/s | 1. Komen | 0.9128 | 0.9307 | 2.9162 |
| 2. Janssen | 0.3781 | 0.4601 | 1.3885 | |
| 3. Belcher and Hunt | 0.5749 | 0.6512 | 1.9150 | |
| 4. Polnikov | 0.4335 | 1.9232 | 1.4870 |
本文使用的数据是欧洲中期数值预报中心(ECMWF)的ERA-interim数据, 根据再分析数据的特点, 10米风速中大多数为中低风速, 同时综合来看, 无论是低风速情况还是高风速情况, Belcher等的计算公式与实验测量值都较为吻合, 相对误差的最大值明显比其他公式小, 因此下文中计算波致应力时, 我们选用Belcher等的波浪增长率计算公式。
1.2 海浪谱敏感性分析 1.2.1 单波近似为使波致应力的求解更加快速有效, 首先只考虑单频率波, 单波情况不考虑方向的改变, 设波浪的能量:
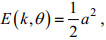 (15)
(15)式中, a是波浪的振幅; 波浪的能量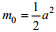
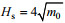
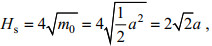 (16)
(16)由公式(2)、(15)可以得到单波近似的波致应力:
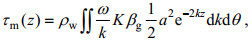 (17)
(17)式中, τm是单波情况[波谱为(15)式]下的波致应力, 是一般情形(2)式的特例。假设:风向沿着x轴; 只存在单波, 波向θ=0;只考虑深水情况。则有:
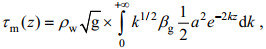 (18)
(18)对于单波近似, 取波浪的波数k=kp, kp为谱峰波数, 则:
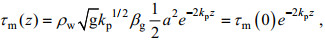 (19)
(19)根据公式(16)可以将振幅用有效波高进行代换, 考虑海表面的波致应力:
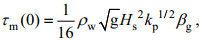 (20)
(20)关于谱峰频率与波龄的关系, Elfouhaily等(1997)提到:
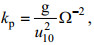 (21)
(21)式中, Ω是波龄, Zhao等(2003)提到波龄与有效波高、风速的关系:
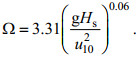 (22)
(22)那么, 当已知10米风速u10、有效波高Hs, 根据公式(20)、(21)、(22)以及波浪增长率的计算公式(10)、(11)就可以计算得到近似求解的波致应力。
1.2.2 JONSWAP谱和Elfouhaily谱海浪波面位移的均值一般取为0, 海浪谱(功率谱)定义为波面位移自相关函数的傅里叶变换。海浪谱表示海浪能量在不同频率、波数和方向上的分布, 对海浪谱积分得到海浪的总能量。
Lucas(2015)提到JONSWAP频率方向谱的表达式:
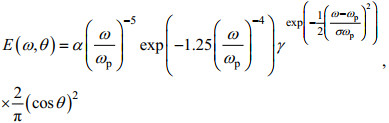 (23)
(23)式中, ωp为谱峰频率; 当ω≤ωp时, σ=0.07, 当ω>ωp时, σ=0.09;只考虑深水情况, 即有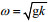
常数α与有效波高有关:
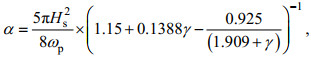 (24)
(24)对于风浪状态, Toba(1972)提到有效波高的计算表达式:
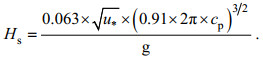 (25)
(25)式中:谱峰相速度cp=g/ωp, 谱峰频率随无因次风区和风速增大而减小; u*为摩擦速度, 可利用公式(5)、(6)计算。
但是一般的JONSWAP谱是风浪低频谱, 对于高频部分没有考虑, 使得计算结果与真实海浪谱可能存在较大的差异。因此, 需要考虑另外一种包含低频部分和高频部分的海浪谱, 该谱由Elfouhaily等人在1997年提出(后文统称作Elfouhaily谱):
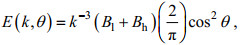 (26)
(26)式中l和h分别表示低频和高频; B表示曲率谱(B=k3E)。
Bl是长波曲率谱(低频部分):
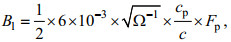 (27)
(27)式中波浪的相速度c=ω/k;
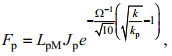 (28)
(28)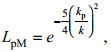 (29)
(29)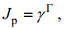 (30)
(30)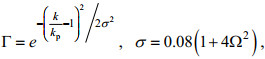 (31)
(31)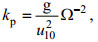 (32)
(32)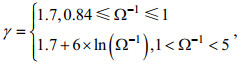 (33)
(33)另外, Bh是短波曲率谱(高频部分):
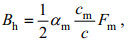 (34)
(34)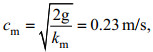 (35)
(35)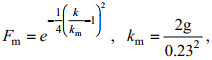 (36)
(36)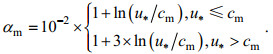 (37)
(37)式中波龄Ω=cp/u10。Elfouhaily谱只适用于反波龄大于0.84(波龄小于1.2)的情况, 即Elfouhaily谱也是风浪谱。
1.2.3 敏感性分析利用单波近似(20)、JONSWAP谱积分公式(23)以及Elfoufaily谱积分公式(26)计算波致应力, 分别控制10m风速变量、波龄变量, 比较三种不同海浪谱公式计算的波致应力随波龄、风速的变化情况以及相互间的差异。
图 2和图 3表明, 在风浪占优的情况下, 单波公式的近似程度并不理想, 计算结果相比JONSWAP谱积分公式和Elfoufaily谱积分公式的计算结果都要小得多, 这与单波公式只考虑谱峰频率有关, JONSWAP谱积分公式没有考虑高频影响, 在波龄、风速增大时计算结果相对Elfoufaily谱积分公式偏小因此当波龄小于1.2时, 使用Elfoufaily谱积分公式计算波致应力较为合理。当波龄大于1.2时, 海域涌浪占优, JONSWAP谱和Elfoufaily谱都是风浪谱, 而目前没有普遍认可的涌浪谱的表达式, 考虑到涌浪频谱通常比较窄, 可以用一个主波近似代替, 为了简单起见, 在涌浪情况下, 我们使用单波公式进行近似求解。
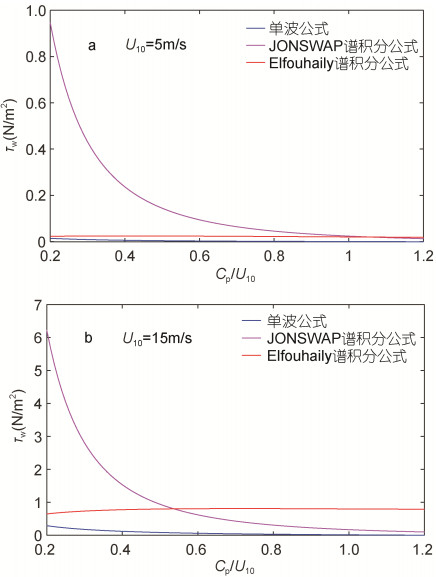 |
| 图 2 取定风速大小时不同谱公式计算的波致应力随波龄的变化 Fig. 2 The variation of wave-induced stress with wave age at given wind speed |
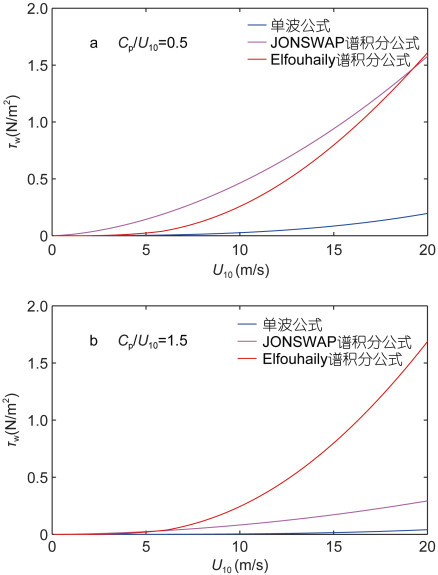 |
| 图 3 取定波龄时不同谱公式计算的波致应力随波龄的变化 Fig. 3 The variation of wave-induced stress with wind speed at given wave age |
本文使用的数据是欧洲中期数值预报中心(ECMWF)的ERA-interim数据, ERA-Interim项目于2006年启动, 为ECMWF之前的再分析[ERA-40 (1957—2002)]和ECMWF设想的下一代扩展再分析提供了桥梁, 同时做了一定的改变:从地面到0.1hpa高度垂向分为60级; T255球面谐波表示为基本动力学领域; 对于表面和其他网格场, 具有大致均匀79km间距的降低高斯网格。时间跨度为1979年至今, 采用的同化方法为4D-VAR, 近地面风速的时间分辨率为6h, 模式近地面风速高度为10m。再分析数据对高风速通常存在一定的低估, 对低风速存在一定的高估, 但整体影响不大。本文中使用到的数据主要有10m风速(包括U分量和V分量)、包含风浪和涌浪的有效波高以及平均波向。所有数据选用的是观测数据, 数据时间为2009年1月、4月、7月以及10月, 时间分辨率为6h, 空间分辨率为85.5°S—65.5°N、90°E—60°W, 数据网格为0.125°×0.125°。
2.2 太平洋波致应力的求解依据上文的分析, 由于Elfouhaily谱和JONSWAP谱是风浪谱, 而单波公式可以计算涌浪占优情况下波致应力的大小, 因此波龄大于等于1.2时使用单波公式来近似求解波致应力。当波龄小于1.2时, 根据分析得出单波公式的计算误差较大, Elfouhaily谱积分公式的计算结果较好, 为更准确的计算不同海况下波致应力的大小, 使用风速和有效波高数据构造Elfouhaily谱.。对不同海况条件, 我们假设:
 (38)
(38)式中, S0i为i点构造的谱能; αi为i点的反演系数; Si为i点原来的Elfouhaily谱能。有效波高与波能的关系:
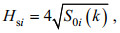 (39)
(39)式中, Hsi是i点的有效波高, 根据公式(38)、(39)以及不同海域的风速、有效波高数据得到反演的系数α:
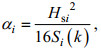 (40)
(40)对不同的海况, 波龄小于1.2时, 利用Elfouhaily谱积分公式得到反演系数α, 波致应力变为:
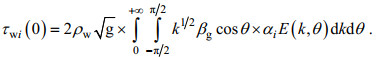 (41)
(41)因此, 本文计算太平洋波致应力之前, 对每一个网格点计算其反演系数, 将计算得出的反演系数与理论Elfouhaily谱积分公式相乘用来修正海浪谱公式, 使得计算得到的海浪谱更加接近真实海况。同时在计算过程中, 首先计算每一个网格点的波龄, 当波龄大于等于1.2时使用单波公式计算波致应力, 当波龄小于1.2时使用Elfouhaily谱积分公式计算波致应力。
2.3 波致应力分布与风场前人的大量研究表明, 浪与风存在着复杂的相互影响的关系, 风时、风区、风速等都会对波浪场产生较大的影响。为分析和解释波致应力的分布与风场存在一定相关性, 选择2009年1月1日00:00时刻的风速和有效波高数据计算波致应力的大小, 得到波致应力在太平洋的总体分布情况。
波致应力大于0, 即风产生的动量通量进入波浪, 此时为风浪占优的情况。波致应力小于0, 快速运动的波浪诱导了一个向上的动量通量, 总动量从水面指向大气, 此时为涌浪占优的情况。图 4表明, 总体而言, 此时刻赤道地区的波致应力的绝对值较小, 接近0;此时刻西北太平洋和澳大利亚以南的波致应力的绝对值较大, 且正值的绝对值要大于负值的绝对值, 即风浪占优情况下的波致应力绝对值大于涌浪占优情况下的波致应力绝对值。并且可以注意到波致应力的正值较大值与波致应力的负值较小值基本会同时出现在一块海域, 多数为风场产生的涡旋处。
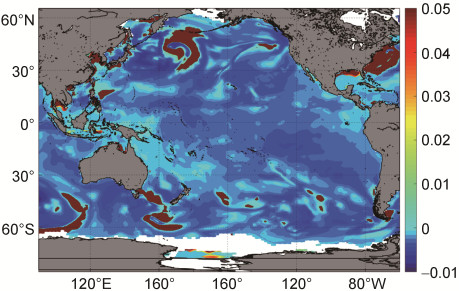 |
| 图 4 2009年1月1日零时刻波致应力(N/m2)在太平洋的分布 Fig. 4 The distribution of wave-induced stress (N/m2) in the Pacific at 0 o'clock on January 1, 2009 |
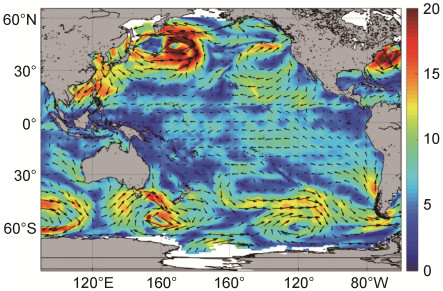 |
| 图 5 2009年1月1日零时刻太平洋的风场(m/s)分布 Fig. 5 The distribution of the wind field (m/s) in the Pacific at 0 o'clock on January 1, 2009 注:箭头表示风向, 填色表示风速大小 |
根据风场图可以发现, 风速较大(接近或大于20m/s)的海域对应的波致应力大多数为正值且绝对值较大, 说明此海域为风浪占优的情况, 即风产生的进入波浪的动量通量较大; 风速为中等大小(接近10 m/s)的海域对应的波致应力大多数为负值, 说明此海域为涌浪占优的情况, 即波浪相速度大于风速, 在弱风条件下, 快速运动的波浪诱导了一个向上的动量通量, 总动量从水面指向大气, 即为负值; 风速很小的海域对应的波致应力接近0, 此处风与浪都较弱, 风产生的进入海浪的动量通量以及波浪诱导的向上的动量通量都很小。
在西北太平洋和澳大利亚以南的东西两侧都存在较强的涡旋, 同时发现存在明显涡旋的这三处海域都有较大的波致应力正值和较小的波致应力负值, 即此处的风浪和涌浪现象都存在且较为明显。风浪离开风直接作用的水域于风区以外形成涌浪, 于风区以内, 由于风速骤然降低或风向骤然改变, 原来的风浪于当地也会变成涌浪(文圣常, 1984)。由此得出, 此处由于风向的骤然改变加上风速的骤然降低, 原来的风浪在当地变成涌浪, 即涡旋中风速大的地方对应波致应力为正值且绝对值大, 风浪占优; 风速小的地方对应波致应力为负值且绝对值大, 涌浪占优。
2.4 太平洋波致应力季节分布特征上节中通过风场的特征解释和分析了波致应力分布的合理性, 此节中继续讨论波致应力分布的季节性变化特征。以2009年1月、4月、7月、10月代表春夏秋冬四个季节, 用它们的风速、有效波高数据来计算月平均波致应力, 并绘制月平均波致应力在太平洋的分布图, 以及使用四个月的风速数据绘制月平均风场图。
图 6表明, 2009年1月份太平洋波致应力的大小在不同海区有较明显的差异, 尤其是北太平洋和南太平洋的西风带海区, 波致应力明显强于其他海区, 西风带的风速较为强盛, 对应的波致应力也较强盛。
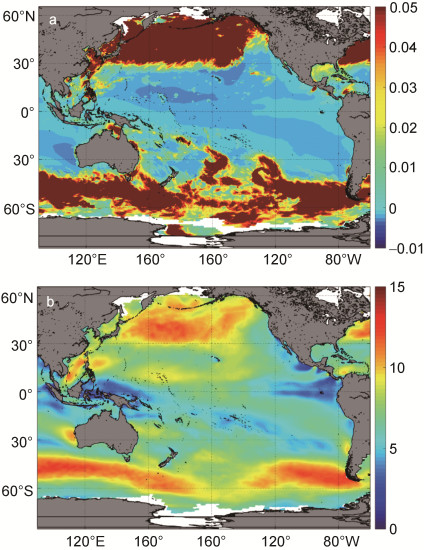 |
| 图 6 2009年1月太平洋的波致应力(a, 单位N/m2)分布和风场(b, 单位m/s) Fig. 6 The distribution of wave-induced stress(a, N/m2) and wind field(b, m/s) in the Pacific in January, 2009 |
图 7表明, 2009年4月份的波致应力相比于1月份整体较弱, 这与4月整体的风场强度整体比较弱有关, 波致应力在南太平洋的西风带明显强于其他海区, 在北太平洋的西风带稍微强于其他海区, 与风场强度的分布比较一致。
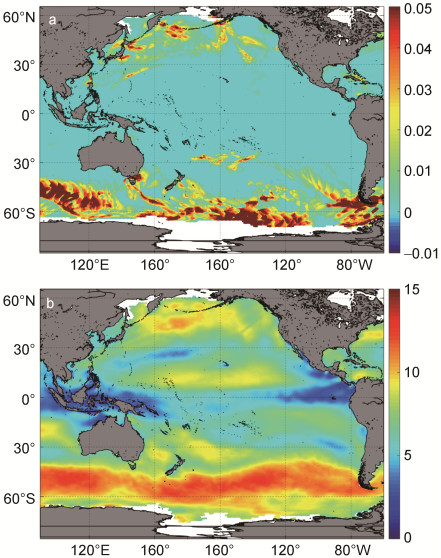 |
| 图 7 2009年4月太平洋的波致应力(a, 单位N/m2)分布和风场(b, 单位m/s) Fig. 7 The distribution of wave-induced stress (a, N/m2) and wind field(b, m/s) in the Pacific in April, 2009 |
图 8表明, 2009年7月份太平洋的波致应力大小分布存在较明显的差异, 南太平洋西风带的波致应力相比其他海域明显强盛, 与对应的风场强弱分布一致。
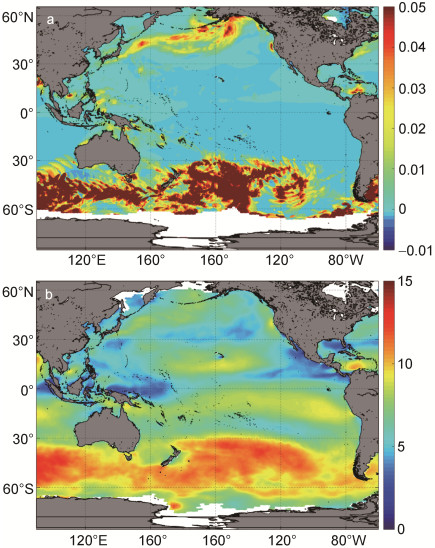 |
| 图 8 2009年7月太平洋的波致应力(a, 单位N/m2)分布和风场(b, 单位m/s) Fig. 8 The distribution of wave-induced stress (a, N/m2) and wind field(b, m/s) in the Pacific in July, 2009 |
图 9表明, 2009年10月份太平洋的波致应力整体较强且分布差异明显, 同样南太平洋和北太平洋西风带的波致应力明显强盛。
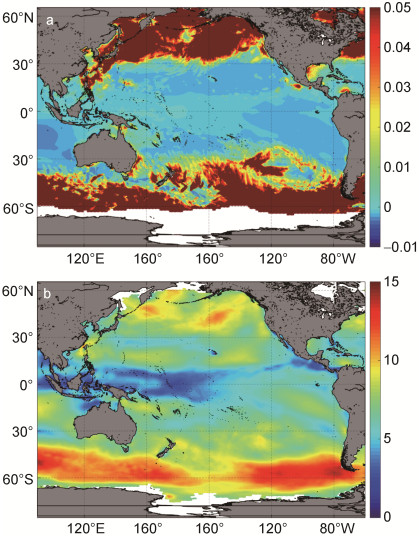 |
| 图 9 2009年10月太平洋的波致应力(a, 单位N/m2)分布和风场(b, 单位m/s)。 Fig. 9 The distribution of wave-induced stress (a, N/m2) and wind field(b, m/s) in the Pacific in October, 2009 |
分析比较2009年四个月份的波致应力分布得到:从空间分布上看, 太平洋西风带的波致应力都较为强盛, 在4月和7月, 南太平洋西风带的波致应力比北太平洋西风带的波致应力要强盛的多; 在时间变化上, 太平洋的波致应力分布整体在1月和10月的时候较为强盛, 波致应力大于0.25的海区面积最多, 同时波致应力的最大值也较大。
3 结论波浪增长率公式对波致应力计算的敏感性分析表明, 相比Komen、Janssen和Polnikov的计算公式, Belcher and Hunt的计算公式虽然在反波龄较大时与实验数据的误差稍微增大, 但总体的吻合度最好; 海浪谱对波致应力计算的敏感性分析表明, 在低风速的情况下, 单波近似的计算结果与Elfouhaily谱积分公式的计算结果较为接近, 但是当高风速时, 单波近似和JONSWAP谱积分公式的计算结果明显小于Elfouhaily谱积分公式的计算结果, 当波龄小于1.2时, 单波公式的近似误差比较大, 当波龄大于等于1.2时, 单波公式可以用来计算涌浪占优情况下海域的波致应力大小。
波致应力的分布与风场存在较大的联系, 风速较大(接近或大于20m/s)的海域对应的波致应力大多数为正值且较大, 此海域为风浪占优, 即风产生的进入波浪的动量通量较大; 风速为中等大小(接近10 m/s)的海域对应的波致应力大多数为负值, 此时涌浪占优, 即波浪相速度大于风速, 在弱风条件下, 快速运动的波浪诱导了一个向上的动量通量, 总动量从水面指向大气; 风速很小的海域对应的波致应力接近0, 此处风与浪都较弱, 风产生的进入海浪的动量通量以及波浪诱导的向上的动量通量都很小。对于太平洋波致应力分布的季节性特征, 从空间分布上看, 西风带的波致应力较其他地区更为强盛, 而在时间变化上1月和10月为波致应力整体较为强盛的时期, 波致应力大于0.25的海区面积最多, 同时波致应力的最大值也较大。
| 文圣常, 1984. 海浪理论与计算原理. 北京: 科学出版社, |
| 邹仲水, 赵栋梁, 黄健, 等, 2014. 海-气界面动量通量的估计方法分析与应用. 海洋学报, 36(9): 75–83 |
| 徐德伦, 于定勇, 2001. 随机海浪理论. 北京: 高等教育出版社, |
| Andreas E L, 2004. Spray stress revisited. Journal of Physical Oceanography, 34(6): 1429–1440 DOI:10.1175/1520-0485(2004)034<1429:SSR>2.0.CO;2 |
| Belcher S E, Hunt J C R, 1993. Turbulent shear flow over slowly moving waves. Journal of Fluid Mechanics, 251: 109–148 DOI:10.1017/S0022112093003350 |
| Benilov A Y, Kuznetsov O A, Panin G N, 1974. On the analysis of wind wave-induced disturbances in the atmospheric turbulent surface layer. Boundary-Layer Meteorology, 6(1-2): 269–285 DOI:10.1007/BF00232489 |
| Davidson K L, Frank A J, 1973. Wave-related fluctuations in the airflow above natural waves. Journal of Physical Oceanography, 3(1): 102–119 DOI:10.1175/1520-0485(1973)003<0102:WRFITA>2.0.CO;2 |
| Donelan M A, Drennan W M, Katsaros K B, 1997. The air sea momentum flux in conditions of wind sea and swell. Journal of Physical Oceanography, 27(10): 2087–2099 DOI:10.1175/1520-0485(1997)027<2087:TASMFI>2.0.CO;2 |
| Edson J B, Fairall C W, 1998. Similarity relationships in the marine atmospheric surface layer for terms in the TKE and scalar variance budgets. Journal of the Atmospheric Sciences, 55(13): 2311–2328 DOI:10.1175/1520-0469(1998)055<2311:SRITMA>2.0.CO;2 |
| Elfouhaily T, Chapron B, Katsaros K, et al, 1997. A unified directional spectrum for long and short wind-driven waves. Journal of Geophysical Research:Oceans, 102(C7): 15781–15796 DOI:10.1029/97JC00467 |
| Grachev A A, Fairall C W, Hare J E, et al, 2003. Wind stress vector over ocean waves. Journal of Physical Oceanography, 33(11): 2408–2429 DOI:10.1175/1520-0485(2003)033<2408:WSVOOW>2.0.CO;2 |
| Hanley K E, Belcher S E, 2008. Wave-driven wind jets in the marine atmospheric boundary layer. Journal of the Atmospheric Sciences, 65(8): 2646–2660 DOI:10.1175/2007JAS2562.1 |
| Harris D L, 1966. The wave-driven wind. Journal of the Atmospheric Sciences, 23(6): 688–693 DOI:10.1175/1520-0469(1966)023<0688:TWDW>2.0.CO;2 |
| Hristov T, Friehe C, Miller S, 1998. Wave-coherent fields in air flow over ocean waves:Identification of cooperative behavior buried in turbulence. Physical Review Letters, 81(23): 5245–5248 DOI:10.1103/PhysRevLett.81.5245 |
| Hristov T S, Miller S D, Friehe C A, 2003. Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature, 422(6927): 55–58 DOI:10.1038/nature01382 |
| Janssen P A E M, 1989. Wave-induced stress and the drag of air flow over sea wave. Journal of Physical Oceanography, 19(6): 745–754 DOI:10.1175/1520-0485(1989)019<0745:WISATD>2.0.CO;2 |
| Janssen P A E M, 1991. Quasi-linear theory of wind-wave generation applied to wave forecasting. Journal of Physical Oceanography, 21(11): 1631–1642 DOI:10.1175/1520-0485(1991)021<1631:QLTOWW>2.0.CO;2 |
| Komen G J, Hasselmann K, Hasselmann K, 1984. On the existence of a fully developed wind-sea spectrum. Journal of Physical Oceanography, 14(8): 1271–1285 DOI:10.1175/1520-0485(1984)014<1271:OTEOAF>2.0.CO;2 |
| Kudryavtsev V N, Makin V K, 2004. Impact of swell on the marine atmospheric boundary layer. Journal of Physical Oceanography, 34(4): 934–949 DOI:10.1175/1520-0485(2004)034<0934:IOSOTM>2.0.CO;2 |
| Larson T R, Wright J W, 1975. Wind-generated gravity-capillary waves:laboratory measurements of temporal growth rates using microwave backscatter. Journal of Fluid Mechanics, 70(3): 417–436 DOI:10.1017/S002211207500211X |
| Lucas C, Guedes S C, 2015. On the modeling of swell spectra. Ocean Engineering, 108: 749–759 DOI:10.1016/j.oceaneng.2015.08.017 |
| Makin V K, Kudryavtsev V N, Mastenbroek C, 1995. Drag of the sea surface. Boundary-Layer Meteorology, 73(1-2): 159–182 DOI:10.1007/BF00708935 |
| Makin V K, Mastenbroek C, 1996. Impact of waves on air-sea exchange of sensible heat and momentum. Boundary-Layer Meteorology, 79(3): 279–300 DOI:10.1007/BF00119442 |
| Makin V K, 2008. On the possible impact of a following-swell on the atmospheric boundary layer. Boundary-Layer Meteorology, 129(3): 469–478 DOI:10.1007/s10546-008-9320-z |
| Miller S, Friehe C, Hristov T et al, 1999. Wind and turbulent profiles in the surface layer over ocean waves. In: Sajjadi S G, Thomas N H, Hunt J C R. Wind-Over-Wave Couplings. Oxford: Clarendon Press, 91-98 |
| Plant W J, 1982. A relationship between wind stress and wave slope. Journal of Geophysical Research:Oceans, 87(C3): 1961–1967 DOI:10.1029/JC087iC03p01961 |
| Polnikov V G, 2011. Integrated model for a wave boundary layer. Marine Science, 1(1): 10–21 |
| Rutgersson A, Smedman A S, Högström U, 2001. Use of conventional stability parameters during swell. Journal of Geophysical Research:Oceans, 106(C11): 27117–27134 DOI:10.1029/2000JC000543 |
| Semedo A, Saetra Ø, Rutgersson A, et al, 2009. Wave-induced wind in the marine boundary layer. Journal of the Atmospheric Sciences, 66(8): 2256–2271 DOI:10.1175/2009JAS3018.1 |
| Shemdin O H, Hsu E Y, 1967. Direct measurement of aerodynamic pressure above a simple progressive gravity wave. Journal of Fluid Mechanics, 30(2): 403–416 DOI:10.1017/S0022112067001508 |
| Smedman A S, Tjernström M, Högström U, 1994. The near-neutral marine atmospheric boundary layer with no surface shearing stress:A case study. Journal of the Atmospheric Sciences, 51(23): 3399–3411 DOI:10.1175/1520-0469(1994)051<3399:TNNMAB>2.0.CO;2 |
| Snyder R L, Dobson F W, Elliott J A, et al, 1981. Array measurements of atmospheric pressure fluctuations above surface gravity waves. Journal of Fluid Mechanics, 102: 1–59 DOI:10.1017/S0022112081002528 |
| Song J B, Fan W, Li S, et al, 2015. Impact of surface waves on the steady near-surface wind profiles over the ocean. Boundary-Layer Meteorology, 155(1): 111–127 DOI:10.1007/s10546-014-9983-6 |
| Stewart R W, 1974. The air-sea momentum exchange. Boundary-Layer Meteorology, 6(1-2): 151–167 DOI:10.1007/BF00232481 |
| Sullivan P P, McWilliams J C, Melville W K, 2004. The oceanic boundary layer driven by wave breaking with stochastic variability. Part 1. Direct numerical simulations. Journal of Fluid Mechanics, 507: 143–174 |
| Sullivan P P, Edson J B, Hristov T, et al, 2008. Large-eddy simulations and observations of atmospheric marine boundary layers above nonequilibrium surface waves. Journal of the Atmospheric Sciences, 65(4): 1225–1245 DOI:10.1175/2007JAS2427.1 |
| Toba Y, 1972. Local balance in the air-sea boundary processes:Ⅰ. on the growth process of wind waves. Journal of Oceanography, 28(3): 109–120 |
| Veron F, Melville W K, Lenain L, 2008. Wave-coherent air-sea heat flux. Journal of Physical Oceanography, 38(4): 788–802 DOI:10.1175/2007JPO3682.1 |
| Wu J, 1971. Slope and Curvature Distributions of Wind-Disturbed Water Surface. Journal of the Optical Society of America, 61(7): 852–858 DOI:10.1364/JOSA.61.000852 |
| Wu H Y, Hsu E Y, Street R L, 1979. Experimental study of nonlinear wave-wave interaction and white-cap dissipation of wind-generated waves. Dynamics of Atmospheres & Oceans, 3(1): 55–78 |
| Zhao D L, Toba Y, 2003. A spectral approach for determining altimeter wind speed model functions. Journal of Oceanography, 59(2): 235–244 DOI:10.1023/A:1025599423405 |
| Zijlema M, Van Vledder G P, Holthuijsen L H, 2012. Bottom friction and wind drag for wave models. Coastal Engineering, 65: 19–26 DOI:10.1016/j.coastaleng.2012.03.002 |
 2018, Vol. 49
2018, Vol. 49


