中国海洋湖沼学会主办。
文章信息
- 孟静, 王树亚, 陈旭, 牟海迪. 2018.
- MENG Jing, WANG Shu-Ya, CHEN Xu, MU Hai-Di. 2018.
- 内孤立波对小直径直立桩柱作用力的实验研究
- AN EXPERIMENTAL STUDY ON THE FORCE OF INTERNAL SOLITARY WAVE ON A CYLINDER OF SMALL DIAMETER
- 海洋与湖沼, 49(3): 535-540
- Oceanologia et Limnologia Sinica, 49(3): 535-540.
- http://dx.doi.org/10.11693/hyhz20171200317
-
文章历史
- 收稿日期:2017-12-19
- 收修改稿日期:2018-03-19
2. 中国海洋大学物理海洋教育部重点实验室 青岛 266100;
3. 中国海洋大学海洋学实验教学示范中心 青岛 266100
2. Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, China;
3. National Oceanography Experimental Teaching Demonstration Center, Ocean University of China, Qingdao 266100, China
内波是发生在层结稳定海洋内部的一种波动, 是海洋能量级串的重要环节, 在海洋混合中发挥着重要作用, 对大尺度热盐环流的维持不可或缺(Alford, 2003; Garrett, 2003; Alford et al, 2015; Kunze, 2017)。内孤立波是一种特殊形式的内波, 能够长距离传播且保持波形基本不变, 具有波形窄、流速大、剪切强的特点, 界面起伏最大可达240m (Dong et al, 2015; Huang et al, 2016)。大振幅的内孤立波除产生等密度面大幅度垂向起伏外, 还产生具有强垂向剪切的往复水平流, 会对海上作业平台产生破坏作用(蔡树群等, 2001, 2002)。
南海北部是一个石油资源丰富且海洋环境复杂的海区, 该海域的内孤立波发生频繁(Guo et al, 2014), 大幅度内孤立波在近海面会产生强剪应力(孙丽, 2006a), 其最大相速度2.55m/s, 可能会对此处的海洋石油资源开发平台的安全造成严重威胁(苗得胜, 2015)。
诸多学者曾进行过内波对垂直桩柱作用力的理论研究。蔡树群等(2002)将小尺度物体受力的Morison公式应用到内孤立波对小直径垂直圆柱形桩柱作用力的求解上, 得到了内孤立波对垂直桩柱作用力的1个渐进估计。叶春生(2005)采用Morison公式, 理论和数值求解了不同水深和圆频率下内波作用于小尺度圆柱体上的荷载, 给出了荷载垂向分布的特性, 并指出内波破坏的可能机制。孙丽(2006b)同样采用Morison公式, 计算了表面波与内孤立波对桩柱的总作用力、力矩以及剪应力, 认为表面波对桩柱的作用力随深度的增大而衰减, 而内孤立波的作用力几乎分布在整个深度范围, 且作用力的量值与方向随深度变化。第一模态内波的作用力在桩柱的上、下部位作用方向相反。此特性影响整个桩柱的所受总作用力和力矩。Xu等(2012)通过建立理论模型研究了两层流体中上凸型与下凹型内孤立波对直立桩柱的作用力, 指出上凸型孤立波可以在下层产生更强的作用力。王旭等(2015)对内孤立波与直立圆柱体的相互作用特性进行了数值模拟, 分析了内孤立波作用下直立圆柱体各种荷载成分的形成机理及其影响程度, 直立圆柱体对内孤立波的波形及其流场特性的影响, 以及Morison公式的适用性等问题。
目前内孤立波对直立桩柱的研究主要集中在实际观测和数值模拟上, 而且结果差别很大, 无法得到很好的验证。关于内孤立波对结构物的作用力的实验研究进行的较少, 徐肇廷等(2006)开展了内孤立波对水平圆柱作用力的实验研究。王玲玲等(2017)对内孤立波环境下圆柱和方柱受力特征进行了物模实验研究。本文在实验水槽中模拟内孤立波与桩柱的相互作用, 通过自行设计的水平微小力测量的测力天平对桩柱受力进行测量, 不仅给出了内波对直立桩柱的受力, 而且给出了垂向受力的分布, 测量结果可为海洋石油平台的设计和使用提供可参考的实验数据。
1 实验设计与理论分析 1.1 实验设置本文的实验在中国海洋大学物理海洋教育部重点实验室的小型内波水槽中进行, 实验水槽的尺寸为1000mm(长)×100mm(宽)×200mm(高)。如图 1所示, 水槽1中放置两层流体, 下层密度ρ2=1.081g/cm3, 厚度为h2=120mm, 上层密度ρ1=1.002g/cm3, 厚度为h1=40mm。较轻密度的盐水需要用漂浮的海绵从下层的顶部慢慢加入, 尽量减少两层盐水的混合。总水深为H=160mm。实验密度剖面采用电导率传感器2测量得到。
 |
| 图 1 实验装置示意图 Fig. 1 The sketch of theexperimental setup 注: 1:水槽; 2:电导率传感器; 3:待测圆柱段; 4:改进的物理摆; 5:楔形刀口; 6:调节螺杆; 7:调节螺帽; 8:托盘; 9:调节平衡螺母; 10:导流柱; 11:塌陷造波板; 12:消波板 |
第一模态的内孤立波是利用重力塌陷的方法生成, 内孤立波产生的流场采用粒子图像测速法(Particle Image Velocimetry, PIV)(Dalzielet al, 2007)进行定量测量。使用Digiflow软件对Charge-coupled Device(CCD)相机拍摄的图片进行处理, 得到流场。
为了测量内孤立波对小直径直立桩柱作用力, 本实验设计了一个水平微小力测量的测力天平。如图 1所示, 为了保证内孤立波与圆柱作用前后的流场真实, 在水槽中放置了导流柱10, 在导流柱上设置了一个待测圆柱段3, 用来测量某位置的圆柱受力情况, 并将待测圆柱段连接在改进的物理摆4下方, 待测圆柱的直径和高度均为20mm, 该天平放在楔形刀口5上, 物理摆的上部调节螺杆6上设置了一个调节螺帽7, 调节它可以改变物理摆的回复力矩。物理摆的两端相同距离l处各设置一个托盘8, 用于放置砝码标定待测圆柱的受力大小。在实验进行之前要调节平衡螺母9使得天平平衡, 这对保证测量结果的准确性和真实性是非常重要的。这样, 通过力矩平衡的原理, 利用天平托盘中砝码的重量可计算出待测圆柱受到的水平作用力。
本实验中我们在直立桩柱上取了4个待测段, 其位置如图 2所示。内孤立波对小直径直立桩柱作用力的测量主要是利用了力矩平衡的原理, 计算公式如下:
 (1)
(1)
 |
| 图 2 直立桩柱受力示意图 Fig. 2 The sketch of the force on the cylinder |
其中, F2是待测圆柱所受到的水平作用力。l为天平的力臂到中心长度, 为60mm; L为力臂中心到待测圆柱中心的距离。x1为待测圆柱受到水平作用力后平移后的位置; x2为待测圆柱平移前的位置; k为单位质量的砝码所造成待测圆柱的平移像素。当F2 > 0时, 待测圆柱受到水平向右的作用力; 当F2 < 0时, 待测圆柱受到水平向左的作用力。其中g=9.8×103mm/s2。
1.2 理论分析本实验采用小桩柱的Morison公式来计算(蔡树群等, 2001; 孙丽, 2006b)内孤立波对小直径直立桩柱的作用力, 表达式如下:
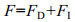 (2)
(2)式中, FD和FI分别为波流过桩柱时所受的“速度力”和“惯性力”。它们的计算公式分别为
 (3)
(3)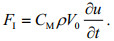 (4)
(4)式中, ρ, A, V0分别为水的密度、桩柱在垂直于流动方向的(单位高度)迎流投影面积和迎流体积; u为无桩柱时位于桩柱轴心处之水平流速; CD和CM分别为实验室确定的速度力系数和惯性力系数, 不同形状的绕流界面有不同的量值, 对圆形截面取CD=1.17, CM=2.0。
由于内孤立波的持续时间较长, 可以估算内孤立波产生的惯性力远小于速度力, 本文只是为了使用Morison公式计算内孤立波对桩柱的作用力, 因此, 计算中仅计算速度力而忽略惯性力。
2 结果与讨论 2.1 内孤立波对直立桩柱作用力的理论计算本实验中, 迎流投影面积A和迎流体积V0由下列公式计算:
 (5)
(5) (6)
(6)通过Morsion公式计算得到速度力分布曲线、惯性力与总作用力分布曲线, 如图 3所示。从图 3a中可以看出, 内孤立波的速度力FD比较大, 最大值可以达到1200μN以上, 且上下两层流体的速度力方向相反, 而惯性力FI(图 3b)相对速度力来说比较小, 最大值在350μN左右, 分布规律与速度力相同。通过将速度力FD与惯性力FI相加, 可以得到总的作用力F(图 3c), 从总作用力的分布曲线可以看出, 使用Morison公式求得的内孤立波对小直径直立桩柱总作用力垂向分布与速度垂向分布规律基本相同, 即在桩柱的上下部分作用力方向相反, 且上层流体作用力的量值大于下层流体。
 |
| 图 3 Morison公式求出的内孤立波对小直径直立桩柱速度力FD(a)、惯性力FI(b)、总作用力F(c)分布 Fig. 3 Distribution of speed force (a), inertia force (b), and total force (c) calculated by Morison equation |
根据PIV测量数据绘制内孤立波的流场时间序列图, 如图 4所示, 可以看出上下两层流体的流速方向相反, 形成很强的垂向剪切, 对直立桩柱造成破坏。
 |
| 图 4 内孤立波流场的时间序列 Fig. 4 The time series of velocity of the internal solitary waves |
当待测圆柱置于距离水面15mm时, 待测圆柱距离水槽底部的距离为145mm, 测力点的力臂L=140mm。在天平左端放置砝码时, 相当于待测圆柱左端受到向右的作用力, 对相应数据线性拟合可以得到单位质量砝码所造成的测力点平移像素k1=0.129px/mg, 在天平右端放置砝码时, 相当于待测圆柱右端受到向左的作用力, 根据线性拟合得到, k2=-0.122px/mg。绘制距离水面15mm处待测圆柱受力曲线如图 5。
 |
| 图 5 距离水面15mm处待测圆柱受力曲线 Fig. 5 The force on the cylinder measured 15mm below the surface |
待测圆柱距离水面15mm处最大受力点的坐标为:最大向右的力(833, 36), 受力大小为1606μN; 最大向左的力(773, 36), 受力大小为1055μN; 因此在距离水面15mm处最大受力为向右的力1606μN。
2.3 待测圆柱受力分析表 1给出了内孤立波在相同位置时, 待测圆柱在不同位置时的最大受力情况及待测圆柱受到的水平作用力。
| 测力点距水面的距离 h(mm) |
测力点受到的最大水平力 F(μN) |
同一时刻待测圆柱受到的水平力 F(μN) |
待测圆柱受到的最大水平力 F(μN) |
| 15 | 1606 | 1606 | 1606 |
| 50 | 840 | 248 | 840 |
| 90 | –1242 | –628 | –1242 |
| 130 | –753 | –468 | –753 |
从表 1可以看出, 第一模态内孤立波经过小直径直立桩柱时, 小直径直立桩柱受到的作用力在垂向上是上下相反的, 上端受到向右的最大作用力, 下端受到向左的最大作用力, 而且上层最大作用力的量值大于下层。同一时刻各位置待测圆柱的水平受力规律同最大水平力类似, 但垂向分布更加明显, 上层与下层水平作用力的量值差异更大。
取待测圆柱受到的最大水平作用力的那个位置以及时刻, 即为待测圆柱在距离水面15mm处时受到水平作用力最大的时刻, 对应的流场如图 6所示。
 |
| 图 6 内孤立波在相同位置时待测圆柱不同位置流场 Fig. 6 Velocity field of the internal solitary waves with the cylinder at different position |
对比内孤立波作用力的实验值与理论值(图 7), 可以得出当内孤立波对小直径直立桩柱产生作用力时, 各点受到作用力的理论值与实验值基本一致, 变化规律也是相同的。理论值与实验值基本一致, 证明了该实验室方法与理论分析方法对研究内孤立波对小直径直立桩柱作用力的可行性, 为数值模拟与理论分析的研究提供了实验参照与标准。
 |
| 图 7 内孤立波对小直径直立桩柱作用力的理论值与实验值 Fig. 7 The force on the cylinder calculated theoretically and measured directly with a scale in the experiment |
实验室条件下研究内孤立波对小直径直立桩柱作用的实验, 主要目标是研究内孤立波对小直径直立桩柱的水平作用力, 内孤立波经过小直径直立桩柱后的波场、流场变化, 以及内孤立波在上下层流体中断面流速的情况等。
从上面的实验结果可以给出内孤立波对小直径直立桩柱影响的几点结论:
(1) 内孤立波的流场、流速以及作用力在铅直方向不但有量值的变化, 也有方向的改变, 且变化规律基本相同。第一模态内孤立波的流速方向以及作用力在桩柱的上下部分方向相反, 且上层流体的量值大于下层流体, 会产生很强的速度切变和扭力, 对小直径直立桩柱造成破坏。内孤立波在传播过程中, 上层流体顶部以及下层流体的底部都会有明显的边界层。
(2) 当内孤立波在相同时刻时, 小直径直立桩柱上下两层的受力情况与受到最大水平力的规律近似, 但是垂向的分布更加的明显, 上层受到的水平作用力与下层差异更大。
(3) 通过Morison公式计算出的内孤立波对小直径直立桩柱作用力与实验室测得的数据基本吻合, 说明了该实验室方法与理论分析方法对研究内孤立波对小直径直立桩柱作用力是可行的。该实验为内孤立波对直立桩柱影响的数值模拟与理论分析提供了可靠的实验参照与标准。
本实验从内孤立波遇到小直径直立桩柱时的流场以及力学方面来分析, 下一步努力将内孤立波对小直径直立桩柱产生的剪应力计算值等各种力学分析中进行进一步的尝试和探讨, 且通过大量的实验来分析内孤立波对小直径直立桩柱的连续作用力, 从而求出速度力系数CD和惯性力系数CM, 使得Morison公式可以更好地应用于内孤立波对直立桩柱作用力的计算与理论分析。海洋中还存在上凸型内孤立波, 因其流场结构与下凹型内孤立波不同, 其引起的作用力规律自然不同, 同时内波因为非线性的作用, 也会出现不对称结构(Xu et al, 2010), 今后我们将开展更系统的实验对这一问题进行研究。
| 王旭, 林忠义, 尤云祥, 2015. 内孤立波与直立圆柱体相互作用特性数值模拟. 哈尔滨工程大学学报, 36(1): 6–11 |
| 王玲玲, 王寅, 魏岗, 等, 2017. 内孤立波环境下圆柱和方柱受力特征——Ⅰ.物理实验. 水科学进展, 28(3): 429–437 |
| 叶春生, 沈国光, 2005. 海洋内波对小尺度圆柱体作用力的分析与计算. 天津大学学报, 38(2): 102–108 |
| 孙丽, 2006a. 南海内孤立波的生成、演变及对桩柱的作用. 青岛: 中国海洋大学硕士学位论文 |
| 孙丽, 杜涛, 李群, 2006b. 内孤立波的研究与数值模型. 海洋湖沼通报,(4): 1–8 |
| 苗得胜, 2015. 基于Fluent的造波技术研究及内孤立波对竖向圆柱体作用力的数值模拟和实验验证. 青岛: 中国海洋大学硕士学位论文 |
| 徐肇廷, 贾村, 陈旭, 等, 2006. 两层分层流体中初始内孤立波分裂的数值研究. 中国海洋大学学报, 36(3): 345–348 |
| 蔡树群, 甘子钧, 龙小敏, 2001. 南海北部孤立子内波的一些特征和演变. 科学通报, 46(15): 1245–1250 DOI:10.3321/j.issn:0023-074X.2001.15.003 |
| 蔡树群, 龙小敏, 甘子钧, 2002. 孤立子内波对小直径圆柱形桩柱的作用力初探. 水动力学研究与进展, 17(4): 497–506 |
| Alford M H, 2003. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature, 423(6936): 159–162 DOI:10.1038/nature01628 |
| Alford M H, Peacock T, MacKinnon J A, et al, 2015. Corrigendum:The formation and fate of internal waves in the South China Sea. Nature, 528(7580): 152 |
| Dalziel S B, Carr M, Sveen J K, et al, 2007. Simultaneous synthetic schlieren and PIV measurements for internal solitary waves. Measurement Science and Technology, 18(3): 533–547 DOI:10.1088/0957-0233/18/3/001 |
| Dong J H, Zhao W, Chen H T, et al, 2015. Asymmetry of internal waves and its effects on the ecological environment observed in the northern South China Sea. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 98: 94–101 DOI:10.1016/j.dsr.2015.01.003 |
| Guo C, Chen X, 2014. A review of internal solitary wave dynamics in the northern South China Sea. Progress in Oceanography, 121: 7–23 DOI:10.1016/j.pocean.2013.04.002 |
| Garrett C, 2003. Internal tides and ocean mixing. Science, 301(5641): 1858–1859 |
| Huang X D, Chen Z H, Zhao W, et al, 2016. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6: 30041 DOI:10.1038/srep30041 |
| Kunze E, 2017. The internal-wave-driven meridional overturning circulation. Journal of Physical Oceanography, 47(11): 2673–2689 DOI:10.1175/JPO-D-16-0142.1 |
| Xu Z H, Yin B S, Hou Y J, 2010. Highly nonlinear internal solitary waves over the continental shelf of the northwestern South China Sea. Chinese Journal of Oceanology and Limnology, 28(5): 1049–1054 DOI:10.1007/s00343-010-9018-1 |
| Xu Z H, Yin B S, Yang H W, et al, 2012. Depression and elevation internal solitary waves in a two-layer fluid and their forces on cylindrical piles. Chinese Journal of Oceanology and Limnology, 30(4): 703–712 DOI:10.1007/s00343-012-1188-6 |
 2018, Vol. 49
2018, Vol. 49


