中国海洋湖沼学会主办。
文章信息
- 诸裕良, 陈伟伦, 储鏖. 2018.
- ZHU Yu-Liang, CHEN Wei-Lun, CHU Ao. 2018.
- 河口潮平均准稳态盐度解析模型
- THE ANALYTICAL MODEL OF ESTUARINE TIDALLY AVERAGED QUASI-STEADY SALINITY
- 海洋与湖沼, 49(3): 541-550
- Oceanologia et Limnologia Sinica, 49(3): 541-550.
- http://dx.doi.org/10.11693/hyhz20171000252
-
文章历史
- 收稿日期:2017-10-09
- 收修改稿日期:2018-01-10
2. 江苏省海岸海洋资源开发与环境安全重点实验室 南京 210098
2. Jiangsu Key Laboratory of Coast Ocean Resources Development and Environment Security, Nanjing 210098, China
河口是河流与海洋衔接过渡的区域, 河流的和海洋的动力条件相互作用, 形成复杂的水动力环境。海洋中的高盐水受潮汐和风等作用向河流上溯, 形成河口独有的盐淡水交汇混合现象。系统化研究盐水入侵主要依靠现场资料分析、解析模型和数值模型。对于河口水流盐度数值模型, 国内研究和应用有丰富的成果, 其中像匡翠萍(1997)、诸裕良等(1998)、包芸等(2001)对以往的三维斜压模型在离散方法等方面进行改进, 在解决特定河口盐水入侵问题上取得了良好效果, 使得原有模型的适用性大大提高。数值模型可以较全面的反映出河口水流盐度的时空变化, 但建立和验证的工作量巨大, 且对内在机制的揭示上比较欠缺。解析模型是对表征水流运动和盐度输运的控制方程进行必要的简化和变形, 从而以解析式呈现河口水流盐度的分布和变化, 是深入分析河口水动力和盐度输运机理的重要方法。
关于河口水流盐度解析模型的研究, 学界存在两种思路, 一种是注重适用性和简便性, 以Savenije(1986, 1993, 2005)为代表, 其基于一维Saint-venant方程建立了一维的盐度预测模型, 得出了涨憩(HWS)、落憩(LWS)和潮平均(TA)三个时刻的断面平均盐度纵向分布, Nguyen等(2006, 2008)在此基础上将Savenije模型由单一河口拓展到分汊河口, Zhang等(2011)将Nguyen的分汊河口模型运用到了长江口。这一思路的优点在于待率定的参数较少, 适用的河口较广泛, 便于工程实际中的快速预测。不足在于垂向的动力变化完全被忽略, 无法阐述各种盐淡水混合机制与河口盐度分布的内在关系。另一种思路是注重对物理机制的阐述, 以Pritchard(1954, 1956)、Hansen等(1965)为代表, 为了揭示重力环流对垂向水流盐度动力的作用, 基于N-S方程组建立了垂向二维的潮平均稳态模型。Hansen模型不足在于: (1)对河口地形的限定过于狭窄, 宽深皆不可变; (2)垂向混合系数依赖率定, 适用性较低; (3)模型假定垂向平均盐度线性降低的区域重力环流和盐度分层大小不变, 不符合实际。为了探究潮汐对流作用对潮平均盐度分布的影响, Jay等(1990)认为对于强混合河口潮致余流对潮平均盐度分布的影响会超过重力环流占据主导, 于是在Ianniello(1977)潮致余流摄动模型的基础上建立了涵盖潮汐正压作用和斜压作用的垂向二维的潮平均水流盐度模型, McCarthy(1993)在此基础上考虑了潮致余流对密度场的影响, 将潮汐正压作用与斜压作用耦合。Jay与McCarthy的摄动模型考虑了潮汐的非线性对流作用以及对盐度梯度和重力环流的影响, 较Hansen模型而言, 后者涵盖了更多的物理机制, 但适用范围缩小, 此外摄动模型成立的前提是垂向混合系数垂向恒定, 与实际不符。MacCready(2004)认为对于存在垂向分层的部分混合河口, 由于垂向紊动应力无法到达分层处水体, 潮汐的非线性作用微乎其微, 潮致余流的影响可以忽略, 可以略去动量方程中的非线性项, 建立了变深变宽情况下潮平均准稳态的河口水流盐度解析模型。MacCready模型是对Hansen重力环流经典模型的改进和发展, 消除了Hansen模型的诸多限定。不足在于: (1)Hansen模型考虑了风的影响, MacCready没有在此基础上改进; (2)垂向混合系数依然依赖率定。虽然MacCready(2007)在Geyer等(2000)的双层双向流速模型基础上推导出垂向紊动黏性系数AV的表达式, 但还存在两个问题: (1)该表达式没有垂向结构, 无法较好反映出Geyer等(2000)中AV的垂向分布; (2)Geyer的双层双向流速模型较为符合底层为向岸盐水上层为向海淡水的盐水楔型混合情况, 但无法反映盐淡水掺混更强的情况, 所以算出的AV量值很小, 用该表达式来研究部分混合和强混合的河口时就会产生较大偏差, 适用性较差。Ralston等(2008)在MacCready模型的基础上加入了风的影响, 但没有考虑垂向混合系数的垂向分布, 也没有考虑表面风应力产生的张力效应(wind straining)以及对垂向紊动混合的影响。
本文的目的是进行与风相关的物理机制的探究, 所以选择第二种思路来进行研究, 运用解析方法对MacCready的河口潮平均准稳态盐度模型进行改进优化, 主要体现在考虑风作用的基础上同时考虑经过盐度分层修正的垂向紊动黏性系数垂向结构分布, 并且在盐度分层中体现出风张力效应和风生紊动混合的作用, 这些改进对于增进风这一重要动力因素对河口盐度分布和盐淡水混合影响机制的认识具有重要意义和参考价值。
1 河口潮平均准稳态盐度模型的改进 1.1 MacCready潮平均准稳态盐度模型简述在MacCready(2004)中, 经过潮周期平均后, 动量守恒方程变为:
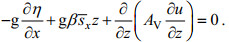 (1)
(1)式中, g为重力加速度, 大小取为9.81。β为盐膨胀系数, 大小取为7.7×10–4。u为纵向流速, η为自由水面水位, 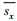
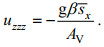 (2)
(2)已知: 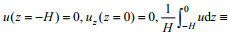
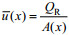
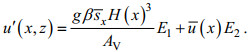 (3)
(3)式中, 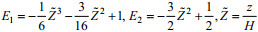
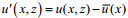
考虑到河口断面面积随x变化, 所以盐度输运方程改写为:
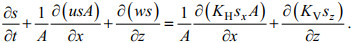 (4)
(4)已知:当z=0或z=H时: w=0且KVsz=0。对式(4)两边垂向平均, 得:
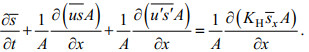 (5)
(5)假定垂向紊动扩散系数KV在垂向上恒定, 则可以有以下关系:
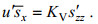 (6)
(6)将(3)式代入(6)式, 对z两次积分, 可得:
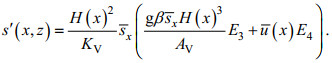 (7)
(7)式中, 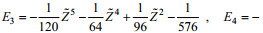
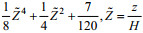
对(5)式从位置x=R到上游方向任意位置对x积分, 得:
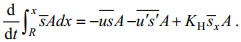 (8)
(8)当河口纵向盐度分布达到准稳态时, 左边为零, 得:
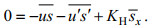 (9)
(9)将u'(x, z)和s'(x, z)表达式代入(9)式, 经整理, 得到以下关于潮平均垂向平均盐度的一阶非线性常微分方程:
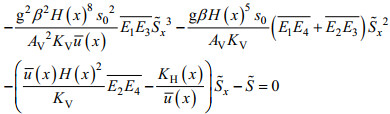 (10)
(10)式中, 第一项代表斜压梯度力的作用; 第二项代表斜压与径流的相互作用; 第三项代表径流的作用; 第四项代表水平扩散的作用。
1.2 基于MacCready盐度模型的改进 1.2.1 垂向紊动黏性系数垂向分布表达式的修正考虑垂向紊动黏性系数的垂向分布, 选用抛物线型的结构型式(陈永平等, 2002), 将其与MacCready原有模型相结合, 得到新的表达形式, 有:
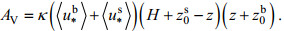 (11)
(11)式中, κ为卡曼常数, 取为0.41, 尖括号代表潮平均。抛物线型式最早源于Nezu等(1986)的水槽实验, Burchard等(2010)在此基础上加入了潮流引起的底部粗糙长度, 以z0b表示。而本文进一步加入了风引起的表面摩阻流速和粗糙长度, 分别以〈u*s〉和z0s表示。
考虑盐度分层的作用, 将Munk-Anderson公式(Munk et al, 1948)概化后的结果作为分层阻尼因子δ乘入到(11)式中, δ=(1+aRi)-b, 其中a取为10, b取为0.5为, Ri为梯度理查森数。所以有
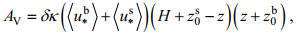 (12)
(12)并且对梯度理查森数Ri进行变化和修正, 加入风的作用, 且使其最终只有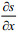
不同于MacCready模型中以静止水面为基准面, 本文以底床为基准面, 更便于推导。经过潮周期平均后, 动量守恒方程变为:
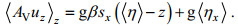 (13)
(13)表面受到风应力作用, 让表面风应力等于表面紊动应力, 有:
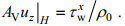 (14)
(14)式中, τwx为表面风应力沿河口方向的分量。ρ0为背景密度, 取为1×103kg/m3。
在(12)式中:
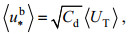 (15)
(15)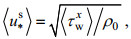 (16)
(16)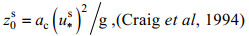 (17)
(17)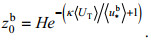 (18)
(18)式中, Cd为拖曳系数, 大小取为2.6×10–3; 〈UT〉为潮平均后的M2分潮潮流强度; 〈τwx〉为潮平均后沿河口方向的风应力。aC取为1400, z0b没有较通用的表达式, 一般通过当地河口的实测拟合可得出与摩阻流速的关系式, 不同河口有不同关系式。本文采取一个简化方法, 对卡曼-普朗特流速垂向分布公式进行垂向平均, 使其等于潮平均潮流强度, 从而反推出z0b表达式。
将(12)式代入(13)式, 按照1.1的方法求解(13)式, 得:
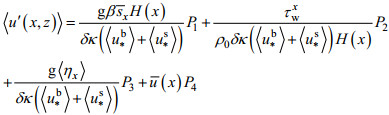 (20)
(20)将(20)式代入(6)式, 得:
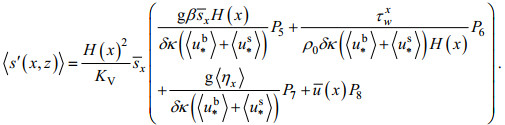 (21)
(21)式中, P1—PS为关于z的结构函数, 纵向流速偏离值和盐度偏离值的垂向分布结构特征就体现在结构函数上。将(20)式和(21)式代入(9)式, 经整理, 得到以下一阶非线性常微分方程:
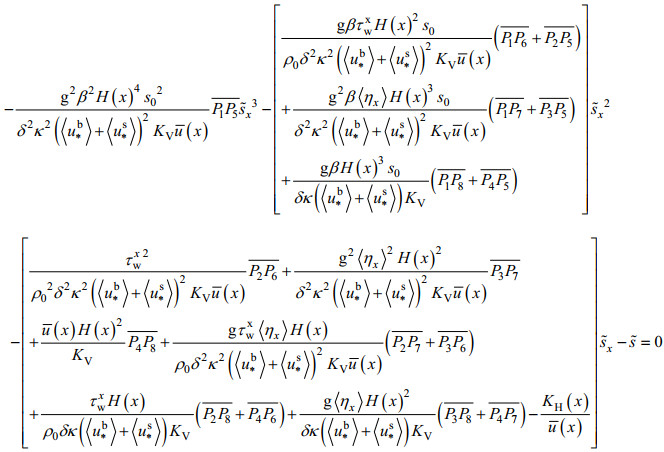 (22)
(22)式中, 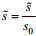
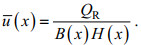 (23)
(23)式中, B(x)和H(x)分别为随纵向变化的河口宽度和水深, QR为径流量。
将(22)式与(10)式相比较, 改进后的盐度分布微分方程中考虑了风的相关项和潮平均正压梯度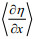
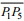
梯度理查森数原有形式为:
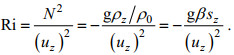 (24)
(24)式中, N为浮力频率, 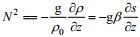
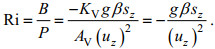 (25)
(25)式中, P表示单位时间内制造紊流所需的能量, B表示单位时间内维持稳定分层所需的势能。我们可以认为紊流只来源于表面边界层和底部边界层黏性底层中的纵向流速剪切作用。这里, 施密特数SC近似取为1, 边界层内垂向混合系数可表示为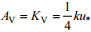
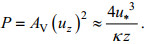 (26)
(26)式中, z在这里表示边界层厚度, 边界层厚度可以代表垂向混合长度, 所以有:
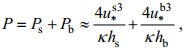 (27)
(27)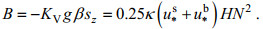 (28)
(28)式中, hs、hb分别为表面紊流边界层和底部紊流边界层厚度, 这里的边界层厚度参考Stacey等(2005)形式:
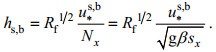 (29)
(29)Rf为通量理查森数, 取为0.2, 所以有:
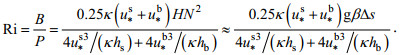 (30)
(30)将盐度输运方程简化为:
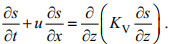 (31)
(31)这里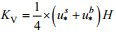
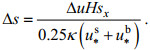 (32)
(32)式中, ∆u表示表底层纵向流速差, 主要由于垂向交换流产生, 所以可以有: ∆u≈ug-uw。ug和uw分别代表重力环流和风生环流重力环流和风生环流引起的表底层流速差。之所以相减, 是因为uw与ug方向相同时符号相反。将(32)代入(30)式, 所以Ri可以变为:
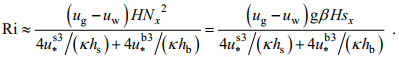 (33)
(33)式中, 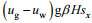
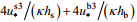
为了比较MacCready盐度模型、只考虑垂向紊动黏性系数垂向分布而未考虑盐度分层作用[见(11)式]的模型和改进模型与实测值的偏差, 本文通过珠江口磨刀门水道和美国Delaware河口的盐度实测资料进行检验。改进模型代表在加入了经过盐度分层修正的垂向紊动黏性系数垂向分布[见(12)式]的潮平均准稳态盐度解析模型。
算例一为珠江口磨刀门水道, 将磨刀门水道概化为一个变深定宽的河口, 尺寸形状如图 1所示。上游径流量为1772m3/s, 距口门89.12km处由于分流减为1000.13m3/s, 距口门55km处再次分流减为777.29m3/s。M2分潮潮流强度为0.45m/s。沿河口方向的风速分量为3m/s, 方向离岸。口门近底处海水盐度s0为15。水平扩散系数和垂向紊动扩散系数由实测资料率定得到。
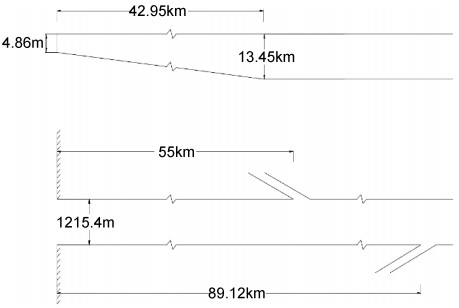 |
| 图 1 磨刀门水道概化尺寸 Fig. 1 Generalization size of the Modaomen waterway |
算例二为美国Delaware河口, 概化后尺寸形状如图 3所示, 河口宽度呈指数变化。径流量为650m3/s, M2分潮潮流强度为0.84m/s。水平扩散系数参照MacCready(2007), 口门处为295m2/s, 上游7.6公里处为50m2/s, 线性变化, 再向上游恒为50m2/s。垂向紊动扩散系数参照MacCready(2004)为垂向紊动黏性系数一半。口门近底处海水盐度s0为32。实测值引自Garvine等(1992)。
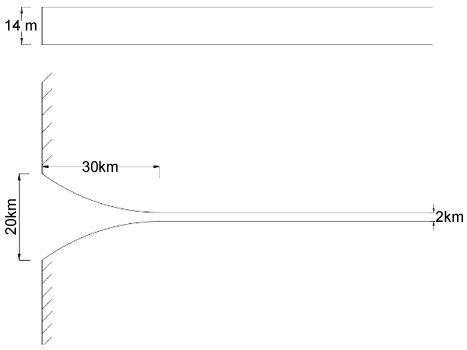 |
| 图 3 Delaware河口概化尺寸 Fig. 3 Generalization size of the Delaware estuary |
从图 2、图 4可以看出改进模型计算结果与实测值吻合得较好, 而未经过盐度分层修正情况的对应结果以及MacCready模型计算结果在盐度分布中段和上游与实测值偏差较大。说明改进模型模拟精度较MacCready模型有较大提高。
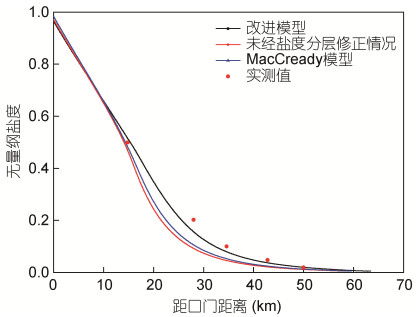 |
| 图 2 不同模型垂向平均盐度纵向分布结果 Fig. 2 Longitudinal distribution of vertical average salinity in different models |
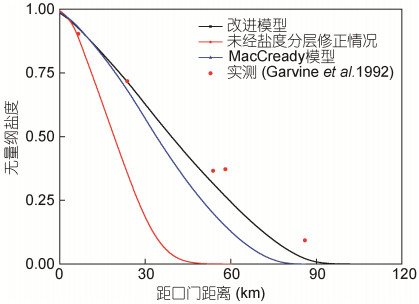 |
| 图 4 不同模型垂向平均盐度纵向分布结果 Fig. 4 Longitudinal distribution of vertical average salinity in different models |
任意方向的风速可分解为平行于河口方向的分量和垂直于河口方向的分量。本文不考虑垂直于河口方向的风速分量对盐度纵向分布的影响, 所以风向变化指平行于河口方向上离岸和向岸两种情况。以下计算河口参数参照算例二。
在准稳态情况下, 风速风向变化对盐度分布的影响体现在对向岸盐通量的影响上。图 6所示, 不同离岸风速下水平扩散盐通量纵向分布基本不变, 说明水平扩散盐通量基本不受离岸风速变化的影响, 对总体盐通量变化没有影响。图 5所示, 不同的离岸风速下离散盐通量的变化趋势总体上是一致的, 先上升至距口门10km左右位置达到最大, 之后逐渐减小至盐水上溯末端为零。
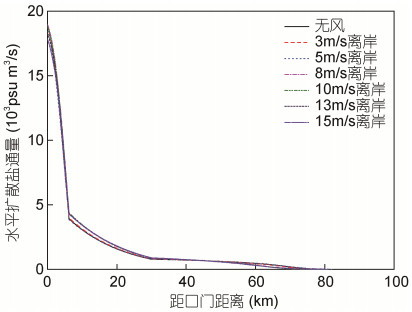 |
| 图 6 不同离岸风速下水平扩散盐通量纵向分布 Fig. 6 Longitudinal distribution of horizontal diffusion salt flux at different offshore wind speeds |
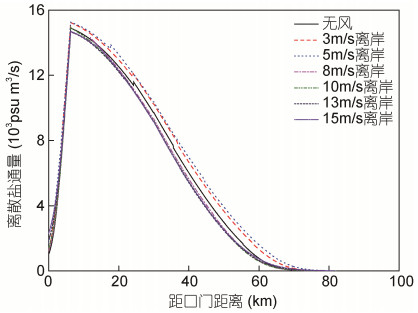 |
| 图 5 不同离岸风速下离散盐通量纵向分布 Fig. 5 Longitudinal distribution of dispersion salt flux at different offshore wind speeds |
上文(8)式表明, 河口某一断面处纵向离散盐通量可以表示为纵向流速偏离值、盐度偏离值与断面面积的乘积。风速变化对离散盐通量的影响体现在对流速偏离值和盐度偏离值的改变上。从流速偏离值[(20)式]和盐度偏离值表达式[(21)式]可以看出, 浮力和水体表面的风切应力产生对密度场的张力效应会促进纵向剪切, δ减小, 使流速偏离值和盐度偏离值增大, 从而使离散盐通量增大。同时, 风的作用使得紊流边界层厚度增加, 垂向紊动混合增强, 垂向紊动混合会抑制纵向剪切, δ增大, 使流速偏离值和盐度偏离值减小, 从而使离散盐通量减小。Scully等(2005)通过对York河口实测流速盐度资料的分析指出, 风对纵向盐度梯度施加的张力效应对河口盐度的垂向分层和混合具有重要影响, 离岸风会增强潮平均纵向剪切, 使得垂向的流速和盐度差值增大。本文认为, 由于风张力效应与风成垂向紊动混合作用相反, 随着离岸风速的增大, 纵向剪切不会持续增强, 而是一个先增强后减弱的过程。在离岸风速从无风增加至5m/s的过程中, 风应力和紊流边界层厚度均增加(图 9), 但张力效应对纵向剪切的促进作用较垂向紊动混合对纵向剪切的抑制作用更明显, 使得流速偏离值和盐度偏离值不断增加, 从而导致离散盐通量的增加(图 5), 各断面盐度值也随之增加(图 7); 在离岸风速由5m/s增加至8m/s过程中, 风应力和紊流边界层厚度均继续增加(图 9), 此时垂向紊动混合对纵向剪切的抑制作用较张力效应对纵向剪切的促进作用更明显, 所以流速偏离值和盐度偏离值减小, 离散盐通量减小(图 5), 所以各断面盐度值也随之减小(图 7); 在离岸风速由8m/s增加至15m/s过程中, 垂向紊动混合对纵向剪切的抑制作用与张力效应对纵向剪切的促进作用基本相当, 后者略大, 两者作用相抵消, 所以流速偏离值和盐度偏离值基本维持不变, 各断面盐度值也总体不变(图 7)。
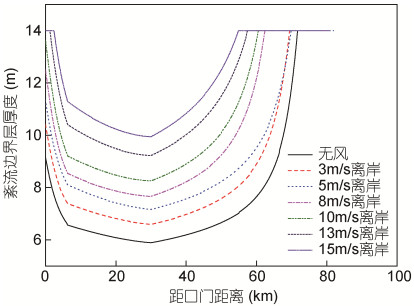 |
| 图 9 不同离岸风速下边界层厚度纵向分布 Fig. 9 Longitudinal distribution of boundary layer in different offshore wind speeds |
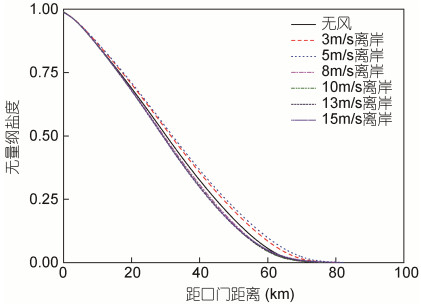 |
| 图 7 不同离岸风速下垂向平均盐度纵向分布 Fig. 7 Longitudinal distribution of vertical-average salinity at different offshore wind speeds |
纵向剪切的增强可以体现在盐度垂向分层的强化上, 而盐度垂向分层的强化反映在其稳定性的增强上, 稳定性判据梯度理查森数Ri体现了张力效应与垂向紊动混合的相对大小关系, 对应着对纵向剪切的促进作用与抑制作用的相对大小关系。Scully等(2005)认为离岸风应力作用会使得盐度垂向分层不断增强, 而本研究表明, 在离岸风速增强的过程中, 两者的相对大小经历了先增大后减小的变化(图 10), 从无风至5m/s时增大, 5m/s至8m/s时明显减小, 8m/s至15m/s时略有减小, 说明盐度垂向分层经历了先增强后减弱的过程。
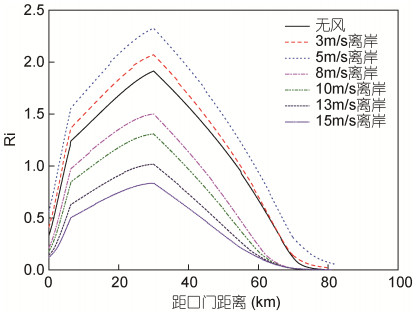 |
| 图 10 不同离岸风速下Ri值纵向分布 Fig. 10 Longitudinal distribution of Ri in different offshore wind speeds |
向岸风速不同时, 盐度分布和盐水上溯距离有明显差异(图 11)。从通量变化角度分析, 水平扩散盐通量变化相对离散盐通量很小(图 14), 所以河口总体盐通量变化取决于离散盐通量变化。由于向岸风切应力产生的张力效应与浮力产生的张力效应对纵向剪切施加的作用是相反的, 向岸风应力的增大会减弱总的张力效应, 所以向岸风应力和垂向紊动混合都会抑制纵向剪切(Scully et al, 2005)。在向岸风速从无风增加至15m/s的过程中, 风应力和紊流边界层厚度均增加(图 15), 反向风张力对纵向剪切的抑制作用与垂向紊动混合对纵向剪切的抑制作用相叠加, 强度远大于浮力产生的张力效应对纵向剪切的促进作用, 使得流速偏离值和盐度偏离值始终明显减小, 从而导致离散盐通量的不断减小(图 13), 各断面盐度值也随之减小(图 11)。
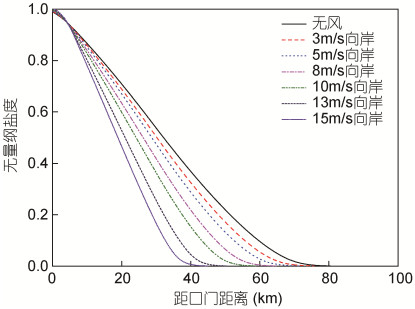 |
| 图 11 不同向岸风速下垂向平均盐度纵向分布 Fig. 11 Longitudinal distribution of vertical-average salinity at different onshore wind speeds |
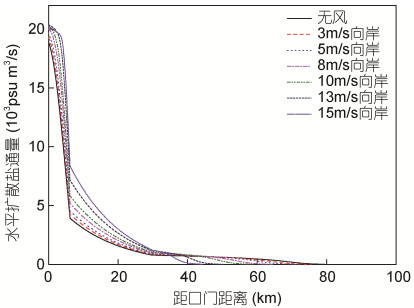 |
| 图 14 不同向岸风速下水平扩散盐通量纵向分布 Fig. 14 Longitudinal distribution of horizontal diffusion salt flux atdifferent onshore wind speeds |
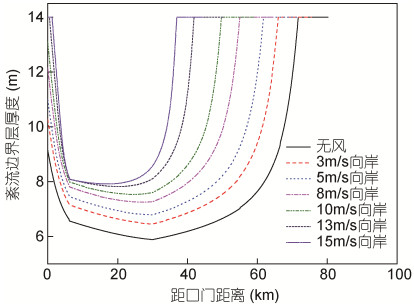 |
| 图 15 不同向岸风速下边界层厚度纵向分布 Fig. 15 Longitudinal distribution of boundary layer at different onshore wind speeds |
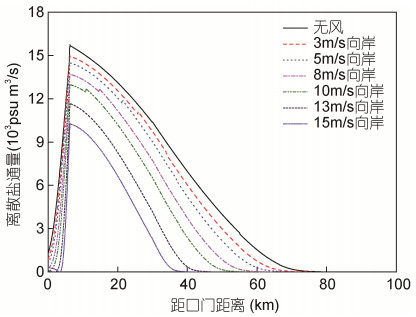 |
| 图 13 不同向岸风速下离散盐通量纵向分布 Fig. 13 Longitudinal distribution of dispersion salt flux at different onshore wind speeds |
从梯度理查森数Ri对向岸风变化的响应来看(图 16), 向岸风速增大的过程最大值基本不变, 但上游区域Ri值有明显下降, 当风速增大到15m/s时, 相较无风时有约一半区域张力效应消失, Ri值为0, 盐度呈现充分混合状态。下游区域Ri值有所增加, 这主要与下游区域纵向盐度梯度明显增加有关(图 12)。
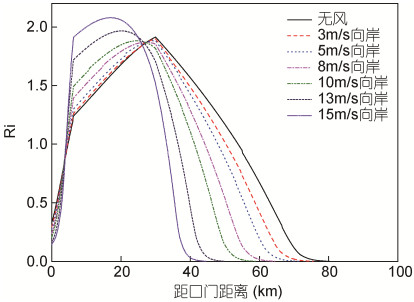 |
| 图 16 不同向岸风速下Ri值纵向分布 Fig. 16 Longitudinal distribution of Ri at different onshore wind speeds |
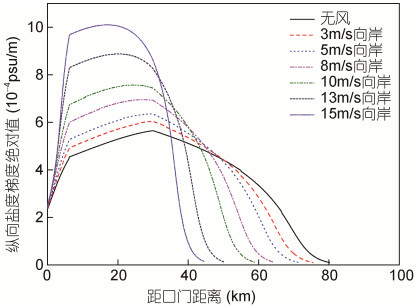 |
| 图 12 不同向岸风速下盐度梯度绝对值纵向分布 Fig. 12 Longitudinal distribution of salinity gradient at different onshore wind speeds |
比较2.2与2.3的结果会发现, 河口潮平均盐度及盐度梯度分布对向岸风的敏感性明显高于离岸风, 且同风速时向岸风作用产生的盐度分布和上溯距离明显大于离岸风作用时(图 7、图 8、图 11、图 12)。这主要由于离岸风作用时总的张力效应与垂向紊动混合对离散盐通量的作用是相抵消的, 而向岸风作用时风张力效应与垂向紊动混合对离散盐通量的作用是相叠加的。
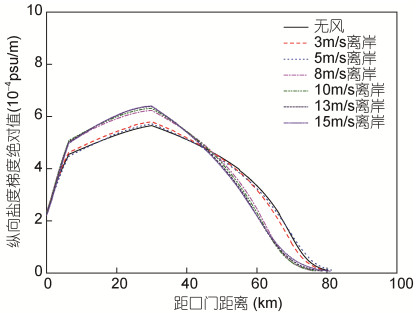 |
| 图 8 不同离岸风速下盐度梯度绝对值纵向分布 Fig. 8 Longitudinal distribution of salinity gradient at different offshore wind speeds |
本文在MacCready潮平均准稳态盐度解析模型基础上考虑了有风情况下垂向紊动黏性系数的垂向分布和盐度分层的作用, 对原有模型进行了改进, 得到以下结论:
(1) 模型计算结果同珠江口磨刀门水道及Delaware河口盐度实测资料对比结果表明, 改进模型的精度较原有模型有较大提升, 与实测盐度资料吻合较好;
(2) 基于Delaware河口的基本参数, 分析了盐度纵向分布对风速风向的响应。结果显示:当离岸风作用时, 在风速增加的前期, 浮力和风的张力效应对离散盐通量的促进作用与风产生的垂向紊动混合对离散盐通量的抑制作用相抵消, 前者强度大于后者, 使得各断面盐度值整体上增加; 在风速增加的后期, 情况与前期一致, 但后者强度大于前者, 使得各断面盐度值整体上有所减少;
(3) 当向岸风作用时, 在风速增加的全过程中, 反向表面风应力产生的张力效应对离散盐通量的抑制作用与风产生的垂向紊动混合对离散盐通量的抑制作用相叠加, 使得各断面盐度值整体上有明显减少。
本文的改进对增进河口水流盐度动力机制的认识有着重要价值, 但还存在着一些不足, 值得进一步研究: (1)未考虑横向的地形变化, 某些情况下横向的离散作用会对河口盐度分布产生重要影响; (2)为了使计算和结果不至过于繁琐, 原有模型和改进模型都令垂向紊动扩散系数KV垂向恒定, 实际上KV也存在垂向分布; (3)本文假定垂向紊动黏性系数AV不随时间变化, 而对于涨潮与落潮AV差异巨大的河口(所谓的盐度周期性分层河口), 潮汐张力(tidal straining)对河口潮平均盐度分布的影响就不可忽略。
| 包芸, 任杰, 2001. 采用改进的盐度场数值格式模拟珠江口盐度分层现象. 热带海洋学报, 20(4): 28–34 |
| 匡翠萍, 1997. 长江口盐水入侵三维数值模拟. 河海大学学报, 25(4): 54–60 |
| 陈永平, 刘家驹, 喻国华, 2002. 潮流数值模拟中紊动黏性系数的研究. 河海大学学报, 30(1): 39–43 |
| 诸裕良, 严以新, 1998. 大江河口三维非线性斜压水流盐度数学模型. 水利水运科学研究,(2): 129–138 |
| Burchard H, Hetland R D, 2010. Quantifying the contributions of tidal straining and gravitational circulation to residual circulation in periodically stratified tidal estuaries. Journal of Physical Oceanography, 40(6): 1243–1262 DOI:10.1175/2010JPO4270.1 |
| Craig P D, Banner M L, 1994. Modeling wave-enhanced turbulence in the ocean surface layer. Journal of Physical Oceanography, 24(12): 2546–2559 DOI:10.1175/1520-0485(1994)024<2546:MWETIT>2.0.CO;2 |
| Garvine R W, McCarthy R K, Wong K C, 1992. The axial salinity distribution in the Delaware estuary and its weak response to river discharge. Estuarine, Coastal and Shelf Science, 35(2): 157–165 DOI:10.1016/S0272-7714(05)80110-6 |
| Geyer W R, Trowbridge J H, Bowen M M, 2000. The dynamics of a partially mixed estuary. Journal of Physical Oceanography, 30(8): 2035–2048 DOI:10.1175/1520-0485(2000)030<2035:TDOAPM>2.0.CO;2 |
| Hansen D V, Rattray Jr M, 1965. Gravitational circulation in straits and estuaries. Journal of Marine Research, 23(2): 104–122 |
| Ianniello J P, 1977. Tidally induced residual currents in estuaries of constant breadth and depth. Journal of Marine Research, 35: 755–786 |
| Jay D A, Smith J D, 1990. Residual circulation in shallow estuaries:2. Weakly stratified and partially mixed, narrow estuaries. Journal of Geophysical Research, 95(C1): 733–748 |
| MacCready P, 2004. Toward a Unified theory of tidally-averaged estuarine salinity structure. Estuaries, 27(4): 561–570 DOI:10.1007/BF02907644 |
| MacCready P, 2007. Estuarine adjustment. Journal of Physical Oceanography, 37(8): 2133–2145 DOI:10.1175/JPO3082.1 |
| McCarthy R K, 1993. Residual currents in tidally dominated, well-mixed estuaries. Tellus A:Dynamic Meteorology and Oceanography, 45(4): 325–340 DOI:10.3402/tellusa.v45i4.14896 |
| Munk W H, Anderson E R, 1948. Notes on a theory of the thermocline. Journal of Marine Research, 7: 276–295 |
| Nezu I, Rodi W, 1986. Open-channel flow measurements with a laser Doppler anemometer. Journal of Hydraulic Engineering, 112(5): 335–355 DOI:10.1061/(ASCE)0733-9429(1986)112:5(335) |
| Nguyen A D, Savenije H H G, 2006. Salt intrusion in multi-channel estuaries:a case study in the Mekong Delta, Vietnam. Hydrology and Earth System Sciences, 10(5): 743–754 DOI:10.5194/hess-10-743-2006 |
| Nguyen A D, Savenije H H G, Pham D N, et al, 2008. Using salt intrusion measurements to determine the freshwater discharge distribution over the branches of a multi-channel estuary:the Mekong Delta case. Estuarine, Coastal and Shelf Science, 77(3): 433–445 DOI:10.1016/j.ecss.2007.10.010 |
| Pritchard D W, 1954. A study of the salt balance in a coastal plain estuary. Journal of Marine Research, 13: 133–144 |
| Pritchard D W, 1956. The dynamic structure of a coastal plain estuary. Journal of Marine Research, 15: 33–42 |
| Ralston D K, Geyer W R, Lerczak J A, 2008. Subtidal salinity and velocity in the Hudson river estuary:Observations and modeling. Journal of Physical Oceanography, 38(4): 753–770 DOI:10.1175/2007JPO3808.1 |
| Savenije H H G, 1986. A one-dimensional model for salinity intrusion in alluvial estuaries. Journal of Hydrology, 85(1-2): 87–109 DOI:10.1016/0022-1694(86)90078-8 |
| Savenije H H G, 1993. Predictive model for salt intrusion in estuaries. Journal of Hydrology, 148(1-4): 203–218 DOI:10.1016/0022-1694(93)90260-G |
| Savenije H H G, 2005. Salinity and Tides in Alluvial Estuaries. Amsterdam: Elsevier, 197 |
| Scully M E, Friedrichs C T, Brubaker J M, 2005. Control of estuarine stratification and mixing by wind-induced straining of the estuarine density field. Estuaries, 28(3): 321–326 DOI:10.1007/BF02693915 |
| Stacey M T, Ralston D K, 2005. The scaling and structure of the estuarine bottom boundary layer. Journal of Physical Oceanography, 35(1): 55–71 DOI:10.1175/JPO-2672.1 |
| Zhang E F, Savenije H H G, Wu H, et al, 2011. Analytical solution for salt intrusion in the Yangtze Estuary, China. Estuarine, Coastal and Shelf Science, 91(4): 492–501 DOI:10.1016/j.ecss.2010.11.008 |
 2018, Vol. 49
2018, Vol. 49


