
中国海洋湖沼学会主办。
文章信息
- 王亚楠, 赵栋梁. 2018.
- WANG Ya-Nan, ZHAO Dong-Liang. 2018.
- 海洋环境因素对白冠覆盖率的影响及其数值估算
- THE EFFECTS OF MARINE ENVIRONMENTAL FACTORS ON WHITECAP COVERAGE AND ITS NUMERICAL ESTIMATION
- 海洋与湖沼, 49(4): 746-755
- Oceanologia et Limnologia Sinica, 49(4): 746-755.
- http://dx.doi.org/10.11693/hyhz20171100284
-
文章历史
- 收稿日期:2017-11-09
- 收修改稿日期:2018-02-05
2. 中国海洋大学物理海洋教育部重点实验室 青岛 266100
2. Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, China
海浪是最常见的海洋波动, 是海-气相互作用与耦合的重要组成部分。海洋表面受风的影响会产生表面张力波, 在风的持续作用下, 风浪开始形成, 并吸收风输入的能量不断成长, 波高增大, 直到波峰附近产生破碎, 将风输入的多余能量耗散, 实现能量平衡。波浪破碎会将空气卷入海水中形成气泡, 气泡上升至海面破裂后形成肉眼可见的白冠区域。波浪破碎是一个强非线性过程, 一般的摄动技术适用于弱的非线性相互作用, 因此无论通过实验方法还是理论方法都很难对该过程进行量化(Zhao et al, 2001)。白冠覆盖率W定义为单位海表面积中白冠区域所占面积的比例, 它可以用来量化波浪破碎的程度。波浪破碎会限制海浪的成长, 还会对海-气相互作用、海面遥感和海洋混合层等产生影响。
白冠覆盖率受风速等一系列水文气象环境因素的影响, 准确量化白冠覆盖率是深入了解波浪破碎等一系列海-气相互作用过程、完善海浪模式和上层海洋湍流模型的关键步骤。在过去的几十年里, 人们通过分析观测数据, 提出白冠覆盖率会受各类环境因素影响, 例如风速(Monahan et al, 1980; wu, 1986)、摩擦风速(Wu, 1979, 1988; Monahan, 1993)、低层大气稳定度(Monahan et al, 1986)、海水温度(Bortkovskii et al, 1993; Bortkovskii, 2012)、波浪能量耗散率(Hanson et al, 1999)、波龄(Sugihara et al, 2007)、风海雷诺数(Zhao et al, 2001)等。
1 白冠覆盖率的参数化风速是影响白冠的最显著因素已成为人们的共识, 最常被用来参数化白冠覆盖率。Monahan等(1990)提出海面上10m处风速U10与白冠覆盖率的立方根W1/3存在线性关系, 即风速U10的指数为3。Monahan(1993)提出参数化形式(1), 当风速U10=UB时, 白冠覆盖率W=0, 从物理意义角度可以将UB看作白冠开始出现时的风速, 一般称为风速阈值, a和n分别为待定系数和指数。
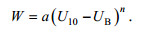 (1)
(1)Zhao等(2001)的表 1和Anguelova等(2006)的表 1总结列出前人的参数化结果, 补充在其之后的数据得到表 1, 其中指数n的取值范围为2.0—4.43, 近年来的研究中指数n取值多处于3—4之间。
| 作者 | a(×10–6) | UB | n | 备注 |
| Blanchard(1963) | 440 | 0 | 2.0 | |
| Monahan(1969) | 12 | 0 | 3.3 | |
| Toba等(1973) | 1.55 | 0 | 3.75 | |
| Tang(1974) | 7.75 | 0 | 3.231 | |
| Wu(1979) | 1.7 | 0 | 3.75 | |
| Monahan等(1980) | 2.95 | 0 | 3.52 | |
| Monahan等(1983) | 4.5 | 0 | 3.31 | |
| Spillane等(1986) | 92.79 | 0 | 2.112 | 冷水 |
| Spillane等(1986) | 47.55 | 0 | 2.525 | 温水 |
| Spillane等(1986) | 3.301 | 0 | 3.479 | 暖水 |
| Bortkovskii(1987) | 0.171 | 0 | 4.43 | 温水 |
| Bortkovskii(1987) | 67.8 | 0 | 2.76 | 暖水 |
| Wu(1988) | 2.0 | 0 | 3.75 | |
| Monahan等(1989) | 0.292 | 0 | 3.204 | ∆T = 0 |
| Hanson等(1999) | 0.204 | 0 | 3.61 | 舍去W < 5×10–5 |
| Villarino等(2003) | 2.32 | 0 | 3.4988 | ∆T < 0 |
| Villarino等(2003) | 0.43 | 0 | 3.6824 | ∆T > 0 |
| Lafon等(2004) | 1.51 | 0 | 3.65 | |
| Lafon等(2007) | 0.81 | 0 | 3.88 | |
| Asher等(1998) | 2.56 | 1.77 | 3 | |
| Asher等(2002) | 3.7 | 1.2 | 3 | |
| Reising等(2002) | 3.5 | 0.6 | 3 | |
| Stramska等(2003) | 41.8 | 4.93 | 3 | |
| Sugihara等(2007) | 8.04 | 2.01 | 3 | |
| Norris等(2013) | 10.3 | 2.63 | 3 | |
| 注:表中∆T为低层大气稳定度, ∆T=Tw−Ta(Tw为海水温度, Ta为气温), νw为海水运动黏度 | ||||
海水温度对白冠覆盖率的影响存在一定争议。Monahan等(1980)发现冷水数据得到的白冠覆盖率参数化结果中, 风速U10的指数小于暖水数据的结果, 因此认为白冠覆盖率与海水温度呈正相关性(Bortkovskii, 1983; Pounder, 1986)。Monahan等(1986)发现不同纬度海域观测数据得到风速U10的指数也存在差异, 海水温度对白冠覆盖率的影响实际为风时的反映(Monahan et al, 1989)。但Wu(1988)认为Monahan等(1986)在研究中所使用冷水的数据量远小于暖水, 以此推论出的水温的作用并不可靠。
目前许多有关白冠覆盖率的经验方程只包含风速、水温等与波浪无关的参量, 而波浪破碎是发生在海-气界面处由风和海浪共同参与的物理过程, 从本质上来看, 该过程与波浪属性关系更密切, 因此除了风的影响, 白冠覆盖率参数化模型还应该包含与波浪有关的参量(Zhao et al, 2001; Yuan et al, 2009)。Toba等(1986)提出无因次破碎波参数
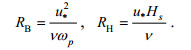 (2)
(2)式中, u*是摩擦风速, ν是空气运动黏度, ωp是风浪的谱峰圆频率, Hs是有效波高, RH又称风海雷诺数。该参数可以总体描述海-气边界处的物理过程, 波浪破碎出现时RB取临界值1000。
波浪能量耗散和白冠覆盖率都可以用来量化波浪破碎, 两者应该有类似的性质, 对此前人发展了破碎波模型(Longuet-Higgins, 1969; 袁业立等, 1988; Zhao et al, 2001; Yuan et al, 2009), 认为白冠覆盖率与波浪能量耗散率成正比(Ross et al, 1974)。波浪能量耗散率εt由破碎耗散源项Sds积分得到, 即
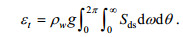 (3)
(3)式中, ρw为海水密度, g为重力加速度, ω为圆频率, θ为波向。Hanson等(1999)利用在阿拉斯加湾的观测数据得到波浪能量耗散率εt与白冠覆盖率的关系式
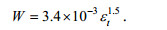 (4)
(4)式中, εt的指数为1.5而不是1, Hanson等(1999)对此解释为波浪能量的耗散或不限于白冠一种表征形式, 对其图像中仍存在的部分离散点解释为测量误差或平衡域理论对波浪能量耗散率εt估测的局限性。Hwang等(2008)根据耗散与风输入平衡得到
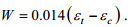 (5)
(5)此处εt=αρaU103, α为系数, 波浪能量耗散阈值εc为0.013—0.038W/m2。Anguelova等(2016)根据Phillips(1985)的破碎峰理论得到
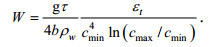 (6)
(6)式中, 泡沫持续时间τ为2s, 破碎强度参数b=0.013, cmax和cmin分别为破碎峰相速上下限, εt依据Hwang等(2008)的εt=αρaU103计算, cmin=αccp, 相速度cp=g/ωp, 常数α、αc、cmax/cmin分别取5.7×10–4、0.3和10。Scanlon等(2016)将摩擦风速u*及其阈值u*T加入Kraan等(1996)的白冠覆盖率表达式中, 得到
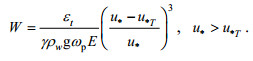 (7)
(7)式中, γ代表每单位白冠所耗散的能量占全部波浪能量的平均比例, 取值0.0078, u*T=0.065m/s, 波浪总能量E=(Hs/4)2。
2 白冠覆盖率与环境参数的关系人们通过多个航次观测得到大量白冠覆盖率数据, 图 1a综合部分前人观测数据, 参照Hanson等(1999)已将W < 5×10–5范围内的数据舍去。图中低风速下的数据分布离散程度较大, 风速小于10m/s时, 白冠覆盖率W的变化最大可超过两个量级, 随风速增大, 散点逐渐收敛, 风速大于10m/s时, W基本控制在一个量级以内, 这与Anguelova等(2006)的分析结果一致。
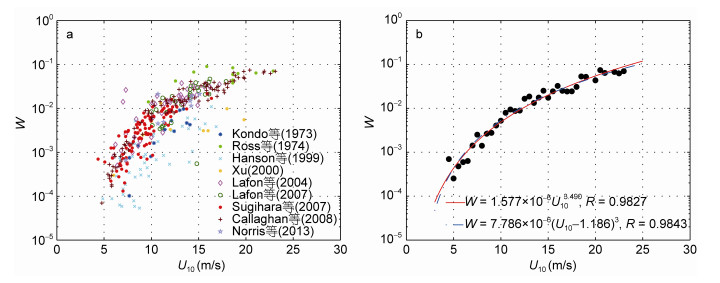 |
| 图 1 白冠覆盖率与风速观测数据分布及其拟合 Fig. 1 The distribution of field observational data of whitecap coverage and the fitting (a)观测数据分布(b)区间平均后的拟合曲线与方程 (a) The field observational data; (b) the fitting curves and equations of interval averaged dada |
用最小二乘法分别以UB等于0和不等于0两种形式对图 1a中数据进行非线性拟合, 其中第二种形式的指数n固定为3, 为避免不同风速下采样密度的不同导致拟合曲线向数据量大的方向倾斜, 以0.5m/s风速区间对白冠覆盖率进行平均, 得到结果式(8)和式(9), 图像如图 1b所示。
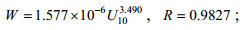 (8)
(8)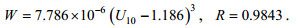 (9)
(9)从相关系数来看, 式(8)和式(9)都达到0.98以上且十分接近, 说明根据风速区间对白冠数据平均处理可以有效减小离散程度, 两种形式都可以很好的刻画数据分布。式(9)风速阈值UB=1.186, 与大部分人认同的3m/s(Blanchard, 1963; Monahan, 1971; Monahan et al, 1986; Hanson et al, 1999; Stramska et al, 2003; Anguelova et al, 2006; Scanlon et al, 2016)存在一定差距, 说明仅以风速阈值为标准来判断白冠是否出现并不严谨, 波浪破碎或许在任意风速下都有可能产生, 支持Monahan等(1986)和Anguelova等(2006)的观点。式(8)指数n=3.490, 符合3—4区间, 该式将作为判断参数化的白冠覆盖率是否与观测符合的依据。
对于海水温度与白冠覆盖率的关系, 如果用类似风速的方法, 单独用海水温度对白冠覆盖率进行参数化得到方程的相关性很低, 图像离散程度很大, 海水温度的影响趋势并不明显(Zhao et al, 2001)。但换个角度来看, 从不同水温环境下得到的白冠覆盖率与风速参数化方程可以发现一定规律。表 2列出前人在不同温度下提出的方程, 图 2示意各个参数化曲线。Monahan(1971)的数据取27.8—29.45℃部分重新使用最小二乘法进行拟合; Monahan等(1980)所用数据来自巴巴多斯海洋气象实验和中国南海实验两组观测, 海水温度分别为26.9℃和24.7℃; Lafon等(2004)和Lafon等(2007)原文中仅给出水温近似值13℃和14℃; Norris等(2013)的数据分布于水温9.04℃—12.3℃范围内。这五组观测数据所处的海水温度依次降低, 各自对应的参数化方程曲线也按同样的顺序由高到低排列, 支持白冠覆盖率随海水温度增加而增大的观点。
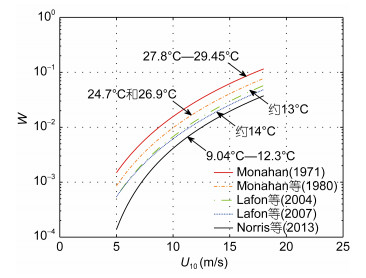 |
| 图 2 不同海水温度下白冠覆盖率参数化曲线对比 Fig. 2 Comparison of whitecap coverage parameterization curves at different sea water temperatures |
| 作者 | 参数化方程 | 海水温度 |
| Monahan(1971) | 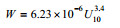 |
27.8—29.45℃ (取该范围内的数据使用最小二乘法重新拟合得到) |
| Monahan等(1980) | 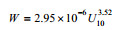 |
24.7℃和26.9℃ |
| Spillane等(1986) | 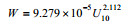 |
冷水 |
| Spillane等(1986) | 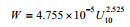 |
温水 |
| Spillane等(1986) | 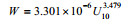 |
暖水 |
| Bortkovskii(1987) | 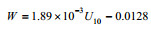 |
冷水 |
| Bortkovskii(1987) | 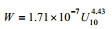 |
温水 |
| Bortkovskii(1987) | 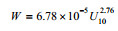 |
暖水 |
| Lafon等(2004) | 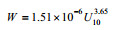 |
约13℃ |
| Lafon等(2007) | 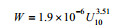 |
约14℃ |
| Norris等(2013) | 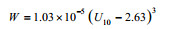 |
9.04—12.3℃ |
根据Wu(1979)的观点, 海水温度对白冠覆盖率的影响体现在式(1)的系数a中。依据前人数据涉及的不同风速范围, 取公共部分5—18m/s, 以1m/s的间隔给定风速值, 由图 2中的各个参数化曲线可以得到不同温度对应的白冠覆盖率W, 除以式(8)中的U103.490算出系数a, 用海水温度Tw对系数a进行参数化, 结合式(8)得到
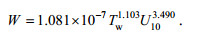 (10)
(10)利用实测风速和实测海水温度分别带入式(8)和式(10)得到白冠覆盖率计算值WU和WUT, 与白冠覆盖率实测值对比结果为图 3, 图中实线为y=x, 虚线分别为WU和WUT与实测数据的正比例函数拟合结果。式(8)比实测值低估17.3%, 考虑水温因素后, 而式(10)比实测值高估3%, 改善了低估问题, 相关系数也提高到0.9以上, 证明将海水温度加入系数a是合理的。
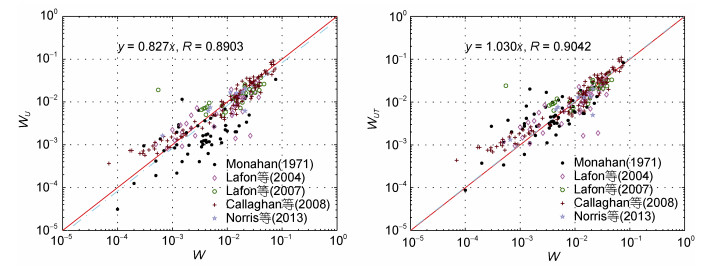 |
| 图 3 式(8)与式(10)拟合效果对比 Fig. 3 Comparison of fitting results of Eq.(8) and Eq.(10) |
Monahan(1993)曾提出同时含有风速U10和海水运动黏度νw的白冠覆盖率参数化形式, 给定10℃、20℃和30℃三个海水温度值, 分别带入Monahan (1993)的参数化形式和式(10)得到图 4。两者的量级和变化趋势一致, 进一步支持式(10)的参数化效果较好。在低风速如U10=5m/s时, 式(10)得到的白冠覆盖率比Monahan(1993)稍大; 而风速增大后, Tw=10℃时的式(10)计算值要小于Monahan(1993)。
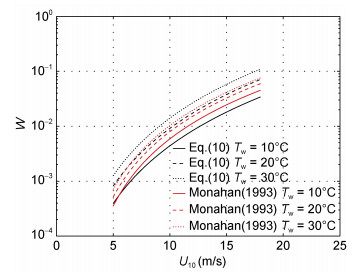 |
| 图 4 式(10)与Monahan(1993)参数化方案对比 Fig. 4 Comparison of Eq.(10) and the equation of Monahan(1993) |
根据Zhao等(2001), 可以用海水运动黏度νw代替空气运动黏度ν, 即RH=u*Hs/νw, 利用Lafon等(2004)、Lafon等(2007)、Sugihara等(2007)和Norris等(2013)的观测数据分别用RH和U10对同一组白冠覆盖率进行参数化得到式(11)和式(12), 图像如图 5所示。
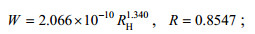 (11)
(11)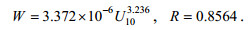 (12)
(12)
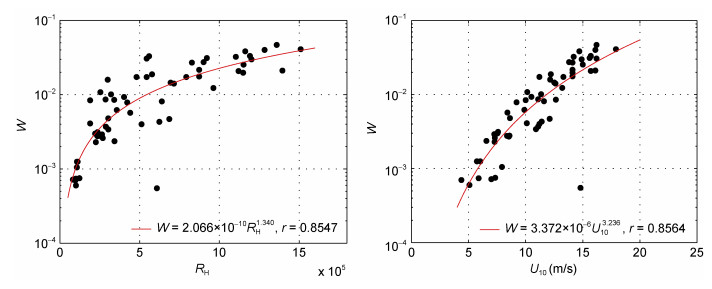 |
| 图 5 相同的白冠覆盖率分别用风海雷诺数和风速参数化结果 Fig. 5 The whitecap coverage parameterized with wind-sea Reynolds number and wind speed |
图 5中W与RH的数据在低RH部分较为离散, 随RH增大而有所改善, W与U10的参数化图像离散程度更小, 两者图像整体都上均匀分布在拟合曲线两侧, 相关系数都达到0.85以上而且相差小于0.002。注意到, 在计算风海雷诺数RH中的海水运动黏度时需要通过海水温度计算, 而前人在文章中并没有给出与白冠覆盖率一一对应的海水温度, 因此只能使用平均水温代替, 这或许是导致图 5中白冠覆盖率与风海雷诺数分布有较大程度离散的原因。风海雷诺数RH在将风速因素保留的前提下, 还引入有效波高和海水运动黏度这两个典型的风浪属性, 所包含的风浪信息更全面。根据以上分析认为, 使用风海雷诺数RH代替风速U10对白冠覆盖率参数化是合理的。另外, 海水温度增加会使海水运动黏度减小, 空气更容易被较暖海水卷入, 有利于波浪破碎(Bortkovskii, 1983; Pounder, 1986), 同时, 海水运动黏度减小还会导致风海雷诺数增大, 白冠覆盖率因而随之增大, 进一步证明了白冠覆盖率与海水温度呈正相关。
3 新参数化方案的提出与检验发展海浪模式有助于了解所有影响波浪成长和衰退的物理过程。第三代海浪数值计算模式SWAN模式(Simulating WAves Nearshore)由荷兰代尔夫特科技大学(Delft University of Technology)研制开发, 目前最新版本为41.10版本。在忽略背景流场的情况下能量平衡方程为
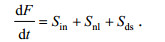 (13)
(13)式中, F为海浪谱, 右边三项包含影响波浪能量发展变化的各个物理过程, 分别为风能输入项、非线性相互作用项和能量耗散项, 深水情况时能量耗散项等效为白冠破碎耗散项。
SWAN模式默认使用Komen模型计算风能量输入项及其对应耗散项, Westhuysen饱和模型则是最新提出的模型。Komen模型的风能输入项为线性增长项与指数增长项的和
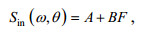 (14)
(14)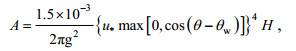 (15)
(15) (16)
(16)式中, θw为风向, H为滤波因子, ρa为空气密度。白冠破碎耗散项为
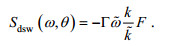 (17)
(17)式中, Г为波陡系数, 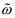
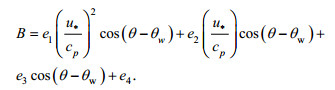 (18)
(18)系数分别为e1=4.0×10–2, e2=5.52×10–3, e3=5.2× 10–5, e4=−3.02×10–4。白冠破碎耗散项为Van Der Westhuysen等(2007)提出的
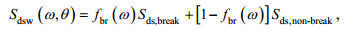 (19)
(19)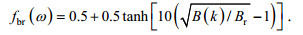 (20)
(20)式中, Sds, break和Sds, non-break分别表示破碎导致的耗散和其它形式的耗散, B(k)表示海浪谱饱和程度, 其阈值Br=1.75×10–3。
利用SWAN模式的耗散项Sds积分可以得到波浪能量耗散率εt, 若得到W与εt的关系就可以直接通过模式计算来了解白冠覆盖率的分布与变化。注意到εt/ρwg的单位m2/s与海水运动黏度νw相同, 利用νw可以有效地结合水温因素, 加入可调参数p和q, 提出白冠覆盖率的新参数化方案
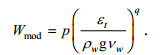 (21)
(21)理想数值实验可以检验新参数化方案效果。设置水深为1000m的平底海域, 范围为150°E—160°E、5°S—5°N, 风场设为定常风, 风速从6m/s —30m/s每2m/s进行一次实验, 计算时长为3天。计算时采用球面坐标系, 网格分辨率为0.1°×0.1°。为削弱边界的影响, 输出151°E — 159°E、4°S — 4°N范围内的数据并将同一风速同一时刻处于相同风区的各变量值分别平均, 海水运动黏度νw取海水温度20℃时的1.05372×10–6m2/s, 根据式(3)计算εt代入式(21)中得到Wmod。用风速U10同样可以对Wmod进行非线性拟合, 以式(8)为标准, 通过对比系数可以计算得到可调参数p和q的值(表 3), 其中, 使用两个模型的第二组参数值可以还原WU103.490关系。当指数q=1时, Wmod与U10拟合结果为
| p | q | |
| Komen模型 | 2.195×10–4 | 1 |
| 2.548×10–4 | 0.9678 | |
| Westhuysen模型 | 1.140×10–4 | 1 |
| 2.181×10–4 | 0.8718 |
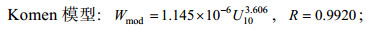 (22)
(22)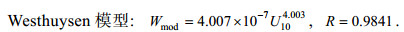 (23)
(23)图像如图 6所示, 两种模型计算结果的相关系数均达到0.98以上, Komen模型的更高一些, 风速U10的指数n基本处于3—4范围, 与近来研究一致, Westhuysen模型计算出的指数n稍大于4, 因此新参数化方案配合使用Komen模型计算效果更好, 之后的研究默认使用Komen模型计算。
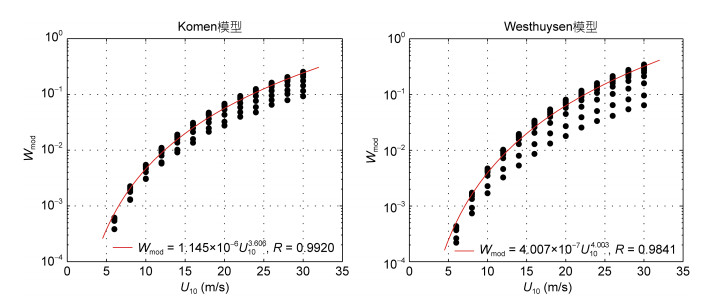 |
| 图 6 Wmod与风速关系示意图 Fig. 6 The relationship of Wmod and wind speed |
第一部分中式(4)—(7)分别为前人使用波浪能量耗散率εt对白冠覆盖率进行参数化的几种方案, 利用SWAN模式计算各个变量代入式中同样可以得到对应的白冠覆盖率, 考察其与风速的关系如图 7所示。以式(22)和式(23)为参照, 使用Hanson等(1999)式(4)和Hwang等(2008)式(5)计算的白冠覆盖率与风速的关系可以保证处于U103和U104之间, 而Anguelova等(2016)式(6)和Scanlon等(2016)式(7)与风速关系很弱, 约为平方关系。近年来研究结果支持白冠覆盖率与风速约为3—4次方关系, 但后两者的参数化方案并不能有效地还原这种关系。
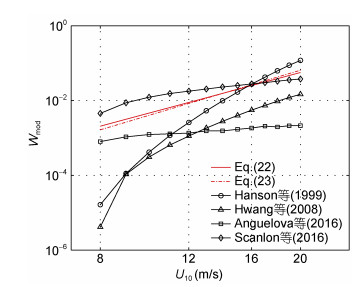 |
| 图 7 其他研究者的参数化方案与式(22)、式(23)对比 Fig. 7 Comparison in the parameterization among other authors', Eq.(22), and Eq.(23) |
图 6中同一风速由于风区和风时不同而对应多个Wmod值, 波龄的变化可以体现风区和风时的变化, 因此考察波龄β对白冠覆盖率的影响。Kraan等(1996)直接用波龄对白冠覆盖率进行参数化, 认为二者呈反比关系。Kleiss等(2010)与Lafon等(2007)观点一致, 认为白冠覆盖率先随波龄增大而增大, 波龄达到0.6时到达最大值, 然后白冠覆盖率随波龄增大而减小。
使用模式计算波龄, 并以0.05波龄区间对白冠覆盖率进行平均, 如图 8所示。Wmod先随波龄增大而增大, 当波龄增大到某个临界值之后, Wmod并没有出现Kleiss等(2010)所说的明显下降趋势, 而是基本趋于稳定。图中可以看出, U10=20m/s时, 波龄临界值约为0.65, U10 = 22m/s、24m/s和26m/s时, 波龄临界值约为0.6, U10=28m/s和30m/s时则为0.55, 因此认为该临界值并不是固定不变, 而是随风速增大而减小。
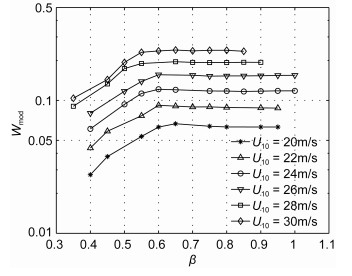 |
| 图 8 不同风速下Wmod随波龄的变化 Fig. 8 Variations in Wmod with wave age at different wind speeds |
风浪吸收风的能量不断成长, 波峰附近会发生波浪破碎使多余的能量耗散, 外观上表现为白冠的形式。白冠覆盖率随海洋环境的影响有明显的时空变化, 其中, 人们广泛认可白冠覆盖率与海面上10m高度处的风速呈指数函数关系, 风速指数的取值大多处于3—4, 根据前人多个观测数据拟合得到更可靠的依赖风速的白冠覆盖率公式, 以此为标准, 其他参数化方案通过检验白冠覆盖率与风速的关系可以判定参数化效果的优劣。除了气象因素, 海水温度和Zhao等(2001)提出的风海雷诺数是影响白冠覆盖率的两个重要海洋因素。观察不同海水温度下得到的白冠覆盖率与风速的参数化方程, 发现高水温时的参数化曲线高于低水温情况, 认为白冠覆盖率随海水温度升高而增大, 与风速的参数化方程中的系数可以表示为海水温度的函数, 因而得到同时包含风速和海水温度的白冠覆盖率参数化形式。随着海水温度升高, 海水运动黏度减小, 风海雷诺数则增大, 白冠覆盖率与风海雷诺数呈正相关进一步支持白冠覆盖率随海水温度升高而增大。
用海水运动黏度对SWAN模式中的白冠耗散项进行无因次化, 可以有效结合海水温度的影响, 利用与风速的关系对系数进行调整, 提出以波浪破碎耗散函数为参数的白冠覆盖率新参数化方案, 配合使用Komen模型可以得到更好的计算效果。根据新参数化方案考察白冠覆盖率与波龄的关系认为, 同一风速下存在一个波龄的临界值, 波龄小于临界值时白冠覆盖率随波龄增大而增大, 大于临界值后白冠覆盖率基本不再变化, 该临界值则会随风速增大而减小。
| 袁业立, 华锋, 潘增弟, 等, 1988. 破碎波统计及其在上层大洋动力学中的应用. 中国科学B辑, 18(10): 1084–1091 |
| Anguelova M D, Webster F., 2006. Whitecap coverage from satellite measurements:A first step toward modeling the variability of oceanic whitecaps. Journal of Geophysical Research:Oceans, 111(C3): C03017 |
| Anguelova M D, Hwang P A., 2016. Using energy dissipation rate to obtain active whitecap fraction. Journal of Physical Oceanography, 46(2): 461–481 DOI:10.1175/JPO-D-15-0069.1 |
| Asher W E, Wanninkhof R., 1998. The effect of bubble-mediated gas transfer on purposeful dual-gaseous tracer experiments. Journal of Geophysical Research:Oceans, 103(C5): 10555–10560 DOI:10.1029/98JC00245 |
| Asher W E, Edson J, Mcgillis W et al, 2002. Fractional area whitecap coverage and air-sea gas transfer velocities measured during GasEx-98. In: Donelan M A, Drennan W M, Saltzman E S et al eds. Gas Transfer at Water Surfaces. Washington, D. C., USA: American Geophysical Union, 199-203 |
| Blanchard D C., 1963. The electrification of the atmosphere by particles from bubbles in the sea. Progress in Oceanography, 1: 73–202 DOI:10.1016/0079-6611(63)90004-1 |
| Bortkovskii R S, 1983. Heat and Moisture Exchange Between Atmosphere and Ocean Under Storm Conditions (in Russian). Leningrad: Hydrometeorological Publishing House, 160 |
| Bortkovskii R S, 1987. Air-sea exchange of heat and moisture during storms. In: Monahan E C ed. Atmospheric and Oceanographic Sciences Library. Dordrecht, Netherlands: Springer, 89-112 |
| Bortkovskii R S, Novak V A., 1993. Statistical dependencies of sea state characteristics on water temperature and wind-wave age. Journal of Marine Systems, 4(2-3): 161–169 DOI:10.1016/0924-7963(93)90006-8 |
| Bortkovskii R S., 2012. Water-temperature effect on the spectral density of wind gravity waves and on sea-surface roughness. Izvestiya, Atmospheric and Oceanic Physics, 48(2): 193–199 DOI:10.1134/S0001433812020028 |
| Callaghan A H, De Leeuw G, Cohen L, et al, 2008. Relationship of oceanic whitecap coverage to wind speed and wind history. Geophysical Research Letters, 35(23): L23609 DOI:10.1029/2008GL036165 |
| Hanson J L, Phillips O M., 1999. Wind sea growth and dissipation in the open ocean. Journal of Physical Oceanography, 29(8): 1633–1648 DOI:10.1175/1520-0485(1999)029<1633:WSGADI>2.0.CO;2 |
| Hwang P A, Sletten M A., 2008. Energy dissipation of wind-generated waves and whitecap coverage. Journal of Geophysical Research:Oceans, 113(C2): C02012 |
| Kleiss J M, Melville W K., 2010. Observations of wave breaking kinematics in fetch-limited seas. Journal of Physical Oceanography, 40(12): 2575–2604 DOI:10.1175/2010JPO4383.1 |
| Kondo J, Fujinawa Y, Naito G., 1973. High-frequency components of ocean waves and their relation to the aerodynamic roughness. Journal of Physical Oceanography, 3(2): 197–202 DOI:10.1175/1520-0485(1973)003<0197:HFCOOW>2.0.CO;2 |
| Kraan G, Oost W A, Janssen P A E M., 1996. Wave energy dissipation by whitecaps. Journal of Atmospheric and Oceanic Technology, 13(1): 262–267 DOI:10.1175/1520-0426(1996)013<0262:WEDBW>2.0.CO;2 |
| Lafon C, Piazzola J, Forget P, et al, 2004. Analysis of the variations of the whitecap fraction as measured in a coastal zone. Boundary-Layer Meteorology, 111(2): 339–360 DOI:10.1023/B:BOUN.0000016490.83880.63 |
| Lafon C, Piazzola J, Forget P, et al, 2007. Whitecap coverage in coastal environment for steady and unsteady wave field conditions. Journal of Marine Systems, 66(1-4): 38–46 DOI:10.1016/j.jmarsys.2006.02.013 |
| Longuet-Higgins M S., 1969. On wave breaking and the equilibrium spectrum of wind-generated waves. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 310(1501): 151–159 DOI:10.1098/rspa.1969.0069 |
| Monahan E C., 1969. Fresh water whitecaps. Journal of the Atmospheric Sciences, 26(5): 1026–1029 DOI:10.1175/1520-0469(1969)026<1026:FWW>2.0.CO;2 |
| Monahan E C., 1971. Oceanic whitecaps. Journal of Physical Oceanography, 1(2): 139–144 DOI:10.1175/1520-0485(1971)001<0139:OW>2.0.CO;2 |
| Monahan E C, Muircheartaigh I ., 1980. Optimal power-law description of oceanic whitecap coverage dependence on wind speed. Journal of Physical Oceanography, 10(12): 2094–2099 DOI:10.1175/1520-0485(1980)010<2094:OPLDOO>2.0.CO;2 |
| Monahan E C, Fairall C W, Davidson K L, et al, 1983. Observed inter-relations between 10m winds, ocean whitecaps and marine aerosols. Quarterly Journal of the Royal Meteorological Society, 109(460): 379–392 DOI:10.1002/qj.v109:460 |
| Monahan E C, Muircheartaigh I ., 1986. Whitecaps and the passive remote sensing of the ocean surface. International Journal of Remote Sensing, 7(5): 627–642 DOI:10.1080/01431168608954716 |
| Monahan E C, Lu M., 1990. Acoustically relevant bubble assemblages and their dependence on meteorological parameters. IEEE Journal of Oceanic Engineering, 15(4): 340–349 DOI:10.1109/48.103530 |
| Monahan E C, Woolf D K., 1989. Comments on "Variations of whitecap coverage with wind stress and water temperature. Journal of Physical Oceanography, 19(5): 706–709 DOI:10.1175/1520-0485(1989)019<0706:COOWCW>2.0.CO;2 |
| Monahan E C, 1993. Occurrence and evolution of acoustically relevant sub-surface bubble plumes and their associated, remotely monitorable, surface whitecaps. In: Kerman B R ed. Natural Physical Sources of Underwater Sound. Dordrecht, Netherlands: Springer, 503-517 |
| Norris S J, Brooks I M, Moat B I, et al, 2013. Near-surface measurements of sea spray aerosol production over whitecaps in the open ocean. Ocean Science, 9(1): 133–145 DOI:10.5194/os-9-133-2013 |
| Phillips O M., 1985. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. Journal of Fluid Mechanics, 156: 505–531 DOI:10.1017/S0022112085002221 |
| Pounder C, 1986. Sodium chloride and water temperature effects on bubbles. In: Monahan E C, Niocaill G M eds. Oceanic Whitecaps. Dordrecht, Netherlands: Springer, 278 |
| Reising S, Asher W, Rose L et al, 2002. Passive polarimetric remote sensing of the ocean surface: The effects of surface roughness and whitecaps. URSI XXVⅡth General Assembly. Maastrict, Netherlands: International Union of Radio Science |
| Ross D B, Cardone V., 1974. Observations of oceanic whitecaps and their relation to remote measurements of surface wind Speed. Journal of Geophysical Research, 79(3): 444–452 DOI:10.1029/JC079i003p00444 |
| Scanlon B, Breivik , Bidlot J R, et al, 2016. Modeling whitecap fraction with a wave model. Journal of Physical Oceanography, 46(3): 887–894 DOI:10.1175/JPO-D-15-0158.1 |
| Spillane M C, Monahan E C, Bowyer P A et al, 1986. Oceanic whitecaps and their role in air-sea exchange processes. In: Monahan E C, Niocaill G M eds. Oceanic Whitecaps. Oceanographic Sciences Library. Dordrecht, Netherlands: Springer, 209-218 |
| Stramska M, Petelski T., 2003. Observations of oceanic whitecaps in the north polar waters of the Atlantic. Journal of Geophysical Research:Oceans, 108(C3): 3086 DOI:10.1029/2002JC001321 |
| Sugihara Y, Tsumori H, Ohga T, et al, 2007. Variation of whitecap coverage with wave-field conditions. Journal of Marine Systems, 66(1-4): 47–60 DOI:10.1016/j.jmarsys.2006.01.014 |
| Tang C C H., 1974. The effect of droplets in the Air-Sea transition zone on the sea brightness temperature. Journal of Physical Oceanography, 4(4): 579–593 DOI:10.1175/1520-0485(1974)004<0579:TEODIT>2.0.CO;2 |
| Toba Y, Chaen M., 1973. Quantitative expression of the breaking of wind waves on the sea surface. Records of Oceanographic Works in Japan, 12(1): 1–11 |
| Toba Y, Koga M, 1986. A parameter describing overall conditions of wave breaking, whitecapping, sea-spray production and wind stress. In: Monahan E C, Niocaill G M eds. Oceanic Whitecaps. Oceanographic Sciences Library. Dordrecht, Netherlands: Springer, 37-47 |
| Van Der Westhuysen A J, Zijlema M, Battjes J A., 2007. Nonlinear saturation-based whitecapping dissipation in SWAN for deep and shallow water. Coastal Engineering, 54(2): 151–170 DOI:10.1016/j.coastaleng.2006.08.006 |
| Villarino R, Camps A, Vall-Ilossera M, et al, 2003. Sea foam effects on the brightness temperature at L-band. In:2003 IEEE International Geoscience and Remote Sensing Symposium. Toulouse, France:IEEE, 5: 3076–3078 |
| Wu J., 1979. Oceanic whitecaps and sea state. Journal of Physical Oceanography, 9(5): 1064–1067 DOI:10.1175/1520-0485(1979)009<1064:OWASS>2.0.CO;2 |
| Wu J., 1986. Stability parameters and wind-stress coefficients under various atmospheric conditions. Journal of Atmospheric and Oceanic Technology, 3(2): 333–339 DOI:10.1175/1520-0426(1986)003<0333:SPAWSC>2.0.CO;2 |
| Wu J., 1988. Variations of whitecap coverage with wind stress and water temperature. Journal of Physical Oceanography, 18(10): 1448–1453 DOI:10.1175/1520-0485(1988)018<1448:VOWCWW>2.0.CO;2 |
| Xu D, Liu X, Yu D., 2000. Probability of wave breaking and whitecap coverage in a fetch-limited sea. Journal of Geophysical Research:Oceans, 105(C6): 14253–14259 DOI:10.1029/2000JC900040 |
| Yan L, 1987. An improved wind input source term for third generation ocean wave modelling. Royal Netherlands Meteorological Institute Scientific Report. De Bilt, Netherlands: WR-87-9, 10 |
| Yuan Y L, Han L, Hua F, et al, 2009. The statistical theory of breaking entrainment depth and surface whitecap coverage of real sea waves. Journal of Physical Oceanography, 39(1): 143–161 DOI:10.1175/2008JPO3944.1 |
| Zhao D L, Toba Y., 2001. Dependence of whitecap coverage on wind and wind-wave properties. Journal of Oceanography, 57(5): 603–616 DOI:10.1023/A:1021215904955 |
 2018, Vol. 49
2018, Vol. 49


