中国海洋湖沼学会主办。
文章信息
- 赵孟欣, 陈旭, 王树亚, 孟静. 2018.
- ZHAO Meng-Xin, CHEN Xu, WANG Shu-Ya, MENG Jing. 2018.
- 非均匀密度层结内潮射线生成与传播的实验研究
- EXPERIMENTAL STUDY ON THE GENERATION AND PROPAGATION OF INTERNAL TIDE BEAM IN NON-UNIFORM STRATIFICATIONS
- 海洋与湖沼, 49(6): 1131-1137
- Oceanologia et Limnologia Sinica, 49(6): 1131-1137.
- http://dx.doi.org/10.11693/hyhz20180100001
-
文章历史
- 收稿日期:2018-01-03
- 收修改稿日期:2018-04-16
2. 中国海洋大学海洋与大气学院 青岛 266100
2. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China
内潮是海洋中普遍存在的发生在密度稳定层化海水内部的一种波动现象, 在海洋的能量分配中起着重要的动力作用, 是能量级串中的一个重要环节(Alford, 2003; Garrett, 2003; Garrett et al, 2007)。海水的层结是影响内潮生成和耗散的主要因素之一, 在忽略地转效应的情况下, 内波的频散关系可表示为:
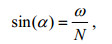 (1)
(1)其中, α为射线与水平方向的夹角, ω为内波的圆频率, N为浮频率, 表达式为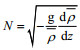
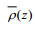
Delisi等(1975)在实验室实验中设置了上层为线性分层、下层为恒定密度的非均匀密度层结, 探究了内潮射线层结突变时的折射问题。内潮射线向上传播遇到跃层时, 会在跃层中激发非线性谐波和平均流(Mercier et al, 2012; Wunsch et al, 2015); 若传播过程遇到浮频率小于内潮频率的流体, 会发生内波隧穿现象(Sutherland et al, 2004)。Mathur等(2009)对密度梯度突变以及存在有限宽度过渡层的非均匀密度层结中内波射线传播开展了实验研究, 计算了能量在层结变化水层中的透射率, 用实验结果解释了夏威夷海脊处内波射线在表层耗散的现象。
为探究地形高度低于转折深度时上层流体生成内潮射线的位置及强度, 本文设置上层强、底层弱的非均匀密度层结, 进行有限水深内潮生成和演化的实验研究, 将针对无转折深度以及转折深度大于地形高度两种情况进行探讨。
1 实验与方法 1.1 实验设置本实验在中国海洋大学物理海洋重点实验室进行, 二维内波水槽长500cm, 宽15cm, 高40cm, 见图 1(a)。实验通过振荡地形, 模拟正压潮流过地形激发内潮, 以5cm和10cm两种高度的高斯地形模拟海洋中的山脊地形, 地形宽度均为40cm。地形固定在75cm长的薄钢板上, 通过金属件与驱动装置连接, 产生正弦运动。将坐标系建立在模型地形的中心位置, z轴向上为正, x轴向右为正。正压潮流的流速为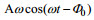
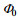
| 组数 | 强迫频率(rad/s) | 地形高度(cm) | 是否存在转折深度 |
| 1 | 0.30 | 5 | 否 |
| 2 | 0.37 | 5 | 否 |
| 3 | 0.44 | 5 | 否 |
| 4 | 0.49 | 5 | 否 |
| 5 | 0.56 | 5 | 否 |
| 6 | 0.71 | 5 | 是 |
| 7 | 0.78 | 5 | 是 |
| 8 | 0.86 | 5 | 是 |
| 9 | 0.98 | 5 | 是 |
| 10 | 0.30 | 10 | 否 |
| 11 | 0.37 | 10 | 否 |
| 12 | 0.42 | 10 | 否 |
| 13 | 0.49 | 10 | 否 |
| 14 | 0.56 | 10 | 否 |
| 15 | 0.64 | 10 | 否 |
| 16 | 0.71 | 10 | 是 |
| 17 | 0.86 | 10 | 是 |
采用改进后的双缸法(马永星等, 2015), 通过控制流量在水槽中放置非均匀层结盐水。实验层结设置为上层层结强, 下层层结弱。实验中采用电导率仪测量电导率进而得到密度剖面, 结果见图 1(b), 0.14m至0.23m为上层强线性分层(以下简称上层), 浮频率N1约为1rad/s; 0至0.14m为下层弱线性分层(以下简称下层), 浮频率N2约为0.65rad/s。
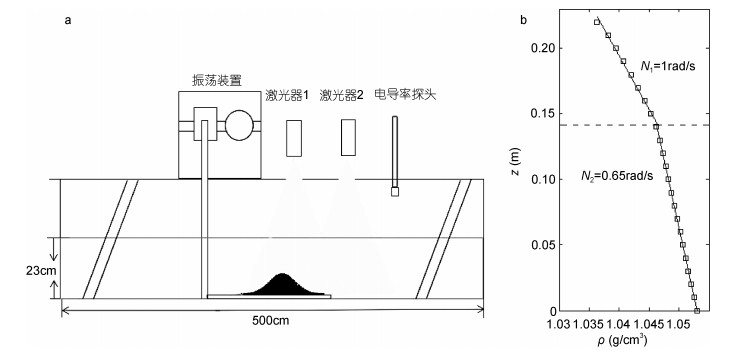 |
| 图 1 a:实验装置示意图, b:密度剖面 Fig. 1 a: sketch of the experiment setup and b: the density profile 注:空心方框代表实测值, 直线是上下层分别线性拟合的结果 |
本文采用粒子图像测速技术(PIV)测量流场, 使用功率3W、波长532nm的激光器, 激光器发射的点光源通过展片展成片光照亮观测平面, 示踪粒子是密度1040kg/m3、直径50μm的聚苯乙烯粒子, 使用一台分辨率为1920×1080像素的CCD相机以10帧/s的帧率采集图像, 相机正对二维水槽侧面拍摄, 视场范围57×101cm。
1.2 数据分析对CCD拍摄得到的图片, 首先利用PIVlab软件包进行处理(Thielicke et al, 2014), 得到流场。对流场数据进行归一化, 分别除以正压潮流速振幅得到归一化水平流速和垂向流速: 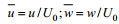
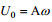
根据Nash等(2005), 内潮能通量的表达式如下:
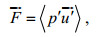 (2)
(2)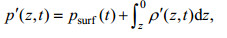 (3)
(3)其中, psurf是表面压强, 根据关系式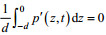
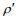
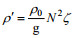
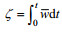
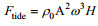
由式(1)可知, 当ω < N时, 有内波射线生成; ω > N时, 流体中无内波射线, 射线在水层中将以指数形式迅速衰减(Gerkema et al, 2008)。本实验中, 0.30rad/s < ω < 0.64rad/s时, ω < N1, ω < N2, 在上下两层流体中均有射线(见图 2a、c); 0.65rad/s < ω < 0.86rad/s时, N1 < ω < N2, 转折深度ztd=0.14m=0.14m以下无内波射线(见图 2b、d)。
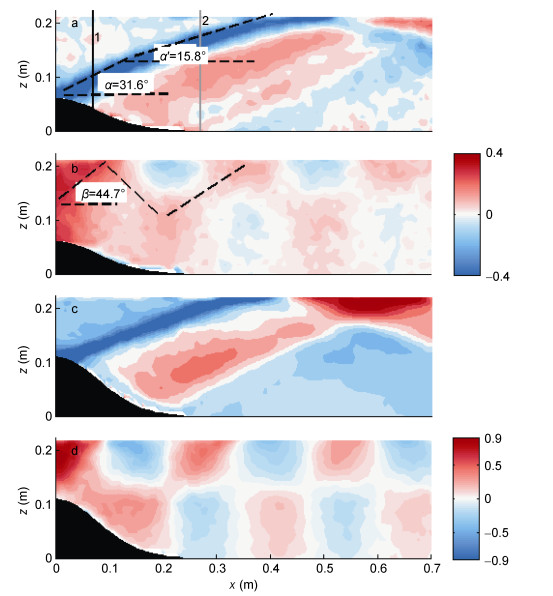 |
| 图 2 内潮的归一化水平流速场 Fig. 2 Snap-shots of normalized horizontal velocity of the internal tide 注: a: ω=0.3rad/s, d=5cm; b: ω=0.71rad/s, d=5cm; c: ω=0.30rad/s, d=10cm; d: ω=0.71 rad/s, d=10cm。a:射线发生折射, 上下水层传播角度不同, 下层与水平方向夹角为α=31.6°, 上层与水平方向夹角为α'=15.8° |
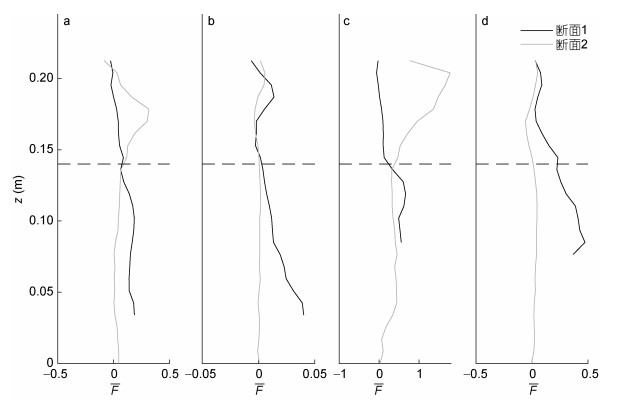
针对第一种情况, 由于上下层流体浮频率不同, 射线在底层生成, 传播至上层后射线发生折射, 角度改变。振荡圆频率ω=0.30rad/s时, 下层射线角度理论值为27.5°, 实测值α=31.6°, 上层射线角度理论值为17.5°, 实测值α'=15.8°。发生折射后射线聚焦, 宽度变窄, 能量更集中, 在x=0.07m和x=0.27m处, 即图 2a中黑色、灰色实线位置, 取垂向断面1、2, 绘制归一化能通量垂向断面分布图, 射线经过断面1时位于下层流体, 经过断面2时在上层流体, 断面2的F最大值大于断面1, 说明射线传播至上层后能通量相对于下层增大(图 3a, c)。而第二种情况下, ω=0.71rad/s时(图 2b、d), 存在转折深度, 下层无内潮射线, 不存能量聚焦, 断面2能通量低于断面1。归一化水平流速分布类似第一模态内波, 射线结构不明显, 流速以上下层界面为界线, 在上层与下层方向相反。相对于第一种情况, 上层流体中内潮射线归一化水平流速更小。
对于第二种情况, 强迫频率ω=0.71—0.86rad/s时, N1 < ω < N2, 此时下层无内波射线, 转折深度ztd=0.14m。此时, 地形高度H(5cm, 10cm)低于转折深度, 正压潮受地形影响产生的扰动依旧能传递到上层, 内潮射线在上层生成并传播, 上层流体成为波导, 见图 2d, 上层射线与水平方向夹角理论值为45.2°, 实测值β=44.7°。上层虽然有射线生成, 从图中可以看到, 其归一化流速较第一种情况更小, 射线强度更弱。下文将通过水平能通量深度积分对两种情况下生成内潮的强度进行比较。
归一化的水平方向的通量Fh=〈u'p'〉, 归一化深度积分能通量:
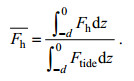 (4)
(4)x=0—0.1m之间是射线的生成区, 不同频率的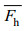
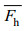
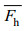
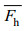
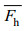
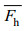
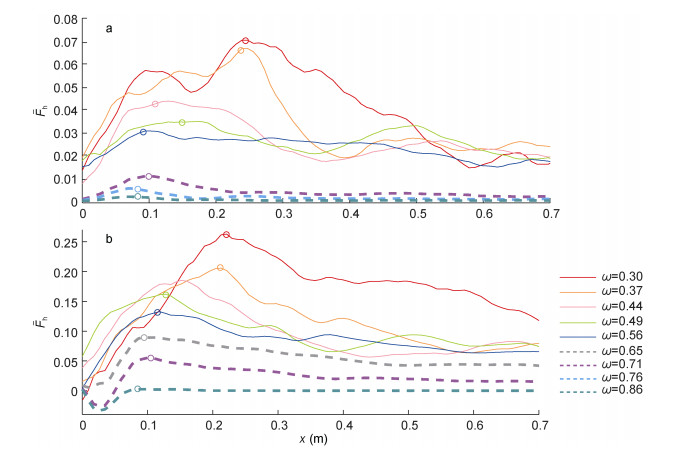 |
| 图 4 内潮的归一化深度积分能通量 Fig. 4 The normalized depth-integrated energy flux 注:实线表示无转折深度, 虚线表示存在转折深度, 空心圆表示最大值位置; ω单位为rad/s |
在衰减区, 随着射线传播, 由于黏性耗散作用, 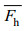
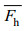
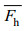
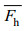
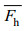
转折深度高于地形高度时, 内潮射线不是在地形处直接生成, 而是在转折深度以上生成并传播, 能量在地形与上层流体之间有一定的衰减。地形越高时, 顶端距离上层内波生成点越近(地形顶距离界面4cm), 相较于矮地形(地形顶距离界面9cm), 有更强的能量传递到上层, 生成的射线强度越强。图 4中, 10cm地形生成内潮水平归一化通量深度积分值是5cm地形的3—4倍, 而ω=0.71rad/s, 存在转折深度时, 10cm高地形生成射线的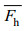
取x=0.35m处的垂向断面, 对该断面上归一化水平流速作EOF分解。分解结果显示, EOF模态结构与内潮的垂向模态结构有对应较好, 前三模态方差贡献率5cm地形实验达到50%以上, 10cm地形实验达到80%(表 2)。10cm地形实验生成内潮射线能量较5cm地形更强, 相同频率下, 第一模态方差贡献率更大, 但两者空间模态结构类似。
| 组数 | 频率(rad/s) | 地形高度(cm) | 第一模态方差贡献率 | 第二模态方差贡献率 | 第三模态方差贡献率 |
| 1 | 0.30 | 5 | 0.41 | 0.28 | 0.06 |
| 5 | 0.56 | 5 | 0.62 | 0.11 | 0.05 |
| 6 | 0.71 | 5 | 0.34 | 0.14 | 0.08 |
| 10 | 0.30 | 10 | 0.69 | 0.23 | 0.02 |
| 14 | 0.56 | 10 | 0.78 | 0.13 | 0.03 |
| 16 | 0.71 | 10 | 0.82 | 0.07 | 0.03 |
当ω=0.30rad/s时, 前三个EOF模态与前三个内潮斜压模态一致(图 5a)。当ω=0.56rad/s、0.71rad/s时, 第一个EOF模态水平速度在流体表面和底层最大且方向相反, 第三个EOF模态水平速度在垂向方向改变三次, 分别对应第一、第二斜压模态(司广成等, 2012), 第二个EOF模态为正压潮模态(图 5b、c、d), 水平流速上下一致。从图 2b、d可以看到, 0.71rad/s时射线结构不明显, 因此高斜压模态对应的EOF模态方差贡献率很小。且强迫频率越大, 正压模态方差贡献率越大, ω=0.86rad/s时, 强迫频率接近上层浮频率N2, 生成的射线能量很弱, 正压模态的方差贡献率最高。
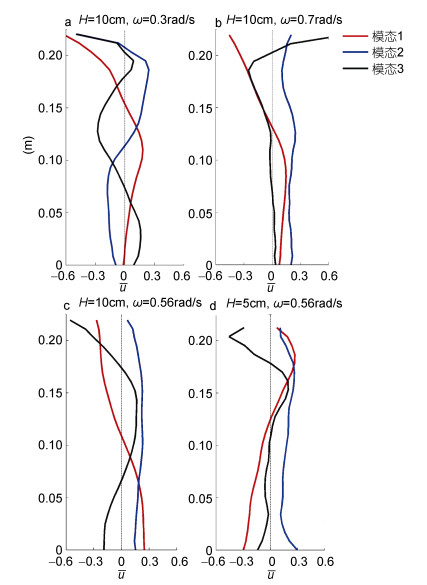 |
| 图 5 EOF分析结果:空间模态 Fig. 5 Results of EOF analysis: the mode structure |
EOF分析结果与图 2b、d中类似第一模态内波的流速分布相吻合, 10cm地形ω=0.71rad/s的实验分解结果表面, 第一个EOF模态与第一斜压模态类似, 方差贡献率达到了81.6%, 速度为0的位置大致在界面处(z=0.14m)而非中间水深位置, 0.1m以下垂向结构基本一致, 类似正压模态结构, 这是由于此时下层无内潮传播, 因此与内潮在全水深传播时的情况不同。
3 结论与展望通过实验室实验, 研究了非均匀密度层结下内潮射线的生成和传播规律, 得到了以下结论:
(1) 内潮射线从浮频率较小的水层(N1=0.65rad/s)传播到浮频率较大的水层(N2=1rad/s)时, 射线传播角度发生改变, 且射线变窄, 能通量变大, 发生能量聚焦;
(2) 当ω < N1, ω < N2时, 存在转折深度ztd=0.14m, 地形高度低于转折深度, 此时底部层结弱的水层无内潮射线, 浮频率变化的界面处生成内潮射线, 在上层流体中传播, 形成波导, 射线强度明显弱于无转折深度存在时的情况;
(3) 无转折深度时, 由于黏性耗散, 归一化水平能通量的深度积分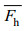
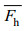
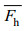
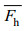
(4) 归一化水平流速的EOF模态与内潮斜压模态对应较好, 内潮频率越接近浮频率时, 正压潮模态的方差贡献率越大。
本文主要进行了高斯地形实验, 在以后的工作中应进一步探究其他不同地形如随机地形、三角地形等作用下内潮生成情况。且实际海洋层结情况复杂多样, 应当结合指数分层、跃层型等不同的层结继续进行研究。
| 马永星, 陈旭, 刘长乐, 等, 2015. 内波水槽中非均匀密度层结的实现及实验验证. 中国海洋大学学报, 45(6): 1–6 |
| 王金虎, 陈旭, 徐洋, 2016. 粗糙地形对内波生成影响的实验研究. 海洋与湖沼, 47(4): 706–713 |
| 司广成, 侯一筠, 2012. 南海北部东沙岛附近的内潮和余流特征. 海洋与湖沼, 43(1): 10–16 |
| Alford M H., 2003. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature, 423(6936): 159–162 DOI:10.1038/nature01628 |
| Chang M H, Lien R C, Tang T Y, et al, 2006. Energy flux of nonlin-ear internal waves in northern South China Sea. Geophysical Research Letters, 33(3): L03607 |
| Delisi D P, Orlanski I., 1975. On the role of density jumps in the reflexion and breaking of internal gravity waves. Journal of Fluid Mechanics, 69(3): 445–464 DOI:10.1017/S0022112075001516 |
| Garrett C., 2003. Internal tides and ocean mixing. Science, 301(5641): 1858–1859 |
| Garrett C, Kunze E., 2007. Internal tide generation in the deep ocean. Annual Review of Fluid Mechanics, 39: 57–87 DOI:10.1146/annurev.fluid.39.050905.110227 |
| Gerkema T, van Haren H., 2012. Absence of internal tidal beams due to non-uniform stratification. Journal of Sea Research, 74: 2–7 DOI:10.1016/j.seares.2012.03.008 |
| Gerkema T, Zimmerman J T F., 2008. An introduction to internal waves. Texel:NIOZ, 207 |
| King B, Stone M, Zhang H P, et al, 2012. Buoyancy frequency profiles and internal semidiurnal tide turning depths in the oceans. Journal of Geophysical Research:Oceans, 117(C4): C04008 |
| Mathur M, Peacock T., 2009. Internal wave beam propagation in non-uniform stratifications. Journal of Fluid Mechanics, 639: 133–152 DOI:10.1017/S0022112009991236 |
| Mercier M J, Mathur M, Gostiaux L, et al, 2012. Soliton generation by internal tidal beams impinging on a pycnocline:laboratory experiments. Journal of Fluid Mechanics, 704: 37–60 DOI:10.1017/jfm.2012.191 |
| Mowbray D E, Rarity B S H., 1967. A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. Journal of Fluid Mechanics, 28(1): 1–16 DOI:10.1017/S0022112067001867 |
| Nash J D, Alford M H, Kunze E., 2005. Estimating Internal Wave Energy Fluxes in the Ocean. Journal of Atmospheric and Oceanic Technology, 22(10): 1551–1570 DOI:10.1175/JTECH1784.1 |
| Paoletti M S, Drake M, Swinney H L., 2014. Internal tide generation in nonuniformly stratified deep oceans. Journal of Geophysical Research:Oceans, 119(3): 1943–1956 DOI:10.1002/2013JC009469 |
| Sutherland B R, Yewchuk K., 2004. Internal wave tunnelling. Journal of Fluid Mechanics, 511: 125–134 DOI:10.1017/S0022112004009863 |
| Thielicke W, Stamhuis E J., 2014. PIVlab-towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. Journal of Open Research Software, 2(1): 1202–1210 |
| Wang J H, Chen X, Wang W, et al, 2015. Laboratory experiments on the resonance of internal waves on a finite height subcritical topography. Ocean Dynamics, 65(9-10): 1269–1274 DOI:10.1007/s10236-015-0874-2 |
| Wunsch S, Delwiche I, Frederick G, et al, 2015. Experimental study of nonlinear harmonic generation by internal waves incident on a pycnocline. Experiments in Fluids, 56(5): 87 DOI:10.1007/s00348-015-1954-2 |
 2018, Vol. 49
2018, Vol. 49