中国海洋湖沼学会主办。
文章信息
- 姜浩, 赵中阔, 樊伟, 宋金宝. 2018.
- JIANG Hao, ZHAO Zhong-Kuo, FAN Wei, SONG Jin-Bao. 2018.
- 基于经验模态分解和小波分解估算海气通量涡相关计算中的截断时间尺度
- ESTIMATE OF CUTOFF TIME SCALE IN THE EDDY COVARIANCE METHOD FOR AIR-SEA FLUX BASED ON EMPIRICAL MODE DECOMPOSITION AND WAVELET DECOMPOSITION
- 海洋与湖沼, 49(6): 1138-1150
- Oceanologia et Limnologia Sinica, 49(6): 1138-1150.
- http://dx.doi.org/10.11693/hyhz20180300060
-
文章历史
- 收稿日期:2018-03-22
- 收修改稿日期:2018-06-07
2. 中国气象局广州热带海洋气象研究所 广州 510640
2. Guangzhou Institute of Tropical and Marine Meteorology, China Meteorological Administration, Guangzhou 510640, China
海洋占地球表面的70%以上, 其运动和变化直接影响和调控着海洋上方的大气结构以及全球气候变化。单位时间内单位面积上海洋和大气发生的物质与能量交换的量称为海气通量, 其强弱直接影响大气和海洋环境(Donelan et al, 2001; Yu et al, 2010), 准确的海气通量计算对全球气候变化预测(Li et al, 2010; Liang et al, 2010; Liu et al, 2012)以及提高海洋数值模拟精度(Ban et al, 2010; Zeng et al, 2010; Zedler et al, 2012)等具有重要影响。
块体参数化方法、廓线法、惯性耗散法以及涡相关法是目前常用的四种海气通量计算方法。海洋观测成本高昂, 每一份海洋数据都来之不易, 高分辨率的观测数据更是少之又少, 也正是这个原因, 使得基于莫宁-奥布霍夫相似理论(MOST)的块体参数化方法成为目前使用最为广泛的海气通量计算方法(Fairall et al, 2003)。而随着近年来科技水平的提高, 现代观测手段不断进步, 高分辨率海洋观测数据逐渐增多, 涡相关海气通量计算方法得到了越来越多的应用, 它直接基于高分辨率观测数据, 没有其它方法中的诸多近似, 因此涡相关法的计算精度是上述几种方法中最高的。截断时间尺度(Cut-off Time Scale, CTS)的选取是海气通量涡相关法计算中的一个关键性问题(Sun et al, 1996; Sakai et al, 2001; Finnigan et al, 2003; 宋朝阳等, 2013; 邹仲水等, 2014), 早期涡相关法通量计算时采用的CTS一般为30至60分钟(Panofsky et al, 1984; Kaimal et al, 1994), 而近几年的研究显示, 在计算海气通量时, CTS的取值应该小于15分钟(Aubinet, 2008; Edson et al, 2013), 目前常用的CTS取值为10分钟, 而Martins等(2017)利用了观测时长为28天的HALOCAST数据进行分析, 结果显示平均CTS只有37秒。
多分辨率分析提出可以用一个“间隙”将信号分为湍和非湍两个部分(Vickers et al, 2003), 将这个“间隙”的时间尺度作为CTS能过滤信号非湍部分对通量的贡献。随着信号处理技术的发展, 人们对CTS做了进一步的研究, 其中黄艳松等(2011)采用了多尺度分解法(Multi-Resolution Decomposition, MRD), Wang等(2013)、邹仲水等(2014)以及Martins等(2017)采用了经验模态分解(Empirical Mode Decomposition, EMD)估算了CTS。而小波分解(Wavelet Decomposition, WD)作为一种新发展的且有效的信号分析方法尚未在相关方面得到应用, 本文分别将EMD和WD这两种信号分解方法应用到海气通量的涡相关计算中, 估算了通量和CTS, 并对这两个方法得到的结果进行了对比、分析和讨论。
1 数据和方法 1.1 数据本研究数据来自广东茂名附近海域(21.44°N, 111.39°E)离岸约6.5公里处的铁塔(如图 1所示, 五角星为铁塔位置)观测, 铁塔上安装了一系列的高分别率传感器, 测量了风速、温度、气压等一系列的海表面气象数据, 这里主要利用风场数据。
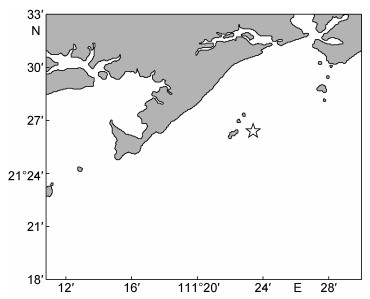 |
| 图 1 观测点(五角星)位置 Fig. 1 The location of the observation point (the star) |
风速数据由三个分量组成, 分别是顺风向风速U、侧风向风速V以及垂直方向风速W, 风速测量仪器为CSAT3, 采样频率为10 Hz, 观测时间为2015年2月4号到3月12号, 观测时长为38天, 数据在经过野点去除、插值之后如图 2所示。
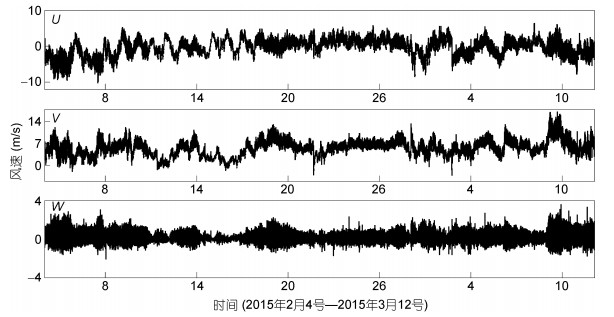 |
| 图 2 茂名铁塔风速数据 Fig. 2 Wind Speed Data observed from Maoming Tower |
相比于浮标, 铁塔更加稳定, 观测数据的处理也更简单, 数据只需要进行野点去除和插值处理即可使用; 由图 1可以看出, 观测位置深入海洋, 受陆地影响较小。
1.2 信号分解方法介绍 1.2.1 经验模态分解方法经验模态分解(Empirical Mode Decomposition, EMD)是Huang等(1998)提出的一种信号分解方法。时间信号序列f(t)经过EMD分解之后可得到一系列固有模态函数(Intrinsic Mode Function, IMF)以及一个余留项(R)。总时长为T的时间信号f(t)的EMD分解过程如下:
(1) 找出f(t)的所有的极值;
(2) 用三次样条拟合的方法分别连接这些极大值和极小值, 得到f(t)的上、下两条包络线, 求出上、下包络线之间的均值曲线m1, 1(T);
(3) 将m1, 1(T)从f(t)中减去, 得到新的时间序列h1, 1(T);
(4) 对新的时间序列重复上述(1)到(3)操作, 直至使中间变量SD满足:
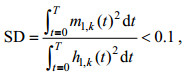 (1)
(1)其中, k为(1)到(3)操作的重复次数, m1, k(t)和h1, k(t)分别为第k次重复之后得到的包络线均值和时间序列,
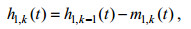 (2)
(2)令IMF1=h1, k(t), IMF1就是从f(t)中分解出的第一个固有模态。
将IMF1从f(t)中去除得到f1(t)=f(t)IMF1, 对f1(t)重复上述(1)到(4)操作, 直到满足fn(t)单调,
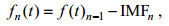 (3)
(3)令R=fn(t), R即为f(t)在T时间段中的变化趋势。由此, 将一个时间信号S进行EMD分解后的结果可以表示为
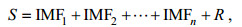 (4)
(4)其中, IMF1, IMF2, …, IMFn为EMD得到的各脉动分量, 代表了信号在不同时间尺度上的脉动, R代表了S的变化趋势, 之后再运用希尔伯特变换(Hilbert Transform, HT)就能计算出各模态对应的时间尺度。需要指出的是, 实际应用中, 往往要考虑到信号的边界效应影响, 计算特征时间尺度时要将瞬时频率ω(t)开始和结束前各去除一小段, 以提高特征时间尺度的精度。
1.2.2 小波分解方法小波变换是一种有效的信号变换分析方法, 它继承并发展了短时傅里叶变换的思想, 具有更高的灵活性, 既可以像傅里叶分析一样用于信号的整体分析, 又可以通过小波基灵活的伸缩、平移实现信号的多尺度细化和信号的细节分析。同时, 小波变换提供了大量的小波基, 可以按照使用者的需求, 针对于不同的信号采用不同的小波基。也正是因为小波变换的这些优点, 自它在1973年被Morlet提出后已应用到许多领域。
一维小波变换的定义:设一个函数ψ(t)∈L2(R), 其中L2(R)为ψ(t)的矢量空间, R为实数, 即ψ(t)具有有限能量, Ψ(ω)为其傅里叶变换,
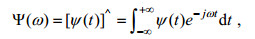 (5)
(5)当满足
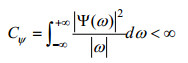 (6)
(6)时, ψ(t)就是所谓的小波基, 它具有振荡性和迅速衰减性。将小波基ψ(t)拉伸或是平移之后得到一个小波序列ψa, b(t),
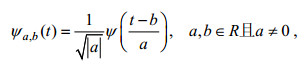 (7)
(7)其中, a为伸缩因子, b为平移因子。对于任意的函数f(t)∈L2(R), 它的连续傅里叶变换为
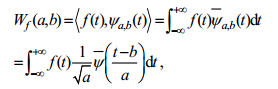 (8)
(8)其中, 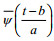
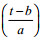
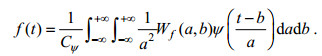 (9)
(9)1986年Mallat和Meyer总结了前人的工作之后, 提出了多分辨率分析(Multi-resolution Analysis, MRA)的概念, 1989年Mallat提出了能够快速进行信号的多分辨率分解与重构的Mallat算法(Mallat, 1989)。将信号f(t)进行多分辨率小波分解(Wavelet Decompo s I t I o n, WD), 假设Aj和Dj分别是其在第j层的近似与细节项, 那么
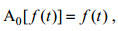 (10)
(10)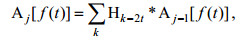 (11)
(11)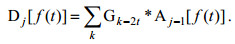 (12)
(12)Mallat重构算法为
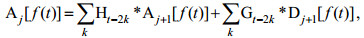 (13)
(13)其中, t=1, 2, 3, …, N(t∈Z), j=1, 2, 3, …, J(j∈Z),J=log2N, H和G是用于分解的一对正交镜像滤波器, H是低通滤波器, G是高通滤波器。由此, 一个时间信号S通过N层小波分解的结果可以表示为
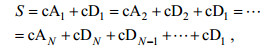 (14)
(14)其中, cAN为信号S的低频近似, 代表了数据在这段时间上的变化趋势, 而cDN, cDN-1, cD1为信号S的高频细节, 它们代表了数据在各个时间尺度上的脉动项。
因此, 应用WD时需要解决两个问题。一是要确定适当的分解层数, 由于EMD分解是完全基于数据自动停止的, 考虑到EMD对数据的分解能力, 我们将EMD分解得到的模态数作为小波分解的层数。二是要选择合适的小波基, 选用不同小波基进行小波分解得到的结果有时会有较大的差异。
MATLAB离散小波分解函数提供了多种小波基, 包括6族共45种。为了选取适合本次研究的小波基, 我们先随机选取了一段风速数据进行EMD分解, 代入所有现有小波基进行小波分解, 之后计算分解出的各层细节项数据与对应的模态数据之间的相关性, 我们认为两者之间的相关性越强, 其对应的小波基就越适合。表 1为基于各小波族中选出的最佳小波基分解得到的各层细节项与对应的模态数据之间的相关系数, 其中db10为Daubechies小波族中第10小波基, coif4为Coiflets小波族中第4小波基, sym9为Symlets小波族中第9小波基, dmey为Discrete Meyer小波基, bior11为Biorthogonal小波族中第11小波基, rbio7为Reverse Biorthogonal小波族中第7小波基。
| 层数 | db10 | coif4 | sym9 | dmey | bior11 | rbio7 |
| No.1 | 0.76 | 0.76 | 0.76 | 0.77 | 0.75 | 0.75 |
| No.2 | 0.58 | 0.57 | 0.57 | 0.59 | 0.54 | 0.54 |
| No.3 | 0.60 | 0.60 | 0.60 | 0.64 | 0.57 | 0.57 |
| No.4 | 0.61 | 0.62 | 0.61 | 0.64 | 0.59 | 0.58 |
| No.5 | 0.62 | 0.59 | 0.59 | 0.62 | 0.54 | 0.59 |
| No.6 | 0.59 | 0.56 | 0.57 | 0.62 | 0.53 | 0.55 |
| No.7 | 0.53 | 0.52 | 0.52 | 0.54 | 0.48 | 0.51 |
| No.8 | 0.48 | 0.45 | 0.47 | 0.46 | 0.46 | 0.44 |
| No.9 | 0.57 | 0.52 | 0.57 | 0.55 | 0.51 | 0.51 |
| No.10 | 0.69 | 0.61 | 0.69 | 0.66 | 0.61 | 0.60 |
| No.11 | 0.53 | 0.54 | 0.55 | 0.54 | 0.42 | 0.56 |
| No.12 | 0.55 | 0.46 | 0.57 | 0.49 | 0.40 | 0.47 |
| No.13 | 0.26 | 0.33 | 0.33 | 0.34 | 0.18 | 0.34 |
从表 1中我们可以看出, 基于dmey小波基分解得到的前8层的相关系数最高, 结合图 3可以看出, 应用dmey小波基分解出的各层数据与各模态数据之间的相关性变化波动也较小, 在总体上也表现出不错的相关性, 综合考虑, 我们认为dmey小波基最适合于本次研究, 本文之后所讨论的小波分解结果, 都是基于dmey小波基得到的。同时, 从图 3中还可以发现, EMD分解与WD分解得到的相对应的结果在前12层都有0.5以上的相关性, 且两者之间的相关性由随着分解层数的增加而减弱。
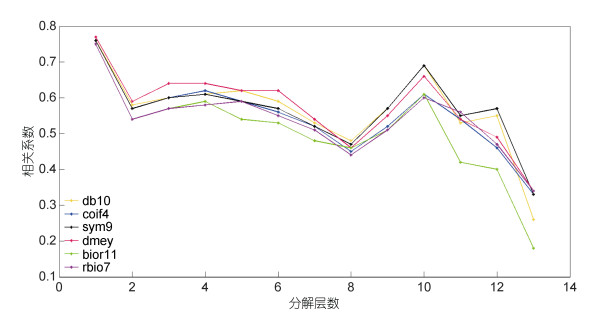 |
| 图 3 基于不同小波基得到的分解结果与EMD分解得到的各模态之间的相关系数 Fig. 3 The correlation coefficients between decomposition results obtained by WD under different wavelets and the modes obtained by EMD |
如图 4a为风速数据经过EMD分解得到的各个模态, 图 4b则为风速数据经过WD分解得到的各层细节数据。如图所示, 随着模态数和层数的增加, 数据线逐渐平滑, 波长逐渐加长, 这说明它们的特征时间尺度在逐渐变大。
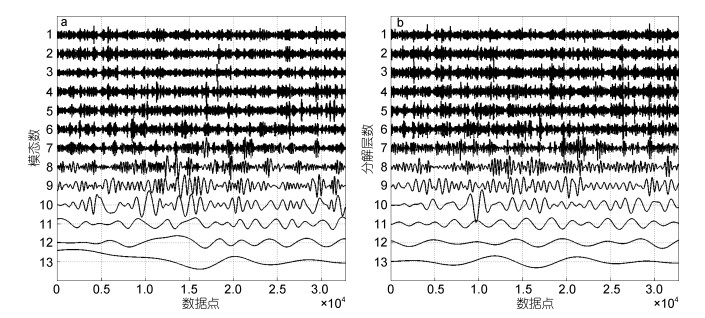 |
| 图 4 分别应用EMD(a)和WD(b)得到的结果 Fig. 4 The results obtained by EMD (a) and WD (b) |
利用HT方法计算各个模态以及各层细节数据的时间尺度(如图 5所示), EMD分解出的各模态的时间尺度分别为0.31、0.60、1.10、1.89、3.59、6.67、13.39、24.24、52.77、109.50、207.20、441.30、1376.20s。WD分解出的各层细节项的的时间尺度分别为0.29、0.57、1.12、2.24、4.44、8.75、17.71、35.71、70.91、138.90、246.36、466.91、931.34s。可以看出两者之间的误差有增加的趋势, 而在前12个模态(对EMD分解结果而言)或者是前12层(对于WD分解的结果而言), 两种方法分解出的信号的时间尺度相差在40s以内, 两者的结果是极相近的。
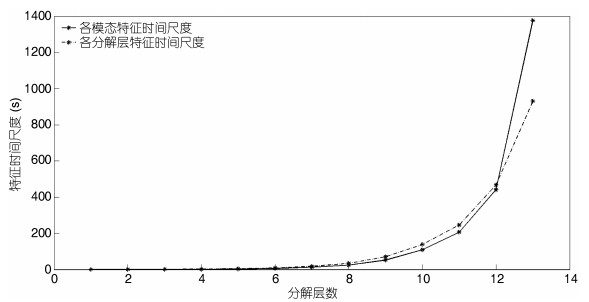 |
| 图 5 分别由EMD(实线)和WD(虚线)得到的各分量的特征时间尺度 Fig. 5 The time scale of the components obtained by EMD (solid line) and WD (dotted line) |
Sun等(1996)在涡相关法海气通量计算中定义了两个时间尺度——截断时间尺度和平均时间尺度, 基于一段时间长度为η的数据φ应用涡相关法计算海气通量F的过程如下:
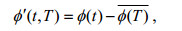 (15)
(15)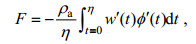 (16)
(16)其中, 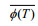
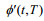
平均时间尺度取值过短, 则无法满足数据的各态历经性, 取值过长则无法保证数据的平稳性, 参考黄艳松等(2011)和Wang等(2013)中数据的分段, 我们将平均时间尺度选定为30分钟。而利用截断时间尺度则能划分数据中的湍与非湍, 适当的截断时间尺度取值, 能去除数据中非湍部分对通量的贡献, 从而提高通量的计算精度。
EMD分解和WD分解本质上都是将一列信号分解为一系列具有不同时间尺度的脉动分量以及它的变化趋势, 一段风速的顺风向U、垂直方向W分量经过EMD分解或是WD分解之后分别可以表示为,
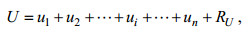 (17)
(17)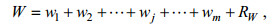 (18)
(18)其中, ui和wj分别表示EMD或WD分解出的U和W不同时间尺度的脉动分量, RU和RW则代表了U和W分解之后的趋势项, 则所有分量的动量通量贡献可以表示为一个矩阵FM,
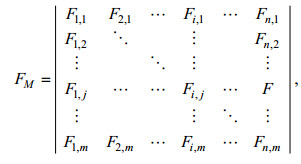 (19)
(19)其中, 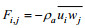
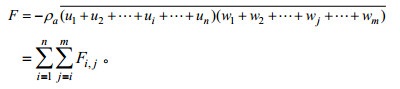 (20)
(20)如图 6a和图 6b所示, 分别是某段风速数据经过EMD分解和WD分解之后得到的通量贡献矩阵。
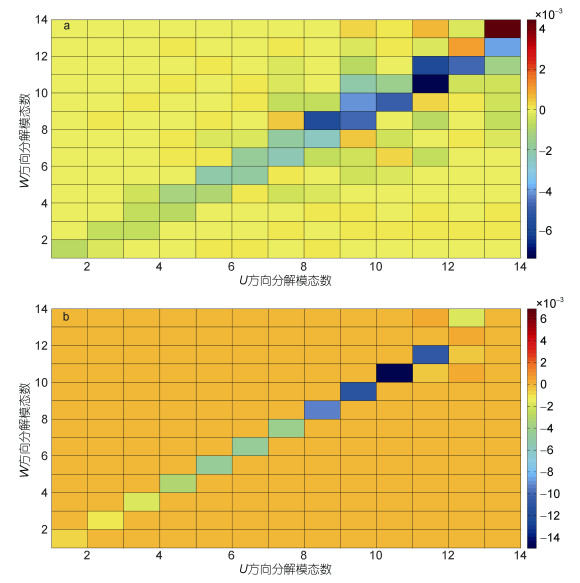 |
| 图 6 分别应用EMD(a)和WD(b)得到的通量贡献矩阵 Fig. 6 The flux contribution matrices from EMD (a) and WD (b) |
从图 6可以看出, 无论是基于EMD方法还是WD方法得到的通量贡献主要都集中在对角线位置, 其他位置的通量贡献值都很小。利用通量贡献矩阵, 参考Wang等(2013)间隙模态寻找方法, 图 6a对角线上的通量贡献量在F12, 12和F13, 13之间出现符号变换, 且F12, 12的通量贡献量在F12, 12和F13, 13之间贡献量较小, 则将第12模态作为间隙模态, 并且在图 6b中也发现了相同的现象, 则将第12层作为间隙层。
同时, 我们还可以从图 6中发现, 通量贡献在对角线位置集中的现象在WD方法得到的通量矩阵中表现的更加明显, 这说明WD分解相对于EMD分解对数据中不同时间尺度的信号分离更加彻底。而EMD方法中的贡献量不集中的现象的产生原因有两个:一是EMD分解的各模态之间有混合, 各时间尺度信号分离不彻底; 二是两个方向上的风速分量EMD分解得到的各模态的时间尺度不够一致。
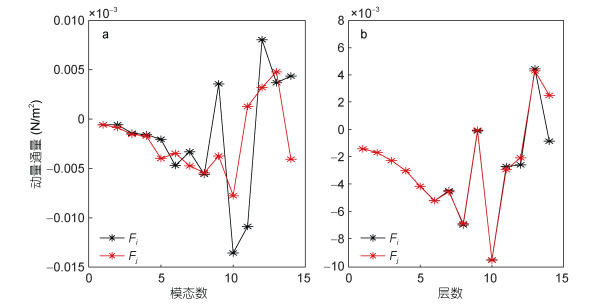
从图像中选择间隙模态不适合用于大量数据的批量处理, Martins等(2017)提出可以将通量贡献矩阵在纵向或是横向上求和, 进而将二维矩阵降维:
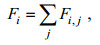 (21)
(21)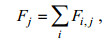 (22)
(22)其中, 式(21)表示通量矩阵在纵向上求和, 式(22)表示通量矩阵在横向上求和, 如此每个通量贡献矩阵都可以得到两条贡献曲线。
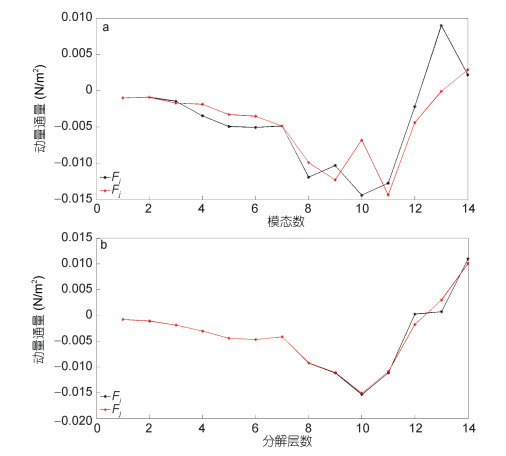
参考黄艳松等(2011)以及Wang等(2013)中的做法, 满足下面两个条件之一的模态或层我们就认为它是间隙模态或间隙层:一、通量变化曲线的跨零点(见图 7); 二、通量变化曲线上的两个极小值点之间的极大值点, 且这个极大值点的贡献量足够小(见图 8)。参考上述方法我们分别对图 6a和图 6b中的通量矩阵在纵向和横向上求和, 对应的通量贡献曲线如图 7所示。
 |
| 图 7 分别采用EMD(a)和WD(b)得到的纵、横向通量贡献曲线(情况一) Fig. 7 The curves of flux contribution in both vertical and horizontal directions from EMD (a) and WD (b), respectively (Situation 1) 注:黑线:纵向通量求和曲线, 红线:横向通量求和曲线 |
 |
| 图 8 分别采用EMD(a)和WD(b)得到的纵、横向通量贡献曲线(情况二) Fig. 8 The curves of flux contribution in both vertical and horizontal directions from EMD (b) and WD (b) (Situation 2) 注:黑线:纵向通量求和曲线, 红线:横向通量求和曲线 |
由图 7所示, 无论是基于EMD分解还是WD分解得到的贡献矩阵, 其纵向求和曲线和横向求和曲线都十分近似, 而WD分解得到的贡献矩阵的纵、横向求和曲线在前11层基本重合, 这说明了不同方向上的风速数据经过WD分解出的各层数据的时间尺度一致性更高。根据间隙模态或是间隙层数的判断规则一, 在第12和第13模态/层之间出现跨零点, 且第12模态/层的动量贡献较小, 则第12模态/层便是我们要找的间隙模态/层。
图 8为满足间隙模态/层的第二个判定规则的情况。对于图 8a, 在第8模态和第10模态两个通量贡献极小值中间, 第9模态为贡献量极大值, 则第9模态为间隙模态, 而对于图 8b, 在第8和第10层两个通量贡献极小值之间, 第9层为通量贡献量很小的极大值点, 则第9层即为间隙层。
一旦找出间隙模态或是间隙层, 应用HT变换计算该间隙模态或是间隙层的时间尺度, 间隙模态或是间隙层的时间尺度就是这段时间的CTS。对应式(21)和式(22)这段数据的通量Fg可表示为
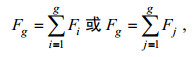 (23)
(23)其中, g表示间隙模态数或是间隙层数。
3 结果与分析 3.1 基于不同方法得到的截断时间尺度的对比将全部数据分段, 每段时间长度为半小时, 总共得到1779个数据段。将每段数据分别用EMD、WD分解之后, 计算每段数据的通量贡献矩阵, 再将矩阵在纵向和横向求和, 则每个通量贡献矩阵得出两条通量贡献曲线, 根据曲线找出每段数据对应的间隙模态和间隙层, 最终得出适合这段数据的截断时间尺度。另外, 我们发现对于少数数据段不能找出截断时间尺度, 这是因为这些数据段中混入了一些涡旋, 而这些涡旋的时间尺度和这段数据的截断时间尺度十分接近, 于是这些涡旋的能量就恰好填充于间隙模态或是间隙层上(Mahrt et al, 2001), 能够得出截断时间尺度的数据段共有1430段, 占全部数据的80.4%。
为了方便描述, 将EMD通量矩阵纵向求和曲线得到的间隙模态称为EGNi, 横向求和曲线得到的间隙模态称为EGNj, 类似的将基于WD方法得到的间隙层数分别称为WGNi和WGNj, 如图 9所示。
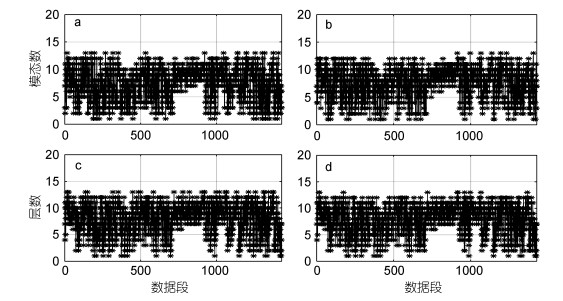 |
| 图 9 间隙模态数和间隙层数变化曲线 Fig. 9 Curves of gap mode number and gap layer number 注: a: EGNi变化曲线, b: EGNj变化曲线, c: WGNi变化曲线, d: WGNj变化曲线 |
表 2为四条曲线相互间的相关系数, 同一贡献矩阵的两个方向上的间隙模态数或是间隙层数曲线具有极高的相关性。总体上, 不同方法获得的曲线之间的相关系数在0.63以上, 也具有较高的相关性, 基于不同的方法对数据进行分析, 却得出相近的结果, 两种结果互为对照, 相互说明了计算的正确性。
| EGNi | EGNj | WGNi | WGNj | |
| EGNi | 1 | 0.63 | 0.68 | 0.66 |
| EGNj | 0.63 | 1 | 0.67 | 0.66 |
| WGNi | 0.68 | 0.67 | 1 | 0.94 |
| WGNj | 0.66 | 0.66 | 0.94 | 1 |
同样为了方便描述, 分别将根据EGNi、EGNj、WGNi、WGNj计算出的截断时间尺度称为ETSi、ETSj、WTSi、WTSj, 截断时间曲线如图 10所示。
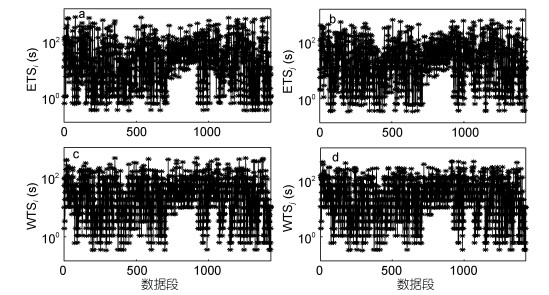 |
| 图 10 不同方法计算出的截断时间尺度 Fig. 10 The cut-off time scale calculated by different methods 注: a: ETSi变化曲线, b: ETSj变化曲线, c: WTSi变化曲线, d: WTSj变化曲线 |
相比于间隙模态和间隙层之间的差异, 不同方法算出的截断时间之间的差异更大, 但是在总体趋势上依旧十分接近。图 11为截断时间尺度的分布概率图, 如图 11所示有约80%的CTS小于200秒。
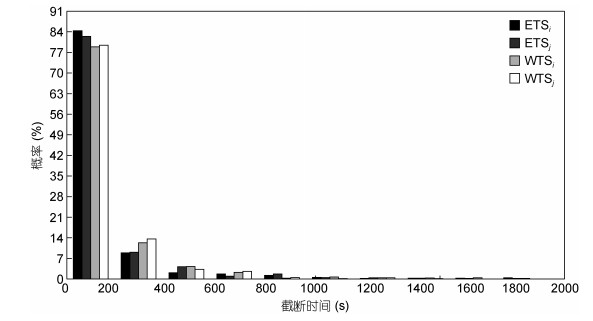 |
| 图 11 CTS的概率分布 Fig. 11 The probability distribution of CTS 注:黑柱: ETSi的概率分布, 灰柱: ETSj的概率分布, 淡灰柱: WTSi的概率分布, 白柱: WTSj的概率分布 |
200秒以下的CTS的概率分布如图 12所示, 其中ETSi、ETSj、WTSi、WTSj的均值分别为39.4秒、43.9秒、47.1秒、47.7秒, EMD方法得到的CTS均值为41.7秒, WD方法得到的CTS均值为47.4秒。
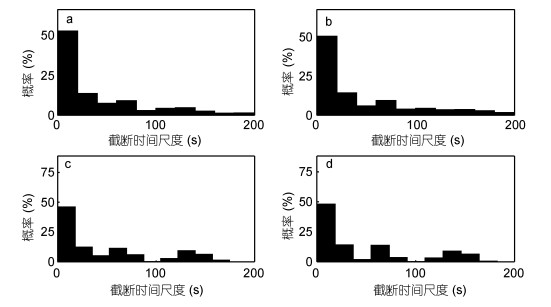 |
| 图 12 200秒以下的CTS分布 Fig. 12 The distribution of CTS below 200 seconds 注: a: ETSi的分布, b: ETSj的分布, c: WTSi的分布, d: WTSj的分布 |
采用EMD和WD计算出的CTS值在2000秒以下均有分布, 去除前20%的大值之后, 均值都在40秒左右, 这个结果远远小于早期学者提出的30至60分钟, 证实了Aubinet(2008)和Edson等(2013)提出的海气通量涡相关法计算时截断时间应该小于15分钟的观点。此外, 传统方法对不同的数据段都采用相同的CTS, 而采用EMD和WD分解后, 得到的CTS是变化的, 每段数据会因为其不同的湍流特性(如:风速数据的标准差和均方根等湍流特征量)而被赋予适合自身的CTS, 根据本文中的方法估算出的截断时间尺度, 有个别数据段会得到比较大的截断时间尺度(接近10分钟), 但是绝大部分数据段得到的截断时间尺度都远小于传统的截断时间尺度取值, 均值略大于Martins等(2017)的研究结果。
我们将应用EMD方法和WD方法计算出的通量和传统的以10分钟作为CTS的通量结果进行比较, 将去除了非湍部分的通量称为湍通量, 传统方法得到的通量称为总通量, 如图 13所示。
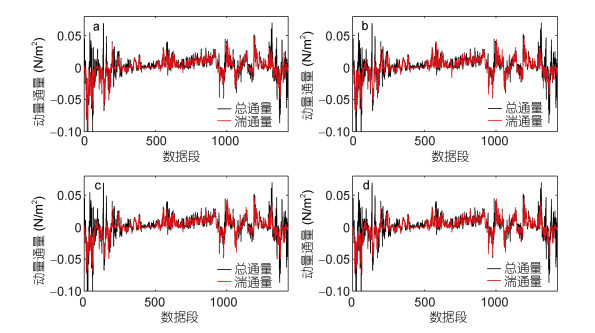 |
| 图 13 新方法和传统方法得到的通量比较 Fig. 13 Comparison of flux obtained by the new method and the traditional method. Figures a, b, c and d are the turbulence flux obtained based on ETSi, ETSj, WTSi and WTSj and the total flux obtained by traditional method, respcetively 注:图a、b、c、d分别为基于ETSi、ETSj、WTSi、WTSj得到的湍通量和传统方法得到的总通量。黑线:传统方法得到的总通量, 红线:新方法得到的湍通量 |
图 13可以看出, EMD和WD方法的运用对通量计算精度的提高主要体现在两个方面: (1)去除了数据非湍部分的通量贡献。这是因为采用了截断时间尺度之后, 将总通量中非湍部分滤去, 造成通量绝对值减小; (2)通量传输方向更加合理。注意到图 13中有些数据段上总通量和湍通量的符号相反, 这是因为采用了EMD分解或是WD分解之后, 将原始数据中的趋势项去除, 只留下了数据的脉动项, 修正了趋势项对通量传输方向的影响。
将采用EMD方法和WD方法之后得到的湍通量和传统方法得到的总通量之间的偏差之比记为γ, 即
 (24)
(24)其中, FTotal为总通量, FTur为湍通量。
图 13中总通量和湍通量之间的偏差比如图 14所示, 图 14a到14b的比率均值分别为47.24%、45.44%、45.61%、45.92%, 四个偏差比均在45%左右, 可见非湍部分对通量的贡献极大, 而采用EMD和WD方法能够有效的去除非湍部分的通量贡献, 提高通量计算精度。
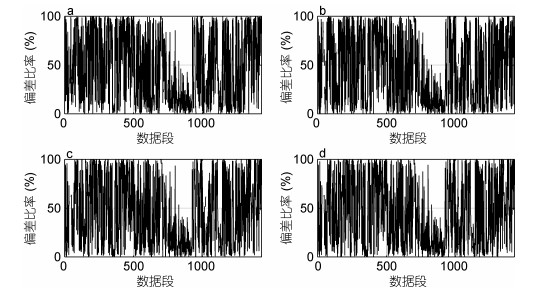 |
| 图 14 不同方法得到的湍通量和总通量的偏差比 Fig. 14 The deviation ratio between the total flux and turbulence flux calculated by different methods |
本文研究了海气通量涡相关法计算中截断时间尺度这一关键性问题, 分别将经验模态分解(EMD)和小波分解(WD)这两种目前十分流行的信号处理方法和涡相关法进行了融合, 基于海上实测数据估算了截断时间尺度, 分析了EMD方法和WD方法之间的优缺点, 对比分析了新方法和传统方法得到的通量结果。主要结论如下:
(1) EMD分解相对于WD分解在操作上有一定的优势。WD分解在开始之前需要设定分解层数和小波基, 如果对数据理解不够, 可能会造成分解层数设置不够和小波基选择不当, 而EMD分解则没有类似小波基选择这样的问题, 且分解层数根据数据自身而定, 相对WD分解EMD分解有更高的自主性。而在EMD和WD对信号的分解能力上面, 依据各自得到的通量矩阵, 发现EMD分解对时间序列信号的分离程度不及WD分解;
(2) 采用EMD和WD分解都能有效的得到通量矩阵, 获得数据的间隙模态或是间隙层数, 最终得到截断时间尺度, 相比较而言, EMD方法估算的截断时间尺度略小于WD方法估算到的结果;
(3) 本文采用EMD方法和WD方法对1700多段数据进行了处理分析, 最终得到的绝大部分数据对应的CTS在40秒左右, 这一结果远远小于传统的截断时间尺度, 并且传统涡相关法使用的截断时间尺度长度是固定的, 而采用了EMD和WD之后, 对于每段数据截断时间都是变化的, 具有更高的灵活度;
(4) 新方法计算出的通量值明显减小, 能有效去除数据非湍部分以及趋势项带来的误差。
本研究计算的全部是动量通量, 一是由于数据的原因, 二是相比于其他气象数据, 风速的变化更加剧烈, 用风速数据进行分解处理更具有代表性, 但是本文提出的通量计算方法对于其他通量的计算都是有效的。而究竟是什么截断时间尺度内在的影响因素, 接下来我们将对它展开研究。
| 邹仲水, 赵栋梁, 黄健, 等, 2014. 海-气界面动量通量的估计方法分析与应用. 海洋学报, 36(9): 75–83 DOI:10.3969/j.issn.0253-4193.2014.09.009 |
| 宋朝阳, 赵栋梁, 张宇铭, 2013. 气体交换速率和时间平均尺度对海-气碳通量估计的影响. 海洋学报, 35(4): 72–79 DOI:10.3969/j.issn.0253-4193.2013.04.009 |
| 黄艳松, 宋金宝, 范聪慧, 2011. 海气通量涡相关法计算中的时间尺度分析. 海洋科学, 35(11): 114–119 |
| Aubinet M., 2008. Eddy covariance CO2 flux measurements in nocturnal conditions:an analysis of the problem. Ecological Applications, 18(6): 1368–1378 DOI:10.1890/06-1336.1 |
| Ban J M, Gao Z Q, Lenschow D H., 2010. Climate simulations with a new air-sea turbulent flux parameterization in the national center for atmospheric research community atmosphere model (CAM3). Journal of Geophysical Research:Atmospheres, 115(D1): D01106 |
| Donelan M, Caniaux G., 2001. Surface heat budget in an oceanic simulation using data from tropical ocean-global atmosphere coupled ocean-atmosphere response experiment. Journal of Geophysical Research:Oceans, 106(C8): 16623–16640 DOI:10.1029/2000JC000224 |
| Edson J B, Jampana V, Weller R A, et al, 2013. On the exchange of momentum over the open ocean. Journal of Physical Oceanography, 43(8): 1589–1610 DOI:10.1175/JPO-D-12-0173.1 |
| Fairall C W, Bradley E F, Hare J E, et al, 2003. Bulk param-eterization of air-sea fluxes:updates and verification for the COARE algorithm. Journal of Climate, 16(4): 571–591 DOI:10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2 |
| Finnigan J J, Clement R, Malhi Y, et al, 2003. A Re-evaluation of long-term flux measurement techniques part Ⅰ:averaging and coordinate rotation. Boundary-Layer Meteorology, 107(1): 1–48 DOI:10.1023/A:1021554900225 |
| Huang N E, Shen Z, Long S R, et al, 1998. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A, 454(1971): 903–995 DOI:10.1098/rspa.1998.0193 |
| Kaimal J C, Finnigan J J., 1994. Atmospheric Boundary Layer Flows:Their Structure and Measurement. Oxford: Oxford University Press, United Kingdom, 289 |
| Li Y B, Gao Z Q, Lenschow D H, et al, 2010. An improved approach for parameterizing surface-layer turbulent transfer coefficients in numerical models. Boundary-Layer Meteoro-logy, 137(1): 153–165 DOI:10.1007/s10546-010-9523-y |
| Liang B C, Lee D Y, Li H J, et al, 2010. Sensitivity study of the effects of wave-induced vertical mixing on vertical exchange processes. Journal of Hydrodynamics, Ser. B, 22(3): 410–418 DOI:10.1016/S1001-6058(09)60072-X |
| Liu B, Guan C L, Xie L A, et al, 2012. An investigation of the effects of wave state and sea spray on an idealized typhoon using an air-sea coupled modeling system. Advances in Atmospheric Sciences, 29(2): 391–406 DOI:10.1007/s00376-011-1059-7 |
| Mahrt L, Moore E, Vickers D, et al, 2001. Dependence of turbulent and mesoscale velocity variances on scale and stability. Journal of Applied Meteorology, 40(3): 628–641 DOI:10.1175/1520-0450(2001)040<0628:DOTAMV>2.0.CO;2 |
| Mallat S G., 1989. A theory for multiresolution signal decomposi-tion:the wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7): 674–693 DOI:10.1109/34.192463 |
| Martins L G N, Miller S D, Acevedo O C., 2017. Using empirical mode decomposition to filter out non-turbulent contributions to air-sea fluxes. Boundary-Layer Meteorology, 163(1): 123–141 DOI:10.1007/s10546-016-0215-0 |
| Panofsky H A, Dutton J A., 1984. Atmospheric Turbulence.Models and Methods for Engineering Applications. New Jersey: Upper Saddle River, 71 |
| Sakai R K, Fitzjarrald D R, Moore K E., 2001. Importance of low-frequency contributions to eddy fluxes observed over rough surfaces. Journal of Applied Meteorology, 40(12): 2178–2192 DOI:10.1175/1520-0450(2001)040<2178:IOLFCT>2.0.CO;2 |
| Sun J L, Howell J F, Esbensen S K, et al, 1996. Scale dependence of air-sea fluxes over the western Equatorial Pacific. Journal of Atmospheric Sciences, 53(21): 2997–3012 DOI:10.1175/1520-0469(1996)053<2997:SDOASF>2.0.CO;2 |
| Vickers D, Mahrt L., 2003. The cospectral gap and turbulent flux calculations. Journal of Atmospheric and Oceanic Technology, 20(5): 660–672 DOI:10.1175/1520-0426(2003)20<660:TCGATF>2.0.CO;2 |
| Wang J J, Song J B, Huang Y S, et al, 2013. Application of the hilbert-huang transform to the estimation of air-sea turbulent fluxes. Boundary-Layer Meteorology, 147(3): 553–568 DOI:10.1007/s10546-012-9784-8 |
| Yu L, Weller R A., 2010. Objectively analyzed air-sea heat fluxes for the global ice-free oceans (1981-2005). Bulletin of the American Meteorological Society, 88(4): 527–539 |
| Zedler S E, Kanschat G, Korty R, et al, 2012. A new approach for the determination of the drag coefficient from the upper ocean response to a tropical cyclone:a feasibility study. Journal of Oceanography, 68(2): 227–241 DOI:10.1007/s10872-011-0092-6 |
| Zeng Z H, Wang Y Q, Duan Y H, et al, 2010. On sea surface roughness parameterization and its effect on tropical cyclone structure and intensity. Advances in Atmospheric Sciences, 27(2): 337–355 DOI:10.1007/s00376-009-8209-1 |
 2018, Vol. 49
2018, Vol. 49


