
中国海洋湖沼学会主办。
文章信息
- 彭浩, 陈杰, 蒋昌波, 何飞, 邓斌, 屈科, 隆院男, 伍志元. 2018.
- PENG Hao, CHEN Jie, JIANG Chang-Bo, HE Fei, DENG Bin, QU Ke, LONG Yuan-Nan, WU Zhi-Yuan. 2018.
- 刚性植物分布方式对海啸波消减影响实验研究
- EXPERIMENTAL INVESTIGATION ON TSUNAMI WAVE ATTENUATION UNDER THE EFFECT OF RIGID VEGETATION DISTRIBUTION
- 海洋与湖沼, 49(6): 1159-1168
- Oceanologia et Limnologia Sinica, 49(6): 1159-1168.
- http://dx.doi.org/10.11693/hyhz20171200303
-
文章历史
- 收稿日期:2017-12-01
- 收修改稿日期:2018-05-01
2. 洞庭湖水环境治理与生态修复湖南省重点实验室 长沙 410114;
3. 水沙科学与水灾害防治湖南省重点实验室 长沙 410114;
4. 湖南省环境保护河湖污染控制工程技术中心 长沙 410114
2. Key Laboratory of Dongting Lake Aquatic Eco-Environmental Control and Restoration of Hunan Province, Changsha 410114, China;
3. Key Laboratory of Water Sediment Sciences and Water Disaster Prevention of Hunan Province, Changsha 410114, China;
4. Engineering and Technical Center of Hunan Provincial Environmental Protection for River-Lake Dredging Pollution Control, Changsha 410114, China
海啸是一种极具破坏性的海洋灾害, 是沿海国家最严重的自然灾害之一, 如何有效减小海啸灾害一直是海岸工程研究的热点(陈杰等, 2013)。大量研究表明, 以红树林为代表的生物海岸植被能显著消减海啸波波能, 降低沿岸地区由海啸灾害所带来的生命财产损失(姚宇等, 2015; 陈杰等, 2016; 何飞等, 2017a, 2018a)。
大量现场观测表明, 海啸波的首波与孤立波非常接近, 因此目前学术界多采用孤立波来近似模拟海啸波(姚宇等, 2015)。近年来, 关于近岸植被对孤立波消减影响研究主要从以下两个方面展开: (1)水动力因素对植物消减孤立波的影响(Giri et al, 2008; 姚宇等, 2015); (2)植物因素对孤立波消减特性的影响。其中, 何飞等(2017a, 2018b)通过物理模型实验分别探讨了植物根、茎、叶对孤立波消减特性及沿程波高衰减特性的影响; Huang等(2011)通过实验和数值模拟探究了植物分布密度对植物消波的影响, 研究发现植物分布密度越大, 孤立波反射系数越大, 而透射系数越小; Irtem等(2009)、Irish等(2014)、Yao等(2015)分别通过物理模型实验研究了不同植物分布密度下孤立波的斜坡爬高值变化情况, 研究结果表明, 孤立波在斜坡的爬高值随植物分布密度的增大而减小。此外, Thuy等(2009)和Iimura等(2012)还探究了植物分布方式对孤立波斜坡爬高的影响。现阶段关于植物分布排列方式对其消波特性影响的研究较为少见。
因此, 本文拟在前人的研究基础上, 设计物理模型实验, 探究刚性植物分布方式对海啸波消减特性的影响。
1 理论分析 1.1 植物排列结构定义现阶段学者研究中大多数采用矩形分布(姚宇等, 2015; 陈杰等, 2016)、交错分布(Hu et al, 2014; 姚宇等, 2015; 陈杰等, 2016)和随机分布(Pujol et al, 2012)三类植物分布方式。Nepf(1999)提出了交错分布植物带的排列结构定义式:
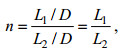 (1)
(1)式中: n为植物排列结构参数, L1为植物间纵向间距, L2为植物间横向间距, D为植物直径。图 1为Suzuki (2011)提出的交错排列植物带结构示意图。
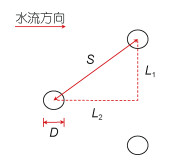 |
| 图 1 植物排列结构 Fig. 1 Vegetation arrangement structure |
图 2为植物尾涡区消浪示意图。图中展示了由于植物存在产生的紊流区和尾涡区, 以及植物排列结构导致的尾涡遮蔽区和尾涡重叠区。当相邻植物间横向间距小于紊流区和尾涡区长度之和或植物尾涡区发生纵向重叠时, 将形成遮蔽效应和重叠效应, 减弱植物的消浪能力(Raupach, 1992)。
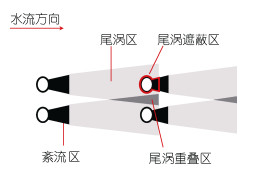 |
| 图 2 植物尾涡区消浪 Fig. 2 Wave attenuation in the tail vortex area of vegetation |
近岸植物的消波作用能有效消减孤立波波能, 而近岸植物对孤立波的影响可以用拖曳力或拖曳力系数来表征。
Tanino等(2008)提出了恒定流条件下非淹没植被拖曳力系数的表达式:
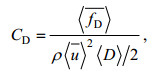 (2)
(2)式中: CD为拖曳力系数, 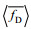
Ergun(1952)提出了关于植被平均拖曳力的表达式:
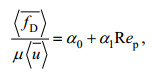 (3)
(3)式中: μ为流体的动力黏滞系数, α0为植物固体体积分数φ的函数, α1为常数, Rep=〈 u〉〈 d〉/μ为基于植被区内孔隙流速〈 u〉的雷诺数。
参考Huang等(2011)和姚宇等(2015), 采用植物固体体积分数φ来估算植物分布密度:
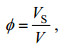 (4)
(4)式中: V为控制体体积, VS为控制体内植被固体所占体积。
将(3)式代入(2)可得出拖曳力系数CD的经验表达式(Tanino et al, 2008):
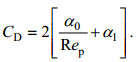 (5)
(5)Tanino等(2008)根据实验数据, 得到α0、α1的表达式:
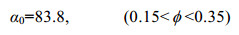 (6)
(6)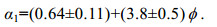 (7)
(7)对于孤立波, 由于惯性力可忽略不计, 恒定流作用下求得的植物拖曳力系数经验表达式可以直接用于孤立波的情况(姚宇等, 2015)。
为便于分析, 定义植物淹没度α:
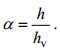 (8)
(8)式中: h为水深; hv为植物高度。同时定义H0为S2浪高仪所测波高, Hi为x轴正向各浪高仪所测波高, 波高参数Hi/H0表征孤立波的沿程波高变化。
本文拟在前人的研究基础上, 开展刚性植物分布方式对海啸波消减影响实验研究。参照式(1)对实验中矩形分布和交错分布植物模型的排列结构进行定义, 讨论分布方式对植物消减海啸波的影响, 并得到矩形分布植物带透射系数与水动力因素和植物因素之间的关系式。同时, 利用式(5)进行植物拖曳力系数计算与分析。
2 实验概述实验在长沙理工大学长40.0m, 宽0.5m, 高0.8m的波浪水槽内进行。水槽前端的液压伺服式不规则波造波机生产实验所需的孤立波, 其主控系统是大连理工大学研发的Wave Make系统。实验布置如图 3所示。
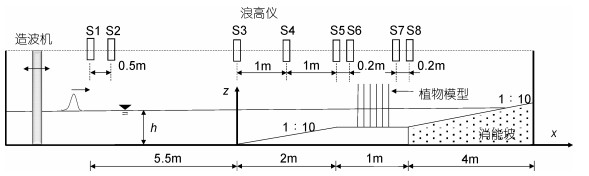 |
| 图 3 实验布置 Fig. 3 The setup of the experimental flume |
在陈杰(2016, 2017a, 2017b, 2018)、何飞(2017a, 2017b, 2018a)等研究基础上, 参考Augustin等(2009)、Sánchez-González等(2011)、Hu等(2014)实验地形布置, 同时考虑实验设备条件的限制, 开展设计实验。实验比尺为1︰20。如图 3所示, 以植物模型前的斜坡坡底为坐标起点, x=0—2.0m为1︰10的斜坡, x=2.0—3.0m为平台, x=3.0—7.0m为1︰10的消能坡。采用PVC圆管概化模拟红树林, 其弹性模量E为2.90—3.92Gpa, 与波浪相互作用时无明显变形现象。PVC圆管高hv=45cm, 直径D=1.1cm, 模拟20—50年树龄直径为20—25cm的红树林。
根据目前学者研究中主要采用的矩形分布(姚宇等, 2015; 陈杰等, 2016)、交错分布(Hu et al, 2014; 姚宇等, 2015; 陈杰等, 2016)和随机分布(Pujol et al, 2012)三类植物分布方式, 并参考前述理论分析内容, 拟设计矩形分布、交错分布和组合分布三类红树林分布方案, 探讨分布排列方式对刚性植物消波特性的影响。本文交错分布排列结构采用植物间距S定义, 矩形分布排列结构采用式(1)中参数n定义。植物排列结构如图 4所示(图 4a为矩形分布, 图 4b为交错分布)。
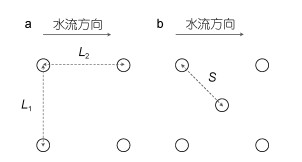 |
| 图 4 红树林模型结构 Fig. 4 Sketch of mangrove model |
如图 5所示, 实验一共设计6种红树林分布方案, 其中模型M1、M2、M3、M4为矩形分布, 模型M5为交错分布, 模型M6为组合分布, 即矩形分布和交错分布的叠加组合分布。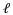
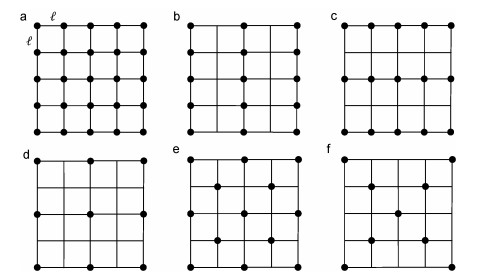 |
| 图 5 红树林模型分布方式 Fig. 5 Mangrove distribution mode 注:图a, b, c…f分别代表模型M1, M2, M3…M6 |
| 植物模型 | 植物分布方式/类型 | 实验水深h(cm) | 入射波波高H(cm) | 植物固体体积分数φ | 模型结构参数n/S |
| M1 | 正方形分布(类型一) | 25.0 30.0 35.0 |
4.0/5.0/6.0/7.0 | 0.331 | 1.0 |
| M2 | 长方形分布(类型一) | 25.0 30.0 35.0 |
0.174 | 2.0 | |
| M3 | 长方形分布(类型一) | 25.0 30.0 35.0 |
0.166 | 0.5 | |
| M4 | 正方形分布(类型一) | 25.0v 30.0 35.0 |
0.087 | 1.0 | |
| M5 | 交错分布(类型二) | 25.0 30.0 35.0 |
0.166 | 1.4 | |
| M6 | 组合分布(类型三) | 25.0 30.0 35.0 |
0.122 | — |
实验首先放置植物模型, 随后对造波机进行预热, 保证造波机性能稳定, 再开启数据采集系统。调整水槽中水位至实验水深, 待水面平静后开始造波, 并测量波高数据。波高测量采用加拿大WG-50型浪高仪。浪高仪最小测量周期为1.5μs, 误差为0.4%, 采样频率为50Hz。为减小波形变化对数据采集的影响, 安排实验组次从小波高到大波高。为避免余浪对入射波的叠加影响, 每完成一个组次实验后需等待水面平静后再进行下一次造波。数据采集时间要经历从造波机开始造波到波浪传播经过植物模型直至水面平静的整个过程, 重复上述步骤直至完成所有实验组次。
3 结果分析 3.1 波形沿程变化图 6给出了模型M1在实验工况h=35.0cm, H0=5.0cm时沿波浪传播方向6个测点(S3—S8)所记录的自由液面时间序列。结果显示, S3和S4记录的自由液面时间序列存在两个明显的峰值:第一个是入射波波峰, 第二个是由于植物模型的存在造成的反射波波峰。当孤立波经过植物模型前S5和S6浪高仪所在位置时, 无明显反射波存在, 且波浪出现壅高现象, 这是由于入射波和反射波发生了叠加, 孤立波峰值增大。孤立波经过植物模型后, 透射波继续以孤立波的形式向前传播, 但波形由尖陡变为平缓, 这是因为波浪与植物模型相互作用时部分波能被植物模型所消减。
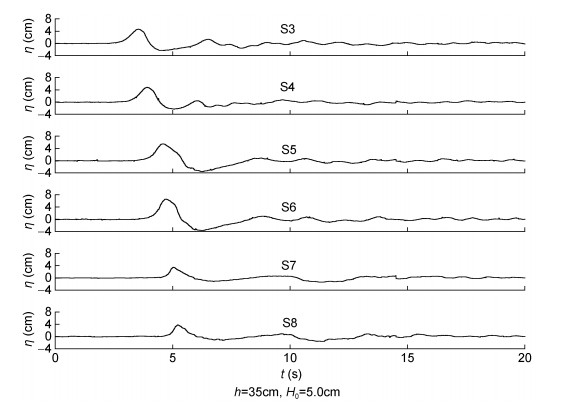 |
| 图 6 模型M1波面历时图 Fig. 6 Surface elevations at different locations for vegetation model M1 |
图 7分别给出了植物模型M1(正方形分布, φ=0.331)、M3(长方形分布, φ=0.166)、M5(交错分布, φ=0.166)和M6(组合分布, φ=0.122)在植物淹没度α=0.67和0.78条件下孤立波沿程波高变化情况。结果显示, 孤立波首先在斜坡地段(0 < x < 2.0m)出现波浪爬高现象, 且爬高主要集中在斜坡后1/2段, 其中M3在H/h=0.2, α=0.67条件下斜坡后1/2段的孤立波爬高值为前1/2段的7.6倍; 当孤立波传播至平台地段(2.0 < x < 2.25m)时, 由于植物的阻挡产生了明显的波浪壅高现象, 其中M1在H/h=0.17, α=0.78条件下出现Hi/H0的最大增量0.27。在本实验地形条件下, 孤立波经过各植物模型前Hi/H0的平均增量比较: M1 > M3 > M6 > M5, 由此可见, 当φ相等时, 孤立波经过M3和M6前的波高增量均大于M5。此外, 当α相同时, 孤立波在斜坡地形的爬高值及各植物摸型前的壅高值均随H/h的增大而增大, 其中M1在α=0.67条件下, H/h=0.20时的Hi/H0增量比H/h=0.13增加了29.1%;孤立波传播至植物模型中时, 由植物引起的水体紊动会造成大量的波能衰减, 使得波高急剧减小, 在此过程中Hi/H0的平均下降值比较: M1 > M3 > M5 > M6;孤立波透过植物模型后, 波高趋于稳定。
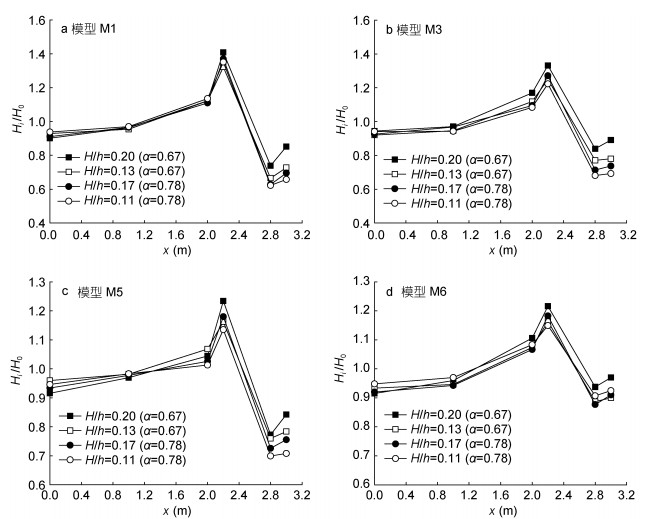 |
| 图 7 孤立波波高沿程变化 Fig. 7 Variation of solitary wave height at different locations |
综上所述, 当α相等时, 孤立波在斜坡地形的爬高值以及植物模型前的壅高值均随H/h的增大而增大; 当φ相等时, 孤立波经过矩形和组合分布植物模型前的壅高值均大于交错分布植物模型。由于M1的分布密度较大, 孤立波在M1前后的波高变化幅度最大。此外, 组合分布方式使得孤立波在植物模型前会产生较大的壅高, 且消浪效果较差。
3.3 孤立波透射系数变化 3.3.1 相对波高的影响图 8分别给出了6种植物模型在植物淹没度α=0.56、0.67、0.78, 入射波高H=4.0cm、5.0cm、6.0cm、7.0cm条件下透射系数Kt随相对波高H/h的变化情况。结果显示, 各植物模型Kt对H/h的敏感度均随H/h的增大而减小。其中, M1(图 8a)在各淹没度α条件下均表现为Kt随H/h的增大而增大, M2—M6(图 8b—f)中Kt与H/h之间的变化关系依赖于α, 具体表现为:当α=0.67和0.78时, Kt随H/h的增大而逐渐增大; 当α=0.56时, Kt随H/h的增大逐渐减小。此外, 在α=0.67和0.78条件下, 各模型Kt在H/h=0.20附近变化趋于平缓; 当α=0.56时, Kt在H/h=0.20附近趋于稳定。同时, 各模型的消浪能力在α=0.56条件下最好, 其中M1在α=0.56, H/h=0.16时达到62%的消浪效果。综上所述, H/h对Kt的影响与φ及α相关。在0.087 < φ < 0.176且α相等的条件下, 各植物模型Kt随H/h的变化趋势相同, 且Kt对H/h的敏感度随H/h的增大而逐渐减小。M1的分布密度较大, 没有出现临界水深, Kt均随H/h的增大而增大且趋于稳定。
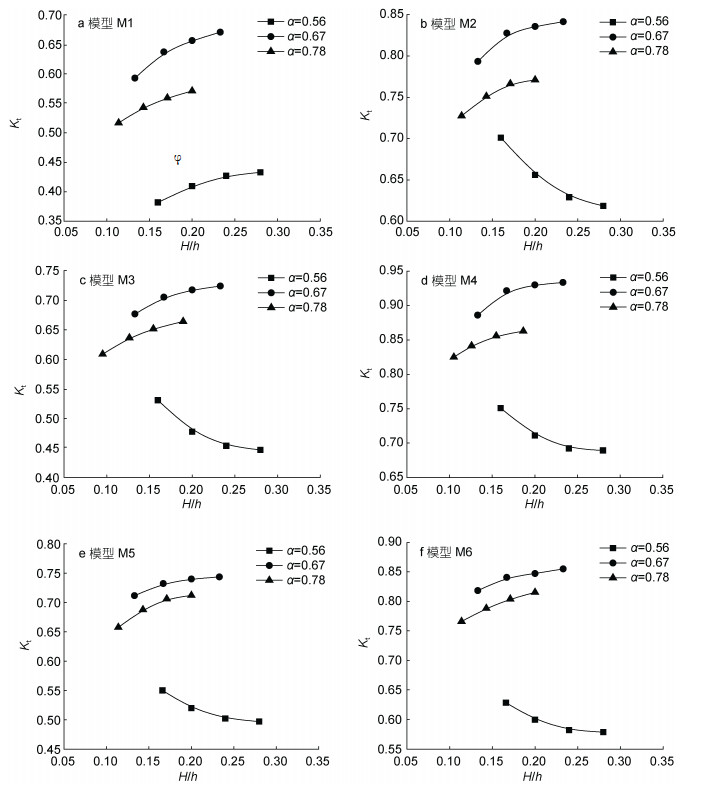 |
| 图 8 不同淹没度下孤立波透射系数随相对波高变化 Fig. 8 The transmission coefficients of solitary waves vary with relative wave heights at different submergence |
图 9a、b分别给出了植物淹没度α=0.67和α=0.78条件下6种植物模型的孤立波透射系数Kt随相对波高H/h的变化情况。本实验中各植物模型的固体体积分数φ大小比较: φM1 > φM2 > φM3=φM5 > φM6 > φM4。结果显示, 入射波要素相同时, 各植物模型Kt大小比较: M4 > M6 > M2 > M5 > M3 > M1。其中, M1的分布密度最大, 消浪效果最好, M2、M3和M5的分布密度相近, 由于分布排列方式不同导致消浪效果也存在差异。例如, M3(长方形分布)与M5(交错分布)的固体体积分数φ相等, 透射系数M5 > M3, 即M3的消浪效果更好。M4的分布密度最小, 消浪效果最差。此外, M1和M4均为正方形分布, 体积分数φM1 > φM4, 透射系数M4 > M1, 因此, 在正方形分布方式下, Kt随φ的增大而减小。综上所述, 在正方形排列方式下, Kt随φ的增大而减小, 当分布排列方式存在差异时, Kt并不是随着φ的变化而单调的变化。
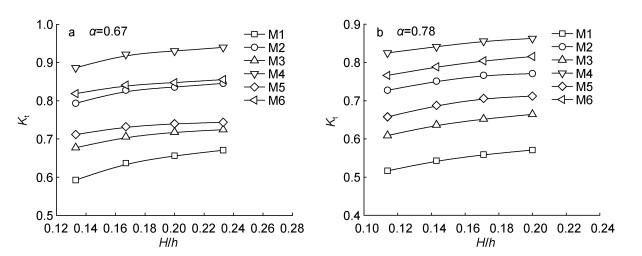 |
| 图 9 相同淹没度下孤立波透射系数随相对波高变化 Fig. 9 The variation of transmission coefficients of solitary waves with relative wave heights at a same submergence |
本实验中植物模型M2和M3的固体体积分数φ基本相等, 且均为长方形分布, 但两者的植物排列结构不同, 其中M2(L1=2 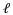
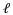
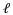
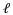
受水动力因素和植物因素的共同作用, 近岸植物影响下的波浪传播变形规律复杂。根据前人的研究(Tanaka et al, 2007; Suzuki et al, 2012; 何飞等, 2017a, 2017b), 发现近岸植物对孤立波消减特性的主要影响因素包括入射波高、水深、波长、植物带长度、植物分布密度、植物淹没度、植物分布方式等。因此近岸矩形分布植物带对孤立波的消浪效果可以用下式表示:
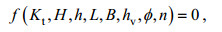 (9)
(9)式中: Kt为透射系数; H为入射波高; h为水深; L为孤立波波长; B为植物带长度; hv为植物高度; φ为植物固体体积分数; n为排列结构参数;
将式(9)中的各影响因素进行无量纲变换可以得到:
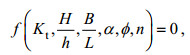 (10)
(10)式中: Kt为透射系数; H/h为相对波高, 可以表征水动力因素; B/L为植物带相对长度、α为植物淹没度、φ为植物分布密度、n为植物排列结构参数, 均可以表征植物因素。
基于本文植物模型M1—M4的实验数据, 如图 10所示, 建立矩形分布植物带孤立波透射系数Kt与各影响因素之间的关系式, 如式(11)所示, 拟合度为0.770, 令关系式右端为П。
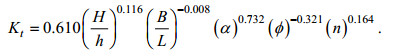 (11)
(11)
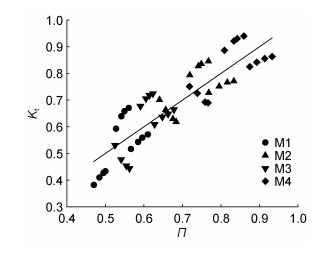 |
| 图 10 孤立波透射系数与各影响因素之间的关系 Fig. 10 Relation between transmission coefficient of solitary wave and various influencing factors |
由于植物消波特性变化非常复杂, 造成部分数据点与拟合曲线偏离较大, 但从整体上看仍呈幂函数关系, 可以看出水动力因素和植物因素均在不同程度上影响植物的消波特性。为了定量考察经验公式的预测值与实测数据的吻合度, 引入均方根偏差(RMSD)变异系数CV:
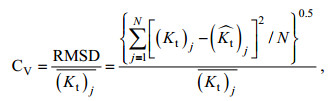 (12)
(12)式中: (Kt)j表示实验实测数据; 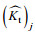
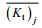
| 模型 | 植物固体体积分数φ | CV% |
| 模型1 | 0.331 | 13.84 |
| 模型2 | 0.174 | 8.32 |
| 模型3 | 0.166 | 12.16 |
| 模型4 | 0.087 | 7.97 |
图 11给出了Tanino等(2008)实验中植物固体体积分数φ=0.15、0.20、0.27、0.35四种工况以及本文中M1、M2、M3、M5四种植物模型的拖曳力系数CD与雷诺数Rep之间的关系曲线。Tanino等(2008)主要研究内容为非淹没状态下随机分布的刚性植物与恒定流之间的相互作用, 并得出结论:在100≤Rep≤700, φ≤0.35条件下, 植物拖曳力系数CD随着固体体积分数φ的增大而增大。值得注意的是, Tanino等(2008)研究中植物模型采用的是随机分布的方式, 并没有考虑分布排列结构对植物拖曳力系数的影响。本文中的M1、M2、M3、M5四种植物模型的φ大小比较: φM1 > φM2 > φM3=φM5, 通过计算求得各植物模型的雷诺数Rep范围: 2000≤Rep≤4000, 利用式(5)求得各植物模型的CD值大小比较: M1最大, M2次之, 而M5和M3基本相等。综上所述, 在2000≤Rep≤4000, φ≤0.331条件下, 符合Tanino等(2008)提出的随着固体体积分数φ的增大, 植物拖曳力系数CD增大的规律, 当φ相等时, 矩形和交错两种不同的分布排列方式对CD的影响较小。
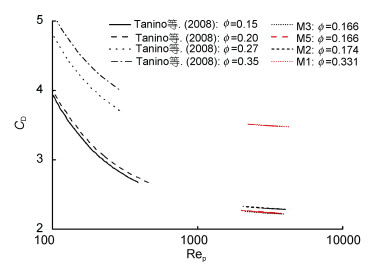 |
| 图 11 Rep-CD关系曲线 Fig. 11 Relationship curves between Rep and CD |
本文通过物理模型实验研究了刚性植物分布方式对孤立波消减影响, 得到以下结论:
(1) 植物固体体积分数φ越大, 孤立波经过植物模型前后的波高变化幅度越大。植物淹没度α相同时, 孤立波在斜坡地形的爬高值以及植物前的壅高值均随相对波高H/h的增大而增大。当φ相等时, 矩形和组合分布植物模型前的波高增量均大于交错分布植物模型。此外, 组合分布方式使得孤立波在植物模型前会产生较大的壅高, 且消浪效果较差。
(2) 相对波高H/h对透射系数Kt的影响与φ及α相关。在0.087≤φ≤0.176且α相等的条件下, 各植物模型Kt随H/h的变化趋势相同且Kt对H/h的敏感度随H/h的增大而减小, 当H/h到达一定数值时, Kt随H/h的增大无明显变化, 此时植物模型的消浪效果趋于稳定。
(3) 当植物分布排列方式为正方形分布时, Kt随φ的增大而减小, 当植物分布方式不同时, Kt并不随φ的变化而单调地变化; 当φ相等时, 植物分布排列方式导致的遮蔽效应与重叠效应将减弱植物的消浪能力, 且遮蔽效应对植物消浪能力的影响比重叠效应更大, 适当增加相邻植物间沿波浪传播方向的间距, 植物带消浪效果增强。
(4) 在雷诺数范围2000≤Rep≤4000, 且φ≤0.331条件下, 植物拖曳力系数CD随固体体积分数φ的增大而增大。当φ相等时, 矩形和交错两种不同的植物分布排列方式对CD的影响较小。
| 何飞, 陈杰, 蒋昌波, 等, 2017a. 考虑根茎叶的近岸植物对海啸波消减实验研究. 热带海洋学报, 36(5): 9–15 |
| 何飞, 陈杰, 蒋昌波, 等, 2017b. 考虑根茎叶影响的刚性植物消浪特性实验研究. 水动力学研究与进展, 32(6): 770–778 |
| 何飞, 陈杰, 蒋昌波, 等, 2018a. 规则波作用下植物带波高衰减特性实验研究. 海洋科学进展, 36(1): 146–158 |
| 何飞, 陈杰, 蒋昌波, 等, 2018b. 植物带影响下孤立波沿程波高衰减特性试验. 水利水电科技进展, 38(1): 75–82 |
| 陈杰, 何飞, 蒋昌波, 等, 2017b. 规则波作用下刚性植物拖曳力系数实验研究. 水利学报, 48(7): 846–857 |
| 陈杰, 何飞, 蒋昌波, 等, 2018. 植物消波机制的实验与理论解析研究进展. 水科学进展, 29(3): 433–435 |
| 陈杰, 赵静, 蒋昌波, 等, 2017a. 非淹没刚性植物对规则波传播变形影响实验研究. 海洋通报, 36(2): 222–229 |
| 陈杰, 蒋昌波, 邓斌, 等, 2013. 海啸波作用下岸滩演变与床沙组成变化研究综述. 水科学进展, 24(5): 750–758 |
| 陈杰, 管喆, 蒋昌波, 2016. 海啸波作用下泥沙运动——Ⅴ.红树林影响下的岸滩变化. 水科学进展, 27(2): 206–213 |
| 姚宇, 杜睿超, 袁万成, 等, 2015. 斜坡非淹没刚性植被影响下孤立波爬高的研究. 水动力学研究与进展, 30(5): 506–515 |
| Augustin L, Irish J, Balsmeier G, et al, 2009. Laboratory measurements of wave attenuation and wave setup by vegetation. Coastal Engineering, 2008, 5: 324–330 |
| Ergun S., 1952. Fluid Flow Through Packed Columns. Chemical Engineering Progress, 48: 89–94 |
| Giri C, Zhu Z, Tieszen L L, et al, 2008. Mangrove forest distributions and dynamics (1975-2005) of the tsunami-affected region of Asia. Journal of Biogeography, 35(3): 519–528 DOI:10.1111/jbi.2008.35.issue-3 |
| Hu Z, Suzuki T, Zitman T, et al, 2014. Laboratory study on wave dissipation by vegetation in combined current-wave flow. Coastal Engineering, 88: 131–142 DOI:10.1016/j.coastaleng.2014.02.009 |
| Huang Z H, Yao Y, Sim S Y et al, 2011. Interaction of solitary waves with emergent, rigid vegetation. Ocean Engineering, 38(10): 1080-1088 |
| Iimura K, Tanaka N., 2012. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Engineering, 54: 223–232 DOI:10.1016/j.oceaneng.2012.07.025 |
| Irish J L, Weiss R, Yang Y Q, et al, 2014. Laboratory experiments of tsunami run-up and withdrawal in patchy coastal forest on a steep beach. Natural Hazards, 74(3): 1933–1949 DOI:10.1007/s11069-014-1286-1 |
| Irtem E, Gedik N, Kabdasli M S, et al, 2009. Coastal forest effects on tsunami run-up heights. Ocean Engineering, 36(3-4): 313–320 DOI:10.1016/j.oceaneng.2008.11.007 |
| Nepf H M., 1999. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resources Research, 35(2): 479–489 DOI:10.1029/1998WR900069 |
| Pujol D, Colomer J, Serra T, et al, 2012. A model for the effect of submerged aquatic vegetation on turbulence induced by an oscillating grid. Estuarine, Coastal and Shelf Science, 114: 23–30 DOI:10.1016/j.ecss.2011.08.020 |
| Raupach M R., 1992. Drag and drag partition on rough surfaces. Boundary-Layer Meteorology, 60(4): 375–395 DOI:10.1007/BF00155203 |
| Sánchez-González J F, Sánchez-Rojas V, Memos C D., 2011. Wave attenuation due to Posidonia oceanica meadows. Journal of Hydraulic Research, 49(4): 503–514 DOI:10.1080/00221686.2011.552464 |
| Suzuki T, 2011. Wave dissipation over vegetation fields. Delft: Doctor Dissertation of Delft University of Technology |
| Suzuki T, Zijlema M, Burger B, et al, 2012. Wave dissipation by vegetation with layer schematization in SWAN. Coastal Engineering, 59(1): 64–71 DOI:10.1016/j.coastaleng.2011.07.006 |
| Tanaka N, Sasaki Y, Mowjood M I M, et al, 2007. Coastal vegetation structures and their functions in tsunami protection:experience of the recent Indian Ocean tsunami. Landscape and Ecological Engineering, 3(1): 33–45 DOI:10.1007/s11355-006-0013-9 |
| Tanino Y, Nepf H M., 2008. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. Journal of Hydraulic Engineering, 134(1): 34–41 DOI:10.1061/(ASCE)0733-9429(2008)134:1(34) |
| Thuy N B, Tanimoto K, Tanaka N, et al, 2009. Effect of open gap in coastal forest on tsunami run-up-investigations by experiment and numerical simulation. Ocean Engineering, 36(15-16): 1258–1269 DOI:10.1016/j.oceaneng.2009.07.006 |
| Yao Y, Du R C, Jiang C B, et al, 2015. Experimental study of reduction of solitary wave run-up by emergent rigid vegetation on a beach. Journal of Earthquake and Tsunami, 9(5): 1540003 DOI:10.1142/S1793431115400035 |
 2018, Vol. 49
2018, Vol. 49


