
中国海洋湖沼学会主办。
文章信息
- 董建宇, 胡成业, 杨晓龙, 李文涛, 张秀梅. 2018.
- DONG Jian-Yu, HU Cheng-Ye, YANG Xiao-Long, LI Wen-Tao, ZHANG Xiu-Mei. 2018.
- 基于GLM模型Logistic回归的菲律宾蛤仔地理群体判别
- DISCRIMINATION BETWEEN GEOGRAPHICAL GROUPS OF RUDITAPES PHILIPPINARUM BY LOGISTIC REGRESSION BASED ON GLM MODEL
- 海洋与湖沼, 49(6): 1318-1324
- Oceanologia et Limnologia Sinica, 49(6): 1318-1324.
- http://dx.doi.org/10.11693/hyhz20180100002
-
文章历史
- 收稿日期:2018-01-04
- 收修改稿日期:2018-04-25
2. 青岛海洋科学与技术国家实验室海洋渔业科学与食物产出过程功能实验室 青岛 266237
2. Function Laboratory for Marine Fisheries Science and Food Production Processes, National Laboratory for Marine Science and Technology, Qingdao 266237, China
菲律宾蛤仔(Ruditapes philippinarum)隶属于软体动物门(Mollusca)、双壳纲(Bivalvia)、帘蛤目(Venerioda)、帘蛤科(Veneridae)、蛤仔属(Ruditapes), 是一种重要的海洋经济贝类(庄启谦, 2001), 其总产量在所有贝类物种中位居世界第二(de Montaudouin et al, 2016)。由于所处海区的地理纬度和生境不同, 菲律宾蛤仔的栖息环境和所面临的环境压力存在差异, 而这一差异正是产生和维持物种不同地理群体形态变异的主要原因(Márquez et al, 2010)。物种地理群体的形态变异属于表型变异的一种, 是物种应对环境压力所做出的适应性改变, 并在一定程度上反映了其生境质量和种群进化史(Márquez et al, 2010)。Krapivka等(2007)研究发现不同地理纬度的智利贻贝(Mytilus chilensis)群体表现出显著的形态学差异, 栖息于更强捕食者压力环境下的野生群体, 比捕食压力较弱环境中的养殖群体具有更厚的外壳以及更高的后闭壳肌指数(Valladares et al, 2010)。物种的形态可塑性恰好为基于形态测量学的物种地理群体判定提供了前提条件。双壳贝类具有坚硬的外壳以及在测量过程中不易变形等特点, 使其成为形态学研究的理想物种(Rufino et al, 2006; Costa et al, 2008, 2010)。然而, 大多数的双壳类尤其是蛤类近似圆形的外壳形态使得其所能测量的形态学指标较少, 限制了基于传统形态学测量方法在双壳类地理群体判别中的应用(Palmer et al, 2004)。Márquez等(2010)应用两种几何形态学方法即轮廓线法(Outlines Method)和地标点法(Landmarks Method)研究了阿根廷不同地理群体条纹蛤(Ameghinomya antiqua)的形态差异并判定了其地理归属, 正确率分别为88.88%和86.66%。Palmer等(2004)结合外壳轮廓椭圆傅里叶分析(Elliptic Fourier Analysis, EFA)也准确判别了来自7个不同产地的一种地中海经济贝类(Chamelea gallina)的地理群体归属。以轮廓线法和地标点法为代表的几何形态测量学(Cadrin, 2000; 陈新军等, 2013)虽然解决了双壳类所能测量的外部形态学指标较少的问题, 但是对双壳类轮廓的提取分析和地标点的鉴定难度较大, 限制了其在快速判别双壳类物种地理群体中的应用。
为了弥补上述分析方法在判定贝类物种地理群体上的不足, 本研究在传统形态测量学基础之上, 假设贝类外壳形态学差异可以通过采样地点来解释(Valladares et al, 2010), 即不同地理群体的菲律宾蛤仔外壳形态不同; 提出将传统形态测量学和广义线性模型(GLM)相结合, 应用GLM模型框架下的逻辑斯蒂(Logistic)回归判别菲律宾蛤仔地理群体的方法。以青岛胶州湾和荣成天鹅湖两个地理群体的菲律宾蛤仔作为研究对象, 对比分析了其形态差异, 探讨了GLM模型Logistic回归方法在菲律宾蛤仔地理群体判别中的可行性和准确性, 以期为双壳类物种地理群体判别提供新的分析方法和技术手段。
1 材料与方法 1.1 样品采集与测量于2017年5月和8月, 从山东青岛胶州湾和荣成天鹅湖采集菲律宾蛤仔样品, 以活体形式运回中国海洋大学海洋生物资源增殖与保护生态学实验室, 静水充气暂养48h, 以排空消化道内的食物。测量前将菲律宾蛤仔壳表面清洗干净, 并用吸水纸吸干壳表面水分。用游标卡尺测量壳长(SL)、壳高(SH)和壳宽(SW), 精确到0.01mm; 用电子天平称量活体重(W), 精确到0.01g。
1.2 数据处理与建模 1.2.1 形态学分析胶州湾与天鹅湖两个地理群体菲律宾蛤仔的外壳形态学差异通过肉眼难以区分。为了定量分析菲律宾蛤仔的形态学差异, 分别用线性函数和幂函数对两个地理群体的SH、SW和W与SL的关系进行了拟合, 分别得到SH、SW和W与SL回归拟合方程。
1.2.2 GLM模型GLM模型是在标准线性模型的基础上发展得到的, 模型假设响应变量不再仅仅只局限于正态分布而是服从于指数分布族中某一种分布, 极大地扩展了标准线性模型。Logistic回归则是GLM模型框架下的用于解决二值型响应变量(Y)即Y服从二项分布的一个模型。GLM模型的一般表达式为:
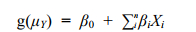 (1)
(1)其中: g(μY)为连接函数, μY为Y的条件均值, Y为响应变量, β0为截距, βi为回归系数, Xi为预测变量。
本研究中将菲律宾蛤仔的采样地点Y以二值响应变量0和1表示(0代表胶州湾, 1代表天鹅湖), Y服从二项分布, 采用Logistic回归进行拟合, 模型的拟合形式为:
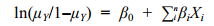 (2)
(2)其中: ln(μY/1–μY)为连接函数。
将(2)化简得Y的条件均值:
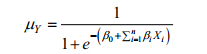 (3)
(3)μY是对应于自变量一系列取值时的响应变量Y发生的概率, 取值范围为[0, 1]。根据模型训练拟合结果判断和选择最适的阈值(μY值), 将μY的取值范围[0, 1]分成[0, μY]和(μY, 1]两个区间, 两个区间分别对应响应变量Y的两个属性值, 便可以实现对响应变量Y的准确分类。
1.2.3 预测变量选择为消除个体间大小差异的影响, 计算其相应的比例性状, 即SH/SL、SW/SL和W/SL以及SW/SH等4个指标, 并将其作为初始预测变量。预测变量间的线性相关会引起多重共线问题进而导致模型参数估计的不稳定和统计推断的偏差(Dormann et al, 2013), 因此在预测变量代入模型之前对其进行Pearson相关分析, 以排除可能出现的上述问题。然后挑选出彼此相互独立的预测变量进行组合, 将得到的各个组合分别代入模型, 根据赤池信息准则(AIC)选择AIC值最小的变量组合进行建模。
1.2.4 模型评估运用受试者工作特征曲线(Receiver Operating Characteristic Curve, ROC曲线)及ROC曲线下方的面积(Area Under ROC Curve, AUC)对模型拟合精度和预测能力进行评估。AUC值大于0.5, 认为模型拟合优于随机判断, AUC值大于0.7, 认为模型是可接受的, AUC值大于0.8和0.9则表明模型良好和极好(Hosmer et al, 2005)。以正确判别个数除以总个数的百分比作为模型的判别正确率:
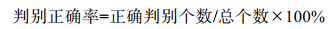 (4)
(4)数据分析和GLM模型Logistic回归构建过程均在R语言(R 3.4.2)(R Development Core Team, 2017)中完成。将全部样本随机分成两组, 即训练集和测试集, 其中训练集占70% (n=122), 用于模型训练并得出拟合模型表达式, 测试集占30%(n=52), 用于评估模型的预测能力。预测变量的Pearson相关性分析在“psych”包(Revelle, 2017)中完成, 模型拟合精度和预测能力的评估均在“pROC”包(Robin et al, 2011)中完成。
2 结果与分析 2.1 菲律宾蛤仔的形态变异本次实验中菲律宾蛤仔样品共计174只, 其中胶州湾84只, 壳长变化范围为19.70-42.90mm; 天鹅湖90只, 壳长变化范围为18.01-41.17mm, t检验显示两个地理群体菲律宾蛤仔壳长差异不显著(P > 0.05)。胶州湾菲律宾蛤仔的壳高、壳宽和活体重与壳长关系表达式分别为(图 1): SHJ=0.6930SL (R2=0.9993)、SWJ=0.4166SL (R2=0.9973)和WJ=0.0006SL2.6512 (R2= 0.9860);天鹅湖菲律宾蛤仔的壳高、壳宽和活体重与壳长关系表达式分别为: SHT=0.7495SL (R2=0.9990)、SWT=0.5058SL (R2=0.9940)和WT=0.0002SL3.0285 (R2= 0.9594)。菲律宾蛤仔的壳高和壳宽与壳长之间的线性关系表明, 壳长、壳高和壳宽都是成比例同步生长的, 且壳长的增加幅度最大, 壳宽的增加幅度最小。在壳长增加量相同的情况下, 天鹅湖群体的壳高和壳宽的增幅分别比胶州湾群体高了8.15%和22.01%, 表明天鹅湖群体比胶州湾群体具有更大的壳高与壳长比和壳宽与壳长比, 壳形椭圆较圆且隆起程度高, “凸”形明显, 更接近于球形。壳长与活体重的幂函数关系显示天鹅湖群体的活体重基本在胶州湾之上, 随着壳长的增加, 两个群体的菲律宾蛤仔的活体重差异逐渐变大, 当壳长大于35mm之后这种差异尤为明显。总之, 相对于胶州湾而言, 天鹅湖菲律宾蛤仔群体的活体重更重, 壳长、壳高与壳宽的增长差异更小, 形状圆而更近似于球形。
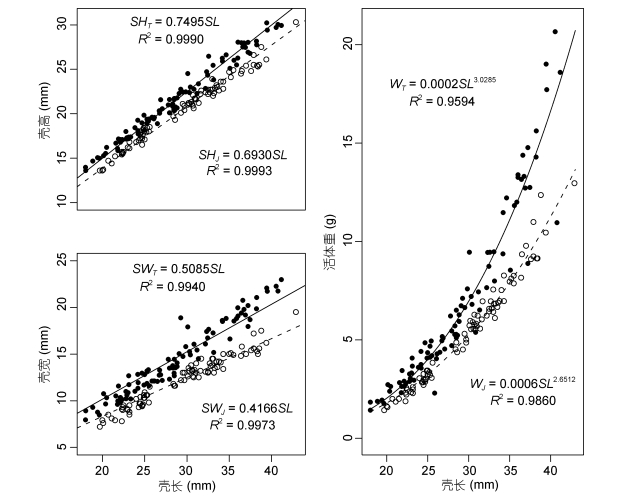 |
| 图 1 壳高(SH)、壳宽(SW)和活体重(W)与壳长(SL)的关系 Fig. 1 The relationship of the shell length (SL) to the shell height (SH), shell width (SW), and live weight (W) 注: J.胶州湾; T.天鹅湖 |
预测变量间的Pearson相关性分析结果表明, 除了SH/SL与W/SL之外的各变量间均呈现显著的线性关系(图 2), 因此符合筛选条件的预测变量组合只有1种, 即SH/SL与W/SL的组合。本研究中只出现了一种变量组合形式, 其AIC值为43.08, 不存在对变量组合间的AIC值大小进行选择和比较, 故SH/SL与W/SL的组合即为构建GLM模型Logistic回归的最优变量组合。
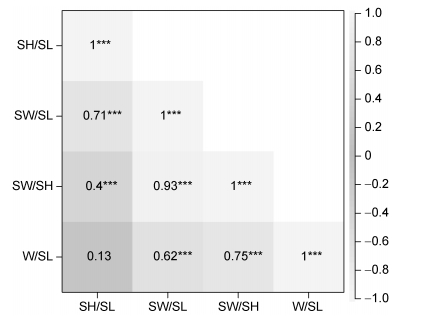 |
| 图 2 预测变量间的Pearson相关系数 Fig. 2 The Pearson correlation coefficient among predictive variables 注: ***: P < 0.001; **: P < 0.01; *: P < 0.05 |
将训练集中预测变量SH/SL和W/SL代入到GLM模型中进行Logistic拟合, 并通过极大似然估计得出模型截距β0和回归系数βi。拟合结果显示, 2个预测变量和截距β0均与响应变量Y显著相关(P < 0.001)。方差膨胀因子检验的结果均小于2, 表明模型预测变量间不存在多重共线, 各个预测变量间是彼此独立的。拟合模型表达式为:
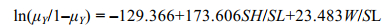 (5)
(5)将(4)化简得:
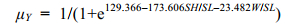 (6)
(6)对训练集拟合得到的响应变量Y的条件概率μY进行排序并绘图可以得到一条近似“S”型的曲线(图 3), 表明GLM模型Logistic回归对训练集的拟合结果比较可靠。
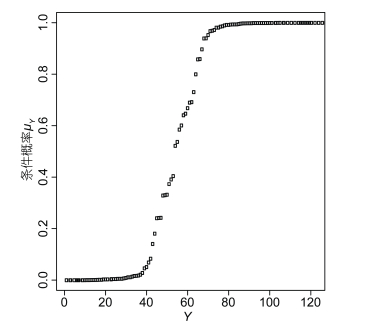 |
| 图 3 训练集响应变量Y的条件概率μY Fig. 3 The conditional probability μY of response variable Y in the train set |
ROC曲线反映了敏感性(Sensitivity)和特异性(Specificity)的相互关系, AUC则表示根据当前拟合模型计算得到的μY值, 随机选择一个正值和负值, 将正值排在负值之前的概率(Hanley et al, 1982), AUC值越接近1表示模型精度越高。用ROC曲线和AUC值对训练集所得模型拟合精度的评估结果如图 4所示。其中AUC的值等于0.984, 拟合结果极好。当Y的条件均值μY的阈值为0.691时, 拟合模型的分类效果最好。此时模型的特异性和敏感性值分别为0.981和0.882, 即拟合模型对于胶州湾群体的正确判别率为98.1%, 对于天鹅湖群体的正确判别率为88.2%, 模型总的正确判别率为92.62%。
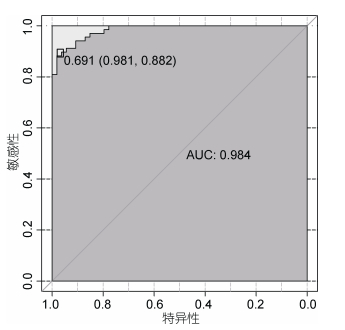 |
| 图 4 ROC曲线 Fig. 4 The (Receiver Operating Characteristic, ROC) curve |
以Y的条件均值μY =0.691为分类判断阈值, 用测试集(其中胶州群体30只, 天鹅湖群体22只)对模型的预测能力进行验证。将测试集的SH/SL和W/SL代入Y的条件均值函数μY中求得对应的μY值, 然后与阈值0.691相比较, 小于0.691的判定为胶州湾群体, 大于0.691的判定为天鹅湖群体。结果显示模型预测的总正确判别率为94.23%, 对胶州湾和天鹅湖群体的正确判别率分别为93.33%和95.45%(图 5)。模型预测的AUC值为0.944, 模型预测精度极好, 表明模型的预测能力极高, 可以准确判别胶州湾和天鹅湖菲律宾蛤仔的地理群体归属。
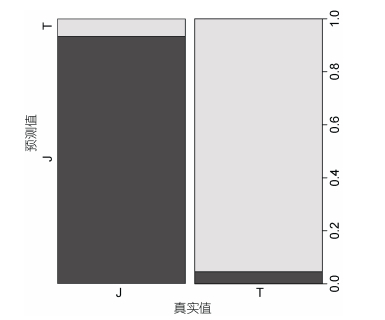 |
| 图 5 模型验证结果 Fig. 5 The result of test of the model 注: J.胶州湾; T.天鹅湖 |
双壳类普遍具有较强的表型可塑性特征(de Montaudouin et al, 2016), 菲律宾蛤仔则是其中的一个重要代表。Kwon等(1999)将韩国沿岸3个不同地理群体, 外壳形态存在显著差异(P < 0.05)的菲律宾蛤仔移殖到同一养殖区域, 13个月后发现这3个群体的外壳形态差异变得不显著(P > 0.05), 证实了栖息地环境条件是影响菲律宾蛤仔外壳形态的主要因素。Watanabe等(2010)对日本4个不同海湾的菲律宾蛤仔的形态学研究表明, 营养条件也会改变蛤仔的外壳形态, 栖息于营养条件状况较好的环境中的个体比生长于贫营养环境中的个体壳宽更小, 壳形椭圆化程度更高。此外, 种群密度和褐色肌肉病(Brown muscle disease, BMD)也会影响菲律宾蛤仔形态, 群体密度较低和BMD疾病感染率较高的菲律宾蛤仔群体往往具有更高的SW/SL值, 因而外形也更近似于球形(Caill-Milly et al, 2012)。本研究中胶州湾是一个半封闭的海湾, 平均水深7m(Fan et al, 2007), 采样点的菲律宾蛤仔群体终年生活于潮下带, 受潮汐作用的影响较小; 而天鹅湖是濒临黄海的一个典型潟湖, 最大水深不足3m(赵鹏等, 2016), 受涨潮和落潮的影响, 采样点菲律宾蛤仔经常暴露于空气中, 不但减少了其滤食时间, 也使得其面临更大的生存和生理压力, 如更高的被捕食风险、夏季的高温和冬季的低温胁迫等, 迫使其通过改变自身的生理代谢和外壳形态等表型特征以适应外界环境的变化。物种的形态变异是物种与其生存环境彼此相互作用的结果, 可以作为其栖息地环境质量的一种反映, Watanabe等(2010)研究表明菲律宾蛤仔的SW/SL可以作为衡量其栖息地营养条件质量的一个指示因子。胶州湾菲律宾蛤仔的SW/SL变化范围为0.35-0.46, 平均值为0.41;天鹅湖菲律宾蛤仔的SW/SL的变化范围为0.43-0.65, 平均值为0.50, t检验显示两者差异极显著(P < 0.001)。且胶州湾菲律宾蛤仔的贝壳干重(均值2.52g)小于天鹅湖(均值3.43g)(P < 0.001), 软体部干重(均值0.26g)大于天鹅湖(均值0.18g)(P < 0.001), 整体表现为壳轻肉重, 肥满度更高。由此表明, 胶州湾菲律宾蛤仔栖息地的营养条件优于天鹅湖(Watanabe et al, 2010; Caill-Milly et al, 2012), 更适合菲律宾蛤仔生长。然而栖息地水深和营养条件是否是造成胶州湾与天鹅湖菲律宾蛤仔形态学差异的主要原因, 尚需进一步研究。
2000年以来, 福建逐渐成为胶州湾底播菲律宾蛤仔苗种的主要产地(郭永禄, 2005), 这种长期的异地苗种底播方式将会对本地野生菲律宾蛤仔种群的遗传结构产生重要影响(Liu et al, 2007; 胡利莎等, 2016), 导致其基因杂合度的升高(Mao et al, 2011)。本研究中的胶州湾样品来自菲律宾蛤仔的底播增殖区, 由于缺乏分子生物学鉴定结果的支持, 尚不能断定其是当地野生种群还是来自福建的苗种亦或是二者的杂交后代。同样, 天鹅湖也曾多次底播产自福建的菲律宾蛤仔苗种。但Kwon等(1999)研究表明, 苗种来源并不影响菲律宾蛤仔的表型性状反映其栖息地环境条件特征。地理群体的表型变异并不总是受基因变异的影响, 而更多的是由栖息地环境条件差异所致(Kwon et al, 1999; Cadrin, 2000; Márquez et al, 2010)。未来的研究则可以进一步定量分析栖息地环境条件对于具有相同基因型的菲律宾蛤仔的形态分化的贡献, 以及影响其表型可塑性的主导因素。
3.2 GLM模型Logistic回归随着形态学分析技术的发展与进步, 基于形态测量学和几何形态测量学的物种鉴定和地理群体判别分析被广泛应用于渔业生物中(Cadrin, 2000; Palmer et al, 2004; Márquez et al, 2010; 陈新军等, 2013; 侯刚等, 2014)。本研究将传统形态测量学和GLM模型中的Logistic回归相结合, 将采样地点胶州湾和天鹅湖抽象成服从二项分布的响应变量Y, 建立了菲律宾蛤仔两个地理群体与预测变量SH/SL和W/SL的条件均值函数回归方程, 并以94.2%总的预测判别正确率实现了对胶州湾和天鹅湖两个地理群体菲律宾蛤仔归属地的判别, 克服了双壳类因外壳近似圆形使得测量指标较少, 难以通过传统形态测量学方法判别其地理群体归属方面的短板。尽管计算机图形处理技术的进步为几何形态测量学分析提供了更加精确的数据收集和更加有效的图形定量分析方法, 然而其并不能突破不同几何形态测量学方法本身所固有的局限性。基于椭圆傅里叶分析的轮廓线法是用傅里叶级数拟合目标轮廓的点坐标, 虽然其能够有效区分不同的群体, 但是对组间差异的解释较为困难(Cadrin, 2000); 而地标点法则必须建立一个坐标空间, 并把全部的地标点按照实际情况固定于坐标系的相应位置之上(Cadrin, 2000)。与几何形态测量学相比, 基于传统形态测量学的GLM模型Logistic回归方法不涉及复杂的图形分析和处理过程, 建模过程相对简单, 得到的条件均值函数表达式明确, 预测准确率较高, 所需预测变量较少(本研究中只涉及SH/SL和W/SL两个预测变量), 不但发挥了传统形态测量学的优势, 也避免了几何形态测量学的劣势。然而, GLM模型Logistic回归中的响应变量Y服从二项分布的前提条件限定了响应变量只能是二值型变量, 即研究的地理群体只能限定为两个, 而不能同时对三个及以上的地理群体归属进行判别。尽管如此, 基于GLM模型的Logistic回归也不失为一种能够快速并且准确判别双壳类地理群体的方法。
4 结论对于菲律宾蛤仔而言, 天鹅湖的栖息地环境选择压力大于胶州湾, 两个地理群体的形态学差异主要表现为壳形和活体重两个方面。基于GLM模型的Logistic回归能够快速准确判别菲律宾蛤仔的地理群体归属, 弥补了基于传统形态测量学方法难以判别贝类物种地理群体方面的不足。
| 庄启谦, 2001. 中国动物志, 软体动物门, 双壳纲, 帘蛤科. 北京: 科学出版社, 278 |
| 陈新军, 方舟, 苏杭, 等, 2013. 几何形态测量学在水生动物中的应用及其进展. 水产学报, 37(12): 1873–1885 |
| 赵鹏, 卢文虎, 杨红生, 等, 2016. 中国北方沿海典型澙湖--山东月湖水深遥感反演. 海洋与湖沼, 47(04): 714–718 |
| 胡利莎, 张振, 马培振, 等, 2016. 10个菲律宾蛤仔野生群体的遗传多样性研究. 海洋与湖沼, 47(3): 549–556 |
| 侯刚, 王学锋, 朱立新, 等, 2014. 基于几何形态测量学的4种金线鱼矢耳石识别研究. 海洋与湖沼, 45(3): 496–503 |
| 郭永禄, 2005.胶州湾底播增殖菲律宾蛤仔(Ruditapes philippinarum)渔业生物学研究.青岛: 中国海洋大学硕士学位论文, 47 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y828488 |
| Cadrin S X, 2000. Advances in morphometric identification of fishery stocks. Reviews in Fish Biology and Fisheries, 10(1): 91–112 DOI:10.1023/A:1008939104413 |
| Caill-Milly N, Bru N, Mahé K, et al, 2012. Shell shape analysis and spatial allometry patterns of manila clam (Ruditapes philippinarum) in a mesotidal coastal lagoon. Journal of Marine Biology,: 281206 |
| Costa C, Aguzzi J, Menesatti P, et al, 2008. Shape analysis of different populations of clams in relation to their geographical structure. Journal of Zoology, 276(1): 71–80 DOI:10.1111/jzo.2008.276.issue-1 |
| Costa C, Menesatti P, Aguzzi J, et al, 2010. External shape differences between sympatric populations of commercial clams Tapes decussatus and T. philippinarum. Food and Bioprocess Technology, 3: 43–48 DOI:10.1007/s11947-008-0068-8 |
| de Montaudouin X, Lucia M, Binias C, et al, 2016. Why is Asari (=Manila) clam Ruditapes philippinarum fitness poor in Arcachon Bay: a meta-analysis to answer?. Estuarine, Coastal and Shelf Science,(179): 226–235 |
| Dormann C F, Elith J, Bacher S, et al, 2013. Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography, 36(1): 27–46 DOI:10.1111/j.1600-0587.2012.07348.x |
| Fan D J, Zhang A B, Yang Z S, et al, 2007. Observations on shell growth and morphology of the bivalve Ruditapes philippinarum. Chinese Journal of Oceanology and Limnology, 25(3): 322–329 DOI:10.1007/s00343-007-0322-3 |
| Hanley J A, McNeil B J, 1982. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 143(1): 29–36 DOI:10.1148/radiology.143.1.7063747 |
| Hosmer D W, Lemeshow S, 2005. Applied Logistic Regression. 2nd ed. Hoboken, New Jersey, USA: John Wiley & Sons, 31-46 |
| Krapivka S, Toro J E, Alcapán A C, et al, 2007. Shell-shape variation along the latitudinal range of the Chilean blue mussel Mytilus chilensis (Hupe 1854). Aquaculture Research, 38(16): 1770–1777 DOI:10.1111/j.1365-2109.2007.01839.x |
| Kwon J Y, Park J W, Lee Y H, et al, 1999. Morphological variation and genetic relationship among populations of the shortnecked clam Ruditapes philippinarum collected from different habitats. Fisheries and Aquatic Sciences, 2(1): 98–104 |
| Liu X Q, Bao Z M, Hu J J, et al, 2007. AFLP analysis revealed differences in genetic diversity of four natural populations of Manila clam (Ruditapes philippinarum) in China. Acta Oceanologica Sinica, 26(1): 150–158 |
| Márquez F, Robledo J, Peñaloza G E, et al, 2010. Use of different geometric morphometrics tools for the discrimination of phenotypic stocks of the striped clam Ameghinomya antiqua (Veneridae) in North Patagonia, Argentina. Fisheries Research, 101(1-2): 127–131 DOI:10.1016/j.fishres.2009.09.018 |
| Mao Y L, Gao T X, Yanagimoto T, et al, 2011. Molecular phylogeography of Ruditapes philippinarum in the Northwestern Pacific Ocean based on COI gene. Journal of Experimental Marine Biology and Ecology, 407(2): 171–181 DOI:10.1016/j.jembe.2011.06.002 |
| Palmer M, Pons G X, Linde M, 2004. Discriminating between geographical groups of a Mediterranean commercial clam (Chamelea gallina (L.): Veneridae) by shape analysis.. Fisheries Research, 67(1): 93–98 DOI:10.1016/j.fishres.2003.07.006 |
| R Development Core Team, 2017. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, https://www.R-project.org/ |
| Revelle W, 2017. psych: Procedures for personality and psychological research. Evanston, Illinois, USA: Northwestern University http://btr0x2.rz.uni-bayreuth.de/math/statlib/R/CRAN/src/contrib/Descriptions/psych.html |
| Robin X, Turck N, Hainard A, et al, 2011. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics, 12: 77 DOI:10.1186/1471-2105-12-77 |
| Rufino M M, Gaspar M B, Pereira A M, et al, 2006. Use of shape to distinguish Chamelea gallina and Chamelea striatula (Bivalvia: Veneridae): linear and geometric morphometric methods. Journal of Morphology, 267(12): 1433–1440 DOI:10.1002/(ISSN)1097-4687 |
| Valladares A, Manríquez G, Suárez-Isla B A, 2010. Shell shape variation in populations of Mytilus chilensis (Hupe 1854) from southern Chile: a geometric morphometric approach. Marine Biology, 157(12): 2731–2738 DOI:10.1007/s00227-010-1532-3 |
| Watanabe S, Katayama S, 2010. Relationships among shell shape, shell growth rate, and nutritional condition in the manila clam (Ruditapes philippinarum) in Japan. Journal of Shellfish Research, 29(2): 353–359 DOI:10.2983/035.029.0210 |
 2018, Vol. 49
2018, Vol. 49


