中国海洋湖沼学会主办。
文章信息
- 蒋暑民, 戴德君, 乔方利, 马洪余. 2019.
- JIANG Shu-Min, DAI De-Jun, QIAO Fang-Li, MA Hong-Yu. 2019.
- 南海北部陆架海域内潮特征的观测研究
- THE INTERNAL TIDES ON CONTINENTAL SHELF OF THE NORTHERN SOUTH CHINA SEA
- 海洋与湖沼, 50(1): 1-11
- Oceanologia et Limnologia Sinica, 50(1): 1-11.
- http://dx.doi.org/10.11693/hyhz20180300046
-
文章历史
- 收稿日期:2018-03-01
- 收修改稿日期:2018-06-19
2. 青岛海洋科学与技术国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266061;
3. 自然资源部数据分析与应用重点实验室 青岛 266061
2. Laboratory for Regional Oceanography and Numerical Modeling, National Laboratory for Marine Science and Technology, Qingdao 266061, China;
3. Key Laboratory of Data Analysis and Applications, MNR, Qingdao 266061, China
内潮波是正压潮流在层结海洋中经过大陆坡折, 海山海沟等变化地形所产生的一类海洋内波(Nash et al, 2006; Garrett et al, 2007; Qian et al, 2010)。内潮波不仅是物质与能量输运的载体, 还是海洋能量级串的重要一环, 海洋湍流的能量源泉之一(Laurent et al, 2002)。并且, 内潮波可以在地形作用下激发出非线性内波, 对于海洋内部混合、生态环境以及海洋工程等都有极大影响(Cai et al, 2002; Zheng et al, 2007; Buijsman et al, 2010; Xu et al, 2010; Li et al, 2011; Li et al, 2011; Vlasenko et al, 2012)。
南海是全球海洋内波活动最强烈的地区之一, 也是内潮波的热点研究区域。方国洪等(1994)结合验潮站观测资料利用数值方法分析了南海正压潮的分布特征, 指出其能量主要是从太平洋通过吕宋海峡传入的。Duda等(2005)根据东沙岛东侧陆架坡折处的观测资料, 分析了内潮流椭圆和能通量等局地内潮特征参量, 发现该海域以全日内潮为主, 全日内潮在向陆架浅水传播的过程中能通量不断增强, 而半日内潮在传播过程中不断减弱。Klymak等(2011)的资料亦有类似结果。此外, 张效谦等(2005)研究了东沙岛西南侧450m以浅海区内潮的时空特征, 指出观测海区内潮流由M2, K1, O1和P1分潮占主导, 并且内潮能通量主要由海底向海表传播。内潮在传播过程中相速度受背景温盐场以及流场的调制, 因此与天文潮的相位差常常会发生变化。内潮流中与天文潮相位差保持不变的潮流称为锁相潮流, 与天文潮相位差不断变化的潮流称为非锁相潮流。Lee等(2012)根据东沙岛东北侧连续8个月现场观测, 发现该海域锁相潮流能量仅占到总潮能的20%。Xu等(2013)分析了东沙岛西南侧400米深度附近的观测资料, 结果表明全日内潮的能量中约60%为锁相潮流, 半日内潮中仅10%锁相。梁辉等(2016)利用南海北部陆坡海区的潜标资料, 研究发现全日内潮的锁相部分占全日内潮能量的70%, 而半日内潮的锁相部分只占半日内潮能量的53%。
由于地形、背景层结的变化以及涡旋的存在, 南海北部不同海区的内潮特征有很大差异, 而之前的大部分观测都集中在东沙岛东侧和南侧陆坡处, 东沙岛西北侧陆架海区的观测研究相对较少, 内潮传到陆架后产生的变化并不清楚。并且前人研究多着重内潮总体特征, 而对内潮垂向模态及其时间演变特征的讨论较少。基于以上考虑, 本文利用南海北部东沙岛西北侧陆架海区近三个月的流速与温度剖面资料, 重点探讨了陆架海域局地内潮及其垂向结构的时间演变特征。
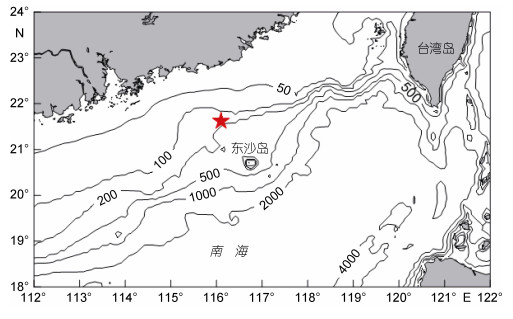
1 数据介绍2014年7月14日—9月24日, 自然资源部第一海洋研究所基于陆丰石油平台(116°E, 21°37′N), 利用锚系潜标开展了南海西北部陆架海域内波观测。观测地点水深约142m, 观测点位置及附近地形分布如图 1所示。潜标系统由一个声学多普勒流速剖面仪(ADCP), 20个温度传感器、5个压力传感器构成, 潜标中传感器及其设置如表 1所示。ADCP(RDI 150kHz)放置在距底10m位置, 向上观测, 采样间隔为2min, 采样垂向间距为4m, 共采样26层, 首层中心距离ADCP 8.4m。由于水面反射影响, 有效测量深度范围约为17—117m。温度传感器和压力传感器的采样间隔均为30秒, 温度传感器的垂向间隔为5m, 测量海面以下平均深度20.5—124m处的水体温度。压力传感器垂向间隔为30米, 通过插值获得温度传感器的实时深度, 由于仪器故障, 50.5m与55.5m深度处的温度数据丢失, 后在数据处理过程中利用线性插值得到对应深度层的温度数据。虽然ADCP无法进行严格的全水深观测, 但是获取的数据已经包含深度范围70%左右, 能够用来分析流速剖面的正压以及斜压信息。为了提取内潮的流速信息, 首先将流速剖面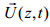
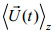
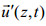
 |
| 图 1 南海北部地形图和潜标观测位置(以黑色五角星表示) Fig. 1 Bathymetry of the northern South China Sea and the location of the mooring (black star) 注:等值线表示水深 |
| 编号 | 仪器类型 | 仪器名称 | 深度(m) | 采样间隔(s) | 备注 |
| 1 | 压力传感器 | 091H010 | 17.5 | 30 | |
| 2 | 温度传感器 | 086S029 | 20.5 | 30 | |
| 3 | 温度传感器 | 086S001 | 25.5 | 30 | |
| 4 | 温度传感器 | 084B039 | 30.5 | 30 | |
| 5 | 压力传感器 | 091H007 | 35.5 | 30 | |
| 6 | 温度传感器 | 084B037 | 35.5 | 30 | |
| 7 | 温度传感器 | 084B043 | 40.5 | 30 | |
| 8 | 温度传感器 | 086S049 | 45.5 | 30 | |
| 9 | 温度传感器 | 084B046 | 50.5 | 30 | 数据缺失 |
| 10 | 温度传感器 | 086S050 | 55.5 | 30 | 数据缺失 |
| 11 | 温度传感器 | 084B049 | 60.5 | 30 | |
| 12 | 压力传感器 | 091H009 | 65.5 | 30 | |
| 13 | 温度传感器 | 086S042 | 65.5 | 30 | |
| 14 | 温度传感器 | 084B045 | 70.5 | 30 | |
| 15 | 温度传感器 | 084B044 | 75.5 | 30 | |
| 16 | 温度传感器 | 084B038 | 80.5 | 30 | |
| 17 | 温度传感器 | 086S045 | 85.5 | 30 | |
| 18 | 温度传感器 | 084B042 | 90.5 | 30 | |
| 19 | 压力传感器 | 091H011 | 95.5 | 30 | |
| 20 | 温度传感器 | 086S041 | 95.5 | 30 | |
| 21 | 温度传感器 | 084B048 | 100.5 | 30 | |
| 22 | 温度传感器 | 086S002 | 105.5 | 30 | |
| 23 | 温度传感器 | 084B041 | 110.5 | 30 | |
| 24 | 温度传感器 | 086S043 | 115.5 | 30 | |
| 25 | 温度传感器 | 086S051 | 120.5 | 30 | |
| 26 | 温度传感器 | 084B047 | 124.2 | 30 | |
| 27 | 压力传感器 | 091H008 | 125 | 30 | |
| 28 | ADCP | Rdi150kHz | 125.5 | 120 |
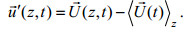 (1)
(1)因为局地的近惯性周期约为32.5h, 并且近惯性振荡常常出现蓝移现象, 可能会与全日内潮频带混淆, 所以我们对原始流速数据进行功率谱分析来确定滤潮的合适周期范围。选择滤波范围的标准是既能最大限度的保留该频带的流速信号, 又能避免其他临近频带信号的干扰(梁辉等, 2016)。图 2显示了东西向斜压流速(图 2a)及正压流速(图 2b)的流速功率谱结果。由图可见, 观测区域以全日潮以及半日潮为主, 其中全日潮以O1和K1分潮频率成典型双峰结构, 峰值略大于半日潮谱峰, 近惯性振荡(周期为32.50小时, 频率为0.73cpd(circle per day, 周期每天))能量并不突出。根据谱分析结果, 分别选取[0.8, 1.2]cpd, [1.8, 2.2]cpd为全日潮以及半日潮的滤波通带(敏感性实验结果显示, 全日潮滤潮周期上限在[0.8, 0.9]cpd之间变化对于滤潮结果影响很小)。
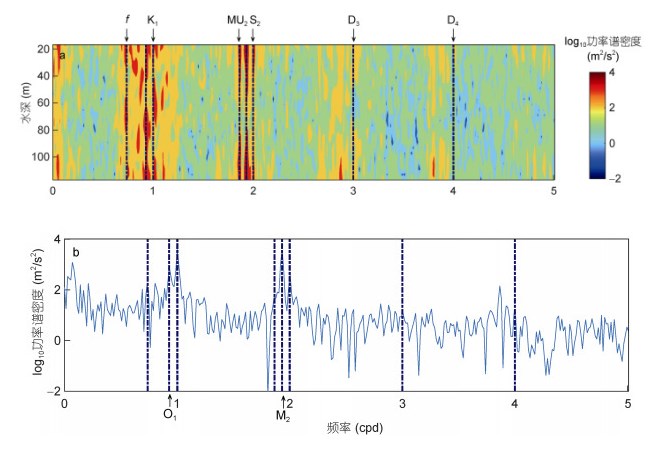 |
| 图 2 潜标位置各深度东西向斜压流速内波功率谱(a)及东西向正压流速内波功率谱(b) Fig. 2 Spectra for zonal baroclinic velocity (a) and for zonal barotropic velocity (b) at different depths |
对整个观测时间段的正压潮流进行标准调和分析, 计算得到正压潮流的潮流要素(表 2)。在观测时间内, 研究区域的正压潮流以K1、O1、M2、S2分潮为主, 其中K1最强, 且全日潮强于半日潮, 这与在南海北部其他海域的观测结果一致(Duda et al, 2005; Klymak et al, 2011; Xu et al, 2011; Lee et al, 2012; Xu et al, 2013)。计算得到潮型数为2.1, 根据我国《港口工程技术规范》(中华人民共和国交通部, 1975), 可以判断当地正压潮流为不规则全日潮。从表 2可以看出, 除O1外, 各大分潮的潮流椭圆的短轴都是负值, 为顺时针运动; 主轴方向基本为东南-西北方向, 这与观测海域正压流以东南-西北方向为主的流场特征相符。
| 分潮 | 长轴(cm/s) | 短轴(cm/s) | 倾角(°) | 迟角(°) |
| O1 | 3.13 | 0.01 | 47.82 | 48.55 |
| K1 | 5.27 | -1.12 | 160.45 | 215.01 |
| M2 | 4.00 | -1.35 | 170.97 | 196.77 |
| S2 | 1.43 | -0.14 | 162.95 | 206.01 |
| 注:倾角标识长轴与正东方向逆时针旋转的夹角, 迟角标识滞后的相位差 | ||||
通过滤波得出的全日和半日内潮流, 再利用式(2)可以分别计算全日和半日内潮的水平动能(HKE):
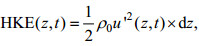 (2)
(2)式中, dz为ADCP采样间距, ρ0为海水密度, 本文中取ρ0=1024kg/m3。图 3展示了全日和半日内潮水平动能的时间变化特征和垂向分布。如图所示, 全日内潮能量略强于半日内潮。在垂向分布中, 全日内潮的垂向变化特征较为杂乱, 难以直观分辨(见图 3a), 而半日内潮清晰表现出强-弱-强的第一模态特征(见图 3b)。为研究内潮的时间变化特征, 我们将半日内潮与全日内潮能量进行深度积分, 并对内潮总水平动能进行谱分析(图 3c), 结果显示内潮能量有约14天的大小潮调制周期, 这主要是由各主分潮之间的相互干涉作用引起的。
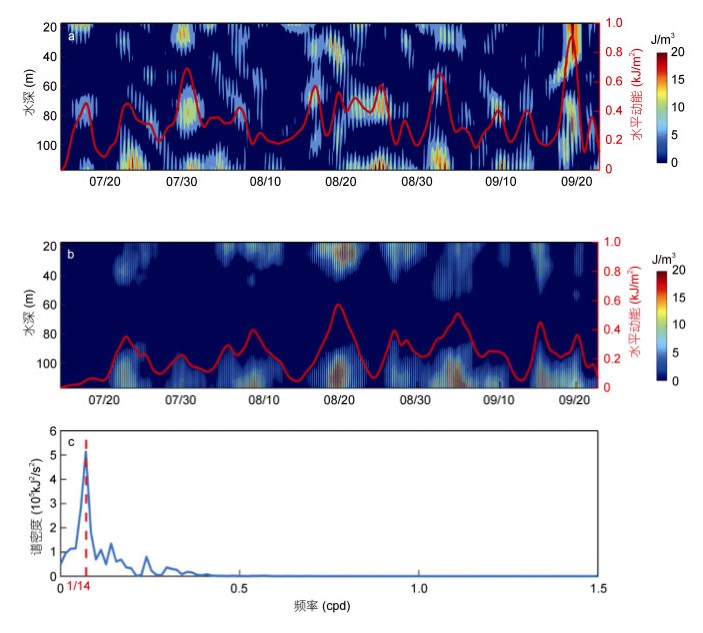 |
| 图 3 全日内潮(a)和半日内潮(b)水平动能的时间变化特征和垂向分布结构以及内潮深度积分水平动能功率谱(c) Fig. 3 The temporal variations and vertical distributions of the HKE of diurnal (a) and semidiurnal (b) internal tides and spectra for depth-integrated HKE of barocline tides (c). 注: 子图中红色曲线代表内潮水平动能的深度积分值, 这里为内潮能量的 1 天低通滤波结果 |
南海内潮波在吕宋海峡生成后, 穿过南海东部海盆向西传播。图 4给出了各层的潮流椭圆, 由图可见, 局地斜压锁相潮流大于正压潮流, 且全日内潮与半日内潮的锁相部分强度相当, 其中O1, M2分潮能量相当, 远大于K1, S2分潮。半日分潮呈现往复流特征, 全日分潮呈现旋转潮流特征; 半日内潮在表层与底层的流速较大, 表现出第一模态特征; 全日内潮则在表层, 中层, 底层均有较强流速, 表现为强-弱-强-弱-强的垂向流速结构, 类似第二模态特征。就斜压流速来看, K1分潮最大流速可达2.89cm/s, O1可达图 3全日内潮(a)和半日内潮(b)水平动能的时间变化特征和垂向分布结构以及内潮深度积分水平动能功率谱(c)7.8cm/s, M2可达8.1cm/s, S2可达2.9cm/s。值得注意的是, 从谱分析以及调和分析结果中, 均发现MU2分潮的斜压能量相当强, 其潮流椭圆长轴可达4.5cm/s, 略小于M2分潮, 远大于S2分潮。同时, 2Q1分潮的斜压能量也非常明显, 其最大流速可达5.57cm/s。MU2周期为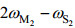

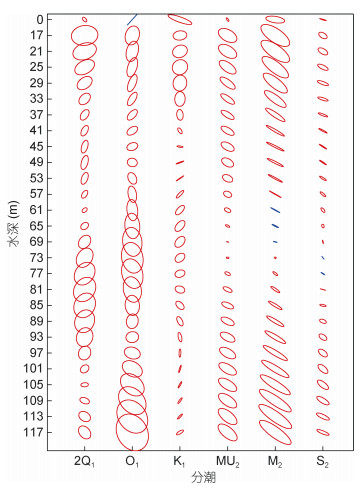 |
| 图 4 内潮主要分潮潮流椭圆随深度的变化 Fig. 4 The tidal ellipses of the internal tide in different layers 注: 0m深度处为正压潮流椭圆, 红色表示顺时针旋转, 蓝色表示逆时针旋转 |
在传播过程中, 由于背景层结以及流场的改变, 内潮波的相速度也随之改变, 进而在观测海区定点观测到的内潮波存在与天文潮相位不一致的部分。通过调和分析, 可以从观测资料的原始斜压流速计算得到各深度斜压潮流的潮流椭圆以及与相位角始终保持一致的潮流, 即锁相潮流。根据调和分析结果, 锁相潮流部分只占总潮流能量的一小部分(各深度调和分析的方差解释率平均约为25%)。这表明观测海域的潮流与天文潮锁相并不明显。为了更细致地探究观测海域内潮的垂向结构及其时间变化特征, 我们利用每层滤波得到的总内潮流减去调和分析计算得出的锁相潮流, 得到内潮流的非锁相部分, 再分别计算全日和半日内潮的锁相和非锁相部分的水平动能, 结果如图 5所示。计算结果显示, 全日内潮中的锁相潮流与半日内潮中的锁相潮流能量相当, 而全日分潮中非锁相潮流强于半日分潮非锁相潮流, 这解释了为何滤波得到的全日内潮强于半日内潮, 而二者的调和分析结果显示强度相当。我们对内潮能量进行了时间平均, 结果表明, 对于全日内潮来说, 锁相潮流占全日内潮能量的17.5%, 而对于半日内潮来说, 锁相潮流占半日内潮能量的30%。
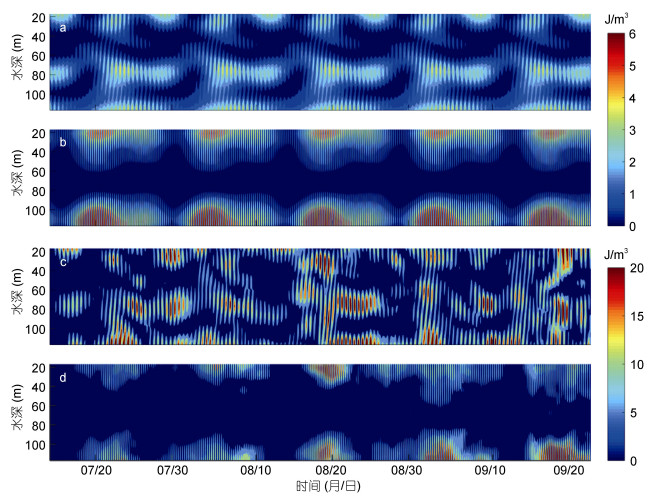 |
| 图 5 锁相(a, b)与非锁相能(c, d)水平动能时间变化与垂向结构 Fig. 5 Time variation and vertical distribution of the coherent and incoherent HKE at diurnal and semidiurnal frequency bands 注: a为全日锁相, b为半日锁相, c为全日非锁相, d为半日非锁相 |
垂向模态是斜压内波的常见特征之一。常见的内波多为低模态内波。由于观测常常难以到达全水深, 所以不同学者也采用了不同的方法计算垂向模态。很多学者采用经验正交函数(EOF)分解方法计算垂向模态(王雪竹等, 2009; Xu et al, 2011; 司广成等, 2012; Gao et al, 2017), 也有很多学者则采用动力模态分解的方法(Klymak et al, 2011; Ma et al, 2013; Shang et al, 2015)。Li等(2015)利用同一组数据对比EOF分解与动力模态分解结果, 发现二者的结果极为相似。然而当观测深度受限时, 不同方法结果是否还一致尚待商榷。为此本文利用观测数据分析对比不同垂向模态计算方法, 并分析局地内潮垂向模态特征。
计算垂向模态需用背景温盐场数据。本文所用潜标的温度传感器的测量范围未达到全水深, 因此本文利用WOA13气候态季节平均温盐资料来补齐全水深的温盐资料。观测时间内, 该海区的温盐变化并不显著, 且观测范围已覆盖上混合层下沿, 再假设WOA数据对于上混合层温度数据变化趋势的反映可信, 本文截取缺测范围内的WOA13气候态夏季温度数据, 将其平移到观测数据之上, 从而得到全水深的温度剖面, 如图 7a所示。在观测海域附近, 盐度的变化对于密度影响并不大, 层结主要受温度变化的影响, 因此我们采用WOA13气候态夏季全水深盐度数据并结合前面得出的温度剖面来计算全水深层结剖面。
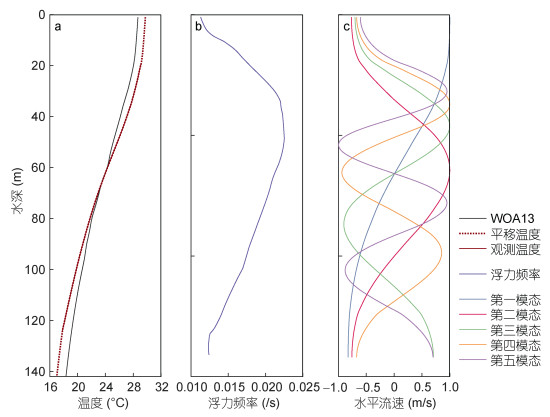 |
| 图 7 观测海区的温度剖面(a), 海洋层结剖面(b)与动力模态分解结果(c) Fig. 7 Temperature profile (a), buoyancy frequency profile (b) and dynamical modes (c) of the study area |
经验正交函数(EOF)分解是一种常见的数据降维分析方法。它把随时间变化、随多个变量变化的标量场分解为不随时间变化的空间函数以及只依赖时间变化的时间函数部分, 原标量场就是这些空间函数分量的线性叠加。因为空间函数的前几个分量就可以解释原标量场的时间变化方差的主要部分, 因此研究这几个分量以及对应的时间变化函数就可以反映原标量场的主要信息。
分别对滤波得到的全日分潮以及半日分潮东西向斜压流速数据进行EOF分解(对南北向流速进行相同分析得到的结果基本一致), 流速正(负)值表示向东(西), 其前5个EOF模态分布函数如图 6所示:
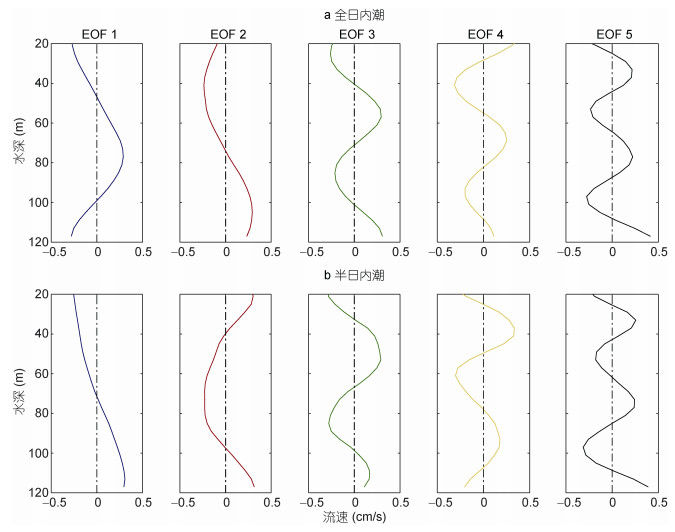 |
| 图 6 全日内潮(a)和半日内潮(b)的EOF垂向模态 Fig. 6 The first five EOF modes for diurnal (a) and semidiurnal (b) internal tides |
全日分潮的前五个EOF模态(为了简便, 下文将EOF第n模态简写为EOFn)的解释率分别为47.1%、34.7%、8.7%、5.0%、2.1%, 其中EOF1跨过0点两次, 表现出明显的第二模态特征; 而EOF2只跨过零点一次, 表现出第一模态特征; EOF3—EOF5在垂向上有变号, 且变号次数随EOF模态数的增加而增加。半日分潮的前五个EOF模态的解释率88.4%、6.7%、1.8%、1.3%、0.8%; EOF1—EOF5跨零点数与EOF模态数相等。EOF结果似乎反映出内潮的垂向模态, 然而EOF分解得出的模态的物理意义并不明确。为了进一步探讨EOF模态的物理意义以及内潮的垂向模态变化特征, 我们进行动力模态分解。
3.4.2 动力模态分解在线性理论框架下, 假设内潮为垂向驻波并同时采用Boussinesq近似, 即刚盖近似, 无耗散近似以及底边界为平底等近似(观测海区已处于大陆架上, 平均坡度约为3°, 因此平底近似合理), 我们可以将内潮水平流速分解为多个离散模态的叠加, 即
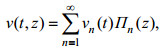 (3)
(3)式中, Πn(z)为内潮水平流速的垂向模态, 可利用质量守恒公式根据垂向速度的垂向模态计算得出:
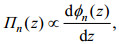 (4)
(4)式中, Φn(z)为垂向速度的垂直模态, 可以通过求解S-L本征值问题来获得:
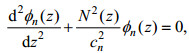 (5)
(5)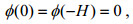 (6)
(6)式中, 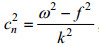
图 7b, c分别对观测海区的浮力频率剖面结构和分解得出的模态垂向结构进行展示。得出各斜压模态后, 在每一时刻都可以利用最小二乘法估计各个模态的振幅系数。Nash等(2004)认为在近表层或者近底层有较多缺测时, 参与最小二乘分解的模态数越多, 分解得到的结果越不稳定, 误差越大。并且由于高模态内潮波通常易于破碎以及耗散, 造成局地的混合, 并不容易远距离传播, 因此实际观测当中非常高模态内潮波的能量也应当并不显著。基于以上考虑, 本文中取模态数n=5。同时更高模态也经过尝试, 但对结果变化影响并不大。图 8展示了内潮前5个模态动能随时间变化及其占总能量的比例(图 7d低通结果)。结果显示, 全日内潮总体呈现高模态结构, 第二模态占优, 可占到全日内潮能量的50%;第一模态次之, 占总能量的27%。而半日内潮第一模态即可占到半日能量的86%, 随着模态数的增加, 能量占总能量的比例逐渐减小。各模态占总能量的比率存在明显的近14天周期变化。
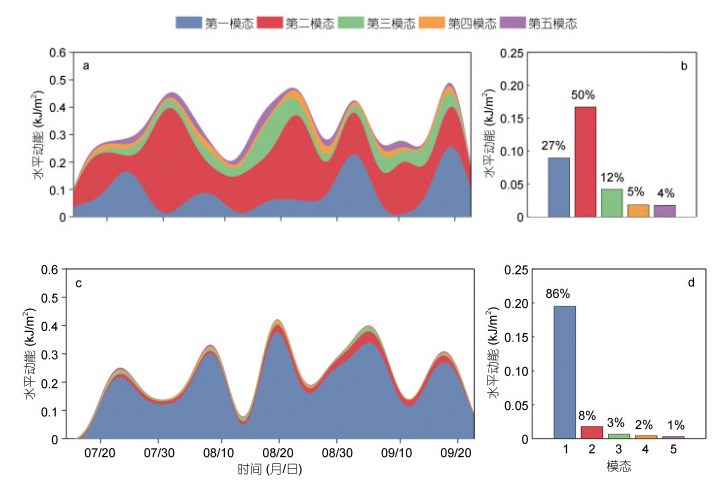 |
| 图 8 内潮前5模态动能的时间序列(a, c)以及占总能量的百分比(b, d) Fig. 8 Time series of HKE of the first five modes diurnal (a) and semidiurnal (c) internal tides, and the corresponding percentage of the total energy (c, d) 注: a, b为全日内潮; c, d为半日内潮 |
为了探讨EOF分解与动力模态分解结果之间的关系, 仿照上述过程, 将其EOF模态也利用动力模态函数进行最小二乘展开。通过检验EOF中各动力模态的占比, 可以有效分析EOF模态的物理意义。
以全日内潮为例进行上述计算, 结果如图 9a所示, EOF1主要对应第二动力模态, 而EOF2反而对应第一动力模态。随EOF模态数的增加, EOF与动力模态的一一对应关系逐渐减弱。这是由于在观测时间范围内, 内潮主要表现出第二模态特征, 所以方差解释率第一的EOF1也就表现为第二模态性质, 而EOF2也相应对应动力第一模态。随着EOF模态数增高, 其所占的方差解释率下降非常迅速, 所以EOF与垂向模态的略微不对应就表现为EOF高模态中多个动力模态的混杂, 如图 9a中EOF5中就已难以找到占主要地位的动力模态。并且由于观测数据常常难以到达全水深, 在观测范围内的动力模态并不正交, 而EOF分解在观测深度范围求正交模态展开, 这就使得二者必然存在着差异。实际上, 观测范围对于EOF结果的物理意义影响非常显著。若将观测范围进一步减小, 例如只取24—109m流场进行EOF分解, 得出的EOF与动力模态之间的一一对应关系会下降非常明显, 如图 9b, 此时的EOF1实际上是动力第一模态与动力第二模态的混合, 而更高阶的EOF2已经难以找到占主导的动力模态项, 混淆现象非常明显。因此, 对于有限观测深度的数据来说, EOF分解的结果难以对应实际的物理意义。
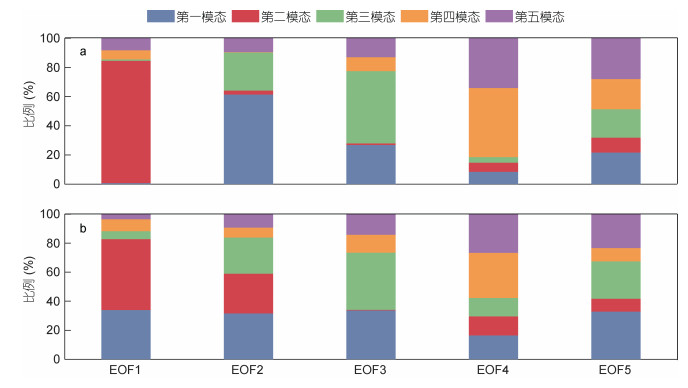 |
| 图 9 EOF模态中各动力模态的占比 Fig. 9 Dynamic modal percentage of EOF modes 注: a 为利用 17—117 米范围全日内潮流速数据得出的 EOF 进行动力分解的结果, b 为利用 25—109 米全日内潮流速数据得出的 EOF 进行动力分解的结果 |
本文通过对2014年南海西北部海域70余天的近全水深流速观测资料的分析, 研究了该海区正压潮、内潮在时间和空间上的结构特点。研究结果表明, 全日正压潮流明显强于半日正压潮流, 且主要以东南-西北方向为主, 潮汐类型为不规则全日潮; 内潮的主轴方向基本沿东南-西北方向, 其中半日分潮呈现往复流特征, 全日分潮呈现旋转潮流特征; 全日内潮强于半日内潮; 通过对各层潮流进行调和分析发现, 除四大分潮外, 内潮中还存在着显著的2Q1、MU2分潮能量, 全日内潮的锁相潮流占全日内潮能量的17.5%, 而对于半日内潮来说, 锁相潮流占半日内潮能量的30%;通过对全日内潮和半日内潮分别进行EOF分解与动力模态分解发现, 全日内潮第二模态占优, 可占到总能量的50%;第一模态次之, 占全日内潮能量的27%。半日内潮以第一模态为主, 占能量的86%。半日内潮与全日内潮垂向模态均表现出约14天的周期变化。随模态增加, EOF与动力模态的一一对应关系逐渐减弱, 到第三模态已经不存在明显的对应关系, 这是由于高模态方差占比太低以及观测深度范围不全导致的。讨论结果显示对于有限深度的潜标观测数据, 利用全水深的温盐剖面进行动力模态分解可能是计算内潮垂向模态更准确的一种方式。
| 王雪竹, 李培良, 张婷婷., 2009. 南海中部深水海盆的潮流垂直结构. 海洋学报, 31(1): 20–27 DOI:10.3321/j.issn:0253-4193.2009.01.003 |
| 中华人民共和国交通部., 1975. 港口工程技术规范. 北京: 人民交通出版社 |
| 方国洪, 曹德明, 黄企洲., 1994. 南海潮汐潮流的数值模拟. 海洋学报, 16(4): 1–12 |
| 司广成, 侯一筠., 2012. 南海北部东沙岛附近的内潮和余流特征. 海洋与湖沼, 43(1): 10–16 |
| 张效谦, 梁鑫峰, 田纪伟., 2005. 南海北部450m以浅水层内潮和近惯性运动研究. 科学通报, 50(18): 2027–2031 DOI:10.3321/j.issn:0023-074X.2005.18.017 |
| 梁辉, 郑洁, 田纪伟., 2016. 南海西北陆坡区内潮与近惯性内波观测研究. 海洋学报, 38(11): 32–42 DOI:10.3969/j.issn.0253-4193.2016.11.003 |
| Buijsman M C, Kanarska Y, McWilliams J C., 2010. On the generation and evolution of nonlinear internal waves in the South China Sea. Journal of Geophysical Research:Oceans, 115(C2): C02012 |
| Cai S Q, Long X M, Gan Z J., 2002. A numerical study of the generation and propagation of internal solitary waves in the Luzon Strait. Oceanologica Acta, 25(2): 51–60 DOI:10.1016/S0399-1784(02)01181-7 |
| Duda T F, Lynch J F, Irish J D, et al, 2005. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea. IEEE Journal of Oceanic Engineering, 29(4): 1105–1130 |
| Gao D L, Jin G Z, Lü X Q., 2017. Temporal variations in internal tide multimodal structure on the continental shelf, South China Sea. Chinese Journal of Oceanology and Limnology, 35(1): 70–78 DOI:10.1007/s00343-016-5168-0 |
| Garrett C, Kunze E., 2007. Internal tide generation in the deep ocean. Annual Review of Fluid Mechanics, 39: 57–87 DOI:10.1146/annurev.fluid.39.050905.110227 |
| Klymak J M, Alford M H, Pinkel R, et al, 2011. The breaking and scattering of the internal tide on a continental slope. Journal of Physical Oceanography, 41(5): 926–945 DOI:10.1175/2010JPO4500.1 |
| Laurent L S, Garrett C., 2002. The role of internal tides in mixing the deep ocean. Journal of Physical Oceanography, 32(10): 2882–2899 DOI:10.1175/1520-0485(2002)032<2882:TROITI>2.0.CO;2 |
| Lee I H, Wang Y H, Yang Y, et al, 2012. Temporal variability of internal tides in the northeast South China Sea. Journal of Geophysical Research:Oceans, 117(C2): C02013 |
| Li D, Chen X, Liu A., 2011. On the generation and evolution of internal solitary waves in the northwestern South China Sea. Ocean Modelling, 40(2): 105–119 DOI:10.1016/j.ocemod.2011.08.005 |
| Li Q, Farmer D M., 2011. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea. Journal of Physical Oceanography, 41(7): 1345–1363 DOI:10.1175/2011JPO4587.1 |
| Ma B B, Lien R C, Ko D S., 2013. The variability of internal tides in the Northern South China Sea. Journal of Oceanography, 69(5): 619–630 DOI:10.1007/s10872-013-0198-0 |
| Nash J D, Alford M H, Kunze E., 2004. Estimating internal wave energy fluxes in the ocean. Journal of Atmospheric and Oceanic Technology, 22(10): 1551–1570 |
| Nash J D, Kunze E, Lee C M, et al, 2006. Structure of the baroclinic tide generated at Kaena Ridge, Hawaii. Journal of Physical Oceanography, 36(6): 1123–1135 DOI:10.1175/JPO2883.1 |
| Qian H, Shaw P T, Ko D S., 2010. Generation of internal waves by barotropic tidal flow over a steep ridge. Deep Sea Research Part I:Oceanographic Research Papers, 57(12): 1521–1531 DOI:10.1016/j.dsr.2010.09.001 |
| Shang X D, Liu Q, Xie X H, et al, 2015. Characteristics and seasonal variability of internal tides in the southern South China Sea. Deep Sea Research Part I:Oceanographic Research Papers, 98: 43–52 DOI:10.1016/j.dsr.2014.12.005 |
| Vlasenko V, Guo C C, Stashchuk N., 2012. On the mechanism of A-type and B-type internal solitary wave generation in the northern South China Sea. Deep Sea Research Part I:Oceanographic Research Papers, 69: 100–112 DOI:10.1016/j.dsr.2012.07.004 |
| Xu Z H, Yin B S, Hou Y J, et al, 2010. A study of internal solitary waves observed on the continental shelf in the northwestern South China Sea. Acta Oceanologica Sinica, 29(3): 18–25 DOI:10.1007/s13131-010-0033-z |
| Xu Z H, Yin B S, Hou Y J., 2011. Multimodal structure of the internal tides on the continental shelf of the northwestern South China Sea. Estuarine Coastal and Shelf Science, 95(1): 178–185 DOI:10.1016/j.ecss.2011.08.026 |
| Xu Z H, Yin B S, Hou Y J, et al, 2013. Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea. Journal of Geophysical Research:Oceans, 118(1): 197–211 DOI:10.1029/2012JC008212 |
| Zheng Q A, Susanto R D, Ho C R, et al, 2007. Statistical and dynamical analyses of generation mechanisms of solitary internal waves in the northern South China Sea. Journal of Geophysical Research:Oceans, 112(C3): C03021 |
 2019, Vol. 50
2019, Vol. 50


