
中国海洋湖沼学会主办。
文章信息
- 柏川棋, 宋金宝, 陈辉. 2019.
- BAI Chuan-Qi, SONG Jin-Bao, CHEN Hui. 2019.
- Stokes漂流近似公式对海洋表层流场估算的影响
- THE IMPACT OF THE ACCURACY OF STOKES DRIFT APPROXIMATION ON ESTIMATION OF OCEAN SURFACE CURRENT
- 海洋与湖沼, 50(1): 12-23
- Oceanologia et Limnologia Sinica, 50(1): 12-23.
- http://dx.doi.org/10.11693/hyhz20180500110
-
文章历史
- 收稿日期:2018-05-08
- 收修改稿日期:2018-06-26
海洋表层是海气动量、热量、水汽交换的主界面, 在气候变化、环境污染等研究中具有重要的地位。Ekman (1905)从理论上解释了由恒定风场驱动的海表洋流偏向主风向右侧这一现象(北半球), 由此开启了对于海洋表层流场的研究。但传统 Ekman 理论与实际观测数据存在不小的偏差, Huang(1979)认为Ekman 流场与风应力的夹角在 10°到 20°之间, 但Cushman-Roisin(1994)得到的偏角在 5°到 10°之间, 为了解决传统 Ekman 理论与观测资料的差异, 后来的研究者对传统的 Ekman 模型进行了修正。
海浪对于海洋上层和大气边界层的动力结构有直接影响, 因此海浪对海洋环流影响一直是研究的焦点。Perrie等(2003)发现在快速发展的强风暴天气下, 由波浪引起的表层海洋流场在传统 Ekman 流场中的比重超过了 40%; Polton等(2005)在传统 Ekman模型中加入了 Stokes-Coriolis 力项, 并用大涡模拟和实测数据进行了检验, 发现该项是上层海洋动力过程的一个重要组分; Tang等(2007)采用 Grand Banks的海洋表层浮标数据和浪流耦合模型研究了海表波浪对于表层流场的影响, 发现考虑波浪效应能够极大地改善模型计算效果; Song(2009)研究了不同垂向涡黏系数结构下海洋随机波浪对于 Ekman 流场的影响, 认为波浪对 Ekman 流场有重要影响。传统的波浪数据主要由浮标观测获得, 相对整个海洋而言, 观测资料十分有限, 因此, 研究者们转而采用近似公式通过波浪要素计算 Stokes漂流, 这些波浪要素来源于海洋卫星遥感观测资料或海浪模式输出结果, 具有非常高的时间和空间分辨率。Breivik等(2016)基于Phillips 谱提出了新的 Stokes 漂流近似公式, 并与单波近似公式和其以前提出的 e 指数近似公式对比, 发现新的近似公式计算的海表 Stokes 漂流剪切项比后两者大得多, 而且新公式计算的 Stokes漂流剖面更接近于实际情况。然而, 到目前为止还没有人研究过Stokes 漂流近似公式精度对海洋表层流场估算的影响, 与谱积分公式计算结果相比, 各种 Stokes 漂流近似公式的偏差有待验证。
第3代海浪数值模式WAVEWATCH III(简称WW3), 由NOAA/NCEP开发用于研究大尺度空间波浪的传播过程, 其考虑了波浪传播过程中地形和海流的空间变化所引起的波浪折射和浅水形变。模式在波浪成长和衰减的能量变化过程中考虑了风生浪作用、白冠的消减作用、海底摩擦和波-波非线性能量传递作用。本文基于海洋卫星遥感数据和WW3模式结果, 采用波浪订正Ekman模型研究Stokes漂流近似公式的精度对于海洋表层流速估算的影响, 并利用拉格朗日浮标观测数据对计算结果进行了验证。
1 数据与方法 1.1 WW3模式设置WW3模式的计算区域位于北太平洋的20°S—70°N, 100°E—310°E, 模式空间分辨率为0.5° × 0.5°, 水深数据来自于ETOPO2, 波浪频率从0.02Hz到0.4852Hz共25个频段, 频率增长因子为1.1421, 波向24个, 分辨率为15°。模式的启动时间设为一个月, 对2013年1月到2013年12月的模拟结果进行计算和分析。模式的风能输入方案采用Ardhuin等(2010)参数化方案, 考虑的主要物理机制包括风能输入、耗散、非线性波-波相互作用。模式在近岸区域考虑了由深度变化引起的波浪破碎和低摩擦效应等近岸物理过程, 并采用了美国国家浮标中心(NDBC, National Data Buoy Center)的有效波高观测数据对WW3模式的输出结果进行验证, 使用了10个浮标共74583条测量数据(WW3模式计算区域和验证浮标站点的位置如图 1所示), 其与WW3模式输出的有效波高的平均相关系数为0.9228, 均方根误差的平均值为0.511m, 说明WW3模式的计算结果是可靠的。
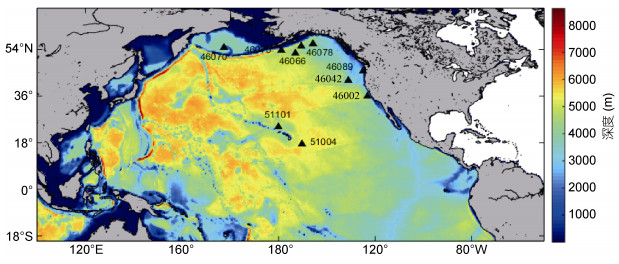 |
| 图 1 模式计算区域地形和NDBC验证浮标的位置 Fig. 1 The bathymetry of model domain and the position of the verifying buoys |
风场作为本文模式的唯一驱动场, 采用了Cross-Calibrated Multi-Platform(CCMP, https://rda.ucar.edu/datasets/ds745.1/)的混合风场数据。该数据由美国宇航局物理海洋学数据分发存档中心(PO.DAAC)提供。CCMP资料的空间分辨率为0.25°, 时间分辨率为6h, 由于其良好的时空分辨率, 该风场资料被广泛的应用于海浪模式中(Zheng et al, 2013; Xu et al, 2017)。
1.2.2 NDBC浮标数据该数据来自美国国家浮标中心(NDBC, http://ww3.ndbc.noaa.gov), NDBC浮标数据包含气象输出资料、连续风资料和海浪频谱资料。气象输出资料有风向、风速、气温、波高、波向等多种数据, 其中波高资料为20min内测量的有效波高平均值, 本文采用NDBC有效波高数据对WW3模式输出结果进行验证。
1.2.3 海表面高度数据该数据来自法国航天局, 海洋卫星数据的归档、验证、处理结果(https://www.aviso.altimetry.fr/en/data/products/sea-surface-height-products), 其空间分辨率为0.25°, 本文采用全球日平均绝对动力地形数据来计算海表地转流场。
1.2.4 拉格朗日浮标数据该数据来自于全球浮标计划(Global Drifter Program, http://www.aoml. noaa.gov/phod/dac/index.php), 用于验证海洋表层流场的计算结果, 拉格朗日浮标测量的流速为拉格朗日速度, 包含了波浪运动, 而本文模型计算的海洋表层流场为欧拉流速, 等于拉格朗日速度减去Stokes漂流速度。我们搜集了57个浮标共55404条观测数据, 其连续观测时长均超过八个月。
1.3 计算方法我们将海洋表层流场分为两部分:地转流场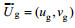
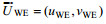
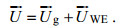 (1)
(1)取笛卡尔坐标系, x向东为正, y向北为正, z向上为正, z = 0为海表面, 采用Boussineq近似, 忽略水平方向的混合, 假设海水密度均匀、流场定常, 此时的地转流场可表示为:
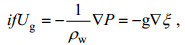 (2)
(2)其中, Ug = ug + ivg为x - y平面上水平复的地转流速, 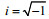
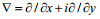
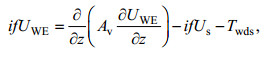 (3)
(3)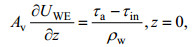 (4)
(4)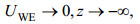 (5)
(5)其中, UWE = uWE + ivWE为x - y平面上水平复的Ekman流速, Us = us + ivs为复的Stokes漂流速度, Twds为波浪破碎引起的动能从波浪向平均流的传递, Av为垂向湍流混合系数, 本文取KPP模型计算(Large et al, 1994; McWilliams et al, 2012), τin为波浪生成引起的风应力减弱, τa = τax + iτay为海表风应力, 由海表 10m高度处的风速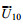
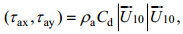 (6)
(6)式中, ρ a为大气密度, Cd为拖曳系数, 根据Jenkins(1989), Twds和τ in可由Sin(f, θ)和Sds(f, θ)源项计算:
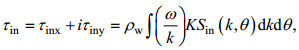 (7)
(7)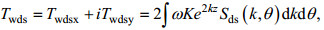 (8)
(8)式中, ω为圆频率, k为波数矢量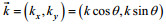
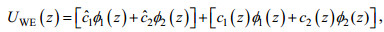 (9)
(9)其中:
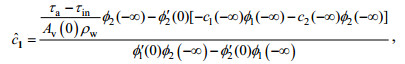 (10)
(10)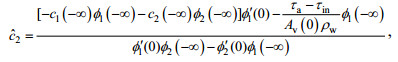 (11)
(11)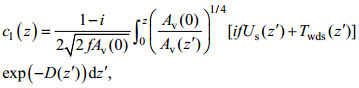 (12)
(12)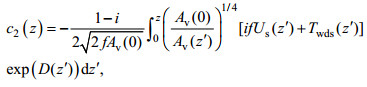 (13)
(13)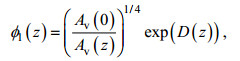 (14)
(14)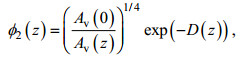 (15)
(15) (16)
(16)WW3模式网格输出的海浪谱是一维的, 根据Webb等(2015), 采用一维海浪谱计算Stokes漂流:
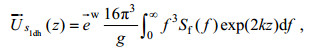 (17)
(17)其中, 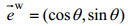
(a) 单波公式(Breivik et al, 2014):
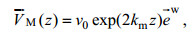 (18)
(18)式中, v0为海表Stokes漂速度, 为了保证单波公式的海表Stokes输送和总的Stokes输送一致, 取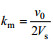
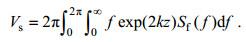 (19)
(19)(b) e指数公式(Breivik et al, 2014):
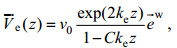 (20)
(20)其中, ke = km/3, Breivik等(2014)发现当C ≈ 8时, 其与Phillips谱计算出的Stokes漂流均方差最小。
(c) Phillips谱近似公式(后面简称Phillips公式, Breivik et al, 2016):
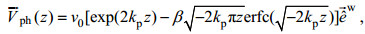 (21)
(21) (22)
(22)Breivik等(2016)使用ERA-Interim北太平洋2010年的再分析资料, 发现取β = 1对大部分海浪谱数据有很好的近似。本文中单波公式、e指数公式和Phillips谱近似公式的v0均为按谱积分公式取值计算出的海表Stokes漂流速度, km、ke、kp均由谱积分公式计算的海表Stokes漂流速度和Stokes输送计算(Breivik et al, 2016)。
2 结果与分析 2.1 Stokes漂流近似公式的敏感性分析为了验证三种Stokes漂流近似公式(18)、(20)、(21)在不同海浪成长状态和风速情况下的精度, 我们取风速5m/s到40m/s, 步长2.5m/s; 波龄0.2到1.2, 步长0.3。分别采用三种近似公式计算Stokes漂流剖面及海表处的剪切项, 并与使用Elfouhaily等(1997)提出的海浪谱公式(后面简称EL谱):
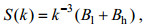 (23)
(23)按积分公式(17)得到的结果进行了对比, 采用标准化均方根误差(NRMS)来描述近似公式和EL谱计算的Stokes漂流剖面偏差, NRMS定义为近似公式与EL谱计算的Stokes漂流剖面速度差的深度积分除以总的Stokes输送(由EL谱计算的Stokes漂流剖面垂向积分获得):
 (24)
(24)式中的H为截断深度, 该深度以下的Stokes漂流速度可以忽略。计算结果如表 1所示, 除了在低风速、低波龄情况下(U10=5m/s、β =0.2), 单波公式的NRMS小于e指数公式和Phillips公式, 其他情况下单波公式的NRMS值均大于其他两个近似公式。当风速达到10m/s后, Phillips公式的NRMS逐渐小于其它两个近似公式, 且随风速增加该趋势愈发明显, 其NRMS值为e指数近似公式的1/4—1/2, 单波公式的1/10—1/6。
| β = 0.2 | β = 0.5 | β = 0.8 | β = 1.2 | ||
| U10 = 5m/s | 1.单波公式 | 0.0013 | 0.1308 | 0.1658 | 0.2036 |
| 2.e指数公式 | 0.0046 | 0.0288 | 0.0268 | 0.0201 | |
| 3. Phillips公式 | 0.0086 | 0.0662 | 0.0771 | 0.0951 | |
| U10 = 10m/s | 1.单波公式 | 0.1452 | 0.2402 | 0.2909 | 0.2918 |
| 2.e指数公式 | 0.0332 | 0.0805 | 0.0989 | 0.0932 | |
| 3. Phillips公式 | 0.0265 | 0.0309 | 0.0336 | 0.0459 | |
| U10 = 20m/s | 1.单波公式 | 0.2241 | 0.3394 | 0.3059 | 0.2032 |
| 2.e指数公式 | 0.0854 | 0.1444 | 0.1291 | 0.0863 | |
| 3. Phillips公式 | 0.0385 | 0.0247 | 0.0196 | 0.0221 | |
| U10 = 40m/s | 1.单波公式 | 0.3176 | 0.2470 | 0.1633 | 0.1198 |
| 2.e指数公式 | 0.1346 | 0.1185 | 0.0720 | 0.0559 | |
| 3. Phillips公式 | 0.0513 | 0.0272 | 0.0213 | 0.0187 |
Elfouhaily等(1997)将Donelan等(1987)提出的海浪谱的低频部分与由大量观测数据约束的高频海浪谱连接起来得到EL谱, 并用风速和波浪观测资料进行了验证, 发现EL谱的计算结果更贴近实测数据。由于WW3模式的可解波浪的最大频率为0.4852Hz, 而高频波浪对于表层Stokes漂流的贡献又十分重要(Breivik et al, 2014), 因此后面采用WW3输出的海浪谱计算Stokes漂流时, 我们将EL谱的高频部分添加到了WW3输出的海浪谱上来考虑高频波浪的影响。
式(23)中的Bl和Bh分别代表长波谱(低频谱)和短波谱(高频谱), Bl的表达式为:
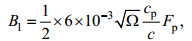 (25)
(25)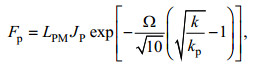 (26)
(26)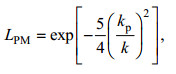 (27)
(27)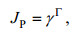 (28)
(28) (29)
(29)Bh的表达式为:
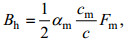 (30)
(30)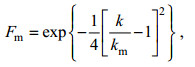 (31)
(31)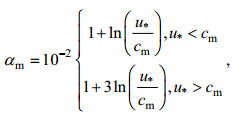 (32)
(32)其中, Ω = U10/cp为反波龄, 取值范围为1 < Ω < 5, U10为10m风速, cp为谱峰相速度, km = 370rad/m, 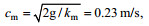
此外, 三种近似公式在不同海浪成长状态和风速下, 在海表z = 0处的Stokes漂流剪切项也存在着明显的差异(图 2), 在低波龄和中、低风速条件下(0m/s < U10 < 17m/s, B = 0.2), 三种公式计算的Stokes漂流剪切项与谱积分(17)的计算结果都很接近, 但随着风速增加, 开始出现差异。其中单波公式与谱积分公式的偏差最大, Phillips公式与谱积分公式的偏差最小, e指数近似公式介于两者之间。此外, 可以看出随风速的增长, 谱积分公式计算的海表Stokes漂流剪切项逐渐增大, 在波龄较小时(B = 0.2), Phillips谱近似公式的计算结果体现了该趋势, 而其他两个公式计算的Stokes漂流剪切项在达到某个阈值后逐渐减小或者稳定不变。最后, 对于给定风速, 海表Stokes漂流剪切项与波龄呈负相关。
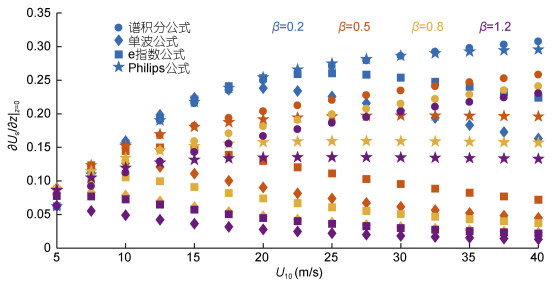 |
| 图 2 不同风速和波龄状态下的海表Stokes漂流剪切项 Fig. 2 The sea surface Stokes drift shear at various wind speeds and wave ages 注:圆点代表谱积分公式, 菱形代表单波公式, 矩形代表e指数公式, 星形代表Phillips公式; 深蓝色代表波龄为0.2, 红色代表波龄为0.5, 橙黄色代表波龄为0.8, 紫色代表波龄为1.2 |
由式(3)可知, Stokes漂流对海表非地转流速估算有直接影响, 我们采用前文给出的波浪订正Ekman模型近似解(9), 将三种不同Stokes漂流近似公式(18)、(20)、(21)和谱积分公式(17)计算的Stokes漂流剖面分别代入其中, 并利用海洋卫星遥感数据和WW3模式输出结果计算了海表非地转流场。Breivik等(2016)指出三种Stokes漂流近似公式计算结果的差异主要集中在海洋表层, 因此我们对计算的非地转流速取5m深度的平均值来进行分析。图 2给出了三种近似公式与谱积分公式计算的非地转流场的相对偏差在北太平洋的年平均结果, 相对偏差的定义为:
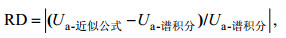 (33)
(33)其中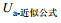
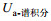
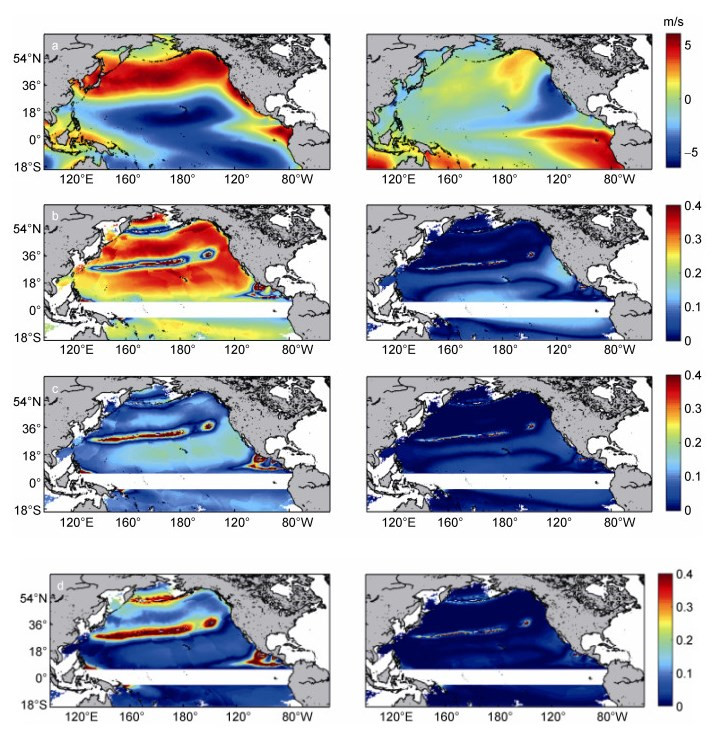 |
| 图 3 三种Stokes漂流近似公式计算的非地转流速的年平均纬向(左)和经向(右)相对偏差: (a)10m高度处的年平均风速(纬向向东为正, 经向向北为正); (b)单波公式的年平均相对偏差; (c)e指数公式的年平均相对偏差; (d)Phillips公式的年平均相对偏差 Fig. 3 The annual average zonal (left) and meridional (right) relative deviation of ageostrophic currents calculated by three different Stokes drift approximations: (a) wind speed at 10m height(The latitudinal direction is positive to the east and the meridional direction is positive to the north); (b) relative deviation of the monochromatic profile (c) relative deviation of the exponential profile (d) relative deviation of Phillips profile |
图 4给出了三种近似公式计算的年平均非地转流速的纬向平均结果[考虑到公式(3)的有效性, 赤道区域除外], 可以看出非地转流速与风速正相关。当风速较小时, 三种近似公式计算出的非地转流速与谱积分公式的计算结果很接近, 但随着风速增大, 单波公式相对于谱积分公式的偏差逐渐加大, 远大于其它两个近似公式。此外, 在低纬度区域(20°S—30°N), Phillips公式计算出的非地转流速比其它两个公式更接近于谱积分公式的计算结果, 在中高纬度区域(> 30°N), Phillips公式和e指数公式的计算结果相差不大。
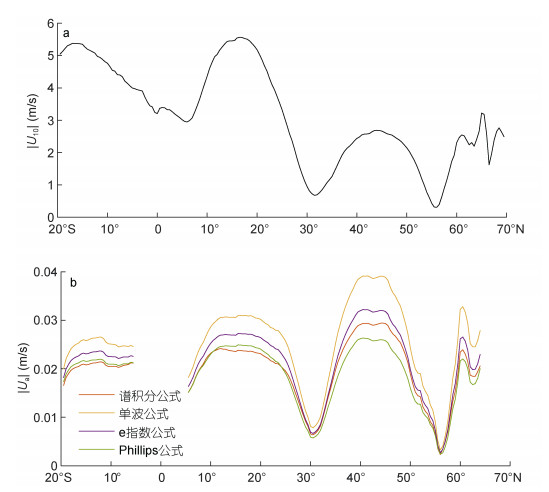 |
| 图 4 三种Stokes漂流近似公式计算出的年平均非地转流速的纬向平均: (a)年平均风速的纬向平均; (b)年平均非地转流速的纬向平均 Fig. 4 The zonal average of annual average ageostrophic currents calculated by three different Stokes drift approximations: (a) zonal average of moduli of annual average wind speed; (b) zonal average of moduli of annual average ageostrophic currents 注:红线为谱积分公式, 橙线为单波公式, 紫线为e指数公式, 绿线为Phillips公式 |
为了进一步验证Stokes漂流近似公式精度对于海洋表层流场计算的影响, 我们选用拉格朗日浮标观测数据对计算结果进行对比验证, 拉格朗日浮标的运动轨迹如图 5所示。
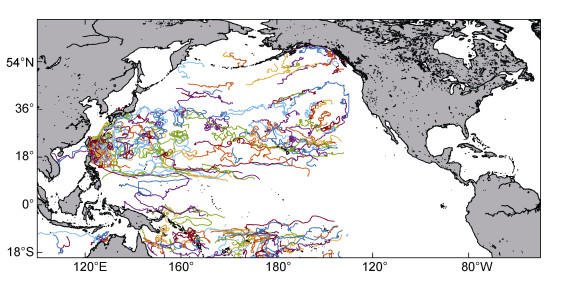 |
| 图 5 拉格朗日浮标运动轨迹 Fig. 5 Trajectories of the Lagrangian drifters for validating the calculated ocean surface currents 注:不同颜色的实线代表不同浮标的运动轨迹 |
由海洋卫星遥感数据估算的海洋表层流场可以代表 15 m深度处的浮标运动(Lagerloef et al, 1999), 浮标测量的流速为15m深度上水团的平均拉格朗日流速:
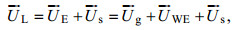 (34)
(34)式中, 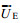
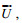
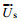
| 浮标ID | 观测量 | 相关系数 | 均方根误差(m/s) | |||||||||||
| 谱积分 公式 |
单波 公式 |
e指数 公式 |
Phillips 公式 |
谱积分 公式 |
单波 公式 |
e指数 公式 |
Phillips 公式 |
|||||||
| 纬向 | 39994 | 1247 | 0.8624 | 0.8565 | 0.8591 | 0.8620 | 0.0856 | 0.0865 | 0.0859 | 0.0856 | ||||
| 经向 | 39994 | 1247 | 0.8443 | 0.8347 | 0.8426 | 0.8447 | 0.0728 | 0.0759 | 0.0733 | 0.0725 | ||||
| 纬向 | 41407 | 1202 | 0.8927 | 0.8881 | 0.8904 | 0.8933 | 0.1708 | 0.1846 | 0.1781 | 0.1731 | ||||
| 经向 | 41407 | 1202 | 0.6203 | 0.6166 | 0.6173 | 0.6206 | 0.1023 | 0.1025 | 0.1034 | 0.1023 | ||||
| 纬向 | 101927 | 1457 | 0.9022 | 0.8983 | 0.8991 | 0.9020 | 0.1850 | 0.2029 | 0.1931 | 0.1858 | ||||
| 经向 | 101927 | 1457 | 0.6267 | 0.6158 | 0.6197 | 0.6261 | 0.1165 | 0.1169 | 0.1180 | 0.1166 | ||||
| 纬向 | 107600 | 1457 | 0.8298 | 0.8292 | 0.8291 | 0.8297 | 0.1930 | 0.1941 | 0.1953 | 0.1930 | ||||
| 经向 | 107600 | 1457 | 0.7689 | 0.7657 | 0.7661 | 0.7695 | 0.1698 | 0.1729 | 0.1722 | 0.1696 | ||||
| 纬向 | 109463 | 1379 | 0.7430 | 0.7340 | 0.7408 | 0.7427 | 0.0959 | 0.1021 | 0.0991 | 0.0962 | ||||
| 经向 | 109463 | 1379 | 0.7124 | 0.7060 | 0.7141 | 0.7124 | 0.1047 | 0.1062 | 0.1044 | 0.1047 | ||||
| 纬向 | 109599 | 1457 | 0.8294 | 0.8219 | 0.8249 | 0.8290 | 0.1209 | 0.1215 | 0.1211 | 0.1209 | ||||
| 经向 | 109599 | 1457 | 0.6937 | 0.6857 | 0.6963 | 0.6927 | 0.1177 | 0.1202 | 0.1172 | 0.1179 | ||||
我们分别计算了三种Stokes漂流近似公式的拉格朗日流速与谱积分公式估算结果的绝对误差和相对偏差, 绝对误差的定义为:
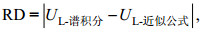 (35)
(35)相对偏差的定义为:
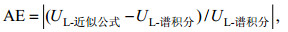 (36)
(36)其中, 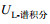
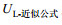
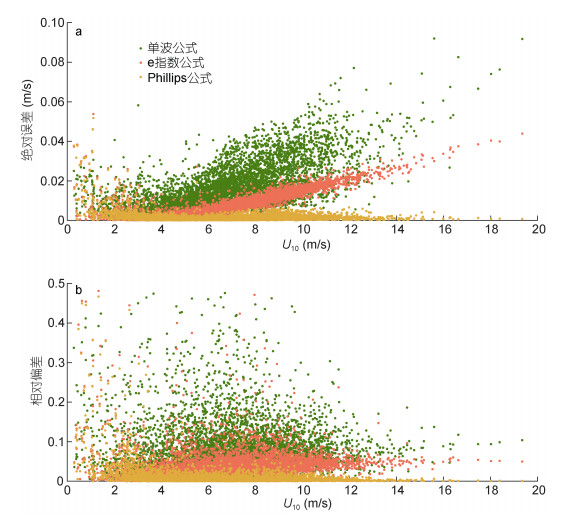 |
| 图 6 不同风速下三种Stokes漂流近似公式计算的拉格朗日流速与谱积分公式计算结果的绝对误差和相对误差: (a)绝对误差; (b)相对偏差 Fig. 6 Absolute error and relative deviation of the Lagrange velocity calculated by three different Stokes drift approximations and spectral integral formula at various wind speeds: (a) absolute error; (b) relative deviation 注:绿点为单波公式, 红点为e指数公式, 橙点为Phillips公式 |
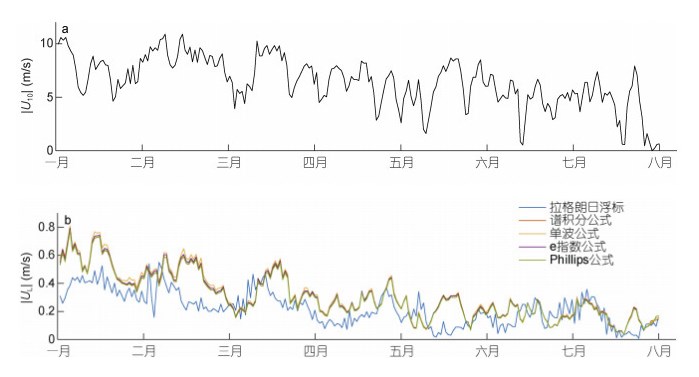 |
| 图 7 不同Stokes漂流公式计算的拉格朗日流速与拉格朗日浮标(42645)观测资料的对比(a)10m高度处风速; (b)拉格朗日流速 Fig. 7 Comparison between the Lagrangian velocities calculated by four different Stokes drift formulas and observations of Lagrangian drifter (42645) observations: (a) wind speed at 10m height; (b) Lagrangian velocities 注:蓝线为浮标数据, 红线为谱积分公式, 黄线为单波公式, 紫线为e指数公式, 绿线为Phillips公式 |
近几年来, 随着海洋遥感卫星的迅速发展, 人们可以获得许多高时空分辨率的海洋观测数据, 然而到目前为止, 遥感卫星还未能够直接对海洋表层流场进行观测, 因此采用能够直接观测的其它海洋环境变量(海表面高度、海表面温度、海表面风速、有效波高等)间接估算是获取海表流场的重要途径。由于海浪谱的实际观测资料较少, 因此人们通常采用近似公式来估算Stokes漂流剖面, 本文分析了不同Stokes漂流近似公式在各种天气条件下与谱积分公式计算结果的偏差, 讨论了Stokes漂流近似公式对海表流场估算的影响。然而, 本文采用了海水密度均匀的假设, 忽略了浮力项对海表流场估算的影响, 因此在下一步的研究中需要考虑浮力项, 深入讨论Stokes漂流近似公式对密度非均匀条件下海表流场估算的影响。
4 结论本文基于海洋卫星遥感数据和WW3模式输出结果, 采用波浪订正的Ekman模型研究了Stokes漂流近似公式精度对于海洋表层流场估算的影响。研究表明, 非地转流速与风速正相关, 且在风速较小时, 三种近似公式计算出的非地转流速与谱积分公式的计算结果接近, 但随着风速增大, 单波公式相对于谱积分公式的偏差逐渐增大, 远超其它两个近似公式。将三种Stokes漂流近似公式计算的海表拉格朗日流速与拉格朗日浮标的观测数据对比, 单波公式的平均相关系数更低, 平均均方根误差更大, 表明Stokes漂流近似公式精度的提高能够优化海表拉格朗日流速的计算结果。与谱积分公式计算的海表拉格朗日流速对比, 单波公式的平均相对偏差为0.0834, e指数公式的平均相对偏差为0.0392, Phillips公式的平均相对偏差为0.0101, 说明Phillips公式在不同风速下均能对谱积分公式有良好的近似效果。在低风速条件下, 计算海洋表层流场时, 由Stokes漂流近似公式精度引起的误差可以忽略不计, 但随着风速增加, 由近似公式精度引起的偏差逐渐变大, 此时应该选择Phillips公式计算Stokes漂流而不是研究者们常用的单波公式, 来减小误差。
| Ardhuin F, Rogers E, Babanin A V, et al, 2010. Semiempirical dissipation source functions for ocean waves. Part I:definition, calibration, and validation. Journal of Physical Oceanography, 40(9): 1917–1941 DOI:10.1175/2010JPO4324.1 |
| Breivik , Janssen P A E M, Bidlot J R., 2014. Approximate stokes drift profiles in deep water. Journal of Physical Oceanography, 44(9): 2433–2445 DOI:10.1175/JPO-D-14-0020.1 |
| Breivik , Bidlot J R, Janssen P A E M., 2016. A Stokes drift approximation based on the Phillips spectrum. Ocean Modelling, 100: 49–56 DOI:10.1016/j.ocemod.2016.01.005 |
| Cushman-Roisin B., 1994. Introduction to Geophysical Fluid Dynamics. Englewood Cliffs N J, USA: Prentice-Hall Press, 320 |
| Donelan M A, Pierson Jr W J., 1987. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry. Journal of Geophysical Research, 92(C5): 4971–5029 DOI:10.1029/JC092iC05p04971 |
| Ekman V W., 1905. On the influence of the earth's rotation on ocean-currents. Arkiv f r Matematik, Astronomi Och Fysik, 2(11): 1–52 |
| Elfouhaily T, Chapron B, Katsaros K, et al, 1997. A unified directional spectrum for long and short wind-driven waves. Journal of Geophysical Research, 102(C7): 15781–15796 DOI:10.1029/97JC00467 |
| Huang N E., 1979. On surface drift currents in the ocean. Journal of Fluid Mechanics, 91(1): 191–208 DOI:10.1017/S0022112079000112 |
| Jenkins A D., 1989. The use of a wave prediction model for driving a near-surface current model. Deutsche Hydrografische Zeitschrift, 42(3-6): 133–149 DOI:10.1007/BF02226291 |
| Komen G J, Cavaleri L, Donelan M, et al, 1994. Dynamics and Modelling of Ocean Waves. Cambridge: Cambridge University Press, |
| Lagerloef G S E, Mitchum G T, Lukas R B, et al, 1999. Tropical pacific near-surface currents estimated from altimeter, wind, and drifter data. Journal of Geophysical Research, 104(C10): 23313–23326 DOI:10.1029/1999JC900197 |
| Large W G, McWilliams J C, Doney S C., 1994. Oceanic vertical mixing:a review and a model with a nonlocal boundary layer parameterization. Reviews of Geophysics, 32(4): 363–403 DOI:10.1029/94RG01872 |
| McWilliams J C, Huckle E, Liang J H, et al, 2012. The wavy ekman layer:langmuir circulations, breaking waves, and reynolds stress. Journal of Physical Oceanography, 42(11): 1793–1816 DOI:10.1175/JPO-D-12-07.1 |
| Perrie W, Tang C L, Hu Y, et al, 2003. The impact of waves on surface currents. Journal of Physical Oceanography, 33(10): 2126–2140 DOI:10.1175/1520-0485(2003)033<2126:TIOWOS>2.0.CO;2 |
| Polton J A, Lewis D M, Belcher S E., 2005. The role of wave-induced coriolis-stokes forcing on the wind-driven mixed layer. Journal of Physical Oceanography, 35(4): 444–457 DOI:10.1175/JPO2701.1 |
| Song J B., 2009. The effects of random surface waves on the steady Ekman current solutions. Deep Sea Research Part I:Oceanographic Research Papers, 56(5): 659–671 DOI:10.1016/j.dsr.2008.12.014 |
| Song J B, Huang Y S., 2011. An approximate solution of wave-modified Ekman current for gradually varying eddy viscosity. Deep Sea Research Part I:Oceanographic Research Papers, 58(6): 668–676 DOI:10.1016/j.dsr.2011.04.001 |
| Tang C L, Perrie W, Jenkins A D, et al, 2007. Observation and modeling of surface currents on the grand banks:a study of the wave effects on surface currents. Journal of Geophysical Research, 112(C10): C10025 DOI:10.1029/2006JC004028 |
| The Wamdi Group., 1988. The WAM model-a third generation ocean wave prediction model. Journal of Physical Oceanography, 18(12): 1775–1810 DOI:10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2 |
| Webb A, Fox-Kemper B., 2015. Impacts of wave spreading and multidirectional waves on estimating stokes drift. Ocean Modelling, 96: 49–64 DOI:10.1016/j.ocemod.2014.12.007 |
| Xu Y, Bi F, Song J B, et al, 2017. The temporal and spatial variations in the pacific wind and wave fields for the period 2002-2011. Acta Oceanologica Sinica, 36(3): 26–36 DOI:10.1007/s13131-017-1039-6 |
| Zheng C W, Pan J, Li J X., 2013. Assessing the China Sea wind energy and wave energy resources from 1988 to 2009. Ocean Engineering, 65: 39–48 DOI:10.1016/j.oceaneng.2013.03.006 |
 2019, Vol. 50
2019, Vol. 50


