中国海洋湖沼学会主办。
文章信息
- 谢成玉, 肖薇, 徐敬争, 朱珊娴, 胡勇博, 李旭辉. 2019.
- XIE Cheng-Yu, XIAO Wei, XU Jing-Zheng, ZHU Shan-Xian, HU Yong-Bo, LI Xu-Hui. 2019.
- 氢和氧稳定同位素示踪湖泊蒸发的对比研究
- COMPARISON OF USING HYDROGEN AND OXYGEN ISOTOPES IN TRACING WATER EVAPORATION IN TAIHU LAKE
- 海洋与湖沼, 50(1): 74-85
- Oceanologia et Limnologia Sinica, 50(1): 74-85.
- http://dx.doi.org/10.11693/hyhz20180300064
-
文章历史
- 收稿日期:2018-03-25
- 收修改稿日期:2018-10-15
2. 南京信息工程大学江苏省大气环境与装备技术协同创新中心 南京 210044;
3. 江苏省无线电科学研究所有限公司 无锡 214073;
4. 清华大学地球系统科学系 北京 100084
2. Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing 210044, China;
3. Jiangsu Radio Scientific Institute Co., LTD, Wuxi 214073, China;
4. Department of Earth System Science, Tsinghua University, Beijing 100084, China
稳定同位素方法能为水文学、古气候学和气象学研究提供独特的示踪信息。由于较轻的水分子(1H216O)和较重的水分子(H2HO和H218O)的饱和水汽压和扩散率不同, 在水汽相变过程中, 较重的水分子会在液态水中富集, 从而形成同位素分馏效应, 这是稳定同位素方法示踪水循环的基础。氢氧稳定同位素(H2HO和H218O)可应用于反演古气候变化(Jouzel et al, 2007; Steffensen et al, 2008), 追踪水分传输过程(Kebede et al, 2012), 量化水资源分布(Evaristo et al, 2015; Wassenaar et al, 2011), 也是探讨湖泊水循环机理的最理想手段(Longinelli et al, 2008; Bouchez et al, 2016)。稳定同位素方法不仅能在全湖尺度上较为准确地计算出蒸发量(包为民等, 2007)和其他水平衡参数(Elmarami et al, 2017), 而且能通过水体中H2HO和H218O的富集信息反映出区域水体的水文状况(Bocanega et al, 2013; Qian et al, 2014)和局地气象要素的变化特征(Yao et al, 2013; Tan, 2014), 提供丰富的时空变化信息(史晓宜等, 2016)。因此, 对于氢氧同位素在自然条件下的富集情况和控制机制研究是非常重要的。
湖泊蒸发是水循环的重要过程, 稳定同位素方法也被广泛用于计算湖泊蒸发。湖泊蒸发既是水循环中的重要过程, 也是地表水耗散中不可忽视的一项(Bateni et al, 2012)。湖泊分布广泛, 约占全球非冰川陆地面积的3.7%(Verpoorter et al, 2014), 湖泊内生物活动极为频繁(Cole et al, 2007)。湖泊是珍贵的地表水资源, 与人类活动密切相关。大型湖泊的蒸发不仅会影响区域地表能量平衡, 甚至会影响区域降水状况和干湿特征(Samuelsson et al, 2010; Zhao et al, 2012), 乃至全球的气候变化(Xu et al, 1998)。因此大型湖泊蒸发的特征、机制及量化是生态、水文、农业和气象等领域一直关注的热点问题(Lenters et al, 2005)。蒸发过程中的氢氧稳定同位素分馏的机制研究是稳定同位素方法在水循环研究中的关键。由于同位素分馏效应, 湖泊水量的各个收支项(包括降水、入湖河水、出湖河水和湖面蒸发)的同位素组分有明显差异。水量平衡方程各项乘以对应的同位素组分, 就形成同位素质量守恒方法。同位素质量守恒方法已经被广泛地用于湖泊水循环的研究, 如北美洲的五大淡水湖(Gat et al, 1994; Jasechko et al, 2014)、非洲的爱德华湖(Russell et al, 2006)、北极湖泊(Gibson, 2002)、日本的琵琶湖(Taniguchi et al, 2000)、俄罗斯的贝加尔湖(Seal II et al, 1998)、中国的青海湖(包为民等, 2007)和青藏高原典型湖泊(高晶等, 2008)等湖泊。
开放水面蒸发的同位素富集机制是稳定同位素方法的关键问题。水面蒸发的同位素组分一般采用Craig和Gordon推出的模型计算(简称Craig-Gordon模型)(Craig et al, 1965)。基于水体和大气水汽的稳定同位素组分(δL和δV)、大气相对于水表温度的相对湿度(h), 并考虑平衡分馏系数(εeq)和动力学分馏系数(εk), Craig-Gordon模型可以计算开放水面蒸发的同位素组分(δE)。其中不确定性较大的是动力学分馏系数(εk)(Xiao et al, 2017)。在野外条件下, 动力学分馏效应既受到分子扩散过程的影响, 也受到湍流传输过程的影响, 而如何量化湍流过程的影响程度是难点。对于湖泊蒸发, 大部分研究中εk的取值是基于实验室的观测结果, 为常数(H2HO和H218O的εk分别是12.5‰和14.2‰, 简称LK系数)(Gonfiantini, 1986; Gibson et al, 2016a; Arnoux et al, 2017)。但是海洋研究中的εk通常是用物理模型推导得到的(Merlivat et al, 1979), 在水面风浪较小的情况下, 取值约为5.5‰和6.2‰(简称OS系数)。由此可见, 湖泊和海洋研究中两种算法差异很大。对于在野外条件下检验湖面εk的研究一度受到δE观测技术的限制, Xiao等(2017)将离轴积分腔输出光谱系统与通量扩散法相结合, 原位在线观测太湖δE, 通过18O稳定同位素对Craig-Gordon模型进行了直接检验, 发现对于太湖δE, OS系数更适用于野外条件下的湖泊蒸发。本文不仅使用18O, 而且通过2H这种稳定同位素手段进一步验证动力学分馏系数的参数化方案在亚热带大型浅水湖泊的适用性。
2H和18O这两种稳定同位素的示踪效果也一直是争议较大的一个问题。迄今为止, 大多数学者采用18O的计算, 因其精度较高, 同位素分馏模拟计算和观测方法更为成熟(Gat, 1970; Vogt, 1976; Gao et al, 2011)。Zimmermann等(1970)认为因2H相对稳定大力提倡2H的使用。而Jasechko等(2014)同时使用两种同位素作为示踪剂, 通过调整蒸发对大气水汽贡献的比例使两种算法的结果逼近, 将逼近的结果作为Great Lakes的蒸发量, 但计算结果明显低于水量平衡法和涡度相关法研究得到的结果。Xiao等(2017)发现采用氢同位素作为示踪剂, 计算得到的湖泊蒸发量对动力学分馏系数的参数化方案不敏感, 从而提出了氢同位素可能更适用于稳定同位素质量守恒方法的假设。但是该文章并未对稳定同位素质量守恒模型中各个变量的时空变化特征及其不确定性进行充分地描述和讨论。那么, 2H和18O这两种稳定同位素哪一个更适用于示踪湖泊蒸发?要明确这个问题, 就需要在稳定同位素质量守恒模型的框架下, 同步观测各个水分收支项的同位素组分, 平行对比两种同位素示踪的结果, 充分讨论其异同及机理。
针对以上问题, 本文将以太湖为研究对象, 在同步观测湖水和大气水汽H2HO和H218O组分的时空变化规律和影响因素的基础上, 将同位素质量守恒方程和Craig-Gordon模型相结合计算湖面蒸发量, 通过详细对比2H和18O在整个参数化方案中的差异及在同位素分馏机理上的差异, 重点检验采用两种同位素作为示踪剂的情况下稳定同位素质量守恒法在大型开放浅水湖泊中的适用性, 探讨动力学分馏系数的参数化方案对蒸发量模拟值的影响, 进一步验证了Xiao等对两种同位素在C-G模型与同位素质量守恒耦合过程中的假设。本文以太湖为例, 结合大量前人的经验, 以开放性的方式讨论了2H和18O稳定同位素对湖泊蒸发的示踪效果和各自的优缺点, 解释了2H稳定性的原因和18O广泛运用的便利, 以期为稳定同位素水文学研究提供数据支持和科学参考。
1 材料与方法 1.1 实验站点本研究以太湖为研究对象, 太湖地处长江三角洲南部, 位于江、浙两省交界处, 湖泊面积约2400km2, 是我国第三大淡水湖泊, 属于典型的大型浅水湖泊。太湖流域位于亚热带季风气候区, 多年平均气温16.2℃, 平均降水量1122mm(Lee et al, 2014), 总蓄水量可达57.7×108m3, 平均水深小于1.9m, 多年平均天然年径流量为160.1×108m3。
1.2 实验观测 1.2.1 水汽同位素观测在中国科学院太湖湖泊生态系统试验站(31°25′11″N, 120°12′50″E), 开展大气水汽H2HO和H218O同位素组分的原位连续观测(图 1)。该试验站位于太湖北部的梅梁湾湾口, 观测仪器为基于离轴积分腔输出光谱技术的水汽同位素分析仪(Model 911-0004, Los Gatos Research, Mountain View, CA, USA), 进气口距离水面3.5m, 同步观测大气水汽δV中H2HO和H218O组分, 其月均值最终输入公式(6)中用于计算δE。
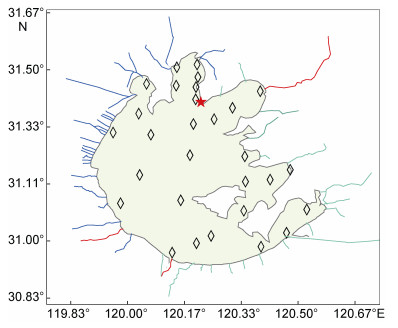 |
| 图 1 太湖采样点示意图 Fig. 1 Sampling sites in the Taihu Lake 注:五角星表示位于太湖北部的梅梁湾湾口处中国科学院太湖湖泊生态系统试验站, 菱形代表湖面上的生态采样点, 蓝线代表入湖河流, 绿线代表出湖河流, 红线代表入/出湖河流 |
湖水同位素组分的采样包括每日定点采样和每季度空间采样(图 1)。在太湖湖泊生态系统试验站内进行定点采样, 采样点距离湖岸250m, 采样时间为每日13:00。空间采样在太湖湖面上的29个采样点进行, 2015年每季度开展一次采样, 具体时间为2月5日、5月22日、8月20日和11月17日。用300ml的玻璃瓶收集水面以下20cm深度处的湖水, 封口后存放在4℃的冰箱内冷藏, 过滤处理后送往中国科学院地理科学与资源研究所生态系统网络观测与模拟实验室, 采用液态水同位素分析仪(Model DLT-100, Los Gatos Research, Mountain View, CA, USA)测定水样中H2HO和H218O的组分。
1.2.3 河水同位素观测观测期间选取51个主要河道采集水样。根据2009年太湖水文巡测资料, 基于监测的总河流水量占太湖的总出入水量80%以上的原则, 且所有断面距太湖段之间没有其他支流汇入, 选择了这51个巡测站点断面。在全湖湖水采样的同一天, 绕湖分别采集这51条河道水样, 并记录各河道的水流方向。河水采样和分析方法同湖水样品。
1.2.4 湖面蒸发和气象要素观测试验期间在太湖湖泊生态系统试验站连续观测湖面蒸发量和气象要素。其中三维超声风速计(CSAT3, Campbell Scientific Inc., Logan, UT)和开路式红外气体分析仪(LI7500, LiCor, Lincoln, NE)观测三维风速、水汽密度和CO2密度; 用四分量辐射计(CNR4, Kipp & Zonen B. V., Delft, The Netherlands)观测向上和向下的长短波辐射, 从而计算净辐射; 在小气候观测系统中, 用温湿度传感器(HMP155A, Vaisala Inc., Helsinki, Finland)观测空气温度和湿度等气象要素。水表面温度根据斯蒂芬-玻尔兹曼定律用天空长波辐射和水面长波辐射的观测值计算得到。
1.3 模型方法 1.3.1 同位素质量守恒法对于一个内陆湖泊而言, 水量平衡方程为:
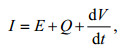 (1)
(1)式中, V为湖泊的蓄水量, dV/dt表示湖泊蓄水量的变化量; I为总入湖水量(包括总入湖河水量i和降水量p, 即I=i+p); E为蒸发量; Q为总出湖水量; 本试验中忽略湖水与地下水之间的交换。
水量平衡方程各项乘以其稳定同位素组分, 即可推导出湖泊的同位素质量守恒方程(Dincer, 1968):
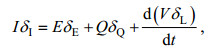 (2)
(2)式中, δL为全湖湖水同位素组分的平均值; δI由δI×I= Σ(δi×i+δP×p)公式计算得出, 即δI=Σ(δi×i+δP×p)/I; δE为湖面蒸发水汽的同位素组分; δQ为太湖的出湖河水同位素组分的权重平均值。
将公式(1)与公式(2)结合消除Q, 即可计算出蒸发量:
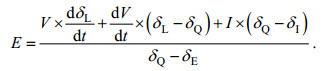 (3)
(3)本文采用公式(3)计算太湖年蒸发量, 时间步长为1个月。太湖入湖水量i、出湖水量Q和蓄水量V来源于太湖网(http://www.tba.gov.cn/)2015年1—12月《水情月报》。降水量p是太湖周边的无锡、东山、湖州气象站降水量的平均值。公式(3)中各同位素组分项的计算方法不尽相同。对于湖水同位素组分而言, 29个采样点的δL值取算数平均值, 作为当天的全湖δL; 然后对时间序列做线性内插, 获得每日δL; 进而算出全湖δL的月均值和该月δL的变化量dδL/dt。对于河水同位素组分而言, 依据燕姝雯等(2009)曾观测环太湖各河道水量, 计算各个分区(湖西区、武澄锡虞区、阳澄淀泖区、杭嘉湖区、浙西区、太浦闸、望亭水利枢纽)的δi和δQ水量权重值; 再根据水情月报中太湖各区水量, 计算入湖和出湖水量权重的δi和δQ; 该δi和δQ代表采样当日的数值, 对时间序列做线性内插, 获得每日δi和δQ, 进而计算出各月δi和δQ。
降水同位素组分根据中国科学院常熟农业生态试验站观测试验得到的经验公式计算(Liu et al, 2014), 降水中氧同位素组分δ18OP根据月平均气温T(℃)和月总日照时数S(h)的经验公式模拟得出(见公式(4)), 降水中的氢同位素组分δ2HP由公式(5)可得:
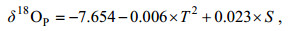 (4)
(4)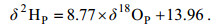 (5)
(5)太湖蒸发水汽中氢氧同位素组分用Craig-Gordon模型计算:
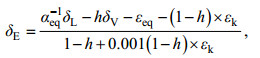 (6)
(6)式中, h代表大气相对于水面的相对湿度, 等于大气实际水汽压ea与水面饱和水汽压es(TS)的比值; δL为全湖湖水同位素组分的平均值; δV是大气水汽的H2HO或H218O组分; εeq和αeq都是平衡分馏系数, 其中αeq > 1, 无量纲; εeq=103(1–1/αeq), 单位为‰。平衡分馏系数主要受温度的影响, 计算方法如下:
对于H2HO:
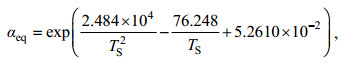 (7)
(7)对于H218O:
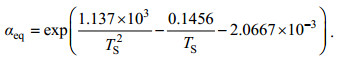 (8)
(8)式中, TS是太湖水表面温度(K), 基于斯蒂芬玻尔兹曼定律用天空长波辐射(Ld, W/m2)和水面长波辐射(Lu, W/m2)计算, 公式为: TS=[(Lu–(1-ε)×Ld)/εσ]1/4, 其中ε代表湖泊表面比辐射率(ε=0.97), σ代表斯蒂芬玻尔兹曼常数(σ=5.67×10–8W/(m2K4))。平衡分馏系数计算方法的不确定性较小, 是目前普遍被接受的计算方法。
在Craig-Gordon模型中, 动力学分馏系数的不确定性比较大(Xiao et al, 2017)。目前大多数人(Gibson et al, 2016b; Gibson et al, 2017)研究湖泊等各类内陆水体时采用εk数值分别为12.5‰(H2HO)和14.2‰ (H218O)。然而Merlivat和Jouzel通过物理学模型得到海洋蒸发的动力学分馏系数εk是风速u的函数关系, 如果采用3.5m高度处的风速, 则函数关系为:
对于H2HO:
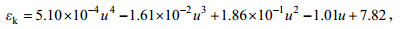 (9)
(9)对于H218O:
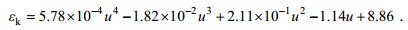 (10)
(10)由于Xiao等(2017)的研究已经表明OS系数更适用于太湖蒸发同位素富集过程研究, 本研究中的默认εk是采用OS系数的算法。
1.3.2 Priestley-Taylor模型Priestley-Taylor模型是基于能量平衡得出的计算水面蒸发的模型(Priestley et al, 1972)。利用该模型计算太湖蒸发的具体公式:
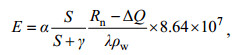 (11)
(11)式中, α为Priestley-Taylor常数(默认值为1.26); S为饱和水汽压-气温曲线的斜率(Pa/℃); γ为干湿表常数(Pa/K); Rn为净辐射(W/m2); λ为蒸发潜热(J/kg); ΔQ为水体热储量变化量(W/m2); ρw为水汽密度(kg/m3)。需要特别指出的是, 由于本文的涡度相关观测站点位于岸边, 只有当风从湖面方向吹来时观测的水汽通量信号能代表湖泊蒸发, 经过风向筛选后的湖面蒸发数据空缺较多, 即便做数据差补, 计算月蒸发量的误差仍然较大。而Lee等(2014)和Wang等(2014)对比Priestly-Taylor模型和太湖多个站点上多年涡度相关法的观测结果, 发现采用默认α值的Priestley-Taylor模型模拟的月蒸发量与观测结果相近(偏差小于4%)。因此, 本文采用该模型的模拟结果作为参考值, 评价稳定同位素质量守恒模型的估算结果。
2 结果与分析 2.1 太湖湖水和河水中氢氧稳定同位素组分的空间和时间变化特征 2.1.1 太湖湖水和河水中氢氧稳定同位素组分的空间变化特征2015年太湖湖水氢氧同位素组分δ2HL、δ18OL和过量氘dL(dL=δ2HL-8δ18OL)的季节空间分布特征如图 2所示。每季度太湖湖水氢氧同位素组分都是在太湖东南部区域最为富集, δ2HL在5月达到最大值-20.7‰, δ18OL也在5月达到最大值-2.9‰。而δ2HL和δ18OL的每季度贫化区域大多出现在太湖北部, δ2HL和δ18OL在2月均达到最小值, 分别是-53.8‰和-7.9‰。湖水δ2HL和δ18OL在5月全湖差异性最小, 分别是6.3‰和1.5‰。δ2HL在11月全湖差异性最大, 可达29.1‰; δ18OL在2月全湖差异性最大, 为4.5‰。在太湖东北角区域, 太湖湖水δ2HL和δ18OL在冬季和秋季都相对较低。太湖湖水过量氘dL空间分布特征与δ2HL和δ18OL相反, 各个季节的dL高值出现在西北部和中部区域, 8月出现最大值11.7‰, 而dL低值主要分布在太湖东部, 5月出现最低值–3.8‰, dL在5月全湖差异性最大, 为14.5‰, 在2月全湖差异性最小, 为9.4‰。
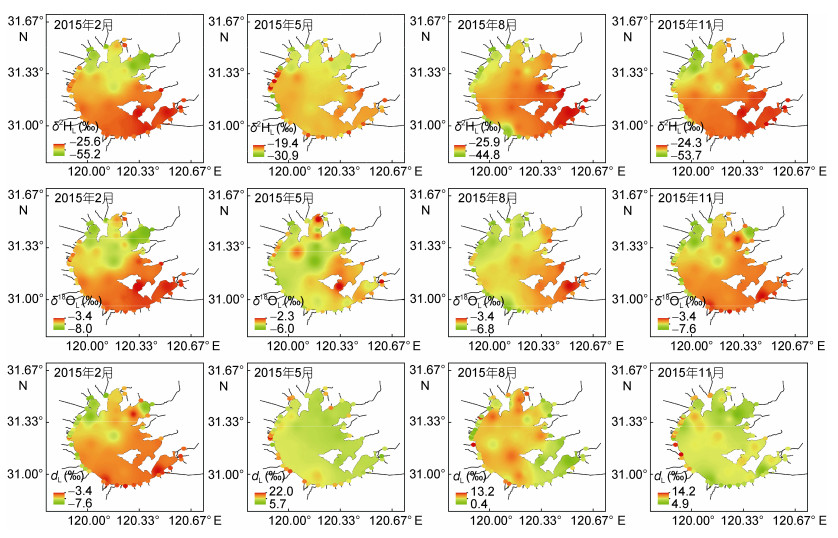 |
| 图 2 2015年太湖湖水和河水同位素组分的空间分布 Fig. 2 The spatial patterns of isotopic compositions of Taihu Lake water and its tributary rivers water in 2015 |
2015年每季度太湖河流中氢氧同位素组分δ2HL、δ18OL和过量氘dL如图 2所示。河流中氢氧同位素组分的分布趋势与太湖湖水的分布特征相似, 呈现东南部的河流氢氧同位素组分较为富集的特征, δ2HL在5月达到最大值-19.4‰, δ18OL也在5月达到最大值-2.3‰, 均比太湖湖水同位素组分的最高值偏高。每季度河流δ2HL、δ18OL的低值大部分出现在太湖的西侧, 其中δ2HL和δ18OL的最低值均出现在2月, 分别为-55.2‰和-8.0‰。河流δ2HL和δ18OL的空间差异性比太湖湖水空间差异性大, 最大值均出现在2月, 可达29.6‰和4.6‰; 河流δ2HL在5月空间差异性最小, 为11.5‰, 河流的δ18OL在8月空间差异性最小, 为3.4‰。河流过量氘dL与湖水dL相似, 河流dL的空间分布与δ2HL和δ18OL相反, 高值大部分在太湖西部, 低值主要分布在太湖东南部, 其中最高值和最低值均在5月出现, 分别为22.0‰和5.6‰, 在5月空间差异性最大, 为27.7‰, 而在2月差异性最小, 为11.4‰。
2.1.2 太湖湖水和河水中氢氧稳定同位素组分的时间变化规律2015年太湖湖水氢氧稳定同位素组分的时间变化规律如图 3所示。对于每季度空间采样而言, 全湖δ2HL和δ18OL的平均值在2月均达到最小值, 分别为-35.9‰±7.4‰(平均值±空间采样点数据的1倍标准差)和-5.1‰±1.2‰; 在5月均达到最大值, 分别为-24.3‰±1.4‰和-3.7‰±0.3‰; 全湖dL平均值在8月达到最大值, 为7.1‰±2.7‰。对于每天定点采样而言, 从梅梁湾湖水同位素组分的时间序列可以看出, δ2HL、δ18OL和dL的全年变化范围分别为-42.5‰— -21.8‰、-6.8‰— -2.7‰和-11.1‰—18.2‰; 2015年δ2HL和δ18OL变化趋势一致, 从4月开始逐渐富集并在6月中旬达到最大值, 随后逐渐贫化, 在7月份达到最小值, dL的变化趋势正好相反。对比空间采样获得的全湖平均值与定点采样获得的单点数据, 可以发现二者变化趋势一致, 但存在系统差异, 全湖δ2HL、δ18OL和dL平均值与同期的梅梁湾湖水同位素组分的差值的变化范围为: 0.7‰—3.7‰、-0.2‰—0.8‰和-3.1‰—2.4‰。
图 3同时展示了2015年每季度太湖入湖河流和出湖河流的氢氧同位素组分的平均值。从时间变化上看, 入湖河流的δ2HL、δ18OL和dL在2月达到最低值, 分别是-43.1‰、-6.2‰和6.6‰, 并在5月达到最大值, 分别是-25.5‰、-4.3‰和9.1‰。同时出湖河流的δ2HL、δ18OL和dL也在5月达到最高值, 分别是-22.3‰、-3.6‰和6.9‰, 但在8月达到最低值, 分别是-31.2‰、-4.7‰和6.7‰。对比发现, 出湖河流的δ2HL、δ18OL最为富集, 湖水其次, 入湖河流最低; 然而三者的dL相差不大, 较为接近。
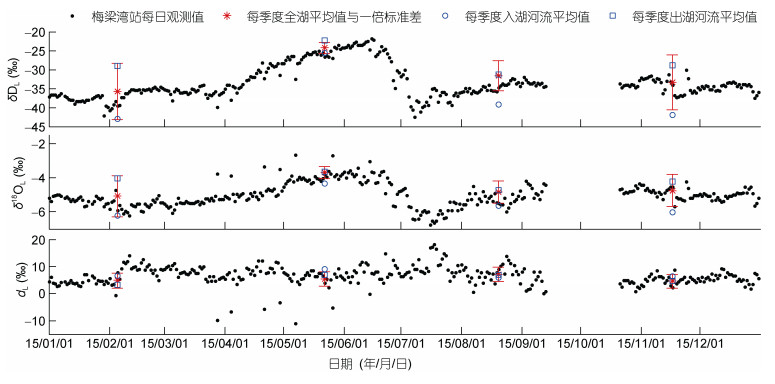 |
| 图 3 2015年太湖湖水和河水的氢氧同位素组分的时间序列 Fig. 3 The time series of isotopic compositions of the Taihu Lake water and its tributary rivers water in 2015 |
2015年太湖水量收支各项的时间序列图如图 4所示。其中总入湖水量和总出湖水量在太湖各项水量收支中所占比重分别为10.9%和11.4%。太湖各项水量存在显著的季节变化, 在夏季较高。2015年6月24日—7月1日太湖遭遇了罕见的连续强降水天气, 6月太湖降水量猛增, 高达599mm, 周边河道的总入水量i也在6月达到最大值, 同期太湖总出水量Q相对较低, 但也高于其它月份。湖泊蓄水量V逐渐增加并在7月达到峰值, 随后太湖水量逐渐降低。
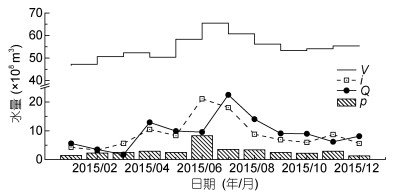 |
| 图 4 太湖各项水量的时间序列图 Fig. 4 The time series of Taihu Lake water budgets 注: V表示湖泊的蓄水量, i表示入湖水量出湖水量, Q表示出湖水量, p表示降水量 |
用Priestley-Taylor模型计算的2015年太湖的月蒸发量的时间序列和气象观测数据如图 5所示。2015年1—5月气温逐渐升高, 近地面大气压强减小, 月蒸发量逐渐增加; 6月因降雨频繁, 水表净辐射明显下降, 该月蒸发量骤减; 7月和8月蒸发量再次升高, 8月达到全年最高(月蒸发量174mm); 9月入秋后气温下降, 蒸发量逐月递减。
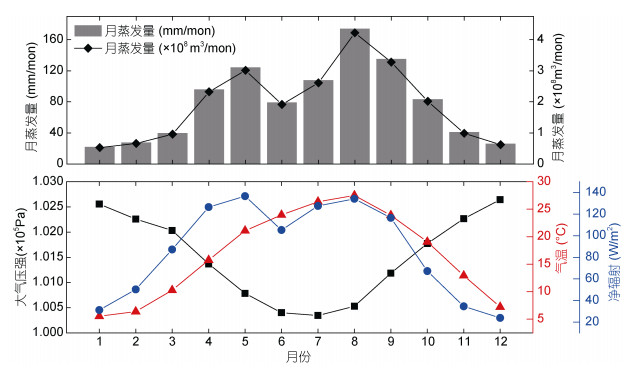 |
| 图 5 2015年每月太湖的蒸发量模拟值、以及气压、气温和水表净辐射观测值 Fig. 5 The simulated monthly evaporation and observed atmospheric pressure, air temperature, and net radiation at water surface in Taihu Lake in 2015 |
就太湖的年蒸发量而言, 研究者们也采用多种方法进行了估算。本文Priestley-Taylor模型估算的2015年太湖总蒸发量总计2.3×109m3, 即953mm。沈行毅采用彭曼修正法估算的太湖年均蒸发量约为1000mm/年(沈行毅, 1984); Qin等(2007)用水量平衡方程计算了太湖在2001年5月—2002年4月的蒸发量约为760mm; 而高雅琦等(2016)通过涡度相关法计算了2012年太湖全年蒸发量为1066mm; Wang等(2014)估算的2011—2012年的太湖年蒸发量为1040mm。由此可见, 不同研究方法和不同时间段太湖年蒸发量变化较大, 2015年太湖蒸发量处于中等水平。
2.3.2 稳定同位素质量守恒方程的计算结果稳定同位素质量守恒方程(公式(3))可以用于计算太湖的年蒸发量, 其中各项的数值和不确定性如表 1所示。太湖年平均蓄水量V为54.2×108m3, 年入湖水总量I为142.6×108m3, 水量不确定性均取其观测值的10%(Xiao et al, 2017)。太湖蓄水的年变化量dV/dt为7.5×108 m3, 其不确定性为观测值的20%。根据本实验液态水同位素分析仪的测量精度, 太湖各项水量的H2HO和H218O同位素组分的不确定性分别为0.3‰和0.1‰, 再根据水量权重计算后, δ2HI、δ2HQ和δ2HL年均值分别为-38.8‰、-27.8‰和-31.0‰, δ18OI、δ18OQ和δ18OL年均值分别为-5.8‰、-4.2‰和-4.6‰。太湖蒸发水汽中的同位素δE由Craig-Gordon模型计算可得, 最终δ2HE为-107.8‰, 不确定性为2.6‰; δ18OE为-18.4‰, 不确定性为0.3‰, 对比发现H218O的计算精度相对于H2HO更高。基于以上数据, 通过蒙特卡洛模拟法得出了2015年太湖的年蒸发量E, 氢同位素的计算结果为21.4(±1.5)×108m3(相当于年蒸发量为880mm), 氧同位素的计算结果为16.8(±1.4)×108m3(相当于年蒸发量为690mm)。
| 稳定同位素种类 | δI(‰) | δQ(‰) | δL(‰) | δE(‰) | dδLdt(‰) | dV/dt(×108m3) | V(×108m3) | I(×108m3) | E(×108m3) |
| H2HO | -38.8±0.4 | -27.8±0.3 | -31.0±0.3 | -107.8±2.6 | 3.0±0.3 | 7.5±1.5 | 54.2±5.4 | 142.6±14.3 | 21.4±1.5 |
| H218O | -5.8±0.1 | -4.2±0.1 | -4. 6±0.1 | -18.4±0.3 | 0.2±0.1 | 7.5±1.5 | 54.2±5.4 | 142.6±14.3 | 16.8±1.4 |
| 注: δI、δQ、δL、δL为水量权重年均值, dδL/dt、dV/dt为年变化量, V为年均值, I、E为年总和量 | |||||||||
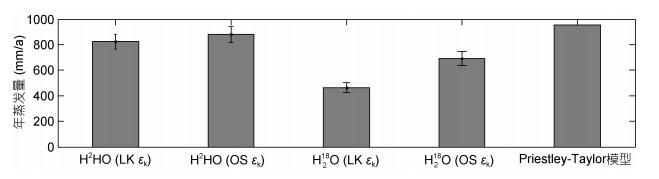
同位素质量守恒法和Priestley-Taylor模型结果对比如图 6所示。同位素质量守恒法中, 使用LK系数, H2HO计算得2015年太湖的年蒸发量为824(±59)mm, H218O计算结果为464(±38)mm; 但使用OS εk, H2HO计算结果为880(±63)mm, H218O计算结果为690(±56)mm; 对比发现, 估算大型浅水湖泊蒸发时, εk采用海洋算法能使结果更接近Priestley- Taylor模型的结果, 且H2HO的计算结果比H218O更稳定。
 |
| 图 6 同位素质量守恒法和Priestley-Taylor模型计算太湖年蒸发量的结果对比 Fig. 6 Comparison in evaporation estimation using isotopic mass balance method and Priestley-Taylor model |
湖水氢氧稳定同位素组分的富集程度是由水面蒸发分馏的强弱和蒸发时间的长短共同决定(Xiao et al, 2016)。太湖中尺度涡度通量网的观测结果表明太湖月蒸发量的空间差异可以忽略不计(王伟, 2014), 所以太湖湖水同位素的空间变化并非是由蒸发量的空间差异引起的。太湖湖水的运动方向是由西北流向东南, 而“引江济太”工程会从太湖东北部的望虞河(图 1中右上角红线所示)将长江水引入太湖, 2015年的“引江济太”发生在1月1日—2月16日和10月26日—11月24日。由此可见, 太湖湖水同位素组分的空间分布主要是受到水流方向的控制, 水在太湖内经历蒸发的时间越长, 湖水δ2H和δ18O值越高, 过量氘值则越低, 因此也呈现出出湖河流的δ2H和δ18O最为富集, 而入湖河流的δ2H和δ18O最为贫化的空间分布特征。
太湖局部氢氧同位素组分存在一定的不规律, 其时空变化的影响因素也有很多, 其中降水是重要因素之一。梅梁湾单点的δ2HL和δ18OL在6月达到峰值却在7月贫化至最低, 因5月太湖全湖随着温度的不断升高(图 5), 湖水同位素不断富集达到最大, 降水量骤减, 5月全湖δ2HL和δ18OL达到峰值(图 4), 因梅梁湾湖水同位素组分与全湖存在一定的时间相位差(图 3), 梅梁湾的湖水同位素信号在六月达到峰值。而6月24日—7月1日太湖遭遇了连续强降水天气, 降水量突增, 因太湖的东侧与黄海相近, 夏季太湖受海洋气团的控制, 海洋气团同位素较贫化, 通过降雨大大降低湖水同位素信号(徐敬争等, 2016), 因此梅梁湾湖水中的δ2HL和δ18OL在7月骤降。
除降水外, 出入湖水和温度对太湖局部氢氧同位素组分时空变化的影响也至关重要。在5月太湖西部即湖西区的河水同位素较为富集, H尤为明显, 同时全湖差异性较小。经分析2015年1—12月《水情月报》数据发现, 湖西区的河流是太湖的主要入湖河流, 其流域的入湖水量占年总入湖水量的67.6%。在地理位置上, 湖西区与无锡市接壤, 主要汇集历经漫长的蒸发富集的河流等内陆水, 而5月是一个明显的升温干旱少雨的月份(图 4、图 5), 湖西区周边的内陆河流中水同位素以分子扩散为主, 即平衡分馏效应显著, 因此造成了5月湖西区的河流水同位素组分2H明显富集的现象(Zimmermann, 1979)。也正因为湖西区的河水同位素局部富集, 原本同位素丰富度较为贫化的西北部湖水同位素得到一定高丰富度的河水的补充, 与太湖东南部的富集同位素之间的差异大大缩小, 使得湖水δ2HL和δ18OL在5月全湖差异性最小。
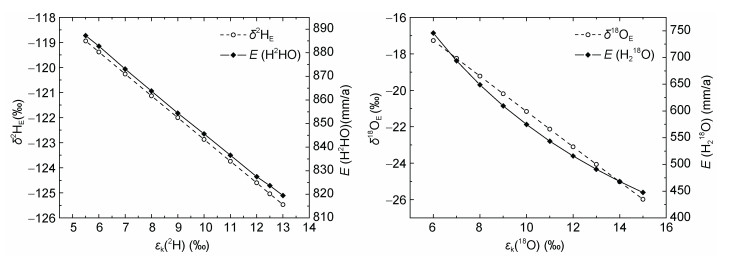
3.2 动力学分馏系数引起的不确定性湖泊蒸发的动力学分馏系数取值是同位素质量守恒法中一个不确定性较大的系数。εk的不同取值直接影响了Craig-Gordon模型的δE, 从而影响蒸发模拟值(Farquhar et al, 1989; Barkan et al, 2007)。同位素质量守恒计算的太湖蒸发对εk的敏感性如图 7所示。以H2HO为示踪剂, εk如果从湖泊系数12.5‰变为海洋系数6.2‰, δ2HE增加6.5‰, 全湖年蒸发量的模拟值将增加57mm。以H218O为示踪剂, εk从湖泊值14.2‰变成海洋值7.1‰, δ2HE增加8.7‰, 模拟的全湖年蒸发量增加226mm。此外, Dansgaard也认为εk若存在4‰的不确定性, 会引起来自海洋的大气水汽中18O的4‰不确定性, 则根据冰芯H218O反演的古温度有5K的偏差(Dansgaard, 1964)。由此可见, εk算法的不确定性会引起湖泊蒸发量估算结果和相关研究结果的明显偏差。
 |
| 图 7 同位素质量守恒法中εk对δE和E的影响 Fig. 7 The influence of εk on δE and E in isotopic mass balance method |
同位素质量守恒法通过2H和18O两种不同种类的稳定同位素示踪太湖蒸发, 差异显著, 从微观角度分析, 因二者的同位素分馏效果不同产生差异。同位素分馏的过程分为两类, 一类因轻重同位素分子之间的饱和水气压差造成的H2O更容易蒸发到空气中, 而H2HO和H218O在水中富集, 称为平衡分馏效应, 另一类则是同位素以分子扩散形式传输的过程, 称为动力分馏效应(Craig et al, 1965; Horita et al, 2008)。在同位素质量守恒法中, εeq和εk分别体现平衡分馏和动力分馏的强弱, C-G模型中的εk (2H)和εk (18O)相近, 无论是OS算法(εk(2H)=5.7‰, εk(18O)=6.4‰)还是LK算法(εk(2H)=12.5‰, εk(18O)=14.2‰), 二者都在同一数量级上, 动力分馏的强度差别不大, 而在平衡分馏过程中, εeq(2H)=81.1‰, εeq(18O)=9.9‰, εeq(2H)约是εeq(18O)的8倍(Majoube, 1971)。对比可见, H218O的εk和εeq量级相当, 因此由C-G模型公式可知, δE对εk的变化响应明显。但是, 2H的εeq比εk大一个数量级, εk的变化对δE的相对影响较弱。所以在太湖蒸发估算的结果中, 2H的计算结果比18O更为稳定。
2H和18O这两种稳定同位素哪一个能更好地示踪蒸发过程, 这是值得探讨的问题。目前, 大部分稳定同位素水文学的研究都采用18O为示踪剂(Gibson, 2002; Coenders-Gerrits et al, 2014)。1970年Gat在Tabgha码头通过蒸发皿试验观测得出εk(18O)应在13.0‰—16.0‰, 并提出在同位素质量守恒的运用中选择18O作为示踪元素的前提是模型中各项数据误差较小。Fontes等(1979)在Titicaca Lake的18O质量守恒试验反向验证了Gat对εk(18O)的结果。由于18O相对于2H的更易测量, 18O的质量守恒法一直并被广泛应用于其他野外观测, 例如, Gao通过18O平衡法证明了融化的冰川水对青藏高原的湖泊水量存在补给作用(Gao et al, 2014); Elmarami等(2017)通过18O的监测结合质量守恒原理, 得出在暴雨期德国Silbersee Lake的湖水存在地表水的大量交换。而对于2H, 1965年Craig和Gordon在实验中发现自然条件下2H的动力学分馏系数与试验的预测不吻合, 当时对于这一现象基本理论无法解释。Zuber(1983)后来认为前者是由于相对湿度较低造成的, 因为相对湿度越低, 野外实测的εk(2H)与实验室预测的εk(2H)偏差越大, 并通过Burdur等三个湖泊的观测数据证实了这一点。另外, 在同位素质量守恒法的运用中Zimmermann较为提倡使用2H作为示踪元素, 2H的同位素分馏过程主要受平衡分馏效应的控制, 其动力学分馏系数较小, 减小了εk(2H)对模型结果带来的误差, 所以2H对动力学分馏系数的误差不敏感, 其计算结果也更为稳定(Zimmermann, 1979)。
有许多科学家在运用同位素手段时会同时观测H2HO和H218O的丰度, 以便提高计算准确性, 例如Dincer利用同位素质量守恒法计算Beysehir湖泊的年入湖量时发现18O的计算结果较2H偏大, 年出湖水量二者较为接近(Dincer, 1968)。Jasechko和Jibson根据2007年北美五大湖的春夏观测数据, 将2H和18O的计算结果无限逼近得出了最优年平均蒸发速率, 但相对于五大湖环境研究实验室的结果和一些观测结果偏低(Jasechko et al, 2014)。本文的研究结果表明2H计算的蒸发量与实测值更为接近, 且对动力学分馏系数敏感性较弱, 从这个角度讲, 2H是更为稳定的示踪剂。
4 结论本文的结果表明2015年太湖湖水和河水中氢氧同位素组分有明显的时间和空间变化特征, 湖水氢氧同位素组分与相连的河水中氢氧同位素组分的空间分布特征基本一致, 呈现东南部富集和北部区域贫化的分布状态, 这种空间变化特征主要受水流方向的控制。太湖湖水的氢氧稳定同位素组分的单点观测和全湖观测的时间变化动态较一致, 但是存在系统偏差。
将稳定同位素质量守恒方程和Craig-Gordon模型相结合估算了太湖蒸发量, 证明了采用稳定同位素质量守恒方程估算亚热带大型浅水湖泊的蒸发是可行的, 同时模型计算结果表明目前被广泛用于湖泊蒸发研究的动力学分馏系数偏高, 而海洋研究中采用的动力学分馏系数更适用于太湖蒸发的示踪。
对比2H和18O这两种稳定同位素, 因氢氧稳定同位素分馏效应存在差异, 氢同位素的分馏过程主要是平衡分馏效应为主导, 动力学分馏效应较小, 而氧同位素的分馏过程中两种分馏效应同等重要, 在模型计算过程中, 动力学分馏系数的不确定性对2H的应用影响较小, 而对18O的影响较大, 因此两种同位素的模拟效果也不同, 结果证明以2H为示踪剂计算太湖蒸发与观测值更接近, 而且更加稳定。我们认为, 检验在自然条件下动力学分馏系数的取值以及2H和18O的适用性对于稳定同位素水文学研究及其它相关研究是非常重要的。
| 王伟, 2014.太湖能量收支及其对气候变化的响应.南京: 南京信息工程大学博士学位论文 |
| 史晓宜, 蒲焘, 何元庆, 等, 2016. 典型温冰川区湖泊的稳定同位素空间分布特征. 环境科学, 37(5): 1685–1691 |
| 包为民, 胡海英, 瞿思敏, 等, 2007. 稳定同位素方法在湖泊水量平衡研究中的应用. 人民黄河, 29(8): 29–30 DOI:10.3969/j.issn.1000-1379.2007.08.014 |
| 沈行毅, 1984. 太湖水面蒸发量的气候学计算. 水文,(4): 12–18 |
| 徐敬争, 肖薇, 肖启涛, 等, 2016. 湖水氢氧同位素组分的时间变化特征及影响因子分析. 环境科学, 37(7): 2470–2477 |
| 高晶, 姚檀栋, 田立德, 等, 2008. 羊卓雍错流域湖水氧稳定同位素空间分布特征. 冰川冻土, 30(2): 338–343 |
| 高雅琦, 王咏薇, 胡诚, 等, 2016. 2012年太湖蒸发量变化特征及蒸发模型评估研究. 气候与环境研究, 21(4): 393–404 |
| 燕姝雯, 余辉, 张璐璐, 等, 2011. 2009年环太湖入出湖河流水量及污染负荷通量. 湖泊科学, 23(6): 855–862 |
| Arnoux M, Barbecot F, Gibert-Brunet E, et al, 2017. Impacts of changes in groundwater recharge on the isotopic composition and geochemistry of seasonally ice-covered lakes:insights for sustainable management. Hydrology and Earth System Sciences, 21(11): 5875–5889 DOI:10.5194/hess-21-5875-2017 |
| Barkan E, Luz B, 2007. Diffusivity fractionations of H216O/H217O and H216O/H218O in air and their implications for isotope hydrology. Rapid Communications in Mass Spectrometry, 21(18): 2999–3005 DOI:10.1002/(ISSN)1097-0231 |
| Bateni S M, Entekhabi D, 2012. Relative efficiency of land surface energy balance components. Water Resources Research, 48(4): W04510 |
| Bocanegra E, Londoño O M Q, Martínez D E, et al, 2013. Quantification of the water balance and hydrogeological processes of groundwater-lake interactions in the Pampa Plain, Argentina. Environmental Earth Sciences, 68(8): 2347–2357 DOI:10.1007/s12665-012-1916-4 |
| Bouchez C, Goncalves J, Deschamps P, et al, 2016. Hydrological, chemical, and isotopic budgets of Lake Chad:a quantitative assessment of evaporation, transpiration and infiltration fluxes. Hydrology and Earth System Sciences, 20(4): 1599–1619 DOI:10.5194/hess-20-1599-2016 |
| Coenders-Gerrits A M J, van der Ent R J, Bogaard T A, et al, 2014. Uncertainties in transpiration estimates. Nature, 506(7487): E1–E2 DOI:10.1038/nature12925 |
| Cole J J, Prairie Y T, Caraco N F, et al, 2007. Plumbing the global carbon cycle:Integrating inland waters into the terrestrial carbon budget. Ecosystems, 10(1): 172–185 DOI:10.1007/s10021-006-9013-8 |
| Craig H, Gordon L I, 1965. Deuterium and oxygen-18 variation in the ocean and the marine atmosphere. In:Tongiorgi E ed. Stable Isotopes in Oceanographic Studies and Paleotemperatures. Pisa, Italy:Lab Geol Nucl, 277: 277–374 |
| Dansgaard W, 1964. Stable isotopes in precipitation. Tellus, 16(4): 436–468 DOI:10.3402/tellusa.v16i4.8993 |
| Dinçer T., 1968. The use of oxygen 18 and deuterium concentrations in the water balance of lakes. Water Resources Research, 4(6): 1289–1306 DOI:10.1029/WR004i006p01289 |
| Elmarami H, Meyer H, Massmann G., 2017. Combined approach of isotope mass balance and hydrological water balance methods to constrain the sources of lake water as exemplified on the small dimictic lake Silbersee, northern Germany. Isotopes in Environmental and Health Studies, 53(2): 184–197 DOI:10.1080/10256016.2016.1206095 |
| Evaristo J, Jasechko S, McDonnell J J, 2015. Global separation of plant transpiration from groundwater and streamflow. Nature, 525(7567): 91–94 DOI:10.1038/nature14983 |
| Farquhar G D, Ehleringer J R, Hubick K T, 1989. Carbon isotope discrimination and photosynthesis. Annual Review of Plant Physiology and Plant Molecular Biology, 40: 503–537 DOI:10.1146/annurev.pp.40.060189.002443 |
| Fontes J C, Boulange B, Carmouze J P, et al, 1979. Preliminary oxygen-18 and deuterium study of the dynamics of Lake Titicaca. In:Isotopes in Lake Studies. Vienna:International Atomic Energy Agency, 207: 207–229 |
| Gao J, Yao T, Joswiak D, 2014. Variations of water stable isotopes (delta O-18) in two lake basins, southern Tibetan Plateau. Annals of Glaciology, 55(66): 97–104 DOI:10.3189/2014AoG66A109 |
| Gat J R, 1970. Environmental isotope balance of Lake Tiberias. In:Isotopes in Lake Studies. Vienna:International Atomic Energy Agency,: 109–127 |
| Gat J R, Bowser C J, Kendall C, 1994. The contribution of evaporation from the Great Lakes to the continental atmosphere:estimate based on stable isotope data. Geophysical Research Letters, 21(7): 557–560 DOI:10.1029/94GL00069 |
| Gibson J J, 2002. Short-term evaporation and water budget comparisons in shallow Arctic lakes using non-steady isotope mass balance. Journal of Hydrology, 264(1-4): 242–261 DOI:10.1016/S0022-1694(02)00091-4 |
| Gibson J J, Birks S J, Jeffries D, et al, 2017. Regional trends in evaporation loss and water yield based on stable isotope mass balance of lakes:The Ontario Precambrian Shield surveys. Journal of Hydrology, 544: 500–510 DOI:10.1016/j.jhydrol.2016.11.016 |
| Gibson J J, Birks S J, Yi Y, et al, 2016a. Stable isotope mass balance of fifty lakes in central Alberta:Assessing the role of water balance parameters in determining trophic status and lake level. Journal of Hydrology:Regional Studies, 6: 13–25 DOI:10.1016/j.ejrh.2016.01.034 |
| Gibson J J, Birks S J, Yi Y, 2016b. Stable isotope mass balance of lakes:a contemporary perspective. Quaternary Science Reviews, 131: 316–628 DOI:10.1016/j.quascirev.2015.04.013 |
| Gonfiantini R, 1986. Environmental isotopes in lake studies. In:Fritz P, Fontes J C H eds. Handbook of Environmental Isotope Geochemistry. Elsevier:Amsterdam, 3: 113–168 |
| Horita J, Rozanski K, Cohen S, 2008. Isotope effects in the evaporation of water:a status report of the Craig-Gordon model. Isotopes in Environmental and Health Studies, 44(1): 23–49 DOI:10.1080/10256010801887174 |
| Jasechko S, Gibson J J, Edwards T W D, 2014. Stable isotope mass balance of the Laurentian Great Lakes. Journal of Great Lakes Research, 40(2): 336–346 DOI:10.1016/j.jglr.2014.02.020 |
| Jouzel J, Masson-Delmotte V, Cattani O, et al, 2007. Orbital and millennial Antarctic climate variability over the past 800, 000 years. Science, 317(5839): 793–796 DOI:10.1126/science.1141038 |
| Kebede S, Travi Y, 2012. Origin of the δ18O and δ2H composition of meteoric waters in Ethiopia. Quaternary International, 257: 4–12 DOI:10.1016/j.quaint.2011.09.032 |
| Lee X H, Liu S D, Xiao W, et al, 2014. The Taihu eddy flux network:an observational program on energy, water, and greenhouse gas fluxes of a large freshwater lake. Bulletin of the American Meteorological Society, 95(10): 1583–1594 DOI:10.1175/BAMS-D-13-00136.1 |
| Lenters J D, Kratz T K, Bowser C J, 2005. Effects of climate variability on lake evaporation:Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). Journal of Hydrology, 308(1-4): 168–195 DOI:10.1016/j.jhydrol.2004.10.028 |
| Liu J R, Song X F, Yuan G F, et al, 2014. Stable isotopic compositions of precipitation in China. Tellus B:Chemical and Physical Meteorology, 66(1): 22567 DOI:10.3402/tellusb.v66.22567 |
| Longinelli A, Stenni B, Genoni L, et al, 2008. A stable isotope study of the Garda lake, Northern Italy:Its hydrological balance. Journal of Hydrology, 360(1-4): 103–116 DOI:10.1016/j.jhydrol.2008.07.020 |
| Majoube M, 1971. Fractionnement en oxygène 18 et en deutérium entre l'eau et sa vapeur. Journal de Chimie Physique et de Physico-Chimie Biologique, 68: 1423–1436 DOI:10.1051/jcp/1971681423 |
| Merlivat L, Jouzel J., 1979. Global climatic interpretation of the deuterium-oxygen 18 relationship for precipitation. Journal of Geophysical Research, 84(C8): 5029–5033 DOI:10.1029/JC084iC08p05029 |
| Priestley C H B, Taylor R J, 1972. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Monthly Weather Review, 100(2): 81–92 DOI:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 |
| Qian H, Wu J H, Zhou Y H, et al, 2014. Stable oxygen and hydrogen isotopes as indicators of lake water recharge and evaporation in the lakes of the Yinchuan Plain. Hydrological Processes, 28(10): 3554–3562 DOI:10.1002/hyp.v28.10 |
| Qin B Q, Xu P Z, Wu Q L, et al, 2007. Environmental issues of Lake Taihu, China. Hydrobiologia, 581(1): 3–14 DOI:10.1007/s10750-006-0521-5 |
| Russell J M, Johnson T C, 2006. The water balance and stable isotope hydrology of lake edward, Uganda-Congo. Journal of Great Lakes Research, 32(1): 77–90 DOI:10.3394/0380-1330(2006)32[77:TWBASI]2.0.CO;2 |
| Samuelsson P, Kourzeneva E, Mironov D, 2010. The impact of lakes on the European climate as simulated by a regional climate model. Boreal Environment Research, 15(2): 113–129 |
| Seal II R R, Shanks III W C, 1998. Oxygen and hydrogen isotope systematics of Lake Baikal, Siberia:implications for paleoclimate studies. Limnology and Oceanography, 43(6): 1251–1261 DOI:10.4319/lo.1998.43.6.1251 |
| Steffensen J P, Andersen K K, Bigler M, et al, 2008. High-resolution greenland ice core data show abrupt climate change happens in few years. Science, 321(5889): 680–684 DOI:10.1126/science.1157707 |
| Tan M, 2014. Circulation effect:response of precipitation δ18O to the ENSO cycle in monsoon regions of China. Climate Dynamics, 42(3-4): 1067–1077 DOI:10.1007/s00382-013-1732-x |
| Taniguchi M, Nakayama T, Tase N, et al, 2000. Stable isotope studies of precipitation and river water in the Lake Biwa basin, Japan. Hydrological Processes, 14(3): 539–556 DOI:10.1002/(ISSN)1099-1085 |
| Verpoorter C, Kutser T, Seekell D A, et al, 2014. A global inventory of lakes based on high-resolution satellite imagery. Geophysical Research Letters, 41(18): 6396–6402 DOI:10.1002/2014GL060641 |
| Vogt H J, 1976. Isotopentrennung bei der Verdunstung von Wasser, Staatsexamensarbeit. Heidelberg:Master Dissertation of Institut fur Umweltphysik, |
| Wang W, Xiao W, Cao C, et al, 2014. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. Journal of Hydrology, 511: 811–824 DOI:10.1016/j.jhydrol.2014.02.012 |
| Wassenaar L I, Athanasopoulos P, Hendry M J, 2011. Isotope hydrology of precipitation, surface and ground waters in the Okanagan Valley, British Columbia, Canada. Journal of Hydrology, 411(1-2): 37–48 DOI:10.1016/j.jhydrol.2011.09.032 |
| Xiao W, Lee X H, Hu Y B, et al, 2017. An experimental investigation of kinetic fractionation of open-water evaporation over a large lake. Journal of Geophysical Research, 122(21): 11651–11663 |
| Xiao W, Wen X F, Wang W, et al, 2016. Spatial distribution and temporal variability of stable water isotopes in a large and shallow lake. Isotopes in Environmental and Health Studies, 52(4-5): 443–454 DOI:10.1080/10256016.2016.1147442 |
| Xu X Y, Zhang R D, Xue X Z, et al, 1998. Determination of evapotranspiration in the desert area using lysimeters. Communications in Soil Science and Plant Analysis, 29(1-2): 1–13 DOI:10.1080/00103629809369924 |
| Yao T D, Masson-Delmotte V, Gao J, et al, 2013. A review of climatic controls on δ18O in precipitation over the Tibetan Plateau:Observations and simulations. Reviews of Geophysics, 51(4): 525–548 DOI:10.1002/rog.v51.4 |
| Zhao L, Jin J M, Wang S Y, et al, 2012. Integration of remote-sensing data with WRF to improve lake-effect precipitation simulations over the Great Lakes region. Journal of Geophysical Research, 117(D9): D09102 |
| Zimmermann U, 1979. Determination by stable isotopes of underground inflow and outflow and evaporation of young artificial groundwater lakes. In:Isotopes in Lake Studies. Vienna:International Atomic Energy Agency,(87): 94 |
| Zimmermann U, Ehhalt D H, 1970. Stable isotopes in the study of the water balance of Lake Neusiedl, Austria. In:Isotopes in Hydrology. Wien:International Atomic Energy Agency,: 129–138 |
| Zuber A, 1983. On the environmental isotope method for determining the water balance components of some lakes. Journal of Hydrology, 61(4): 409–427 DOI:10.1016/0022-1694(83)90004-5 |
 2019, Vol. 50
2019, Vol. 50


