
中国海洋湖沼学会主办。
文章信息
- 王卓越, 郑建, 杨宇星, 王法明. 2019.
- WANG Zhuo-Yue, ZHENG Jian, YANG Yu-Xing, WANG Fa-Ming. 2019.
- 南太平洋副热带偶极子模式模拟评估
- PERFORMANCE OF FIFTEEN CMIP5 MODELS ON THE SOUTH PACIFIC DIPOLE:COMPARISON AND COMMENT
- 海洋与湖沼, 50(2): 237-247
- Oceanologia et Limnologia Sinica, 50(2): 237-247.
- http://dx.doi.org/10.11693/hyhz20180700185
-
文章历史
- 收稿日期:2018-07-25
- 收修改稿日期:2018-11-16
2. 中国科学院大学 北京 100049;
3. 中国科学院海洋环流与波动重点实验室 青岛 266071;
4. 青岛海洋科学与技术国家实验室海洋动力过程与气候功能实验室 青岛 266071
2. University of Chinese Academy of Science, Beijing 100049, China;
3. Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Qingdao 266071, China;
4. Laboratory for Ocean and Climate Dynamics, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
南半球拥有比北半球更广的海域, 观测显示南半球海域存在着年际SST变化模态。Saji等(1999)首先在热带印度洋发现了海温偶极模态, Venegas等(1997)发现在南大西洋存在SST偶极模态, Behara等(2001)发现在南印度洋也存在有偶极模态, Chiang J C H(2004)等讨论了太平洋与大西洋的经向模态与赤道的相关关系。Wang(2010, 2010a, 2010b)从理论上猜想并验证了在全南半球副热带地区一致存在海表面温度(sea surface temperature, SST)偶极模态, 观测资料分析显示在南太平洋副热带的确存在SST偶极模态, 并根据Behera等(2001)之前发现的印度洋副热带偶极子(Indian Ocean Subtropical Dipole, IOSD)定义南太平洋的模态为南太平洋副热带偶极子(South Pacific Subtropical Dipole, SPSD)。SPSD是一个存在于南太平洋呈东北-西南向分布的SST偶极模态。有研究(Reason, 2001; 李琼等, 2016)显示副热带偶极子可以通过大气环流调整的形式来影响局地的气候以及降水。
作为研究气候变化的有力工具, 耦合模式可以弥补海洋观测资料在时间和空间上的不足, 用来研究气候系统的变异规律和变异机理, 是目前气候研究的重要手段。但是, 模式本身存在模拟误差, 因此评估模式的模拟能力具有重要意义。
Morioka等(2012)研究了SINTEX-F模式对南印度洋副热带偶极子的模拟结果并进行评估。JE Chu等(2013)利用国际耦合模式比较计划(Coupled Model Intercomparison Project Phase 5, CMIP5)研究评估了印度洋海盆模态和偶极模态在未来可能发生的变化。Morioka Y(2013)系统分析了南太平洋副热带偶极子的生成机制, 较完整的描述了偶极子的发展消亡过程。Yuan C X(2014)利用模式研究了副热带偶极子的预报可能性, 从物理场量上一定程度上给出了预测因子。Zheng等(2017)使用观测与模式资料对南太平洋存在的多极SST模态进行了对比分析, 指出潜热通量变化是南太平洋多极模态生成的主要因素。但是, 基于CMIP5对偶极子的模拟评估尚未展开(Taylor K E, 2012)。
本文利用CMIP5历史模拟结果评估了模式与观测中偶极子的空间结构、模态强度、生成消亡以及影响气候方面的差距, 并初步讨论了可能的原因。第一部分简单介绍了CMIP5模式资料和处理数据的方法; 第二部分分析了观测到的偶极子的特征以及生成过程; 第三部分主要是模式与观测的总体对比, 其中讨论了模式与观测, 模式与模式之间的差异; 第四部分挑选了个别模式进行合成分析, 讨论了模态生成过程的主要影响因素; 最后进行了总结讨论。
1 资料与方法 1.1 资料本文使用的历史SST资料来自英国哈德莱中心(Met Office Hadley Center)分辨率为1°×1°、时间跨度为1950—2005年。热通量资料来自NCEP/ NCAR (National Centers for Environmental Prediction, National Center for Atmospheric Research)再分析数据集、分辨率为1.9°×1.875°。模式资料来自CMIP5历史模拟, 为了方便与观测进行对比模式资料均插值到了1°×1°。本文选取CMIP5的15个耦合模式的数据, 模式试验为历史试验(historical run)。该试验是在工业革命试验(piControl)基础上选取初始场进行积分, 积分时间为1850—2012年。采用随时间变化的强迫场包括温室气体、太阳常数、火山活动、臭氧和气溶胶。其中, 1850—2005年的强迫场为观测值。用于对比的模式资料时间跨度与观测相同, 为1950—2005年, 同时所有资料都扣除了年循环与长期线性趋势。
1.2 研究方法本文采用奇异值分解(singular value decomposi tion, SVD)方法来分析偶极模态, 变量场使用海平面气压场和SST场。不同于其他文献所采用的经验正交函数分解(Empirical Orthogonal Function, EOF)分析方法, SVD分析方法考虑两个变量场之间的相关关系, 在分析SST模态与大气耦合方面, 相较EOF来说更为适合。在做SVD分析之前, 为避免年循环与厄尔尼诺影响到分析结果, 本文中的数据都预先进行处理, 去除年循环与厄尔尼诺影响的部分, 其中扣除的厄尔尼诺部分使用公式(1)计算得出:
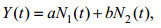 (1)
(1)| 序号 | 模式名称 | 研究机构 (国家/机构名称) |
海洋模式格点数 x×y(个) |
大气模式格点数 x×y(个) |
| 1 | ACCESS1-3 | 澳大利亚/联邦科学与工业研究组织(CSIRO-BOM)和气象局(BOM) | 360×300 | 192×145 |
| 2 | BCC-CSM1-1 | 中国/国家气候中心 | 360×300 | 128×64 |
| 3 | CanESM2 | 加拿大/气候模拟与分析中心 | 256×192 | 128×64 |
| 4 | CSIRO-Mk-3-6-0 | 澳大利亚/英联邦科学与工业研究组织与昆士兰州气候变化卓越中心合作 | 192×189 | 192×96 |
| 5 | GFDL-CM3 | 美国/地球物理流体动力学实验室(GFDL) | 360×200 | 144×90 |
| 6 | GISS-E2-R | 美国/NASA/GISS (戈达德空间研究所) | 144×90 | 144×90 |
| 7 | HadGEM2-CC | 英国/哈德利气候预测和研究中心, 气象局 | 360×216 | 192×145 |
| 8 | HadGEM2-ES | 英国/哈德利气候预测和研究中心, 气象局 | 360×216 | 192×145 |
| 9 | INM-CM4 | 俄国/数值数学研究所 | 360×340 | 180×120 |
| 10 | IPSL-CM5A-LR | 法国/皮埃尔-西蒙拉普拉斯研究所(IPSL) | 182×149 | 96×96 |
| 11 | MIROC5 | 日本/大气与海洋研究所(东京大学), 国立环境研究所和日本海洋地球科学与技术局 | 360×368 | 256×224 |
| 12 | MIROC-ESM | 日本/日本海洋地球科学与技术, 大气与海洋研究所和国家环境研究所 | 256×192 | 128×64 |
| 13 | MPI-ESM-MR | 德国/马克斯普朗克气象研究所(MPI) | 256×220 | 192×96 |
| 14 | NorESM1-M | 挪威/挪威气候中心 | 384×320 | 144×96 |
| 15 | NorESM1-ME | 挪威/挪威气候中心 | 384×320 | 144×96 |
其中, a、b为线性回归系数, N1、N2分别为EOF分解得到的前两个主成分模态。以下如无特殊说明, 默认所有数据均已采取如上处理。
为了更好地评估多模式的模拟能力, 从而将模式与观测进行对比, 引入技巧评分方法(Hirota et al, 2011; Taylor, 2001), 采用公式(2):
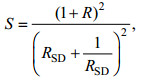 (2)
(2)其中, R为模式与观测空间相关系数,
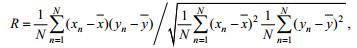 (3)
(3)RSD为模式与观测空间标准偏差的比率,
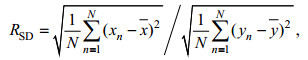 (4)
(4)其中, xn和yn分别为具有N个格点(可以指时间也可以指空间)的模式模拟和观测所得的物理量。
2 观测与模式中的偶极子 2.1 观测中的偶极子李琼等(2016)研究显示, 在南太平洋区域存在偶极型的SST模态, 并且具有季节锁相的特性, 即在南半球的春季开始生成, 于当年夏季发展成熟。为了分析这种模态, 本文将观测资料外理为季节平均资料(JFM, 春季平均), 然后对1950—2005年时段进行SVD计算得图 1。区域边界敏感性分析显示, 模态受边界的选取影响很小, 南北与东西边界10°的变化模态几乎没有改变。从图 1中可以看到在0°—60°S、160°—60°W存在偶极型的SST分布与负的气压异常中心。模态沿东北西南向分布, 正极位于东北方向, 负极位于西南方向。海表面气压对应一个大的负气压中心, 中心位于105°W, 35°S附近。其中正极的振幅要比负极强, 且正极的范围要比负极大。将SST模态的时间序列振幅作为表征偶极子的指数, 参考文献(李琼等, 2016)以超过0.6个标准差作为判定的依据, 可以得出如下的事件年:正事件为1952、1957、1960、1965、1972、1977、1980、1984、1993年, 负事件为1956、1958、1962、1964、1966、1971、1974、1978、1991、1998、2003年。
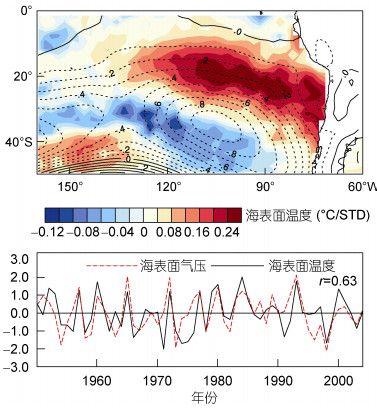 |
| 图 1 利用奇异值分解法分析得出的1950—2005年春季海表面温度(sea surface temperature, SST)与气压模态 Fig. 1 Spring sea surface temperature and pressure mode from 1950 to 2005 by SVD(singular value decompositon)analysis 注:等值线线为海表面气压(Sea Level Pressure, PSL)(单位: hPa/STD), STD为海温标准差, r为SST与海表气压时间序列线性(Pearson)相关系数 |
对模式资料做SVD计算, 结果如图 2所示。从图中可以看到模式在SST模态的模拟上与观测较为接近, 绝大多数模式都可以模拟出偶极模态, 但在模拟的强度和位置上模式之间有着不小的差距, 其中HadGEM2-CC与HadGEM2-ES模式模拟的SST模态强度要比观测强许多, 但在偶极的位置上与观测较为接近。两个HadGEM2模式在负极以及负气压范围上有一定的差距。HadGEM2-CC模式模拟的负极较为西伸, 对应负气压也向西延伸, 同时负气压中心也相对偏北。
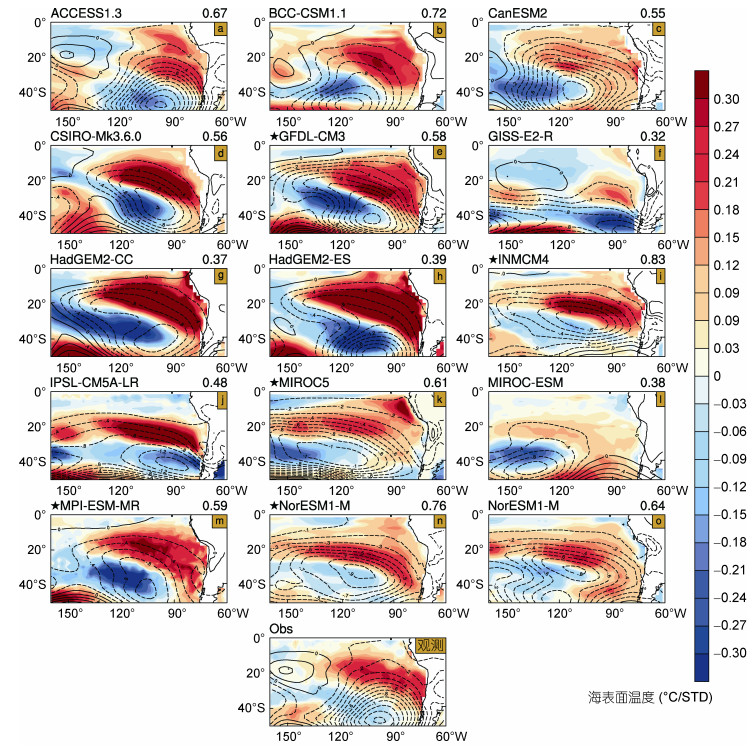 |
| 图 2 利用奇异值分解法分析模式与观测结果 Fig. 2 SVD analysis mode and observation results 注:图片右上角数字为模式模拟的气压模态的技巧评分, 等值线为海表面气压(单位: hPa/STD) |
为了挑选出几个相对模拟较好的模式进行分析对比, 本文采用了前文提到的模态技巧评分作为评判依据, 在表 2中列出。其中SST与气压的技巧评分进行等权相加作为最终的评估标准, 选出了5个最佳模式, 这5个模式在模态的位置模拟上与观测都有着较好的对应, 在图中以星号标识。分别是GFDL- CM3、INM-CM4、MIROC5、MPI-ESM-MR和NorESM1-M五个模式。这5个模式模拟的SST模态强度和气压强度都与观测较为接近, 值得一提的是其中MIROC5模式模拟的负极强度比观测强, 位置也较为偏西, 并且正极与观测不同, 有分裂为3个次正极。在岸边的正极强度最强, 向西南方向逐渐减弱。对应的负气压范围也比观测大出许多, 形态呈东西分布。但由于SST在与观测对应的区域模拟较好, 同时气压模拟的强度与观测较为接近, 所以综合来看, MIROC5模式的技巧评分要高于其他模式。剩下的模式模拟的情况各不相同, GISS-E2-R、MIROC-ESM、IPSL-CM5A-LR模式模拟的模态与观测出入较大。IPSL-CM5A-LR模拟出了多个极, 且均呈南北向分布而非东北西南向分布。在MIROC-ESM模式中, 正极在60°S以南。GISS-E2-R模式中负极模拟与观测差距较大。其余的模式中, ACCESS1.3、HadGEM2-CC、HadGEM2-ES和BCC-CSM1.1模式模拟的SST负极比观测要强, 对应的负气压中心强度也要比观测强。NorESM1-ME模式模拟的正极区域相比观测东西延伸较长, 南北范围较小, SST模态的强度与观测较为接近。
| 模式名称 | 气压评分 | SST评分 | 总分 |
| NorESM1-M | 0.88 | 0.76 | 1.64 |
| INM-CM4 | 0.7 | 0.83 | 1.53 |
| GFDL-CM3 | 0.92 | 0.58 | 1.5 |
| MIROC5 | 0.88 | 0.61 | 1.49 |
| MPI-ESM-MR | 0.89 | 0.59 | 1.48 |
| ACCESS1-3 | 0.77 | 0.67 | 1.44 |
| NorESM1-ME | 0.78 | 0.64 | 1.42 |
| BCC-CSM1-1 | 0.65 | 0.72 | 1.37 |
| CanESM2 | 0.82 | 0.55 | 1.37 |
| CSIRO-Mk-3-6-0 | 0.8 | 0.56 | 1.36 |
| IPSL-CM5A-LR | 0.81 | 0.48 | 1.29 |
| HadGEM2-CC | 0.67 | 0.37 | 1.04 |
| HadGEM2-ES | 0.65 | 0.39 | 1.04 |
| GISS-E2-R | 0.59 | 0.32 | 0.91 |
| MIROC-ESM | 0.44 | 0.38 | 0.82 |
大多数模式中SST模态与气压中心都有较好的对应, 表明这些模式在海气耦合方面模拟的较好, 但是在个别几个模式中, 虽然能够模拟好海气耦合的过程, 但由于对偶极模态模拟较差, 使得气压中心与偶极都与观测有着较大的出入。如GISS-E2-R、IPSL-CM5A-LR、MIROC-ESM。GISS-E2-R模式模拟的模态强度偏低, 同时位置也与观测不同, 呈南北向分布, 在海平面上方并没有对应负气压中心, 无论在正极还是负极都对应负的气压异常, 未能模拟出系统性的环流异常。IPSL-CM5A-LR模式与GISS-E2-R模式的情况类似, 但在模态的强度上相比GISS-E2-R模式要强。MIROC-ESM模式模拟的正极较弱, 负极较强, 位置较观测偏西南, 对应的负气压中心也较为偏弱, 强度只有观测的一半左右。
为了分析影响模态生成发展过程中潜热通量的变化, 利用SVD分析得出的模态时间序列, 将提前一个月的潜热通量回归到南太平洋区域, 结果如图 3所示。从图中可以看到, 观测与模式在SST正极上方有明显的向下潜热通量。同时在负极上方有向上的潜热通量。观测中的潜热通量负中心与SST负极中心有一定的偏差, 潜热通量中心偏东南, 这可能是由于负气压引起的东南风异常驱动海流, 使较冷的水团向西北移动。几乎所有模式都可以模拟出SST模态对应的潜热通量异常, 这表明了SST偶极模态是受潜热通量控制的。在较强的五个模式中, SST正极中心偏东部分有向上的潜热通量, 这可能是由于较暖水团受风异常驱动在区域内堆积, 从而对大气产生了反馈效应。这在其他模式中也有相应体现。其中在HadGEM2两个模式中, 模拟的模态偏强, 且正极区域的向上热通量也相对偏西。在MPI-ESM-MR模式中则只有对应的向下热通量, 并无向上的热通量区域, 这有可能是MPI-ESM-MR模式模拟的风场异常强度与观测相比较弱, 从而使SST异常更广泛的分布, 没有达到反馈大气的强度。在CSIRO-Mk3.6.0模式中, 正极与负极的模拟强度都相对较强, 但区域相比观测较小, 正极附近出现了向上的热通量输送。图 4为模式模拟的SST与海表气压模态的泰勒图表, 从图中可以看到使用技巧评分得出的最佳5个模式在泰勒图表中与观测较为接近。其中在海表气压模态的模拟上模式整体模拟较好, 这是由于对应气压为单极, 与SST的偶极相比更容易模拟, 所以在泰勒图中模式模拟表现整体相较SST更为接近观测。总体上符合技巧评分得出的排名, 也佐证本文使用的技巧评分公式能够评估模式模拟偶极子的能力。
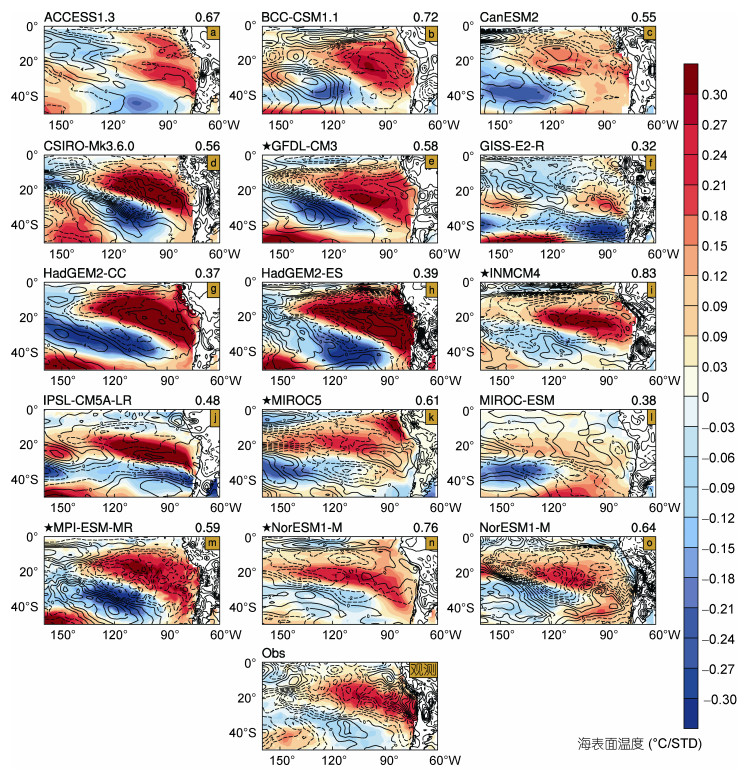 |
| 图 3 以奇异值分解法SST模态为基础, 将潜热通量回归得出的分布图 Fig. 3 The distribution of latent heat flux is obtained based on the SVD sea temperature mode 注:模式右上角的数字为SST模态的技巧评分, 等值线为海表面潜热通量(单位: W/m2) |
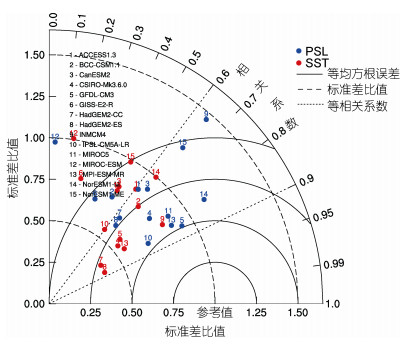 |
| 图 4 CMIP5模式模拟泰勒图 Fig. 4 The Taylor diagram of the CMIP5 |
为了详细分析模式在模态生成发展过程中潜热与SST对应关系, 本文将观测和模拟相对较强的两个模式中1950—2005年所有正事件分别进行合成, 得出提前三个月的SST分别与潜热和风场叠加的空间分布。从图 5中可以看到观测中在提前一个月时, SST正极区域已经有正的异常出现, 同时在90°W、40°S附近有气旋式环流异常, 在气旋中心对应有向上的潜热通量, 而在正极偏北也有一块向上潜热通量区域。风场显示在正极上方有明显的西北风异常, 使得东南季风减弱, 热量在正极区域堆积。在负极有西北风异常, 使前一个月出现的SST负极向东传播, 由图可以看到原本一整块的负极分裂为几个小的区域。在发展最强的时候, 气压中心强度进一步增加, 南侧气流也随之加强, 使得南部的冷水团运动到了原来的负极区, 进一步使负极增强。同时也可以看到在正极上方西北风异常加强, 热量在正极更多的堆积。在南美西海岸有向上的潜热通量。
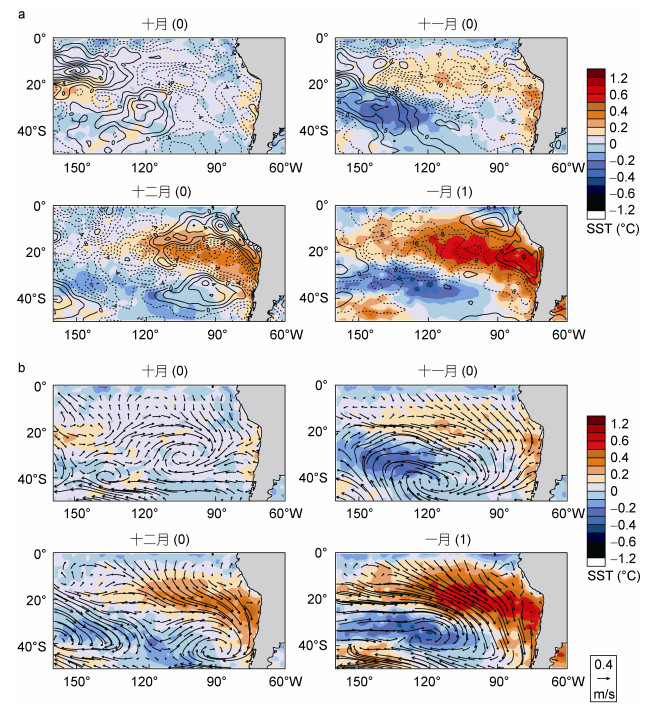 |
| 图 5 观测中的合成分析 Fig. 5 Synthetic analysis in observations a中等值线为潜热(单位: W/m2), b为风场(单位: m/s), 0代表事件年的前一年, 1代表事件年 |
CSIRO-Mk3-6-0模式在模拟模态发展阶段时与观测较为不同, 如图 6, 从提前三个月的风场与潜热通量来看, 首先是在20°—30°S, 120°—90°W区域产生了正SST异常, 同时在此区域下方生成了气旋式环流异常, 南侧偏冷的海水向西北流动。提前两个月时正极与负极开始加强, 气旋式环流的强度也随之变强。提前一个月时, 负极上方风场异常继续增强, 促使负极区域向东延伸。当模态发展成熟时, 气旋的南支气流最强, 使负极区域SST向北发展并进一步增强。结合潜热通量分布可以看到负极上方有着较强的向上潜热通量, 这也是该区域SST降低的主要原因。而在正极区域, 随着SST的不断升高, 在正极堆积的热量开始向大气输送, 从潜热分布可以清楚的看到在正极区域有正潜热通量区域。相比观测而言, CSIRO-Mk-3-6-0模式模拟的模态区域更为集中, 强度也更强。体现在发展阶段, 模式比观测更早的模拟出SST的异常变化, 气旋中心也相对偏西。
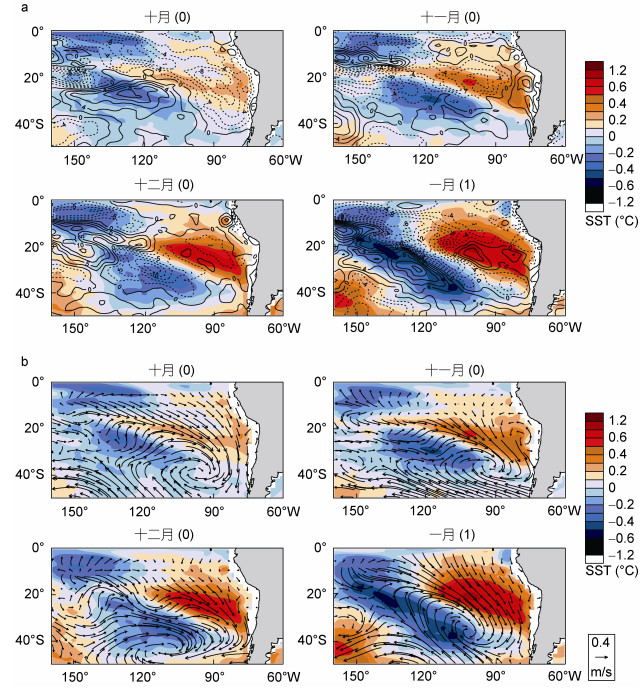 |
| 图 6 CSIRO-Mk3.6.0模式的合成分析 Fig. 6 Synthetic analysis in CSIRO-Mk3.6.0 model 注: a中等值线为潜热(单位: W/m2), b为风场(单位: m/s), 0代表事件年的前一年, 1代表事件年 |
HadGEM2-ES模式模拟的SST模态如图 7, 强度较观测强出许多, 无论从正极还是负极。同时SST模态区域也相对较观测更广。从图 7来看, 提前三个月时, 在10°—40°S, 90°—120°W范围就已经产生了跷跷板式的SST分布, 120°—100°W, 60°—30°S区域有较强的东南风异常, 该区域的SST也呈现出了负距平。在20S°, 100°W附近随着西北风的异常, 从热带地区带来了暖气流, 通过潜热传递给海洋, 使得该区域SST产生正异常。到提前两个月时, 正极与负极都进一步加强, 同时在负极偏南生成了一个强气旋式环流异常, 正极区域中心强度达到了0.6℃。提前一个月时与前者相比, 正极与负极的区域与强度都得到了更进一步的加强与扩大, 气旋北支气流与正极的西北气流合并。当模态发展最强时, 正极与负极区域达到最大, 强度也达到了顶峰, 其中负极的中心比正极高出0.2℃左右, 极值达到了-1.2℃左右。与观测相比, 正极与负极的区域都相对较广, 强度超过了观测, 并且对应气旋中心也较为偏南。南美西岸海区大部分区域都达到了0.6℃或更高的SST距平, 同时在气旋东支气流的引导下延伸到了60°S以南, 对比观测来看, 观测中由于气旋中心偏西且强度稍弱, 正极的SST异常并未能继续向南延伸。并且极值也局限于20°S一带。
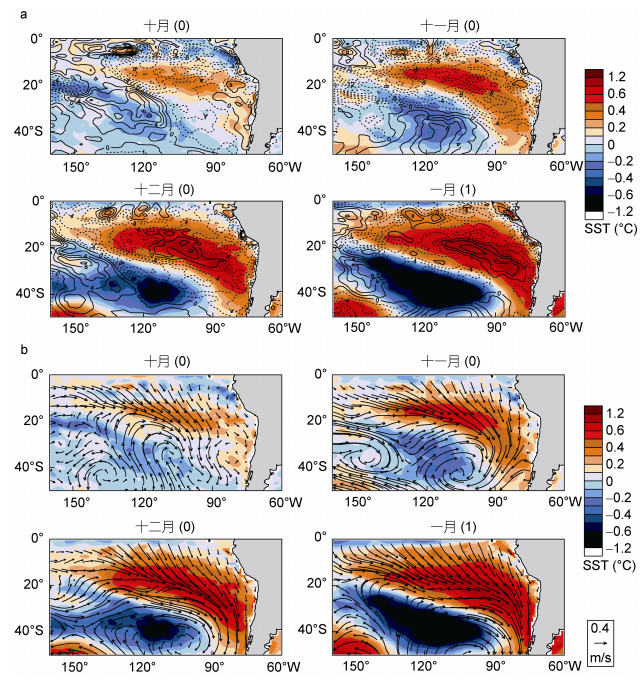 |
| 图 7 HadGEM2-ES模式合成结果 Fig. 7 Synthetic analysis in HadGEM2-ES model a中等值线为潜热(单位: W/m2), b为风场(单位: m/s), 0代表事件年的前一年, 1代表事件年 |
通过上述分析可以发现: HadGEM2两个模式与CSIRO-Mk3.6.0模式与观测更为接近, 但SST模态强度模拟偏强, 使得技巧评分较其他模式低。在气压模态方面, 所有模式模拟的强度都与观测较为接近, 从而使得气压模态模拟位置成为影响技巧评分的重要因素。HadGEM2两个模式在气压的强度上与观测有一定差距, 从而使得其技巧评分偏低。GFDL-CM3模式模拟的气压与观测对应很好, 技巧评分在所有模式中最高, 达到了0.92, 但其模拟的SST模态负极强度偏强, 正极区域也较大, 技巧评分只有0.58。综合技巧评分, NorESM1-M模拟SST偶极子模态的能力较强, 且模态位置与强度与观测都拟合较好, INMCM4模式次之, 正极模拟强度较观测强。HadGEM2-CC、HadGEM2-ES、MPI-ESM-MR、GFDL-CM3模式模拟的SST模态与观测都拟合较好, 但比观测强出许多的模态强度使得技巧评分偏低。
3.2 模式分组回归分析为了验证模拟较好的模式与模拟较差的模式热力耦合的不同, 根据技巧评分高低将15个CMIP5模式分为了三组, 分别为技巧评分高、中、低组, 每组5个模式。为了对比分析模式模拟偶极模态的能力, 选用了技巧评分高和低的两个组, 将这两组五个模式SVD计算得出的的偶极模态进行平均(图略)。两组模式分别选取SST(潜热通量)正极(负极)区域进行平均, 其中潜热通量为提前一个月。使用55a的数据做回归分析, 得出结果如图 8。图中分组标题数字分别代表回归系数, 相关系数。组1、组2分别为技巧评分高、低的组。从图中可以看到, 观测中的SST与潜热通量呈负相关关系, 回归系数为-0.018表明在正极区域SST的变化与潜热通量有着明显的联系。而技巧评分较高的组在这一点上与观测较为接近, 回归系数为-0.020。技巧评分低的回归系数为-0.032, 相较观测偏强, 体现在SST模态上为偶极强度比观测高出许多。即SST与潜热通量耦合关系越密切, 偶极子的强度就越强, 这从侧面佐证了影响偶极子发展的物理量主要是潜热通量, 偶极子对潜热通量的变化较为敏感。
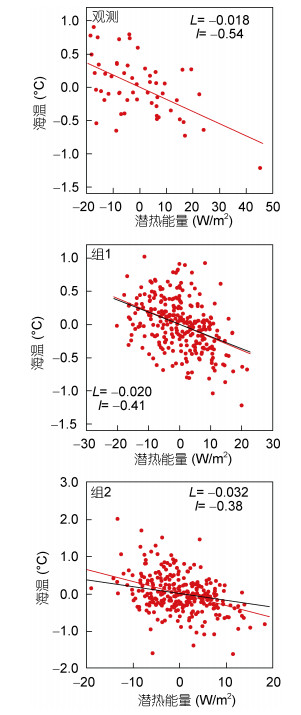 |
| 图 8 模式与观测中正极模态区域平均回归分析 Fig. 8 Regression analysis of the mean positive mode region in model and observation 注:潜热通量提前SST 1个月, L和l分别代表回归系数与相关系数 |
通过上面的分析, 关于模式在模拟副热带偶极子的能力上, 可以得出如下结论:
(1) 本文评估的15个模式中有13个模式都可以模拟出偶极模态和与SST对应的气压异常中心, 在模拟SST异常方面, 绝大多数模式模拟都相较观测更强, 而在气压方面则与观测强度较为一致。MIROC5、NorESM1-M模式模拟的强度和位置与观测最为接近, HadGEM2、CSIRO-Mk3.6.0、INM-CM4、IPSL-CM5A- LR模式模拟的模态位置与观测较为接近, 但是模态强度均超过观测值20%—30%。
(2) 模式在模拟偶极模态发展阶段较观测具有一定的提前性, 观测中在提前两个月时可以看出SST的跷跷板式分布, 而在3/4模式中提前三个月就有类似SST分布, HadGEM2-ES、HadGEM2-CC、CSIRO- Mk-3-6-0模式中甚至可以提前到六个月, 这种现象有待于进一步的研究。
(3) 偶极模态的生成与传播在相当的程度上是受大气环流调制的, 其中潜热通量的人造毛尤为重要。大气环流产生的风场异常引起潜热通量的变化, 之后通过潜热的形式传递给海洋, 使模态进一步发展。在HadGEM2-ES、HadGEM2-CC、CSIRO-Mk-3-6-0模式中偶极模态发展到成熟阶段时会模态正极上方会产生正的潜热通量异常, 即模态通过潜热通量的形式将热量反馈给大气, 进一步加强大气环流异常。
李琼, 郑建, 王法明. 2016. 南太平洋副热带偶极子对南太平洋辐合带的影响. 海洋科学, 40(10): 143-150 DOI:10.11759//hykx20151201002 |
Behera S K, Yamagata T, 2001. Subtropical SST dipole events in the southern Indian Ocean. Geophysical Research Letters, 28(2): 327-330 DOI:10.1029/2000GL011451 |
Chiang J C H, Vimont D J, 2004. Analogous Pacific and Atlantic meridional modes of tropical atmosphere-ocean variability. Journal of Climate, 17(21): 4143-4158 DOI:10.1175/JCLI4953.1 |
Chu J E, Ha K J, Lee J Y et al, 2014. Future change of the Indian Ocean basin-wide and dipole modes in the CMIP5. Climate Dynamics, 43(1-2): 535-551 DOI:10.1007/s00382-013-2002-7 |
Hirota N, Takayabu Y N, Watanabe M et al, 2011. Precipitation reproducibility over tropical oceans and its relationship to the double ITCZ problem in CMIP3 and MIROC5 climate models. Journal of Climate, 24(18): 4859-4873 DOI:10.1175/2011JCLI4156.1 |
Morioka Y, Ratnam J V, Sasaki W et al, 2013. Generation mechanism of the South Pacific Subtropical Dipole. Journal of Climate, 26(16): 6033-6045 DOI:10.1175/JCLI-D-12-00648.1 |
Morioka Y, Tozuka T, Masson S et al, 2012. Subtropical dipole modes simulated in a coupled general circulation model. Journal of Climate, 25(12): 4029-4047 DOI:10.1175/JCLI-D-11-00396.1 |
Reason C J C, 2001. Subtropical Indian Ocean SST dipole events and southern African rainfall. Geophysical Research Letters, 28(11): 2225-2227 DOI:10.1029/2000GL012735 |
Saji N H, Goswami B N, Vinayachandran P N et al, 1999. A dipole mode in the tropical Indian Ocean. Nature, 401(6751): 360-363 |
Taylor K E, 2001. Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research:Atmospheres, 106(D7): 7183-7192 DOI:10.1029/2000JD900719 |
Taylor K E, Stouffer R J, Meehl G A, 2012. An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society, 93(4): 485-498 DOI:10.1175/BAMS-D-11-00094.1 |
Venegas S A, Mysak L A, Straub D N, 1997. Atmosphere-ocean coupled variability in the South Atlantic. Journal of Climate, 10(11): 2904-2920 DOI:10.1175/1520-0442(1997)010<2904:AOCVIT>2.0.CO;2 |
Wang F M, 2010a. Thermodynamic coupled modes in the tropical atmosphere-ocean:An analytical solution. Journal of the Atmospheric Sciences, 67(5): 1667-1677 DOI:10.1175/2009JAS3262.1 |
Wang F M, 2010b. Subtropical dipole mode in the Southern Hemisphere:A global view. Geophysical Research Letters, 37(10): L10702 |
Wang F M, Chang P, 2010. Coupled variability and predictability in a stochastic climate model of the Tropical Atlantic. Journal of Climate, 21(23): 6247-6259 |
Yuan C X, Tozuka T, Luo J J et al, 2014. Predictability of the subtropical dipole modes in a coupled ocean-atmosphere model. Climate Dynamics, 42(5-6): 1291-1308 DOI:10.1007/s00382-013-1704-1 |
Zheng J, Wang F M, 2017. On the formation of the South Pacific quadrupole mode. Theoretical and Applied Climatology, 130(1-2): 331-344 DOI:10.1007/s00704-016-1885-8 |
 2019, Vol. 50
2019, Vol. 50


