
中国海洋湖沼学会主办。
文章信息
- 周春, 李予国, 张宝强. 2019.
- ZHOU Chun, LI Yu-Guo, ZHANG Bao-Qiang. 2019.
- 变速海水运动感应电磁场数值模拟及特征分析
- NUMERICAL SIMULATION OF THE ELECTROMAGNETIC FIELD INDUCED BY SEAWATER MOVEMENT
- 海洋与湖沼, 50(2): 261-268
- Oceanologia et Limnologia Sinica, 50(2): 261-268.
- http://dx.doi.org/10.11693/hyhz20180700186
-
文章历史
- 收稿日期:2018-07-26
- 收修改稿日期:2018-12-10
2. 青岛海洋科学与技术国家实验室 海洋矿产资源评价与探测技术功能实 验室 青岛 266100;
3. 国家海洋技术中心 天津 300112
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, China;
3. National Ocean Technology Center, Tianjin 300112, China
海水是一种高电导率的流体, 处于不停地运动之中。根据法拉第定律和安培定律, 海水运动因切割地磁场而产生感应电流, 从而感生时变电磁场, 称为海水运动感应电磁场。早在1832年, 法拉第就指出, 在地磁场中流动的河流和海水会产生感应电动势。Wollaston(1851)在穿过英吉利海峡海底电缆上检测出与海洋潮汐周期相同的电势变化, 证实了法拉第的预言。从此以后, 人们开始研究海水运动感应电磁现象。Longuet-Higgins等(1954)分析了各种海水运动产生的微弱电流, 并考虑了表面波和稳定流引起的电场及电流。Weaver(1965)和Larsen(1973)利用直接微分法推导了海洋表面波感应磁场表达式。Beal等(1970)利用直接微分法计算了内波所引起的海洋磁场。Chave(1983)利用格林函数法计算海水运动感应电磁场, 并分析了表面重力波和开尔文波感应电磁场特证。陈标等(2001)计算了典型海流产生的磁场强度, 认为当海流宽度较大时, 海流感应磁场不应被忽略。林春生等(2003)根据电磁感应原理计算了海流感应电磁场。张自力等(2006)利用海浪谱理论分析了半无限空间海浪波动感应电磁场的频谱特性。林智恒等(2019)从毕奥萨伐尔定律出发, 推导了二维海水运动磁场方程, 并分析了海水运动周期、振幅和水深对感应磁场的影响。
Bhatt(2011)假设海水在整个海水层中沿一个方向匀速运动, 采用格林函数法计算一维和二维海水运动感应电磁场, 并讨论了其在海水中的分布特征。Bhatt(2011)所述的海水运动模型可称为常速度海水运动模型。通常情况下, 海水运动速度是随着海水深度的变化而变化的, 故而研究变速度海水运动感应电磁场十分必要。本文提出一种计算变速度海水运动感应电磁场的新方法。计算了常速度海水运动感应电磁场, 并与格林函数法计算结果进行了对比。然后计算了变速度海水运动感应电磁场, 较详细地讨论了海水运动周期和海底介质电导率对海水运动感应电磁场的影响。
1 海水运动感应电磁场表达式运动的海水因切割地磁场而产生感应电磁场, 感应电场强度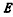
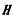
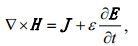 (1)
(1)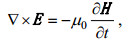 (2)
(2)式中,
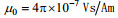
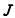
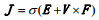
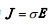
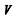
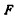
建立如图 1所示地电模型, 坐标原点位于海平面上, 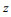
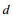
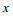
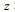
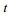
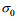
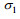
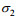
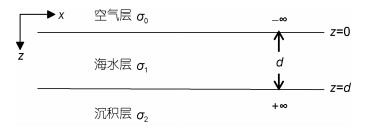 |
| 图 1 地电模型示意图 Fig. 1 Seawater movement and the geoelectric model |
根据法拉第电磁感应定律, 沿x向运动的海水因切割沿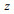
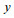
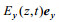
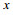
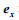
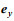
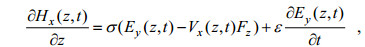 (3)
(3)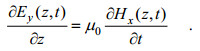 (4)
(4)假设海水运动速度场为时谐函数(Coulson, 1955), 即认为海水行进波具有简谐波的形式。一维速度场为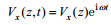
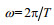
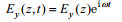
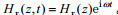
于是, 方程(3)和(4)变为
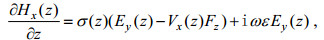 (5)
(5)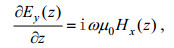 (6)
(6)对方程(6)关于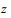
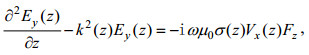 (7)
(7)其中,
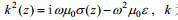
对方程(5)关于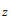
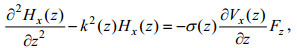 (8)
(8)在一定边界条件下, 求解偏微分方程(7)和方程(8), 即可得到海水运动感应电磁场。
Bhatt(2011)利用格林函数法求解偏微分方程(7), 得到电场分量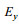
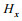
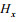
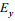
对于如图 1所示地电模型, 方程(8)可以写成为
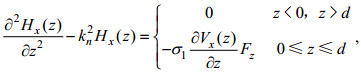 (9)
(9)其中,
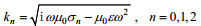
由方程(5), 得
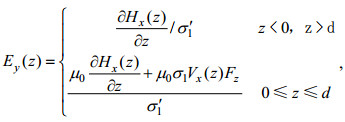 (10)
(10)其中, 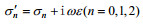
方程(9)的解具有下列形式:
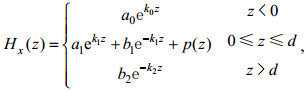 (11)
(11)式中,
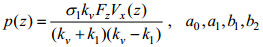
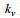
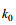
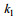
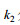
将方程(11)代入方程(10), 可得
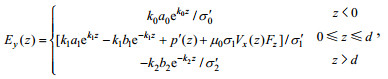 (12)
(12)式中,
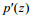
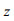
由于在海水表面(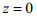
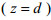
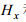
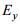
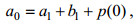 (13)
(13)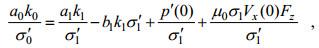 (14)
(14)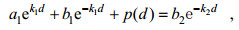 (15)
(15)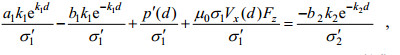 (16)
(16)由上述方程组可以求得系数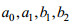
为验证前述方法和计算机程序的正确性, 建立了一个常速度海水运动模型, 分别用本文方法和格林函数法计算一维海水运动感应电磁场, 并比较两种方法的计算结果。然后, 分析海水运动周期和海底介质电导率对感应电磁场的影响。
假设在整个海水层中海水以相同的速度V0=0.1m/s, 沿x方向运动, 即海水运动速度不随深度的变化而变化, 称为常速度模型。本文中采用Constable等(1996)提出的典型一维海洋地电模型, 即假定图 1所示模型中海水层和海底介质的电导率分别为3.33和1.0S/m。海水层厚度为2000m, 垂直地磁场为Fz=5×10-5T。利用本文方法和格林函数法分别计算海水运动感应电磁场响应。图 2为海水运动周期为10s时, 感应电场和感应磁场振幅随深度变化曲线。由图 2可知:
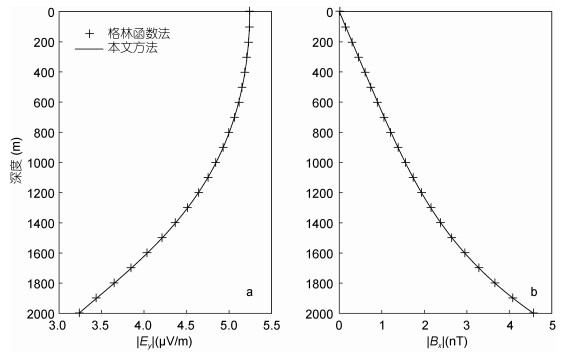 |
| 图 2 常速度模型海水运动感应电场Ey和感应磁场Bx振幅随深度变化曲线 Fig. 2 The depth-related variation of amplitude of the electric field (Ey) and electromagnetic fields (Bx) induced in a homogeneous velocity model |
(1) 本文方法计算得到的常速度海水运动感应电场和感应磁场曲线与格林函数法(Bhatt, 2011)所得曲线完全重合。
(2) Ey分量在海表面处有最大值5.241µV/m, 随着深度的增加而减小, 在海底界面处达到最小值3.239µV/m; Bx分量在海表面处有最小值1.762×10-5nT, 随着深度的增加而增大, 在海底界面处达到最大值4.572nT。
(3) 海水运动感应电磁场是海底大地电磁探测数据中的主要噪声(张自力, 2009), 模拟结果表明海水运动感应电磁场的量级与海洋大地电磁场的量级相当, 因而在解释海洋大地电磁场资料时, 应设法抑制或消除海水运动感应电磁场的影响, 否则可能会对海洋电磁探测方法的应用效果产生影响。
2.1.1 海水运动周期对海水运动感应电磁场的影响海水是一种良导体, 电磁场在海水中传播时会衰减, 而衰减的快慢程度与电磁场的周期有关。周期越短, 电磁场在海水层中衰减越快。研究表明, 海洋表面重力波的周期范围在0.1—100s。本文选取三个不同的海水运动周期(T=1、10、100s), 来讨论海水运动周期对感应电场和感应磁场的影响。
图 3为不同海水运动周期感应电场和感应磁场振幅随深度变化曲线。由图 3可知:
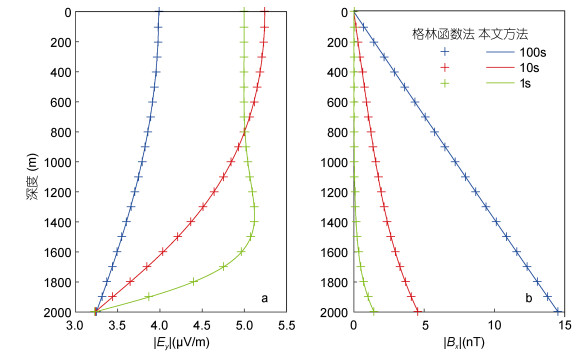 |
| 图 3 不同海水运动周期的感应电场Ey和感应磁场Bx振幅随深度变化曲线 Fig. 3 The depth-related variation of amplitude of the electric field (Ey) and electromagnetic fields (Bx) in different seawater movement periods |
(1) 对于三种不同的海水运动周期, 本文方法计算得到的常速度模型感应电场和磁场曲线与用格林函数法计算结果完全重合。电场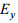
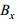
(2) 短周期时(1s), 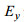
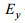
(3) 磁场分量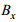
常速度情形下, 海水层中海水速度不随深度变化, 即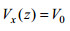
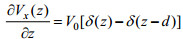
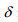
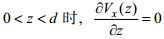
图 4为海底介质电导率分别为0.1、1.0和10S/m时海水运动感应电磁场振幅随深度变化曲线。由图 4可知:
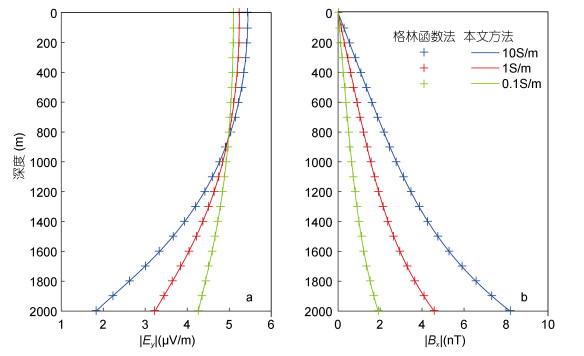 |
| 图 4 不同海底介质电导率的海水运动感应电场Ey和感应磁场Bx振幅随深度变化曲线 Fig. 4 The depth-related variation of the amplitude of the electric field (Ey) and electromagnetic fields (Bx) of seawater movement in different seafloor conductivities |
(1) 海底介质电导率对海水层深部电场的影响比浅部明显。在海水浅部(水深0—800m), 海底介质电导率越大, 电场振幅值越小, 且随深度增加衰减越快。
(2) 海底介质电导率越大, 磁场振幅值越大。随着海水深度的增大, 海底介质对感应磁场的影响越明显。
2.2 变速度海水运动假设海水运动速度随深度增加呈指数衰减, 即为变速度海水运动。假设海水速度场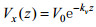
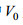
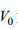
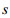
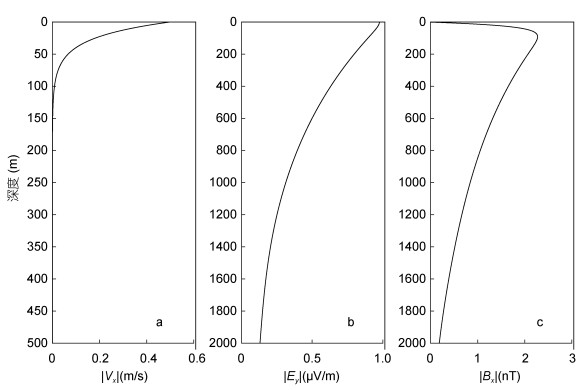 |
图 5 海水运动速度Vx(z)随深度指数衰减(a)、感应电场  |
(1) 
(2) Bx在海表面处为零, 随着深度的增加快速增大, 在93m深处达到最大值2.273nT, 然后随着深度的继续增大单调减小, 在海底界面处达到最小值0.186nT。这与常速度模型Bx分量在海水层中的变化规律不同。
2.2.1 海水运动周期对海水运动感应电磁场的影响海水运动周期越短, 速度场衰减越快(图 6a)。图 6b和图 6c分别为三种不同海水运动周期(5、10、16.7s)的海水运动感应电场和磁场振幅随深度变化曲线。由图 6可知:
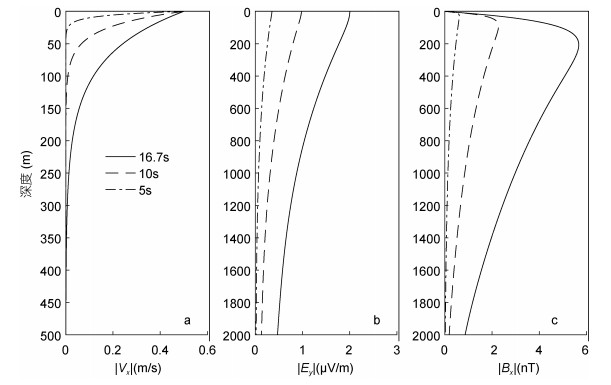 |
| 图 6 不同海水运动周期变速度Vx(z)模型及感应电场Ey和感应磁场Bx振幅随深度变化曲线 Fig. 6 Various velocity models in different seawater movement periods and the depth-related variation in the amplitude of the inductive electromagnetic field |
(1) Ey在海表面处有最大值, 随着海水深度的增大而单调衰减, 海水运动周期越短, 电场振幅值随深度衰减越快。海水运动周期越长, 感应电场振幅值越大。
(2) Bx在海表面处为零, 随着深度的增加快速增大到最大值, 然后随着深度的继续增大单调减小, 在海底界面处达到极小值。海水运动周期越长, 其波长越长。海水运动速度随深度衰减越慢, 感应磁场振幅值越大, 且其最大值出现的位置离海平面越远。
2.2.2 海底介质电导率对海水运动电磁场的影响下面讨论变速度情形下, 海底介质电导率对海水运动感应电磁场的影响。假定海水运动速度随深度指数衰减(图 7a), 海水运动周期为10s, 海平面处海水速度为V0=0.5m/s。我们计算了海底介质电导率分别为0.0、1.0、10S/m时的海水运动感应电磁场响应, 其振幅随深度变化曲线如图 7b和图 7c所示。
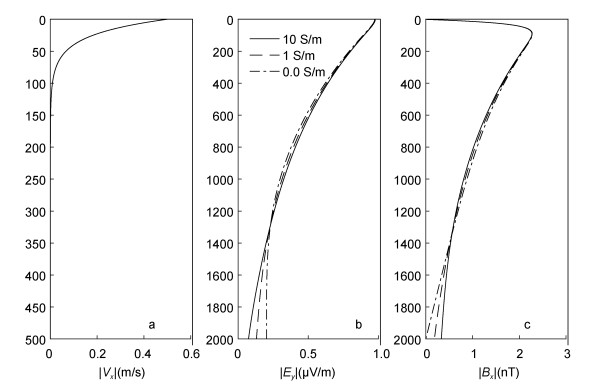 |
| 图 7 速度场Vx(z)及不同海底介质电导率感应电场Ey和感应磁场Bx振幅随深度变化曲线 Fig. 7 The depth-related variation of velocity field and amplitude of inductive electromagnetic field of seawater movement in different seafloor conductivities |
由图 7可知, 相较于海水运动速度保持不变的情形(图 4), 在海水运动速度随深度指数衰减情形下, 海底介质电导率对海水运动感应电磁场的影响较小, 且其影响只体现在海水深部(1400m以下)。在浅部, 三种不同海底介质电导率的感应电场Ey和感应磁场Bx曲线重合在一起。在深部, Ey随着海底介质电导率的增大而减小, 与之相反, Bx则随着海底介质电导率的增大而增大。
3 结论本文提出了一种计算一维海水运动感应电磁场的新方法。首先推导出了一维速度场海水运动感应电磁场偏微分方程, 利用电磁场在海水面和海底面上的连续性条件, 得到了海水运动感应电磁场表达式。计算了常速度海水运动感应电磁场, 并与格林函数法计算结果进行了对比, 两种方法的计算结果一致。然后计算了变速度海水运动模型感应电磁场, 并讨论了海水运动周期和海底介质电导率对海水运动感应电磁场的影响。计算结果表明, 海水运动速度对感应电场和感应磁场都有影响, 但影响程度与海水运动速度的特征有关。海水运动速度越大, 感应电场和感应磁场幅值也越大。对变速度海水运动而言, 海水运动周期越短, 其电磁场随深度衰减越快。海底介质电导率对变速度海水运动感应电磁场的影响主要体现在海水深部近海底面处, 且其影响要比常速海水运动小得多。在本文所述模型和参数条件下, 常速度长周期海水运动感应电场和磁场振幅分别可达6µV/m和10nT; 变速度长周期海水运动感应电场和磁场振幅分别可达3µV/m和6nT。海水运动感应电磁场数量级与海洋大地电磁场的量级相当, 在利用海洋大地电磁法探测海底地下结构时, 海水运动感应电磁场是不可忽略的干扰源。
张自力, 2009.海洋电磁场的理论及应用研究.北京: 中国地质大学(北京)博士学位论文
|
张自力, 魏文博, 李庚伟, 等. 2006. 海浪感应磁场的频谱特性. 渤海大学学报(自然科学版), 27(4): 354-357 DOI:10.3969/j.issn.1673-0569.2006.04.016 |
陈标, 祝传刚, 张铁军, 等. 2001. 典型海流磁场的数值模拟. 青岛大学学报, 14(2): 1-3 |
林春生, 任德奎. 2003. 海流感应电磁场的分析与计算. 海军工程大学学报, 15(4): 19-22, 41 DOI:10.3969/j.issn.1009-3486.2003.04.005 |
林智恒, 李予国. 2019. 海水运动感应磁场的数值计算方法. 中国海洋大学学报, 49(2): 74-78 |
Beal H T, Weaver J T, 1970. Calculations of magnetic variations induced by internal ocean waves. Journal of Marine Research, 75(33): 6847-6852 |
Bhatt K M, 2011. Motion induce noise in marine electromagnetic data. Technical University, Braunschweig, Lower Saxony, Germany
|
Chave A D, 1983. On the theory of electromagnetic induction in the earth by ocean currents. Journal of Geophysical Research, 88(B4): 3531-3542 DOI:10.1029/JB088iB04p03531 |
Constable S, Cox S C, 1996. Marine controlled-source electromagnetic sounding:2. The PEGASUS experiment. Journal of Geophysics Research, 101(B3): 5519-5530 DOI:10.1029/95JB03738 |
Coulson C A, 1955. Waves. 7th ed. Edinburgh: Oliver and Boyd, 16-18
|
Ellis E, Banker S M, Smith W et al, 1881. Discussion on Mr. Adams' paper on "Earth currents". Journal of the Society of Telegraph Engineers and of Electricians, 10(36): 71-96 DOI:10.1049/jste-2.1881.0007 |
Larsen J C, 1973. An introduction to electromagnetic induction in the ocean. Physics of the Earth and Planetary Interiors, 7(3): 389-398 DOI:10.1016/0031-9201(73)90063-0 |
Longuet-Higgins M S, Stem M E, Stommel H M, 1954. The electrical field induced by ocean currents and waves, with applications to the method of towed electrodes. Papers in Physical Oceanography and Meteorology, 13(1): 1-37 |
Weaver J T, 1965. Magnetic variations associated with ocean waves and swell. Journal of Geophysical Research, 70(8): 1921-1929 DOI:10.1029/JZ070i008p01921 |
 2019, Vol. 50
2019, Vol. 50


