中国海洋湖沼学会主办。
文章信息
- 郜婕, 毛新燕, 郭新宇. 2019.
- GAO Jie, MAO Xin-Yan, GUO Xin-Yu. 2019.
- 吐噶喇海峡内潮的能量收支和大小潮变化
- ENERGY BUDGET AND SPRING-NEAP VARIATION OF INTERNAL TIDES IN TOKARA STRAIT, JAPAN
- 海洋与湖沼, 50(2): 269-277
- Oceanologia et Limnologia Sinica, 50(2): 269-277.
- http://dx.doi.org/10.11693/hyhz20181000251
-
文章历史
- 收稿日期:2018-10-25
- 收修改稿日期:2018-11-16
2. 中国海洋大学 环境科学与工程学院 青岛 266100;
3. 爱媛大学 沿岸环境科学研究中心 爱媛 790-8577;
4. 日本海洋研究开发机构 神奈川 236-0001
2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China;
3. Center for Marine Environmental Studies, Ehime University, Ehime 790-8577, Japan;
4. Japan Agency for Marine-Earth Science and Technology, Kanagawa 236-0001, Japan
吐噶喇海峡位于琉球岛链北部, 是大隅海峡南端屋久岛与奄美大岛之间水域的总称。其宽约203km, 平均水深634m, 是连接东海与西太平洋的重要水道(林葵等, 1995;孙湘平, 2006)。吐噶喇海峡潮能量显著, 地形复杂, 水体层化较强, 适宜内潮生成与传播, 是西北太平洋中非常重要的内潮生成区域(Varlamov et al, 2015)。内潮生成后, 进一步通过非线性演化与耗散将能量向海洋小尺度运动转化, 促进海洋内部混合(Baines, 1982; Munk et al, 1998; Laurent et al, 2002);同时, 它所造成的营养盐输入促进浮游植物的生长以及珊瑚的繁殖, 对海洋生态学具有重要的意义(方欣华等, 2005; Sharples et al, 2007; Jan et al, 2009; Lucas et al, 2011)。
太平洋M2内潮能量约为338GW, 其中84%产生于岛屿陆坡等地形处(Munk et al, 1998)。由于地形和层结的不同, 西太平洋的内潮能量约比东太平洋大2—3个量级(Niwa et al, 2001)。西北太平洋中约有35GW正压潮能量转化为内潮能量, 其中吐噶喇海峡、吕宋海峡、伊豆群岛、小笠原群岛为M2内潮主要生成区域(Varlamov et al, 2015)。吐噶喇海峡处M2分潮内潮能量仅次于吕宋海峡, 为西北太平洋第二大内潮产生区域(Niwa et al, 2001; 2004)。Zhu等(2017)利用船载ADCP(Acoustic Doppler Current Profiler)观测数据研究了吐噶喇海峡处潮流和表层环流, 结果表明:吐噶喇海峡处半日潮以M2分潮为主, 最大潮流振幅约为0.27m/s; 全日潮以K1分潮为主, 最大潮流振幅约为0.21m/s; 潮流椭圆的垂向结构中则显示表层以下的潮流流速呈现复杂的变化规律, 甚至多次反向, 有明显的内潮信号。前人也利用船载CTD(Conductivity Temperature Depth profiler)和ADCP探测吐噶喇海峡处内潮的产生和传播, 发现吐噶喇海峡处生成的内潮在向外海传播过程被黑潮地转涡度所阻碍(Rainville et al, 2004)。Tsutsumi等(2017)利用ADCP观测数据分析了吐噶喇海峡处的湍流混合, 认为内潮引起的水平流速的垂向剪切会显著影响当地的湍流耗散。
前人对吐噶喇海峡做了多方面的研究工作, 但是对于内潮生成及传播过程尚缺乏明确的量化, 尤其是大小潮期间内潮能量的具体收支变化还不清楚。因此, 本文将利用高分辨率的海洋模式结果开展相关研究, 明确量化吐噶喇海峡处内潮能量的收支及其随大小潮的变化。
1 数据简介和验证JCOPE-T(Japan Coastal Ocean Predictability Experiment—Tides)模式是日本海洋研究开发机构(Japan Agency for Marine-Earth Science and Technology, JAMSTEC)基于POM(Princeton Ocean Model)模式所研发的, 采用三维斜压原始控制方程组的有限体积海洋模型。它是一个嵌套在JCOPE2模式(Miyazawa et al, 2009)的高分辨率潮汐驱动的海洋环流预报模式。JCOPE-T由表面动量、热量和淡水通量驱动, 包括潮汐过程和淡水径流(日本的47条主要河流, 朝鲜半岛的3条河流, 7条中国主干线陆地河流和1条台湾省的河流)。模式的水平分辨率为1/36°(约为3km), 覆盖了西北太平洋的一部分: 24°—48°N和125°—148°E; 垂向分辨率为47个σ层, 适用于吐噶喇海峡区域地形复杂、岸线曲折且岛屿众多的情况。模式内模时间步长为2s, 外模时间步长为60s, 计算结果每小时输出一次。水平湍黏性系数和水平物质扩散系数采用Smagorinsky(1963)给出的公式计算。垂向的黏性和扩散系数使用了改进的Mellor-Yamada 2.5阶湍流封闭模型(Mellor et al, 1982)。
JCOPE-T海洋环流预报模式已经成功地应用于日本海洋预报及科研的各项工作中: Varlamov等(2015)比较JCOPE-T模式结果和卫星观测数据, 指出该模式可以较好地模拟反映西北太平洋的潮汐特征, 并进一步分析了西北太平洋内潮的能量分布及内潮主要产生区域的影响因素。Takagi等(2017)则在JCOPE-T模拟结果的基础上利用轨迹追踪计算了日本海海底甲烷气体泄漏后的运移路径。
本文选择JCOPE-T模式在126°—132°E和27°—32°N海域(图 1a红线所围区域)2015年11月的模拟结果, 对吐噶喇海峡处的内潮产生和传播机制进行研究。
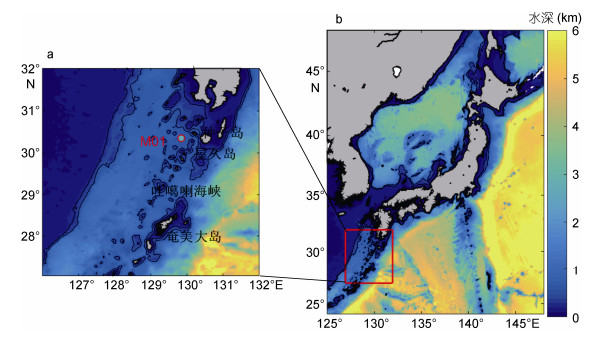 |
| 图 1 研究区的水深和M01观测站位置(a)以及区域位置(b) Fig. 1 The topography of model domain showing the mooring location M01 (a) and the geographical background (b) |
此外, 本文分析了日本OMIX项目(Ocean Mixing Processes, http://omix.aori.u-tokyo.ac.jp/en/ )2015年M01潜标观测数据, 用于验证JCOPE-T模式结果。M01(129°51′E, 30°21′N)处水深为650m, 于573m处放置75kHz的ADCP向上观测。观测时间为2015年11月15日8: 00—2015年11月21日12:00, ADCP数据时间分辨率为1min; 数据的垂向分辨率为8m。
为进一步分析比较该点的潮流特征, 对观测数据和JCOPE-T模拟的结果做了下述处理:先利用Matlab自带的Butter带通滤波器(通带截止频率8.4×10-6Hz通带最大衰减5dB, 阻带截止频率0.7×10-6, 阻带最大衰减30dB)和低通滤波器, 得到各自的潮频流速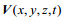
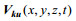
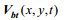
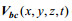
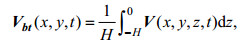 (1)
(1)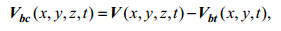 (2)
(2)将JCOPE-T模拟结果与M01点的观测数据结果对比可知(图 2), 模拟结果可以基本反应该点的黑潮特征:黑潮在该处弯曲, 流动方向在该处转向东南; 东西向流速大于南北向流速, 东西向流速最大值约为0.85m/s, 而南北向流速最大值约为0.5m/s; 表层至200m处流速较大, 200m以深, 随着深度的增加, 黑潮的流速逐渐减小。同时, 模拟结果可以很好地反映M01点的潮流:两者正压潮流的大小和变化特征基本一致, 正压潮流以半日潮和全日潮周期为主, 其流速最大值约为0.15m/s; 两者内潮流速的大小和变化周期也基本一致, 内潮能量的传播方向也基本一致。由于模式采用一般σ分层, 在水深较深的海域底层的垂向分辨率较低, 模式模拟结果不能充分显示内潮的复杂垂向结构特征。
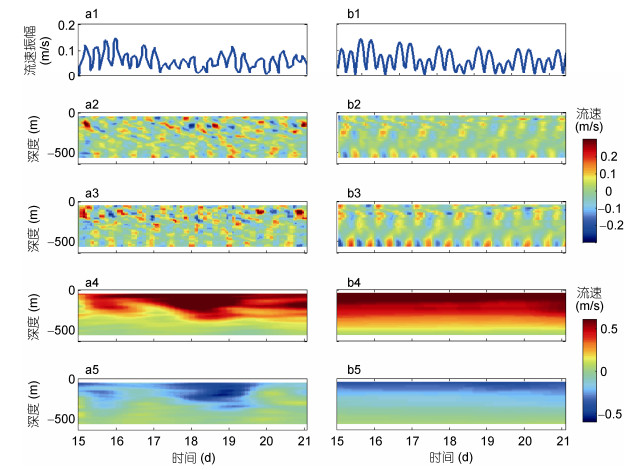 |
| 图 2 M01观测点的正压潮流速的振幅(1)、东西向内潮流速(2)、南北向内潮流速(3), 东西向低频黑潮流速(4)和南北向低频黑潮流速(5) Fig. 2 The amplitude of barotropic tidal velocity(1), the east-west baroclinic tidal velocity (2), the south-north baroclinic tidal velocity (3), the east-west Kuroshio velocity (4), the south-north Kuroshio velocity (5) 注:左列为ADCP观测结果(a); 右列为JCOPE-T模式数据(b) |
综合比较可得, JCOPE-T模式模拟结果和ADCP观测结果基本一致, 模式较好地反映了该地正压潮流和内潮流速的大小和位相等基本特征, 基本体现了该地的黑潮信号, 可用于分析吐噶喇海峡处内潮产生和传播特征。应该指出, 由于观测站点有限, 观测时间较短, 仅对观测数据的分析是很难揭示内潮在该海区的产生和传播。
2 等密面起伏分析海水内部等密度面的起伏情况能够很好地刻画内潮的生成、传播以及分布情况。因此, 本文选取了100、250、500和1000m不同深度来探讨等密面起伏的分布情况。首先根据当地月平均的密度场, 计算得到密度垂向梯度, 并据此将每层的密度扰动反算得到密度起伏(公式3)。由于JCOPE-T模式采用的是一般σ分层, 因此绘制水平分布图时通过线性插值的方法, 计算出各个深度层上密度起伏的水平分布状况, 进行绘图。
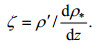 (3)
(3)其中, ζ为等密面起伏, ρ*为月平均的密度场, ρ‘为密度扰动。图 3a中, 内潮在吐噶喇海峡附近时产生的等密度面起伏最大, 其振幅可达30m;东海陆坡和奄美群岛处也有较大的等密度面起伏产生。内潮自吐噶喇海峡向外传播过程中, 颜色深的黄色条纹后面紧接着蓝色条纹, 并且在两条颜色深的黄色条纹中间存在着数条浅黄色和浅蓝色的条纹, 这是由于复杂地形处的内潮波多次反射导致的。而东海陆坡处产生的内潮, 随着水深变浅, 在海底和海面之间多次反射, 其等密度面起伏的振幅由20m迅速衰减为5m。
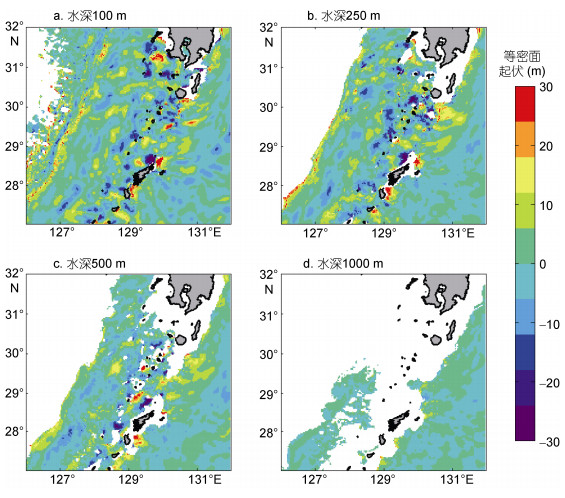 |
| 图 3 模式2015年11月14日0时, 水深100、250、500和1000m等密面起伏 Fig. 3 The movement of Isopycnal at the depth of 100, 250, 500 and 1000 m, at 0:00, Nov. 14, 2015 |
比较图 3a和图 3b, 250m处的密度起伏状况与100m处很相似, 但在九州岛东南海域的200m等密面起伏较100m更为明显一些。对比图 3不同深度处的等密面起伏情况可知, 内潮在吐噶喇海峡向太平洋传播时引起的等密面起伏与上层相比显著减小, 在向东海陆架传播时也有不同程度的衰减。值得注意的一点是, 该区域向太平洋内部传播的内潮能够影响的深度超过1000m。由于吐噶喇海峡处复杂的地形特征, 各岛屿、海山地形处产生的内潮在传播过程中相互影响, 难以区分。因此, 从能量的角度去分析, 有助于对于该海域内潮的进一步认识。
3 内潮能量收支分析 3.1 正压潮能通量正压潮能通量, 又称正压潮能通量密度, 即单位时间内通过海底至海面单位宽度断面的正压潮能。本文正压潮能通量计算公式如下(吴頔等, 2015;单位: W/m):
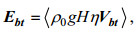 (4)
(4)其中,
Ebt为正压潮能通量, 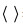
 |
| 图 4 吐噶喇海峡处的正压潮能通量分布 Fig. 4 Distribution of barotropic energy flux at the Tokara Strait 注:红色(蓝色)数字表示传入(传出)吐噶喇海峡深度积分的能通量; 蓝框表示积分区域(余同) |
计算得到, 通过西北边界的正压潮能通量约为-43.15GW(以进入到图 4蓝框所示边界为正), 通过西南边界的正压潮能通量为-5.10GW, 通过东南边界的正压潮能通量为60.06GW, 通过东北边界的正压潮能通量为2.11GW。即绝大部分正压潮能量通过东南边界传入, 在吐噶喇海峡转向后经西北边界向外传播, 其净正压潮能通量为13.92GW。
3.2 内潮能转化率目前人们普遍接受的内潮生成机制是潮地生成机制, 即内潮是由正压潮流、层化的海水和变化的地形共同作用生成。本文参照Legg等(2006)提出的公式, 利用正压潮流速和内潮导致的扰动压强估算内潮潮能转化率(Conversion rate, 单位: W/m2)。周期平均的内潮能转化率可以用公式(5)计算:
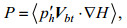 (5)
(5)其中,
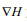
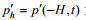
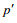
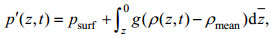 (6)
(6)其中, ρmean为月平均的密度, ρsurf为斜压的海表面压强。由于垂向积分的扰动压强为零(Kunze et al, 2002), 即: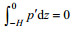
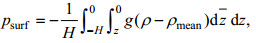 (7)
(7)从图 5可以看出, 内潮主要生成在海山、海岛等地形陡峭处(等深线较密处)。吐噶喇海峡是主要的内潮生成区域, 除此之外东海陆坡、奄美大岛南端也有大量内潮生成。由于吐噶喇海峡处岛屿众多, 其内潮的生成区域也零星散布, 十分复杂。这一分布特征也与Niwa等(2004)通过POM模式模拟的结果相一致。
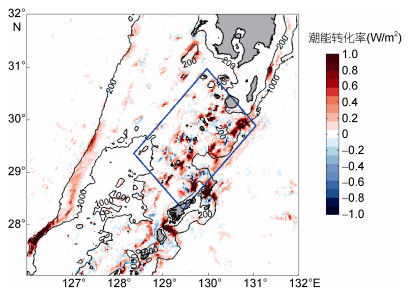 |
| 图 5 吐噶喇海峡处内潮的潮能转化率的水平分布 Fig. 5 Distribution of conversion rate from barotropic tide to baroclinic tide at the Tokara Strait 黑线表示等深线(单位: m) |
对图 5所示的蓝框内的潮能转化率进行积分可得, 吐噶喇海峡处由正压潮向内潮转化的能通量约为3.73GW, 这和Varlamov等(2015)计算所得的吐噶喇海峡处M2内潮能转化率为3.8GW大小基本一致。结合前文计算结果分析可得, 吐噶喇海峡处正压潮净能通量约为13.92GW, 其中有3.73GW(26.80%)转化为内潮能量, 两者的差值10.19GW(73.20%)的正压潮能量由于底摩擦等耗散在吐噶喇海峡。
3.3 内潮能通量为了进一步研究内潮能量在该区域附近的传播情况, 可以利用内潮流速和内潮导致的压强扰动在垂向上的积分计算内潮能通量(Holloway, 1996)。周期平均的内潮能通量可以用公式(8)计算(单位, W/m)(Munroe et al, 2005):
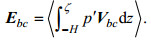 (8)
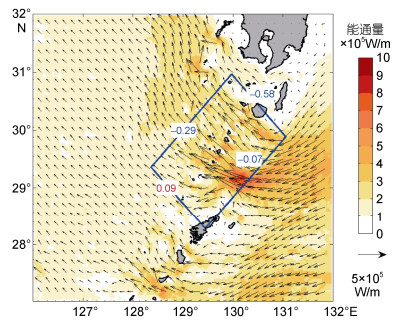
(8)由图 6可以看出, 内潮自吐噶喇海峡产生并逐渐向其周围海域传播。该地产生的内潮由于岛屿地形的阻碍主要分为两支, 大部分垂直于等深线向东南传入太平洋深层; 小部分向西北传入浅海陆架区, 这一结果和Guo等(2012)得到的结论基本一致。
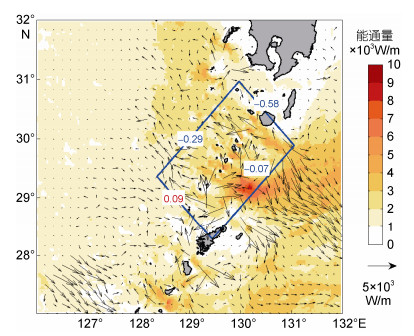 |
| 图 6 吐噶喇海峡处的内潮能通量分布 Fig. 6 Distribution of barotropic energy flux at the Tokara Strait |
其中, 通过西北边界的内潮能通量约为0.29GW, 通过西南边界的内潮能通量为-0.09GW, 通过东南边界的内潮能通量为-0.58GW, 通过东北边界的内潮能通量为-0.07GW。该区域内产生3.73GW内潮能量中约-0.84GW的内潮能量通过边界传至浅海和太平洋, 绝大部分能量经过东南边界、西北边界传出, 特别的, 尽管吐噶喇海峡内部产生的能量部分通过西南边界向外传出, 仍有大量内潮能量(约0.14GW)自奄美大岛南端产生并经西南边界传入吐噶喇海峡。东海陆架陆坡处对于M2分潮为亚临界地形, 内潮在浅海区继续传播直至耗散。
观测和数值模拟的结果显示, 高模态的内潮在源地耗散, 促进当地的混合; 低模态内潮传播到东海和太平洋深层, 最远可到距源地1000km之外的海区(Jan et al, 2009)。区域内积分的内潮潮能转化率减去通过边界上传出的内潮能通量即为当地耗散的内潮能通量。因此, 吐噶喇海峡处耗散的内潮能量约为2.89GW(77.2%)。
4 大小潮能量变化为进一步计算大小潮期间, 吐噶喇海峡处内潮在边界和区域内的能量收支的变化, 本文首先计算了大小潮期间吐噶喇海峡通过4个边框的正压潮能通量、内潮能通量随时间的变化(图 7)。图中蓝线为正压潮能通量(单位: ×102GW), 红线为内潮能通量(单位: GW)。
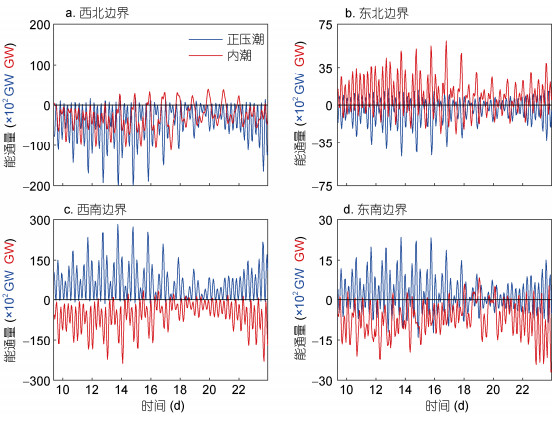 |
| 图 7 通过4个边界的正压潮能通量(蓝色, 单位: ×102GW)、内潮能通量(红色, 单位: GW)随时间的变化 Fig. 7 Time series of barotropic (blue, unit: ×102GW) and baroclinic energy flux (red, unit: GW) through four lateral boundaries: a. northwest; b. northeast; c. southwest; d. southeast |
由图 7可知, 通过西北和东南两个边界的正压潮(内潮)能通量显著大于其他两个边界, 且在大小潮期间保留着一致的变化趋势。对于四个边界来说, 大潮时期传入(传出)四个边界的能量显著大于小潮时期传入(传出)的能量, 但是其正负(传入/传出)不受大小潮影响。即, 大小潮仅仅会影响正压潮和内潮传入(传出)的能量的大小, 而不影响其方向。
进一步分别取14个全日潮周期平均和大小潮期间25h平均, 计算平均潮、大潮和小潮正压潮能通量和内潮能转化率、内潮能通量, 绘制其分布图(图 8)并计算通过各个边界的值和区域内积分(表 1)。
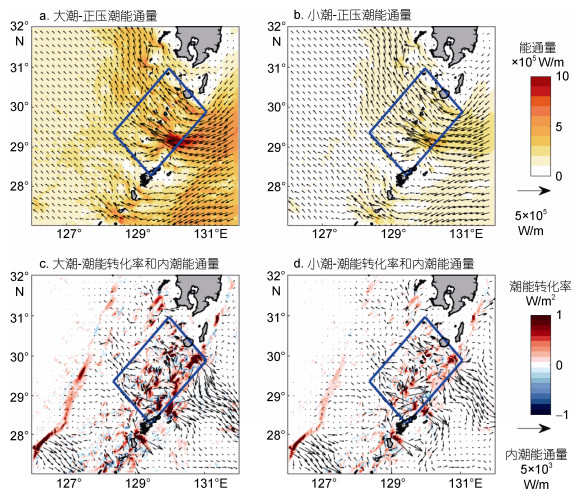 |
| 图 8 25h平均的大潮和小潮时的正压潮能通量和内潮能转化率 Fig. 8 25-h-averaged barotropic tidal energy flux and the conversion rate from barotropic tide to baroclinic tide during the spring and neap period |
| 边界 | 西北 | 西南 | 东南 | 东北 | 区域内积分 | 潮能转化率 | 耗散比率 | |
| 正压潮 | 大潮 | -59.87 | -8.00 | 82.56 | 3.05 | 17.74 | ||
| 小潮 | -26.78 | -2.26 | 38.15 | 0.64 | 9.75 | |||
| 平均潮 | -43.15 | -5.10 | 60.06 | 2.11 | 13.92 | |||
| 内潮 | 大潮 | -0.41 | 0.11 | -0.78 | -0.07 | -1.15 | 4.98 | 76.91% |
| 小潮 | -0.15 | 0.05 | -0.36 | -0.05 | -0.51 | 2.44 | 79.10% | |
| 平均潮 | -0.29 | 0.09 | -0.58 | -0.07 | -0.85 | 3.73 | 77.21% |
综合图 4—图 8和表 1可得:大潮和小潮时期, 吐噶喇海峡正压潮能量的传入和传出方向不变, 主要通过东南边界传入、西北边界传出; 大潮时期自太平洋传入吐噶喇海峡的正压潮能量(17.74GW)约为小潮时期传入能量(9.75GW)的1.8倍; 吐噶喇海峡内潮的产生区域基本一致, 但产生的内潮能量大小不同, 大潮时期吐噶喇海峡处产生的内潮能量(4.98GW)是小潮期间产生内潮能量(2.44GW)的2倍; 吐噶喇海峡内潮能量的传入和传出方向不变, 绝大部分能量通过东南、西北边界传出, 仍有少量能量自西南边界传入; 大潮时期吐噶喇海峡处传出的内潮能量(1.15GW)约为小潮时期传出能量(0.51GW)的2.1倍, 这与Holloway等(2003)模拟夏威夷群岛处内潮的大小潮变化所得结论一致; 大潮和小潮期间, 吐噶喇海峡内潮的耗散比率基本不变, 约为76%—79%。
5 结论本文利用JCOPE-T模式对吐噶喇海峡内潮的生成与传播过程进行了探究分析, 得到以下结论:
吐噶喇海峡处地形复杂、层结深厚, 是西北太平洋内潮的主要产生区域, 内潮所致的等密面起伏可达30m。吐噶喇海峡处的内潮主要产生在陡峭的海山、海岛地形处附近, 产生后垂直于等深线分为两支向外传播:一支向西北传入东海陆架, 能量在海面与海底之间不断反射、迅速衰减; 另一支向东南传入太平洋深层。
吐噶喇海峡处潮能丰富, 其平均潮时期的计算结果显示:该区域内, 输入的正压潮净能通量为13.92GW, 约有3.73GW转化为内潮能量, 其中有77.21%在当地耗散, 传出的内潮能通量为0.84GW, 主要通过西北、东南两个边界传出。
大小潮影响吐噶喇海峡处的内潮的产生:大潮期间输入的正压潮能通量约为小潮期间的2倍, 其产生的内潮能量也约为2倍, 但主要转化区域基本不变。尽管大小潮期间, 内潮自正压潮转化的能量不同, 其传播方向并不受影响, 仍主要通过西北、东南两个边界传出, 且在当地的内潮能量耗散比率均在76%—79%。即, 大小潮仅影响吐噶喇海峡处产生的内潮能量的大小, 不影响其产生区域、传播方向和耗散比率。
该海域受黑潮和天气系统(主要是风)影响, 其层结有显著的季节变化。因此, 根据公式(8), 除作为能量输入的正压潮的大小潮变化外, 层结的深度和强弱也会影响该区域的内潮产生和传播。本文基于一个月内的模式结果, 仅研究了大小潮时期内潮能量的变化, 可不考虑层结在这段时间的变化。未来会对该区域长时间尺度下内潮的能量变化和基本特征进行分析, 并进一步在理想地形下研究强背景流对于内潮传播的影响。
方欣华, 杜涛. 2005. 海洋内波基础和中国海内波. 青岛: 中国海洋大学出版社
|
孙湘平. 2006. 中国近海区域海洋. 北京:海洋出版社 |
吴頔, 方国洪, 崔欣梅, 等. 2015. 泰国湾及邻近海域潮汐潮流的数值模拟. 海洋学报, 37(1): 11-20 DOI:10.3969/j.issn.0253-4193.2015.01.002 |
林葵, 汤毓祥, 郭炳火. 1995. 吐噶喇海峡黑潮流速结构和流量的研究. 海洋与湖沼, 26(3): 247-253 DOI:10.3321/j.issn:0029-814X.1995.03.004 |
Baines P G, 1982. On internal tide generation models. Deep Sea Research Part A:Oceanographic Research Papers, 29(3): 307-338 DOI:10.1016/0198-0149(82)90098-X |
Guo P, Fang W D, Liu C J et al, 2012. Seasonal characteristics of internal tides on the continental shelf in the northern South China Sea. Journal of Geophysical Research:Oceans, 117(C4): C04023 |
Holloway P E, 1996. A numerical model of internal tides with application to the Australian north west shelf. Journal of Physical Oceanography, 26(1): 21-37 |
Holloway P E, Merrifield M A, 2003. On the spring-neap variability and age of the internal tide at the Hawaiian Ridge. Journal of Geophysical Research:Oceans, 108(C4): 3126 DOI:10.1029/2002JC001486 |
Jan S, Chen C T A, 2009. Potential biogeochemical effects from vigorous internal tides generated in Luzon Strait:A case study at the southernmost coast of Taiwan. Journal of Geophysical Research:Oceans, 114(C4): C04021 |
Kunze E, Rosenfeld L K, Carter G S et al, 2002. Internal waves in Monterey submarine canyon. Journal of Physical Oceanography, 32(6): 1890-1913 DOI:10.1175/1520-0485(2002)032<1890:IWIMSC>2.0.CO;2 |
Laurent L C S, Simmons H L, Jayne S R, 2002. Estimating tidally driven mixing in the deep ocean. Geophysical Research Letters, 29(23): 21-1 DOI:10.1029/2002GL016021 |
Legg S, Huijts K M H, 2006. Preliminary simulations of internal waves and mixing generated by finite amplitude tidal flow over isolated topography. Deep Sea Research Part Ⅱ:Topical Studies in Oceanography, 53(1-2): 140-156 DOI:10.1016/j.dsr2.2005.09.014 |
Lucas A J, Franks P J S, Dupont C L, 2011. Horizontal internal-tide fluxes support elevated phytoplankton productivity over the inner continental shelf. Limnology and Oceanography:Fluids and Environments, 1(1): 56-74 DOI:10.1215/lof3.v1.1 |
Mellor G L, Yamada T, 1982. Development of a turbulence closure model for geophysical fluid problems. Reviews of Geophysics, 20(4): 851-875 DOI:10.1029/RG020i004p00851 |
Miyazawa Y, Zhang R C, Guo X Y et al, 2009. Water mass variability in the western North Pacific detected in a 15-year eddy resolving ocean reanalysis. Journal of Oceanography, 65(6): 737-756 DOI:10.1007/s10872-009-0063-3 |
Munk W, Wunsch C, 1998. Abyssal recipes Ⅱ:energetics of tidal and wind mixing. Deep Sea Research Part I:Oceanographic Research Papers, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
Munroe J R, Lamb K G, 2005. Topographic amplitude dependence of internal wave generation by tidal forcing over idealized three-dimensional topography. Journal of Geophysical Research:Oceans, 110(C2): C02001 |
Niwa Y, Hibiya T, 2001. Numerical study of the spatial distribution of the M2 internal tide in the Pacific Ocean. Journal of Geophysical Research:Oceans, 106(C10): 22441-22449 DOI:10.1029/2000JC000770 |
Niwa Y, Hibiya T, 2004. Three-dimensional numerical simulation of M2 internal tides in the East China Sea. Journal of Geophysical Research:Oceans, 109(C4): C04027 |
Rainville L, Pinkel R, 2004. Observations of energetic high-wavenumber internal waves in the Kuroshio. Journal of Physical Oceanography, 34(7): 1495-1505 DOI:10.1175/1520-0485(2004)034<1495:OOEHIW>2.0.CO;2 |
Sharples J, Tweddle J F, Green J A M et al, 2007. Spring-neap modulation of internal tide mixing and vertical nitrate fluxes at a shelf edge in summer. Limnology and Oceanography, 52(5): 1735-1747 DOI:10.4319/lo.2007.52.5.1735 |
Smagorinsky J, 1963. General circulation experiments with the primitive equations:I. The basic experiment. Monthly Weather Review, 91(3): 99-164 DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
Takagi Y, Kawahara S, Okano Y et al, 2017. Numerical Simulation of Methane Seeping from the Seabed in the Japan Sea. Journal of Chemical Engineering of Japan, 50(4): 244-253 DOI:10.1252/jcej.16we069 |
Tsutsumi E, Matsuno T, Lien R C et al, 2017. Turbulent mixing within the Kuroshio in the Tokara Strait. Journal of Geophysical Research:Oceans, 122(9): 7082-7094 DOI:10.1002/2017JC013049 |
Varlamov S M, Guo X Y, Miyama T et al, 2015. M2baroclinic tide variability modulated by the ocean circulation south of Japan. Journal of Geophysical Research:Oceans, 120(5): 3681-3710 DOI:10.1002/2015JC010739 |
Zhu X H, Nakamura H, Dong M H et al, 2017. Tidal currents and Kuroshio transport variations in the Tokara Strait estimated from ferryboat ADCP data. Journal of Geophysical Research:Oceans, 122(3): 2120-2142 DOI:10.1002/2016JC012329 |
 2019, Vol. 50
2019, Vol. 50


