中国海洋湖沼学会主办。
文章信息
- 端和阳, 刘保昌, 何宜军, 李秀仲. 2019.
- DUAN He-Yang, LIU Bao-Chang, HE Yi-Jun, LI Xiu-Zhong. 2019.
- 一种改进的基于逆Omega-K算法的海面场景SAR原始数据仿真方法
- AN IMPROVED RAW DATA SIMULATION METHOD FOR MEASURING OCEAN SURFACE CURRENT
- 海洋与湖沼, 50(2): 291-300
- Oceanologia et Limnologia Sinica, 50(2): 291-300.
- http://dx.doi.org/10.11693/hyhz20180900226
-
文章历史
- 收稿日期:2018-09-27
- 收修改稿日期:2019-01-17
运用SAR对海面要素(如海流、海浪以及海面漂浮物)进行观测是目前研究海洋表面特性的一个重要手段。由于海洋表面时刻处于运动状态, 其相对于陆地多了许多复杂的物理调制过程, 包括倾斜调制(Rouault et al, 2010)、水动力调制(Hara et al, 1994)、多普勒频移调制(Statman et al, 2007)、波流相互作用(Martin, 2014)等。如果不能研究清楚这些物理调制过程的机制, 就必然给SAR海面观测造成不利影响, 而原始数据仿真可以通过控制参数生成典型的海洋场景, 以便研究调制之间的相互作用, 也可以通过参数的开启或关闭某些调制(Liu et al, 2016), 从而详细了解这些物理调制过程。
正是由于上述的海表面运动的复杂性, 海洋表面原始数据级仿真的工作并不多, 大部分研究都是基于静止的陆地场景。早期的基于图像域海洋表面原始数据仿真主要有Franceschetti(1998, 2002)等, Franceschetti在前人(Hargerl, 1980, 1981, 1986)等人对分布式表面(DS)与速度聚束(VB)这两大类不同模型的基础上, 依据Bragg散射机理建立了更加有效的原始海洋一般场景的数据仿真, 重点考虑了非线性水动力调制下的Bragg共振, 同时考虑了不连续波纹, 并加入了一个随机相位项。然而, Franceschetti基于图像域的仿真会损失诸如多普勒中心频率这样的有效信息(Hansen et al, 2011)。此后, Franceschetti等(2002)又提出了基于DS模型的SAR原始数据级仿真, 但是没有考虑与径向速度有关的分辨率单元内的后向散射的随机传播过程; 同时也没有考虑到海洋表面波浪随空间变化。Liu等(2016)针对Franceschetti原始数据仿真算法的缺点提出了基于逆Omega-K(IOK)的海面要素原始数据仿真算法, 弥补了上述缺陷; 同时针对海浪运动参数的空间变化, IOK算法要求所有参与频率空间映射函数的参数保持空间无关, Liu等人提出了批处理方法来解决这个问题, 即根据海面径向速度的取值范围, 设置一系列离散化的径向速度值, 然后对于每一个径向速度值, 均实施一次逆Omega-K算法; 每实施一次逆Omega-K算法, 海面上所有具有该径向速度值的散射单元将会同时被仿真。
Liu等(2016)的原始数据仿真方法很好的体现出了速度聚束效应, 与Franceschetti仿真方法相比, 大大提高了仿真算法的真实性, 同时考虑了海表面流场因素, 采用IOK原始数据仿真方法能够精确地将流场信息包含到原始数据中去。但是Liu等(2016)的仿真算法也存在局限性, 第一, 该文仅考虑了正侧视情况, 并没有推广到斜侧视, 这样应用范围受限。第二, 该文并没有考虑Bragg散射所造成的Bragg相速度误差项。第三, 也没有考虑大尺度波运动所造成的Stokes漂流(Wang et al, 2015)所导致的海水净位移。斜侧视对于SAR测流十分重要, 如果仅仅是正侧视, 我们只能获得雷达视线方向速度, 即径向速度一维流场, 无法一次性获得二维流场。即使采用卫星重访的方式获得两幅图像合成获的二维流场也会因为时间差造成不同程度的去相干而影响测流精度。为了精确获得流矢量, 就必须采用以大斜侧视为基础的双波束干涉合成孔径雷达(DBI)来提供至少两个不同方向的观测结果, 这样就可以借助大斜侧视来一次性获取二维流场。但是大斜视测流的问题在于由于斜侧视角的存在, 会造成目标的距离向迁移变得不可忽略, 从而产生严重的距离方位耦合。与此同时, 当雷达波长与海面毛细波波长相比拟的时候, 会产生Bragg散射, 从而产生一个虚拟的波形速度, 我们称之为Bragg相速度。这个速度的量级是不可忽略的, 所以在仿真时必须要考虑, 不然就会造成比较大的测流误差。最后需要考虑的是Stokes漂流。由于海面风或者是涌浪的存在会产生表面重力波, 并且表面重力波的非线性作用导致海表面的水质点轨迹不封闭, 使得在波浪传播方向上产生一个拉格朗日净输运, 称之为Stokes漂流。Stokes漂流对于能否精确获取海表面流至关重要, 因为其产生的物质输运表现形式就是流。
综上所述, 大斜侧视与Bragg相速度与Stokes漂流都是流仿真中十分有必要考虑的, 本文通过引入以上三个要素来完善海洋原始数据仿真模型, 使其更具有普适性和延伸性。下一节将描述海面原始数据仿真方法, 第二节给出具体的仿真结果, 最后给出了结论。
1 海面原始数据仿真方法本节主要讨论斜侧视海面原始数据仿真的主要过程。1.1节介绍斜侧视海面原始数据仿真的几何模型, 1.2节回顾Liu(2016)正侧视情况下的海面原始数据仿真, 1.3节进行正侧视到斜侧视海面原始数据仿真方法的推导, 1.4节介绍了如何在斜侧视仿真中加入Stokes漂流和Bragg相速度。
1.1 SAR几何模型如图 1所示为斜侧视海面要素SAR原始数据仿真算法所用到的坐标系, 入射角为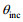
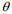
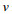
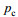
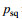
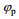
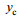
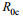
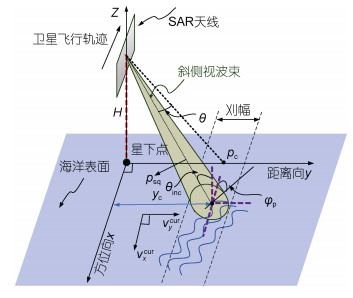 |
| 图 1 SAR原始数据仿真几何模型 Fig. 1 SAR geometric model for ocean surface |
设雷达观测到的径向速度为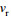
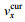
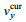
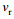
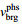
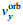
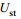
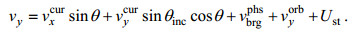 (1)
(1)基于IOK的正侧视海面要素SAR原始数据仿真算法的基本思想是将一个像元内的海面认为是一个“水质点”, “水质点”的运动包含两种速度分量:对应于海浪的轨道速度与海流速度的合成速度以及像元内的小尺度海浪随机运动。
在一个SAR分辨率单元内的“水质点”, 我们必须要保证径向传播速度的随机特征, 否则在多普勒域内后向散射的信号的随机多普勒波动就无法体现。因此, 要在分辨率单元内把局部长波轨道速度的随机扰动加入SAR原始数据。这个分辨率单元内的径向速度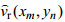
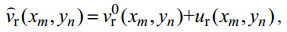 (2)
(2)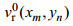
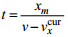
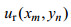
与长波轨道速度相关的VB效应对SAR成像是非常重要的, 在原始数据仿真中需要通过长波轨道速度来生成。方法就是把描述雷达照射场景的后向散射面到雷达的瞬间距离纳入SAR原始信号的距离方程。此时散射面在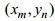
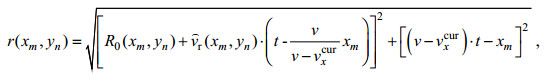 (3)
(3)其中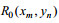
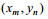
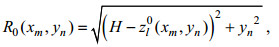 (4)
(4)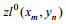
基于以上公式, 加入倾斜调制、水动力调制、大尺度波浪轨道速度信息、小尺度波浪运动信息等海面信息, 可以推导出二维时域的海洋SAR原始数据表达式。但时域海洋SAR原始数据方程包含双重求和, 如果直接使用时域表达式将导致庞大的计算量而使算法效率低下。所以我们使用快速傅里叶变换(FFT)将其变换到频域内从而大大加快计算速度, 则海面SAR回波信号的二维频率谱为
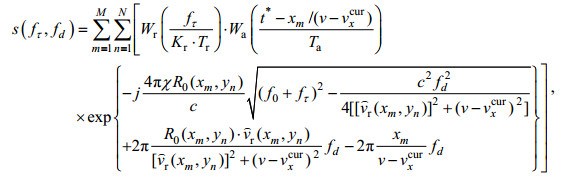 (5)
(5)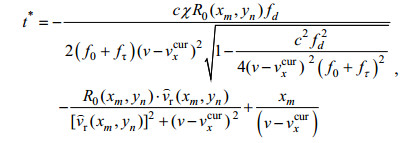 (6)
(6)其中fi表示方位向频率, fd表示距离向多普勒频率, f0表示雷达载波频率, 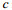
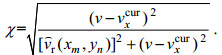 (7)
(7)由于在SAR波束范围内, 目标在波束内与雷达平台的相对运动变化会超过一个距离分辨率单位, 导致目标的回波不在一条距离向直线上造成距离方位耦合, 产生距离徙动(Cafforio et al, 1991a, 1991b)。要应对沿距离向的变化问题, 在二维频率域需要进行参考函数相乘。原理就是通过距离频率映射函数(RFMF), 将两重求和转化为二维快速傅里叶变换(FFT)。设新的距离频率量为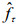
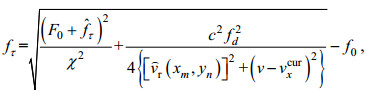 (8)
(8)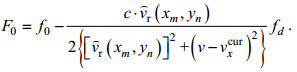 (9)
(9)但是海洋一直处于运动中, 这导致RFMF是随着空间坐标变化的, 而IOK算法需要RFMF不依赖于空间坐标, 为此Liu(2016)提出了一种称为“批处理”的解决方案。即同时模拟具有相同径向速度的海洋表面反向散射元素的集合。“批处理”方法主要包括三个子步骤:首先根据海面径向速度的取值范围, 设置一系列离散化的径向速度值; 然后对于每一个径向速度值, 均实施一次IOK算法, 结果就是对应某个特定的径向速度值, 海面上所有具有该径向速度值的散射单元将会同时被仿真。
但是映射之前需要将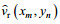
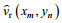
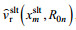
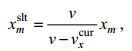 (10)
(10)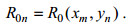 (11)
(11)根据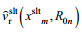
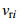
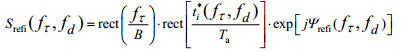 (12)
(12)其中:
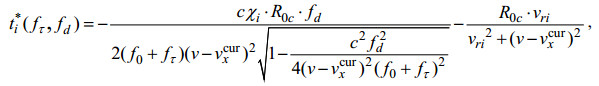 (13)
(13)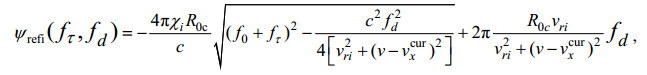 (14)
(14)上式中rect()表示矩形函数运算, 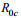
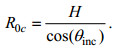 (15)
(15)上一节我们回顾了正侧视情况下的海面测流原始数据仿真, 它的问题在于正侧视下的海面流场原始数据仿真一般只能应用于获取一维海面运动信息, 而斜侧视可应用于多波束SAR流场观测来便于一次性获取二维流场, 尤其是大斜侧视情况下的海面测流原始数据仿真对于多波束SAR测流至关重要。为了达到大斜侧视仿真的目的, 我们希望能够在原有基础上增加一些额外的步骤通过改进来实现, 而不是完全推倒重来。
首先要矫正由于斜侧视引起的距离向耦合, 也就需要先重新计算零方位时刻斜视波束中心的坐标位置, 加入斜侧视角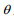
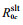
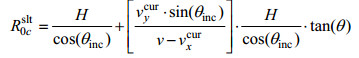 (16)
(16)接下来需要根据波束的斜视角来计算SAR多普勒中心频率。存在流速的情况下, 由于斜侧视角的存在, 卫星平台速度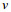
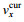
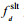
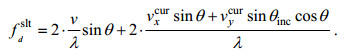 (17)
(17)根据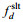
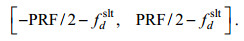 (18)
(18)其中PRF为脉冲重复频率, 将斜侧视下的波束中心斜距和多普勒中心代入参考函数, 斜侧视下的Omega-K参考函数为
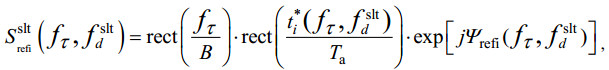 (19)
(19)其中:
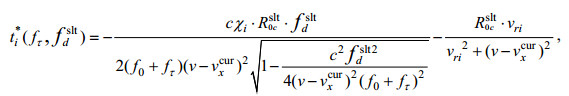 (20)
(20)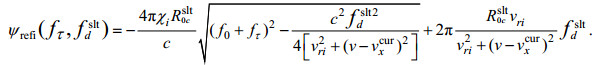 (21)
(21)至此, 由正侧视到斜侧视的推导就已经结束, 根据式(16)和(17)可以看出, 当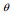
目前广泛采用三阶深水Stokes波近似迭代法来推导Stokes漂流具体表达式, 根据高山等人(2002), 时域Stokes漂流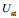
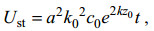 (22)
(22)其中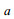
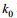
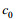
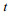
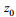
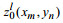
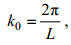 (23)
(23)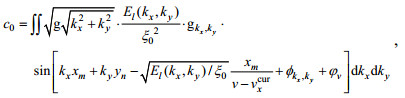 (24)
(24)其中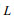
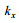
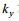
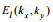
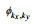
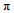
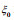
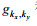
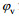
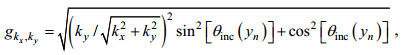 (25)
(25)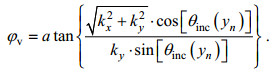 (26)
(26)最后, Stokes漂流的计算公式变为
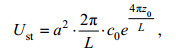 (27)
(27)其中, 波面振幅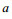
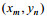
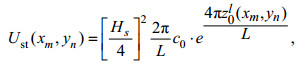 (28)
(28)其中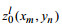
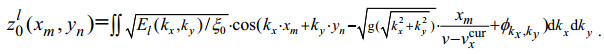 (29)
(29)另外还有一个重要的参数就是长波传播方向与流向之间的夹角, 即长波角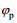
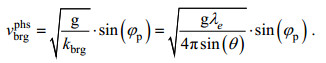 (30)
(30)其中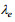
本节主要对斜侧视算法进行仿真, 并将结果与正侧视的相比较, 同时为了仿真的真实性, 对原始数据加入白噪声, 信噪比设为10dB, 仿真区域的对应的实际面积为5km×5km。为进行对比验证仿真实验斜侧视角和长波主波方向角选用了两个相差较大的角度值, 在验证斜侧视的正确性之后加入Stokes漂流来讨论Stokes漂流对于整个仿真流场的影响。
表 1里列出了仿真所需要的参数选择, 在整个区域内考虑为同一流动方向, 以便验证结果的正确性。
| 参数名 | 参数值 |
| 雷达载波频率 | 9.6GHz |
| 脉冲持续时间 | 5×10–6s |
| 带宽 | 40MHz |
| 雷达平台速度 | 7600m/s |
| 雷达平台高度 | 700km |
| 雷达入射角 | 40° |
| 雷达斜侧视角 | 5° 35° |
| 雷达方位向流速 | 0.5m/s |
| 雷达距离向流速 | 0.7m/s |
| 海面19.5m高处的风速 | 5m/s |
| 有效波高 | 4m |
| 长波波长 | 200m |
| 长波主波方向 | 5° 45° |
| 方位向离散面元数m | 2048 |
| 距离向离散面元数n | 2048 |
根据1.1节公式(1), 在验证流场正确与否之前需要去除由海浪和卫星平台共同作用引起的轨道速度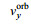
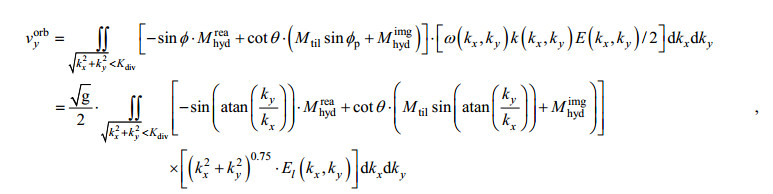 (31)
(31)上面公式中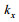
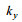
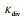
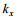
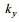
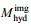
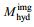
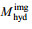
在斜侧视角为35°的情况下轨道速度如图 2所示, 距离向和方位向出现正负值是以雷达波束中心点(图像中心)为坐标原点所导致的, 速度的正值表示速度矢量顺着雷达视线方向, 负值表示逆着雷达视线方向(下同)。图 3表示JONSWAP谱在长波角为45°情况下的海浪方向谱。在去除轨道速度相关的速度后, 我们先来讨论Bragg相速度加入与未加入的区别, 图 4a、b是从原先2048×2048个离散元中经过64×64窗的平均滤波之后得到的流场图, 采用多普勒中心频率估计法(曹福祥等, 2009)。从图 4a、b可以清楚的看到在加入Bragg相速度之后雷达观测到的海面径向速度有了明显的变化, 说明Bragg相速度在实际观测中不可忽略, 在仿真中需要加入。
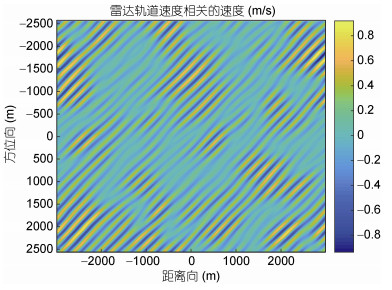 |
| 图 2 海洋表面轨道速度分布 Fig. 2 Orbital velocity distribution of ocean surface |
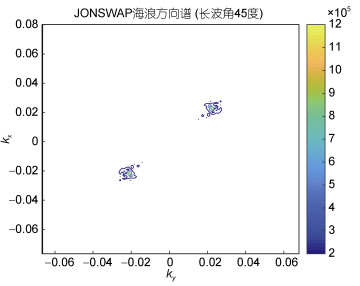 |
图 3 JONSWAP海浪方向谱(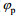 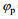 |
 |
| 图 4 是否考虑Bragg相速度情况下的海面径向流速对比 Fig. 4 Bragg phase velocity contrast 注: a:未加入Bragg相速度; b:加入Bragg相速度 (a) Without Bragg phase velocity adding; (b) With Bragg phase velocity adding |
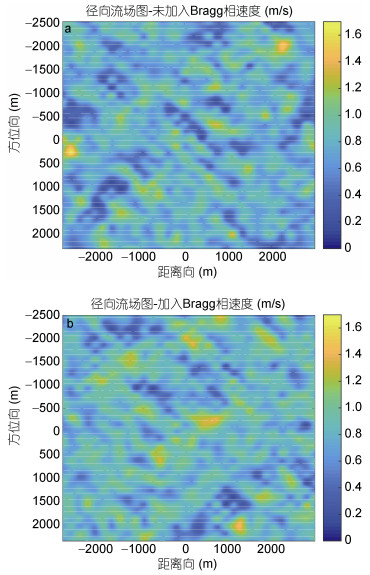
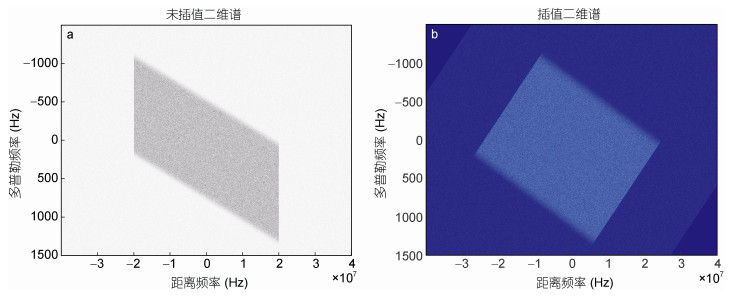
对仿真得到的海面要素SAR原始数据采用多普勒中心估计法反演获得总径向速度。图 5a给出了35°斜侧视角、长波主波方向为45°情况下的未插值原始数据仿真二维谱, 图 5b表示仿真阶段的Stolt(李俊慧等, 2016)插值的二维谱。图 6则是聚焦成像后的时域图像, 表示的是幅度值, 可以清晰地看到海浪波纹, 图 7则为雷达观测流速。
 |
| 图 5 35°斜侧视角海面原始数据仿真二维谱 Fig. 5 The 2-dimensional spectrum of ocean surface raw data at a squint side-looking angle of 35° 注: a:未经过Stolt插值; b:经过Stolt插值 |
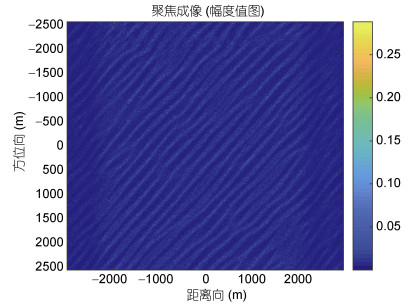 |
| 图 6 35°斜侧视角情况下的海面成像 Fig. 6 Sea surface SAR simulation imaging at 35° squint side-looking angle |
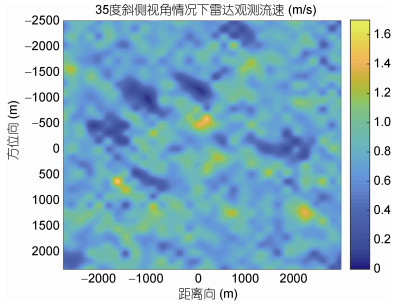 |
| 图 7 35°斜侧视角情况下的海面径向流速 Fig. 7 The current radial velocity at 35° squint side-looking angle |
去除Bragg速度、轨道速度后即可得到海表面径向流速(如无特别说明下面的流速均为校正后流速)。为使仿真结果尽量精准, 采用蒙特卡洛方法计算20次独立仿真实验的平均值, 下面的图 5至图 7均展示了20次独立仿真实验中的第1次结果。采用多普勒流速估计进行反演, 对整个流场20次反演的结果均值为0.6184m/s。流场的理论流速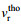
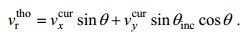 (32)
(32)根据理论流速计算公式, 整个流场的理论流速为0.6554m/s, 误差为5.7%, 二者结果基本吻合。
为了更好的验证斜侧视情况下的仿真结果的准确性, 只讨论一个斜侧视角是不够的, 所以本文增加了5°斜侧视角情况下的仿真做对比验证, 同样为了结果的精准采用了20次独立仿真实验的平均值, 图 8至图 9展示了20次独立仿真实验中的第1次实验结果。
图 8a表示5°斜侧视角情况下的未插值二维谱, 图 8b表示经过Stolt插值后的二维谱, 图 9是雷达观测到的海面流速。通过多普勒中心估计法得到的整个流场的20次反演结果均值为0.5087m/s, 同时计算得到的理论流速结果为0.4918m/s, 误差为3.4%, 二者的结果依然基本吻合。
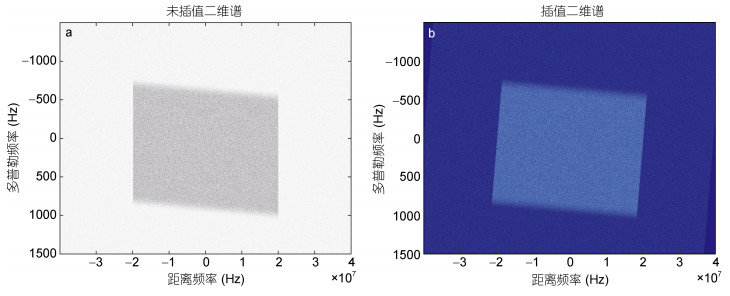 |
| 图 8 5°斜侧视角海面原始数据仿真二维谱(a)未经过Stolt插值(b)经过Stolt插值 Fig. 8 Frequency 2-d spectrum of ocean surface raw data at a squint side-looking angle of 5° a. without the Stolt interpolation; b. with the Stolt interpolation |
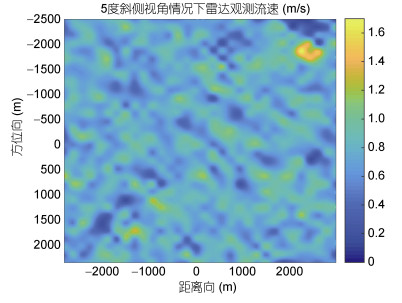 |
| 图 9 5°斜侧视角情况下的海面径向流速 Fig. 9 The current radial velocity at 5° squint side-looking angle |
在验证了斜侧视SAR仿真的准确性之后, 加入Stokes漂流, 如图 10所示, 可以看到与不加入Stokes漂流的情况存在明显不同。在斜侧视角为35°, 长波角为45°的情况下采用多普勒流速计算法得到的反演结果为0.7709m/s。而根据上面结果, 在不加入Stokes漂流的情况下流速为0.6554m/s。这个结果说明Stokes漂流对于海表面流速有重要影响。
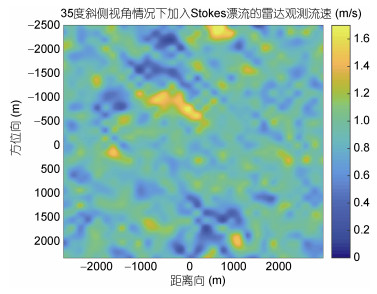 |
图 10 35°斜侧视角情况下加入的海面径向流速(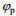 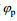 |
通过改变长波主波传播方向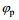
图 11是JONSWAP谱在长波角为5°情况下的海浪方向谱, 从图 12可以看到当主波传播方向为5°时stokes漂流的影响明显减弱, 通过多普勒中心频率估计的结果为0.7088m/s。在考虑Stokes漂流的情况下计算径向速度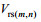
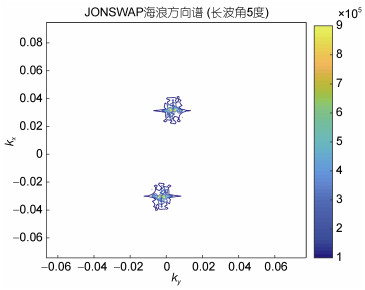 |
图 11 JONSWAP海浪方向谱(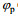 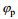 |
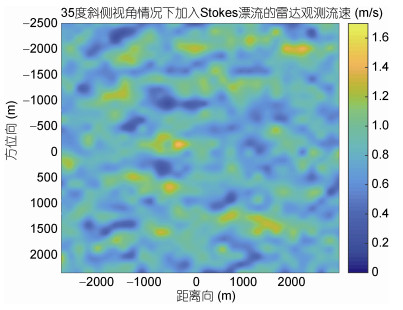 |
图 12 35°斜侧视角情况下加入的海面径向流速(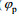 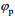 |
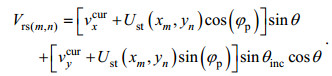 (33)
(33)根据上面的公式, 长波主播方向角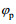
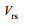
在本文中我们讨论了斜侧视SAR原始数据仿真的重要意义, 从正侧视仿真算法出发, 通过加入一些必要步骤来实现由正侧视到斜侧视的推广。通过分析以及大量的仿真实验得到了如下的结论: (1)斜侧视下的海流仿真结果与利用多普勒质心分析的结果能够很好的贴合, 表明了大斜侧视模型的准确性。(2)长波主波方向角度越小, 其对雷达径向流场影响会逐渐减小, 若接近90°对径向流场的结果可以忽略。基于此可以根据长波角和长波信息(即海浪谱)和风速估计Stokes漂流流速, 除了风速是外部输入参数, 其他的参数均可通过本文模型得到, 这不仅提高了流速反演的精度, 同时也能在一定程度上实现流成分分离。以上结论能够为双波束测流系统研究提供了一定的理论参考, 以此来获得二维流场。这说明斜侧视逆Omega-K算法能够获得海洋表面的空间运动参数, 并且在多波束等SAR海表面观测中比正侧视的应用范围更广。
李俊慧, 王洪, 汪学刚, 等. 2016. 步进频SAR的波数域成像算法研究. 现代雷达, 38(7): 25-31 |
高山, 钱成春, 王伟, 等. 2002. 深水Stokes漂流公式的一种新形式. 海洋湖沼通报, (2): 1-9 DOI:10.3969/j.issn.1003-6482.2002.02.001 |
曹福祥, 胡东辉, 洪文. 2009. 一种改进的基于全数据集的星载ScanSAR多普勒中心估计方法. 中国科学院研究生院学报, 26(1): 97-101 |
Cafforio C, Prati C, Rocca F, 1991a. Full resolution focusing of seasat sar images in the frequency-wave number domain. International Journal of Remote Sensing, 12(3): 491-510 DOI:10.1080/01431169108929668 |
Cafforio C, Prati C, Rocca F, 1991b. SAR data focusing using seismic migration techniques. IEEE Transactions on Aerospace and Electronic Systems, 27(2): 194-207 DOI:10.1109/7.78293 |
Calini A, Schober C M, 2017. Characterizing JONSWAP rogue waves and their statistics via inverse spectral data. Wave Motion, 71: 5-17 DOI:10.1016/j.wavemoti.2016.06.007 |
Franceschetti G, Migliaccio M, Riccio D, 1998. On ocean SAR raw signal simulation. IEEE Transactions on Geoscience and Remote Sensing, 36(1): 84-100 DOI:10.1109/36.655320 |
Franceschetti G, Iodice A, Riccio D et al, 2002. SAR raw signal simulation of oil slicks in ocean environments. IEEE Transactions on Geoscience and Remote Sensing, 40(9): 1935-1949 DOI:10.1109/TGRS.2002.803798 |
Hansen M W, Collard F, Dagestad K F et al, 2011. Retrieval of sea surface range velocities from Envisat ASAR Doppler centroid measurements. IEEE Transactions on Geoscience and Remote Sensing, 49(10): 3582-3592 DOI:10.1109/TGRS.2011.2153864 |
Hara T, Plant W J, 1994. Hydrodynamic modulation of short wind-wave spectra by long waves and its measurement using microwave backscatter. Journal of Geophysical Research:Oceans, 99(C5): 9767-9784 DOI:10.1029/93JC03514 |
Harger R O, 1980. The side-looking radar image of time-variant scenes. Radio Science, 15(4): 749-756 DOI:10.1029/RS015i004p00749 |
Harger R O, 1981. SAR ocean imaging mechanisms. In:Beal R C, DeLeonibus P S, Katz I eds. Spaceborne Synthetic Aperture Radar for Oceanography. Baltimore, MD, USA: John Hopkins University Press, 41-52
|
Harger R O, 1986. The SAR image of short gravity waves on a long gravity wave. In:Phillips O M, Hasselmann K eds. Wave Dynamics and Radio Probing of the Ocean Surface. MA:Springer: 371-392 |
Liu B C, He Y J, 2016. SAR raw data simulation for ocean scenes using inverse omega-k algorithm. IEEE Transactions on Geoscience and Remote Sensing, 54(10): 6151-6169 DOI:10.1109/TGRS.2016.2582525 |
Mao Y, Guo L X, Ding H F, 2011. Numerical simulation for the sea echo spectrum of OTHR radar based on JONSWAP sea spectrum. In: Proceedings of 2011 IEEE International Conference on Microwave Technology & Computational Electromagnetics. Beijing, China: IEEE, 3.
|
Martin S, 2014. An Introduction to Ocean Remote Sensing. New York: Cambridge University Press, 251-260
|
Rouault M J, Mouche A, Collard F et al, 2010. Mapping the agulhas current from space:an assessment of ASAR surface current velocities. Journal of Geophysical Research:Oceans, 115(C10) |
Statman J I, Rodemich E R, 2007. Parameter estimation based on Doppler frequency shifts. IEEE Transactions on Aerospace and Electronic Systems, AES-23(1): 31-39 |
Wang Z F, Wu K J, Dong S et al, 2015. Effect of wave-induced Stokes drift on the dynamics of ocean mixed layer. Chinese Journal of Oceanology and Limnology, 33(1): 233-242 DOI:10.1007/s00343-015-4036-7 |
Yu Y, Pei H L, Xu C Z, 2017. Parameter identification of JONSWAP spectrum acquired by airborne LIDAR. Journal of Ocean University of China, 16(6): 998-1002 DOI:10.1007/s11802-017-3271-2 |
 2019, Vol. 50
2019, Vol. 50


