中国海洋湖沼学会主办。
文章信息
- 陈耀祖, 高磊, 刘子洲, 孙利元, 顾艳镇, 翟方国, 李培良. 2019.
- CHEN Yao-Zu, GAO Lei, LIU Zi-Zhou, SUN Li-Yuan, GU Yan-Zhen, ZHAI Fang-Guo, LI Pei-Liang. 2019.
- 山东半岛海洋牧场潮汐特征分析
- TIDAL CHARACTERISTICS OF MARINE PASTURES AROUND SHANDONG PENINSULA
- 海洋与湖沼, 50(4): 719-727
- Oceanologia et Limnologia Sinica, 50(4): 719-727.
- http://dx.doi.org/10.11693/hyhz20180900227
文章历史
-
收稿日期:2018-09-27
收修改稿日期:2019-02-15
2. 国家海洋局北海环境监测中心 山东省海洋生态环境与防灾减灾重点实验室 青岛 266100;
3. 山东省水生生物资源养护管理中心 烟台 264000;
4. 浙江大学 海洋学院 舟山 316021
2. North China Sea Environmental Monitoring Center, State Oceanic Administration; Shandong Provincial Key Laboratory of Marine Ecology and Environment & Disaster Prevention and Mitigation, Qingdao 266100, China;
3. Shandong Hydrobios Resources Conservation and Management Center, Yantai 264000, China;
4. Ocean College, Zhejiang University, Zhoushan 316021, China
潮汐和潮流是近海潮波运动的主要表现形式, 在海岸带侵蚀与沉积物输运过程中起到关键作用。了解近海潮汐特征, 对近岸水产养殖、船舶航行、港口建设、开发工程建设和防灾减灾等都具有重要意义。
山东省海洋牧场观测网系统于2015年开始建设, 其核心组成部分为“海洋环境有缆在线观测系统” (孟鑫等, 2017), 可以根据需求集成搭载海流计、波浪仪、温盐深仪(Conductivity-Temperature-Depth, CTD)、水质仪等观测仪器, 实现多要素长期、实时监控。利用CTD观测的水位数据, 可以分析海洋牧场潮汐特征分布, 为海洋牧场生产生活和防灾减灾提供科学指引。
国内外关于潮汐的工作较多, 学者对于潮汐的形成原因以及潮汐基本性质已有共识, 潮汐理论较为完备。计算区域潮汐特征几乎是所有近海水动力研究不可或缺的一环, 而这一过程一般通过实测数据如验潮站数据、卫星高度计数据等进行分析, 或者通过数值模式模拟得到, 而观测数据往往被用来检验模式的准确性。为了获取更加准确的调和常数, 实现更加准确的潮汐拟合与预报, 前人在潮汐分析方法上做了许多工作, 目前比较常用的分析方法有调和分析方法(Foreman et al, 1991; Pawlowicz et al, 2002; Lü et al, 2009)和正交潮响应法(Groves et al, 1975; 李培良等, 2002)等, 后者在处理非天文潮时效果较好。Smith等(1997)比较了调和分析法和响应法对T/P高度计数据的分析效果, 并将结果与FES95.2和大量验潮站的结果进行对比, 发现二者差距很小。El-Diasty等(2018)将小波网络分析与调和分析相结合, 建立了一个新的预报模式, 该模式对长期和短期资料都具有预报准确性。一般而言, 对于30天以上的逐时水位资料, 基于最小二乘法的调和分析(陈宗镛, 1980)已经可以较准确地估计各分潮的调和常数, 反映海区的潮汐特征。
在近海区域, 由于水深较浅, 大洋传入的潮波波速发生变化, 使得潮波变形, 这种变形潮波是由原潮波与高阶潮波叠加而成的。此外, 潮波与近岸地形的摩擦作用, 使得潮波能量耗散, 振幅减小, 相位发生变化。在河口区, 潮汐与河道几何形状、底摩擦以及径流之间的非线性相互作用相对于近海水域而言更强(Friedrichs et al, 1988)。因此, 在近海以及河口研究中, 潮波与地形的非线性相互作用对潮汐特征分析以及数值模式准确性都具有重要影响。Friedrichs等(1988)对比数值模型与实测数据结果, 分析了非线性相互作用对河口区潮波变形的影响; Hall等(2005)指出, 当考虑非线性作用产生的浅水分潮时, 使用短期资料就可以实现准确的调和分析; Matte等(2014)使用NS_TIDE模型探讨了圣劳伦斯河河口非线性作用导致的非平稳潮流过程。虽然所用模式不同, 但上述研究都考虑了非线性相互作用的影响, 从而提高了数值模式的准确性。中国近海潮波系统的研究已经较为完备, 无论是实测数据还是数值模型, 都给出了中国近海潮汐、潮流的基本特征, 结论较为一致。朱学明(2009)、李秉天(2014)和黄学智(2016)用FVCOM (Finite Volume Community Ocean Model)模式研究了中国近海潮汐潮流的分布特征, 并将结果与验潮站资料进行分析对比, 无潮点、圆流点位置以及主要分潮调和常数都和前人研究相近, 取得了较好的模拟效果。罗丹等(2015)用POM(Princeton Ocean Model)模式模拟了渤海区域4个主要分潮, 与实际观测吻合较好。不管是基于观测(胡景, 2007; 于玲等, 2010; 赵云霞等, 2012)还是上述模式, 中国近海的潮汐特征已较为明确, 但目前的潮汐研究仍存在一些不足。一方面, 中国近海潮汐特征主要是通过零星的验潮站数据和数值模式得出的, 在中国近海复杂海岸和地形背景下, 这些潮汐特征的准确性受到一定限制。为了得到更准确的潮汐特征, 多点、长时间的观测数据是必须的, 而海洋牧场的观测数据满足这一需求。另一方面, 对中国近海潮汐特征的研究大多只局限于调和常数以及潮汐类型的讨论上, 而对潮汐日不等现象的分析并不多见。此外, 对于一般海区而言, 调和常数具有极大的稳定性, 在不特别长的时间内可近似认为是常数, 但海岸侵蚀以及人为改造使得近海水深以及岸线不断变化, 进而会导致区域潮汐特征发生改变(李秉天, 2014)。本文详细分析了山东半岛海洋牧场所在海域的潮汐特征, 也可以为这些工作以及近海模式的优化提供指引。
1 数据本文所使用水深数据来自于山东省海洋牧场观测网项目。海洋牧场水下观测平台均搭载Hydrocat CTD, 该仪器的观测变量包括温度、电导率、压强和溶解氧等。其中, 压强的量程为350m, 初始精度为量程的0.1%, 即±0.35m, 分辨率达到了量程的0.002%, 观测间隔为1min。
本文基于海洋牧场观测系统中15个海洋牧场(图 1) Hydrocat CTD的观测水深数据, 分析这些海洋牧场的潮汐特征。为了便于展示与说明, 本文对所有海洋牧场按A—O进行编号, 具体海洋牧场信息如表 1所示。
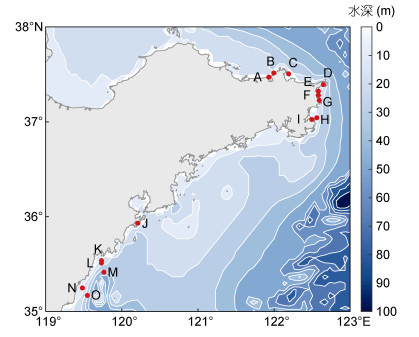 |
| 图 1 山东半岛周边海域水深分布图 Fig. 1 Map of bathymetry around Shandong Peninsula 注:红色实心点表示海洋牧场位置, 对应名称见表 1; 用于绘制该图的水深数据来自ETOPO1(https://www.ngdc.noaa.gov/mgg/global/global.html) |
| 牧场编号 | 名称 | 观测时间 | 资料长度(d) |
| A | 威海瑜泰游钓型海洋牧场 | 2016.06.24—2017.04.04 | 284 |
| B | 威海西港游钓型海洋牧场 | 2016.06.02—2017.12.27 | 573 |
| C | 威海刘公岛游钓型海洋牧场 | 2016.07.19—2017.08.04 | 381 |
| D | 西霞口集团国家级海洋牧场 | 2016.07.20—2016.08.27 | 38 |
| E | 荣成天鹅湖游钓型海洋牧场 | 2016.08.11—2017.10.04 | 419 |
| F | 荣成烟墩角游钓型海洋牧场 | 2017.11.10—2018.03.10 | 120 |
| G | 荣成成山鸿源投礁型海洋牧场 | 2017.11.16—2018.04.20 | 155 |
| H | 荣成东楮岛游钓型海洋牧场 | 2016.06.26—2017.06.12 | 352 |
| I | 荣成鸿泰游钓型海洋牧场 | 2017.11.25—2018.04.06 | 132 |
| J | 青岛鲁海丰游钓型海洋牧场 | 2016.03.14—2016.06.30 | 109 |
| K | 日照万宝游钓型海洋牧场 | 2017.06.21—2018.05.23 | 337 |
| L | 日照欣慧投礁型海洋牧场 | 2017.06.29—2017.11.27 | 151 |
| M | 日照国美投礁型海洋牧场 | 2017.05.20—2017.11.26 | 190 |
| N | 日照水产集团投礁型海洋牧场 | 2017.05.20—2017.09.26 | 129 |
| O | 日照岚山阳光游钓型海洋牧场 | 2017.06.22—2017.11.05 | 137 |
本文使用T_TIDE程序(Pawlowicz et al, 2002)对海洋牧场水深资料进行调和分析, 并选取主要分潮的调和常数做进一步分析, 具体包括2个全日分潮K1、O1, 2个半日分潮M2、S2, 以及1个浅水分潮M4。
由于仪器布放时间和实际工作时长存在差异, 各海洋牧场的水深资料长度不尽相同(表 1), 对于同一个海洋牧场而言, 不同长度的资料所得到的调和分析结果可能存在差异。本文将每个海洋牧场的资料划分为15d、30d、60d、90d以及90d以上5种资料长度, 每种长度的资料起始时间相同, 均为该海洋牧场观测起始时间, 90d以上资料取该海洋牧场完整观测资料。以威海瑜泰游钓型海洋牧场(A)为例, 该海洋牧场观测起始时间为2016年6月24日, 以此为起点, 截取15d、30d、60d、90d以及284d共5种长度的资料, 并选取合适的分潮进行分析。根据Rayleigh判据, 如果两分潮频率分别为f1和f2, 当|f1-f2|≥2fc/N时, 二者才能分离开来, 其中fc为截止频率。故两分潮频率差越小, 分辨二者所需要的时间序列越长, 因此Liu等(2008)在对不同时间长度资料进行调和分析时所考虑的分潮数量也有所不同。而本文所选取的分潮在最短的分析资料长度即15d情况下也不会发生相互混淆。
如图 2所示, 威海瑜泰游钓型海洋牧场(A) 15d资料长度下的调和分析重构潮位与观测水深异常在振幅与相位上都对应良好, 二者相关系数达到了0.95, 重构潮位方差解释率为90.1%, 说明该调和分析方法可以较好地估计海洋牧场的调和常数。
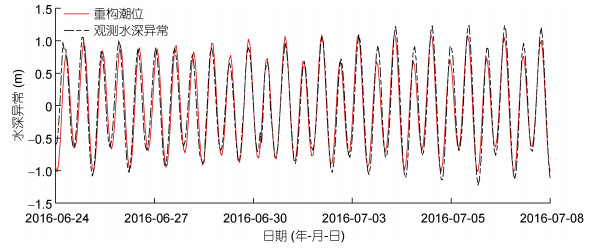 |
| 图 2 原始观测水位异常(黑色点划线)与重构潮位(红色实线)时间序列 Fig. 2 The time series of the observed depth anomaly (black dash line) and the returned tidal level (red line) in harmonic analysis |
基于上述方法, 计算得到了各海洋牧场在不同资料长度下的调和常数。图 3展示了各海洋牧场主要分潮调和常数即振幅和迟角的分布情况, 对每个海洋牧场调和常数变化进行分析, 可以得到以下结论:
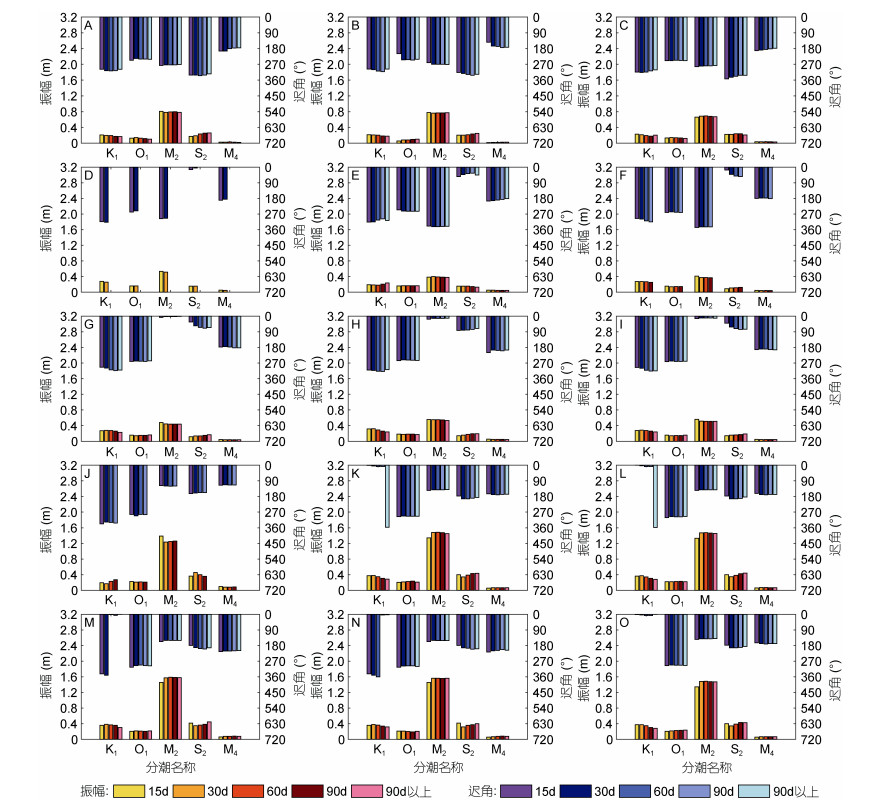 |
| 图 3 各海洋牧场利用不同时间长度资料计算得到的调和常数的比较 Fig. 3 Comparison in harmonic constant computed in different time lengths for each marine pasture |
(1) 所有海洋牧场中M2分潮的振幅最为显著, 其平均振幅为0.87m。K1、O1、S2分潮也具有较大的分潮振幅, 其平均振幅分别为0.23m、0.16m和0.26m。M4分潮振幅较小, 其平均振幅为0.05m。
(2) 各海洋牧场调和常数估计的准确性随资料长度增加不断提高。以荣成东楮岛游钓型海洋牧场(H)为例, 基于T_TIDE调和常数误差算法(Pawlowicz et al, 2002), 图 4展示了该海洋牧场调和常数误差随资料长度的变化曲线, 其他海洋牧场的误差变化曲线呈现类似的特征, 为避免赘述, 本文仅对该海洋牧场的情况进行展示和说明。图 4表明, 随着资料长度的增加, 分潮振幅误差(图 4a)和迟角误差(图 4b)随资料长度增加均呈现下降趋势, 表明调和常数估计准确性不断提高。因此, 在后文潮汐特征空间变化的分析中, 调和常数取自各海洋牧场完整资料下的调和分析结果。
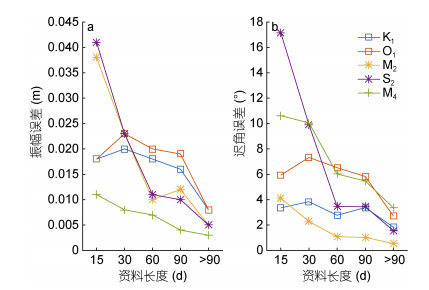 |
| 图 4 荣成东楮岛游钓型海洋牧场(H)分潮振幅(a)、迟角(b)误差随资料长度的变化 Fig. 4 Evolution of tidal amplitudes (a) and phases (b) in H marine pasture with the increase in data length |
基于2.1的结果, 本文对各个海洋牧场的完整资料进行调和分析, 并进一步利用所得调和常数, 分析调和常数、潮汐类型、潮差以及潮汐日不等现象等潮汐特征的空间变化。
2.2.1 调和常数以M2分潮为例, 山东半岛M2分潮振幅的区域分布差异较为明显, 东北部沿海M2分潮振幅较东南部小约2到3倍, M2分潮振幅(图 5)从威海瑜泰游钓型海洋牧场(A)沿着山东半岛沿岸向东先缓慢减小, 在荣成烟墩角游钓型海洋牧场(F)达到最小值0.37m, 之后呈上升趋势, 在日照国美投礁型海洋牧场(M)达到最大值1.58m。M2分潮迟角(图 6)从威海瑜泰游钓型海洋牧场(A)沿着山东半岛沿岸向东缓慢增大, 在荣成烟墩角游钓型海洋牧场(F)达到最大值344°, 继而在荣成成山鸿源投礁型海洋牧场(G)回到0°附近, 在青岛鲁海丰游钓型海洋牧场(J)之后维持在140°左右。图 7直观展示了M2分潮以及其它分潮的调和常数的变化, 从振幅的相对大小上不难看出, 各海洋牧场的K1分潮振幅均大于O1分潮振幅, M2分潮振幅均大于S2分潮振幅, M4分潮振幅在所选取的分潮中最小。由于大洋潮汐受天体引潮力驱动, 在其传入近海后, 受几何地形与摩擦作用影响, 分潮振幅和迟角发生改变, 因此, 上述分潮调和常数的空间变化, 是天体引潮力、几何地形与摩擦共同作用的结果。
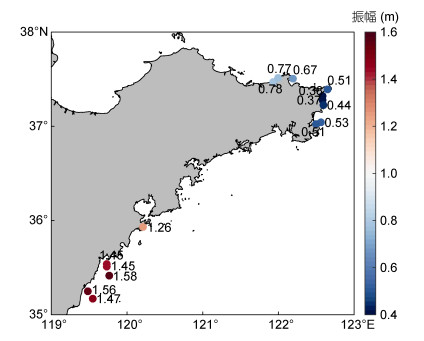 |
| 图 5 M2分潮振幅空间分布 Fig. 5 Spatial distribution of M2 amplitudes |
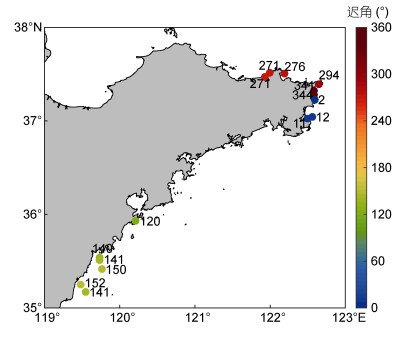 |
| 图 6 M2分潮迟角空间分布 Fig. 6 Spatial distribution of M2 phases |
 |
| 图 7 主要分潮调和常数空间变化 Fig. 7 Spatial evolution of harmonic constants |
潮汐是不同频率和相位的分潮叠加而形成的, 通常M2、S、K、O1的分潮振幅最大, 因此实际中常用上述4个分潮的平均振幅比值来作为潮汐类型的判据(陈宗镛, 1980)。在中国, 除了某些M2分潮与S2分潮振幅相近的海域, 大多采用如下标准确定潮汐类型(孙湘平, 2006):

其中, HK1、HO1和HM2分别为K1、O1和M2分潮的平均振幅。在本文所关心的海洋牧场中, S2分潮的振幅都显著小于M2分潮, 因此采用上述标准是合理的。
根据上述计算公式, 计算所有海洋牧场的潮型系数, 如图 8所示, 在山东半岛东北部, 除A、B、C海洋牧场外, 大部分海洋牧场潮型系数大于0.5, 潮汐类型属于不规则半日潮; 山东半岛东南部海洋牧场潮型系数均小于0.5, 潮汐类型属于规则半日潮。此外, K1和O1分潮的振幅(图 7a)自威海瑜泰游钓型海洋牧场(A)沿山东半岛海岸到日照岚山阳光游钓型海洋牧场(O)呈上升的趋势, 考虑山东半岛东北部海洋牧场(D—I)与东南部海洋牧场(J—O), 随着K1和O1的振幅的增加, 山东半岛东北部海洋牧场的潮型系数相对于东南部并未增大反而减小, 这是因为东南部海洋牧场M2分潮的平均振幅(图 7c)较大, 其振幅更为显著, 主导作用更强。
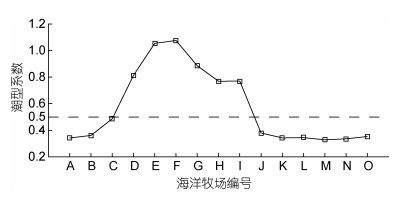 |
| 图 8 潮型系数曲线 Fig. 8 Coefficient of tidal types 注:黑色虚线表示潮型系数为0.5的曲线 |
潮差主要考虑平均潮差和最大可能潮差, 平均潮差按2HM2计算, 最大可能潮差按2×(1.29HM2+1.23HS2+HK1+HO1)(孙湘平, 2006)计算。一般地, 在平均潮差较大的海域, 其最大可能潮差也较大。从上述最大可能潮差计算式也可以看出, 当M2分潮振幅较大时, 上式括号中第一项大小也最为显著, 对计算结果的贡献最大。图 9展示了所各海洋牧场平均潮差以及最大潮差的变化曲线, 其中平均潮差与最大可能潮差变化趋势几乎相同。平均潮差与最大可能潮差均在日照国美投礁型海洋牧场(M)达到最大值, 分别为3.48m和5.70m, 二者均在荣成烟墩角游钓型海洋牧场(F)达到最小值分别为0.82m和2.27m。潮差在山东半岛东南部海洋牧场(J—O)尤为显著, 该区域平均潮差达到了3m以上。潮差变化受地形影响显著, 一般在近岸潮差大, 远岸潮差小, 旋转潮波系统中心潮差小, 边缘潮差大(孙湘平, 2006)。考虑到海洋牧场均处于近岸, 山东半岛东北部海洋牧场(A—I)所在区域的低潮差可能是其与M2分潮无潮点距离较近导致的。
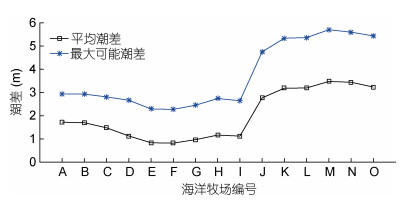 |
| 图 9 平均潮差和最大可能潮差 Fig. 9 Mean tidal range and utmost tidal range 横坐标为海洋牧场编号 |
潮汐日不等现象表现为潮高日不等和潮时日不等。首先, S2分潮对于潮高的影响较为显著, 可以用S2分潮与M2分潮振幅的相对比值来衡量潮高不等现象的显著程度, HS2/HM2若大于0.4则一般认为潮高不等现象显著。而迟角差gM2-(gK1+gO1)则用来判断潮高不等的类型, 当其值位于0°、180°、270°附近时, 分别对应高潮高不等、低潮高不等、高潮高和低潮高不等, 其中gM2、gK1、gO1、分别是M2、K1、O1分潮的迟角, 计算所得的角度差如果大于360°或者小于0°, 都将订正到0°—360°范围内。其次, 在大部分海洋牧场, 最显著的M2分潮倍潮是M4分潮, 可以用二者相对振幅大小HM4/HM2和迟角差2gM2-gM4来刻画潮时日不等现象。HM4/HM2越大, 则说明潮时不等现象越显著, 而当其值小于0.01时, 实际上可以不考虑浅水分潮的影响。当2gM2-gM4的值位于90°和270°附近时, 分别对应更长的落潮历时和更长的涨潮历时(陈倩, 2002)。
图 10展示了潮高不等和潮时不等的参数变化曲线。图 10a中, 所有海洋牧场的HS2/HM2均小于0.4, 表明潮高不等在各海洋牧场均不显著。其次, 对于潮时不等, 考虑M4分潮与M2分潮的振幅比(图 10a), 潮时不等现象的强弱表现出区域性差异, 在山东半岛东北部(D—I)较强, 在东南部相对较弱。而从M4分潮与M2分潮的迟角差上来看(图 10b), 威海瑜泰海洋牧场、威海西港海洋牧场、威海刘公岛海洋牧场(A、B、C)与荣成成山鸿源海洋牧场、荣成东楮岛海洋牧场、荣成鸿泰海洋牧场(G、H、I)迟角差分别接近0°与180°, 表明除A、B、C与G、H、I海洋牧场以外, 其他海洋牧场的落潮历时均大于涨潮历时, 表现为涨潮主导的特征。
 |
| 图 10 潮高不等现象和潮时不等现象的参数变化 Fig. 10 Variations of tidal height asymmetry and flood-ebb duration difference |
上述分析中, A、B、C海洋牧场与G、H、I海洋牧场迟角差分别接近0°与180°, 表明涨潮历时与落潮历时相当接近, 这似乎与G、H、I牧场相对较大的M4分潮和M2分潮振幅比相悖。Friedrichs等(1988)提出, M4分潮和M2分潮振幅的比值HM4/HM2, 可以衡量非线性潮波变形的程度, 但潮波变形不一定导致涨潮历时与落潮历时发生偏差, 在M4分潮和M2分潮迟角差满足一定关系时, 二者并不会发生偏差, 该系数较大时才对潮时不等有显著影响。考虑到各海洋牧场的HM4/HM2均小于0.15(图 10a), 可以认为, 潮时不等主要是M4分潮与M2分潮的相位差(图 10b)导致的。
3 结论本文利用山东半岛15个海洋牧场的观测水深数据, 对比了不同资料长度对于调和分析结果的影响, 并分析了海洋牧场潮汐特征的空间变化, 得到了以下结论:
(1) 调和常数估计误差随着资料长度的增加而减小, 调和常数估计准确性不断提高。
(2) 各海洋牧场的M2分潮振幅在所选取的分潮中最为显著。全日分潮K1和O1的平均振幅分别为0.23m和0.16m, 半日分潮M2和S2的平均振幅分别为0.26m和0.87m, 浅水分潮M4的平均振幅为0.05m。
(3) 各海洋牧场潮汐类型均为以M2分潮为主导的半日潮潮型。除威海瑜泰游钓型海洋牧场(A)、威海西港游钓型海洋牧场(B)、威海刘公岛游钓型海洋牧场(C)三个海洋牧场外, 山东半岛东北部海洋牧场潮汐类型均属于不规则半日潮, 山东半岛东南部海洋牧场潮汐类型为规则半日潮。
(4) 平均潮差与最大可能潮差变化趋势几乎一致, 二者均在日照国美投礁型海洋牧场(M)达到最大值, 均在荣成烟墩角游钓型海洋牧场(F)达到最小值。
(5) 潮高不等现象在各海洋牧场均不显著, 潮时不等现象在威海瑜泰游钓型海洋牧场(A)、威海西港游钓型海洋牧场(B)、威海刘公岛游钓型海洋牧场(C)、荣成成山鸿源投礁型海洋牧场(G)、荣成东楮岛游钓型海洋牧场(H)、荣成鸿泰游钓型海洋牧场(I)不显著, 而在其他海洋牧场均表现为落潮历时大于涨潮历时。
于玲, 方国洪. 2010. 中国近海验潮站长期观测资料的潮汐调和分析. 海洋科学进展, 28(2): 133-141 DOI:10.3969/j.issn.1671-6647.2010.02.001 |
朱学明, 2009.中国近海潮汐潮流的数值模拟与研究.青岛: 中国海洋大学硕士学位论文, 43-52 http://cdmd.cnki.com.cn/Article/CDMD-10423-2009172297.htm
|
孙湘平, 2006.潮汐与风暴潮.见: 孙湘平.中国近海区域海洋.北京: 海洋出版社, 130-157
|
李秉天, 2014.渤海地形演变对潮波系统影响的数值研究.青岛: 国家海洋局第一海洋研究所硕士学位论文, 34-44 http://cdmd.cnki.com.cn/article/cdmd-85301-1015518080.htm
|
李培良, 左军成, 李磊, 等. 2002. 南海TOPEX/POSEIDON高度计资料的正交响应法潮汐分析. 海洋与湖沼, 33(3): 287-295 DOI:10.3321/j.issn:0029-814X.2002.03.009 |
陈倩, 2002.浙江近海潮汐潮流的三维数值模拟.杭州: 浙江大学博士学位论文, 18-19 http://cdmd.cnki.com.cn/article/cdmd-10335-2003110051.htm
|
陈宗镛. 1980. 潮汐学. 北京: 科学出版社, 127-234
|
罗丹, 刘浩. 2015. 渤海潮汐潮流的数值研究. 上海海洋大学学报, 24(3): 457-464 |
孟鑫, 王冬, 李培良, 等. 2017. 海洋牧场溶解氧生态模型初探. 海洋技术学报, 36(5): 120-126 |
赵云霞, 魏泽勋, 王新怡. 2012. 利用T/P卫星高度计资料调和分析南海潮汐信息. 海洋科学, 36(5): 10-17 |
胡景, 2007.卫星高度计数据提取海洋潮汐信息及气候变化研究.青岛: 中国海洋大学硕士学位论文, 25-34 http://cdmd.cnki.com.cn/article/cdmd-10423-2008011421.htm
|
黄学智, 2016.基于FVCOM的黄渤海潮汐潮流的数值模拟.大连: 大连海洋大学硕士学位论文, 32-48 http://cdmd.cnki.com.cn/Article/CDMD-10158-1016757930.htm
|
El-Diasty M, Al-Harbi S, Pagiatakis S, 2018. Hybrid harmonic analysis and wavelet network model for sea water level prediction. Applied Ocean Research, 70: 14-21 DOI:10.1016/j.apor.2017.11.007 |
Foreman M G G, Neufeld E T, 1991. Harmonic tidal analyses of long time series. International Hydrographic Review, 68(1): 85-108 |
Friedrichs C T, Aubrey D G, 1988. Non-linear tidal distortion in shallow well-mixed estuaries:a synthesis. Estuarine, Coastal and Shelf Science, 27(5): 521-545 DOI:10.1016/0272-7714(88)90082-0 |
Groves G W, Reynolds R W, 1975. An orthogonalized convolution method of tide prediction. Journal of Geophysical Research, 80(30): 4131-4138 DOI:10.1029/JC080i030p04131 |
Hall P, Davies A M, 2005. The influence of sampling frequency, non-linear interaction, and frictional effects upon the accuracy of the harmonic analysis of tidal simulations. Applied Mathematical Modelling, 29(6): 533-552 DOI:10.1016/j.apm.2004.09.015 |
Liu Z L, Hu D X, Chu Z X, 2008. Observation of currents in the southern Yellow Sea in the summers of 2001 and 2003. Journal of Ocean University of China, 7(1): 17-26 DOI:10.1007/s11802-008-0017-1 |
Lü H Q, Hu J J, 2009. Tidal analysis in the venturi-shaped area between Zhenhai and Shenjiamen in the East China Sea. Chinese Journal of Oceanology and Limnology, 27(1): 103-111 DOI:10.1007/s00343-009-0103-2 |
Matte P, Secretan Y, Morin J, 2014. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary:an application of nonstationary tidal harmonic analysis. Journal of Geophysical Research, 119(9): 5724-5744 |
Pawlowicz R, Beardsley B, Lentz S, 2002. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Computers & Geosciences, 28(8): 929-937 |
Smith A J E, Ambrosius B A C, Wakker K F et al, 1997. Comparison between the harmonic and response methods of tidal analysis using TOPEX/POSEIDON altimetry. Journal of Geodesy, 71(11): 695-703 DOI:10.1007/s001900050137 |
 2019, Vol. 50
2019, Vol. 50


