中国海洋湖沼学会主办。
文章信息
- 赵新华, 侯一筠, 刘泽, 庄展鹏, 王凯迪. 2019.
- ZHAO Xin-Hua, HOU Yi-Jun, LIU Ze, ZHUANG Zhan-Peng, WANG Kai-Di. 2019.
- 基于卫星高度计和浮标漂流轨迹的海洋涡旋特征信息对比分析
- ANALYSIS OF THE GLOBAL EDDIES BASED ON ALTIMETER SNAPSHOTS AND BUOY DRIFTING TRAJECTORY DATA
- 海洋与湖沼, 50(4): 759-764
- Oceanologia et Limnologia Sinica, 50(4): 759-764.
- http://dx.doi.org/10.11693/hyhz20181100269
文章历史
-
收稿日期:2018-11-09
收修改稿日期:2019-01-07
2. 中国科学院大学 北京 100049;
3. 中国科学院海洋大科学研究中心 青岛 266071;
4. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 青岛 266000;
5. 自然资源部第一海洋研究所 青岛 266061;
6. 中国海洋大学 青岛 266100
2. University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
4. Pilot National Laboratory for Marine Science and Technology(Qingdao), Laboratory for Ocean and Climate Dynamics; Chinese Academy of Sciences, Center for Ocean Mega-Science, Qingdao 266000, China;
5. First Institute of Oceanography, Ministry of Natural Resources of China, Qingdao 266061, China;
6. Ocean University of China, Qingdao 266100, China
海洋涡旋在大洋和边缘海中普遍存在, 是与大尺度环流并列的海洋中最为基本的运动形式之一(Chelton et al, 2011; Zhang et al, 2014)。涡旋自身的保守性特征(Chaigneau et al, 2011; Early et al, 2011; Dong et al, 2014)使其在全球海洋物质和能量的输运中起着不可忽视的作用(Chen et al, 2010)。近年来, 随着卫星遥感平台的不断发展和现场观测资料的持续积累, 我们对于海洋涡旋的时空特征和变化规律的认识也不断深入(Lankhorst et al, 2006; Beron-Vera et al, 2008; Griffa et al, 2008; 胡冬等, 2018)。基于多源数据的探测特点和获取频率, 目前主流的涡旋识别方法主要分为两类:一种是基于矢量或标量空间场快照数据(如海表高度异常、海表温度)提取椭圆几何图形或闭合等值线, 称为欧拉涡旋(Isern-Fontanet et al, 2003; Cecilio et al, 2014; 崔凤娟等, 2015); 另一种是基于水团或者物质颗粒(例如漂流浮标)轨迹数据追踪闭合回路, 称为拉格朗日涡旋(Veneziani et al, 2005; Lilly et al, 2006; Dong et al, 2011; Lumpkin et al, 2013; Lumpkin, 2016)。
由于数据源的不同, 通过上述两种方法获取海洋涡旋的全球分布信息是有显著差异的, 在追踪单个涡旋的特征信息时, 不同方法也具有其各自的优势。在本文中, 首先介绍基于卫星高度计和浮标漂流轨迹提取涡旋特征信息的差别; 其次, 对两种数据源得到的全球海洋涡旋进行时空配对, 在全球尺度上分析涡旋配对结果中出现显著空间差异的原因; 最后, 统计配对涡旋的涡旋半径、涡旋强度等特征信息, 分析同一涡旋特征量在不同识别方法中的差异。
1 材料与方法本文选取Chelton提供的涡旋数据集(04版本)作为欧拉涡旋数据源, 该数据集基于1993年1月—2015年5月共269个月的卫星高度计观测的海表高度异常(Sea Level Anomaly, SLA)识别涡旋特征信息, 在确定涡旋范围之后, 在该范围内计算涡旋质心作为涡旋的中心位置, 围绕涡旋中心的封闭流线作为涡旋边界; 由于卫星高度计观测的海面动力高度信息自动满足地转平衡条件, 因此基于卫星高度计数据探测的欧拉涡旋一般为中尺度涡。对该数据集中的涡旋Rossby数(定义为整个涡旋内部的相对涡度ζ与局地行星涡度f之比)进行统计, 发现卫星高度计提取的涡旋Rossby数几乎都小于0.1(占96.3%), 这也表明中尺度涡控制区域内环流结构维持了较好的地转平衡关系。另外, 由于卫星高度计数据获取SLA在时间和空间上的连续性, 我们可对某个特定区域内的中尺度涡进行整个生命周期内的追踪, 掌握其生消过程和演变规律, 这也是卫星高度计数据在识别和追踪中尺度涡时的一大优势。
本文选取NOAA提供Argos表层浮标漂流轨迹数据作为拉格朗日涡旋数据源, 轨迹数据包括每隔6h水帆位于水下15m的浮标经纬度定位信息和速度数据, 时间跨度与卫星高度计数据相同。我们依据Dong等(Dong et al, 2011)提出的基于漂流浮标轨迹的几何特征的螺旋轨迹搜索法, 基于浮标轨迹是否形成闭合回路来判定是否探测到涡旋, 闭合回路中所有点的平均位置被认为是涡旋中心, 并剔除惯性振荡的影响。与卫星高度计数据自动满足地转关系不同, 浮标漂流轨迹是对局地水体运动总趋势的直接观测, 追踪浮标漂流轨迹形成的闭合回路并不受地转平衡约束, 即这种轨迹回路可以是中尺度涡、亚中尺度涡或更小尺度的局地动力扰动产生, 这也是浮标漂流轨迹数据在识别不同尺度海洋涡旋时的一大优势。定义由浮标漂流轨迹识别拉格朗日涡旋的相对涡度ζ为闭合回路上平均速度与回路平均半径之比, 并根据与欧拉涡旋相同的方法计算得到拉格朗日涡旋的Rossby数。我们发现, 全球拉格朗日涡旋对应的涡旋Rossby数中有35.2%大于0.1(即控制涡旋的动力机制存在高阶准地转或非地转因素), 这是与欧拉涡旋特征信息进行比较发现的最大不同。
为了定量找出不同涡旋识别方法对同一个海洋涡旋过程进行涡旋特征信息提取时出现的差异, 我们将相同时间段内的卫星高度计欧拉涡旋与浮标漂流轨迹拉格朗日涡旋进行配对。定义满足以下两个条件, 则认为基于两种不同方法识别的涡旋配对成功(即两种方法识别到同一个涡旋):
(1) 浮标漂流轨迹提取闭合回路的时间段在卫星高度计提取涡旋的生命周期内;
(2) 提取两类涡旋的中心位置相距不超过±0.5个经纬度。
2 结果与讨论我们遴选了生命周期大于4周的卫星高度计欧拉涡旋共245389个、成环周期大于2d(剔除惯性振荡影响)的浮标漂流轨迹拉格朗日涡旋175236个。在全球大洋中漂流浮标由于位置不确定, 不能全部提取到所有的海洋涡旋, 因此在本文中, 我们以卫星高度计欧拉涡旋为基准, 涡旋的配对成功率定义为匹配的涡旋数量占卫星高度计欧拉涡旋数量的百分比。结果表明, 约有16.5%的拉格朗日涡旋可以和同期的欧拉涡旋结果进行配对, 其中冷涡(北半球逆时针闭合回路)14066个、暖涡(北半球顺时针闭合回路)14864个, 涡旋极性分布在数量上基本持平。
2.1 涡旋配对成功率的空间分布特征基于涡旋配对条件, 在全球范围内卫星高度计欧拉涡旋和浮标漂流轨迹拉格朗日涡旋的配对成功率在空间分布上并不均衡, 具有随纬向的变化特征(见图 1)。在中纬度(20°—60°S, 20°—60°N)具有较高的配对成功率, 平均成功率约为17.9%, 最大成功率可达25%;而在高纬度极地区域(60°—90°S, 60°—90°N), 由于高度计在极地区域数据缺失, 这导致Chelton提供的涡旋数据集在该区域中尺度涡旋数量显著减少, 进一步导致涡旋配对的成功率降低至3%。在低纬度赤道区域(20°S—20°N), 涡旋配对成功率已经不到10%, 这是由于低纬度区域内地转效应并不显著, 卫星高度计无法有效观测到欧拉涡旋; 但通过浮标漂流轨迹识别出的拉格朗日涡旋却大量存在, 这说明在低纬度区域内, 采用漂流浮标手段对涡旋进行观测, 能够有效的弥补卫星高度计识别涡旋的区域限制。
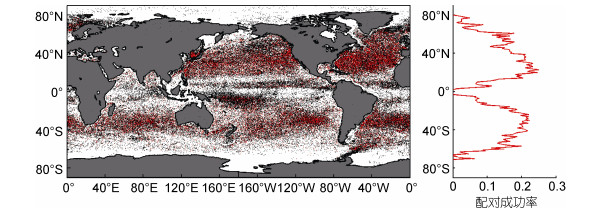 |
| 图 1 涡旋配对的全球分布 Fig. 1 The global distribution of Lagrangian eddies that match Eulerian eddies (red dots) and those who do not match (black dots) 注: 红色为配对成功的拉格朗日涡旋中心点, 黑色为未配对的拉格朗日涡旋中心点 |
在典型的涡旋多发区域, 例如中国南海区域, 共有72个拉格朗日涡旋可以和同期的欧拉涡旋结果进行配对, 涡旋配对率为17.4%, 这与同纬度区域的涡旋配对率大致持平。此外在黑潮延伸体区域, 该处受黑潮影响, 涡旋分布众多, 且经过该处的漂流浮标分布密集, 在配对时间范围内共提取到1760个拉格朗日涡旋, 其中23.6%的拉格朗日涡旋可以和同期的欧拉涡旋进行配对, 这也与同纬度区域的涡旋配对率大致持平。而在同为强西边界流的湾流区域, 在配对时间范围内共提取到5635个拉格朗日涡旋, 涡旋配对率也增长至26.6%, 这比同纬度区域的涡旋配对率略有增长。
2.2 配对涡旋半径的空间分布变化与台风风圈类似, 涡旋半径是表征涡旋过程对局地水体水平影响范围的一项重要指标, 而基于两种不同识别方法获得的涡旋过程均能够提取相应的涡旋半径信息。我们对能够配对的28930个涡旋过程进行分析, 将不同涡旋识别方法针对同一涡旋过程获得的涡旋半径的差异进行量化。图 2显示了能够配对的卫星高度计欧拉涡旋半径与浮标漂流轨迹拉格朗日涡旋闭合回路半径比值的全球分布。由于浮标漂流轨迹的闭合回路不一定就是涡旋的最外围, 因此从半径比值的总体分布上看, 欧拉涡旋半径要大于拉格朗日涡旋闭合回路半径; 特别是半径比值在2—3范围内的涡旋数量, 超过配对涡旋总数的54%。与涡旋配对成功率相似, 半径比值的全球分布也具有区域性特征, 中纬度(20°—50°S, 20°—50°N)的副热带和中纬度海区的半径比值基本在1, 即两种识别方法获得的涡旋(闭合回路)半径大致相当; 在20°S—20°N (特别是近赤道区域)、高纬度区域以及西边界流区域, 欧拉涡旋半径是同期拉格朗日涡旋闭合回路半径的3倍或更多。
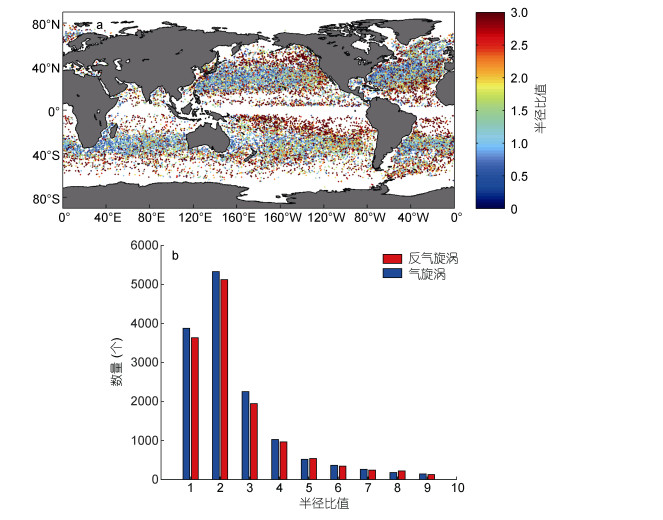 |
| 图 2 针对同一涡旋过程, 卫星高度计识别欧拉涡旋半径和浮标漂流轨迹识别拉格朗日涡旋闭合回路半径比值的全球分布(a)及数量直方图分布(b) Fig. 2 The global distribution of the ratios of Eulerian eddy radiuses identified from altimeter snapshot data and the corresponding Lagrangian eddy radiuses identified from buoy drifting trajectory data (a) and histograms of cyclonic (blue lines) and anticyclonic (red lines) eddies (b) |
在黑潮延伸体区域, 该处受黑潮影响, 不断有涡旋产生, 产生欧拉涡旋半径是同期拉格朗日涡旋闭合回路半径的1.8倍左右, 显著高于同纬度大洋内部海区。与黑潮区域类似, 在湾流区域, 产生欧拉涡旋半径是同期拉格朗日涡旋闭合回路半径的2.1倍。这表明受强西边界流作用的区域, 产生的涡旋受背景流影响, 提取的欧拉涡旋半径与同期拉格朗日涡旋闭合回路半径之比显著高于副热带和中纬度大洋内部海区。
2.3 配对涡旋Rossby数的空间分布特征Rossby数是表征大尺度运动的无量纲数, 也是描述地转效应重要性的首选指标。如前所述, 有超过1/3的拉格朗日涡旋对应的涡旋Rossby数大于0.1;这其中, 与欧拉涡旋配对的16.5%拉格朗日涡旋对应的涡旋Rossby数大于0.1的比例下降至22.3%, 而剩余未能配对的拉格朗日涡旋对应的涡旋Rossby数大于0.1的比例则上升至37.8%。这种比例分布说明, 受局地地转平衡的影响, 中尺度涡控制范围内(即欧拉涡旋内)的闭合回路也表现出较强的地转效应。
在涡旋Rossby数中, 若忽略局地科氏力的影响, 则涡旋Rossby数将直接反应涡旋过程的平均相对涡度, 也就是涡旋的强度信息。线性条件下, 涡旋控制范围内的平均相对涡度在涡旋中心处最大, 并沿半径方向递减; 但受到局地其他因素(如背景流剪切、侧摩擦、海底地形等)的影响, 这种线性分布的情况很难在现实中被观测到。在图 3中, 我们给出了能够配对的卫星高度计欧拉涡旋Rossby数与浮标漂流轨迹拉格朗日涡旋Rossby数比值的全球分布。该比值小于1的涡旋数量(即拉格朗日涡旋Rossby数大于同期欧拉涡旋Rossby数), 占配对涡旋总数的83.3%, 空间分布主要集中在低纬度和高纬度海区、以及边缘海(如中国南海和东海, 日本海, 鄂霍次克海等)。在这些区域内形成的拉格朗日涡旋由于受到局地其他因素(如背景流剪切、侧摩擦、海底地形等)的影响, 导致控制涡旋的高阶准地转或非地转因素增强, 进而导致了拉格朗日涡旋Rossby数增大。而该比值大于1的涡旋, 则主要集中在大洋的内区, 在中纬度(20°—50°S, 20°—50°N)的副热带和中纬度大洋内部海区, 在该海区内, 远离背景流区域, 且海底地形相对平缓, 在该处的涡旋受高阶准地转或非地转因素影响较小, 因此拉格朗日涡旋Rossby数和同期欧拉涡旋Rossby数大致相当。结合半径比值的空间分布结果, 我们发现, 拉格朗日涡旋较小的闭合回路对应较大的平均相对涡度; 也就是说, 浮标在被中尺度涡俘获后, 更容易在相对涡度较大的地方(如中尺度涡中心、中尺度涡边缘等)形成闭合回路。
 |
| 图 3 高度计探测涡旋Rossby数和配对的漂流浮标探测涡旋Rossby数比值的全球分布(a)及数量直方图分布(b) Fig. 3 The global distribution of the ratio of Eulerian eddy Rossby numbers identified from altimeter snapshot data and the corresponding Lagrangian eddy Rossby numbers identified from buoy drifting trajectory data (a) and histograms of cyclonic (blue lines) and anticyclonic (red lines) eddies (b) |
本文利用自1993年1月—2015年5月共269个月的Chelton提供的高度计探测涡旋结果和表层浮标漂流轨迹提取的涡旋回路进行配对分析, 结果表明在该时间段内, 表层浮标漂流轨迹提取的涡旋有16.5%可以和高度计涡旋结果配对, 且配对成功的涡旋在空间分布上并不均衡, 在中纬度(20°—60°S, 20°—60°N)有较高的配对成功率(17.9%), 在高纬度极地区域, 由于高度计数据缺失, 在极地区域无法用高度计探测中尺度涡旋, 这导致涡旋配对的成功率降低至3%。而在赤道地区, 由于地转关系失效, 高度计在该区域无法有效观测到欧拉涡旋, 采用漂流浮标能够有效的弥补高度计在该区域探测涡旋的不足。
进一步我们对于配对成功的28930个涡旋的半径和涡旋Rossby数进行统计, 表明在全球海洋中高度计识别中尺度涡的半径一般是浮标轨迹识别海洋涡旋的2—3倍左右, 约占总体的54%。从空间分布上看, 在中纬度(20°—50°S, 20°—50°N)的副热带和中纬度海区, 两种识别方法获得的涡旋(闭合回路)半径大致相当, 而在20°S—20°N以内(特别是近赤道区域)、高纬度区域以及西边界流区域, 欧拉涡旋半径是同期拉格朗日涡旋闭合回路半径的3倍或更多。同时, 涡旋Rossby数比值小于0.6的占56%。对两种方法配对涡旋Rossby数的比值分析表明, 拉格朗日涡旋较小的闭合回路对应较大的平均相对涡度, 在低纬度和高纬度海区、以及边缘海(如中国南海和东海, 日本海, 鄂霍次克海等)区域内, 形成的拉格朗日涡旋由于受到局地其他因素(如背景流剪切、侧摩擦、海底地形等)的影响, 导致控制涡旋的高阶准地转或非地转因素增强, 进而导致了拉格朗日涡旋Rossby数增大。通过对配对成功的涡旋个例分析, 我们发现, 当漂流浮标被一个中尺度涡俘获时, 其更容易在中尺度涡内部相对涡度较大的地方(如中尺度涡中心、中尺度涡边缘等)形成闭合回路。
胡冬, 陈希, 毛科峰, 等. 2018. 黑潮延伸体邻近区域中尺度涡特征统计分析. 海洋与湖沼, 49(3): 497-511 |
崔凤娟, 匡晓迪, 王玉. 2015. 南海中尺度涡年际变化特征及动力机制分析. 海洋与湖沼, 46(3): 508-516 |
Beron-Vera F J, Olascoaga M J, Goni G J, 2008. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures. Geophys Res Lett, 35(12): L12603 |
Cecilio C M, Gherardi D F M, Souza R B et al, 2014. Spatio-temporal variability of the eddy kinetic energy in the south Atlantic ocean. IEEE Geosci Remote Sens Lett, 11(11): 2010-2014 DOI:10.1109/LGRS.2014.2317414 |
Chaigneau A, Le Texier M, Eldin G et al, 2011. Vertical structure of mesoscale eddies in the eastern South Pacific Ocean:a composite analysis from altimetry and Argo profiling floats. J Geophys Res, 116(C11): C11025 DOI:10.1029/2011JC007134 |
Chelton D B, Schlax M G, Samelson R M, 2011. Global observations of nonlinear mesoscale eddies. Prog Oceanogr, 91(2): 167-216 DOI:10.1016/j.pocean.2011.01.002 |
Chen G X, Hou Y J, Zhang Q L et al, 2010. The eddy pair off eastern Vietnam:interannual variability and impact on thermohaline structure. Cont Shelf Res, 30(7): 715-723 DOI:10.1016/j.csr.2009.11.013 |
Dong C M, Liu Y, Lumpkin R et al, 2011. A scheme to identify loops from trajectories of oceanic surface drifters:an application in the Kuroshio extension region. J Atmos Oceanic Technol, 28(9): 1167-1176 DOI:10.1175/JTECH-D-10-05028.1 |
Dong C M, McWilliams J C, Liu Y et al, 2014. Global heat and salt transports by eddy movement. Nat Commun, 5: 3294 DOI:10.1038/ncomms4294 |
Early J J, Samelson R M, Chelton D B, 2011. The evolution and propagation of quasigeostrophic ocean eddies. J Phys Oceanogr, 41(8): 1535-1555 DOI:10.1175/2011JPO4601.1 |
Griffa A, Lumpkin R, Veneziani M, 2008. Cyclonic and anticyclonic motion in the upper ocean. Geophys Res Lett, 35(1): L01608 |
Isern-Fontanet J, García-Ladona E, Font J, 2003. Identification of marine eddies from altimetric maps. J Atmos Oceanic Technol, 20(5): 772-778 DOI:10.1175/1520-0426(2003)20<772:IOMEFA>2.0.CO;2 |
Lankhorst M, 2006. A self-contained identification scheme for eddies in drifter and float trajectories. J Atmos Oceanic Technol, 23(11): 1583-1592 DOI:10.1175/JTECH1931.1 |
Lilly J M, Gascard J C, 2006. Wavelet ridge diagnosis of time-varying elliptical signals with application to an oceanic eddy. Nonlin Processes Geophys, 13(5): 467-483 DOI:10.5194/npg-13-467-2006 |
Lumpkin R, 2016. Global characteristics of coherent vortices from surface drifter trajectories. J Geophys Res, 121(2): 1306-1321 DOI:10.1002/2015JC011435 |
Lumpkin R, Johnson G C, 2013. Global ocean surface velocities from drifters:mean, variance, El Ni o-Southern Oscillation response, and seasonal cycle. J Geophys Res, 118(6): 2992-3006 DOI:10.1002/jgrc.20210 |
Veneziani M, Griffa A, Garraffo Z D et al, 2005. Lagrangian spin parameter and coherent structures from trajectories released in a high-resolution ocean model. J Mar Res, 63(4): 753-788 DOI:10.1357/0022240054663187 |
Zhang Z G, Wang W, Qiu B, 2014. Oceanic mass transport by mesoscale eddies. Science, 345(6194): 322-324 DOI:10.1126/science.1252418 |
 2019, Vol. 50
2019, Vol. 50


