
中国海洋湖沼学会主办。
文章信息
- 曹川川, 孙建, 张文清. 2019.
- CAO Chuan-Chuan, SUN Jian, ZHANG Wen-Qing. 2019.
- ASAR波模式数据反演参数误差与海浪条纹清晰度的相关性分析
- THE CORRELATION ANALYSIS BETWEEN IMAGES STRIPE DEFINITION AND INVERSION PARAMETERS ERROR IN ASAR WAVE MODE
- 海洋与湖沼, 50(4): 777-787
- Oceanologia et Limnologia Sinica, 50(4): 777-787.
- http://dx.doi.org/10.11693/hyhz20181100273
文章历史
-
收稿日期:2018-11-14
收修改稿日期:2019-01-23
欧洲环境卫星(Environmental Satellite, Envisat)是欧空局(European Space Agency, ESA)于2002年3月1日发射升空, 搭载C波段(5.33GHZ)的先进合成孔径雷达(Advanced Synthetic Aperture Radar, ASAR), 其波模式数据包含Level-0原始数据(ASA_WV_0)、Level-1单视复图像(single-look complex phase- preserving, ASA_WVI_1)与影像交叉谱(complex cross spectra, ASA_WVS_1), 以及Level-2海浪谱(SAR ocean wave spectra, ASA_WVW_2)三种产品(Schöttler B et al, 2003)。
波模式数据提供全球的海浪信息, 广泛应用于海浪研究和数值预报。其反演算法起源于Hasselmann等(1991)提出的非线性变换算法MPI(the Max- Planck-Institute)和Engen等(1995)提出用合成孔径雷达(Synthetic Aperture Radar, SAR)影像交叉谱来反演海浪谱的方法。在此基础上Schulz-Stellenfleth等(2007)提出CWAVE反演算法, 应用于ERS-1/2 (European Remote-Sensing Satellite-1/2)和Envisat卫星。目前ESA官方处理ASAR波模式数据是应用Li等(2011)基于CWAVE提出的CWAVE_ENV (CWAVE for Envisat)算法。与此同时, 对波模式数据精度的验证也在不断地进行, 如Kerbaol等(2005)、Abdalla等(2006)、王贺等(2008)、Collard等(2009)、Li等(2011)、Ren等(2011)、Wang等(2014)。以上研究都是基于Level-2数据对比浮标或模式数据进行验证, 波模式反演算法已经十分成熟, 但仍然存在一定的误差, 所以精度的提升需要更多地从Level-1数据入手。截至目前, 仍没有学者对SAR成像海浪条纹清晰度与反演质量的关系进行研究。
一幅SAR图像可认为是后向散射截面σ0的空间分布图, 根据不同地物反射方式的差异, 在影像中显示出不同的纹理特征, 它是确定影像中感兴趣区域或目标的重要特征之一(Haralick et al, 1973)。对于海洋视场的SAR图像, 则显示为清晰度不一的明暗相间的海浪条纹。条纹清晰的图像纹理显著, 方向和尺度明确, 而条纹不清晰的图像则纹理模糊, 图像灰度分布无规律。图 1分别为条纹清晰和不清晰的SAR图像, 两种条纹清晰度的目视差别十分明显。本文通过与实时同步观测的浮标匹配, 结合SAR图像条纹的清晰度, 检验ASAR波模式数据的误差。为SAR数据反演和修正方法的更新提供了有价值的参考, 对提高数据精度具有重要意义。
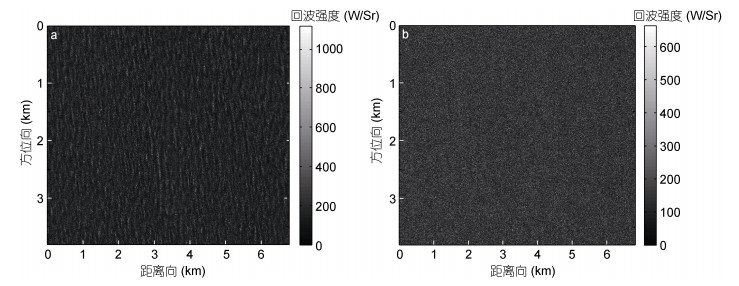 |
| 图 1 不同成像条纹清晰度的先进合成孔径雷达(Advanced Synthetic Aperture Radar, ASAR)图像 Fig. 1 The ASAR images in different stripe definition 注: a表示海浪条纹清晰的SAR图像, b表示海浪条纹不清晰的SAR图像 |
Envisat-ASAR波模式Level-1数据(ASRA_WVI_ 1), 也称单视复图像与影像交叉谱。该数据沿着卫星飞行路径每隔100km生成一次, 每一轨道最多生成400幅影像, 空间分辨率在方位向和距离向分别为6m和9m(方位向为卫星飞行方向, 距离向为垂直于卫星飞行的方向), 图幅范围5×5km—10×5km(ESA, 2014)。该数据是生成海浪谱数据的基础, 利用软件和程序处理可得到SAR图像和SAR谱。
1.2 Level 2数据(ASA_WVW_2)Envisat-ASAR波模式Level 2数据(ASA_WV W_2), 该数据为NetCDF格式的海浪谱产品, 由ESA发布, 可从GlobWave官方免费下载。本文研究数据的范围为2010年1月1日00时09分19秒—2011年1月1日00时04分16秒, 与Level-1b数据对应。已通过官方的反演方法处理, 包含海浪谱及完整的海浪参数。其反演方法是Li等(2011)提出的CWAVE_ENV, 该算法可以从SAR数据中获取整体的海浪参数, 而不需要任何辅助数据(Globwave, 2013a)。
1.3 NODC(The National Oceanographic Data Centre)浮标数据浮标每隔1h输出一组海浪测量数据。测量结果已被官方整理为每月一个文件, 本文所用数据为全球2010年1—12月的全部浮标数据。图 2标示了与波模式数据匹配成功的532个浮标点的分布情况, 其中红色方块为条纹清晰的SAR图像匹配的浮标点, 蓝色为条纹不清晰的图像匹配的浮标点, 黑色为目视分类后剩余图像匹配的浮标点。
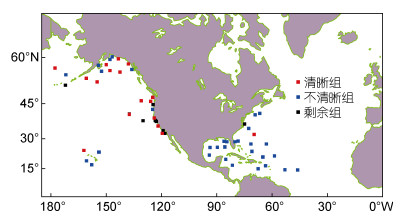 |
| 图 2 NODC (The National Oceanographic Data Centre)浮标的位置分布 Fig. 2 The location of NODC buoys |
研究SAR海浪成像与反演数据精度的关系, 需要获得成像区域对应的真实海况信息, 目前公认可信度最高的数据还是浮标测量。GlobWave官方曾对2002—2009年的ASAR数据与浮标进行匹配, 设定的匹配空间和时间标准是60km和60min, 但发现匹配成功的数量很少, 为了增加匹配数量采用一个动态的同步方法, 即官方所说的虚拟观测(Globwave, 2013b)。如附录表 1, 可发现匹配时间小于60min, 但匹配与源距离远大于60km。为了严格验证SAR图像反演参数的质量和保证数据量, 将重新设定匹配阈值来匹配浮标。
| 浮标号 | 浮标纬度(°N) | 浮标经度(°W) | 卫星纬度(°N) | 卫星经度(°W) | 匹配与源距离(m) | 距离差 (m) | 时间差 (m) |
| 41041 | 14.35667 | -46.0083 | 13.9982 | -44.7806 | 125905 | 51860 | 683 |
| 41041 | 14.35667 | -46.0083 | 14.8874 | -44.9742 | 81020 | 95682 | 698 |
| 41041 | 14.35667 | -46.0083 | 14.8874 | -44.9742 | 105263.15 | 49747.65 | 698 |
| 41041 | 14.35667 | -46.0083 | 15.7768 | -45.1678 | 176076 | 45124 | 713 |
| 41041 | 14.35667 | -46.0083 | 16.6659 | -45.3625 | 265178 | 10453 | 728 |
| 41041 | 14.35667 | -46.0083 | 17.5546 | -45.5581 | 356299 | 11729 | 743 |
| 41041 | 14.35667 | -46.0083 | 18.4433 | -45.7545 | 443274 | 99001 | 758 |
| 注:文件名NODC_GW_L2P_SAR_ENVI_NRT_20091231_005651_20091231_011235_0085_0331.nc | |||||||
本文通过匹配数据, 进行海浪参数与SAR图像的结合分析。将2010年全年的ASAR波模式数据WVI (Level-1)产品、WVW (Level-2)产品, 以及NODC的浮标这三种数据进行匹配, 用实时同步的浮标测量值来对比官方反演的海浪参数。考虑到官方发布的Level-2级海浪参数都会进行修正, 本文保留了修正前后的两类海浪参数, 因此可同时检验官方修正前、后的海浪参数质量。
2.1 ASA_WVI_1P数据与ASA_WVW_2P数据匹配ASAR波模式Level-1数据中包含无效数据, 在剔除海面被海冰和陆地覆盖时的无效数据后, 2010年Level-1数据集包含821424幅SAR图像数据。对应的2010年Level-2海浪谱数据共8683个文件(每个文件包含1轨的信息)。利用软件计算和匹配成像的经、纬度与时间, 成功匹配出436083个数据图像。主要从匹配成功的L2级数据中提取的参数有:有效波高(SWH)、主波波长(dwl)、风速(wsp), 得到具有海浪参数的SAR图像。
2.2 ASAR数据与浮标匹配结合GlobWave官方和前人的匹配方法, 匹配采用时间间隔60min和以浮标为中心的边长为120km的方框为区域(方框内距浮标的最大直线距离小于85km)。用文章2.1的匹配结果再与浮标匹配, 得到532组有效匹配结果。因每幅匹配成功的SAR图像均存在两组相邻的浮标测量值, 所以采用两次浮标测量的平均值作为真实值进行误差分析。
2.3 验证目视分类结果与参数转换检查全部匹配成功的532幅SAR图像, 进行目视判读分类, 从中严格选出43幅海浪条纹清晰和211幅条纹不清晰的SAR图像, 剩余图像的条纹清晰度介于两者之间(为突出成像条纹清晰度差异对SAR反演质量的影响, 不再讨论中间清晰度的情况)。
为了表明目视分类结果的可靠性, 提出参数——谱峰显著度(Spectral Peak Saliency, SPS), 它是通过对SAR影像的子图像做快速傅里叶变换和滤波处理, 将回波信号由空间域转换为频率域计算得到的参数值, 定义为谱峰值与背景平均值之比; Sun等(2009)使用这一概念作为判据筛选SAR影像, 认为SPS值越高, 其对应SAR影像的背景噪声在回波信号中的占比越低, 成像质量就越好。图 3a和3b分别为条纹清晰组和不清晰组SAR影像对应的SPS值的分布情况, 横坐标为谱峰显著度, 纵坐标为出现的频数。
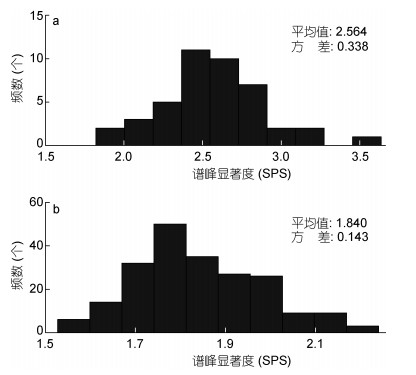 |
| 图 3 不同清晰度合成孔径雷达(Synthetic Aperture Radar, SAR)图像对应的谱峰显著度 Fig. 3 The Spectral Peak Saliency of SAR images in different definition 注: a表示条纹清晰SAR图像对应谱峰显著度的分布, b表示条纹不清晰SAR图像对应谱峰显著度的分布 |
图 3中成像条纹清晰组的SPS主要集中在2.5附近, 而不清晰组SPS则集中在1.8附近, 两者有较好的区分性, 说明以上目视分类影像清晰度的结果是可靠的。匹配到的浮标信息以条纹清晰图像为例, 部分展示在附录表 2, 包含浮标和SAR图像的经纬度、匹配时间间隔(s), 以及图像中心距离浮标的直线距离(km)。
| 浮标文件名 | 浮标纬度 (°N) | 浮标经度 (°W) | 影像纬度 (°N) | 影像经度(°W) | 时间间隔1 (s) | 时间间隔2 (s) | 距离间隔(km) |
| 51101_201001.nc | 24.321 | -162.058 | 24.254 | -161.779 | -52 | 3548 | 29.30 |
| 46001_201001.nc | 56.300 | -148.021 | 56.548 | -147.262 | -1896 | 1704 | 54.26 |
| 46075_201001.nc | 53.926 | -160.806 | 53.617 | -160.683 | -1278 | 522 | 35.24 |
| 46080_201002.nc | 58.035 | -149.994 | 57.970 | -150.206 | -2732 | 868 | 14.39 |
| 46001_201002.nc | 56.300 | -148.021 | 56.434 | -147.299 | -1895 | 1705 | 46.93 |
| 51101_201002.nc | 24.321 | -162.058 | 24.525 | -162.436 | -218 | 3382 | 44.45 |
| 46075_201003.nc | 53.926 | -160.806 | 53.589 | -159.999 | -1105 | 2495 | 64.94 |
| 46085_201003.nc | 55.855 | -142.559 | 55.630 | -143.351 | -876 | 2724 | 55.57 |
| 46035_201003.nc | 57.069 | -177.750 | 57.252 | -177.130 | -1926 | 1674 | 42.55 |
| 46001_201003.nc | 56.300 | -148.021 | 56.645 | -148.658 | -2238 | 1362 | 54.84 |
| 46080_201003.nc | 58.035 | -149.994 | 58.396 | -149.287 | -2553 | 1047 | 57.72 |
| 46080_201003.nc | 58.035 | -149.994 | 57.526 | -149.702 | -2568 | 1032 | 59.25 |
| 46085_201003.nc | 55.855 | -142.559 | 55.999 | -142.481 | -697 | 2903 | 16.72 |
用官方反演值与浮标测量值进行对比验证。因浮标只提供主波周期(dwp), 而官方ASAR反演只提供主波波长(dwl); 核实浮标位置的水深与波长的关系后, 采用深水波的频散关系得到周期(T)与波长(L)的转换公式:
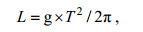 (1)
(1)其中, g表示重力加速度。风速作为海浪能量的输入源是极其重要的参数, 因此后文主要对比有效波高(SWH)、主波波长(dwl)和风速(wsp)三项参数修正前、后的值。因官方修正后的风速普遍为异常值, 故在下文的图中仅展示修正前的风速。
3 结果与分析 3.1 ASAR反演海浪参数的误差分析图 4为匹配成功的532组ASAR图像反演的海浪参数与实时同步的浮标测量值对比。图中横坐标为浮标测量值, 纵坐标为ASAR反演值。图 4a-4d分别对应有效波高、主波波长、风速和主波周期的参数分布。每张图有两种散点:分别是官方反演海浪谱后直接计算的海浪参数和经过修正处理后得到的海浪参数(后面统称为修正前和修正后的海浪参数)。图中标注了参数对比的均方根误差RMSE和偏差Bias数据, 计算公式如公式(2)和公式(3):
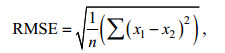 (2)
(2) (3)
(3)
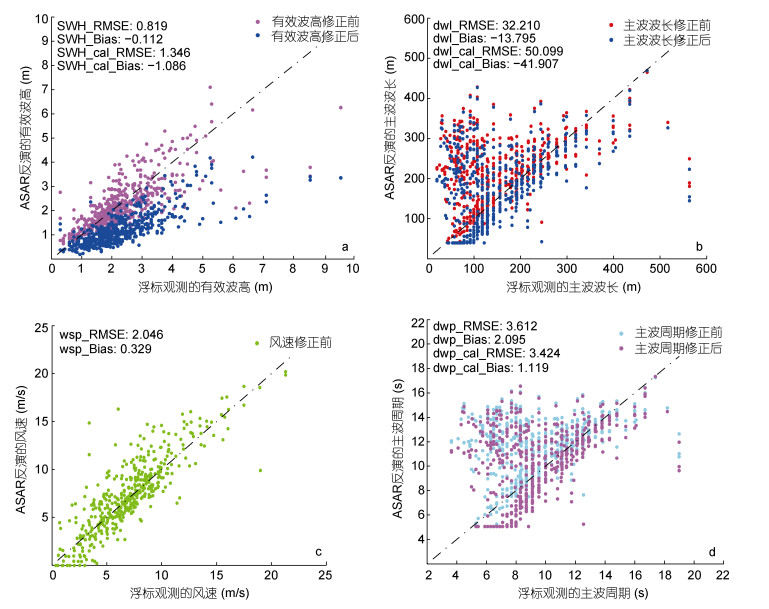 |
| 图 4 ASAR反演海浪参数与浮标测量值对比 Fig. 4 Scatter plots of ocean wave parameters derived by ASAR-WVW compared to buoy in situ measurements 注: RMSE:修正前的均方根误差, Bias:修正前的偏差值, cal_RMSE:修正后的均方根误差, cal_Bias:修正后的偏差, SWH:有效波高, dwl:主波波长, wsp:风速, dwp:主波周期 |
其中, x1为ASAR反演的参数值, x2为浮标测量参数值, n为数据量。
图 5和图 6分别为海浪条纹清晰组和不清晰组SAR图像反演的海浪参数与实时同步的浮标观测对比。两图的子图像a-d分别是有效波高、主波波长、风速和主波周期; 横坐标为浮标测量值, 纵坐标为ASAR反演值。两种散点分别代表官方修正前、后的海浪参数。详细的误差情况如表 1。
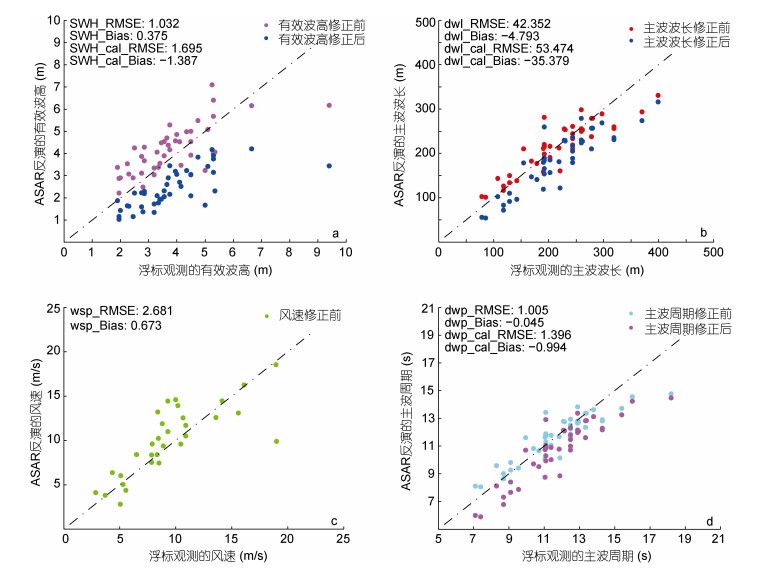 |
| 图 5 条纹清晰组海浪参数与浮标测量值对比 Fig. 5 Ocean wave parameters compared to buoy in situ measurements in the clear stripe group |
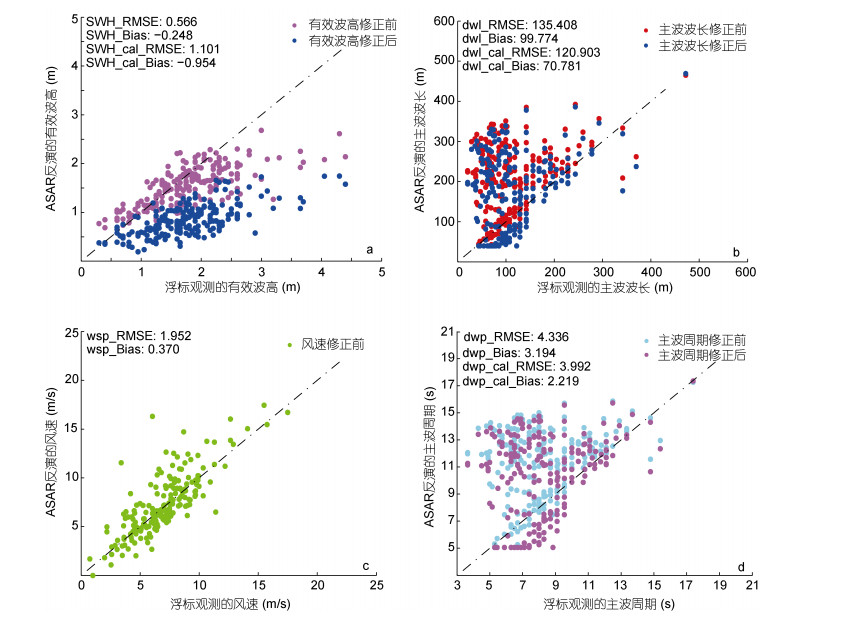 |
| 图 6 条纹不清晰组海浪参数与浮标测量值对比 Fig. 6 Ocean wave parameters compared to buoy in situ measurements in the unclear stripe group |
| 参数 | 清晰组RMSE | 清晰组 Bias | 不清晰组RMSE | 不清晰组 Bias |
| SWH(m) | 1.032 | 0.375 | 0.566 | -0.248 |
| SWH修正后(m) | 1.695 | -1.387 | 1.101 | -0.954 |
| dwl(m) | 42.352 | -4.793 | 135.408 | 99.774 |
| dwl修正后(m) | 53.474 | -35.379 | 120.903 | 70.781 |
| wsp(m/s) | 2.681 | 0.673 | 1.952 | 0.370 |
全年的Envisat-ASAR波模式数据量很大, 但受限于现有浮标的数量和布设位置, 仅得到532组匹配结果。对比发现: SWH修正前的误差(RMSE=0.819, Bias=-0.112)对比Li等(2011)的验证结果(深水中RMSE=0.7m, Bias=0.06m, 浅水中RMSE=1.02m, Bias=-0.19m), 其误差还在可接受范围, 但主波波长、主波周期和风速的反演误差明显偏大。
一般公认官方修正后的数据误差更小, 更具有应用价值, 但在本文的研究中, SWH、dwl和wsp三种参数经过官方修正后RMSE和Bias的值都变得更大。查阅GlobWave官方用户手册, 发现官方进行海浪参数修正时, 依旧沿用Johnsen等(2004)和Collard等(2009)的修正方法(Globwave, 2013a)。如有效波高的修正:
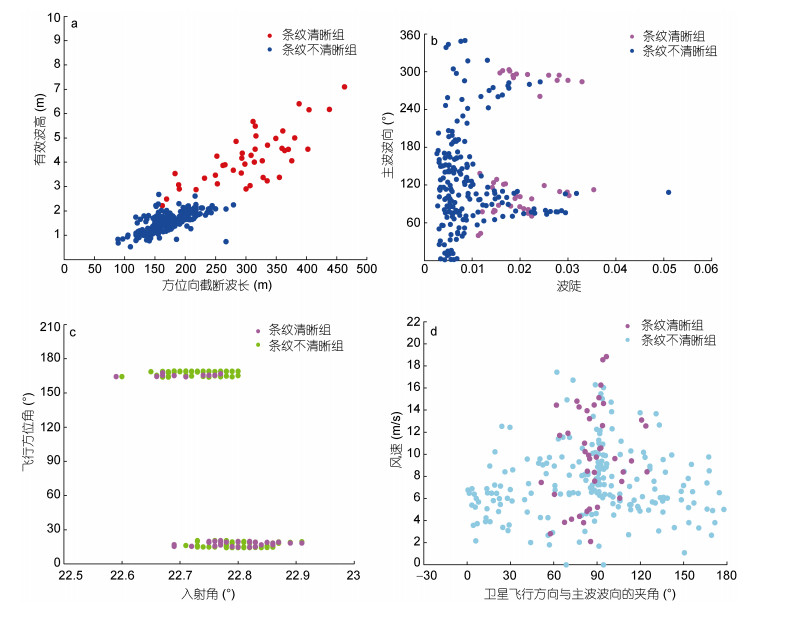
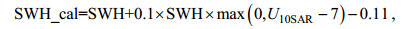 (4)
(4)其中, SWH_cal指修正后的有效波高, U10SAR指代风速, 由公式(4)可知SWH的修正易受到SAR反演风速的影响。文献中提出此公式是针对涌浪的SWH进行修正, 引入对全部数据进行修正实为不妥。而且Johnsen等(2006)通过2003年6月—2005年9月的监测数据, 证实传感器接受增益有所变化。从反演算法上来分析, 当时的反演算法CWAVE现在已更新为CWAVE_ENV, 且Li等(2011)已论证两种算法的反演值差异, 所以官方的修正方法理论上也需要进行相应的更新。
图 5和图 6分别为SAR图像条纹清晰组和不清晰组与浮标测量相比的误差情况, 从数据误差结果上看, 条纹清晰图像反演的海浪参数的精度并非完全优于不清晰图像。主要分以下几点详细说明:
(1) 有效波高(SWH):可以发现不同条纹清晰度SAR图像反演的SWH值有很好的区分度。条纹清晰组反演的SWH最小值为2.215m, 而不清晰组反演的SWH有84.83%在2m以内。与浮标相比, 清晰组SWH的反演值高于浮标测量值, 而不清晰组则低于浮标测量值, 但清晰组反演的SWH误差更大。官方的修正方法将两种清晰度下反演的SWH值都变小, 但修正后的结果具有更大误差, 建议根据不同条纹清晰度来合理修正反演值。
(2) 主波波长(dwl): 图 5b和图 6b中, 两种清晰度下SAR反演的dwl值分布比较重叠。对比浮标测量值发现, 不清晰组dwl < 150m的数据量高达79.15%, 但此处SAR反演值相比于浮标测量值, 把dwl高估了2—4倍左右, 使得Bias达到了99.774m。以浮标为准, 所以不清晰组对应的波长是以短波为主。两组计算的RMSE和Bias的结果很明显, 条纹清晰图像反演的主波波长误差更小, 修正后带来更大误差, 而不清晰图像则相反。
(3) 风速(wsp):条纹清晰组数据量少, 主要在4—20m/s分布, 其中wsp > 7m/s占74.42%。而条纹不清晰组主要集中在10m/s以内, 其中wsp < 7m/s占51.18%。与浮标测量相比, SAR的反演值偏高, 不清晰组图像风速的反演值误差更小。
(4) 主波周期(dwp):对比浮标数据误差很明显, 清晰组反演误差更小, 不清晰组误差较大。误差原因是在10s以内大量SAR反演值计算的dwp明显偏高, 与SAR反演的dwl < 150m时的数据相对应。而浮标测量的波周期, 对应清晰组有79.07%的dwp > 10s, 而不清晰组有79.15%的dwp < 10s, 说明清晰图像实际的波浪周期要高于不清晰图像。对比图 4d与图 5d、图 6d就会发现, 因为修正降低了不清晰组反演的主波周期值, 才使得总体主波周期修正后的值误差更小。
综上, 海浪条纹清晰的SAR图像对应较大的有效波高、主波波长和风速。相比浮标测量, 条纹清晰图像反演得到的主波波长和主波周期误差更小, 而不清晰图像反演得到的有效波高和风速误差更小。经过官方的修正方法降低了SAR的反演值, 却使反演的海浪参数误差变大。数据匹配验证的结果和官方修正方法的说明都证明目前的修正方法需要修正更新。
3.2 ASAR成像条纹清晰度与海浪参数的关系根据SAR成像理论, 普遍认同卫星入射角在20°—60°时, 其回波机制就是海面微尺度波的Bragg散射, 更长尺度的波浪通过调制这些微尺度波的方向、能量和运动, 使得SAR能对海浪成像(Hasselmann et al, 1991)。任何海洋研究人员感兴趣的现象, 只要对海水微尺度波的产生和分布产生影响, 就会在合成孔径雷达图像上得以显现(孙建, 2005)。
海面SAR成像过程主要有三种调制机制: (1)倾斜调制, 通过长波波陡改变局部入射角, (2)流体动力调制, 短波和长波之间的流体动力相互作用, 形成汇聚区和发散区, 调制短Bragg散射波的波数和能量, (3)速度聚束调制, 由于长波轨道速度引起回波信号的多普勒效应, 使得海面的散射面位移和导致散射面元在图像平面也产生一个方位向的位移。前两种调制Hasselmann将其归结为真实孔径雷达(Real-Aperture Radar, RAR)成像机制, 通常被认为是线性过程, 第三种为SAR调制, 具有很强的非线性。当位移小于长波的波长时, 这个调制能被看成线性过程, 当位移大于波长时, 这个过程就变成非线性, 并且当位移明显的超出波长时, 图像就会完全模糊(Hasselmann et al, 1991)。
方位向截断波长是一个表征SAR成像过程的非线性的量(Alpers et al, 1986; Vachon et al, 1994), Beal等(1983), Lyzenga等(1986)和Monaldo等(1986, 1988)已经实验性的证实方位向截断尺度与轨道速度分量或整体波浪场的属性成比例, Stopa等(2015)用ASAR数据也证实方位向截断波长与轨道波浪速度整体的方差成比例。Hasselmann等(1989)提出SAR调制传递函数(MTF)的结果对SAR视像和飞行方向依赖性非常强。Jain(1981)认为SAR成像与海浪在有效波高上的调制相关, 同时GlobWave官方手册也说明三种调制机制均随波高的增加而增加(Globwave, 2012)。此外, 波向和卫星飞行方向以及两者之间的夹角都能够产生方位向速度分量, 即带来成像的非线性。
根据不同条纹清晰度的SAR图像, 从Level-2级数据中提取和计算对应的海浪参数, 对比参数在不同清晰度下的分布情况。包含参数:有效波高(SWH)、方位向截断波长(ACW)、波陡(S)、主波波向(ddr)、飞行方向角、电磁波入射角、风速(wsp)、卫星飞行方向与主波波向的夹角。
图 7的数据来自波模式Level-2产品修正前的海浪参数和设备参数。图 7a的横坐标为方位截断波长, 纵坐标为有效波高, 可看出SWH和ACW在两种清晰度下的聚类分布较明显, 计算两参数的相关系数高达0.891。图 7b横坐标为波陡, 纵坐标为主波波向, 波陡是由有效波高和主波波长计算得到(S=SWH/dwl), 但两参数在不同清晰度下的区分度不高。不清晰图像的波陡在0.01以内聚集, 可对照图 5b, 因波长的SAR反演值明显偏高于浮标, 所以计算的波陡值更小; 而清晰组的波陡值相对较大, 但两种波陡值分布重叠。看波向, 清晰组分布更集中, 主要在300°附近和60°—150°范围内, 而不清晰组则广泛分布没有规律。图 7c横坐标为电磁波入射角, 纵坐标为卫星飞行方向角, 看图可知这两参数与成像清晰度无关。飞行方向角集中在18°和165°附近, 即卫星运行过程中的升降轨形成的现象; 而电磁波入射角分布于22.5°—23°范围内, 可说明ASAR波模式数据符合Bragg散射条件。图 7d横坐标为卫星飞行方向与主波波向的夹角, 纵坐标为风速, 这两个参数对条纹清晰度的响应不好。条纹清晰SAR图像的夹角值集中在90°附近, 即海浪是沿着距离向附近传播, 而不清晰SAR图像的夹角值分布无规律, 但也包含90°附近的值, 说明还有其他因素导致沿距离向传播的波浪在SAR影像上成像的条纹不清晰, 仍需深入研究; 对比两种清晰度的风速分布也无显著差别。
 |
| 图 7 SAR成像有关的海浪参数在不同清晰度图像下的散点分布图 Fig. 7 Scatter plots of wave parameters related to SAR imaging in different definition |
检验的参数主要取自于SAR成像理论和前人的研究, 分析的结果又与成像理论相一致。如有效波高和波陡的增大对海面微尺度波的分布产生影响:使波峰后的回波信号加强, 波峰前的回波信号减弱, 即加强了倾斜调制, 使微尺度波的汇聚和发散作用加强, 即加强了流体动力调制, 这两种作用都会增加回波信号之间的差异, 表现在SAR影像上就是更加显著的黑白相间的条纹。按照速度聚束调制理论, 非线性作用是影像模糊的主要原因, 所以方位向截断波长对成像清晰度的响应敏感。此外, 距离方向传播的波产生的调制以倾斜和流体动力调制为主, 而随着偏离距离向的角度的增大, 这两种调制的影响就会减小。然而波浪的传播方向一旦偏离距离方向, 则会产生相当明显的速度聚束(孙建, 2005), 这解释了清晰SAR图像的条纹方向基本与距离向相一致的现象; 敏感性分析中选取卫星飞行方向与主波波向的夹角, 即是为了验证是否有方位向分量, 发现清晰影像的夹角主要集中在90°附近, 也就是速度聚束作用未产生或者很弱, 成像基本为线性过程, 所以表现在SAR影像上条纹清晰。总言之, 海浪是否能在SAR影像上清晰成像, 是一个非常复杂的过程。根据本文的分析首先要满足成像调制机制, 又要避免成像过程的非线性作用; 波浪沿距离方向传播, 且波高越高、方位向截断波长较长、波陡更大的波, 更具备成像清晰的可能性。
4 结论本文通过匹配2010年全年的Envisat-ASAR波模式数据WVI(Level-1)产品、WVW(Level-2)产品, 以及NODC的浮标数据, 对比不同条纹清晰度SAR图像对应的海浪参数, 得到以下结论:
(1) 证实目前官方处理波模式数据的修正方法需要更新。修正后的海浪参数反而具有更大的误差。如532组匹配浮标的SAR图像反演值, 修正后有效波高的RMSE和Bias分别增加了0.53m和0.97m, 主波波长的RMSE和Bias分别增加了17.89m和28.11m。基于本文对条纹清晰度不同现象的研究, 建议在新的反演参数的修正公式中, 加入SAR图像条纹清晰度的评估项, 来合理修正ASAR波模式数据反演的海浪参数。
(2) 不同条纹清晰度SAR图像反演参数的精度具有较大差别。条纹清晰图像的主波波长和主波周期的反演误差更小, 但有效波高和风速的反演误差更大, 而条纹不清晰图像则相反; 且条纹清晰图像对应的海浪参数值普遍高于不清晰图像的同一参数值。这个结果刷新了对SAR成像海浪参数反演精度的认知, 并提出了SPS来检验目视分类影像条纹清晰度的效果。
(3) 通过分析海浪参数对海浪条纹清晰度的敏感性, 证明了有效波高和方位向截断波长对SAR图像清晰度的响应最好, 波陡次之, 而波向、风速和角度偏差值的响应不明显, 且图像清晰度与卫星飞行方位角和入射角无关。波浪沿距离方向传播, 且波高越高、方位向截断波长较长、波陡更大的波, 更具备成像清晰的可能性。
本文的研究基于NODC的浮标数据, 通过核实浮标位置的水深情况, 发现浮标位置的水深与波长满足深水重力波的频散关系, 因此本文的结论应该可以推广到深水大洋。从整体误差分析的结果来看, 区分SAR图像的条纹清晰度是一个有效衡量反演质量的新思路, 若能结合图像的条纹清晰度对SAR的反演参数进行修正, 将会有效提高SAR反演海浪参数的精度; 同时下一步将尝试加入高度计或者对其他卫星的SAR波模式数据进行验证, 如sentinel-1和高分三号。扩展对SAR成像海浪条纹清晰度的研究, 以及开展不同清晰度图像分类的工作。
王贺, 杨劲松, 黄韦艮, 等. 2008. 对ENVISAT ASAR level 2算法固有误差的分析. 海洋学报, 30(3): 72-76 |
孙建, 2005. SAR影像的海浪信息反演.青岛: 中国海洋大学博士学位论文, 6-7 http://cdmd.cnki.com.cn/Article/CDMD-10423-2005140461.htm
|
Abdalla S, Bidlot J R, Janssen P, 2006. Global validation and assimilation of Envisat ASAR wave mode spectra. In: Proceedings of SEASAR 2006. Frascati, Italy: ESA, 8.1
|
Alpers W R, Bruening C, 1986. On the relative importance of motion-related contributions to the SAR imaging mechanism of ocean surface waves. IEEE Transactions on Geoscience and Remote Sensing, 24: 873-885 |
Beal R C, Tilley D G, Monaldo F M, 1983. Large- and small-scale spatial evolution of digitally processed ocean wave spectra from Seasat Synthetic Aperture Radar. Journal of Geophysical Research, 88: 1761-1778 DOI:10.1029/JC088iC03p01761 |
Collard F, Ardhuin F, Chapron B, 2009. Monitoring and analysis of ocean swell fields from space:New methods for routine observations. Journal of Geophysical Research, 114: 7-23 |
Engen G, Johnsen H, 1995. SAR-Ocean Wave Inversion Using Image Cross Spectra. IEEE Transactions on Geoscience and Remote Sensing, 33: 1047-1056 DOI:10.1109/36.406690 |
ESA (European Space Agency), 2014. ENVISAT-1 products specifications volume 8: ASAR products specifications, 2.2: Organisation of products, http://envisat.esa.int/handbooks/asar/CNTR2-2.html#eph.asar.prodalg.orgprod
|
Globwave, 2012. Deliverable D.9 Wave data handbook, 5.3 SAR wave imaging. Logica UK: ESA (European Space Agency), 28-31, http://globwave.ifremer.fr/download/GlobWave_D.9_WDH_v1.1.pdf
|
Globwave, 2013a. Globwave product user guide phase 3. Logica UK: ESA (European Space Agency), 27-43, http://globwave.ifremer.fr/download/GlobWave_D.7_PUG3_v1.0.pdf
|
Globwave, 2013b. Satellite/Buoy Match-ups. Logica UK: ESA(European Space Agency), http://globwave.ifremer.fr/products/globwave-satellite-data/satellite-buoy-match-ups
|
Haralick R M, Shanmugam K, Dinstein I, 1973. Textural features for image classification. IEEE Transactions on Systems, Man, and Cybernetics, 3: 610-621 |
Hasselmann K, Hasselmann S, Brfining C et al, 1989. Application of a new closed ocean wave-SAR spectral transform relation to LEWEX data, paper presented at Conference on measuring, modeling, predicting and applying directional ocean wave spectra. Johns Hopkins Univ., Baltimore, Md
|
Hasselmann K, Hasselmann S, 1991. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. Journal of Geophysical Research, 96: 10713-10729 DOI:10.1029/91JC00302 |
Jain A, 1981. SAR imaging of ocean waves:Theory. IEEE Journal of Oceanic Engineering, 6: 130-139 DOI:10.1109/JOE.1981.1145496 |
Johnsen H, Collard F, 2004. ASAR wave mode processing -Validation of reprocessing upgrade. Europe: ESA-ESRIN
|
Johnsen H, Engen G, Collard F et al, 2006. Envisat ASAR wave mode products - Quality assessment and algorithm upgrade. In: Proceedings of SEASAR 2006. Frascati, Italy: European Space Agency, SP-613
|
Kerbaol V, Johnsen H, Chapron B et al, 2005. Quality assessment of ENVISAT ASAR Wave mode products based on regional and seasonal comparisons with WAM model outputs. In: Proceedings of the 2004 ENVISAT/ERS Symposium. Salzburg, Austria: ESA
|
Li X M, Lehner S, Bruns T, 2011. Ocean wave integral parameter measurements using Envisat ASAR wave mode data. IEEE Transactions on Geoscience and Remote Sensing, 49: 155-174 DOI:10.1109/TGRS.2010.2052364 |
Lyzenga D R, 1986. Numerical simulation of synthetic aperture radar image spectra for ocean waves. IEEE Transactions on Geoscience and Remote Sensing, 24: 863-872 |
Monaldo F M, Lyzenga D R, 1986. On the estimation of wave slope- and height-variance spectra from SAR imagery. IEEE Transactions on Geoscience and Remote Sensing, 24: 543-551 |
Monaldo F M, Lyzenga D R, 1988. Comparison of shuttle imaging radar-B ocean wave image spectra with linear model predictions based on aircraft measurements. Journal of Geophysical Research:Oceans, 93: 15374-15388 DOI:10.1029/JC093iC12p15374 |
Ren Q F, Zhang J, Meng J M et al, 2011. Comparison and analysis of Envisat ASAR ocean wave spectra with buoy data in the northern Pacific Ocean. Chinese Journal of Oceanology and Limnology, 29: 10-17 DOI:10.1007/s00343-011-9926-8 |
Schöttler B, Rosich B, Closa J et al, 2003. A first assessment of the ASAR wave mode properties and its complex imagette product characteristics. In: Proceedings of CEOS Working Group on Calibration/Validation-SAR WORKSHOP (ESA SP-526). London, England: European Space Agency
|
Schulz-Stellenfleth J, KäNig T, Lehner S, 2007. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data. Journal of Geophysical Research, 112: 3-19 |
Stopa J E, Ardhuin F, Chapron B et al, 2015. Estimating wave orbital velocity through the azimuth cutoff from space-borne satellites. Journal of Geophysical Research:Oceans, 120: 7616-7634 DOI:10.1002/2015JC011275 |
Sun J, Kawamura H, 2009. Retrieval of surface wave parameters from SAR images and their validation in the coastal seas around Japan. Journal of Oceanography, 65: 567-577 DOI:10.1007/s10872-009-0048-2 |
Vachon P W, Krogstad H E, Scott Paterson J, 1994. Airborne and spaceborne synthetic aperture radar observations of ocean waves. Atmosphere-Ocean, 32: 83-112 DOI:10.1080/07055900.1994.9649491 |
Wang H, Zhu J H, Yang J S, 2014. Error analysis on ESA's Envisat ASAR wave mode significant wave height retrievals using triple collocation model. Remote Sensing, 6: 12217-12233 DOI:10.3390/rs61212217 |
 2019, Vol. 50
2019, Vol. 50


