中国海洋湖沼学会主办。
文章信息
- 张先毅, 黄竞争, 杨昊, 欧素英, 刘锋, 蔡华阳, 杨清书. 2019.
- ZHANG Xian-Yi, HUANG Jing-Zheng, YANG Hao, OU Su-Ying, LIU Feng, CAI Hua-Yang, YANG Qing-Shu. 2019.
- 长江河口潮波传播机制及阈值效应分析
- THE GOVERNING MECHANISM OF TIDAL WAVE PROPAGATION AND THRESHOLD EFFECT IN THE CHANGJIANG RIVER ESTUARY
- 海洋与湖沼, 50(4): 788-798
- Oceanologia et Limnologia Sinica, 50(4): 788-798.
- http://dx.doi.org/10.11693/hyhz20181200305
文章历史
-
收稿日期:2018-12-28
收修改稿日期:2019-03-25
2. 河口水利技术国家地方联合工程实验室 广州 510275;
3. 广东省海岸与岛礁工程技术研究中心 广州 510275
2. State and Local Joint Engineering Laboratory of Estuarine Hydraulic Technology, Guangzhou 510275, China;
3. Guangdong Provincial Engineering Research Center of Coasts, Islands and Reefs, Guangzhou 510275, China
河口是陆海相互作用的过渡区域, 受流域径流和外海潮汐的双重作用, 径潮动力非线性相互作用具有独特性和复杂性(Guo et al, 2015; 欧素英等, 2017)。自上个世纪以来, 上游建坝、口门围垦、河道挖沙等高强度人类活动对河口环境的破坏已远超河口自身的修复能力, 河口海岸面临着巨大挑战(陈吉余等, 2002)。位于我国长江的三峡大型水利工程和珠江三角洲的口门围垦、无序采沙等就是典型的强人类活动, 受其影响河口的来水来沙条件及河道地形变化剧烈(陈吉余等, 1995; 胡光伟等, 2014), 直接影响河口区的潮波传播及径潮相互作用(蒋陈娟等, 2012; 石盛玉等, 2017, 2018), 进而影响盐淡水混合、泥沙输运及河口区的地貌演变(刘锋等, 2011; 蒋陈娟等, 2012; 袁丽蓉等, 2013; 谢丽莉等, 2015)。因此, 揭示河口区径潮非线性相互作用特征及潮波传播机制不仅是河口海岸动力学研究的重要科学问题, 亦可为河口区的水资源管理及整治规划, 有效控制盐水入侵和风暴潮灾害等提供科学依据。
目前, 数据分析(欧素英等, 2004, 2017; Pan et al, 2018)、数值模拟(李秉天等, 2015; 朱建荣等, 2016; 鲍道阳等, 2017a, b; Zhang et al, 2018)、解析理论模型(Horrevoets et al, 2004; Cai et al, 2014a, 2016)等方法已被广泛应用到河口区径流对潮波传播的影响研究。其中, 解析理论方法因其模型所需地形、动力边界条件简单易得, 能够快速探讨系统扰动对水动力的影响, 并揭示径潮动力的非线性作用机制, 在河口区潮波传播过程及其变化机制研究中取得良好的应用效果(Horrevoets et al, 2004; Cai et al, 2012, 2013, 2014a, 2014b, 2016, 2019)。在解析模型中, 潮波振幅和余水位(即潮平均水位)是反映河口径潮相互作用的两个重要指标, 在此基础上, 可进一步探讨潮波振幅衰减率和余水位坡度对径潮动力非线性作用的响应。研究表明, 径流和河口地形是影响潮波传播变形两个主要因素(路川藤等, 2010; Zhang et al, 2016; Abdullah et al, 2016)。径流一方面通过增大流速来增大潮波的衰减效应, 使潮波振幅趋于减小; 而另一方面径流通过增大河口沿程的余水位、水深以及摩擦项中的水深项, 减小潮波衰减率, 使潮波振幅趋于增大。而河床下切以及河口地形的辐聚效应增强, 使潮波能量汇聚, 沿程潮波衰减率小, 有利于潮波向上游传播。因此, 通过研究潮波振幅、余水位及其空间梯度值的变化, 可以定量分析不同外部动力因素(径潮动力边界及地形边界等)对潮波传播的影响程度, 从而揭示河口区径流影响下的潮波传播过程及机制。
国内外学者对长江河口径流影响下的潮波传播过程及机制进行了一系列研究, 成果丰硕。例如, 基于长江感潮河段的潮位及流量数据, 分析潮波传播与径流的关系, 结果表明越往上游感潮河段的潮波传播特征值(如潮差、余水位等)的季节性变化越明显(刘新成等, 1999; 李国芳等, 2006)。径潮相互作用的强弱也影响了长江河口潮区界、潮流界和滞流点的移动, 上游河段径流作用强, 靠近河口的区域潮汐动力作用强, 潮区界距离上游的距离与流量输入呈正相关关系, 与下游潮流上溯强弱呈负相关关系(黄李冰等, 2015; 路川藤等, 2016; 石盛玉等, 2018; 刘鹏飞等, 2018)。径流输入相当于增加涨潮阻力, 使潮波传播能量损耗增大, 导致潮波衰减增加(欧素英等, 2016), 感潮河段的潮能也相应减小。但在径流主导的区域由于回水效应使得向陆方向的水位坡度增大, 余水位及相应的水深值随流量增大而增加, 季节性变化显著(Cai et al, 2014a, 2014b, 2016)。另外, 研究表明潮波在长江口北支的喇叭形河道往上游传播时潮差本应持续增加, 但在径流顶托、河道辐聚和底床摩擦的共同作用下潮差出现先增大后减小的规律(徐汉兴, 1990; 宋永港等, 2011)。郭磊城等(2017)通过谱分析方法研究南京、徐六泾和牛皮礁3个潮位站不同分潮的传播变化规律, 指出潮波以江阴潮位站为界, 上游为径流优势段, 下游为潮流优势段, 不同动力优势河段潮的波振幅对径流的响应不同。
综上所述, 径流和径潮相互作用对长江乃至世界其它河口的潮波传播起着主导作用, 因此对潮波传播的机制分析仍有不少值得深入探讨的地方。本文基于长江河口天生港至芜湖感潮河段的逐日高、低潮位资料及上游大通水文站的逐日流量数据, 重点分析径流影响下不同河段的潮波衰减率和余水位坡度的时空变化特征。在此基础上, 采用Cai等(2016)提出的一维水动力解析模型反演长江河口主要潮波变量的时空变化, 进而揭示长江河口潮波传播及径潮相互作用的过程及机制。
1 研究区域与数据长江是我国最长(近6300km)亦是水量最丰富(约占我国径流量的36%)的河流(如图 1a所示), 其下端长江河口为典型的径潮相互作用区域。据长江河口上游控制水文站(大通站)的资料统计, 其多年平均流量为28700m3/s, 其中最大日均流量达92600m3/s, 最小日均流量为4260m3/s(夏云峰等, 2010), 流量季节性变化显著。长江河口每日有两次涨潮两次落潮, 半日潮特征显著, 且口外为正规半日潮而口内为不正规半日浅海潮(沈焕庭等, 1979)。长江河口是一个中潮河口, 其拦门沙附近的中浚站多年平均潮差为2.67m, 最大潮差为4.62m (Zhang et al, 2012)。
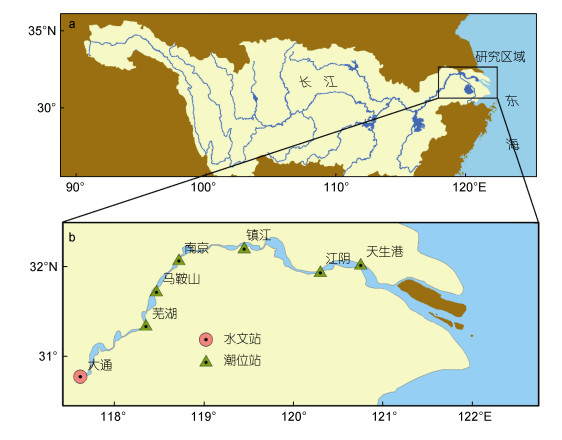 |
| 图 1 长江(a)及长江河口(b)概化示意图 Fig. 1 Sketch of the study area: Changjiang (Yangtze) River(a) and its estuary (b) |
本文重点探讨长江河口主干的潮波传播过程及机制, 所用水文数据取自《长江流域水文资料-长江下游干流区》第6卷第6册中天生港、江阴、镇江、南京、芜湖、马鞍山6个潮位站2007—2009年逐日高、低潮位数据及相应时段大通站的逐日流量数据。图 2为由长江河口沿程6个潮位站的月均振幅和余水位随流量变化图, 可以发现天生港、江阴两站的潮波振幅和余水位在年内没有明显的洪枯季变化, 而镇江、南京、马鞍山和芜湖4个站点的振幅和余水位表现出明显的洪枯季变化。本文将天生港至江阴河段简称为下段, 镇江、南京、马鞍山和芜湖简称为上段。从空间上看, 潮波振幅在口门处最大, 往上游逐渐减小。余水位则相反, 口门处最小, 往上游逐渐增大。从时间上看, 各站潮波振幅具有明显的周期性变化, 但上、下段差异显著, 即随着流量增加, 下段两个站点的潮波振幅不存在明显的季节性变化(洪枯季平均振幅之差小于0.05m), 而上段四个站点的潮波振幅随着流量增大而显著减小, 季节性变化明显(洪枯季平均振幅之差大于0.1m)。
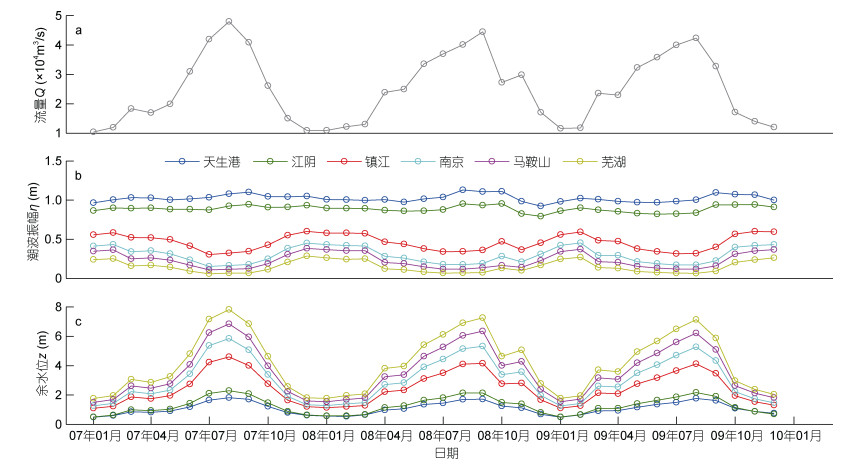 |
| 图 2 2007—2009年大通站月均流量(a)、长江沿程各站点月均潮波振幅(b)与月均余水位(c) Fig. 2 Temporal variation of the monthly average river discharge at Datong Station (a), the monthly average tidal amplitude (b), and residual water level (c) in the Changjiang River estuary |
为分析长江河口潮波传播的时空变化特征, 本文采用逐潮平均数据, 即在原始数据中选取同一潮周期内相邻的低潮位(HHW)和高潮位(HLW), 每天两组数据分别统计计算。高低潮位之差即为潮差, 振幅为潮差的一半, 即振幅的表达式为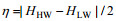
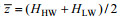
潮波衰减率定义为两潮位站间单位潮波振幅的振幅变化率:
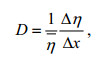 (1)
(1)其中, 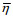
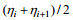
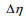
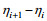
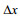
水位坡度定义为余水位随距离的变化率:
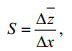 (2)
(2)其中, 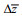

通过数理统计方法得出潮波传播时空变化的一般规律之后, 进一步采用Cai等(2016)提出的考虑径流影响的一维潮波传播解析模型, 对长江河口(天生港至芜湖)近500km感潮河段的潮波传播过程及机制进行探讨。解析模型采用概化地形, 河口的横截面积及河宽采用公式(3)和公式(4)表示:
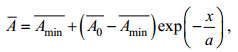 (3)
(3)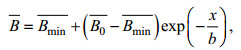 (4)
(4)其中, A和B表示潮平均的河道横截面积和宽度,
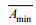
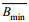
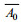
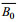
基于2007年长江河口实测的横截面积和河宽数据(相对国家85高程基准), 通过ArcGIS软件生成数字高程模型(DEM), 并提取沿程断面0m等深线以下的断面面积和河宽, 通过公式(3)和公式(4)率定得出相应的地形参数, 作为模型的地形边界(见表 1)。模型下边界采用天生港的潮波振幅, 上边界为相应时段大通站的流量数据。
| 地形参数 | 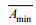 (m2), (m2),
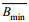 (m) (m)
|
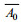 (m2), (m2),
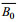 (m) (m)
|
a, b (km) |
| 横截面积 | 12135 | 51776 | 150.55 |
| 河宽 | 2005 | 6735 | 43.59 |
注: 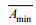 和 和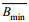 表示收敛至上游河段的最小横截面积和宽度, 表示收敛至上游河段的最小横截面积和宽度, 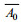 和 和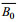 表示口门处的横截面积和宽度, a和b表示横截面积和宽度的收敛长度 表示口门处的横截面积和宽度, a和b表示横截面积和宽度的收敛长度 |
|||
解析模型的输入为4个无量纲参数:潮波振幅系数ζ(代表口门潮汐动力的大小), 河口形状系数γ(代表河道横截面积的收敛程度), 摩擦系数χ(代表底床摩擦耗散), 径流量系数φ(代表上游径流动力的影响)。将得到的4个无量纲变量代入4个隐式方程(见表 2)可得描述潮波传播变化的4个无量纲潮波变量, 即衰减系数δ、流速振幅系数μ、波速系数λ、高潮位与高潮憩流或低潮位与低潮憩流之间的相位差ε(见表 2)。表 2中, ω=2π/T表示潮波频率, T为潮周期, g表示重力加速度, 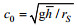

|
图 3为沿程各河段的潮波衰减率和余水位坡度随流量的变化图。由图 3可见沿程各河段潮波衰减率均为负值, 其中靠近口门的天生港-江阴段的衰减率的绝对值最小(表明潮波衰减作用最弱), 江阴-马鞍山段的衰减率的绝对值大体与下段相同但均比天生港-江阴段大(表明潮波衰减作用较强), 而马鞍山-芜湖段的衰减率的绝对值最大(表明潮波衰减作用最强)。余水位坡度随着流量的增大而增大, 且上游余水位坡度比下游大。
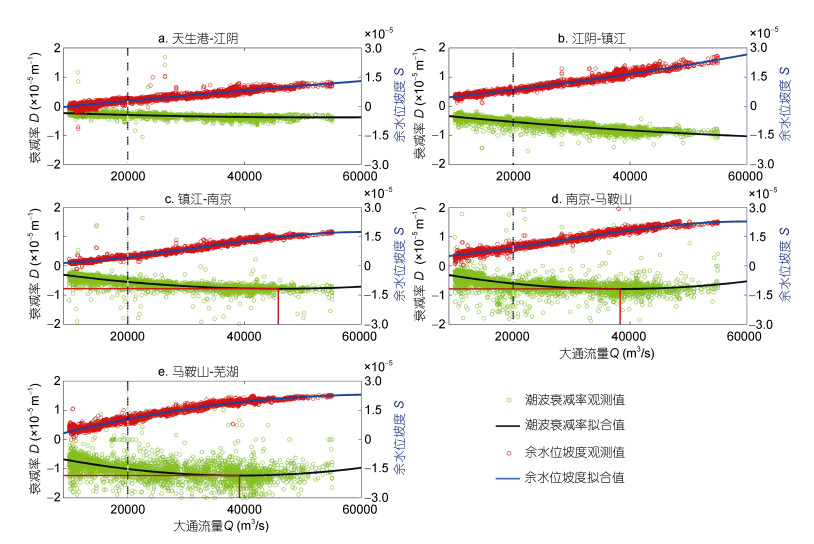 |
| 图 3 长江河口沿程各河段潮波衰减率与余水位坡度随流量的变化 Fig. 3 Variations of tidal damping and residual water level slope with river discharge in the Changjiang River estuary in the sectors of Tianshenggang-Jiangyin (a), Jiangyin-Zhenjiang (b), Zhenjiang-Nanjing (c), Nanjing-Ma'anshan (d) and Ma'anshan-Wuhu (e) 注:黑色虚线表示洪枯季分界线, 红色实线表示衰减率的阈值 |
由图 3还可见潮波衰减率与余水位坡度随流量的变化并非线性, 特别是在洪季有大流量下泄情况下, 上游河段两特征潮波变量随流量变化的斜率明显减小。采用三次多项式拟合出流量与各河段潮波变量的关系:
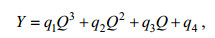 (5)
(5)其中, Y表示潮波衰减率(D)或者余水位坡度(S), Q表示大通站的流量, qi (i=1, 2, 3, 4)为多项式回归系数。由图 2可见, 镇江站以下河段的三次多项式拟合结果依然呈现出较明显的线性相关, 而在镇江以上河段潮波衰减率和余水位坡度随流量的变化呈非线性, 且存在一个流量阈值, 对应潮波衰减率的极小值和余水位坡度的极大值。对拟合出的三次多项式进行求导, 可估算出极值条件下的流量阈值(见表 3)。潮波衰减率在南京-芜湖河段对应的流量阈值小于40000m3/s, 而镇江-南京段其阈值流量达到45795m3/s。当流量超过阈值时潮波衰减率呈增大趋势, 潮波衰减作用有所减弱。镇江以下河段由于受流量影响相对较小, 其潮波衰减率在正常流量条件下难以达到最小值。余水位坡度亦有类似的现象, 其出现极大值所对应的流量阈值如表 3所示。天生港-镇江河段在正常流量条件下没有出现极大值, 而镇江至芜湖河段的流量阈值约为59000—65000m3/s。
| 特征量 | 极值 | 天生港-江阴 | 江阴-镇江 | 镇江-南京 | 南京-马鞍山 | 马鞍山-芜湖 |
| 潮波衰减率 | Qmax (m3/s) | 53811 | 96245 | 45795 | 38313 | 39142 |
| Dmin (m-1) | -3.79×10-6 | -11.67×10-6 | -7.82×10-6 | -7.90×10-6 | -12.36×10-6 | |
| 余水位坡度 | Qmax(m3/s) | - | - | 60265 | 59907 | 63161 |
| Smax(-) | - | - | 1.74×10-5 | 2.28×10-5 | 2.31×10-5 | |
| 注: Qmax:潮波衰减率与余水位坡度的极值所对应的大通站流量阈值; Dmin:潮波衰减率的极小值; Smax:余水位坡度的极大值; Smax:天生港-江阴、江阴-镇江的余水位坡度; -:无法达到阈值 | ||||||
以上统计结果表明, 潮波衰减率和余水位坡度随流量变化存在一个流量阈值效应, 即超过一定的流量阈值, 潮波衰减率绝对值和余水位坡度随流量增大反而有所减小。计算结果还表明镇江以上河段潮波衰减率和余水位坡度在正常洪峰流量条件下出现明显的极小值和极大值, 而镇江以下河段由于受径流动力影响较小, 阈值效应不明显。
4 潮波传播机制分析为探讨不同河段潮波衰减率和余水位坡度极值对应的流量阈值的形成变化过程及径潮动力的非线性作用机制, 本文采用一维水动力解析模型(Cai et al, 2015)反演长江河口2007—2009年沿程主要潮波变量的形成变化过程。解析模型的率定参数为曼宁摩擦系数的倒数K, 天生港站往上游42km的河段模型率定的K值为80m1/3/s, 而42km以上的河段K值为55m1/3/s。下段的K值较大与该段动力为潮流优势有关, 底质以淤泥为主, 上游的K值较小与该段动力为河流优势有关, 底质以细砂和砂为主(Cai et al, 2016, 2019)。模型计算出的潮波振幅和余水位与实测值的线性相关系数R2均大于0.9(见图 4), 表明解析模型可较好的反演出本研究区域的潮波变化特征。
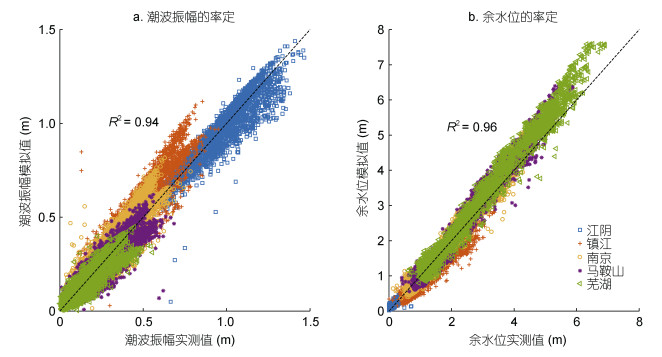 |
| 图 4 解析模型的计算值与实测值的比较 Fig. 4 Comparison between analytically computed results and observations |
图 5为解析模型计算得出的不同流量条件下(对应2007—2009时段)的潮波振幅、余水位及其相应梯度值的沿程变化等值线图。由图 5a可知, 流量越大潮波振幅衰减得越快, 当流量为10000m3/s时, 潮波振幅在距离口门200km处衰减约65%, 而当流量为55000m3/s时, 潮波振幅在相同距离内衰减约86%。由图 5b可知潮波衰减率的极小值(对应的潮波衰减作用最强)出现在200—500km的河段上, 即潮波衰减率存在位置阈值, 且这一位置随着流量增大逐渐向外海推移, 当流量为10000m3/s时, 对应的极小值出现在490km, 而当流量为55000m3/s时, 该极值对应的位置在280km。在同一河段上潮波衰减率随流量的变化也是非线性的, 即存在流量阈值。在200km处潮波衰减率在35000m3/s流量时达到极小值, 而在500km处流量为20000m3/s时潮波衰减率达到极小值, 说明上游河段达到阈值所需的流量较下游小。图 5c显示余水位的时空变化等值线图, 可见余水位的增幅与流量呈正相关关系, 当流量为10000m3/s时, 500km处的余水位仅为2m, 而当流量为55000m3/s时, 500km处余水位可达11m。由图 5d可见余水位坡度的位置阈值与潮波衰减率对应的位置相似, 当流量为10000m3/s时, 余水位坡度在490km处才达到极大值, 而当流量为55000m3/s时, 极大值对应位置在280km。这主要是因为潮平均条件下余水位坡度主要与摩擦项相平衡(Cai et al, 2016), 坡度越大对应的有效摩擦越大, 因而潮波衰减作用越强。余水位坡度也存在流量阈值, 且与潮波衰减率相似也有上游阈值流量小于下游的特征, 但上游流量阈值所对应的余水位坡度比下游小。在500km处流量阈值约为40000m3/s, 对应的余水位坡度为1.5×10-5, 而在300km处流量阈值约为50000m3/s, 对应的余水位坡度为2.5×10-5。
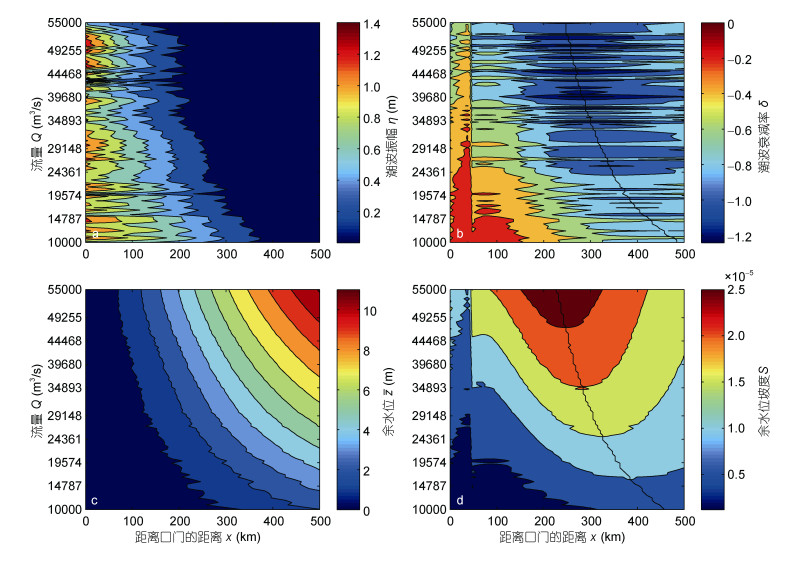 |
| 图 5 潮波振幅η(a)、潮波衰减率δ(b)、余水位Z (c)及余水位坡度S(d)随距离和流量变化的等值线图 Fig. 5 Profiles of longitudinal variations vs different river discharge in the tidal amplitude η(a), the tidal damping (b), the residual water level Z (c) and the residual water level slope S (d) 注:黑色粗实线表示该流量条件下的位置阈值 |
图 6为解析模型计算的潮波传播速度和高潮位与高潮憩流(或低潮位与低潮憩流)的相位差的时空变化图。由图 6a可见传播速度极小值亦存在明显的位置阈值与流量阈值。传播速度极小值的位置随着流量增大逐渐往下游推移, 如在10000m3/s流量条件下传播速度在490km处达到极小值, 而在55000m3/s流量条件下传播速度在200km处达到极小值。另一方面, 传播速度与潮波衰减率类似, 亦有越往上游达到极小值所需的流量阈值越小的特点, 如在200km处传播速度在49000m3/s流量时达到极小值, 而在500km处在10000m3/s流量时即可达到极小值。可见传播速度与潮波衰减率具有明显的正相关, 即衰减率越小(衰减效应越强)对应的传播速度越小。而图 6b显示相位差的极大值位置与传播速度极小值位置基本对应, 当流量为10000m3/s时相位差极大值位于410km, 而当流量为55000m3/s时极大值向外海推移至100km。可见相位差与传播速度呈负相关关系, 这主要是由于相位差越大, 表示高潮位与高潮憩流所间隔的时间越长, 潮波传播速度越小。
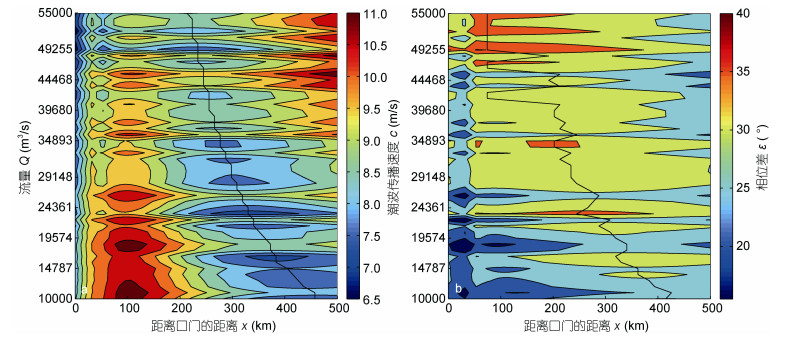 |
| 图 6 潮波传播速度(a)和高潮位与高潮憩流(或低潮位与低潮憩流)的相位差(b)随距离和流量变化等值线图 Fig. 6 Profiles of longitudinal variations vs different river discharge in the wave celerity (a), the phase lag between high water and high water slack (or low water and low water slack)(b) 注:黑色粗实线表示该流量条件下的位置阈值 |
通过对潮波衰减率、余水位坡度及传播速度等值线图的分析, 结果表明这些潮波变量在空间和时间上分别有位置阈值和流量阈值。潮波的衰减受余水位坡度影响, 余水位坡度越大等同于潮波传播受到的有效摩擦越大, 潮波衰减作用越强, 因而潮波传播速度越小。而影响河口潮波传播的主要因素除有效摩擦外还有河口形状, 在一维水动力解析模型中采用河口形状参数γ表征河口的辐聚程度, 由表 2定义可知, γ大于0则河口呈辐聚形, 且γ越大表示辐聚程度越强(河道横截面积减小得越快)。
图 7显示河口形状参数γ与水深h随流量的沿程变化等值线图。由图 7a可见γ极大值位于200km以下河段, 这是由于此区域地形(即横截面积)辐聚程度大。而在200km以上河段出现γ等于0的位置, 表示此河段横截面积基本不变。γ为0的位置与上述各潮波变量(潮波衰减率、余水位坡度和潮波传播速度)的位置阈值基本一致, 说明各潮波变量达到位置阈值时的河段地形辐聚程度最小, 余水位坡度达到极大值, 而与其等价的有效摩擦使潮波衰减率达到极小值。图 7b为水深的时空变化图, 黑色实线表示不同流量下水深出现极小值的位置。可见由于上游河段存在较强的回水效应, 水深出现极小值。而水深的极小值对应余水位坡度的极大值, 说明余水位坡度的阈值现象源于余水位变化引起的水深变化。水深达到极小值时河道横截面积基本不变, 对应γ为0的位置。河口形状参数γ在达到0后还将继续减小, 这是由于水深增加导致横截面积增大, 使该河段地形由辐聚转为辐散。但水深导致的河口辐散程度较小, 河口形状参数仅为-0.05, 地形辐散导致的衰减不足以弥补有效摩擦的减小, 因而使潮波衰减率反而有所增大(衰减作用减弱)。
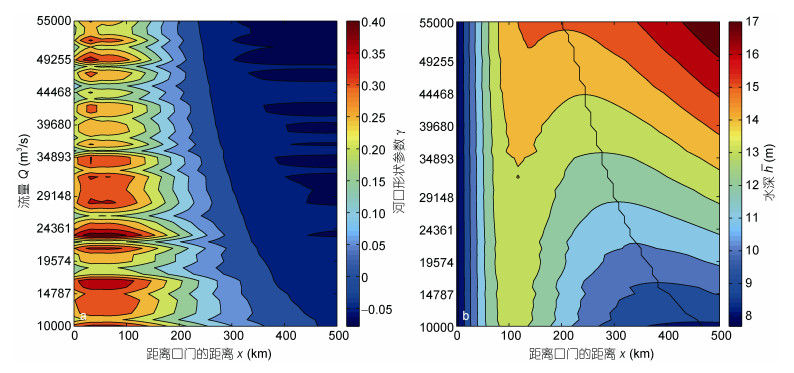 |
| 图 7 河口形状参数γ(a)和水深h(b)随距离和流量变化等值线图 Fig. 7 Profiles of longitudinal variations vs different river discharges in the estuary shape number γ (a) and the water depth h(b) 注:黑色粗实线表示该流量条件下的位置阈值 |
基于长江河口沿程6个潮位站2007—2009年的逐日高低潮位数据, 统计分析潮波衰减率和余水位坡度时空变化特征, 指出随着流量增大, 潮波衰减率减小(衰减作用增强)而余水位坡度增大, 且江阴以上河段衰减率和余水位坡度随流量的季节性变化较下游明显。但是这两个潮波特征量随流量的变化呈非线性, 存在流阈值效应, 即超过一定流量值潮波特征量发生趋势逆转, 这种现象在上游河段尤为明显。为探讨流量阈值现象并揭示径潮相互作用的动力学机制, 本文采用考虑径流作用的一维水动力解析模型对长江河口主要潮波变量的时空变化进行反演, 得到如下主要结论:
(1) 潮波衰减率和余水位坡度由于径潮动力非线性作用存在位置与流量阈值效应。位置阈值随着流量增大逐渐向下游推移, 而流量阈值越往上游值越小。
(2) 余水位坡度主要与潮波传播的有效摩擦相平衡。在达到位置或流量阈值后余水位坡度逐渐减小, 潮波传播所受的有效摩擦减小, 导致潮波衰减率增大(衰减作用减弱), 相应的传播速度逐渐增大。
(3) 河口潮波传播是河口地形辐聚与有效摩擦综合作用的结果。潮波衰减率和余水位坡度的阈值效应主要是由于余水位变化引起水深变化, 进而影响控制径潮相互作用的河口形状系数和有效摩擦(即余水位坡度)。
致谢 本研究所用水文资料由水利部长江水利委员会水文局提供, 地形资料由上海华东师范大学河口海岸学国家重点实验室提供, 特此致谢。
石盛玉, 程和琴, 玄晓娜, 等. 2018. 近十年来长江河口潮区界变动. 中国科学:地球科学, 48(8): 1085-1095 |
石盛玉, 程和琴, 郑树伟, 等. 2017. 三峡截流以来长江洪季潮区界变动河段冲刷地貌. 海洋学报, 39(3): 85-95 DOI:10.3969/j.issn.0253-4193.2017.03.008 |
朱建荣, 鲍道阳. 2016. 近60年来长江河口河势变化及其对水动力和盐水入侵的影响Ⅰ. 河势变化.海洋学报, 38(12): 11-22 |
刘锋, 田向平, 韩志远, 等. 2011. 近四十年西江磨刀门水道河床演变分析. 泥沙研究, (1): 45-50 |
刘鹏飞, 路川藤, 罗小峰, 等. 2018. 基于数学模型的长江潮流界变化特性. 科学技术与工程, 18(3): 346-353 DOI:10.3969/j.issn.1671-1815.2018.03.056 |
刘新成, 杨清书. 1999. 长江河口段潮差变化研究. 华东师范大学学报(自然科学版), (2): 89-94 |
李国芳, 谭亚, 张秀菊. 2006. 感潮河段上游流量对潮位预报的影响. 河海大学学报(自然科学版), 34(2): 144-147 DOI:10.3321/j.issn:1000-1980.2006.02.007 |
李秉天, 王永刚, 魏泽勋, 等. 2015. 渤海主要分潮的模拟及地形演变对潮波影响的数值研究. 海洋与湖沼, 46(1): 9-16 |
沈焕庭, 潘定安. 1979. 长江河口潮流特性及其对河槽演变的影响. 上海师范大学学报:自然科学版, (1): 133-144 |
宋永港, 朱建荣, 吴辉. 2011. 长江河口北支潮位与潮差的时空变化和机理. 华东师范大学学报(自然科学版), (6): 10-19 DOI:10.3969/j.issn.1000-5641.2011.06.002 |
陈吉余, 陈沈良. 2002. 中国河口海岸面临的挑战. 海洋地质动态, 18(1): 1-5 DOI:10.3969/j.issn.1009-2722.2002.01.001 |
陈吉余, 徐海根. 1995. 三峡工程对长江河口的影响. 长江流域资源与环境, 4(3): 242-246 |
欧素英, 田枫, 郭晓娟, 等. 2016. 珠江三角洲径潮相互作用下潮能的传播和衰减. 海洋学报, 38(12): 1-10 DOI:10.3969/j.issn.0253-4193.2016.12.001 |
欧素英, 杨清书. 2004. 珠江三角洲网河区径流潮流相互作用分析. 海洋学报, 26(1): 125-131 DOI:10.3321/j.issn:0253-4193.2004.01.014 |
欧素英, 杨清书, 杨昊, 等. 2017. 河口三角洲径流和潮汐相互作用模型及应用. 热带海洋学报, 36(5): 1-8 |
胡光伟, 毛德华, 李正最, 等. 2014. 三峡工程运行对洞庭湖与荆江三口关系的影响分析. 海洋与湖沼, 45(3): 453-461 |
袁丽蓉, 杨清书, 谢莉莉等, 2013.人类活动干扰下伶仃洋河口湾地形演变趋势变化.见: 中国海洋工程学会.第十六届中国海洋(岸)工程学术讨论会(下册).大连: 中国海洋工程学会, 6
|
夏云峰, 闻云呈, 梁婷. 2010. 长江下游典型代表性潮型选择研究初探. 水道港口, 31(5): 501-505 DOI:10.3969/j.issn.1005-8443.2010.05.047 |
徐汉兴. 1990. 长江口潮位变化规律及其工程应用. 海洋与湖沼, 21(4): 311-319 |
郭磊城, 朱春燕, 何青, 等. 2017. 长江河口潮波时空特征再分析. 海洋通报, 36(6): 652-661 |
黄李冰, 李义天, 韩剑桥, 等. 2015. 径潮动力对长江河口滞流点的影响. 水科学进展, 26(4): 572-578 |
蒋陈娟, 杨清书, 戴志军, 等. 2012. 近几十年来珠江三角洲网河水位时空变化及原因初探. 海洋学报, 34(1): 46-56 |
谢丽莉, 刘霞, 杨清书, 等. 2015. 人类活动驱动下伶仃洋洪季大潮水沙异变. 泥沙研究, (3): 56-62 |
路川藤, 罗小峰, 陈志昌. 2010. 长江口不同径流量对潮波传播的影响. 人民长江, 41(12): 45-48 DOI:10.3969/j.issn.1001-4179.2010.12.012 |
路川藤, 罗小峰, 陈志昌. 2016. 长江潮流界对径流、潮差变化的响应研究. 武汉大学学报(工学版), 49(2): 201-205 |
鲍道阳, 朱建荣. 2017a. 近60年来长江河口河势变化及其对水动力和盐水入侵的影响Ⅱ. 水动力.海洋学报, 39(2): 1-15 |
鲍道阳, 朱建荣. 2017b. 近60年来长江河口河势变化及其对水动力和盐水入侵的影响Ⅲ. 盐水入侵.海洋学报, 39(4): 1-15 |
Abdullah A D, Gisen J I A, Van Der Zaag P et al, 2016. Predicting the salt water intrusion in the Shatt al-Arab estuary using an analytical approach. Hydrology and Earth System Sciences, 20: 4031-4042 DOI:10.5194/hess-20-4031-2016 |
Cai H Y, Savenije H H G, Jiang C J, 2014b. Analytical approach for predicting fresh water discharge in an estuary based on tidal water level observations. Hydrology and Earth System Sciences, 18: 4153-4168 DOI:10.5194/hess-18-4153-2014 |
Cai H Y, Savenije H H G, Jiang C J et al, 2016. Analytical approach for determining the mean water level profile in an estuary with substantial fresh water discharge. Hydrology and Earth System Sciences, 20: 1177-1195 DOI:10.5194/hess-20-1177-2016 |
Cai H Y, Savenije H H G, Garel E et al, 2019. Seasonal behaviour of tidal damping and residual water level slope in the Yangtze River estuary:identifying the critical position and river discharge for maximum tidal damping. Hydrology and Earth System Sciences, 23(6): 2779-2794 DOI:10.5194/hess-23-2779-2019 |
Cai H Y, Savenije H H G, Toffolon M, 2013. The effect of river discharge on tidal dynamics in three alluvial estuaries: the Scheldt, Modaomen and Yangtze Cases. In: Proceedings of HP1, IAHS-IAPSO-IASPEI Assembly. Gothenburg, Sweden: IAHS Publ., 39-47
|
Cai H Y, Savenije H H G, Toffolon M, 2014a. Linking the river to the estuary:influence of river discharge on tidal damping. Hydrology and Earth System Sciences, 18: 287-304 DOI:10.5194/hess-18-287-2014 |
Cai H Y, Savenije H H G, Yang Q S et al, 2012. Influence of river discharge and dredging on tidal wave propagation:Modaomen estuary case. Journal of Hydraulic Engineering, 138(10): 885-896 DOI:10.1061/(ASCE)HY.1943-7900.0000594 |
Guo L C, Van Der Wegen M, Jay D A et al, 2015. River-tide dynamics:exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. Journal of Geophysical Research:Oceans, 120(5): 3499-3521 DOI:10.1002/2014JC010491 |
Horrevoets A C, Savenije H H G, Schuurman J N et al, 2004. The influence of river discharge on tidal damping in alluvial estuaries. Journal of Hydrology, 294(4): 213-228 DOI:10.1016/j.jhydrol.2004.02.012 |
Pan H D, Lv X Q, Wang Y Y et al, 2018. Exploration of tidal-fluvial interaction in the Columbia river estuary using S_TIDE. Journal of Geophysical Research:Oceans, 123(9): 6598-6619 DOI:10.1029/2018JC014146 |
Zhang E F, Savenije H H G, Chen S L et al, 2012. An analytical solution for tidal propagation in the Yangtze Estuary, China. Hydrology and Earth System Sciences, 16: 3327-3339 DOI:10.5194/hess-16-3327-2012 |
Zhang F Y, Sun J, Lin B L et al, 2018. Seasonal hydrodynamic interactions between tidal waves and river flows in the Yangtze Estuary. Journal of Marine Systems, 186: 17-28 DOI:10.1016/j.jmarsys.2018.05.005 |
Zhang M, Townend I H, Cai H Y et al, 2016. Seasonal variation of tidal prism and energy in the Changjiang River estuary:a numerical study. Chinese Journal of Oceanology and Limnology, 34(1): 219-230 DOI:10.1007/s00343-015-4302-8 |
 2019, Vol. 50
2019, Vol. 50


