中国海洋湖沼学会主办。
文章信息
- 曾侃, 李恒宇. 2019.
- ZENG Kan, LI Heng-Yu. 2019.
- Gerris在海洋大振幅内孤立波数值模拟中的应用
- APPLICATION OF GERRIS IN NUMERICAL SIMULATION OF OCEAN LARGE-AMPLITUDE INTERNAL SOLITARY WAVES
- 海洋与湖沼, 50(4): 799-810
- Oceanologia et Limnologia Sinica, 50(4): 799-810.
- http://dx.doi.org/10.11693/hyhz20181200283
文章历史
-
收稿日期:2018-12-02
收修改稿日期:2019-03-17
海洋内波是密度层化海水内部的一种波动现象。由于内波的恢复力是由层化海水密度差导致的约化重力, 相比于作为海表面波恢复力的重力而言, 只有其千分之一的量级, 所以海洋内波的振幅比海浪大得多而其直接引起的海表面起伏却几乎为零。例如, Osborne等(1980)在安达曼海观测到振幅约60m的内孤立波; Tessler等(2012)在苏禄海观测到振幅约40m的内孤立波; Xie等(2013)在比斯开湾观测到振幅约40—70m的内孤立波; Klymak等(2006)及Lien等(2014)在南海观测到约为170m振幅的内孤立波。
海洋内波几乎不引起海表起伏的特性使其难以通过现场观测手段发现和定位, 而卫星遥感观测, 尤其是卫星合成孔径雷达(Synthetic Aperture Radar, SAR)观测, 可以获得清晰反映内波特征的图像, 便于发现和定位内波(孙丽娜等, 2018)。正是遥感观测帮助人们建立起了全球海域内波分布的清晰图景, 让人们意识到海洋内波在世界海域范围内的普遍存在(Jackson, 2004)。在SAR图像上看到的内波通常是内孤立波或者内孤立子。尽管存在多种内孤立波的生成机制, 但目前普遍认为内孤立波主要由正压潮与地形(如海峡, 海山等)的相互作用产生的内潮波在传播过程中逐渐裂变而成(方欣华等, 2005; 王金虎等, 2016)。
从遥感获得的内波图像特征来获得内波的垂直特征却并不直接。基于内波孤立波的非线性理论, 内孤立波的半宽度与振幅存在某种函数关系。这依赖于对内波动力学特征的准确描述(Zheng et al, 2001; Zhang et al, 2016)。
在内波理论方面, 最简单的是在弱非线性弱频散假设下的KdV方程, 它能很好地描述浅水分层流体中的小振幅内波。根据上下两层水厚度的不同情况, 该方程被推广到了无限深海的Benjamin-Ono方程(Benjamin, 1967; Ono, 1975)和有限深海的Joseph方程(Joseph, 1977)。受制于弱非线性假设的约束, 上述KdV类方程不适于描述大振幅内波。在KdV基础上引入三阶非线性项的eKdV方程使得这一情况有所改善, 它可以描述实际海洋中观测到的波形变宽且有一个平底波谷的情况, 且在振幅的适用范围上比KdV更大(Helfrich et al, 2006)。进一步, Miyata(1988)提出了完全非线性的Miyata方程, 可以描述大振幅内波, 但其频散项依然只有一阶, 所以只适于描述长波, 且只能用于两层流体。在数值计算方面, 主要分为两类。一类为直接数值求解内孤立波理论方程, 如Liu等(1998)运用变系数KdV方程来数值计算南海和东海海域的内波从深水向浅水传播过程中的结构变化; 蔡树群等(2001)基于规则化长波(RLW)方程, 来探讨南海北部内波的结构特征和演变; 张善武等(2015)运用变系数eKdV方程数值求解中国南海大振幅内孤立波的振幅和波宽等特征参数。另一类基于N-S(Navier-Stokes)方程组、Euler方程组的全域离散化网格进行计算, 如Vlasenko等(2000)基于Euler方程组探讨了稳态大振幅内孤立波的结构; Zhang等(2014)基于Euler方程利用有限体积法建立了一个适应水深变化的二维内波数值模式, 并在等深水域求解等密度线随时间变化的数值解; Shen等(2006)基于N-S方程组建立内波二维数值模型, 并进行内波速度场分析, 从而根据SAR成像原理来成像仿真等。Stastna等(2002)用从Euler方程组推导的描述完全非线性内波的DJL(Dubreil-Jacotin-Long)方程讨论了在非均匀背景流场下浅水层化海洋中内孤立波振幅的上限; Preusse等(2012)也用DJL方程研究了不同背景层化下内孤立波振幅的上限以及内波破碎机制。鉴于DJL的完全非线性属性, 本文将之也归到第二类中。
由于内波KdV理论模型及其变种是基于各种不同的假设条件下简化导出, 在定量模拟实际海洋的内波时存在较大误差, 所以当以模拟现实作为需求时, 采用基于N-S方程组、Euler方程组或DJL方程进行的数值模拟更为可靠, 可以获得实测连续海水层化条件下的完全非线性内孤立波解。然而数值模拟的主要问题是计算量大, 计算时间长。为了准确反映海洋中的密度层化, 层化区的网格必须足够密集。若采用均匀网格, 必然导致大计算量。在内波模拟中, 数值模型为降低计算量, 常在不同的维度设定不同的分辨率(Vlasenko et al, 2000, 2002, 2010; Du et al, 2008; Zhang et al, 2014)。而本文采用的Gerris软件可通过自适应网格来降低模型的计算量。Gerris根据涡度、密度梯度等物理量在模型运行期间动态调节局部网格尺寸, 在保证二阶计算精度的前提下加快计算速度。实验表明, 用Gerris实现的Euler模型获得一次稳定内孤立波解的时间约7min, 从而可以当做一个方便的完全非线性连续层化内孤立波计算工具。
基于KdV理论模型从SAR图像提取的内孤立波半宽度反演的振幅常常被低估甚至严重低估。采用连续层化的KdV模型比两层模型有一定改善(曾侃, 2002)。更进一步的改善是采用高阶非线性方程(Xue et al, 2013)。然而Euler模型的模拟结果表明除了内波半宽度与振幅的关系不同外, 内波半宽度还随水层深度增加而增大, 而非KdV理论模型所述那样上下一致, 因此基于从SAR图像上提取的内波在海表面的半宽度再利用KdV理论模型或其变种反演内波振幅的方法存在缺陷。
本文按如下方式组织:第一节介绍用Gerris实现的用于内孤立波数值模拟的二维Euler模型的基本特征以及进行内波数值拟的参数设置方法; 第二节讨论了用Gerris实现的Euler数值模型与用KdV模型获得的大振幅内孤立波的结构差异; 第三节用现场的内孤立波观测数据对Gerris实现的Euler模型的有效性进行验证; 第四节总结了研究结果并讨论了其对SAR内波振幅反演的意义。为简化表述, 下文将“Gerris实现的Euler数值模型”简称为“Euler模型”。
1 模型与实验设置 1.1 模型与软件介绍本文采用的Euler数值模型是用新西兰水文和大气国家研究所Stephen博士开发的流体动力学开源软件Gerris建立的。Gerris是一个基于四叉树(三维是八叉树)动态自适应网格的偏微分方程组求解框架。
动态自适应网格技术是一种根据流场实际情况通过动态调整局部网格尺寸来减小计算量的技术。其基本原理是以一个或者多个物理量为判断准则, 动态决定网格是加密还是稀化(王亮等, 2015), 这可以在保证计算精度的同时有效提高计算速度。在流体力学数值模式应用中常采用涡度作为网格自适应控制的判断准则:
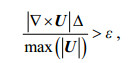 (1)
(1)其中, Δ为网格尺度, U为水质点的速度矢量, ε为自定义的阈值(0<ε<1)。当速度矢量满足公式(1)时, 网格进行加密, 反之, 网格稀化。在本文的内波模拟实验中, 还将密度梯度也作为一个判断准则。当同时定义了多个判断准则时, 其中任何一个准则得到满足均导致网格加密; 反之, 只当所有准则均不满足的情况才导致网格稀化(Popinet, 2003; Popinet et al, 2007)。在网格被动态调整后, Gerris再根据CFL条件来动态调节时间步长。
实际海洋中, 黏性的最大长度特征尺度在厘米量级, 而内波的水平特征尺度基本在百米到千米量级之间, 故可忽略流体黏性。本文关心的内孤立波属于高频内波, 可忽略地转效应。因此本文用于内波模拟的控制方程为在Bossinesq近似下且忽略地转效应的二维Euler方程组(Phillips, 1977)
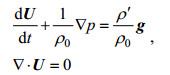 (2)
(2)其中, g=(0, -g)是重力加速度矢量, ρ0是作为密度参考量的海表面密度均值, ρ'是海水密度场ρ(x, z, t)与密度参考量的差。p是实际压强场与密度为ρ0的流体静压强的差。gρ'/ρ0是约化重力项, 它是内波的恢复力, 在模型设定中体现为源项。
1.2 模型初始化将Euler模型的初始流场设定为连续层化流体的内波KdV方程的一模态定形内孤立波解(Leonov et al, 1975)。
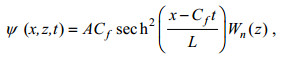 (3)
(3)其中, 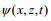
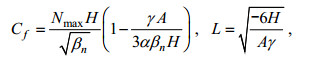 (4)
(4)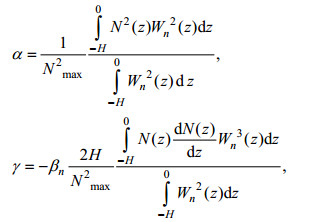 (5)
(5)其中, H为水深, N(z)为浮性频率剖面, Nmax是其最大值, βn和Wn(z)是Sturm-Liouville型边值问题(见公式(5))的本征值βn及对应的本征函数Wn(z)。n代表模态, 这里只考虑1模态。
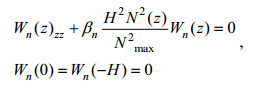 (6)
(6)若未扰动密度垂直剖面ρ0(z)已知, 并指定一个振幅A, 则可以计算出内波的流函数, 进而获得速度场和密度场:
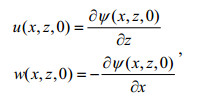 (7)
(7)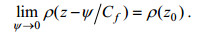 (8)
(8)模型的坐标系设为速度等于内波初始相速度Cf的移动坐标系, 使得内波在计算域内相对静止, 可减小计算域的长度从而降低计算量。移动坐标相当于在整个计算域引入了一个均匀的背景流场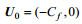
 (9)
(9)模型的左边界满足:
 (10)
(10)假设海表面满足刚盖近似, 海底平坦, 则上、下边界条件为:
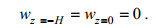 (11)
(11)当用KdV解设定模型的初始场后, 随着模型的运行, 初始波形将发生变化, 部分波成分被分离出来并被色散掉, 最终剩下的波形稳定部分便是该数值模型获得的稳定内孤立波解。稳定的判断条件是各物理量在20T时间内变化不超过0.1%, 其中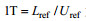
除自适应网格外, Gerris还可以通过多核并行处理来提高计算速度。测试表明, 使用Intel® Xeon(R) E5-2603 v3主频1.60GHz处理器进行8核并行处理, 获得一个内孤立波解的时间约为7min。这个计算效率使得将之当作一个可多次调用的内孤立波数值计算工具纳入到更复杂的应用框架成为可能。
2 Euler数值模型与KdV模型的比较本文采用Vlasenko(1994)提出的参数化浮性频率公式来描述海洋的主密跃层, 见公式(12)和图 1。
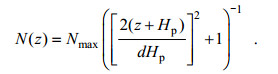 (12)
(12)
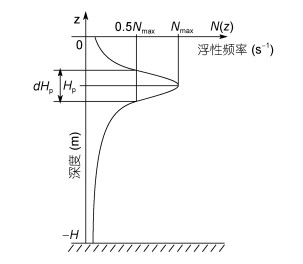 |
| 图 1 参数化浮性频率示意图(Vlasenko, 1994) Fig. 1 The profile of parametric buoyancy frequency (Vlasenko, 1994) 注: Nmax表示最大浮性频率, Hp表示密跃层的深度, dHp表示密跃层的厚度 |
公式(12)将密度剖面用密跃层的深度(Hp)、厚度(dHp)以及浮性频率最大值(Nmax)这3个物理意义明确的参量表示。采用参数化浮性频使得本征方程(5)有解析解, 见公式(14)(Vlasenko, 1994), 便于和Euler模型的数值解进行比较。
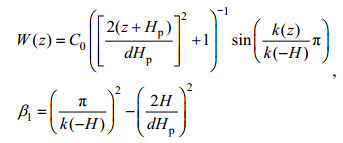 (13)
(13)其中, C0为使得W(z)最大值为1的归一化系数, 且
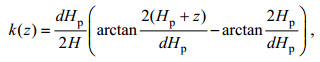 (14)
(14)另外, 根据浮性频率的定义
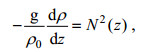 (15)
(15)可得到未扰动时参数化密度垂直剖面(曾侃, 2002):
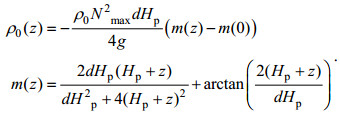 (16)
(16)其中ρ0为海表参考密度。
下面讨论在不同海水层化条件和不同振幅条件下的内孤立波结构特征。表 1按最大浮性频率由强到弱列出4种层化条件, 图 2是对应的密度剖面和浮性频率剖面。参数设定方法如下:首先固定海表密度为1000kg/m3, 水深为300m, 跃层深度Hp为35m, 再设定dHp为不同值, 然后调节相应的Nmax使得海底密度相同。
| 分层 | Nmax(s-1) | Hp (m) | dHp (m) |
| 1 | 0.03 | 35 | 35 |
| 2 | 0.0195 | 35 | 95 |
| 3 | 0.016 | 35 | 155 |
| 4 | 0.015 | 35 | 196.5 |
| 注: Nmax表示最大浮性频率, Hp表示密跃层的深度, dHp表示密跃层的厚度 | |||
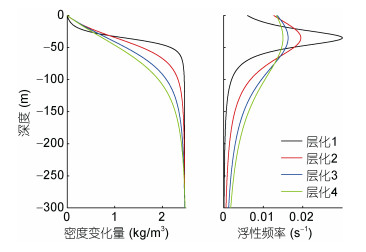 |
| 图 2 不同层化条件的密度和浮性频率剖面 Fig. 2 The density and buoyancy frequency profiles of different stratification conditions |
图 3为层化条件1时用Gerris模拟的内孤立波的演变图, 色标以ρ'的最大值归一化, 其中ρ'为密度变化量。图 3a—图 3d分别是0, 5, 10, 20T时刻的密度分布图, 它们给出了初始波形在Euler方程控制下分裂并色散的过程。分离出的小振幅波成分由于运动速度偏慢而与主波成分逐渐远离直至超出计算域。图 3d表明在20T时刻仅剩下已处于稳定状态的主要波成分, 它即为该数值模型获得的内孤立波解。自适应网格的疏密由涡度和密度梯度共同控制, 图 4为图 3d黄框位置放大显示的网格分布。注意, 为了显示清楚, 这里少绘了最细一层次的网格。
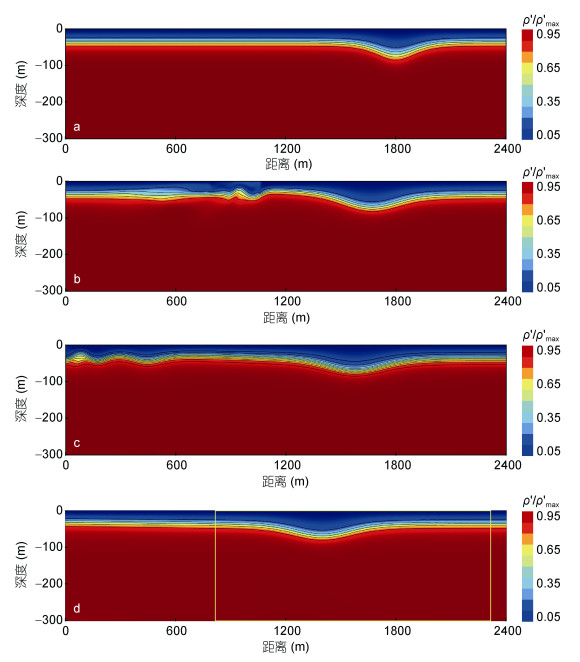 |
| 图 3 用Gerris模拟的内孤立波演变图 Fig. 3 Evolution of the internal solitary wave simulated by Gerris 注: a、b、c、d依次为0, 5, 10, 20T时刻密度分布图; ρ'表示密度变化量, ρmax'表示其最大值 |
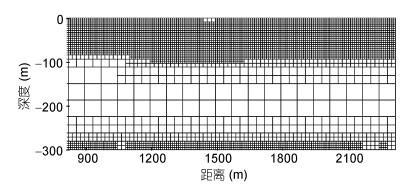 |
| 图 4 在内孤立波模拟时Gerris动态生成的网格 Fig. 4 The mesh dynamically generated by Gerris during the simulation of internal solitary wave |
图 5是分别用自适应网格和均匀网格模拟的速度场在图 3d中黄框所示区域的差异分布图。显然, 在内孤立波中心位置附近差异较大。水平速度场和垂直速度场的平均偏差分别为-0.0015m/s和-5.38× 10-5m/s, 标准差分别为0.0062m/s和0.0026m/s, 可以忽略不计。可见自适应网格在保障计算精度的同时降低了计算量。
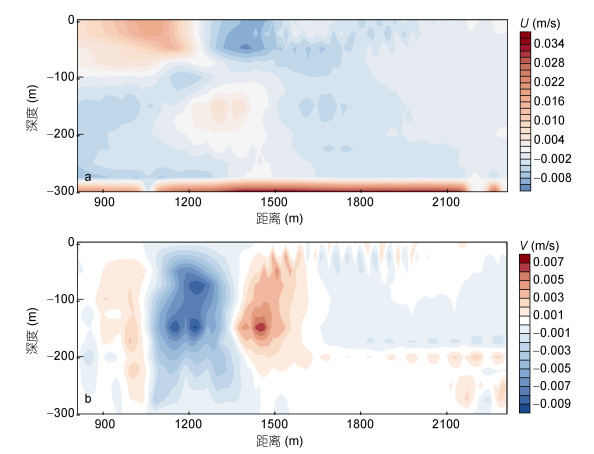 |
| 图 5 用Gerris在分别采用自适应网格和均匀网格的情况下模拟的速度场的差异分布图 Fig. 5 Difference in velocity field simulated between adaptive grid and uniform grid 注: a.水平速度场U差异分布; b.垂向速度场V差异分布 |
图 6为在层化1条件下, 振幅为33m时, 分别用KdV模型与Euler模型模拟得到的内孤立波等密度线分布。图 6表明, 对水下46m处水层, 两个模型等密度线的垂向最大位移恰好相等; 对46m以浅的水层, Euler模型的等密度线的垂向最大位移大于KdV模型; 对46m以深的水层, 则情况相反。由于KdV模型将内波运动分解成水平和垂直两个独立的部分相乘, 因而仅垂向位移在不同深度有变化, 而孤立波半宽度则是上下一致的。然而, Euler模型的垂向位移和孤立波半宽度均随水层深度不同而变化。就这点而言, 两个模型存在本质区别。下文将从不同方面讨论两个模型在垂直结构上的区别。
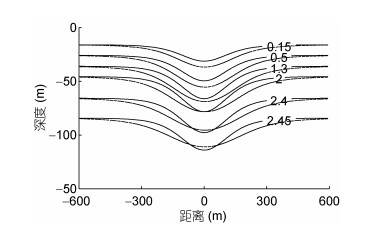 |
| 图 6 KdV模型(实线)和Euler模型(虚线)在同一振幅下的内孤立波等密度线(单位: kg/m3)垂向剖面(水深H=300m) Fig. 6 Isopycnal profiles (unit: kg/m3) of KdV model (solid line) and Euler model (dashed line) at the same amplitude (depth H = 300m) |
图 7为在层化1的条件下, KdV模型和Euler模型在不同振幅时的垂向结构对比图。图 7a、图 7b和图 7c均以与Euler模型结果相同振幅下的KdV模型解析解为标准将Euler模型数值解进行归一化处理。归一化后, KdV模型各物理量垂向结构不随振幅变化, 而Euler模型对应的各物理量垂向结构随振幅而改变, 这样可以突出Euler模型结果与KdV模型结果的比例关系。图 7a为内孤立波中心位置等密度线垂向位移的垂直剖面, 可见, 振幅越大, Euler模型给出的中心位置等密度线垂向位移最大值所对应深度越小。图 7b和图 7c分别为内孤立波中心位置水平速度分量和垂向速度分量最大位置的垂向速度分量的垂向剖面, 它们表明随着振幅增加, 水平速度分量为0对应的深度及垂向速度分量最大值对应的深度均增加, 并且Euler数值模型的最大水平速度分量和最大垂向速度分量均小于KdV模型的对应值。总的说来, 在相同层化条件下, 振幅越大, Euler模型数值解与KdV模型解析解的差异越大。KdV方程是在弱非线性和弱频散条件下导出的, 小振幅是其可忽略高阶非线性的条件。然而, 随着振幅增大, 高阶非线性效应必然越来越大而越来越难以忽略, 故舍弃它们导致的误差也越来越大。
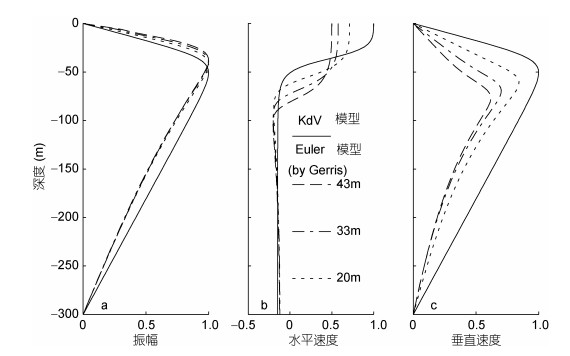 |
| 图 7 KdV模型和Euler模型在不同振幅下的归一化内波垂向结构 Fig. 7 Vertical profiles of KdV model and Euler model at different amplitudes 注: a.振幅归一化; b.水平速度归一化; c.垂直速度归一化 |
稳态内孤立波数值解的半宽度采用等效方波长的定义(Miyata, 1988; Vlasenko et al, 2000)
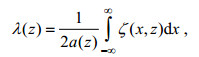 (17)
(17)其中, a(z)为未扰动时在深度为z处的密度层在孤立波中心位置的垂向位移, 称为内孤立波在深度z处等密度线的振幅; ζ(x, z)为深度为z的等密度线在不同水平位置上的垂向扰动。显然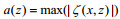
下面讨论内波半宽度在不同深度的变化特征。既然密度是深度的单调增函数, 因此也可以等效讨论内波半宽度随密度增加的变化性。而且半宽度本身也是通过等密度线计算获得的, 因此讨论半宽度与密度而非深度的关系更为方便。接下来将不同密度层的内孤立波半宽度视为密度的函数, 并且将KdV模型和Euler模型均以深度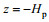
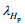
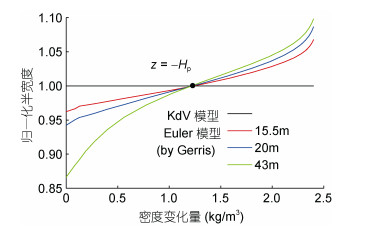 |
| 图 8 KdV模型和Euler模型给出的在不同振幅下归一化内孤立波半宽度随密度的变化曲线 Fig. 8 The normalized half width of internal solitary waves simulated by KdV and Euler model with different amplitudes |
卫星SAR是观测内波的重要手段。既然SAR图像上的内波条纹的明暗变化与内波表面流场的梯度相关, 那么就有必要研究下内波表面流场及其梯度的规律。当用KdV及其变种理论来解释SAR的内波成像机制时, 可将内波表面流场梯度最大值和最小值之间的距离Lu与内波半宽度关联起来, 进而计算出内波振幅。然而从Euler模型结果可知, 在完全非线性条件下, 内波不同密度层的半宽度不同, 因而表面流场梯度极值的间距与内波最大振幅密度层的半宽度的关系不再固定。图 9a为在振幅33m的情况下, 内波表面流速在不同层化(见表 1)的分布。图 9a表明在相同的振幅下, 层化越弱, 表面水平流速的极大值越小。在表层, 由于水层垂直起伏为0, 基于等效方波长的半宽度定义失效, 但我们依然可以将Lu当作一个与半宽度作用类似的表面流速特征尺度, 见图 9b。Lu随跃层厚度的变化如图 9c所示。图 9c表明在海表和海底密度以及跃层深度不变的情况下, 随着跃层厚度增加, 层化强度变弱, Lu呈现上升趋势。综合图 9表明表面流速、表面流速梯度分布在一定程度上可以反映密跃层的强弱变化。对于KdV解析解, Lu与内孤立半宽度的关系是确定的, 而在Euler模型中, Lu与内波半宽度不再有简单的对应关系, 这也就增大了从Lu反演内波振幅的难度。
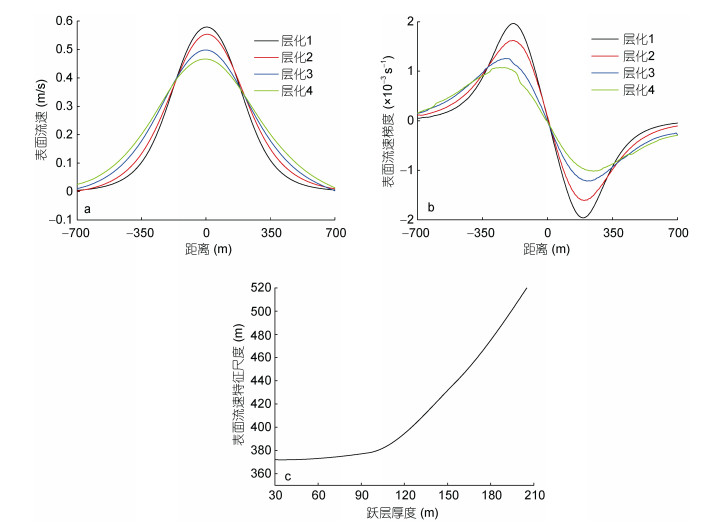 |
| 图 9 Euler模型模拟的不同层化下内孤立波海表流场 Fig. 9 Surface velocity field of internal solitary waves simulated by Euler model with different stratifications |
本节用两组大振幅内孤立波实测数据来验证Gerris实现的Euler模型的有效性。第一组数据着重验证内孤立波的水平与垂向结构特征; 第二组数据着重验证其流场分布。
3.1 墨西拿海峡北部内孤立波验证第一组实测数据(Vlasenko et al, 2000)是1995年大西洋爱奥尼亚海巡航期间在墨西拿海峡海底山脊北部25km处测得的振幅为55m的内孤立波。该内波所处位置总水深300m, 内波传播方向为东, 它被认为是潮地作用下形成的山后波在脱离地形逆流传播过程中演变而成(Brandt et al, 1997)。温度、盐度和深度数据通过温盐深剖面仪(Conductivity Temperature Depth, CTD)及温度链获取; 流场数据通过75kHz ADCP(Acoustic Doppler current profiler)获取。图 10为实测数据密度剖面布, 其中参数化密度剖面为Euler数值模型的初始化密度场, 如公式(16)所示。
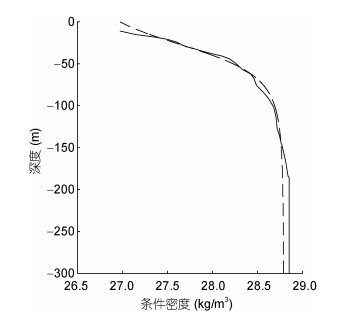 |
| 图 10 墨西拿海峡北部实测密度剖面(实线, 从Vlasenko et al, 2000提取)及及其参数化密度剖面(虚线) Fig. 10 The observed density profile (solid line, extracted from Vlasenko et al, 2000) in the north of Messina Strait and its parametric density profile (dashed line) |
图 11为用KdV模型、Euler模型得到的墨西拿海峡北部大振幅内孤立波的垂向结构与实测数据的对比图。图 11a为内波中心位置的垂向位移剖面, 可见Euler模型得到的内孤立波最大振幅的深度较KdV模型更接近实测。图 11b为内孤立波中心位置的水平速度场的垂向剖面, Euler模型得到的最大水平速度以及水平速度为0时的深度均较KdV模型更接近实测。图 11c为内孤立波最大垂向速度位置处的垂直速度场的垂向剖面, 同样, 与KdV模型相比, Euler模型得到的最大垂直速度及其对应深度均与实测数据更为接近。综合图 11表明, 与KdV模型相比, 在垂向剖面上, Euler模型得到的垂向位移、水平速度场及垂直速度场的特征参数、变化趋势均与实测数据吻合更好。部分参数对比见表 2。
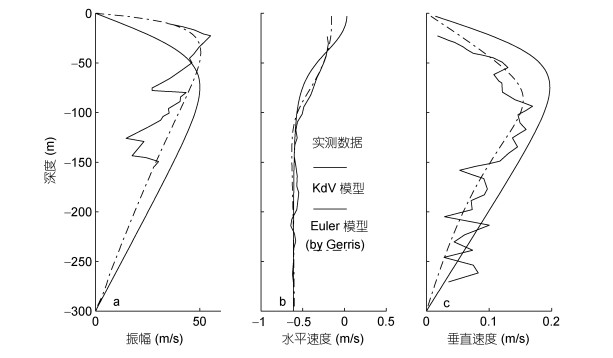 |
| 图 11 用Euler模型和KdV模型模拟的墨西拿海峡北部内孤立波的垂向结构与实测数据(Vlasenko et al, 2000)的比较 Fig. 11 Comparison of the vertical structure between the observed data (thick solid line, extracted from Vlasenko et al, 2000), and the Euler model (thin solid line) and KdV model (dashed line) in the northern of the Messina Strait |
| 特征参数 | 实测 | Euler模型 | KdV模型 |
| 振幅(m) | 55 | 50 | 50 |
| 相速度(m/s) | 1.0 | 0.9 | 0.9 |
| 最大水平东向速度(m/s) | 0.61 | 0.68 | 1.06 |
| 最大垂向速度(m/s) | 0.16 | 0.15 | 0.20 |
| 最小垂向速度(m/s) | -0.11 | -0.15 | -0.20 |
图 12为墨西拿海峡北部大振幅内孤立波实测数据与KdV模型、Euler模型各密度层半宽度对比图。从图 12中可以看出, Euler模型变化趋势较KdV模型与实测数据更为吻合, 即在一定范围内, 随密度值的增加, 半宽度呈现上升趋势。而KdV模型的半宽度并不随密度变化而变化。
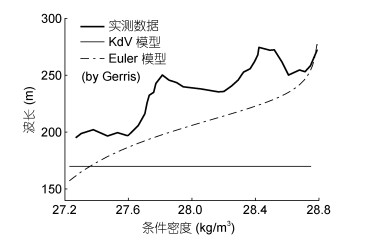 |
| 图 12 墨西拿海峡北部内孤立波在不同模型下的水平特征尺度与实测数据(Vlasenko et al, 2000)对比图 Fig. 12 The contrast of the horizontal characteristic scales of internal waves between different models and observed data (extracted from Vlasenko et al, 2000) in the northern Messina Strait |
第二组实测数据(于博, 2015)为国家“973计划”项目在南海深水区投放的ME2潜标测得, 潜标布放的位置是(20.99°N, 118.16°E), 水深为2029m, 内孤立波振幅为186m, 传播方向为西向。该海域内波被认为是潮地作用下, 下凹波在传播过程中裂变形成或者混合区的塌陷对周围层化的水体产生的冲击作用演变而成(Du et al, 2008)。图 13为实测密度剖面分布以及拟合的参数化密度剖面。
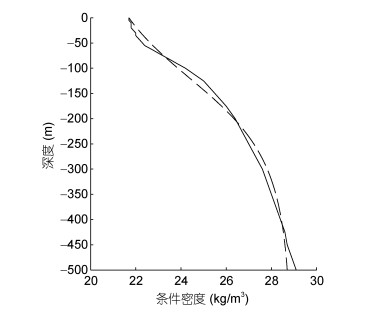 |
| 图 13 南海深水区实测密度剖面(实线)及参数化密度剖面(虚线)示意图(水深H=2000m) Fig. 13 Map of observed density profile (solid line) and parametric density profile (dashed line) in the deep-water area of the South China Sea (depth H = 2000m) |
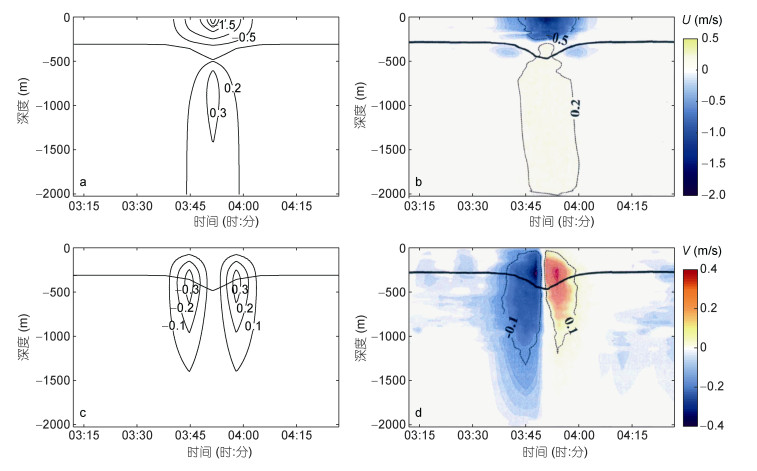
图 14为南海深水区内孤立波的一个垂直剖面的水平速度和垂直速度时序变化图。其中右侧是剔除了背景流场的实测流场, 时间跨度是75min。左侧两幅图为对应的Euler模型模拟的结果。当模式时间大于40T时(1T=400s), 模拟的内孤立波处于稳定状态, 故选取40T以后11.25T(75min)时间段内的数据与实测数据进行比较, 确保模式数据与实测数据的时间跨度相同。而且为方便与实测数据的速度场分布图进行比较, 还将Euler模型结果换算成与实测数据相同的时间标尺。粗实线为最大垂向位移的等密度线。图 14表明Euler模型结果比较准确的反映了实测内孤立波的内部结构, 例如, 内孤立波的周期, 垂向位移最大的等密度线的初始深度, 水平速度及垂向速度的极值等。表 3中所示为南海深水区两模型特征参数对比数据。数据再次表明, Euler模型的结果优于KdV模型的结果。
| 特征参数 | 实测 | Euler模型 | KdV模型 |
| 振幅(m) | 186 | 180 | 180 |
| 相速度(m/s) | 3.51 | 3.44 | 3.69 |
| 最大水平西向速度(m/s) | -1.81 | -1.87 | -3.38 |
| 最大垂向速度(m/s) | 0.35 | 0.35 | 0.50 |
| 最小垂向速度(m/s) | -0.39 | -0.35 | -0.50 |
通过与两组实测数据的对比, 无论就大振幅内孤立波的结构特征还是其速度场而言, Euler模型均能够较好的模拟大振幅内孤立波, 且优于KdV模型给出的模拟结果。在上述两个实验中, 若以同一层化同一振幅下的KdV解为单位1, 则在Euler模型解中, 最大水平速度分别为0.65和0.55, 最大垂向速度分别为0.8和0.75, 可见KdV模拟的水平和垂向速度分量的最大值均偏大, 即KdV模型高估了非线性效应(Vlasenko et al, 2000)。由于KdV模型是弱非线性方程, 要求振幅远小于较浅水层, 而以上两实例均不满足这个要求, 故高阶非线性不可忽略, 这应是造成KdV模型与实测及Euler模型结果相去甚远的一个重要原因。
4 结论本文采用开源的流体动力学软件Gerris建立的Euler数值模型模拟了不同层化条件下的稳态大振幅内孤立波。由于Gerris采用了自适应网格和并行处理技术, 该模型兼具高精度和高效率的特点。并且, 由于采用Euler方程作为控制方程, 故该模型可获得完全非线性的稳态内孤立波解。比较Euler模型与KdV模型的结果表明Euler模型克服了KdV模型在分析大振幅内波结构时的局限性。
Euler模型的结果表明, 内孤立波的振幅、波中心位置水平速度分量、等密度层最大垂向速度分量均随着深度的变化而变化, 但变化趋势与KdV理论不同。尤其, 在KdV理论中, 各等密度层的半宽度是相同的, 而Euler模型获得的半宽度却随深度而改变。
与两组现场观测数据的比较结果表明, Euler模型的模拟结果无论在波参数上还是在速度流场分布上均比KdV模型的结果更接近实测数据。因此, 有理由认为Euler模型获得的大振幅内孤立波的结构比KdV更准确。基于此, 再反观KdV模型给出的最大水平和垂直速度分量均大于Euler模型的对应结果这一现象, 可以认为KdV高估了大振幅内孤立波的非线性效应。
从文中给出的多组比较数据可以看出, 对于大振幅内孤立波, 高阶非线性效应不应忽略。
另外, 考虑到在Euler模型的内孤立波解中等密度面半宽度也随深度变化这一事实, 在SAR内波振幅反演研究工作中, 若能与Euler模型或者其它完全非线性模型(例如DJL模型)相结合, 有望获得更为准确的SAR内波振幅反演算法。
于博, 2015.南海北部内孤立波能量和水体输运研究.青岛: 中国海洋大学硕士学位论文, 17-20
|
王亮, 毛科峰, 陈希, 等. 2015. Gerris数值方案及其在海洋数值模拟中的应用. 南京信息工程大学学报:自然科学版, 7(1): 92-96 |
王金虎, 陈旭, 徐洋. 2016. 粗糙地形对内波生成影响的实验研究. 海洋与湖沼, 47(4): 706-713 |
方欣华, 杜涛. 2005. 海洋内波基础和中国海内波. 青岛: 中国海洋大学出版社
|
孙丽娜, 张杰, 孟俊敏. 2018. 基于遥感与现场观测数据的南海北部内波传播速度. 海洋与湖沼, 49(3): 471-480 |
张善武, 范植松, 石新刚. 2015. 变系数EKdV模型在模拟南海北部大振幅内孤立波传播和裂变中的应用. 中国海洋大学学报(自然科学版), 45(4): 9-17 |
曾侃, 2002.从卫星合成孔径雷达海表图像研究海洋内波的三个问题.青岛: 青岛海洋大学博士学位论文, 48-55 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y468620
|
蔡树群, 甘子钧, 龙小敏. 2001. 南海北部孤立子内波的一些特征和演变. 科学通报, 46(15): 1245-1250 DOI:10.3321/j.issn:0023-074X.2001.15.003 |
Benjamin T B, 1967. Internal waves of permanent form in fluids of great depth. Journal of Fluid Mechanics, 29(3): 559-592 DOI:10.1017/S002211206700103X |
Brandt P, Rubino A, Alpers W et al, 1997. Internal waves in the strait of Messina studied by a numerical model and synthetic aperture radar images from the ERS 1/2 satellites. Journal of Physical Oceanography, 27(5): 648-663 DOI:10.1175/1520-0485(1997)027<0648:IWITSO>2.0.CO;2 |
Du T, Tseng Y H, Yan X H, 2008. Impacts of tidal currents and Kuroshio intrusion on the generation of nonlinear internal waves in Luzon Strait. Journal of Geophysical Research:Oceans, 113(C8): C08015 |
Helfrich K R, Melville W K, 2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics, 38(1): 395-425 |
Jackson C R, 2004. An Atlas of Internal Solitary-like Waves and their Properties. 2nd ed. Washington DC, USA: NOAA
|
Joseph R I, 1977. Solitary waves in a finite depth fluid. Journal of Physics A:Mathematical and General, 10(12): L225-L227 DOI:10.1088/0305-4470/10/12/002 |
Klymak J M, Pinkel R, Liu C T et al, 2006. Prototypical solitons in the South China Sea. Geophysical Research Letters, 33(11): L11607 DOI:10.1029/2006GL025932 |
Leonov A I, Miropol'sky, Y Z, 1975. Toward a theory of stationary nonlinear internal gravity waves. Izvestiya, Atmospheric and Oceanic Physics, 11(5): 298-304 |
Lien R C, Henyey F, Ma B et al, 2014. Large-amplitude internal solitary waves observed in the northern South China Sea:properties and energetics. Journal of Physical Oceanography, 44(4): 1095-1115 DOI:10.1175/JPO-D-13-088.1 |
Liu A K, Chang Y S, Hsu M K et al, 1998. Evolution of nonlinear internal waves in the East and South China Seas. Journal of Geophysical Research:Oceans, 103(C4): 7995-8008 DOI:10.1029/97JC01918 |
Miyata M, 1988. Long internal waves of large amplitude. In: Proceedings of the IUTAM Symposium. Tokyo, Japan: Springer, 399-406
|
Ono H, 1975. Algebraic solitary waves in stratified fluids. Journal of the Physical Society of Japan, 39(4): 1082-1091 DOI:10.1143/JPSJ.39.1082 |
Osborne A R, Burch T L, 1980. Internal solitons in the Andaman Sea. Science, 208(4443): 451-460 DOI:10.1126/science.208.4443.451 |
Phillips O M, 1977. The Dynamics of the Upper Ocean. 2nd ed. Cambridge, UK: Cambridge University Press
|
Popinet S, 2003. Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries. Journal of Computational Physics, 190(2): 572-600 DOI:10.1016/S0021-9991(03)00298-5 |
Popinet S, Rickard G, 2007. A tree-based solver for adaptive ocean modelling. Ocean Modelling, 16(3-4): 224-249 DOI:10.1016/j.ocemod.2006.10.002 |
Preusse M, Stastna M, Freistühler H et al, 2012. Intrinsic breaking of internal solitary waves in a deep lake. PLoS One, 7(7): e41674 DOI:10.1371/journal.pone.0041674 |
Shen H, He J Y, 2006. SAR imaging simulation of horizontal fully two-dimensional internal waves. Journal of Hydrodynamics, Ser. B, 18(3): 294-302 DOI:10.1016/S1001-6058(06)60006-1 |
Stastna M, Lamb K G, 2002. Large fully nonlinear internal solitary waves:the effect of background current. Physics of Fluids, 14(9): 2987-2999 DOI:10.1063/1.1496510 |
Tessler Z D, Gordon A L, Jackson C R, 2012. Early stage soliton observations in the Sulu Sea. Journal of Physical Oceanography, 42(8): 1327-1336 DOI:10.1175/JPO-D-11-0165.1 |
Vlasenko V, Brandt P, Rubino A, 2000. Structure of large- amplitude internal solitary waves. Journal of Physical Oceanography, 30(9): 2172-2185 DOI:10.1175/1520-0485(2000)030<2172:SOLAIS>2.0.CO;2 |
Vlasenko V, Hutter K, 2002. Numerical experiments on the breaking of solitary internal wavesover a slope-shelf topography. Journal of Physical Oceanography, 32(6): 1779-1793 DOI:10.1175/1520-0485(2002)032<1779:NEOTBO>2.0.CO;2 |
Vlasenko V, Stashchuk N, Guo C et al, 2010. Multimodal structure of baroclinic tides in the South China Sea. Nonlinear Processes in Geophysics, 17(5): 529-543 DOI:10.5194/npg-17-529-2010 |
Vlasenko V I, 1994. Multimodal soliton of internal waves. Atmospheric and Oceanic Physics, 30(2): 161-169 |
Xie X H, Cuypers Y, Bouruet-Aubertot P et al, 2013. Large- amplitude internal tides, solitary waves, and turbulence in the central Bay of Biscay. Geophysical Research Letters, 40(11): 2748-2754 DOI:10.1002/grl.50533 |
Xue J S, Graber H C, Lund B et al, 2013. Amplitudes estimation of large internal solitary waves in the Mid-Atlantic Bight using synthetic aperture radar and marine X-band radar images. IEEE Transactions on Geoscience and Remote Sensing, 51(6): 3250-3258 DOI:10.1109/TGRS.2012.2221467 |
Zhang H S, Jia H Q, Gu J B et al, 2014. Numerical simulation of the internal wave propagation in continuously density- stratified ocean. Journal of Hydrodynamics, 26(5): 770-779 DOI:10.1016/S1001-6058(14)60086-X |
Zhang X D, Wang J, Sun L N et al, 2016. Study on the amplitude inversion of internal waves at Wenchang area of the South China Sea. Acta Oceanologica Sinica, 35(7): 14-19 DOI:10.1007/s13131-016-0902-1 |
Zheng Q N, Yuan Y L, Klemas V et al, 2001. Theoretical expression for an ocean internal soliton synthetic aperture radar image and determination of the soliton characteristic half width. Journal of Geophysical Research:Oceans, 106(C12): 31415-31423 DOI:10.1029/2000JC000726 |
 2019, Vol. 50
2019, Vol. 50