中国海洋湖沼学会主办。
文章信息
- 王振霄, 王彩霞. 2019.
- WANG Zhen-Xiao, WANG Cai-Xia. 2019.
- 基于遥感图像的南海北部内孤立波及相互作用研究
- INTERNAL SOLITARY WAVE AND INTERACTION IN THE NORTHERN SOUTH CHINA SEA BASED ON REMOTE SENSING IMAGES
- 海洋与湖沼, 50(5): 958-970
- Oceanologia et Limnologia Sinica, 50(5): 958-970.
- http://dx.doi.org/10.11693/hyhz20190400065
文章历史
-
收稿日期:2019-04-02
收修改稿日期:2019-05-09
内波是密度相对稳定的层化流体内部的振荡。它们不仅频繁地发生在海洋中, 而且对海洋声学、海洋光学、海洋生物以及海洋工程等有重要的影响, 是海洋中起着重要作用的动力学过程(Thorpe, 1975; Garrett et al, 1979)。内孤立波是一种特殊的内波, 在非线性效应和频散效应的平衡作用下, 波形可以在传播过程中实现上百公里保持不变, 因此可以形成巨大的物质和能量输运(Osborne et al, 1980; Grimshaw et al, 2002)。海洋中, 内孤立波以波包的形式传播。当两列内孤立波在其传播过程中以倾斜的夹角相遇, 这会导致它们彼此发生非线性相互作用(Miles, 1977; Matsuno, 1998; Liu et al, 1998; Wang et al, 2012)。此过程可能会导致内波的振幅发生叠加, 传播方向发生改变, 还可能导致内波之间发生共振能量转移。此外, 内波也可能直接穿过彼此。这种现象频繁地被遥感图像所拍摄到(Liu et al, 1998; Xue et al, 2014)。目前内波观测的手段主要包括现场观测以及卫星遥感图像。传统的基于锚定潜标或者走航船只的现场观测手段虽然可以有效地跟踪某列内波的波包并研究其演化过程, 但是这种观测手段不仅受多方面因素的影响, 而且费用昂贵难以大范围开展, 对内波传播过程中发生的现象, 例如内波-波相互作用, 更是无法很好地进行观测。相比于传统的观测手段, 基于遥感图像的观测手段具有大范围、长距离以及高分辨率等优点。内波的遥感成像原理分为以下3个过程(Alpers, 1985; Thompson, 1986): (1)由内波引起表面流场的辐散或者辐聚; (2)由表面流场调制的海表面粗糙度变化; (3)毛细波与遥感卫星雷达相互作用。随着观测手段的不断改进, 遥感图像的时间以及空间分辨率不断提升, 使得结合多种手段相调查研究内波成为可能(Wang et al, 2019)。
本文使用遥感图像对南海北部的内孤立波以及相互作用现象进行了研究。南海北部是一个半封闭的深水海盆, 范围为105°—123°E、15°—25°N, 平均水深超过1800m, 最大水深可达5420m, 通过台湾海峡和吕宋海峡分别与中国东海以及西太平洋连接。该海区内岛屿众多, 并且存在复杂多变的海底地形, 既有宽阔的大陆架, 又有坡度急剧变化的大陆坡, 还有辽阔的深海盆地(杨海军等, 1998)。南海北部是全球内波最为活跃的海区之一(Liu et al, 1998; Hsu et al, 2000; Alford et al, 2015), 是国际公认的“天然内波实验场”(杜涛, 2000)。南海北部现场观测得到的内波振幅最大可达240m(Huang et al, 2016), 传播速度最大可达3m/s左右(孙丽娜等, 2018)。内波的振幅以及传播速度是了解内波演化、能量传递以及混合过程的关键参数(Xue et al, 2013)。通过遥感图像中的内波信号对内波振幅以及传播速度进行反演可以使我们进一步了解内波。目前最常见的用于研究内波的一维方程是Korteweg-de Vries(KdV)方程。Zheng等(2001)最早提出通过提取遥感图像中内波截面处信号强度峰值间的距离, 结合KdV方程计算内波振幅的方法。Yang等(2003)将该方法运用于南海内波振幅的反演上。南海北部内波相互作用的研究主要为数值模拟, 李群等(2007)运用二维Kadomtsev-Petviashvili(KP)方程对东沙岛附近的内波相互作用进行了数值模拟。李娟等(2014)基于柱KP模型研究了东沙岛附近内波的弹性碰撞。南海北部关于内波相互作用观测的研究十分匮乏。卫星遥感图像可以拍摄到海洋中的内波相互作用现象, 是观测和研究该现象特征最有效的手段之一。
本文尝试通过统计南海北部大量的遥感图像, 得出图像中内孤立波和相互作用现象的时间与空间分布特征。并且结合遥感图像和观测数据, 运用KdV方程以及Benjamin-One(BO)方程对南海北部的内波进行参数反演。
1 数据介绍与研究方法 1.1 数据介绍本文一共下载了南海北部所拍摄到内波现象的遥感图像共计869张, 卫星的基本参数如表 1所示。其中ERS-1、ENVISAT-1以及SENTINEL-1为合成孔径雷达(Synthetic Aperture Radar, SAR)遥感卫星, GF-1为光学遥感卫星。遥感图像的成像质量受到海表面风场、拍摄角度、极化方式等多种条件影响(Da Silva et al, 1998; Xue et al, 2013)。对遥感图像中的内孤立波以及相互作用现象进行识别, 整理得到853组内波, 208处相互作用现象。
| 卫星 | 运行时间 | 往返周期 (d) |
分辨率 (m) |
图片数量 (张) |
内孤立波数量(组) | 相互作用现象数量(处) |
| ERS-1 | 1991年7月17日—2011年1月19日 | 35 | 30 | 399 | 401 | 106 |
| ENVISAT-1 | 2002年3月1日—2011年4月21日 | 35 | 30 | 265 | 295 | 88 |
| SENTINEL-1 | 2014年4月3月至今 | 12 | 5×5 | 81 | 103 | 5 |
| GF-1 | 2013年4月26日至今 | 16 | 16 | 124 | 54 | 9 |
自2004年至今, 南海北部海洋观测开放航次由中科院南海海洋研究所负责实施, 调查船为“实验3”号科考船, 调查海区为南海北部海区及西部局部海区, 观测范围大致位于18°—23°N, 110°—120°E以及12°—18°N, 110°—112°E。每年9月在航次调查海域进行为期约30d的大面站观测, 每年观测站点略有不同。为对遥感图像进行内波参数反演实验, 选取其中距离遥感图像拍摄海域最近的2005年的部分站点的温盐深(Conductivity-Temperature-Depth, CTD)数据作为反演实验中所需的层结数据。
1.2 研究方法为了模拟内波的传播特性, 通常会根据内波的水平尺度与水深的关系, 来选择合适的一维内波传播模型。以两层层化水体为例, 对于浅水长内波, 即内波波长远大于水深, 一般会选用KdV方程(Benjamin, 1967; Benney, 1966); 如果内波的波长大于其中一层水深, 但是远小于另一层水深, 可以采用BO方程(Benjamin, 1967; Ono, 1975; Wang et al, 2019)。两层流体的KdV方程的形式为:
 (1)
(1)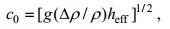 (2)
(2)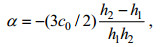 (3)
(3)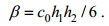 (4)
(4)其中, η为内孤立波的垂向位移, c0、α、β分别为线性内波的相速度、非线性项系数、频散项系数。h1和h2分别为上下层水深, heff=h1h2/(h1+h2)被定义为有效水深。Δρ为上下层海水密度的差, ρ约为上层海水密度。
通过上述的参数, 可以给出方程(1)的孤立解, 其形式为:
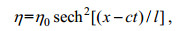 (5)
(5)其中, c为相速度, l为内波的特征半波宽:
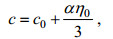 (6)
(6)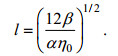 (7)
(7)得到振幅η0与特征半波宽l的关系:
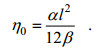 (8)
(8)Zheng等(2001)提出了卫星信号强度与海表面流场关系的理论模型。内波图像上的后向散射强度与内波引起的海表面流场的梯度正相关, 即:
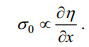 (9)
(9)单列内波条纹最亮点和最暗点之间的距离可以通过遥感图像的后向散射强度截面曲线相邻的波峰和波谷之间的距离确定, 称其为峰-峰距离dp-p, 而且其满足:
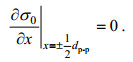 (10)
(10)内波的半波宽l和峰-峰距离dp-p之间存在以下关系:
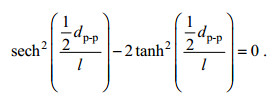 (11)
(11)方程(11)解得:
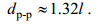 (12)
(12)结合方程(6)和方程(8)即可计算内波振幅以及传播速度。
KdV方程由于形式简单, 经常被用于反演两层层化海水的内波参数, 但是其反演结果往往与实际情况相差甚远, 这是由于实际海洋中的内波并不满足KdV方程的条件导致的。南海北部大陆坡折区域的平均水深约为250m, 上层海水深度约为10—20m左右。因此, 我们认为该海域所观测到的内波为深水非线性内波, 可以选用BO方程对内波振幅及传播速度进行反演。BO方程的形式如下:
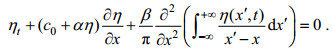 (13)
(13)其中的线性相速度c0, 非线性项系数α和离散项系数β形式如方程(14)—方程(16):
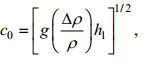 (14)
(14)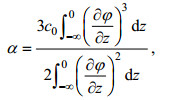 (15)
(15)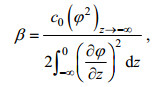 (16)
(16)其中, φ是Taylor-Goldstein方程的振型解(Baines, 1995), h1为上层深度。现实海洋大多数情况下海水为连续层结, 为方便研究对海水进行两层层化假设, 认为当φ到达最大值时的深度为上层海水的厚度h1。
方程(13)解得形式如方程(17):
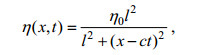 (17)
(17)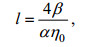 (18)
(18)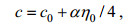 (19)
(19)其中, η0为孤立波的振幅, l为特征半波宽, c为内波的相速度, 它们的形式分别如方程(18)和方程(19)所示。
内波振幅与半波宽的关系:
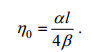 (20)
(20)Wang等(2019)通过一级近似给出遥感图像的图像对比度与内波传播过程中引起的流动的梯度呈正相关, 即:
 (21)
(21)根据BO方程的解, 由内波引起的表面流可以通过简化进而给出其表达形式:
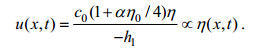 (22)
(22)将式(22)代入式(21), 可以得到内波信号在遥感图像上的表现的表达式:
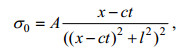 (23)
(23)其中, A为常数。在t=0时刻的情况下, 根据上式可以得到单列内波的截面上最亮点与最暗点之间的距离, 即峰-峰距离dp-p与内波的特征半波宽的关系为:
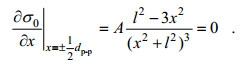 (24)
(24)因此得到:
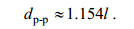 (25)
(25)结合式(19)和式(20)即可反演内波的振幅以及传播速度。
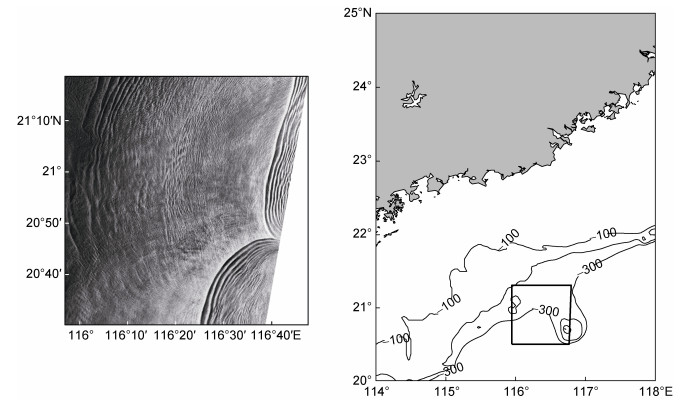
为确定内波特征半波宽, 我们采用的方法是经验模态分解法(Empirical Mode Decomposition, EMD)。EMD分解是由N.E.Huang等提出的一种用于对非线性不平稳信号进行平稳化处理的方法(甘锡林等, 2007)。EMD分解过程:提取原数据中σ0(t)所有极大值和极小值, 对于没有数据的部分, 采用三次样条插值拟合得到完整连续的曲线, 分别为上包络线和下包络线; 定义b(i)为上包络线和下包络线的均值; 定义一个新的序列c(i)为原数据σ0(t)减去平均包络b(i)的差值, 即:
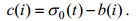 (26)
(26)得到的新序列c(i)就是原数据经过EMD分解得到的本征模态分量(Intrinsic Mode Functions, IMF)。通过计算IMF分量的归一化方差来估计每个IMF的相对能量, 认为能量最大的分量为内波信号。测量该IMF分量极大值和相邻极小值之间的距离, 该距离为遥感图像上内波截面处的峰-峰距离dp-p。
2 结果与分析 2.1 内孤立波及相互作用的时空分布我们对下载的869张遥感图像进行分析整理, 提取了其中的内孤立波及相互作用现象发生时内孤立波交汇处的位置信息并绘制在海图上, 分别得到南海北部的内孤立波空间分布图以及相互作用空间分布图。另外我们还对这些内孤立波及相互作用发生的时间进行了记录, 分别绘制了南海北部内孤立波个数和相互作用次数的月分布图以及日分布图。
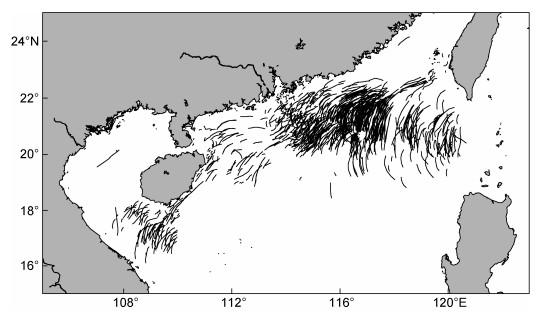
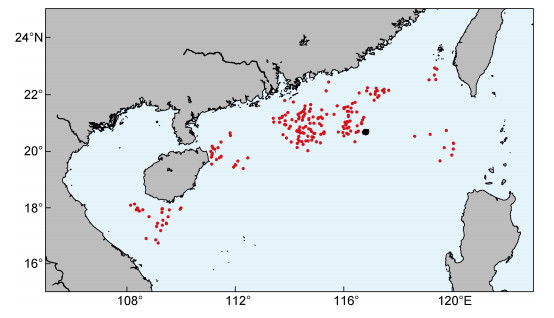
南海北部内孤立波的空间分布如图 1所示。从图 1中可以发现该海域的内波主要分布在东沙群岛以及海南岛附近大陆架浅海区, 其中东沙群岛附近存在大量的内孤立波, 符合甘锡林等(2007)和孙丽娜等(2018)根据遥感图像统计的结果。南海北部内孤立波相互作用的空间分布如图 2所示。从图 2中可以发现该海域发生的内孤立波相互作用现象主要集中在东沙岛西北部以及海南岛南部海域, 这两个区域也属于南海北部内波发生频率最高的区域(甘锡林等, 2007; 孙丽娜等, 2018)。根据已有的研究结果, 南海东北部内波主要是内潮在吕宋海峡处与海底山脊发生相互作用产生的(Alford et al, 2015)。这些内波在其传播过程中非线性不断增强, 并在传播至东沙岛后发生反射和绕射现象(甘锡林等, 2007), 受其影响内波传播方向发生改变, 一部分向西北传播, 另一部分向西南传播。因此我们猜测之所以东沙岛附近频繁地发生内孤立波相互作用现象, 有以下两个原因:对于西侧的内孤立波相互作用现象, 是由于内波传播至东沙岛发生绕射, 一列内波波包有可能分裂为两列且传播方向发生改变, 这两列内波在传播过程中彼此相遇, 发生相互作用; 另一方面, 内波传播至东沙岛后也可能发生反射, 反射的内波可能会与后续传来的内波相遇, 发生相互作用。图 3是2002年6月24日ERS-1卫星拍摄到的内孤立波相互作用的遥感图像, 图中可以看见两列内孤立波正在发生相互作用。我们认为这两列内孤立波是由经过东沙岛的内波分裂形成的, 它们的传播方向发生了改变, 在后续的传播过程中发生相互作用。对于第二种猜想, 我们并没有在所统计的遥感图像上发现类似现象, 对此我们将在后续研究中进行验证。海南岛附近的内波主要生成于大陆架水深变化剧烈的区域并向西北传播, 我们认为这些内波传至大陆架浅海处发生反射, 进而与后续传来的内波发生相互作用。图 4为2004年6月8日ENVISAT-1卫星拍摄到的内孤立波相互作用的遥感图像, 图中内孤立波A和内孤立波B正在发生相互作用。我们认为内孤立波A为从海南岛大陆架浅海处反射的内孤立波, 内孤立波B为传播至此的内孤立波, 两者相遇发生相互作用。
 |
| 图 1 内孤立波空间分布图 Fig. 1 The spatial distribution of internal solitary waves 注:黑色曲线为内孤立波波锋线 |
 |
| 图 2 内孤立波相互作用现象的空间分布图 Fig. 2 The spatial distribution patterns of internal solitary wave interaction patterns 注:红点代表内孤立波交汇处的位置, 黑点代表东沙岛 |
 |
| 图 3 2002年6月24日ERS-1卫星拍摄到发生内孤立波相互作用的遥感图像 Fig. 3 An ERS-1 satellites image taken on June 24 2002 showing internal solitary wave interaction 注:等值线表示水深, 单位: m; 余同 |
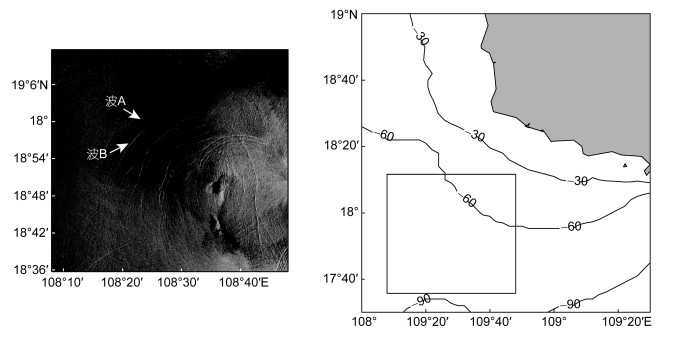 |
| 图 4 2004年6月8日ENVISAT-1卫星拍摄到发生内孤立波相互作用的遥感图像 Fig. 4 An ENVISAT-1 satellites image taken on June 8 2004 showing internal solitary wave interaction |
图 5a、图 5b分别为南海北部内孤立波个数的月分布图和日分布图, 图 6a、图 6b分别为南海北部内孤立波相互作用次数的月分布图和日分布图。可以发现南海北部内孤立波以及相互作用现象主要集中在4—9月份, 6月份内孤立波数量以及相互作用次数最多。这是由于南海北部的海水夏季层结强于冬季的结果(甘锡林等, 2007)。内孤立波数量多的月份, 相互作用发生的次数也相应的多。个别内孤立波数量少的月份, 并没有内孤立波相互作用现象发生。内孤立波相互作用次数的日分布也有类似情况, 内孤立波数量多的日期, 相互作用现象也相应的多, 且个别日期内没有内孤立波相互作用现象发生。
 |
| 图 5 内孤立波个数月分布以及日分布图 Fig. 5 The monthly and daily distributions of the internal solitary waves 注: a为内孤立波个数的月分布图, b为内孤立波个数的日分布图 |
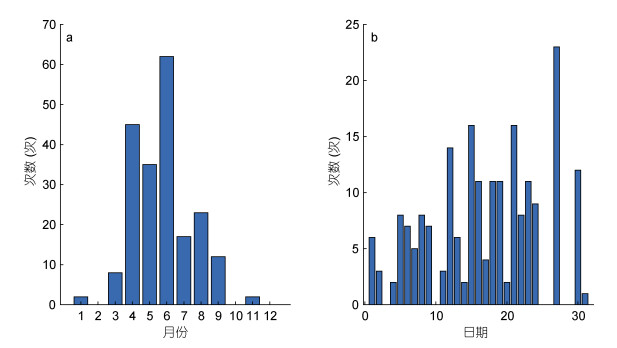 |
| 图 6 内孤立波相互作用次数的月分布以及日分布图 Fig. 6 The monthly and daily distributions of the internal solitary wave interaction 注: a为内孤立波相互作用次数的月分布图, b为内孤立波相互作用次数的日分布图 |
本文选用三张遥感图像进行振幅和传播速度的反演实验, 图像分别为2005年5月9日的ENVISAT-1、ERS-1卫星拍摄的遥感图像各一幅、2005年9月7日拍摄的ERS-1图像一幅。2005年5月9日ENVISAT-1、ERS-1拍摄的遥感图像分别如图 7、图 8所示, 两幅图像的极化方式为VV极化, 产品等级level1B, 成像模式为精密成像模式, 空间分辨率为25m。可以从图像中看到明显的明暗相间的条纹带, 其长度约为106km, 传播方向大致为西北方向。两幅图像拍摄的时间间隔约为29min, 图像中具有相同传播方向的内孤立波可以认为是同一列, 如图 9所示, 两幅图像中内孤立波的波锋线位置相距大约2.5km。因此可以直接从遥感图像中提取内孤立波的传播速度为1.43m/s。
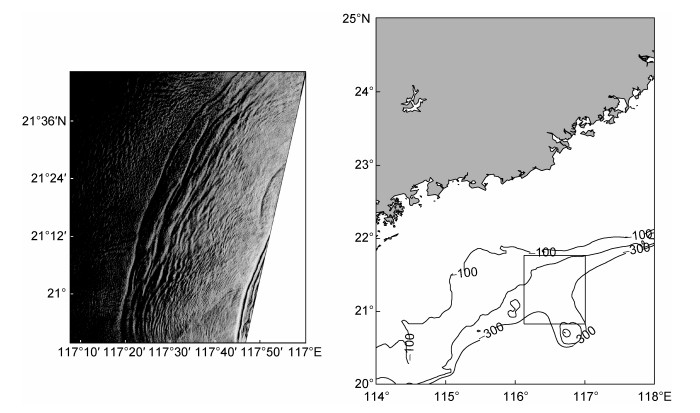 |
| 图 7 2005年5月9日ENVISAT-1卫星拍摄到的内孤立波遥感图像 Fig. 7 An ENVISAT-1 satellite image taken on May 9 2005 showing internal solitary wave |
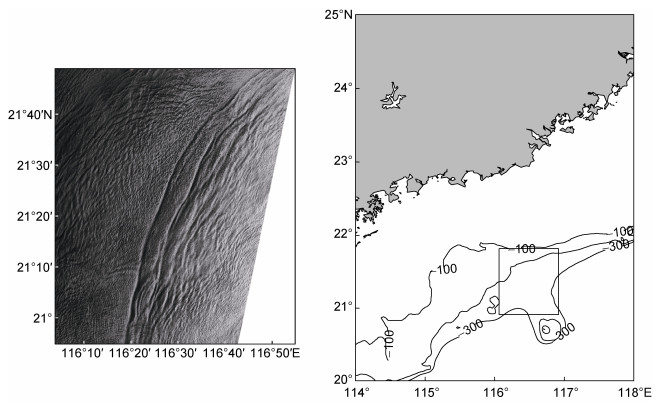 |
| 图 8 2005年5月9日ERS-1卫星拍摄到的内孤立波遥感图像 Fig. 8 An ERS-1 satellite image taken on May 9 2005 showing internal solitary wave |
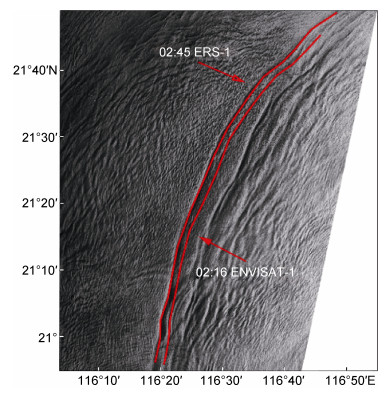 |
| 图 9 ENVISAT-1和ERS-1图像中内孤立波波锋线的叠加图 Fig. 9 The stacking diagram of internal solitary wave crests of ENVISAT-1 and ERS-1 images |
另一张图像如图 10所示, 为2005年9月7日拍摄的ERS-1遥感图像, 其极化方式为VV极化, 产品等级level1B, 成像模式为精密成像模式, 空间分辨率为25m。图片位于东沙岛东北方向。
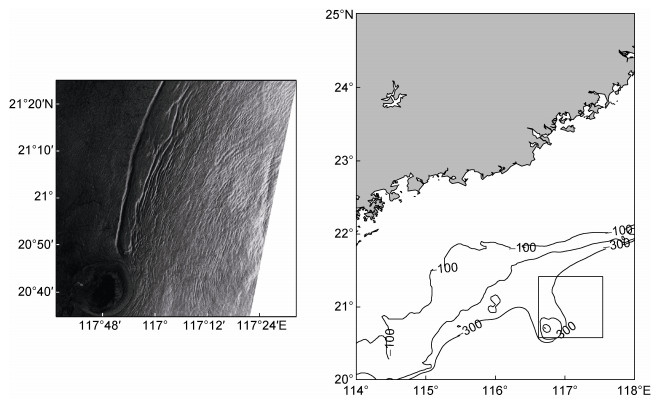 |
| 图 10 2005年9月7日ERS-1卫星拍摄到的内孤立波遥感图像 Fig. 10 An ERS-1 satellite image taken on September 7 2005 showing internal solitary wave |
对于图 7、图 8中两张遥感图像中的内孤立波, 我们选取2005年南海北部海洋观测开放航次CTD大面站E103号站位观测的CTD数据, 作为该海区的层结数据, 如图 11a、11b所示。该海域海水密度的变化范围约为1018—1024kg/m3, 上层深度约为20m。
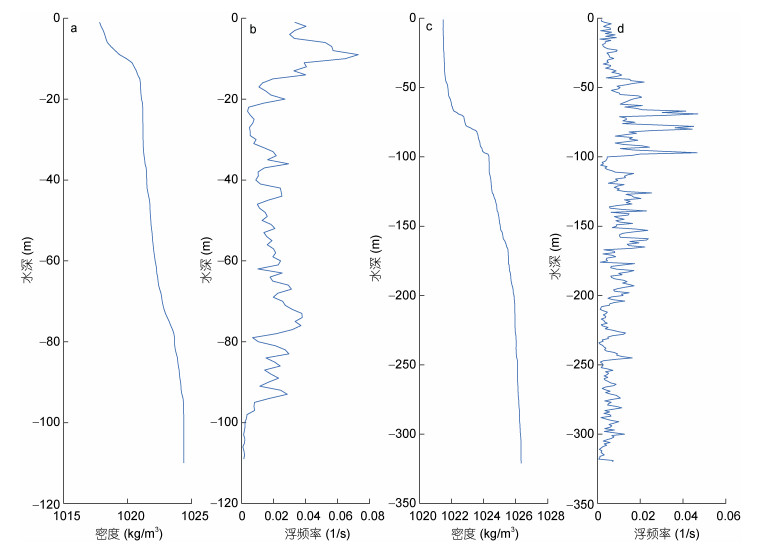 |
| 图 11 CTD测得的密度剖面(a、c)和浮频率剖面(b、d) Fig. 11 The CTD data of density profile (a, c) and buoyancy frequency profile (b, d) |
对于图 10中的内孤立波, 我们选取2005年南海北部海洋观测开放航次CTD大面站E203_2号站位观测的CTD数据, 作为该海区的层结数据, 如图 11c、图 11d所示。该海域海水密度的变化范围约为1021—1026kg/m3, 上层深度约为95m。
对2005年5月9日的两幅遥感图像, 以及2005年9月7日的遥感图像, 我们分别截取三张图像中内孤立波波包的第一列波峰线(图 12a、图 12b、图 12c为选取的内孤立波截面, 图像的像元间距为25m), 并对选取的截面进行EMD分解以提取图像中内孤立波截面处的dp-p, 用以计算内孤立波的特征半波宽。
 |
| 图 12 内孤立波截面位置示意图 Fig. 12 Locations of internal solitary wave transects |
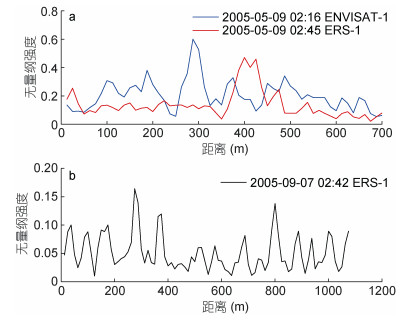
对遥感图像强度经过归一化处理后, 得到图像的无量纲强度值σ0, 图 13为选取的三个内孤立波截面处的无量纲强度值曲线, 其中图 13a的两条曲线为2005年5月9日的两张遥感图像的内孤立波截面, 分别用不同颜色标出, 图 13b为2005年9月6日的遥感图像的内孤立波截面。
通过计算EMD分解所得IMF分量的归一化方差, 得到图像强度截面中的内波信号。内波信号的提取结果如图 14、图 15和图 16所示。对于截面a, 归一化方差最大的是IMF3, 占比70.8%;对于截面b, 归一化方差最大的是IMF3, 占比73.1%;对于截面c, 归一化方差最大的是IMF4, 占比49.3%。我们认为这三个IMF分量分别对应三个截面处的内波信号, 三个截面处的dp-p分别为88.5、87.5和362.5m。在实际的海洋中, 卫星遥感的传感器接收的信号可以认为是多种不同尺度的海洋信号相互叠加而成, 因此其捕捉到的内波信号中必然会夹杂着许多其他信息, 这也导致通过未经处理的原始内波截面的图像强度直接提取的dp-p并不能准确代表真实的内波信号, 如图所示, 直接从内波截面处提取的dp-p与经过EMD分解后提取的dp-p并不相同, 我们认为EMD分解所得到的内波信息更加接近实际的内波信息。
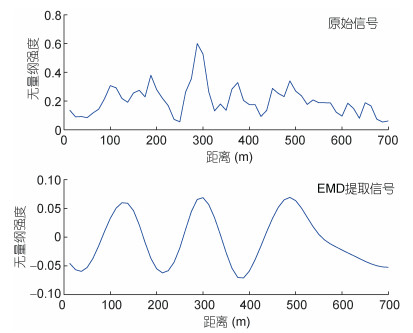 |
| 图 14 经验模态分解提取的截面a处图像强度相邻峰值的间隔 Fig. 14 Extraction of peak-peak spacing at Transect a by Empirical Mode Decomposition (EMD) |
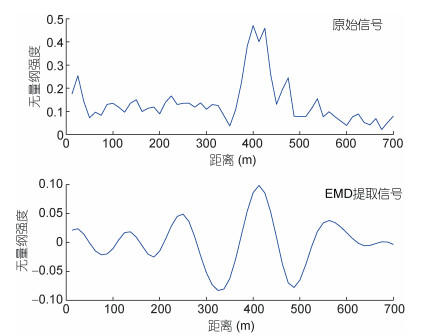 |
| 图 15 经验模态分解提取的截面b处图像强度相邻峰值的间隔 Fig. 15 Extraction of peak-peak spacing at Transect b by EMD |
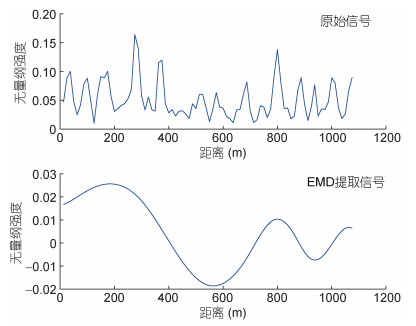 |
| 图 16 经验模态分解提取的截面c处图像强度相邻峰值的间隔 Fig. 16 Extraction of peak-peak spacing at Transect c by EMD |
结合海水层结以及dp-p, 我们运用两种不同的内波一维传播方程计算三张遥感图像中内孤立波的振幅及传播速度。对于2005年5月9日, ENVISAT-1和ERS-1卫星所拍摄的两张遥感图像, 其dp-p分别为88.5m和87.5m, 上层深度和水深分别为h1=20m, H=250m, 上层密度为ρ1=1018kg/m3, 下层密度为ρ2=1024kg/m3。通过KdV方程计算得到内孤立波的振幅分别为29.9m和30.6m, 传播速度分别为1.78m/s和1.79m/s; 通过BO方程计算得到内孤立波的振幅为7.0m和7.1m, 传播速度分别为1.22m/s和1.22m/s。对于2005年9月7日, ERS-1卫星所拍摄的遥感图像, 其dp-p为362.5m, 上层深度和水深分别为h1=95m, H=350m, 上层密度为ρ1=1021kg/m3, 下层密度为ρ2=1026kg/m3。通过KdV方程计算得到内孤立波的振幅为64.8m, 传播速度为2.53m/s, 通过BO方程计算得到内孤立波的振幅为38.5m, 传播速度为2.46m/s。
通过不同方程反演所得的内波振幅与传播速度都存在比较大的差别。为判断反演结果是否合理, 我们将反演所得的振幅与前人对南海北部内波振幅情况的统计结果进行比较。甘锡林等(2007)曾对南海北部内波的振幅分布情况进行了统计分析, 根据其绘制的内波振幅统计分布图可以发现, 内孤立波截面a与截面b所处海域的内波振幅范围约为10—20m, 内孤立波截面c所处海域的内波振幅范围约为20—60m。由此可见KdV方程反演的结果偏大, 而BO方程的反演结果更接近这一范围。孙丽娜等(2018)通过遥感图像提取了南海北部内波的传播速度, 指出南海北部内波传播速度随水深增加逐渐增大, 变化范围在0.4—3.0m/s之间。根据其给出的水深与内波传播速度的对比, 当水深在200—400m范围, 内波的传播速度约为1.1—1.5m/s。由此可见KdV方程反演的结果超出这一范围, 而BO方程的反演结果相较于KdV方程的反演结果更接近这一范围。因此我们认为相比于KdV方程, BO方程反演所得振幅以及传播速度更加符合该海域的实际情况。由于没有与遥感图像时间同步的现场观测数据, 所以我们无法对两种方法反演所得的振幅以及传播速度的精确度做出判断, 我们认为BO方程相较于KdV方程更适合用于反演该海域内波参数。另一方面, 遥感图像的分辨率以及dp-p的提取方法都有可能导致反演结果的变化, 尤其是dp-p对反演精确度尤为关键, 这也导致反演结果的不确定性增加。
3 结论南海北部是全球内波最为活跃的海区之一, 内波在传播过程中可能会发生相互作用, 这种现象频繁地被遥感图像所拍摄到, 内波的相互作用可能导致内波振幅的剧烈变化, 从而对水下结构构成威胁。内波振幅以及传播速度对我们了解认识内波具有重要的研究意义。本文对南海北部多颗卫星所拍摄到的大量遥感图像进行整理, 统计分析了其中的内孤立波以及相互作用现象时空分布特征, 并对统计结果做出合理的解释:内波传播至东沙岛发生绕射, 绕射的内波分裂成两列, 继续西传过程中发生相互作用; 内波传至海南岛附近浅滩处发生反射, 与后续传至的内波发生相互作用。南海北部的内孤立波及相互作用现象主要集中在4—9月份, 其中6月份内波数量最多, 这是由于南海北部夏季海水层结强于冬季。与此同时我们还结合遥感图像和观测数据, 分别采用KdV方程和BO方程对东沙岛附近海域的内孤立波振幅以及传播速度进行了反演实验。根据反演结果, 我们认为BO方程所得内孤立波振幅以及传播速度更加接近该海域的实际情况, 通过遥感图像和观测数据对内波参数进行反演的方法是可行的。接下来我们将针对南海北部的内波相互作用展开进一步研究。
致谢 感谢“国家科技基础条件平台-国家地球系统科学数据共享服务平台-南海及其邻近海区科学数据中心(http://ocean.geodata.cn) ”提供数据支撑。
甘锡林, 黄韦艮, 杨劲松, 等. 2007. 利用多源遥感卫星数据研究南海内波的时空分布特征. 遥感技术与应用, 22(2): 242-245 DOI:10.3969/j.issn.1004-0323.2007.02.024 |
甘锡林, 黄韦艮, 杨劲松, 等. 2007. 基于希尔伯特-黄变换的合成孔径雷达内波参数提取新方法. 遥感学报.2007, 11(1): 39-47 |
孙丽娜, 张杰, 孟俊敏. 2018. 基于遥感与现场观测数据的南海北部内波传播速度. 海洋与湖沼, 49(3): 471-480 |
李娟, 刘苗, 王春梅, 等. 2014. 基于柱Kadomtsev-Petviashvili模型的海洋内孤立波非线性相互作用传播特征仿真模拟研究. 河北科技大学学报, 35(6): 512-517 |
李群, 孙丽, 徐肇廷. 2007. 内孤立波波-波相互作用的数值模拟. 中国海洋大学学报, 37(6): 868-872 |
杜涛. 2000. 浅强跃层大振幅内波研究. 地学前缘.2000, 7(S1): 179-188 |
杨海军, 刘秦玉. 1998. 南海海洋环流研究综述. 地球科学进展, 13(4): 364-368 DOI:10.3321/j.issn:1001-8166.1998.04.007 |
Alford M H, Peacock T, MacKinnon J A et al, 2015. The formation and fate of internal waves in the South China Sea. Nature, 521(7550): 65-69 DOI:10.1038/nature14399 |
Alpers W, 1985. Theory of radar imaging of internal waves. Nature, 314(6008): 245-247 DOI:10.1038/314245a0 |
Baines P G, 1998. Topographic Effects in Stratified Flows. Cambridge: Cambridge University Press
|
Benjamin T B, 1967. Internal waves of permanent form in fluids of great depth. Journal of Fluid Mechanics, 29(3): 559-592 DOI:10.1017/S002211206700103X |
Benney D J, 1966. Long non-linear waves in fluid flows. Journal of Mathematics and Physics, 45(1-4): 52-63 DOI:10.1002/sapm196645152 |
Da Silva J C B, Ermakov S A, Robinson I S et al, 1998. Role of surface films in ERS SAR signatures of internal waves on the shelf:1. Short-period internal waves. Journal of Geophysical Research:Oceans, 103(C4): 8009-8031 |
Garrett C, Munk W, 1979. Internal waves in the ocean. Annual Review of Fluid Mechanics, 11(1): 339-369 |
Grimshaw R, Pelinovsky E, Poloukhina O, 2002. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlinear Processes in Geophysics, 9(3-4): 221-235 |
Huang X D, Chen Z H, Zhao W et al, 2016. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6: 30041 DOI:10.1038/srep30041 |
Liu A K, Hsu M K, 1998. Nonlinear internal wave interaction in the China seas. The 1998 WHOI/IOS/ONR Internal Solitary Wave Workshop: Contributed Papers, 140-142
|
Matsuno Y, 1998. Oblique interaction of interfacial solitary waves in a two-layer deep fluid. Proceedings of the Royal Society of London. Series A:Mathematical, Physical and Engineering Sciences, 454(1971): 835-856 DOI:10.1098/rspa.1998.0188 |
Miles J W, 1977. Obliquely interacting solitary waves. Journal of Fluid Mechanics, 79(1): 157-169 |
Ono H, 1975. Algebraic solitary waves in stratified fluids. Journal of the Physical Society of Japan, 39(4): 1082-1091 DOI:10.1143/JPSJ.39.1082 |
Osborne A R, Burch T L, 1980. Internal solitons in the Andaman Sea. Science, 208(4443): 451-460 DOI:10.1126/science.208.4443.451 |
Thompson D R, Gasparovic R F, 1986. Intensity modulation in SAR images of internal waves. Nature, 320(6060): 345-348 DOI:10.1038/320345a0 |
Thorpe S A, 1975. The excitation, dissipation, and interaction of internal waves in the deep ocean. Journal of Geophysical Research, 80(3): 328-338 DOI:10.1029/JC080i003p00328 |
Wang C, Pawlowicz R, 2012. Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia. Journal of Geophysical Research:Oceans, 117(C6): C06031 |
Wang C X, Wang X, Da Silva J C B, 2019. Studies of internal waves in the strait of georgia based on remote sensing images. Remote Sensing, 11(1): 96 |
Xue J S, Graber H C, Lund B et al, 2013. Amplitudes estimation of large internal solitary waves in the Mid-Atlantic Bight using synthetic aperture radar and marine X-band radar images. IEEE Transactions on Geoscience and Remote Sensing, 51(6): 3250-3258 DOI:10.1109/TGRS.2012.2221467 |
Xue J S, Graber H C, Romeiser R et al, 2014. Understanding internal wave-wave interaction patterns observed in satellite images of the Mid-Atlantic Bight. IEEE Transactions on Geoscience and Remote Sensing, 52(6): 3211-3219 DOI:10.1109/TGRS.2013.2271777 |
Yang J S, Huang W G, Zhou C B et al, 2001. Simulation study on optimal conditions for internal wave observation by SAR. In: Scanning the Present and Resolving the Future. Proceedings IEEE 2001 International Geoscience and Remote Sensing Symposium. Sydney, NSW, Australia, Australia: IEEE
|
Zheng Q A, Yuan Y L, Klemas V et al, 2001. Theoretical expression for an ocean internal soliton synthetic aperture radar image and determination of the soliton characteristic half width. Journal of Geophysical Research:Oceans, 106(C12): 31415-31423 DOI:10.1029/2000JC000726 |
 2019, Vol. 50
2019, Vol. 50