
中国海洋湖沼学会主办。
文章信息
- 杜砚冰, 王彩霞, 苏梦. 2019.
- DU Yan-Bing, WANG Cai-Xia, SU Meng. 2019.
- 内孤立波过凹陷地形的实验探究
- EXPERIMENTAL STUDY OF CANYON TOPOGRAPHY IMPACT ON INTERNAL SOLITARY WAVE
- 海洋与湖沼, 50(5): 971-978
- Oceanologia et Limnologia Sinica, 50(5): 971-978.
- http://dx.doi.org/10.11693/hyhz20190400067
文章历史
-
收稿日期:2019-04-03
收修改稿日期:2019-05-10
2. 国家海洋局烟台海洋环境监测中心站 烟台 264000
2. Yantai Marine Environment Monitoring Central Station of State Oceanic Administration, Yantai 264000, China
内波是在重力场作用下发生在密度稳定层化的流体内部的一种波动, 其波动的频率介于惯性频率与浮性频率之间(方欣华等, 2005)。内波通常分为内潮波(线性或弱线性潮成内波)和内孤立波(强非线性潮成内波)。本文的观测对象为内孤立波, 它在非线性作用和频散作用相平衡的情况下产生。在密度稳定层化的海水中, 正压潮流经过剧烈变化的地形(例如陆架边缘, 海底山脉等)时受地形的强迫作用激发产生内潮波(Vlasenko et al, 2005)。由于实际海洋环境因素的复杂性, 内潮波的传播也很不稳定, 尤其在陆坡和海槛区域内潮波常常与海底和跃层相互作用产生内孤立波。
在对内孤立波传播的研究中, 底地形对内波传播的影响一直是研究的热点, 20世纪80年代以来, 一些理论和实验陆续研究了内孤立波经过各种底地形的传播情况(Small, 2003)。Helfrich等(1984)的实验研究了内孤立波在两层流体中随水深不断增加情况下的散射情况。在进一步的论文中(Helfrich et al, 1986)又使用实验室实验和理论模型结合的方法对长波形内孤立波在海底地形上的演变实验结果进行了检验。他们的实验考虑了下凹型内孤立波从下层水厚的区域经过斜坡地形传播经过上下层水厚度相等的拐点到上层水厚的区域的形态变化情况。他们的eKdV (Korteweg-de Vries)方程数值模拟研究结果表明, 当入射波传播通过上下层厚度相等的拐点时可能会出现多个发生了极性转换的波, 即内孤立波将扩散为震荡的一系列波包。Kao等(1985)的实验也研究了两层流体中内孤立波在斜坡地形上的传播过程。在他们的实验设置中下层水始终比上层厚, 内孤立波波形一直保持为下凹型。他们用KdV方程检验了连续分层流体中密度跃层内部的孤立波形态, 并且在弱分层盐水溶液中研究了内孤立波从深水生成后传播到斜面上的演变和破碎情况。与上凸波的实验结果对比, 发现在下凹型内孤立波破碎之前波形尾部变陡。经过定量测量发现, 内孤立波波形破碎是由界面剪切不稳定支配的。之后大振幅内孤立波经过正向和反向陡坡的破碎实验也被广泛研究(Djordjevic et al, 1978)。他们发现内孤立波向浅水区传播可能导致波浪破碎和多个上凸型类孤子波的产生和沿斜坡向上的传播(Michallet et al, 1999; Cheng et al, 2009, 2011)。
虽然前人已经进行了许多内孤立波经过斜坡或山脊地形的演化实验(Wessels, 1996; Chen, 2007), 但我们对内孤立波与凹陷地形作用情况的理解有限。凹陷的峡谷状地形普遍存在于海底地形中, 当内孤立波传播经过峡谷时, 流体的厚度变化会导致内孤立波的演化。故本文设计实验记录了下凹型内孤立波在凹陷地形上传播的演化过程。本实验结果可作为研究内孤立波在海洋中传播时受海底凹陷地形影响的参考, 为内波理论研究、数值模拟及内波观测提供较为准确的依据。
1 实验装置本实验地点为中国海洋大学物理海洋教育部重点实验室, 实验在密度分层水槽中进行, 实验所用水槽为玻璃钢架构造, 规格为长3m×宽0.2m×高0.3m。在水槽前布设CCD (Charge Coupled Device)相机用于数据采集, 由于所需拍摄范围不同, 实验中使用分辨率分别为1920像素×1080像素和4096像素×3000像素的两种相机, 对应的观测区水平范围分别约为0.5m和1.2cm。数据分析利用MATLAB软件编程完成。实验布局示意图如图 1所示。在内孤立波与凹陷地形作用实验中, 在水槽底部铺设地形, 用以改变孤立波的传播特性, 所用地形是两个截面为直角梯形的棱柱, 如图 2所示, 模型表面经抛光处理, 地形与水槽内壁距等宽、放置水槽中无缝隙。两地形尖角端相对, 拼成凹陷地形, 左侧地形紧贴水槽左侧, 右侧地形与左侧地形尖角端相距一定距离d放置。
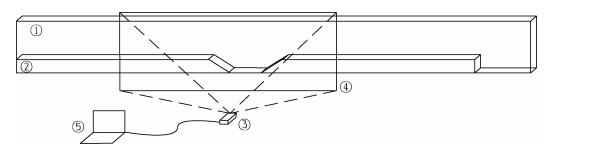 |
| 图 1 实验现场示意图 Fig. 1 Schematic illustration of the laboratory setup 注: ①:实验水槽, ②:实验地形, ③:工业相机, ④:实验观测区域, ⑤:图像采集所用电脑 |
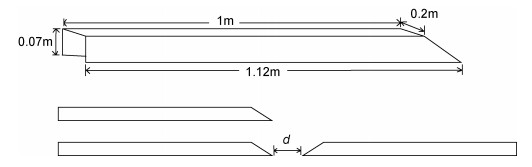 |
| 图 2 地形示意图 Fig. 2 Schematic illustration of the topography 注: d表示右侧地形与左侧地形尖角端之间的距离 |
图 3为在水槽内用重力塌陷法造波的示意图。在两层流体系统中, 上层染色淡水厚度为h1、密度为ρ1, 下层盐水厚度为h2、密度为ρ2。水槽的左端设置重力塌陷造波, 内孤立波生成后的传播路径是从左至右。挡板左侧为造波区, 挡板两侧的界面高度差为塌陷高度η, 抽出挡板后内孤立波在水槽最左端生成并向右传播, 在距水槽左端一定距离的观测位置处设置垂直断面, 记录内孤立波经过时的两层流体界面高度变化情况作为初始振幅a。
 |
| 图 3 初始波形观测位置 Fig. 3 Observing location of initial waveform 注: h1为上层染色淡水厚度, h2为下层盐水厚度, η为塌陷高度 |
在同一层结条件下, 仅改变造波的塌陷高度η, 观察生成内孤立波振幅a的变化规律。图 4中给出了实测内孤立波初始振幅与塌陷高度之间相关关系的系列实验结果, 图 4a是上层流体厚度h1=1cm, 下层流体厚度h2=10cm的层结下生成下凹型内孤立波的造波结果, 图 4b是上层流体厚度h1=12cm, 下层流体厚度h2=3cm的层结下生成上凸型内孤立波的造波结果。每种层结下都进行了8次造波实验, 在图中以圆点标记。由图可知, 无论对于下凹波还是上凸波实验组的层结, 塌陷高度均要比前导波初始振幅大, 但两者之间是正相关关系, 即塌陷高度越大, 初始振幅也越大。通过对比两组实验发现, 相同层结、相同塌陷高度时生成的内孤立波振幅仍然可能不完全相同, 这是由于应用重力塌陷法造波时, 手动抽出挡板的速度和方向的不稳定造成的波形不稳定。
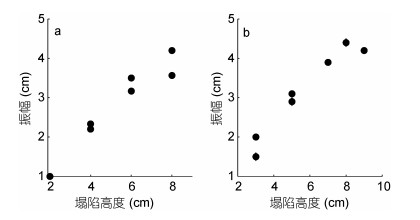 |
| 图 4 前导波初始振幅与塌陷高度关系图 Fig. 4 Relation between the measured wave amplitude and step depth |
Korteweg-de Vries (KdV)方程是建立在弱非线性、弱频散性且两者平衡条件下的一类内孤立波理论模型, 其表达式如下:
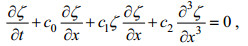 (1)
(1)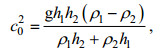 (2)
(2)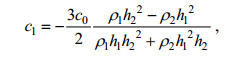 (3)
(3)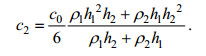 (4)
(4)KdV的理论解如下:
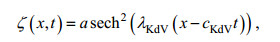 (5)
(5)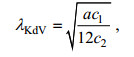 (6)
(6)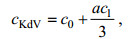 (7)
(7)其中, ζ为两层流体界面起伏, 它是水平位移x和时间t的函数; 方程各项系数c0、c1和c2分别可由重力加速度g、上下层流体厚度h1、h2和密度ρ1、ρ2求得; a为内孤立波振幅, cKdV和λKdV为KdV理论解的相速度和波长。
KdV方程适用于小振幅内孤立波, 随着内孤立波振幅的增大, 高阶非线性项的影响会逐渐增大, 非线性和色散效应不再保持平衡, 故KdV理论不再适用。可以通过在KdV方程中加入立方非线性项使其适用于大振幅内孤立波, 所得修正方程为eKdV方程。而mKdV理论是对eKdV理论的进一步修正, mKdV方程可以应用于上下层流体深度比接近其临界值, 即当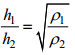
mKdV方程的表达式为:
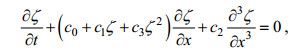 (8)
(8)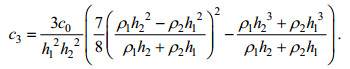 (9)
(9)mKdV的理论解为:
 (10)
(10)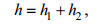 (11)
(11)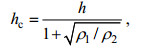 (12)
(12)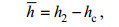 (13)
(13) (14)
(14)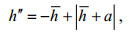 (15)
(15)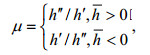 (16)
(16)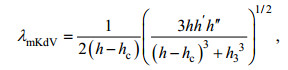 (17)
(17)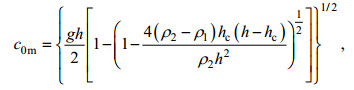 (18)
(18)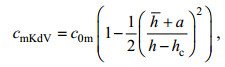 (19)
(19)其中, cmKdV和λmKdV为mKdV理论解的相速度和波长。
图 5给出了当上层流体厚度h1=1cm, 下层流体厚度h2=10cm, 塌陷高度η分别为2、4、6、8cm四种情况下的实验生成的下凹型内孤立波波形与理论波形的比较图。图中黑色实线为实验中生成的实际内孤立波波形, 虚线为KdV理论波形, 点线为mKdV理论波形。在图 5a中, 实验生成的下凹型前导内孤立波波形更接近KdV理论波形, mKdV波形更宽, 而在图 5b—图 5d中, 前导内孤立波的波形变宽, 实验波形更符合mKdV方程模拟结果。
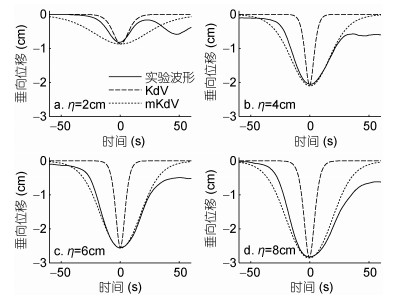 |
| 图 5 下凹型内孤立波实验与理论结果比较 Fig. 5 Comparison between experimental and theoretical results for depression-type internal solitary waves |
通过比较实验波形和理论波形在振幅半值处的波形宽度值差异大小来判断实验波形与理论波形的符合程度。记振幅值半值处对应的KdV波形与实验波形波宽差为dKdV, mKdV波形与实验波形波宽差为dmKdV, 定义当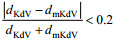
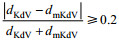
| h1(cm) | h2(cm) | d(cm) | η(cm) | a(cm) | ε | 适用理论 |
| 1 | 10 | 0 | 2 | 0.9 | 0.08 | KdV |
| 1 | 10 | 0 | 4 | 2.2 | 0.2 | mKdV |
| 1 | 10 | 0 | 6 | 2.5 | 0.23 | mKdV |
| 1 | 10 | 0 | 8 | 2.9 | 0.26 | mKdV |
| 1 | 10 | 20 | 2 | 1 | 0.09 | mKdV |
| 1 | 10 | 20 | 4 | 2.2 | 0.2 | mKdV |
| 1 | 10 | 20 | 6 | 3.5 | 0.32 | mKdV |
| 1 | 10 | 20 | 8 | 4.2 | 0.38 | mKdV |
| 1 | 10 | 41 | 2 | 1 | 0.09 | mKdV |
| 1 | 10 | 41 | 4 | 2.6 | 0.24 | mKdV |
| 1 | 10 | 41 | 6 | 3.5 | 0.32 | mKdV |
| 1 | 10 | 41 | 8 | 3.6 | 0.33 | mKdV |
| 1 | 8.5 | 0 | 2 | 1.3 | 0.14 | mKdV |
| 1 | 8.5 | 0 | 4 | 2.2 | 0.23 | mKdV |
| 1 | 4 | 0 | 3 | 1.1 | 0.22 | mKdV |
| 1 | 4 | 15 | 3 | 1.4 | 0.28 | mKdV |
| 1 | 3 | 0 | 2 | 1 | 0.25 | mKdV |
| 1.5 | 6 | 0 | 3 | 1 | 0.13 | mKdV |
| 1.5 | 6 | 0 | 5 | 2.2 | 0.29 | mKdV |
| 注: h1为上层流体厚度, h2为下层流体厚度, d为左右两侧地形距离, η为塌陷高度, a为内孤立波振幅, ε为非线性参数 | ||||||
在上凸型内孤立波实验中, 保持流体层结不变, 随着内孤立波初始振幅的增加, 内孤立波波形从接近KdV理论波形逐渐转变为mKdV理论波形。图 6给出了h1=12cm, h2=3cm的层结下, 塌陷高度η分别为3、5、7、9cm四种情况下实验波形与理论波形的比较图。图中黑色实线为实验中生成的实际内孤立波波形, 虚线为KdV理论波形, 点线为mKdV理论波形。从图中可以观察到当塌陷高度η=3cm时, 实验波形接近KdV理论模拟结果; 随着塌陷高度增加, 在η=5cm和7cm的实验中, 实验波形宽度介于KdV理论和mKdV理论波形之间; 当η=9cm时, 上凸型内孤立波的实验波形变为更接近mKdV波形的形态。
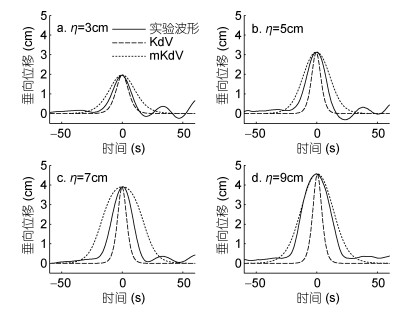 |
| 图 6 上凸型内孤立波实验与理论结果比较 Fig. 6 Comparison between experimental and theoretical results for elevation-type internal solitary waves |
将上凸型内孤立波的各组实验波形与理论波形比较发现, 实验波形不完全适用于某一理论。计算了各组实验非线性参数ε, 将结果整理为列表 2, 由表可知, 对于本文中进行的上凸型内孤立波实验, 非线性参数ε≤0.22时, KdV理论波形与上凸型内孤立波实验波形符合较好; 当内孤立波初始振幅增大, 非线性参数也随之增大, 上凸型内孤立波波形介于Kdv理论和mKdv理论波形之间; 当非线性参数ε≥0.27时, mKdV理论与实验波形符合较好。
| h1 (cm) | h2 (cm) | η(cm) | a(cm) | ε | 适用理论 |
| 6 | 3 | 5 | 1.9 | 0.21 | KdV |
| 8 | 3 | 3 | 1.75 | 0.16 | KdV |
| 8 | 3 | 5 | 2.4 | 0.22 | KdV |
| 8 | 3 | 7 | 2.7 | 0.25 | - |
| 10 | 3 | 3 | 2.2 | 0.17 | KdV |
| 10 | 3 | 5 | 2.7 | 0.21 | KdV |
| 10 | 3 | 7 | 3.5 | 0.27 | m KdV |
| 12 | 3 | 3 | 2 | 0.13 | KdV |
| 12 | 3 | 5 | 3.1 | 0.21 | - |
| 12 | 3 | 7 | 3.9 | 0.26 | - |
| 12 | 3 | 9 | 4.2 | 0.28 | m KdV |
| 注: “-”代表实验波形介于两种理论波形之间 | |||||
在水槽底部放置凹陷地形, 通过拉开右侧地形不同距离d改变凹陷地形的宽度, 观察下凹型内孤立波传播经过不同宽度的凹陷地形的演化过程。在本实验中, ρ1=1000kg/m3, ρ2=1041kg/m3, 由内孤立波理论我们知道, 当上层流体厚度和下层厚度满足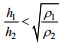
图 7为h1=1.5cm, h2=6cm, d=41cm时的实验波形图, 其他各组实验中波形演化情况基本一致, 总体而言内孤立波整体波形并无明显转变, 在经过凹陷地形的过程中维持下凹形态。从细节上看, 下凹型主波前半部分基本没有变化, 而主波的尾部界面有所抬升, 波形后半部分变陡。推测造成下凹型内孤立波尾部形态演化的原因有两方面:第一, 受限于水槽和地形尺寸, 在水槽左端重力塌陷法生成下凹型内孤立波在遇到地形前的过程中仍未形成一个稳定传播的波形, 所以在波形传播过程中还在进行波形稳定前的演化, 尾部界面逐渐抬升, 波形变得更完整, 结合对照实验得出这是波形演化的主要原因; 第二, 凹陷地形的上坡段对内孤立波的作用。在下凹型内孤立波的爬坡阶段, 可以观察到主波后半部分波形变陡峭, 这是由于内孤立波受到上坡地形作用波形变得不稳定, 在内孤立波爬坡过程中为保证质量守恒, 界面处的剪切效应增加导致内孤立波尾波波形变陡(Kao et al, 1985)。
 |
| 图 7 h1=1.5cm, h2=6cm, d=41cm情况下的波形图 Fig. 7 Photos of the waveform in case of h1=1.5cm, h2=6cm, d=41cm |
下凹型内孤立波传播经过凹陷地形时受到其作用, 振幅大小发生变化, 通过观测内孤立波振幅的变化趋势, 有助于理解凹陷地形作用影响下凹型内孤立波能量演化过程。
3.2.1 无地形实验内孤立波在水槽中传播时, 除了受凹陷地形部分作用造成内孤立波振幅变化, 还会受到流体黏滞力和水槽侧壁和底部摩擦力的作用, 引起振幅衰减(赵国君等, 2013), 若要讨论凹陷地形本身对内孤立波的作用, 需排除地形以外的干扰, 为此我们设置了无地形的对照组实验:无地形实验两层流体分层结构为h1=1cm, h2=10cm, 进行了塌陷高度η分别为2、4、6、8cm的四次实验。
将内孤立波水平传播单位距离的振幅减小量定义为衰减率, 即R=da/dx(R为衰减率, da为内孤立波传播水平距离dx过程中对应的振幅减小量)。表 3给出了四次无地形实验中内孤立波的振幅衰减率, 从表 3中数据来看, 随着塌陷高度增加, 虽然没有观察到振幅衰减的变化趋势, 几次实验振幅衰减率的量级是一致的, 于是我们对四次实验的衰减率求平均, 得到的数值0.0042作为无地形条件下内孤立波实验水槽中传播的平均衰减率。
| η(cm) | a(cm) | R |
| 2 | 0.9 | 0.0035 |
| 4 | 3.5 | 0.0041 |
| 6 | 4.6 | 0.0037 |
| 8 | 4.4 | 0.0057 |
| 注: η为塌陷高度, a为内孤立波振幅, R为振幅平均衰减率 | ||
图 8为h1=1cm, h2=10cm层结下, 凹陷地形逐渐拉开距离, 左右地形距离d分别为0、20、41cm时, 不同初始振幅内孤立波过凹陷地形对应的振幅变化滤波后结果。三组实验共性在于, 当振幅过小时凹陷地形对振幅大小影响很微弱, 当振幅足够大时, 内孤立波振幅变化整体趋势是一致的, 下凹型内孤立波与凹陷地形相遇时会发生振幅的减小, 而离开凹陷地形阶段振幅有变大趋势, 离开地形后振幅减小。推测下凹型主波接近凹陷地形时的振幅减小是地形对内孤立波产生扰动使振幅有轻微的衰减, 而进入凹陷地形后振幅的增加的可能原因有两个: 1)经过下坡地形后地形的扰动结束, 内孤立波进入新的层结, 上层流体厚度保持1cm不变而下层从10cm到17cm逐渐变大, 随着内孤立波在新的层结重新回归稳定状态, 下凹型内孤立波振幅增加; 2)由于凹陷地形后半段可看成一个斜坡地形, 结合前人内孤立波与斜坡作用的实验(Chen et al, 2007), 内孤立波与上坡地形作用, 地形会对迎面而来的内孤立波做功, 于是推测振幅的增加趋势部分来自凹陷地形后半段迎波面对内波做功能量增加的结果。
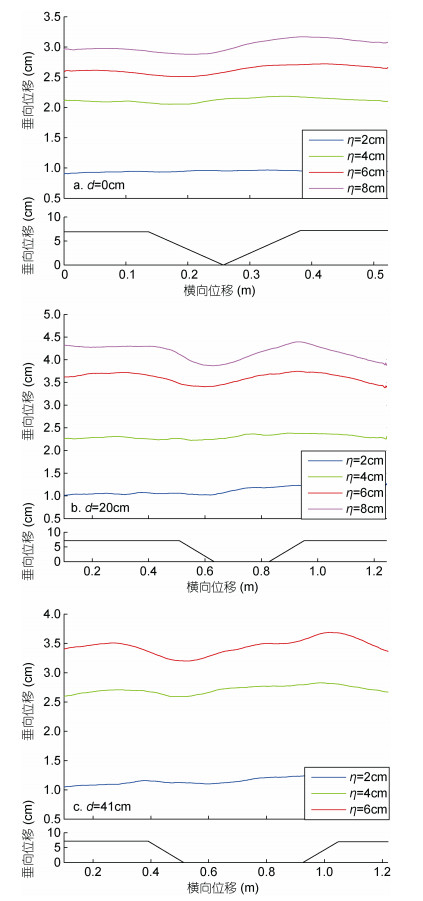 |
| 图 8 主波振幅随传播位置的变化 Fig. 8 Wave amplitude changes with horizontal displacement 注:黑线表示底地形高度随横向位移的变化 |
通过振幅变化趋势我们发现小振幅内孤立波振幅变化平缓, 内孤立波振幅越大, 其变化越剧烈。在流体分层结构为h1=1cm, h2=10cm外, 额外设置了h1=1cm, h2=8.5、4、3cm的实验组, 观察其主波振幅受地形影响的变化情况。参考前人内孤立波与山脊作用的实验(赵国君等, 2013), 引入无量纲参数障碍比ξ来描述控制波传播和反射的能量水平, 对于下凹波与山脊地形作用其定义为(h1+a)/(h1+h2+hs), a为下凹型内孤立波振幅, hs为山脊地形高度, 在本实验下凹波与凹陷地形作用中, 我们将障碍比定义为ξ=(h1+a)/(h1+h2+hc), hc为凹陷地形总厚度, 以凹陷地形前后10cm范围内的振幅变化曲线极大值与极小值之差Δa作为振幅变化剧烈程度的衡量标准, 各组实验结果如表 4所示。
| h1(cm) | h2(cm) | d(cm) | η(cm) | a(cm) | ξ | Δa(cm) |
| 1 | 10 | 0 | 2 | 0.9 | 0.11 | 0.04 |
| 1 | 10 | 0 | 4 | 2.2 | 0.18 | 0.14 |
| 1 | 10 | 0 | 6 | 2.5 | 0.19 | 0.21 |
| 1 | 10 | 0 | 8 | 2.9 | 0.22 | 0.29 |
| 1 | 10 | 20 | 2 | 1 | 0.11 | 0.23 |
| 1 | 10 | 20 | 4 | 2.2 | 0.18 | 0.16 |
| 1 | 10 | 20 | 6 | 3.5 | 0.25 | 0.34 |
| 1 | 10 | 20 | 8 | 4.2 | 0.29 | 0.52 |
| 1 | 10 | 41 | 2 | 1 | 0.11 | 0.16 |
| 1 | 10 | 41 | 4 | 2.6 | 0.2 | 0.24 |
| 1 | 10 | 41 | 6 | 3.5 | 0.25 | 0.49 |
| 1 | 8.5 | 0 | 2 | 1.3 | 0.14 | 0.12 |
| 1 | 8.5 | 0 | 4 | 2.2 | 0.19 | 0.26 |
| 1 | 4 | 0 | 3 | 1.1 | 0.18 | 0.11 |
| 1 | 4 | 15 | 3 | 1.4 | 0.2 | 0.13 |
| 1 | 3 | 0 | 2 | 1 | 0.18 | 0.18 |
| 注: h1为上层流体厚度, h2为下层流体厚度, d为左右两侧地形距离, η为塌陷高度, a为内孤立波振幅, ξ为障碍比, Δa为凹陷地形前后10cm范围内的振幅变化曲线极大值与极小值之差 | ||||||
将表 4中振幅极值差Δa与障碍比ξ数据列作图, 得到图 9振幅极值差与障碍比关系图。从图 9可知, 振幅变化的剧烈程度与障碍比值是近似正相关的关系, 当障碍比较小, 下凹型内孤立波的振幅变化并不明显, 当ξ > 0.25时, 下凹型内孤立波的振幅变化较大, 凹陷地形与下凹型内孤立波的作用明显。
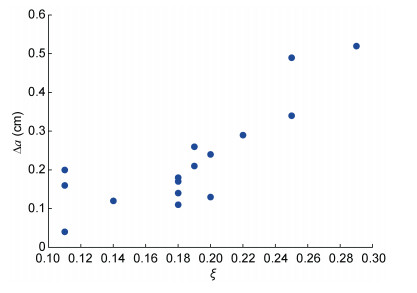 |
| 图 9 振幅极值差与障碍比关系图 Fig. 9 Relationship between amplitude differences and obstacle ratios 注: ξ为障碍比, Δa为凹陷地形前后10cm范围内的振幅变化曲线极大值与极小值之差 |
实验中发现重力塌陷法造波时塌陷高度与初始振幅的正相关关系。对于下凹型内孤立波实验组, 与KdV理论相比, mKdV理论与实测波形在总体上更加符合; 而对上凸型内孤立波实验, 非线性参数ε≤0.22时, KdV理论波形较窄, 与上凸型内孤立波实验波形符合较好, 当内孤立波初始振幅增大, 非线性参数也随之增大, 上凸型内孤立波波形介于KdV理论和mKdV理论波形之间, 当非线性参数ε≥0.27时, mKdV理论与实验波形符合较好。下凹型内孤立波经凹陷地形波形演化并不明显, 内孤立波传播过程中前半部波形维持稳定, 尾部界面抬升, 尾部波形变陡。凹陷地形的存在会使下凹形内孤立波的振幅先减小再增加。下凹型内孤立波与凹陷地形作用振幅变化的强度与地形障碍比存在近似的正相关关系:小障碍比ξ实验中凹陷地形与下凹型内孤立波的作用比较微弱; 随着ξ数值增加, 下凹型内孤立波振幅变化增强; 当ξ > 0.25时, 下凹型内孤立波的振幅变化较强, 凹陷地形与下凹型内孤立波的作用明显。
方欣华, 杜涛. 2005. 海洋内波基础和中国海内波. 青岛: 中国海洋大学出版社, 7
|
赵国君, 邵利民, 陈旭. 2013. 内孤立波过山脊地形演化实验研究. 海洋工程, 31(4): 42-47 |
Chen C Y, 2007. An experimental study of stratified mixing caused by internal solitary waves in a two-layered fluid system over variable seabed topography. Ocean Engineering, 34(14-15): 1995-2008 DOI:10.1016/j.oceaneng.2007.02.014 |
Cheng M H, Hsu J R C, Chen C Y et al, 2009. Modelling the propagation of an internal solitary wave across double ridges and a shelf-slope. Environmental Fluid Mechanics, 9(3): 321-340 |
Cheng M H, Hsu J R C, Chen C Y, 2011. Laboratory experiments on waveform inversion of an internal solitary wave over a slope-shelf. Environmental Fluid Mechanics, 11(4): 353-384 |
Djordjevic V D, Redekopp L G, 1978. The fission and disintegration of internal solitary waves moving over two-dimensional topography. Journal of Physical Oceanography, 8(6): 1016-1024 DOI:10.1175/1520-0485(1978)008<1016:TFADOI>2.0.CO;2 |
Helfrich K R, Melville W K, Miles J W, 1984. On interfacial solitary waves over slowly varying topography. Journal of Fluid Mechanics, 149: 305-317 DOI:10.1017/S0022112084002664 |
Helfrich K R, Melville W K, 1986. On long nonlinear internal waves over slope-shelf topography. Journal of Fluid Mechanics, 167: 285-308 DOI:10.1017/S0022112086002823 |
Kao T W, Pan F S, Renouard D, 1985. Internal solitons on the pycnocline:generation, propagation, and shoaling and breaking over a slope. Journal of Fluid Mechanics, 159: 19-53 DOI:10.1017/S0022112085003081 |
Michallet H, Ivey G N, 1999. Experiments on mixing due to internal solitary waves breaking on uniform slopes. Journal of Geophysical Research:Oceans, 104(C6): 13467-13477 DOI:10.1029/1999JC900037 |
Pedlosky J, 2003. Waves in the Ocean and Atmosphere:Introduction to Wave Dynamics. Berlin: Springer, 260
|
Small J, 2003. Refraction and shoaling of nonlinear internal waves at the malin shelf break. Journal of Physical Oceanography, 31(12): 2657-2674 |
Vlasenko V, Stashchuk N, Hutter K, 2005. Theoretical Modelling and Observational Evidence. Cambridge: Cambridge University Press, 351
|
Wessels F, Hutter K, 1996. Interaction of internal waves with a topographic sill in a two-layered fluid. Journal of Physical Oceanography, 26(1): 5-20 |
 2019, Vol. 50
2019, Vol. 50


