
中国海洋湖沼学会主办。
文章信息
- 刘兴兴, 张东, 韩飞. 2019.
- LIU Xing-Xing, ZHANG Dong, HAN Fei. 2019.
- 基于PCA和WNN的潮滩沉积物粒度与运移趋势的遥感研究
- REMOTE SENSING STUDY ON SEDIMENT GRAIN SIZE DISTRIBUTION AND ITS MIGRATION TREND ANALYSIS IN TIDAL FLAT BASED ON PCA AND WNN MODEL
- 海洋与湖沼, 50(6): 1168-1180
- Oceanologia et Limnologia Sinica, 50(6): 1168-1180.
- http://dx.doi.org/10.11693/hyhz20190500092
文章历史
-
收稿日期:2019-05-16
收修改稿日期:2019-08-06
2. 南京师范大学 海洋科学与工程学院 南京 210023;
3. 江苏省地理信息资源开发与利用协同创新中心 南京 210023
2. College of Marine Science and Engineering, Nanjing Normal University, Nanjing 210023, China;
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
潮滩主要是指淤泥质海岸的潮间带浅滩, 是在各种动力以及环境因素作用下, 受潮汐变动影响的海陆交汇地带(王爱军等, 2006), 在海洋资源开发利用中占有突出地位。江苏省拥有丰富的潮滩资源, 受自然和人类活动等因素影响, 潮滩冲淤变化的强度与频率呈逐年增加趋势(陈玮彤等, 2018)。潮滩冲淤演变与潮滩沉积动力及水动力过程的协调作用有关, 其中沉积物粒度参数可用于提取沉积环境和物质来源信息, 反映沉积物发生沉积时的水动力条件; 通过分析粒度参数的空间分布与变化特征, 反演沉积物的净输运趋势, 可了解沉积物输运格局、地貌变化特征及其与潮滩冲淤的联系。因此, 监测潮滩沉积物分布与粒径运移趋势, 对分析潮滩冲淤演变规律具有重要意义。
在沉积物粒径运移趋势研究方面, McLaren等(1985)建立了一维粒径趋势模型; Gao等(1992, 1994)改进并提出了二维粒径趋势模型(Grain Size Trend Analysis, GSTA), 通过将平均粒径、分选系数以及偏态三个粒度参数在同一沉积环境下不同地点的差异转化为物质输运信息, 使粒径趋势分析技术趋于成熟。GSTA模型在智利的Izmir湾(Duman et al, 2004)、西班牙的Camposoto海滩(Poizot et al, 2013)、中国的胶州湾及邻近海域(汪亚平等, 2000)、山东月湖(薛允传等, 2002)等地貌单元得到了广泛应用。由于GSTA分析局限于采样区内部, 无法拓展到更大的空间范围, 而遥感具有大范围空间信息提取的技术特点, 因此利用遥感技术结合GSTA模型分析, 是潮滩粒径趋势研究的一个新的方向。
GSTA分析需由特定的粒度参数驱动。目前, 基于定量遥感的潮滩表层沉积演变研究大都利用单波段或波段组合因子作为相关变量, 通过建立粒度参数与光谱之间的线性或非线性统计模型, 来实现沉积物类型、粒度参数的遥感反演(van der Wal et al, 2007;张东等, 2008;郑晓丹等, 2009)。影响潮滩表层光谱特征的因素包括沉积物组成、含水量差异、有机物含量等, 其内在响应机理十分复杂, 因此建立统计模型来进行沉积物粒度参数的遥感反演是一种可行的方案。但是, 波段因子之间的相关性、遥感影像噪声等原因, 使得基于简单统计模型的粒度参数遥感反演精度往往难以突破。相比较而言, 人工神经网络模型在复杂非线性回归方面有着突出优势, 在地物要素定量遥感反演中得到成功应用(De et al, 2012;陈晓琳等, 2015), 将人工神经网络模型用于潮滩沉积物粒度参数遥感反演, 通过非线性拟合, 提高沉积物粒度参数的反演精度, 将是一种有益尝试。
据此, 本文综合运用野外实地采样与多光谱遥感数据, 结合主成分分析法和小波神经网络模型, 研究并实现一种基于遥感粒度参数驱动的沉积物粒径运移趋势分析方法, 以期更加有效、准确地获得大范围的潮滩沉积物粒径运移趋势, 为潮滩资源的合理开发利用及保护提供参考。
1 研究区与数据 1.1 研究区概况以江苏省中部淤泥质潮滩为研究对象, 选择盐城市的运粮河口至川东港口岸段为研究区, 开展潮滩沉积物粒度与粒径运移趋势遥感研究, 位置如图 1a所示。研究区地处江苏省东部黄海之滨, 岸滩坡度平缓, 平均坡度约为1.1‰—2.3‰, 近年来由于滩涂围垦开发, 岸滩呈逐年陡化趋势(张东等, 2018)。岸外海域水动力受东海前进潮波和南黄海旋转潮波控制(任美锷, 1986), 潮流作用呈现季节性变化, 潮流输沙是泥沙的主要运动形式(张存勇, 2013)。沿海潮汐类型主要是正规半日潮, 研究区内平均潮差自北向南逐渐增大, 近岸浅水区浅海分潮作用显著, 潮汐变形明显。在水动力的搬运、沉降和分选作用下, 潮滩沉积物平均粒径为4Φ左右, 主要为正偏态(张长宽, 2013)。
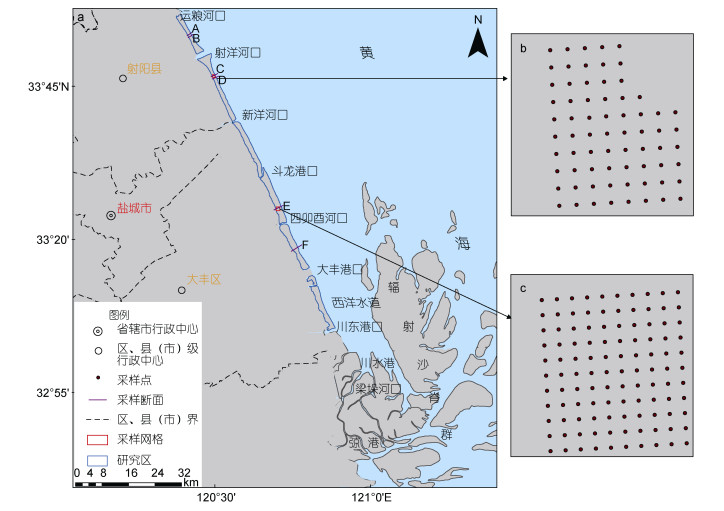 |
| 图 1 研究区及采样点示意图 Fig. 1 Sketch map of the study area and the sampling points 注: a:研究区示意图, 其中A为SY01断面, B为SY02断面, C为SY03断面, D为SY04断面, E为DF01断面, F为DF02断面; b:射阳网格采样区; c:大丰网格采样区 |
2014年7月5—10日低潮时, 在江苏省中部潮滩自北向南、从陆向海布设6条断面, 依次编号为SY01、SY02、SY03、SY04、DF01、DF02断面, SY01、SY02断面位于射阳河口北侧, SY03、SY04断面位于射阳河口南侧, DF01断面位于四卯酉河口北侧, DF02断面位于大丰港一期工程北侧, 共采集表层沉积物样本72个, 采样间隔为60m;在大丰区与射阳县各设置一个矩形网格采样区, 采集了179个有效样本, 网格采样间隔为90m。采样时潮间带基本完全出露, 土壤水分充分下渗, 采样深度为表层1—2cm。采样断面和采样网格位置分布如图 1所示, 其中断面样本数据和网格样本数据用于沉积物粒度参数遥感建模及反演精度评价; 此外, 网格样本数据还用于沉积物粒径运移趋势验证。
沉积物样品在实验室经去除有机质、贝壳碎屑等预处理后, 利用Malven MasterSizer2000激光粒度仪进行沉积物粒度参数分析, 获得Φ/4间隔的粒度分布数据。然后利用矩法公式计算得到样品的平均粒径、分选系数和偏态。
1.3 遥感影像获取和预处理下载了野外采样时间段前后的Landsat、HJ-1A等多景卫星遥感影像数据, 通过目视分析和比选, 剔除其中云量影响大的影像, 最终选取2014年5月7日低潮时覆盖研究区的HJ-1A多光谱遥感影像作为沉积物粒度参数遥感反演的数据源, 影像空间分辨率为30m, 成像时太阳高度角为57.328°, 方位角为290.773°。同时选取覆盖部分研究区的两景Landsat 7 ETM+影像(成像时间为2014年4月25日和8月13日)和一景Landsat 8 OLI影像(成像时间为2014年5月8日)进行平行分析试验, 用于了解影像成像时间与野外采样时间不同步对粒度参数遥感反演结果可能产生的影响。
遥感影像首先利用ENVI FLAASH大气校正模块, 根据影像成像时间和位置, 选择中纬度夏季大气模式(Mid-Latitude-Summer)和海洋气溶胶模型(Maritime)进行大气校正处理; 然后以2014年1—3月的多景几何精校正的GF-1号影像为参照, 采用image to image校正方式完成影像的几何精校正(边金虎等, 2014), 几何校正误差小于0.05个像元; 最后进行光滩分离处理, 通过计算影像归一化差值植被指数(Normalized Difference Vegetable Index, NDVI), 利用光滩与植被NDVI值的差异进行掩膜, 剔除滩涂植被; 光滩与水体则根据两者在近红外波段的反射率差异, 采用单波段阈值法进行分离, 最终获得潮间带光滩的地表反射率影像数据。
2 研究方法潮滩沉积物粒径运移趋势遥感研究主要包含两部分, 一是沉积物粒度参数的遥感反演, 通过筛选合适的粒度参数遥感反演因子和构建遥感反演模型, 获得平均粒径、分选系数、偏态的空间分布; 二是基于遥感反演的粒度参数驱动粒径运移趋势模型, 得到沉积物可能的空间输运特征。具体方法阐述如下。
2.1 沉积物粒度参数遥感反演方法 2.1.1 基于PCA(Principal Component Analysis)的粒度参数遥感反演因子筛选方法现有的沉积物粒度参数遥感反演因子主要有单波段因子(韩飞, 2015)、波段组合因子(郑晓丹等, 2009)、遥感指数因子(张东等, 2008)等, 一般以相关系数为指标对其进行筛选。其问题在于多光谱影像的各波段之间具有高度相关性, 在一定程度上存在信息冗余, 利用相关性高的波段进行波段组合, 可能会进一步加大信息分离和提取的难度。
已有研究表明, PCA主成分分析是一种去除波段之间多余信息、将多波段图像信息压缩到比原来波段更有效的少数几个转换波段的方法, 转换后的主分量信噪比大, 噪声减小(许石罗等, 2017)。因此利用ENVI5.3对潮间带光滩反射率影像进行主成分分析处理, 首先计算出所有波段的协方差矩阵, 然后使用该矩阵计算主成分和特征向量(梁菲等, 2011), 处理后得到4个主成分波段, 计算其特征值及各主成分波段特征值对总体方差的贡献率及累计贡献率。结果表明, 第一主成分波段对粒度参数信息的贡献率为84.31%, 前3个主成分波段的累计贡献率达到99.95%, 可见前3个主成分波段在去相关、降噪的基础上, 对原影像波段中的粒度信息进行了较全面的表达, 因此提取前3个主成分波段作为粒度参数的遥感反演因子。
2.1.2 基于小波神经网络(Wavelet Neural Network, WNN)的粒度参数反演模型构建方法近年来, 人工神经网络模型(Artificial Neural Network, ANN)由于高度的非线性映射及自学习能力, 被广泛应用于地物信息遥感提取。WNN是人工神经网络的一种, 于1992年由ZHANG Qinghua博士等人提出, 其基本思想是采用小波元来代替神经元, 利用一致逼近的小波分解来建立小波变换与神经网络的连接。与其它ANN相比, WNN具有更强的模式识别及容错能力, 且结构简单、收敛速度快、精度高。小波神经网络模型拓扑结构包括:输入层、隐含层和输出层等三层, 具体结构如图 2所示(沈利华, 2014)。
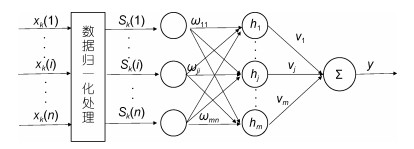 |
| 图 2 小波神经网络模型结构图 Fig. 2 The model structure of wavelet neural network 注: {xk(1), xk(2), …, xk(n)}:小波神经网络的输入, 对应PCA分析得到的主成分波段; {Sk(1), Sk(2), …, Sk(n)}:输入样本归一化处理后的数据序列; n:输入层节点数; {h(1), h(2), …, h(m)}:隐含层数据序列; m:隐含层节点数; ωji和vj:网络连接权值; y:输出, 即为所需模拟的粒度参数 |
借鉴前人小波分析中的一些经验并结合实际需要, 最终确定的隐含层激励函数为Morlet小波函数f(x), 如公式(1)所示。
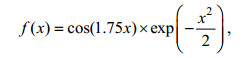 (1)
(1)其中, x表示输入隐含层的数据序列。
小波神经网络有训练和学习两种模式。建模点应具有空间位置广泛, 由海向陆分布均匀等特点, 因此选取SY02、SY03、DF01、DF02等4条断面共48组断面样本数据作为建模组, 进行小波神经网络模型训练; SY01、SY04断面以及射阳和大丰网格采样的203组样本数据作为模型检验组, 检验模型应用到独立数据集中的预测效果。
以PCA图像中采样点所在位置的前3个主成分波段特征值作为输入参数, 以采样点沉积物粒度参数作为输出参数, 分别建立平均粒径、分选系数及偏态的小波神经网络模型。随机初始化网络连接权值ωji、vj, 设置小波神经网络参数, 然后将建模组数据输入网络进行训练。网络的训练过程是先进行信号前向传播, 然后计算网络输出与期望输出间的误差并将其反向传播, 按梯度下降方向自动调整权值ωji、vj, 反复训练, 直至满足终止条件。采用平均绝对误差MAE、平均相对误差APE及变异系数CV。为指标, 对粒度参数的模型预测结果与实测结果进行比较, 当模型达到满意精度后, 最终确定的模型网络参数设置如表 1所示。
| 参数 | 设置 |
| 隐含层节点数 | 6个 |
| 隐含层激励函数 | Morlet小波函数 |
| 学习速率 | 0.01 |
| 最大训练次数 | 2000次 |
| 控制误差 | 0.001 |
获得空间分布的遥感反演粒度参数后, 将其输入Gao等(1992, 1994)提出的二维粒径趋势模型(GSTA模型)获取沉积物粒径运移趋势信息, 具体步骤为: (1)定义特征距离, 判断两点是否相邻, 若相邻两点间满足①沉积物在运移方向上粒径变细、分选变好、更加正偏或②沉积物在运移方向上粒径变粗、分选变好、更加负偏, 则在两点之间定义一个单位矢量; (2)对每个点的所有单位矢量相加得到该点的粒径趋势矢量; (3)将每个点的合矢量与相邻点合矢量取平均, 以消除“噪声”影响, 得到该点的最终趋势矢量, 所有采样点的合矢量分布共同构成沉积物粒径趋势分布图。
2.2.2 粒径运移趋势矢量精度验证方法GSTA模型模拟得到沉积物的粒径运移趋势矢量, 包含角度与长度信息, 角度表示沉积物净搬运方向, 长度表示粒径趋势的显著性, 并不代表实际搬运速率的大小。利用采样点所在像素中心点作为采样的相同点位, 采用两种方法对反演粒径运移趋势与实测粒度参数模拟的粒径运移趋势进行精度验证:一是差值分级法, 二是矢量相似法。
(1) 差值分级法
分别计算实测粒度参数模拟的粒径运移趋势矢量与反演粒径运移趋势矢量的长度差及角度差, 并根据两者的差值进行分级。趋势矢量的长度差直接取两者差值的绝对值, 角度差采用两向量共线表示相似性程度高, 夹角越大则差异越大, 因此两个矢量的角度差θ计算公式如下:
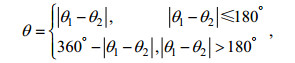 (2)
(2)其中, θ1、θ2分别为反演与实测粒度参数模拟的矢量与平面直角坐标系X轴正方向的夹角。获得长度及角度差值后, 根据差值大小进行分级, 以对反演结果是否适用于粒径趋势反演进行评价。
(2) 矢量相似法
分别进行角度相似性与长度相似性计算, 然后对二者加权求和得到矢量相似性。
由于相似度非负, 矢量x1、x2的角度相似性SD算法为:
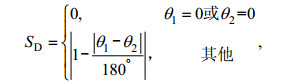 (3)
(3)式中变量含义同公式(2)。SD为1表示两矢量角度完全相似; SD为0表示两矢量角度完全不相似。
矢量x1、x2的长度相似性SL算法为:
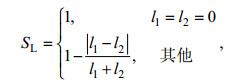 (4)
(4)式中l1、l2分别为矢量x1、x2的长度。同样, SL为1表示两矢量长度完全相似, SL为0表示两矢量长度完全不相似。
由于角度与长度在矢量中同等重要, 因此将角度与长度的相似性权重系数均取0.5, 得到沉积物粒径输运趋势图的相似性系数S为:
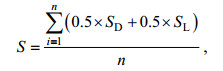 (5)
(5)式中n为粒径输运趋势矢量的个数。
3 结果与分析 3.1 实测沉积物粒度参数统计特征对现场采样的251个样本进行粒度分析, 发现研究区表层沉积物平均粒径为3.60—5.32Φ, 分选系数为0.51—1.92, 偏态为0.01—3.75。利用矩法粒度参数分级表对沉积物粒度参数进行分级(贾建军等, 2002), 结果如图 3所示。
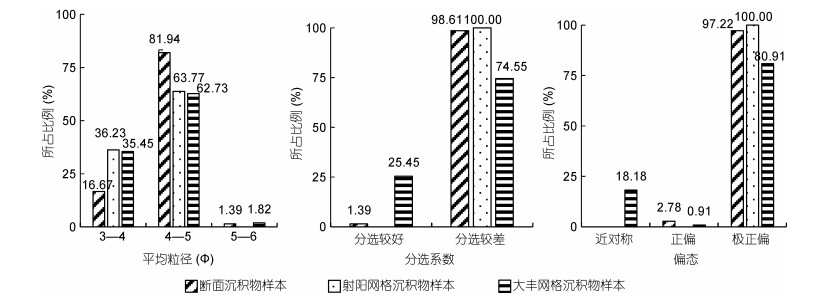 |
| 图 3 实测沉积物粒度参数统计特征图 Fig. 3 Statistical characteristics of particle size parameters of measured sediment |
断面沉积物样本平均粒径以4—5Φ为主, 比例达81.94%;分选情况以分选较差为主, 比例达98.61%;正偏与极正偏情况样本的比例分别为2.78%、97.22%。射阳网格沉积物样本情况与断面沉积物样本基本相似, 平均粒径以4—5Φ为主, 比例为63.77%;但分选较差与极正偏情况的样本有所增加, 比例均达到100.00%。大丰网格沉积物样本与断面沉积物样本存在较大差异, 分选较好的沉积物样本比例达到25.45%;近对称情况的样本全部位于大丰网格范围内, 占大丰网格样本总数的18.18%。
3.2 沉积物粒度参数遥感反演结果 3.2.1 沉积物粒度参数建模组模型检验表 2为建模组48个样本的粒度参数小波神经网络模型检验结果。
| 粒度参数 | r | MAE | APE(%) | CV(%) |
| 平均粒径 | 0.88 | 0.11Φ | 2.56 | 3.30 |
| 分选系数 | 0.86 | 0.07 | 6.25 | 8.63 |
| 偏态 | 0.88 | 0.21 | 8.41 | 9.59 |
| 注: r:相关系数; MAE:平均绝对误差; APE:平均相对误差; CV :变异系数 | ||||
总体来看, 平均粒径、分选系数及偏态的相关系数r分别为0.88、0.86及0.88, 模型构建效果比较理想。从粒度参数反演结果来看, 平均粒径反演结果最好, 平均绝对误差为0.11Φ, 平均相对误差仅为2.56%, 表明实测值与反演值的差距相对较小, 模型准确程度高; 变异系数为3.30%, 说明模型反演结果比较稳定。其次为分选系数, 平均绝对误差、平均相对误差及变异系数分别为0.07、6.25%、8.63%。偏态反演结果相对较差, 平均绝对误差0.21, 平均相对误差为8.41%, 变异系数为9.59%。
图 4为最终构建的平均粒径、分选系数及偏态小波神经网络模型建模组输出结果, 可以看出, 沉积物粒度参数实测值与反演值的拟合度比较理想, 可以较好地反映沉积物各粒度参数的变化情况。
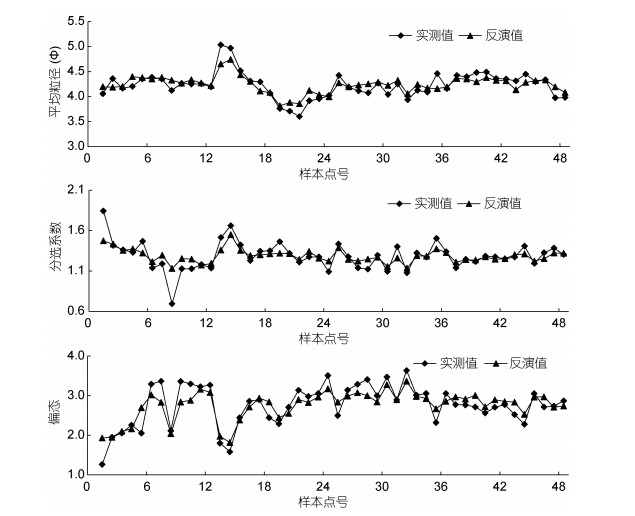 |
| 图 4 小波神经网络建模组输出结果图 Fig. 4 The output of the wavelet neural network modeling group |
将203个模型检验组数据代入模型, 为了保证结果的可靠性, 将模型运行10次, 对比分析其差异(朱婧婧, 2018), 结果如图 5所示, 图中数值分别为运行结果的最大值、平均值及最小值。可以看出, 平均粒径、分选系数、偏态的平均绝对误差均值分别为0.22Φ、0.15、0.42, 实测值与反演值的差距相对较小。根据三种沉积物粒度参数对比, 平均粒径的平均相对误差均值最小, 分选系数次之, 偏态最大; 同时, 平均粒径、分选系数、偏态的变异系数范围分别为5.99%—7.05%、14.71%—18.19%、23.49%—28.80%, 表明反演值与实测值总体差距比较稳定, 且多次反演结果均在一个合理的范围内, 粒度参数反演效果较好。
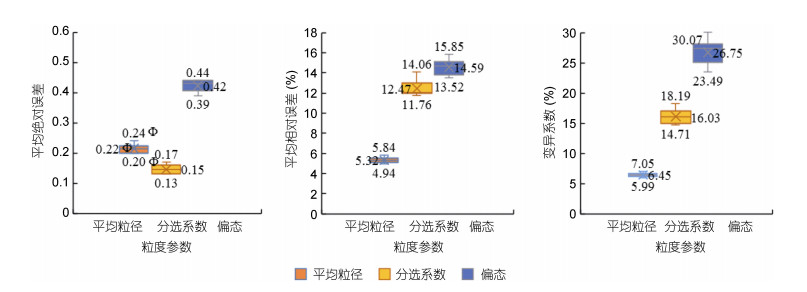 |
| 图 5 小波神经网络模型检验组输出结果图 Fig. 5 Graph of the test group output in wavelet neural network model |
总体来看, 三种粒度参数反演结果中, 平均粒径反演精度最好, 分选系数次之, 偏态最差。表明随着粒度参数阶数的增加, 反演值与实测值间的偏差逐渐增大, 模拟精度降低。
3.2.3 与单波段线性模型遥感反演结果的精度对比已有研究发现, 近红外波段较其他波段组合因子相比具有形式简单、与各沉积物粒度参数线性相关显著等特点, 因此单波段线性模型在沉积物粒度参数遥感反演中取得了良好结果(韩飞, 2015)。将基于WNN的粒度参数反演模型(模型1)与单波段线性模型(模型2)反演结果进行精度对比, 结果如表 3所示。可以看出, 两种模型均能很好地反演平均粒径, 其原因在于不同粒径的沉积物具有不同的反射光谱能力, 并在近红外波段能有明显的灰度区分, 从而使得平均粒径与近红外波段反射率之间存在较好的线性相关关系; 而分选系数及偏态分别为平均粒径的一阶矩和二阶矩, 代表平均粒径粒级分布的统计特征, 由于人工神经网络模型在复杂非线性回归拟合方面有着突出优势, 因此相较于单波段线性模型, 基于WNN的粒度参数反演模型对于分选系数和偏态的反演精度有较大提高。
| 粒度参数 | MAE | APE(%) | |||||||
| 模型1 | 模型2 | 模型1 | 模型2 | ||||||
| 建模组 | 模型检验组 | 建模组 | 模型检验组 | 建模组 | 模型检验组 | 建模组 | 模型检验组 | ||
| 平均粒径 | 0.11Φ | 0.22Φ | 0.12Φ | 0.21Φ | 2.56 | 5.32 | 2.89 | 4.53 | |
| 分选系数 | 0.07 | 0.15 | 0.09 | 0.19 | 6.25 | 12.47 | 6.90 | 12.50 | |
| 偏态 | 0.21 | 0.42 | 0.27 | 0.66 | 8.41 | 14.59 | 10.70 | 15.98 | |
将实测的90m间隔网格状粒度参数用Gamma GS+软件进行克里金插值分析, 绘制半方差图, 得到各粒度参数的变程值(马菲等, 2008)。结果表明采用偏态变程值180m作为特征距离的计算结果与当地水动力条件更为吻合。以此作为特征距离, 分别运行GSTA模型, 计算射阳网格与大丰网格的沉积物粒径运移趋势。考虑到粒径趋势图像的边缘效应, 因此解释时需去除最外圈采样点对应的趋势矢量(贾建军等, 2005)。去除“边缘效应”影响的粒径趋势矢量后, 获得的射阳网格与大丰网格粒径趋势矢量如图 7所示。可以看到, 实测粒度参数模拟与遥感反演的沉积物粒径输运均表现出总体上向偏北方向的运移趋势。射阳和大丰潮滩位于辐射沙脊群北翼, 已有研究表明, 该区域的潮流受地形约束显著, 涨潮时水流顺着西洋水道由北向南汇集, 落潮时以弶港为核心, 水流由南向北运动(陈可锋等, 2019), 夏季在弶港以北的近岸浅滩及附近海域有北上的流动(王辉, 1996), 射阳与大丰海岸附近潮余流为偏北向(张长宽, 2013)。因此可见射阳和大丰网格的潮滩表层沉积物输运趋势与当地的潮余流对泥沙的搬运有关, 主要受潮余流运动控制。
 |
| 图 6 网格沉积物粒径趋势图 Fig. 6 Trend of particle size the grid sediment 注: a:射阳网格实测粒度模拟粒径运移趋势; b:射阳网格遥感反演粒径运移趋势; c:大丰网格实测粒度模拟粒径运移趋势; d:大丰网格遥感反演粒径运移趋势 |
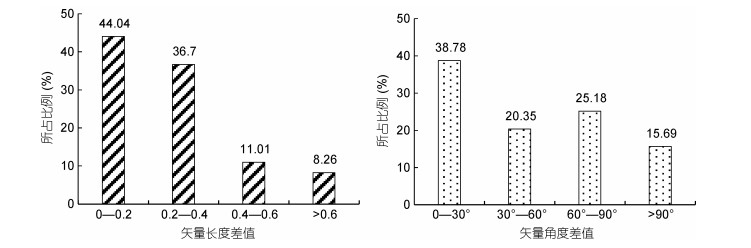 |
| 图 7 矢量长度及角度差值统计图 Fig. 7 Statistics of vector length and angle difference |
去除“边缘效应”影响的粒径趋势矢量后, 计算所有矢量的长度及角度差值, 统计结果如图 7所示。矢量长度差值小于0.2的矢量占44.04%, 小于0.4的矢量占80.74%, 长度差值大于0.6的矢量仅占总体的8.26%, 说明遥感反演的粒径趋势矢量与实测粒度参数模拟的粒径趋势矢量在长度方面差异较小。角度差值结果略差于长度差值, 两向量间呈现锐角表明两者在角度方面较为相似, 角度差值大于90°的矢量占总体的15.69%, 而差值小于30°的矢量占比达38.78%, 表明矢量在角度方面差异可以接受, 遥感反演和实测参数模拟得到的粒径矢量总体能够表现一致性的输运方向趋势。
3.3.3 矢量相似性计算结果检验去除“边缘效应”影响的粒径趋势矢量后, 对所有采样点位的矢量相似性值取平均得到两图的矢量相似性系数, 计算结果为0.67, 表明遥感反演与实测粒度参数模拟得到的粒径运移趋势图之间有较高的相似性。具体来说, 反演的沉积物粒径输运趋势与实测结果的角度相似性为0.63, 长度相似性为0.71, 长度相似性略好于角度相似性, 也表明两者在沉积物粒径搬运方向和粒径趋势显著性方面有较高的契合度, 遥感反演得到的沉积物粒径运移趋势具有一定的代表性, 可以体现沉积物的净输运趋势。
射阳网格与大丰网格的沉积物粒径运移趋势矢量相似性系数分别为0.73与0.63, 角度相似性分别为0.72、0.58, 长度相似性分别为0.75、0.67, 相比较而言, 射阳网格反演结果略好于大丰网格。在射阳网格的小型潮沟附近, 存在着由两侧指向潮沟中心的净搬运趋势, 表明局部地形也是潮滩物质输运格局的重要影响因素(贾建军等, 2005)。
3.4 研究区潮滩沉积物粒径趋势遥感反演粒径趋势图像的质量与采样空间尺度息息相关, 为把握研究区整体粒径运移趋势, 把遥感影像重采样为90m, 以平均粒径、分选系数及偏态的空间分布图层驱动GSTA模型, 去除“边缘效应”影响的粒径趋势矢量后, 获得的研究区沉积物粒径运移趋势图如图 8所示。
 |
| 图 8 研究区沉积物粒径运移趋势图 Fig. 8 Trends of sediment particle migration in the study area 注: a:运粮河口—射阳河口岸段; b:射阳河口—新洋河口岸段; c:新洋河口—斗龙港口岸段; d:斗龙港口—四卯酉河口岸段; e:四卯酉河口—大丰港口岸段; f:大丰港口—川东港口岸段 |
在潮滩不同的位置, 研究区沉积物粒径趋势呈现一定的规律性, 主要表现为: 1)在靠近海岸线附近的潮间带高潮坪, 沉积物主要呈北向或北偏东方向的运移趋势, 沉积物的运移方向与滩面小型沙波走向方向接近垂直; 2)在潮间带中潮坪, 滩面宽平, 沉积物主要呈北向或北偏西方向的运移趋势, 沉积物运移与海岸线的走向方向相近, 体现了北向的潮余流作用; 3)在中潮坪上同时能观测到粒径运移趋势不一致的矢量, 这部分矢量主要集中在在潮滩上的大型潮沟特别是自然河流的入海河口附近, 在局部地形的影响下, 这些区域的沉积物具有从水道两侧向潮沟轴线方向的运移趋势, 沉积物向潮沟汇聚, 通过水流的搬运带到破波带外的潮间带下部区域; 4)在潮间带上部盐沼边缘, 由于植被的阻挡, 水流运动减缓, 携沙能力降低, 沉积物运移趋势稍显混乱, 其中多数呈与植被边缘垂直偏北方向运移趋势, 少量受滩面入海潮沟水流运动的影响, 沿植被边缘由潮沟向两侧滩面运移。此外, 在射阳河口南北两侧防波堤及大丰港一期、二期码头等海堤堤脚附近的滩面, 由于不透水堤坝阻挡了泥沙沿岸方向的输运, 造成沉积物粒径运移趋势在堤坝两侧不一致。总的来说, 堤坝北侧由于堤岸的阻挡作用, 水流在堤脚附近流速减弱, 变化的流向使细颗粒泥沙在滩面沉积, 形成浮泥层, 沉积物沿堤向岸输运; 堤坝南侧由于堤坝与岸的双重折射, 沉积物呈现沿堤向海的输运趋势, 这也体现了人类建设活动对当地沉积物的扰动作用。
4 讨论 4.1 影像成像时间与野外采样时间间隔对粒度参数遥感反演精度的影响江苏中部淤泥质海岸的泥沙主要来自于岸外辐射沙脊群海底泥沙的自主调节(朱大奎等, 1986;王颖等, 1990)。在物源供应相对稳定的情况下, 潮滩表层沉积物的粒径与组成的变化主要受水动力条件的影响。而在同一沉积环境或输运系统内, 相似的水动力条件通常需要较长的时间尺度才能体现潮滩表层沉积物粒度参数的变化以及净输运过程(高抒, 2009)。已有研究表明, 沉积物粒度变化及粒径输运趋势所反映的泥沙运移时间尺度与沉积物的活动层深度有关(Yamashita et al, 2018)。以大丰潮滩为例, 在正常天气条件下, 介于大小潮期间一个潮周期的时间尺度内, 潮滩表层沉积物的活动层厚度约为2cm左右(贾建军等, 2005)。沉积物在活动层厚度范围内不断混合, 沉积物粒度参数相对稳定, 同时潮滩表层沉积物净输运也没有发生显著变化(Dolphin et al, 1995;贾建军等, 2005), 而超过一个潮周期, 水动力过程的季节性变化以及极端气象条件是改变潮滩表层沉积物的主要因素。本研究中, 影像成像时间与野外采样时间集中在2014年的5月上旬与7月上旬的夏季, 台风暴潮尚未对潮滩沉积物产生影响, 因此可以认为采集自活动层的沉积物粒径与组成不会发生明显变化, 滞后约2个月的现场采样与遥感影像成像时间可看作近似准同步, 遥感影像能够有效反映沉积物粒度参数的分布特征。
为进一步分析时间间隔长度对粒度参数遥感反演结果的影响, 另外选取了2014年4月25日、5月8日和8月13日的Landsat7 ETM+、Landsat8 OLI影像进行平行分析试验, 由于研究区内上述影像均有部分被云层覆盖, 因此裁剪出其中的大丰区斗龙港口—大丰港口岸段潮滩进行分析。考虑到Landsat影像与HJ-1A影像波段之间的可比性, 将Landsat7 ETM+影像的第1、2、3、4波段及Landsat8 OLI影像的第2、3、4、5波段进行主成分分析提取反演因子; 以DF01、DF02断面样本数据作为建模组训练小波神经网络模型。表 4列出了DF01、DF02断面及110组大丰网格样本的精度验证结果。可以看到, WNN模型给出的模拟结果相对稳定, 三个粒度参数的平均绝对误差MAE及平均相对误差APE均较小。但随着时间间隔长度的增加, 除了平均粒径的变异系数Cv保持稳定以外, 分选系数和偏态的变异系数Cv呈增加趋势, 表明虽然活动层内沉积物粒径的变化不大, 但是组成变化开始体现。因此可见, 1—2个月左右的影像成像与野外采样时间间隔不会对沉积物粒度参数的遥感反演精度产生实质影响。
| 日期(年.月.日) | MAE | APE(%) | CV (%) | ||||||||
| 平均粒径 | 分选系数 | 偏态 | 平均粒径 | 分选系数 | 偏态 | 平均粒径 | 分选系数 | 偏态 | |||
| 2014.08.13 | 0.22 | 0.17 | 0.42 | 5.51 | 14.15 | 15.53 | 7.55 | 15.66 | 16.12 | ||
| 2014.05.08 | 0.21 | 0.16 | 0.42 | 5.01 | 14.90 | 15.33 | 6.98 | 16.01 | 18.46 | ||
| 2014.04.25 | 0.23 | 0.16 | 0.41 | 5.62 | 14.93 | 15.61 | 7.01 | 16.22 | 19.09 | ||
WNN神经网络是一种以BP神经网络拓扑结构为基础, 把小波基函数作为隐含层节点的传递函数, 信号前向传播的同时误差反向传播的神经网络, 通过不断地对已知数据训练然后进行模型预测。由于小波理论是全尺度分析, 具有全局最优解, 从而避免了追求局部最优而造成的过拟合和收敛速度慢等问题。因此WNN神经网络不会对模拟序列中个别的极大值或极小值进行过多的关注, 而是着眼于整体更高的拟合精度。这样就要求建模组样品应尽量满足粒度参数取值区间较大且数量分布相对均匀, 能尽量涵盖本区域的粒度参数分布范围。
本研究在进行GSTA粒径运移趋势分析时, 分别对长度、角度差值较大及相似性较低的趋势矢量进行统计分析, 发现矢量所在位置的粒度参数大多属于分选较好或近对称情况, 或者周围分选较好或近对称情况的点位较多。根据实测沉积物粒度参数的统计结果, 建模组中这类情况的样品仅占5%左右, 所以导致这些点位的粒度参数反演结果精度降低, 由于沉积物粒径运移趋势分析对分选系数的敏感度很高, 从而影响了局部点位的沉积物粒径运移趋势相似性。这类情况的样本基本都位于大丰网格范围内, 这也是射阳网格沉积物粒径运移趋势反演结果好于大丰网格的主要原因。但是由于WNN模型的全局最优特性, 大部分点位的分选系数具有最优的模拟精度, 从而保证了研究区整体上粒径输运趋势的正确性。
5 结论利用野外采样数据与HJ-1A多光谱遥感影像数据, 提出了一种基于影像PCA主成分分析和WNN小波神经网络模型的潮滩表层沉积物粒径输运趋势遥感反演方法。得出的主要结论如下:
(1) 粒度参数遥感反演因子的质量会影响建模效果。考虑到多光谱影像各波段之间的高度相关性, 需要对遥感影像首先进行主成分分析, 以获取特征值大的主成分波段, 然后进行反演因子构建。
(2) WNN小波神经网络模型在潮滩沉积物粒度参数遥感反演方面具有较大优势。经验证, 模型检验组平均粒径、分选系数、偏态的平均绝对误差分别为0.22Φ、0.15、0.42。平均粒径的平均相对误差最小, 为5.32%;分选系数次之, 为12.47%;偏态最大, 为14.59%。同时, 平均粒径、分选系数、偏态的变异系数范围分别为5.99%—7.05%、14.71%—18.19%、23.49%—28.80%, 且多次反演结果均在一个合理的范围内, 沉积物粒度参数反演效果较好。相较于直接利用影像反射率因子建立数学统计模型, WNN小波神经网络模型模拟的平均粒径精度接近, 分选系数与偏态的模拟精度有较大提高。
(3) 对比遥感反演与实测沉积物粒度参数模拟得到的粒径趋势图, 趋势矢量的长度差小于0.4的矢量占总体的80.74%, 角度差小于90°的矢量占总体的84.31%, 两者矢量相似性系数为0.67, 具有较高的相似性。通过对研究区的沉积物粒径趋势模拟分析, 可以看出在潮滩的不同位置, 沉积物粒径运移趋势总体呈现不同的规律性特征, 与当地水动力条件较为吻合, 表明遥感方法能够有效用于潮滩沉积物的粒径趋势反演。
(4) 基于遥感技术实现潮滩沉积物粒度反演与运移趋势分析, 不受限采样范围, 可应用于沉积环境复杂、实地测量困难的淤泥质潮滩, 为大范围的潮滩沉积特性研究及冲淤演变分析提供了一种快速且有效的方法。
致谢 南京邮电大学应益强对小波神经网络模型构建提出了中肯建议, 华东师范大学贾建军教授对沉积物粒径输运趋势制图方法及泥沙运动的活动层厚度等问题提出了宝贵建议, 审稿专家也对论文修改提出了宝贵建议, 谨致谢忱!
马菲, 汪亚平, 李炎, 等. 2008. 地统计法支持的北部湾东部海域沉积物粒径趋势分析. 地理学报, 63(11): 1207-1217 |
王辉. 1996. 东海和南黄海夏季环流的斜压模式. 海洋与湖沼, 27(1): 73-78 DOI:10.3321/j.issn:0029-814X.1996.01.013 |
王颖, 朱大奎. 1990. 中国的潮滩. 第四纪研究, 10(4): 291-300 DOI:10.3321/j.issn:1001-7410.1990.04.001 |
王爱军, 高抒, 贾建军. 2006. 互花米草对江苏潮滩沉积和地貌演化的影响. 海洋学报, 28(1): 92-99 DOI:10.3321/j.issn:0253-4193.2006.01.013 |
边金虎, 李爱农, 雷光斌, 等. 2014. 环境减灾卫星多光谱CCD影像自动几何精纠正与正射校正系统. 生态学报, 34(24): 7181-7191 |
朱大奎, 柯贤坤, 高抒. 1986. 江苏海岸潮滩沉积的研究. 黄渤海海洋, 4(3): 19-27 |
朱婧婧, 2018.潮滩表层沉积物粒度定量遥感反演研究.烟台: 鲁东大学硕士学位论文, 28-39 http://cdmd.cnki.com.cn/Article/CDMD-10451-1018063824.htm
|
任美锷. 1986. 江苏省海岸带和海涂资源综合调查报告. 北京: 海洋出版社, 122-134
|
许石罗, 牛瑞卿, 武雪玲, 等. 2017. 基于主成分分析与粒子群优化的遥感影像变化检测. 测绘科学, 42(4): 151-156 |
汪亚平, 高抒, 贾建军. 2000. 胶州湾及邻近海域沉积物分布特征和运移趋势. 地理学报, 55(4): 449-458 DOI:10.3321/j.issn:0375-5444.2000.04.007 |
沈利华. 2014. 基于小波神经网络的城市建设用地预测. 计算机应用与软件, 31(10): 180-182 DOI:10.3969/j.issn.1000-386x.2014.10.042 |
张东, 张鹰, 李欢, 等. 2008. 基于组分反演的高光谱潮间带表层沉积物自动分类研究. 海洋学报, 30(3): 62-71 DOI:10.3321/j.issn:0253-4193.2008.03.008 |
张东, 崔丹丹, 吕林. 2018. 江苏省海岸线时空动态变化遥感监测技术、方法与应用. 北京: 海洋出版社, 12
|
张长宽. 2013. 江苏省近海海洋环境资源基本现状. 北京: 海洋出版社, 119-123
|
张存勇. 2013. 连云港近岸海域沉积物运移趋势. 海洋学报, 35(3): 172-178 DOI:10.3969/j.issn.0253-4193.2013.03.020 |
陈可锋, 郑金海, 陆培东, 等. 2019. 南黄海辐射沙脊群形成演变的动力地貌过程数值模拟. 水科学进展, 30(2): 230-242 |
陈玮彤, 张东, 崔丹丹, 等. 2018. 基于遥感的江苏省大陆岸线岸滩时空演变. 地理学报, 73(7): 1365-1380 |
陈晓琳, 孙根云, 徐方建, 等. 2015. 青岛灵山湾潮间带沉积物粒度参数高光谱定量反演. 海洋科学, 39(8): 95-102 |
郑晓丹, 张东, 张鹰, 等. 2009. 基于高光谱的潮间带表层沉积物粒度参数空间分布规律研究. 海洋学报, 31(3): 57-66 DOI:10.3321/j.issn:0253-4193.2009.03.007 |
贾建军, 汪亚平, 高抒, 等. 2005. 江苏大丰潮滩推移质输运与粒度趋势信息解译. 科学通报, 50(22): 2546-2554 DOI:10.3321/j.issn:0023-074X.2005.22.017 |
贾建军, 高抒, 薛允传. 2002. 图解法与矩法沉积物粒度参数的对比. 海洋与湖沼, 33(6): 577-582 DOI:10.3321/j.issn:0029-814X.2002.06.002 |
高抒. 2009. 沉积物粒径趋势分析:原理与应用条件. 沉积学报, 27(5): 826-836 |
梁菲, 谭衢霖, 刘亚岚, 等. 2011. 国产"环境一号"(HJ-1)卫星遥感影像桥梁提取研究. 测绘工程, 20(5): 13-17 DOI:10.3969/j.issn.1006-7949.2011.05.004 |
韩飞, 2015.淤泥质海岸潮滩表层沉积特征遥感研究.南京: 南京师范大学硕士学位论文, 39-41 http://cdmd.cnki.com.cn/Article/CDMD-10319-1015430382.htm
|
薛允传, 贾建军, 高抒. 2002. 山东月湖的沉积物分布特征及搬运趋势. 地理研究, 21(6): 707-714 DOI:10.3321/j.issn:1000-0585.2002.06.006 |
De C, Chakraborty B, 2012. Estimation of mean grain size of seafloor sediments using neural network. Marine Geophysical Research, 33(1): 45-53 DOI:10.1007/s11001-011-9145-x |
Dolphin T J, Hume T M, Parnell K E, 1995. Oceanographic processes and sediment mixing on a sand flat in an enclosed sea, Manukau Harbour, New Zealand. Marine Geology, 128(3-4): 169-181 DOI:10.1016/0025-3227(95)00097-I |
Duman M, Avcı M, Duman S et al, 2004. Surficial sediment distribution and net sediment transport pattern in Izmir Bay, western Turkey. Continental Shelf Research, 24(9): 965-981 DOI:10.1016/j.csr.2004.03.001 |
Gao S, Collins M, 1992. Net sediment transport patterns inferred from grain-size trends, based upon definition of "transport vectors". Sedimentary Geology, 81(1-2): 47-60 DOI:10.1016/0037-0738(92)90055-V |
Gao S, Collins M B, Lanckneus J et al, 1994. Grain size trends associated with net sediment transport patterns:an example from the Belgian continental shelf. Marine Geology, 121(3-4): 171-185 DOI:10.1016/0025-3227(94)90029-9 |
McLaren P, Bowles D, 1985. The effects of sediment transport on grain-size distributions. Journal of Sedimentary Petrology, 55(4): 457-470 |
Poizot E, Anfuso G, Méar Y et al, 2013. Confirmation of beach accretion by grain-size trend analysis:Camposoto beach, Cádiz, SW Spain. Geo-Marine Letters, 33(4): 263-272 DOI:10.1007/s00367-013-0325-3 |
van der Wal D, Herman P M J, 2007. Regression-based synergy of optical, shortwave infrared and microwave remote sensing for monitoring the grain-size of intertidal sediments. Remote Sensing of Environment, 111(1): 89-106 DOI:10.1016/j.rse.2007.03.019 |
Yamashita S, Naruse H, Nakajo T, 2018. Reconstruction of sediment-transport pathways on a modern microtidal coast by a new grain-size trend analysis method. Progress in Earth and Planetary Science, 5(1): 7 DOI:10.1186/s40645-018-0166-9 |
 2019, Vol. 50
2019, Vol. 50


