中国海洋湖沼学会主办。
文章信息
- 史剑, 朱超, 刘经东, 刘振宇. 2019.
- SHI Jian, ZHU Chao, LIU Jing-Dong, LIU Zhen-Yu. 2019.
- 台风过程中浪致Stokes漂流对海洋上层温度影响的数值模拟
- NUMERICAL SIMULATION OF INFLUENCE OF WAVE-INDUCED STOKES DRIFT ON UPPER OCEAN TEMPERATURE DURING TYPHOON
- 海洋与湖沼, 50(6): 1209-1222
- Oceanologia et Limnologia Sinica, 50(6): 1209-1222.
- http://dx.doi.org/10.11693/hyhz20190600114
文章历史
-
收稿日期:2019-06-14
收修改稿日期:2019-07-15
2. 河海大学海岸灾害及防护教育部重点实验室 南京 210098
2. Key Laboratory of Coastal Disaster and Defense, Ministry of Education, Hohai University, Nanjing 210098, China
海浪作为海洋中的典型小尺度现象, 无时无刻不存在于海面。近年来, 随着对海洋大尺度物理过程研究的逐渐深入, 研究者们发现海浪对海洋大尺度物理过程存在重要的作用。海浪主要以浪致搅拌混合、Stokes漂流、辐射应力和波浪破碎等方式作用于上层海洋, 影响着海洋上层的温度、盐度、流速等海洋环境要素。
有限振幅波理论中提到, 在无旋、无粘条件下, 非线性作用会使波浪在传播方向上产生随深度变化的净位移, 并影响着上层海洋动力过程, 此净位移为Stokes漂流。Longuet-Higgins(1953)提出, 在海水有粘性的条件下, Stokes漂流不仅会影响海洋上层流动, 而且会引起净质量输运。Weber(1983)通过研究发现, 真实的海洋存在粘性, 不管粘性多小, Stokes漂流均会引起净质量输运。McWilliams等(1999)在研究Stokes输运大小时发现, 高风速下的Stokes输运与风生环流输运具有相当的量级, 并发现Ekman输运的量值中Stokes输运最大可达50%, Tamura等(2012)、毕凡(2013)在Stokes输运的研究中也得到了相同的结论。Hasselmann(1970)则提出在行星涡度的影响下, Stokes漂流与涡度作用产生Coriolis-Stokes力, 虽然此力只穿透很浅的海洋深度, 但对海洋混合层的能量输入输出、剖面流场结构和海表流场分布具有一定的影响。Huang(1979)则证明了Coriolis-Stokes力能够改变混合层内Ekman平衡和流速剖面的现象。Lewis等(2004)在经典的Ekman模型中加入了Coriolis- Stokes力项, 发现模拟的海洋动力过程与实际更加相符。Craik等(1976)则提出在Stokes漂流与风生流作用过程中, 会产生Stokes-Vortex力, 该力是Langmuir环流的主要源动力。Li等(1995)研究海洋上层环流结构时发现, Langmuir环流通过增强上层环流的剪切不稳定性, 加剧了上层海洋的混合作用, Polton等(2007)也得出了相同的结论。Li等(2008)则利用MY2.5(Mellor et al, 1974)阶湍封闭模型进行数值模拟, 引入了参数化的Stokes漂流, 改变垂向混合系数, 结果表明, 相较于海浪破碎仅对海洋表层产生影响, Stokes漂流的影响可贯穿整个混合层。从Stokes漂流全球分布来说, 由于南北半球西风带的作用, 高纬度海域出现大浪区, 形成较大的Stokes漂流:冬季北半球西风带的不断加强, 北半球高纬度海区产生了更大的Stokes漂流(Zhang et al, 2014; Wang et al, 2015)。
Stokes漂流影响着海洋上层的动力过程, 对于海洋上层温盐场的分布具有重要作用。Deng等(2012)在Stokes漂流的研究中, 将Coriolis-Stokes力加入POM模式的动量方程中, 发现考虑Coriolis-Stokes力作用后, 海表温度和混合层厚度更加符合实际。Zhang等(2014)在HYCOM(Hybrid Coordinate Ocean Model)模式的中加入Stokes漂流作用, 发现Stokes漂流对海洋上层温度的变化具有重要的贡献。基于NEMO环流模式, Breivik等(2015)讨论了Coriolis-Stokes力作用对海洋混合层的影响, 发现Coriolis-Stokes力对减小海表面温度偏差具有重要的作用。
台风能够在海面产生台风浪, 这些剧烈的海浪会产生Stokes漂流, 显著地影响着海洋上层流场结构。国内外学者对于台风过程中海洋上层温度的变化做了大量的研究(Price, 1981; Shay et al, 1992;刘增宏等, 2006;杨晓霞等, 2010), 得出了台风过程中海水降温右偏性、延迟性等结论, 并从台风强度、移速、海洋上层环境等方面进行了降温因素的分析。然而, 针对台风过程中浪致Stokes漂流对海洋上层温度变化影响的研究较少, 因此研究台风过程中Stokes漂流对海洋上层温度的影响, 有利于深入了解台风过程中海洋上层温度变化的物理机制。本文在浪流耦合模式中考虑波浪产生的Stokes漂流作用, 分析研究Stokes漂流在台风过程中对海洋上层温度的影响。
1 模型介绍 1.1 耦合模型文中采用的海洋环流数值模型为FVCOM(The Unstructured Grid Finite Volume Community Ocean Model), 该模型采用了有限体积法, 结合了有限差分法和有限单元法的优点, 在数值计算方面具有高效性和稳定性。该模型已发展至第四代, 随着物理方案不断改进, 加入了浪流耦合模块、冰模块、水质模块、生物模块、泥沙模块、同化模块和河口分析模块等。本文以FVCOM3.1.6版本为基础, 采用浪流耦合模块(FVCOM- SWAVE)和环流模块进行海洋上层温度的数值模拟。
1.2 Stokes漂流及其效应目前计算Stokes漂流的公式主要分为两种, 一种是采用海浪谱计算Stokes漂流(Breivik et al, 2016), 另一种则采用海浪的波高、周期和波数等要素计算Stokes漂流。模型采用第二种方式计算Stokes漂流并与环境流场矢量叠加, 形成新的流场结构。Stokes漂流的计算公式可表示为:
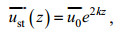 (1)
(1)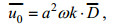 (2)
(2)式中, 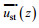
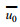
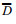
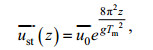 (3)
(3)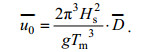 (4)
(4)Stokes漂流的存在引起了非零的净输移被称为Stokes输运, 对Stokes漂流在水深方向上进行垂向积分, 可得Stokes漂流产生的输运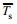
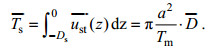 (5)
(5)Stokes输运能够促进海洋上层的质量输移和能量的传递, 在全球大洋中的输运过程具有不可忽略的作用。McWilliams等(1999)为了比较Stokes输运与总输运的大小关系, 定义了Ekman-Stokes数Es, 其含义是海浪产生的输运在净Ekman输运中所占比例, 具体表达式为:
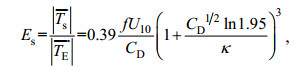 (6)
(6)其中, 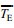
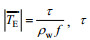
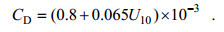 (7)
(7)台风过程会使海洋上层温度发生变化, 本文选择的台风过程为2014年9号台风“麦德姆(Matmo)”, 其前一号和后一号台风的路径与“麦德姆”不同, 而且台风过程与“麦德姆(Matmo)”无重叠。台风“麦德姆(Matmo)”于2014年7月18日左右在太平洋西岸海域生成, 20日左右加强为强热带风暴, 23日凌晨在台湾省台东县登陆, 之后穿越台湾海峡在福建省福清市再次登陆, 影响福建、江西、浙江、江苏等地区, 最后穿越山东半岛, 26日凌晨从黄渤海域登陆朝鲜半岛, 此台风对我国影响时间长, 范围广。台风路径资料来源国家气象局(Ying et al, 2014), 具体见图 1。
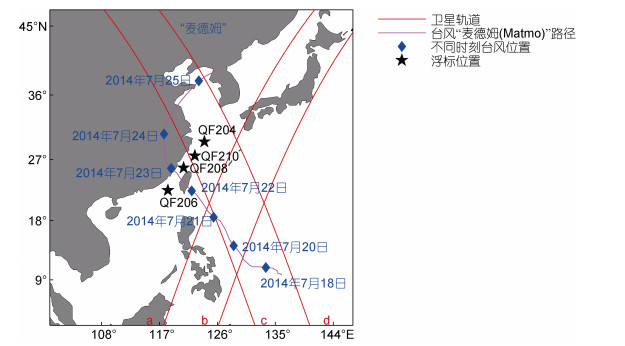 |
| 图 1 台风路径、高度计轨道和浮标位置图 Fig. 1 The typhoon path, altimeter track and buoy location 注: a、b、c、d为四个时刻卫星轨道的编号 |
本文模拟的区域涉及了中国海及其外海, 经纬度为100°-147°E, 2°-47°N。研究区域较大, 包括了菲律宾群岛、台湾岛、日本岛、琉球岛链等众多复杂地形, 地形如图 2。本文采用高精度海岸线GSHHS (Global Self-consistent Hierarchical High-resolution Shoreline)刻画研究区域, 并采用无结构化三角形网格贴合复杂的岸线和地形, 水深数据则采用ETOPO1(1-Minute Gridded Global Relief Data Collection)高精度地形数据插值得到。
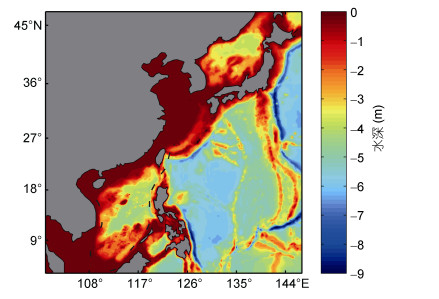 |
| 图 2 区域地形图 Fig. 2 The regional topographic map |
采用欧洲中期天气预报中心ECMWF(European Centre for Medium-Range Weather Forecasts)每6h一次, 分辨率为0.125°×0.125°的风场驱动模型:采用HYCOM资料作为温度初始场:与风场精度一致的NCEP(National Centers for Environmental Prediction)的热通量资料作为温度变化的源汇项:本文主要采用Argo实测的浮标资料进行海洋上层温度的验证, 采用中国近海浮标QF204、QF206、QF208、QF210资料和Jason-2卫星高度计资料进行波高验证。
2.3 模型设置由于本文着重考虑浪致Stokes漂流对温度场的影响, 因此, 在浪流耦合机制方面, FVCOM模型中只考虑了浪致Stokes漂流的作用, 并将Stokes漂流作用加在环流模块对应的动量方程中。模型区域水平方向采用非结构化的三角形网格, 分别包括50244个单元和26073个节点, 空间最小步长约10km。模型设置了陆地、岛屿和海洋开边界, 海岸处采用干湿网格法, 当水深小于0.05m时定义为干点, 其速度为0, 开边界设置为海绵边界条件。模型垂向上分为40层, 采用σ-S混合坐标, σ坐标用于水深较小处, 混合坐标适用于水深较大的区域。模型采用内外模算法, 内模时间步长为3s, 用来计算湍动能、温盐和三维水流速度, 外模时间步长为30s, 用来计算水位和平均流速。
3 台风浪的模拟及验证 3.1 台风浪的模拟“麦德姆(Matmo)”台风过程中伴随着强烈的台风浪, 引起了浪致的Stokes漂流, 为了表明Stokes漂流模拟的可靠性, 需要进行台风浪的可靠性验证。模拟的台风过程时间段为2014年7月18-26日, 图 3选择了期间4个典型时刻进行分析。
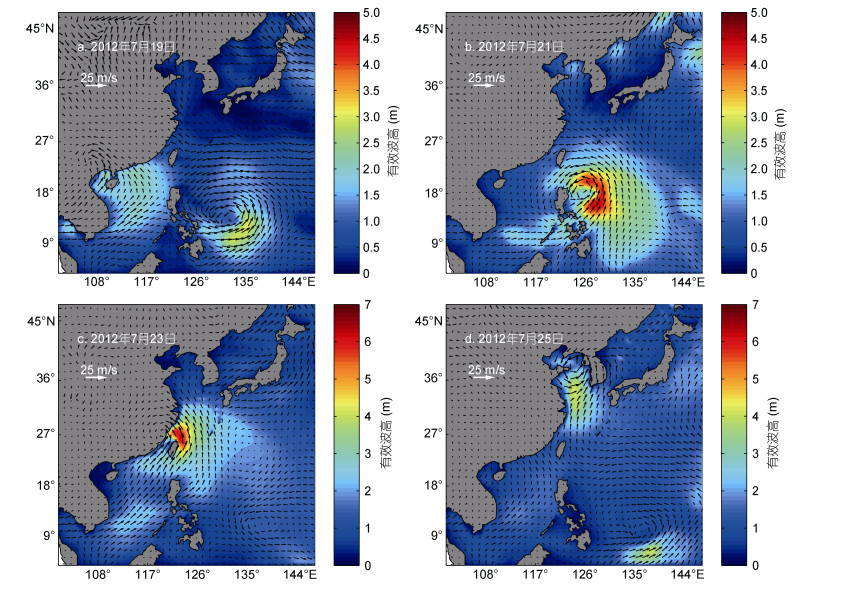 |
| 图 3 4个典型时刻风场矢量和有效波高分布图 Fig. 3 Distribution of wind field vectors and significant wave heights at four typical moments |
由图 3a可以看出, 7月19日左右“麦德姆(Matmo)”就形成了较大的台风浪, 风场与浪场相对应, 大风区域对应着大浪区域, 有效波高值达3.5m左右。随着时间的推进, 台风的风场变强, 影响的海域变大, 台风浪表现出典型的右偏性, 台风中心右侧产生了约4.5m的大浪。如图 3c所示, 7月23日, “麦德姆(Matmo)”穿过台湾海峡在福建登陆, 地形作用导致波浪分布区域变小, 但在大风作用下, 台风的最大有效波高达到了约6.5m, 且总体表现出了台风浪的右偏性。7月25日, “麦德姆(Matmo)”移向黄渤海域, 受陆地的影响, 台风风场相对减弱, 但在黄渤海域中依旧产生了4.5m左右的大浪, 影响了较大的海域范围。
3.2 台风浪的验证为了进一步说明海浪数值模拟的准确性, 采用Jason-2卫星高度计和四个近岸浮标的有效波高值对模型模拟的海浪做进一步的验证。高度计Ku波段反演的波高值优于C波段反演的波高值, 因此, 本文采用Ku波段反演的有效波高值验证外海的模拟波高。QF204、QF206、QF208和QF210四个浮标以及卫星轨道的位置分布如图 1, 其中a轨道为2014年7月20日8时左右、b轨道为2014年7月26日5时左右、c轨道为2014年7月23日6时左右、d轨道为2014年7月20日18时左右。岛屿、陆地等因素影响着高度计反演值的精度, 离岸越远, 有效波高值越准确(王娟娟等, 2016), 因此选取远离岸线的有效波高反演值进行验证, 不同轨道的取值范围以对比图的横坐标为准, 图 4为反演值与模拟值的对比结果, 图 5为浮标测量值与模拟值的对比结果。
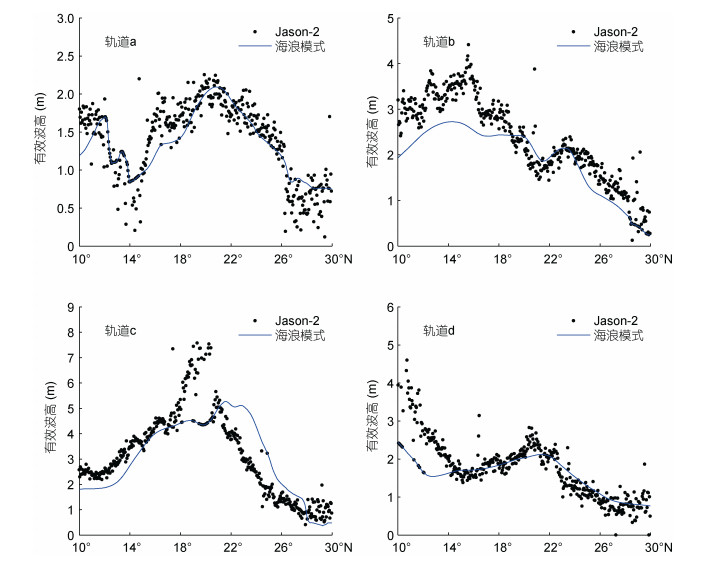 |
| 图 4 有效波高模拟值与高度计值比较 Fig. 4 Comparison in significant wave heights between simulated and altimeter data |
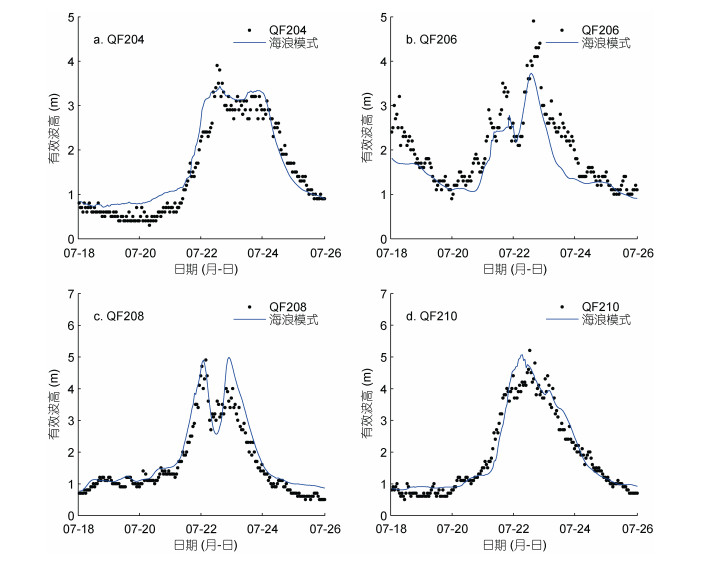 |
| 图 5 有效波高模拟值与浮标实测值比较 Fig. 5 Comparison in significant wave heights between simulated and measured data |
通过与卫星高度计和近岸浮标资料的对比发现, 模型可以较准确的模拟出有效波高。通过比较相关系数(R), 平均误差(ME), 平均绝对误差(MAE)和均方根误差(RMSE)来衡量波高模拟结果的准确性, 具体公式如下:
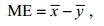 (8)
(8)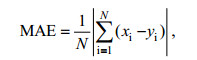 (9)
(9) (10)
(10)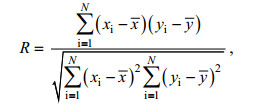 (11)
(11)式中, xi和yi分别代表模拟值与实测值(反演值), 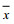
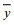
| 浮标、轨道名称 | 个数N(个) | 相关系数R | 平均误差ME(m) | 平均绝对误差MAE(m) | 均方根误差RMSE(m) |
| 轨道a | 406 | 0.8160 | -0.2494 | 0.2326 | 0.3863 |
| 轨道b | 406 | 0.8861 | -0.3946 | 0.4806 | 0.5920 |
| 轨道c | 408 | 0.7828 | -0.0417 | 0.6093 | 0.8781 |
| 轨道d | 402 | 0.7708 | -0.1530 | 0.3391 | 0.4027 |
| QF204 | 193 | 0.9622 | 0.1744 | 0.2767 | 0.4224 |
| QF206 | 193 | 0.8933 | -0.3237 | 0.3651 | 0.4956 |
| QF208 | 193 | 0.9515 | 0.2596 | 0.3212 | 0.4247 |
| QF210 | 193 | 0.9673 | 0.0759 | 0.2657 | 0.3520 |
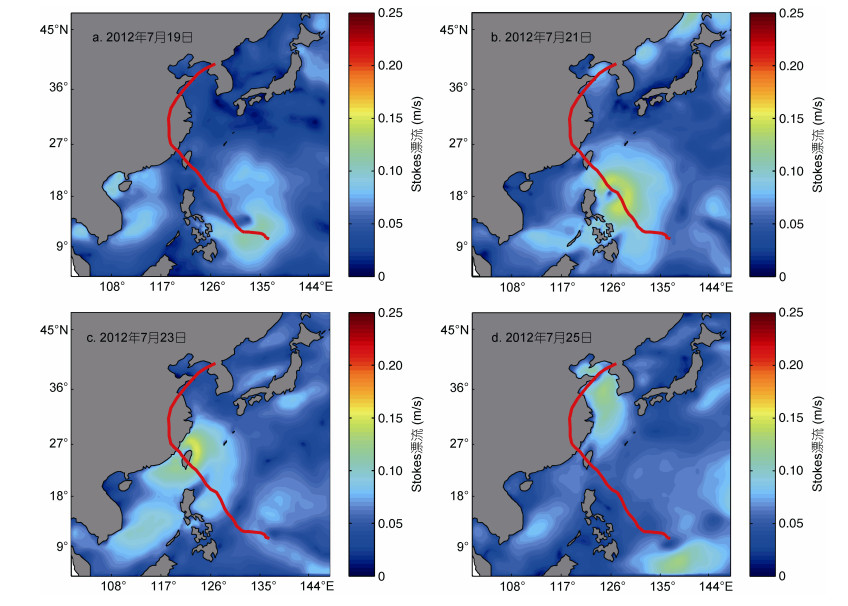
通过对有效波高模拟精度的验证, 保证了Stokes漂流模拟的可靠性, 如图 6是台风过程中Stokes漂流的时空分布。通过分析可以发现, Stokes漂流的分布总体上与风场强度、有效波高的分布呈正相关, 风场强度越大, 风能输入越大, 引起的波浪相对较强, 从而产生了较强的Stokes漂流。如图 6a, 台风生成初期风浪场强度均较小, 形成的Stokes漂流只有0.1m/s左右; 如图 6b, 随着波浪的成长, 波浪引起的Stokes漂流也逐渐增大, 由于台风浪的右偏性, 使得Stokes漂流的分布也出现了右偏性, 漂流最大值位于台风路径右侧, 约为0.15m/s; 由图 6c、图 6d可以看出, 台风登陆福建和朝鲜半岛时, 对我国东海、黄海、渤海海域均产生了较大的Stokes漂流, 漂流的速度在0.10-0.15m/s不等, 而位于台风影响外的海域, Stokes漂流流速较小, 仅为0.05m/s及以下。
从全球角度讲, 空间上Stokes漂流流速大小与纬度高低有关, 纬度越高, Stokes漂流流速越大; 时间上, 西太平洋冬春秋季月平均Stokes漂流流速大于夏季的Stokes漂流(Zhang et al, 2014; Wang et al, 2015)。在南北半球西风带作用下, 高纬度海域出现大浪区, 形成较大的Stokes漂流; 冬季太阳直射南半球, 北半球副热带高压减弱, 温差变大, 西风带加强, 使得冬季长时间出现较大海浪, 冬季海域产生的Stokes漂流大于夏季的Stokes漂流。
我国海域及外海虽然位于中低纬度, 夏季受到西风带的影响较小, 但是会受到台风的影响, 台风过程伴随着剧烈的海浪作用, 从而产生较大的Stokes漂流, 其量值可达0.15m/s不等, 因此台风过程中的Stokes漂流在海洋研究中不应该被忽略。
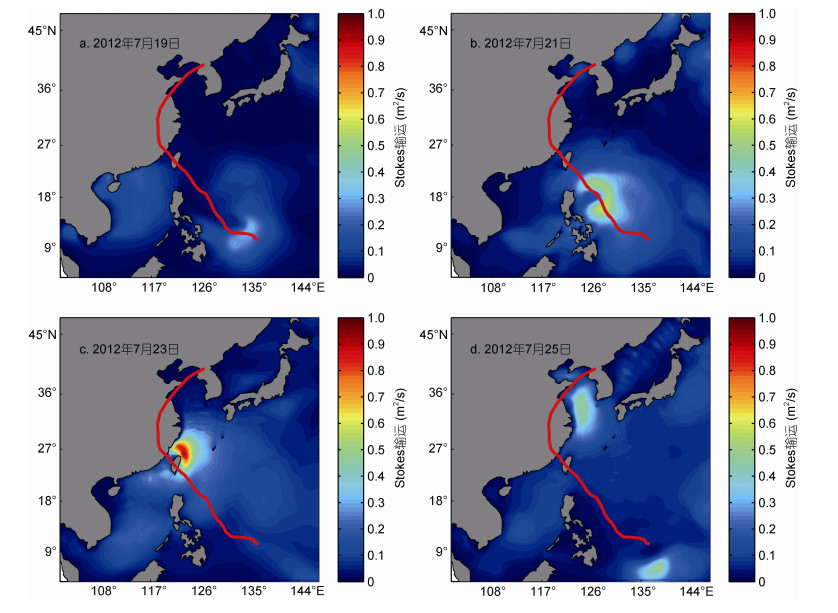
4.2 台风过程中Stokes输运的分布Stokes漂流会产生输运现象, 这种现象对海洋上层环境的质量和能量交换具有重要的作用, 影响着台风过程中海洋上层温度的分布。通过式(5)计算台风过程中Stokes输运, 结果如图 7所示。结合图 6、图 7可以看出Stokes输运与Stokes漂流的分布特征具有一致性, Stokes输运的高值区与漂流的高值区是吻合的, Stokes输运分布的高值区主要在台风路径处。风场浪场越大, Stokes漂流越大, 对于质量、能量的输运越大。台风过程初期, 如图 7a, Stokes漂流较弱, 相应的Stokes输运也较小, 输运量在0.2m2/s左右。7月21日随着浪场的加强, Stokes漂流及输运都变大, 输运量达到了0.6m2/s, Stokes输运与Stokes漂流分布一样呈现右偏性。在台风登陆福建时, Stokes输运达到了最大值1m2/s左右, 出现在台湾海峡及东海海域。随着台风移动, Stokes输运分布在整个东中国海海域。
 |
| 图 7 4个典型时刻Stokes输运分布图 Fig. 7 Distribution of the Stokes transport at four typical moments |
本文为了研究台风过程中Ekman-Stokes数的变化, 确定一条以台风路径为基础, 从“麦德姆(Matmo)”生成海域, 经钓鱼岛海域延伸至东海、黄海、渤海的轨迹线, 分析台风过程中轨迹线上的Ekman-Stokes数变化。通过式(6)计算典型时刻的Ekman-Stokes数, 如图 8。从图 8a可以看出, 台风初期位于低纬度时, 此时Stokes输运占净输运的比例为25%左右; 随着台风的成长和移动, Stokes输运占比逐渐增大, 7月21日, 在15°-20°N附近其最大输运比例达到32%, 输运比例明显的大于其他区域, 输运比值与输运量的大小呈正相关; 在台风7月23日登陆福建和7月25日登陆朝鲜半岛过程中, 如图 8c、图 8d, 台风附近产生的输运位于25%-30%, 也大于其他海域的输运比值。台风过程中Stokes输运对海洋上混合层的影响集中在台风路径附近, 与Stokes漂流密切相关, Stokes漂流越大, Stokes输运以及Ekman-Stokes数相对越大。Stokes输运在净输运中占比越大, 海浪对上层海洋的混合作用越强, 在输运方向后方易产生辐散, 致使下层海水上翻, 进而对海表温度场产生影响。
 |
| 图 8 Ekman-Stokes数随纬度变化 Fig. 8 Variation of Ekman-Stokes number with latitude |
Stokes漂流在垂向上是呈指数形式分布, 因此它影响着一定深度的上层海洋流场结构, 将此深度定义成Stokes漂流的影响深度Ds, 表达形式如下:
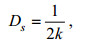 (12)
(12)其中, k表示波数。通过式(12)求出台风过程中Stokes漂流的影响深度, 如图 9。台风过程中, 影响深度Ds的分布与Stokes漂流的大小分布一致, 在台风登陆前表现最明显, 最大影响深度达到了12m左右。随着影响深度的增大, Stokes漂流越能促进海洋上层质量、能量的交换, 加强垂向的湍流作用, 使得下层冷水上翻, 从而降低了上层海水的温度。
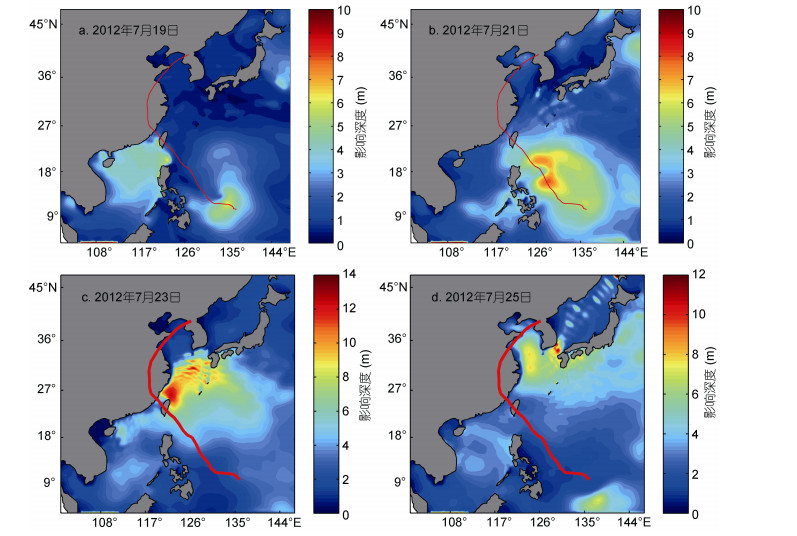 |
| 图 9 Stokes漂流影响深度分布图 Fig. 9 Distribution of the Stokes drift affected depth |
为了清晰的体现Stokes漂流在台风过程中对上层海水温度变化的影响, 对考虑和未考虑Stokes漂流作用模拟的海表面温度(Sea Surface Temperature, SST)进行作差, 使用水深约为3m处的模式数据作为海表面温度, 定义改善量α, 具体表达形式如下:
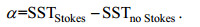 (13)
(13)通过式(13)计算出的改善量见图 10, 其中, SSTStokes为考虑Stokes漂流影响的海表面温度, SSTno Stokes 为未考虑Stokes漂流影响的海表面温度。从α的分布可以看出, 在考虑Stokes漂流后的海表面温度呈明显的降低趋势, 温度降低的区域与图 6中Stokes漂流的分布具有一致性。台风过程初期, 风场浪场强度较小, 引起的Stokes漂流不明显, 从而产生的降温现象不明显; 7月21日, 随着台风的成长, Stokes漂流速度变大, 达到0.15m/s, 产生了明显的Stokes输运, 加大了影响深度, 加强了上下层水体的交换, 因此对海域内产生了较大的降温, 最大降温达到2℃, 降温区域也逐渐变大, 遍布了整个菲律宾群岛的东部海域; 降温的区域随着台风的移动而变化, 7月23日, 台风登陆福建, Stokes漂流对福建、台湾海域产生了2℃左右的降温, 此时由于南海存在较大Stokes漂流, 南海区域也出现了较明显的温度降低现象。在随后台风移动的过程中, 降温区继续扩大, 延伸至整个中国海域。
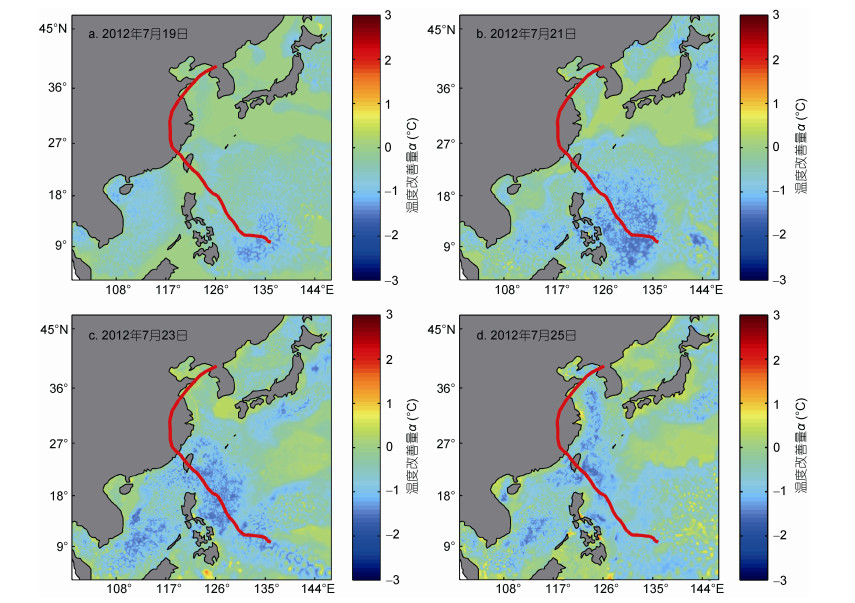 |
| 图 10 温度改善量α的分布 Fig. 10 Distribution of the improvements α |
结合图 6-图 10, 可以发现温度改善量α的分布与Stokes漂流、输运、影响深度以及Ekman-Stokes数都存在相关性。波浪诱导应力项之一的Coriolis- Stokes力会改变海洋上混合层的能量输入、流速剖面结构以及海表流场分布, 流场的变化又会直接对能量守恒方程产生影响, 进而影响海洋表层的温度。Stokes漂流则通过Coriolis-Stokes力使上层海洋的温盐和密度分布发生变化, 改变流速剪切项, 使得不稳定性增强并造成海表流场发生改变, 海表流场的改变导致输运变化, 在输运后方产生上升流并引起SST的减小。此外, Stokes漂流与风驱水平流相互作用下, 会导致Langmuir环流, Langmuir环流的存在改变了海洋上层的湍动能, 进而会影响SST(王智峰, 2012), Stokes漂流越大, Langmuir湍效应占主导地位, 湍动能变大, 直接增强了海水的对流, 使得SST减小。为了能够进一步解释Stokes漂流对海表降温的影响, 以靠近台风路径(降温明显)和远离台风路径(降温不明显)的两个研究位置为例(如图 12中所示红色圆点), 对比分析了考虑和未考虑Stokes漂流作用研究位置处的上层垂向混合系数, 选择对比时刻为7月21日12时, 坐标分别为(128.35°E, 11.53°N)和(135.18°E, 27.18°N), 对比结果见图 11。由图 11可知, 对比考虑和未考虑Stokes漂流作用的垂向混合系数发现, 考虑Stokes漂流作用模拟的垂向混合系数更大, 与Stokes漂流的理论影响深度12m相比, 其产生的垂向混合作用可以影响整个混合层, 有利于上层海水的混合。
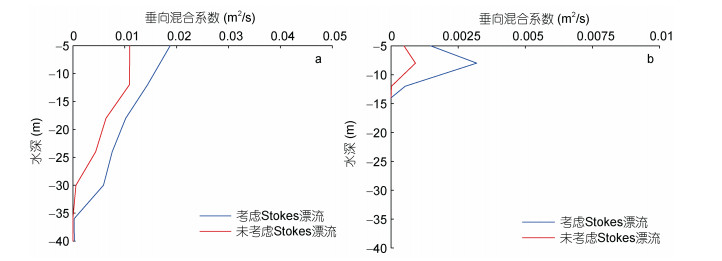 |
| 图 11 两个研究点处垂向混合系数分布 Fig. 11 Vertical mixing coefficient in two research sites 注: a:靠近台风路径的研究点; b:远离台风路径研究点 |
台风过程中, 由于路径附近的Stokes漂流及其效应均较大, 使得路径附近处上层海水降温较明显, Stokes漂流速度越大, 输运量及占净输运的比例越大、影响深度越深, 从而加快了上下层水体能量的交换, 温度降低的越明显。反之, 台风路径外侧海域受到Stokes漂流及其效应的影响较小, 所以温度降低的不明显。
5.2 台风过程中海洋上层温度的验证为了分析在Stokes漂流作用下上层海水温度模拟的可靠性, 对考虑和未考虑Stokes漂流的情况下模拟的温度进行验证。采用模拟区域内每天Argo浮标资料的表层温度数据与模拟的表层温度数据进行对比验证, 通过比较实测值与模拟值的相关系数(R), 平均误差(ME), 平均绝对误差(MAE)和均方根误差(RMSE)来衡量模拟结果的准确性, R越大, 说明相关程度越好; ME值越大, 说明模拟温度出现偏高情况; MAE和RMSE值越小, 说明与实测值越接近。选择台风路径处一个代表性Argo浮标进行剖面温度比较, 位置为(134.5°E, 12.28°N), 利用该浮标处的实测温度与模拟温度进行比较, 由于Stokes漂流对深层海水的影响较小, 因此采用Argo浮标100m以内的温度数据, 将模拟的温度插值到Argo剖面测量点上, 取绝对误差的绝对值作为判断模拟结果的依据。图 12中粉色星为进行剖面温度比较的Argo浮标研究点位置, 红点为混合系数研究点位置, 图 13为考虑和未考虑Stokes漂流作用下温度绝对误差的绝对值随时间变化, 表 2为考虑和未考虑Stokes漂流情况下模拟值与Argo浮标第一层实测值的统计量分析。
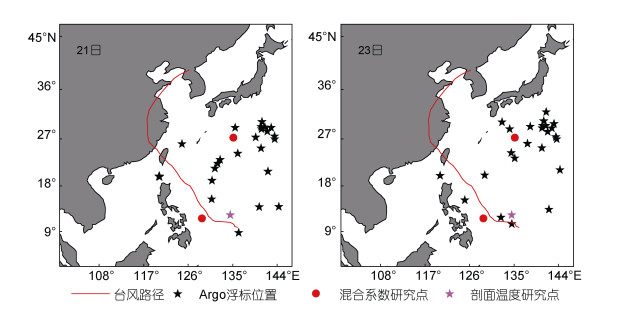 |
| 图 12 Argo浮标和研究点位置 Fig. 12 Locations of Argo buoys and research sites |
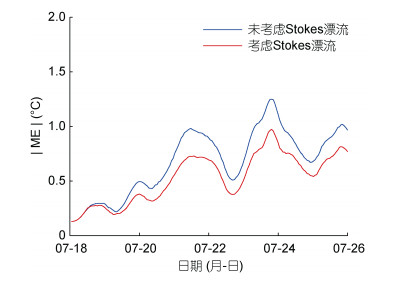 |
| 图 13 台风路径处代表性Argo浮标处模拟温度的平均误差(ME)绝对值随时间变化 Fig. 13 The ME absolute value of simulated temperature at the representative Argo buoy along the typhoon path changes with time |
| 日期(月-日) | 浮标数(个) | R | ME(℃) | RMSE(℃) | MAE(℃) | |||||||
| 考虑Stokes漂流 | 未考虑Stokes漂流 | 考虑Stokes漂流 | 未考虑Stokes漂流 | 考虑Stokes漂流 | 未考虑Stokes漂流 | 考虑Stokes漂流 | 未考虑Stokes漂流 | |||||
| 07-18 | 20 | 0.8330 | 0.7928 | 0.3410 | 0.3548 | 0.5774 | 0.7884 | 0.4625 | 0.5213 | |||
| 07-19 | 29 | 0.9375 | 0.8785 | -0.2307 | 0.3125 | 0.6995 | 0.7481 | 0.4069 | 0.5832 | |||
| 07-20 | 33 | 0.8137 | 0.7380 | -0.3800 | 0.9395 | 0.6986 | 1.5339 | 0.5090 | 1.2512 | |||
| 07-21 | 30 | 0.8531 | 0.8553 | 0.6070 | 0.9289 | 0.5521 | 1.2702 | 0.3919 | 1.0507 | |||
| 07-22 | 24 | 0.8587 | 0.7316 | 0.5610 | 0.6719 | 0.7692 | 1.2060 | 0.4224 | 0.9616 | |||
| 07-23 | 24 | 0.8463 | 0.7006 | 0.3870 | 1.0995 | 0.6044 | 1.3349 | 0.4564 | 1.4021 | |||
| 07-24 | 23 | 0.8480 | 0.6706 | 0.3085 | 1.2499 | 0.6932 | 1.1117 | 0.5976 | 0.8691 | |||
| 07-25 | 23 | 0.7276 | 0.6305 | 0.6458 | 0.9886 | 0.8742 | 1.4485 | 0.7234 | 1.1950 | |||
| 07-26 | 26 | 0.6672 | 0.4486 | 0.8955 | 1.4200 | 0.8977 | 1.3385 | 0.7635 | 1.6818 | |||
| 均值 | 26 | 0.8206 | 0.7163 | 0.2576 | 0.8851 | 0.7074 | 1.1978 | 0.5260 | 1.0573 | |||
由表 2可知, 在考虑Stokes漂流作用的误差统计量的均值R为0.82, ME为0.26℃, RMSE为0.71℃, MAE为0.53℃, 未考虑Stokes漂流作用的误差统计量的均值R为0.72, ME为0.89℃, RMSE为1.12℃, MAE为1.06℃, 通过对比发现, 考虑了Stokes漂流的作用, 模拟与实测温度的相关系数更高、均方根更小, 温度偏高现象得到了改善, 模拟的温度与实际更加相符。在整个台风过程中, 根据与实测浮标资料对比发现, 随着模拟时间的增加, 两种试验结果出现了相关系数降低、平均绝对误差和均方根误差增大的情况, 并且模拟的温度具有升高的趋势, 说明模拟时间越长, 模型计算失真的可能性越大。图 13中, 随着时间的增加, 虽然模拟温度的误差具有增加的趋势, 但是对比未考虑Stokes漂流作用的模拟结果发现, 考虑Stokes漂流作用后模拟温度的误差相对较小, 说明模拟效果得到了改善。
6 结论浪致Stokes漂流是海洋上层不可忽视的物理过程。台风作用形成的台风浪会产生较大的Stokes漂流, Stokes漂流则会引起Stokes输运, Stokes漂流和Stokes输运最大值分别可达0.15m/s和1m2/s, 两者在台风过程中的分布与浪场的分布相对应。Stokes漂流越大, Stokes输运占净输运的比例越大, 通过计算Ekman-Stokes数表明Stokes输运在台风过程中总输运中占有很大比例。
基于浪流耦合模型, 将考虑和未考虑Stokes漂流作用的模拟结果进行对比发现, 台风过程中Stokes漂流、Stokes输运等会使海洋上层温度的模拟值降低, 温度降低幅度与Stokes漂流等大小相关, Stokes漂流越大, 温度降低幅度越大, 降温主要分布在台风路径附近, 最大降温约为2℃。采用了Argo实测资料与模拟的海洋上层海温进行对比发现, 考虑了Stokes漂流后, 模拟的海洋上层温度得到改善, 与实测温度更接近。
王娟娟, 高志一, 王久珂, 等. 2016. Jason-2有效波高产品在中国海域的准确性评估. 海洋与湖沼, 47(3): 509-517 |
王智峰, 2012. Stokes_drift对上层海洋的影响研究.青岛: 中国海洋大学博士学位论文
|
毕凡, 2013.波浪对环流输运影响和涌浪传播耗散特征研究.青岛: 中国海洋大学博士学位论文
|
刘增宏, 许建平, 朱伯康, 等. 2006. 利用Argo资料研究2001-2004年期间西北太平洋海洋上层对热带气旋的响应. 热带海洋学报, 25(1): 1-8 DOI:10.3969/j.issn.1009-5470.2006.01.001 |
杨晓霞, 唐丹玲. 2010. 台风引起南海海表面降温的位置变化特征. 热带海洋学报, 29(4): 26-31 DOI:10.3969/j.issn.1009-5470.2010.04.005 |
Breivik Ø, Bidlot J R, Janssen P A E M, 2016. A stokes drift approximation based on the Phillips spectrum. Ocean Modelling, 100: 49-56 DOI:10.1016/j.ocemod.2016.01.005 |
Breivik Ø, Mogensen K, Bidlot J et al, 2015. Surface wave effects in the NEMO ocean model:forced and coupled experiments. Journal of Geophysical Research:Oceans, 120(4): 2973-2992 DOI:10.1002/2014JC010565 |
Craik A D D, Leibovich S, 1976. A rational model for Langmuir circulations. Journal of Fluid Mechanics, 73(3): 401-426 DOI:10.1017/S0022112076001420 |
Deng Z A, Xie L A, Han G J et al, 2012. The effect of Coriolis-Stokes forcing on upper ocean circulation in a two-way coupled wave-current model. Chinese Journal of Oceanology and Limnology, 30(2): 321-335 DOI:10.1007/s00343-012-1069-z |
Hasselmann K, 1970. Wave-driven inertial oscillations. Geophysical Fluid Dynamics, 1(3-4): 463-502 DOI:10.1080/03091927009365783 |
Huang N E, 1979. On surface drift currents in the ocean. Journal of Fluid Mechanics, 91(1): 191-208 DOI:10.1017/S0022112079000112 |
Lewis D M, Belcher S E, 2004. Time-dependent, coupled, Ekman boundary layer solutions incorporating Stokes drift. Dynamics of Atmospheres and Oceans, 37(2004): 313-351 |
Li S, Song J B, Sun Q, 2008. Effect of Stokes drift on upper ocean mixing. Acta Oceanologica Sinica, 27(2): 11-20 |
Li M, Zahariev K, Garrett C, 1995. Role of Langmuir circulation in the deepening of the ocean surface mixed layer. Science, 270(5244): 1955-1957 DOI:10.1126/science.270.5244.1955 |
Longuet-Higgins M S, 1953. Mass transport in water waves. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 245(903): 535-581 DOI:10.1098/rsta.1953.0006 |
McWilliams J C, Restrepo J M, 1999. The wave-driven ocean circulation. Journal of Physical Oceanography, 29(10): 2523-2540 DOI:10.1175/1520-0485(1999)029<2523:TWDOC>2.0.CO;2 |
Mellor G L, Yamada T, 1974. A hierarchy of turbulence closure models for planetary boundary layers. Journal of the Atmospheric Sciences, 31(7): 1791-1806 DOI:10.1175/1520-0469(1974)031<1791:AHOTCM>2.0.CO;2 |
Polton J A, Belcher S E, 2007. Langmuir turbulence and deeply penetrating jets in an unstratified mixed layer. Journal of Geophysical Research:Oceans, 112(C9): C09020 |
Price J F, 1981. Upper ocean response to a hurricane. Journal of Physical Oceanography, 11(2): 153-175 DOI:10.1175/1520-0485(1981)011<0153:UORTAH>2.0.CO;2 |
Shay L K, Black P G, Mariano A J et al, 1992. Upper ocean response to hurricane gilbert. Journal of Geophysical Research:Oceans, 97(C12): 20227-20248 DOI:10.1029/92JC01586 |
Tamura H, Miyazawa Y, Oey L Y, 2012. The Stokes drift and wave induced-mass flux in the North Pacific. Journal of Geophysical Research:Oceans, 117(C8): C08021 |
Wang Z F, Wu K J, Dong S et al, 2015. Effect of wave-induced Stokes drift on the dynamics of ocean mixed layer. Chinese Journal of Oceanology and Limnology, 33(1): 233-242 DOI:10.1007/s00343-015-4036-7 |
Weber J E, 1983. Attenuated wave-induced drift in a viscous rotating ocean. Journal of Fluid Mechanics, 137: 115-129 DOI:10.1017/S0022112083002311 |
Wu J, 1980. Wind-stress coefficients over sea surface near neutral conditions-A revisit. Journal of Physical Oceanography, 10(5): 727-740 DOI:10.1175/1520-0485(1980)010<0727:WSCOSS>2.0.CO;2 |
Ying M, Zhang W, Yu H et al, 2014. An overview of the china meteorological administration tropical cyclone database. Journal of Atmospheric and Oceanic Technology, 31(2): 287-301 DOI:10.1175/JTECH-D-12-00119.1 |
Zhang X S, Wang Z F, Wang B et al, 2014. A numerical estimation of the impact of Stokes drift on upper ocean temperature. Acta Oceanologica Sinica, 33(7): 48-55 DOI:10.1007/s13131-014-0507-5 |
 2019, Vol. 50
2019, Vol. 50