
中国海洋湖沼学会主办。
文章信息
- 闫西荡, 杨坤德. 2020.
- YAN Xi-Dang, YANG Kun-De. 2020.
- 蒸发波导环境下风浪对电磁波传播影响的数值模拟研究
- INFLUENCE OF WIND SPEED ON ELECTROMAGNETIC WAVE PROPAGATION UNDER EVAPORATION DUCT CONDITION BASED ON SEA SURFACE MODEL
- 海洋与湖沼, 51(1): 13-19
- Oceanologia et Limnologia Sinica, 51(1): 13-19.
- http://dx.doi.org/10.11693/hyhz20190700129
文章历史
-
收稿日期:2019-07-01
收修改稿日期:2019-09-12
2. 国家海洋声学信息感知工业和信息化部重点实验室(西北工业大学) 西安 710072
2. Laboratory of Ocean Acoustics and Sensing(Northwestern Polytechnical University), Ministry of Industry and Information Technology, Xi'an 710072, China
蒸发波导是一种大气波导, 其产生的机理是:随着海面水汽的蒸发及扩散, 海面上方产生大气湿度负梯度, 相应的大气折射指数会随着海拔高度的增加而减小, 同样产生负梯度变化趋势(史阳, 2017; Yang et al, 2016; Zhang et al, 2016)。大气折射指数的负梯度会使得电磁波向下折射, 当折射的曲率大于地球曲率时, 电磁波信号就被陷获在蒸发波导大气层中, 实现超视距传播(康士峰等, 2014;张永刚, 2014)。受蒸发波导环境、微波频率、粗糙海面及传播距离等的影响, 海洋蒸发波导环境中的电磁波传播特性起伏变化很大, 规律比较复杂(刘成国等, 1998;刘成国, 2003;黄小毛等, 2006; Zhang et al, 2017)。以往的工作主要通过计算这些气象因素对蒸发波导条件下大气折射率剖面的影响来分析它们对路径损失的作用, 其结果与实验数据仍有较大差异。本文则是在蒸发波导的背景条件下, 研究其中的电磁波传播特性受风速带来的海面变化的影响, 可作为对原模型的修正。
在研究海面波浪对电磁波传播影响时寻找一种合适的海面模型是非常重要的。早期很多是利用Monte Carlo等方法结合实际海面谱反演海面模型(Mandelbrot, 1982)。后来有很多学者利用经典带限Weierstrass分形模型来模拟粗糙海面, 这些分形模型的表面谱满足负幂率关系, 一定程度上可以模拟整个海面的完全海谱。人们改进了分形模型以模拟产生满足PM谱分布的实际海面, 并给出了模型中各参数与海面上风速之间的关系。通过此模型, 可以在一定风速情况下产生相应的海面。
本文利用一维带限海面模型产生的海面“地形”, 将其作为抛物方程电磁波传播模型的边界条件进行计算, 得到相应的路径损失与传统计算方法进行对比, 并分析了不同蒸发波导高度、不同频率及不同接收天线高度时的情况。
1 背景模型 1.1 一维分形海面模型Mandelbrot指出Weierstrass函数(Mandelbrot, 1982;王运华等, 2007; Yan et al, 2017)
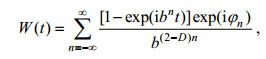 (1)
(1)具有分形的性质。这是一个处处连续但处处不可导的函数, t是自变量, φn为任意的随机相位函数, D近似等于豪斯道夫维数, b是空间基频。
为了说明问题我们取φn为零时Weierstrass函数的实部C(t), 即
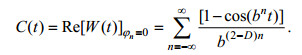 (2)
(2)可以证明, 这种函数无论是空间基频b>1还是b < 1都满足自相似的分形特征。基于此式, 经典的分形模型通常是用一维带限Weierstrass函数来模拟一维动态海面, 该函数通常表示为:
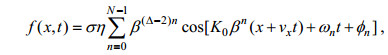 (3)
(3)其中, f为海面高度, x为水平距离, σ为海面高度起伏均方根, 其单位均为m, η为归一化因子, Δ是分形模型的分维数(1 < Δ < 2), β为尺度因子(β >1), K0为海表面的空间基波波数, 它决定空间频谱的位置, ωn为第n个谱分量的角速度, 其单位为rad/s, n是[-π, π]上均匀分布的随机相位, vx是观测雷达平台的水平运动速度, 其单位为m/s。风与波浪条件之间的关系可以使用经典的Pierson- Moskowitz(PM)谱来定义。PM谱是根据经验推导出来的, 并使用距离海表面高度19.5m处的海上风速U19.5作为定义波能量谱的单一参数。由式(3)所模拟粗糙面的功率谱满足负幂率指数谱, 正好对应于海面PM谱中的一段。
海上风速和海面高度起伏均方根及其基波波数满足如下关系:
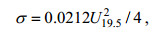 (4)
(4)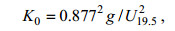 (5)
(5)其中, g为重力加速度。不同风速条件下利用分形模型生成的粗糙海面如图 1。
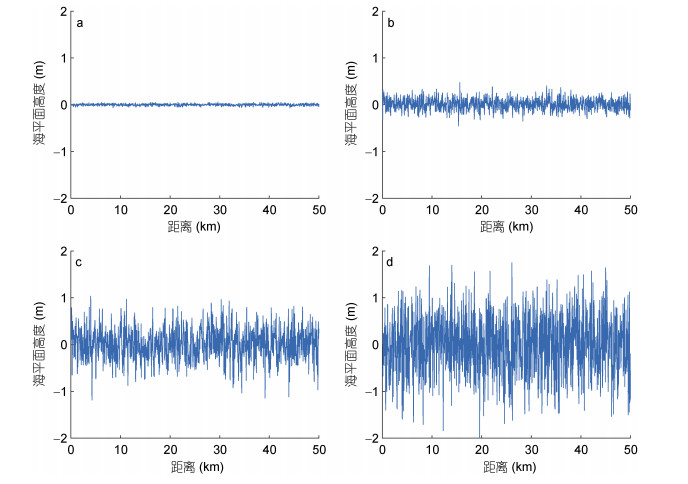 |
| 图 1 2m/s(a)、5m/s(b)、8m/s(c)及11m/s(d)风速下产生的海面 Fig. 1 Sea surface generated under different wind speed conditions |
从图 1中可以看出, 风速越大, 海面的高度起伏幅值越大。事实上, 根据式(5), 可以得到海面高度起伏均方根与风速的关系曲线, 如图 2所示。
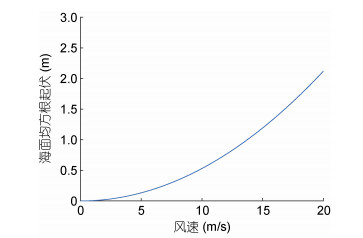 |
| 图 2 海面高度起伏均方根与风速的关系 Fig. 2 Relationship between RMS fluctuation of sea surface and wind speed |
抛物方程(Parabolic Equation, PE)模型使用了对亥姆霍兹波动方程的近轴近似(Dockery, 1988), 可适用于复杂边界条件的建模。在发展出基于分步傅里叶变换的计算方法后, PE方法已成为一种被广泛接受的计算蒸发波导条件下电磁波传播的技术(Thomson et al, 1983; Hyaric, 2001)。
对于2D窄角传播, PE的标量形式如下:
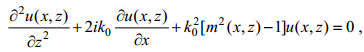 (6)
(6)其中, z与x分别代表海面上高度与距离, k0为自由空间波数, u是垂直极化电磁场中的磁场标量分量或水平极化电磁场中的电场标量分量, m是修正折射率指数。
距离xk、高度z处的参量u可被记作u(xk, z), 则利用分步傅里叶变换, 可得到u(xk+1, z)如下:
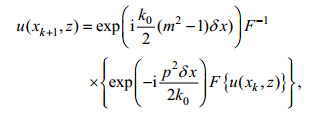 (7)
(7)其中, F[·]与F-1[·]分别代表傅里叶与逆傅里叶变换。δx=xk+1-xk是距离上的步长。在包含地形边界条件的情况下, 可通过相应位置u值的置零来体现地形的遮蔽效应等。
最终, 可利用u(x, z)计算得到路径损失PL:
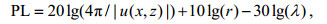 (8)
(8)其中, γ是水平距离, 其单位为m, λ为电磁波波长, 单位为m。
2 风速对蒸发波导中电磁波传播的影响本文设定了某典型蒸发波导环境条件进行数值模拟, 研究风浪对电磁波近海面传播的影响。人们利用海面上有限的气象参数及基于Monin-Obukhov理论的蒸发波导模型, 就可以计算出一定高度范围内的修正折射率剖面(Yan et al, 2018), 这些模型中较为常见的一种即Naval Postgraduate School(NPS)模型(Shi et al, 2015)。
NPS模型的核心是长期海上调查得到的海气通量整体算法COARE(Coupled Ocean–Atmosphere Response Experiment)耦合海洋大气响应实验, 该算法广泛应用于边界层中, 经过了大量的试验验证。本文采用COARE3.0算法来进行海表层尺度, 并利用以下公式计算温湿度剖面(Yang et al, 2017):
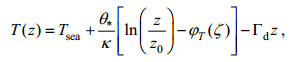 (9)
(9)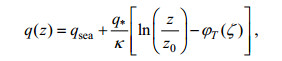 (10)
(10)式中均采用国际单位制, T为温度, q为比湿, z为表面层中的高度, Tsea为海表温度, qsea为海表处的比湿, θ*和q*分别为比湿及位温的尺度参数, z0是表面粗糙度长度, 函数φT是相似性函数, κ是von Karman常数, L是Monin-Obukhov长度, ζ = z/L称为Monin-Obukhov参数, Γd取值0.00976K/m。
为了计算折射率剖面, 还要知道大气压随高度分布的情况。大气压剖面可通过联立流体静力学方程及理想气体定律并积分得到, 即:
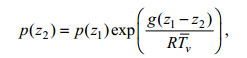 (11)
(11)式中, z1为观测高度, z2为表面层中的任一高度, R为通用气体常数(287.04J/(kgK)), 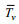
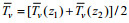
利用式(9)-式(11)获得的温度、湿度和大气压剖面, 结合式(12)和式(13)就可以得到修正折射率剖面。
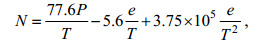 (12)
(12)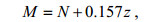 (13)
(13)式中, N是大气折射率, P是大气压强, 单位为hPa, e是水汽分压, 单位为hPa, T是大气温度, 单位为K, M为修正折射率, z为海面上高度, 单位为m。
设海表温度为24.3℃, 大气压为1018.6hPa, 2m高处气温为20.8℃, 2m高处比湿为9.4g/kg, 10m高处风速为8.4m/s。则对于以上设定的气象参数, 利用NPS模型计算可得到相应的修正折射率剖面如图 3所示。同时可得到此时蒸发波导高度为15.7m。
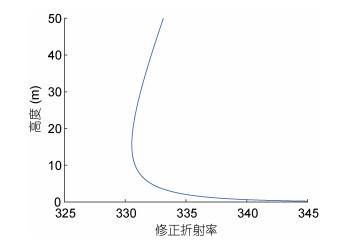 |
| 图 3 蒸发波导修正折射率剖面 Fig. 3 Modified refractive index profile of the evaporation duct |
数值模拟参数设定为:电磁波频率8GHz, 天线高度3m, 天线极化方式为水平极化, 最远计算距离为100km。将生成的海浪模型作为地形信息, 与计算得到的修正折射率剖面作为抛物方程模型的输入, 计算可得到风浪影响情况下的近海面传播路径损失, 如图 4所示。
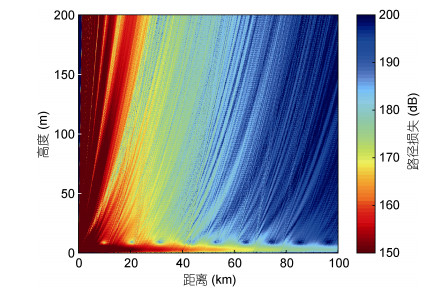 |
| 图 4 考虑风浪时蒸发波导中微波传播的路径损失 Fig. 4 The path loss of microwave propagation in the evaporation duct in consideration of the topography of sea surface |
为了与不考虑风浪地形影响时的情况进行对比, 我们计算了后者的电磁波传播路径损失如图 5。
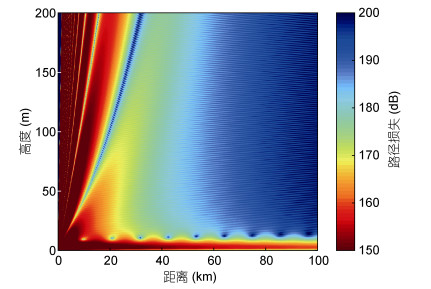 |
| 图 5 不考虑风浪时蒸发波导中的微波传播的路径损失 Fig. 5 The path loss of microwave propagation in the evaporation duct in no consideration of the topography of sea surface |
对比图 4与图 5, 可看出, 考虑风浪地形影响时, 蒸发波导陷获层以内的电磁波能量随距离衰减更快, 大约60km后路径损失就增大到170dB以上; 对于蒸发波导高度以上的区域, 由于海浪表面的遮挡及反射等, 电磁波互相干涉产生不平滑的条纹。
图 6给出了若干个接收高度处, 电磁波传播路径损失随距离变化的曲线。其中图 6a是考虑风浪地形影响时的情况, 图 6b为不考虑时的情况。从二者的对比可以看出, 无论接收天线高度为3、5或7m, 考虑风浪影响时的路径损失都会大于不考虑时。在传播距离较近时, 两种情况的差值较小, 40km处对应的差值大约为8dB; 随着传播距离的增大, 两种情况的差值会逐渐变大, 在100km处达到了约20dB。在给定的条件下, 不考虑风浪地形时的路径损失曲线都比较平缓, 而考虑风浪地形时曲线多了很多起伏, 并且曲线上毛刺的起伏程度随着接收天线的高度增加而有所增加。
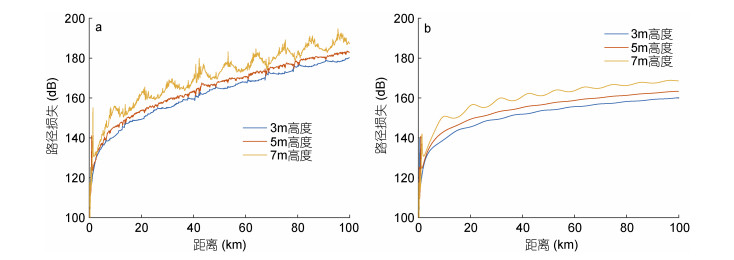 |
| 图 6 考虑海浪(a)与不考虑海浪(b)时不同接收高度处电磁波路径损失随距离变化的曲线 Fig. 6 The path loss of electromagnetic wave as a function of distance at different receiving heights |
图 7给出了若干个接收距离处, 电磁波传播路径损失随高度变化的曲线。其中图 7a是考虑风浪地形影响时的情况, 图 7b为不考虑时的情况。从图中可以看出, 在近海面低高度的十几米的范围内, 无论接收天线距离为40或100km, 考虑风浪影响时的路径损失都会大于不考虑时, 并且两种情况下路径损失随高度变化的曲线起伏都比较小。超过一定的高度范围后, 两种情况路径损失的最小值差距并不大, 但有风浪影响时的路径损失却会在某些高度处有一些比较大的起伏, 与无风浪影响时的差值可能达到30dB以上。由于模拟海面的随机性, 这些较大路径损失出现的高度并不稳定, 也会给接收信号强度带来比较强的随机性。
 |
| 图 7 考虑海浪(a)与不考虑海浪(b)时不同接收距离上电磁波路径损失随高度变化曲线 Fig. 7 The path loss of electromagnetic wave versus height at different receiving distances |
为了深入分析风速海浪地形对传播的影响, 本文继续采用更多的参数设置, 以研究不同频率、不同风速等条件下的路径损失分布。
(1) 考虑风浪地形时, 不同蒸发波导高度对微波传播路径损失的影响(情况1);
(2) 风浪地形对不同频率微波传输的影响(情况2);
(3) 不同风速产生的海浪对微波传播的影响(情况3)。
三种条件下抛物方程模型的数值模拟输入参数如表 1所示, 蒸发波导中其他环境条件则与图 3中一致。
| 情况1 | 情况2 | 情况3 | |
| 天线高度(m) | 3 | 3 | 3 |
| 发射频率(GHz) | 8 | 1-15 | 8 |
| 天线极化方式 | 水平极化 | 水平极化 | 水平极化 |
| 传输距离(km) | 100 | 100 | 100 |
| 计算高度(m) | 200 | 200 | 200 |
| 蒸发波导高度(m) | 1-15 | 15.7 | 15.7 |
| 19.5m高风速(m/s) | 8.4 | 8.4 | 1-15 |
蒸发波导高度不同的情况下, 电磁波传播路径损失对应的曲线如图 8所示。数值模拟条件即表 1的情况1, 微波传播距离为100km。从图中可知, 当蒸发波导高度小于7m时, 对于频率为8GHz的电磁波, 路径损失随着蒸发波导高度的增加而有所减小, 但减小的速率比较小。蒸发波导高度在7-12m时, 8GHz电磁波传播路径损失随着波导高度的增加而急剧减小至180dB左右。蒸发波导高度超过12m时, 路径损失则相对变化不大。
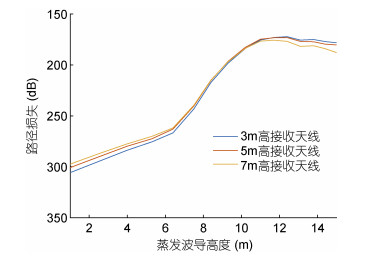 |
| 图 8 不同蒸发波导高度对微波传播的影响 Fig. 8 Influence of different evaporation duct heights on microwave transmission |
图 9为不同频率电磁波在不考虑风浪与考虑风浪时的路径损失, 接收天线距离为100km, 数值模拟参数如表 1中情况2。从图 9中可以看出, 无论风浪大小及接收天线高低, 频率较低情况下的电磁波传播路径损失计算结果都比较近似, 而高频时计算结果则有较大差异。蒸发波导中的微波频率约小于4.5GHz时, 风浪带来的地形对传播损失影响不大; 随着频率的增大, 路径损失有所减小, 3m高处的接收天线比10m高处的接收天线测量得到的路径损失大3dB左右。微波频率在6-10GHz时, 四种情况下的路径损失差距比较明显, 不考虑风浪地形影响且3m接收天线的路径损失最小, 考虑风浪地形且10m高接收天线的路径损失最大, 其他两者比较近似, 各路径损失差大体小于20dB。微波频率超过11GHz时, 考虑风浪地形影响的路径损失明显变大, 且在11.5GHz处存在一个极大值点。
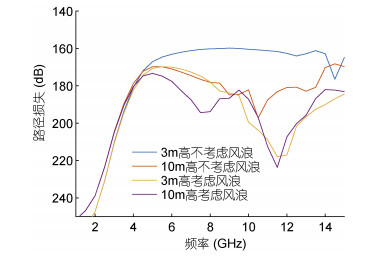 |
| 图 9 风浪地形对不同频率微波传输的影响 Fig. 9 Influence of wind speed on microwave transmission at different frequencies |
图 10是不同风速产生的海浪对微波传播路径损失的影响, 数值模拟参数如表 1情况3, 传输距离为100km。从图 10中可知, 风速较低时, 微波传播路径损失随风速的变化很小, U19.5超过一定范围后, 风速越大, 形成的海面越粗糙, 微波在蒸发波导中传播的路径损失越大。当风速小于4m/s时, 各高度处的天线路径损失几乎与不考虑风浪地形时相同, 并随着天线高度的增加而增大。当U19.5大于6m/s时, 风速每增加1m/s, 路径损失约增大10dB, 并且此时接收天线高度对路径损失的影响不明显。
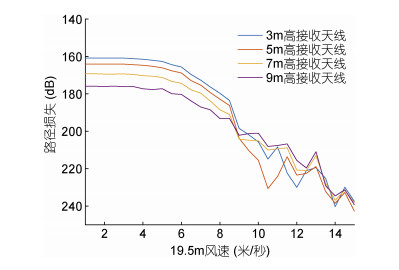 |
| 图 10 不同风速产生的海浪对微波传播的影响 Fig. 10 Influence of sea surfaces generated by different wind speeds on microwave propagation 注: U19.5表示距离海表面高度19.5m处的海上风速 |
本文利用一维分形海面模型产生的海面“地形”, 并将其作为抛物方程电磁波传播模型进行计算, 得到相应的路径损失与传统计算方法进行对比, 并分析了不同蒸发波导高度、不同频率及不同接收天线高度时的情况。考虑风浪地形影响时, 对于频率为8GHz的电磁波, 路径损失随着蒸发波导高度的增加而有所减小。蒸发波导中的微波频率约小于4.5GHz时, 风浪带来的地形对传播损失影响不大, 微波频率在6-10GHz时, 路径损失差距会比较明显。风速较低时, 微波传播路径损失随风速的变化很小, U19.5超过一定范围后, 风速越大, 形成的海面越粗糙, 微波在蒸发波导中传播的路径损失越大。风浪地形对不同情况下微波传输路径损失的影响有很大不同, 在设计舰艇通信系统或者雷达系统的时候需要加以考虑。
王运华, 郭立新, 吴振森. 2007. 改进的一维分形模型在海面电磁散射中的应用. 电子学报, 35(3): 478-483 DOI:10.3321/j.issn:0372-2112.2007.03.019 |
刘成国, 2003.蒸发波导环境特性和传播特性及其应用研究.西安: 西安电子科技大学博士学位论文
|
刘成国, 潘中伟, 蔺发军, 等. 1998. 一种预测低层大气折射率剖面的实用方法. 电波科学学报, 13(4): 403-406 |
张永刚. 2014. 海洋声光电波导效应及应用. 北京: 电子工业出版社
|
黄小毛, 张永刚, 王华, 等. 2006. 蒸发波导中雷达异常性能的仿真与分析. 系统仿真学报, 18(2): 513-516 DOI:10.3969/j.issn.1004-731X.2006.02.063 |
康士峰, 张玉生, 王红光. 2014. 对流层大气波导. 北京: 科学出版社
|
史阳, 2017.蒸发波导建模及微波传输特性研究.西安: 西北工业大学
|
Dockery G D, 1988. Modeling electromagnetic wave propagation in the troposphere using the parabolic equation. IEEE Transactions on Antennas and Propagation, 36(10): 1464-1470 DOI:10.1109/8.8634 |
Hyaric A Z L, 2001. Wide-angle nonlocal boundary conditions for the parabolic wave equation. IEEE Transactions on Antennas and Propagation, 49(6): 916-922 DOI:10.1109/8.931149 |
Mandelbrot B B, 1982. The Fractal Geometry of Nature. New York: W. H. Freeman and Company
|
Shi Y, Yang K D, Yang Y X et al, 2015. A new evaporation duct climatology over the South China Sea. Journal of Meteorological Research, 29(5): 764-778 DOI:10.1007/s13351-015-4127-6 |
Thomson D J, Chapman N R, 1983. A wide-angle split-step algorithm for the parabolic equation. The Journal of the Acoustical Society of America, 74(6): 1848-1854 DOI:10.1121/1.390272 |
Yan X D, Yang K D, Ma Y L, 2018. Calculation method for evaporation duct profiles based on artificial neural network. IEEE Antennas and Wireless Propagation Letters, 17(12): 2274-2278 DOI:10.1109/LAWP.2018.2873110 |
Yan X D, Yang K D, Zhang Q et al, 2017. The investigation of vertical space correlation for electromagnetic propagation under evaporation duct conditions. In: OCEANS 2017- ANCHORAGE. Anchorage: IEEE, 1-4
|
Yang S B, Li X F, Wu C et al, 2017. Application of the PJ and NPS evaporation duct models over the South China Sea (SCS) in winter. PLoS One, 12(3): e0172284 DOI:10.1371/journal.pone.0172284 |
Yang K D, Zhang Q, Shi Y et al, 2016. On analyzing space-time distribution of evaporation duct height over the global ocean. Acta Oceanologica Sinica, 35(7): 20-29 DOI:10.1007/s13131-016-0903-0 |
Zhang Q, Yang K D, Shi Y, 2016. Spatial and temporal variability of the evaporation duct in the Gulf of Aden. Tellus A: Dynamic Meteorology and Oceanography, 68(1): 29792 DOI:10.3402/tellusa.v68.29792 |
Zhang Q, Yang K D, Yang Q L, 2017. Statistical analysis of the quantified relationship between evaporation duct and oceanic evaporation for unstable conditions. Journal of Atmospheric and Oceanic Technology, 34(11): 2489-2497 DOI:10.1175/JTECH-D-17-0156.1 |
 2020, Vol. 51
2020, Vol. 51


