中国海洋湖沼学会主办。
文章信息
- 张志欣, 郭景松, 蔡燕红, 乔方利, 郭炳火. 2020.
- ZHANG Zhi-Xin, GUO Jing-Song, CAI Yan-Hong, QIAO Fang-Li, GUO Bing-Huo. 2020.
- 一种用于海洋层化数据的插值方法改进
- IMPROVED INTERPOLATION FOR MARINE STRATIFICATION DATA
- 海洋与湖沼, 51(2): 228-234
- Oceanologia et Limnologia Sinica, 51(2): 228-234.
- http://dx.doi.org/10.11693/hyhz20190900165
文章历史
-
收稿日期:2019-09-04
收修改稿日期:2019-11-12
2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室 青岛 266237;
3. 自然资源部海洋环境和数值模拟重点实验室 青岛 266061;
4. 自然资源部数据分析与应用重点实验室 青岛 266061;
5. 自然资源部宁波海洋环境监测中心站 宁波 315012
2. Laboratory for Regional Oceanography and Numerical Modeling, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China;
3. Key laboratory of Data Analysis and Applications, Ministry of Natural Resources, Qingdao 266061, China;
4. Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources, Qingdao 266061, China;
5. Ningbo Marine Environment Monitoring Center Station, Ministry of Natural Resources, Ningbo 315012, China
海洋环境调查数据的客观分析图像是调查结果的直观体现, 也是进一步科学研究的基础。对于规整的海洋要素格点数据, 资料点分布相对均匀, 因而图像绘制可以选择的插值方法比较多; 但是对于资料点空间分布不均匀的情况, 网格化插值结果受插值方法和具体参数选择影响较大。目前的大量研究表明, 采用不同的空间插值方法得到的结果具有明显的差异(Stohl et al, 1995; Dirks et al, 1998; Jeffrey et al, 2001; 范银贵, 2002; 陈欢欢等, 2007; 杜红娟等, 2012; 张海平等, 2017)。近些年来, 有学者提出对原始数据进行一定的处理, 如引入月平均总云量影响因子的协同克里金插值方法(孔令娜等, 2012)、对气象数据先进行距平处理再做空间插值(刘琰琰, 2017)等, 在一定程度可以提高插值结果的精度。在海洋环境监测的同时, 人们也对空间插值方法在不同海湾和近海区域的最优插值方法和参数选择等进行探索研究(刘瑞民等, 2002; 尹维翰等, 2007; 李峋等, 2009; 潘楚东等, 2010; 吴翠晴等, 2012; 尹维翰等, 2012; 李俊龙等, 2015; 王兴等, 2016)。这些工作对空间插值方法的最优选择给出了一些有益的建议。
然而, 海洋环境状况受制于外部、内部诸多动力因子以及热力和物质交换等, 特别是陆架区、近岸海域及陆架坡区, 还受复杂的海底地形影响, 海洋环境要素场必然有着更复杂的空间分布特征。在使用现有的插值方法绘制的温度和盐度断面图中, 我们发现之前没有被关注到的一些明显异常现象, 如图 1和图 2中的“藕”状或“台阶状”的跃层结构, 给人们对海洋环境认识和科学研究带来虚假信息。本文试图针对这类异常现象, 分析其出现的原因, 并对现有插值方法提出一种改进方案。
 |
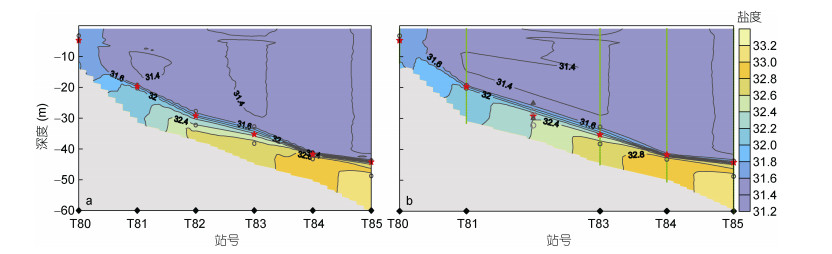
| 图 1 南海北部一断面盐度分布图 Fig. 1 Salinity section distribution in the northern South China Sea 注: a: 三角网线性插值方法插值得到的; b: Kriging方法插值得到的; 黑色圆圈: “台阶”状或“藕”状异常结构 |
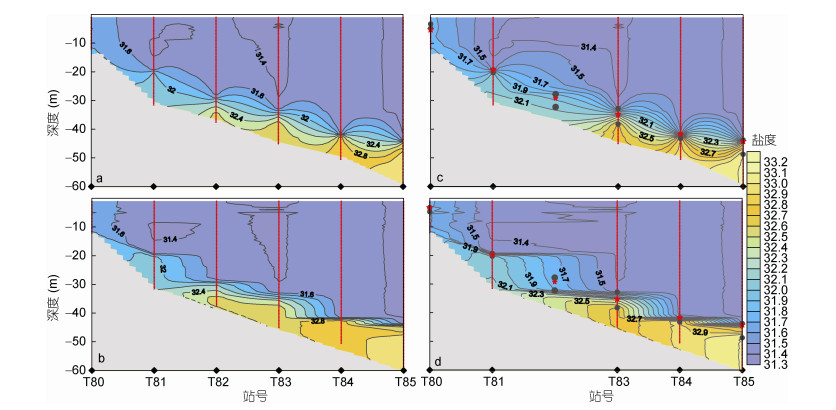 |
| 图 2 泰国湾内的一条盐度断面分布图 Fig. 2 Salinity section distribution in the Gulf of Thailand 注: a: Kriging方法插值得到的; b: 三角网线性插值方法插值得到的; 为了检验2种不同方法的插值结果与实际数据的偏差情况, 将图 2a和图 2b的盐度断面中T82测站去除, 由其他5个测站组成一比对断面, 再分别采用Kriging方法和三角网插值方法插值得到图 2c和图 2d; 图 2c和图 2d中灰色圆点: 观测盐度值垂向变化(一阶导数) > 0.1/m的深度层的上下界位置; 红色五角星: 各测站跃层中心位置 |
在利用海洋调查数据绘制要素空间分布状况图时, 人们通过选择合适的插值方法及恰当的搜索域参数、输出参数等配置, 通常经过几次调整后, 可以得到一个比较满意的客观分析图像。然而, 有时仍可能出现局部异常, 而且无论如何调整相关配置参数都无法消除。目前, 在海洋水文要素插值中应用比较广泛的有Kriging、三角网线性插值法等。三角网线性插值法得到的结果能够很好地呈现原始数据信息, 缺点是数据边界舍去较多, 且用所得格点数据绘制的图像线条不平滑, 有时会出现或轻或重的“台阶状”层化结构异常(图 1a)。Kriging方法, 又称空间自协方差最佳插值法, 它是建立在变异函数理论结构分析基础之上的统计格网化方法, 且可以适当地外推插值到观测点区之外, 从而得到较完整的图像, 但有时也会有或清晰或模糊的“藕”状层化结构出现(图 1b)。
类似的异常结构在海洋要素平面图、断面图中经常会被看到, 其中断面图异常多出现在海底地形倾斜较大, 且水文要素层化结构显著的区域。仔细探寻图 1a & b, 在两测站之间区域, 这些“藕”状或“台阶”状层化结构并没有观测数据支持, 其海洋要素分布特征也与测站处的情况不同, 两测站之间的“藕”状结构显示要素的垂向变化的范围大于测站处, 而“台阶”状结构中甚至显示要素几乎垂向均匀, 在这些区域明显出现了不同于测站处观测数据所体现的环境信息。无论是两测站间区域的“藕”状还是“台阶”状结构, 其呈现的层化结构范围都与测站处要素特征不同。这些异常结构的出现给我们认识真实的海洋环境状况带来了一些信息干扰。
本文将以泰国湾内的一条盐度断面为例进行详细探讨。泰国湾内一条由6个测站T80-T85组成的断面, 这里分别采用Kriging和三角网线性插值法插值得到盐度断面分布图(图 2a和b)。这两种插值方法的插值结果显示盐跃层处出现了两种明显不同的结构。对于Kriging插值方法, 两测站间跃层呈“藕”状结构, 相对于测站处的跃层厚度明显增大, 强度则减弱; 对于三角网线性插值法, 两测站间呈“台阶”状结构, 两台阶之间盐度几乎垂直均匀。针对这两种异常现象, 我们认为: 1)在测站处由于该站观测数据占绝对优势的权重, 两种插值法得到的结果并无差异, 其层化结构图像是真实的; 2)在两测站之间区域则由周边测站的观测数据插值得到, 其结果与采用的插值方法密切相关。这意味着这两种异常结构是插值带来的。为此, 我们把图 2a和b中盐度断面数据中的T82测站剔除, 由其他5个测站组成一个比对断面, 并继续采用Kriging和三角网线性插值法对其插值得到图 2c和d所示的一组盐度断面分布图。该分布图显示这两种插值方法的插值结果在T82站均产生了更强的“藕”状和“台阶”状结构, 其跃层垂向范围竟比图 2a和b中该测站的测量情况增大了3倍多。以上分析比对可以确定图像中“藕”状和“台阶”状结构是插值带来的假象。
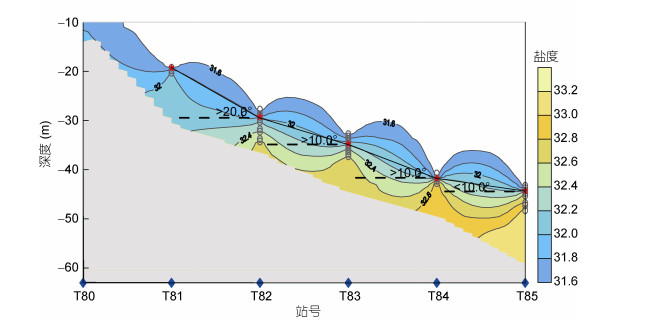
2 坐标变换改进的插值方法上面的分析表明, 这种“藕”状或者“台阶”状假象出现在跃层中。我们分别计算了图 2中原断面中T81—T85各测站的盐度垂向变化一阶导数, 并根据盐跃层强度的国标规定(GB/T 12763.7-1991, 1991), 挑选出其中盐度垂向变化率 > 0.1/m的值, 并以灰色圆圈标注于图 3, 其相应的深度位置即是盐跃层所在处。由图 3可见, 盐跃层是倾斜的, 而且倾斜角是变化的。其中测站T81—T82之间大于20.0°, T82—T84之间为10°—20°, 而T84—T85之间小于10°。显然, 该断面的盐跃层各段具有不同的倾斜角。然而现有的插值方法对参与插值的离散数据的搜索域参数(包括搜索半径和搜索域长轴方向等)只能给定一个值, 搜索域长轴方向等参数预先设定后就不能再改变, 而不能同时选择几个不同的倾斜角进行插值计算。然而对于跃层所在深度位置呈多角度倾斜变化的断面, 如果设置参与插值的搜索域长轴方向只取某一数值, 则难以兼顾整个断面跃层的多角度倾斜变化情况。我们认为这可能是现有插值方法设计没有考虑到这种跃层倾斜角变化的情况, 才导致了图像跃层中出现“藕”状或者“台阶”状结构。
一般说来, 在近岸海域、陆架海域及陆坡区盐度和温度跃层位置随地形而倾斜, 倾斜角度往往是变化的。正是这种多角度倾斜变化增添了假象出现的机会。然而, 如果盐跃层分布位置是水平的或倾斜角是不变的, 则选用现有的插值方法, 只要调整参与插值的搜索域的长、短轴半径和长轴方向等, 就可以兼顾水文要素分布特征, 插值出该要素的客观图像。但这里的问题是盐跃层倾斜角度是变化的, 不同于我们平时经常遇到的水平或者单一倾斜角的跃层。针对上面提出的问题, 我们试图通过深度坐标变换, 使图 3中各测站的跃层中心位于新坐标中同一深度上, 然后应用现有的方法进行插值, 之后再把插值数据还原到原有深度坐标中, 我们称之为“坐标变换改进的插值方法”。具体步骤如下:
(1) 首先分别计算各测站盐度垂向分布一阶导数, 并挑选出其最大值所在深度, 记为Di(i=1, 2, 3, 4, 5, 6), 这就是各测站盐跃层中心深度(图 3中的红色五角星标示)。取所有Di的平均值得到各测站跃层中心位置在该断面内的平均深度, 记为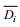
(2) 采用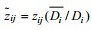
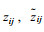
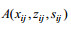
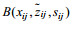
(3) 采用三角网线性插值法对数据组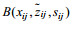
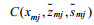
(4) 对由(3)形成的格点数据组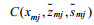
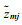
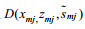
(5) 选用Kriging插值法对数据组D继续插值, 得到规整的格点数据E, 并据此绘制等值线图(见图 4)。这里三角网线性插值法和Kriging方法的组合使用, 即最大化的呈现了原始数据信息, 又完好保留了数据边界且所绘图像等值线线条平滑, 实现了两种方法的优势互补。
图 4a是采用深度坐标变换改进后得到的插值结果, 由图可见盐跃层贴近海底, 并随地形由深向浅变化, 在测站处其跃层上下限位置与测量结果相一致, 在两测站之间也没有出现图 2a和b中的“藕”状或者“台阶”状结构。跃层之下有一高盐水顺势向岸爬升, 盐度值逐渐变小, 而跃层之上盐度混合均匀, 表现为典型的三层结构。整体很好地呈现了观测数据的客观真实性, 符合物理海洋学的基本认识。
为了验证坐标变换改进后的插值效果, 本文特意对去除第三测站(T82)数据的比对断面插值结果进行比较。直接用Kriging方法、三角网线性插值法插值得到的结果在T82测站处出现明显的“藕”状(图 2c)和“台阶”状(图 2d)假象, 而运用本文的坐标变换改进后的插值方法得到的盐度断面分布图在T82测站的分布特征与原6点组成的盐度断面结果非常接近(图 4b), 插值出的跃层厚度与该测站测量结果基本相当, 可以较好地表现出盐跃层的分布特征, 只是跃层上限位置略浅些, 这是受该处不同倾斜角度的跃层位置影响所致。
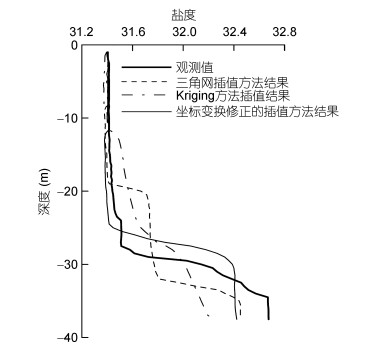
在该组比对断面插值结果中, 我们分别提取出图 2c和d、图 4b中T82站处三种插值结果, 与该站观测值一起绘制盐度垂向分布图(见图 5)。比较表明, 在10m以浅, Kriging方法、三角网线性插值方法、采用坐标变换改进后的插值结果与实测值相差不大, 但10m以深的盐度垂向分布差别较大。观测得到的该站盐度层化为典型的三层结构, 即上均匀层-跃层-下均匀层, 盐跃层位于27.5—34.5m, 厚度为7.0m, 强度为0.16/m。三角网线性插值方法得到T82站的结果出现双盐跃层, 如同图 2d看到的台阶状结构, 跃层范围也因此比观测的放大了将近2倍, 强度为0.06/m, 比观测的缩小了近一半。Kriging方法得到的T82站盐跃层也出现类似于三角网线性插值结果的双跃层结构, 显现为弱化的多层层化结构: 12.0m处盐度垂向变化较强略 < 1.0/m; 之后随着水深增加盐度近乎均匀分布; 直到27.0m处盐度垂向变化增大, 且 > 1.0/m; 27.0—37.5m之间的盐度垂向变化缓慢, 近乎均匀变化, 这部分厚度约为10.0m, 强度为0.04/m; 近底37.5m处盐度垂向变化增大, 且 > 1.0/m。本文提出的“坐标变换改进的插值方法”得到的盐度垂向分布表现为典型的三层结构, 盐跃层位于25.0—29.0m, 厚度为4.0m, 强度为0.20/m, 其分布态势和跃层强度都更接近于观测结果。由此可见, 利用“坐标变换改进的插值方法”得到的结果在跃层分布形态、厚度、强度方面更能客观地反映其实际特征。
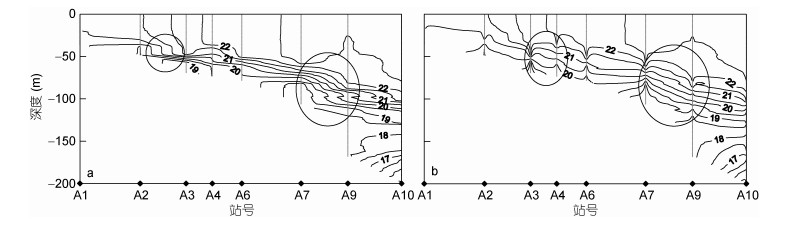
现在, 我们把前面提出的坐标变换改进的插值方法应用于舟山东南东海陆架区的一条断面。该断面共有11个观测站, 水深均浅于110m。图 6中绿色标示的区间是实测温度梯度大于0.2℃/m的温跃层, 它位于近底层。图 6a中红线和黑线分别为应用本文坐标变换改进的插值法和三角网线性插值法得到的等温线分布。结果表明, 两种方法得到的等温线分布大部分区域基本一致, 但温跃层及附近区域差别明显。应用本文坐标变换改进的插值法得到的结果显示在温跃层中等温线密集, 两测站之间接近直线性地自然连接, 十分接近人工绘图结果。然而三角网线性插值结果中出现由一组密集的等温线构成一种类似台阶状的图像异常, 即两台阶面之间是垂直均匀的水层, 从而呈现似双跃层的结构。这种异常现象在29.22°—29.1°N、28.87°—28.72°N、28.15°—27.84°N三个区间较明显, 尤其28.87°—28.72°N区间。
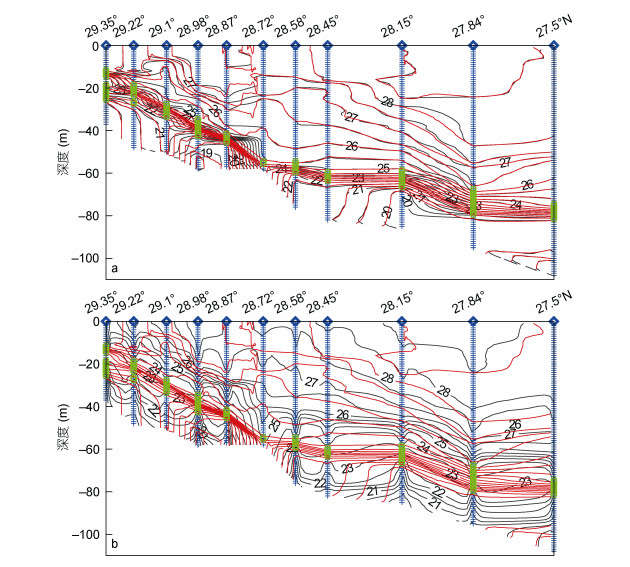 |
| 图 6 8月初舟山东南东海陆架海域的一条观测断面的温度分布 Fig. 6 A temperature section distribution in the continental shelf of East China Sea to the southeast of Zhoushan in early August 注: 绿色: 各测站实测温度梯度大于0.2℃/m的水层; 蓝色菱形: 各测站位置; 蓝色鱼骨线: 各测站的测点位置; 红色等值线: 采用本文坐标变换改进的插值方法得到的结果; 黑色等值线在图 6a、图 6b中分别表示采用三角网线性插值法和采用Kriging插值法所得到的结果 |
图 6b与图 6a比较, 可以看到Kriging方法与本文改进方法插值结果的差异更明显, 尤其在温跃层及其附近区域的等温线分布。Kriging法插值结果(图 6b)显示在该区域内等温线分布略显复杂。在测站处等温线在温跃层高度聚集。而在两测站之间等温线分别向上、下弯曲, 从而被分为上、下两个等温线密集水层, 这两等值线密集区之间的水层等温线略稀疏, 温度接近垂直均匀态, 整体呈现双跃层特征, “藕”状结构明显。结合前面的分析, 这种类似“藕”状的结构可以被认为是Kriging方法插值带来的假象。本文坐标变换改进的插值方法得到的等温线则在近底层各个测站间近直线性连接, 呈现出随地形变化的强温跃层。由此可见, 这种坐标变换修正的插值方法得到的结果更符合水文要素的客观分布特征, 能更好的体现海洋要素数据的客观真实性, 是对现有插值方法的改进与补充。
3 结论插值方法的合理选用是海洋环境要素得以客观成像过程中的重要一步。插值方法各有特色, 如何把插值方法恰当地应用于各种各样的海洋环境调查数据中是我们使用这些方法的关键。这不仅需要我们熟知各类插值方法的优缺点, 还要对所使用的数据环境有一个初步的了解。在此基础上, 以海洋数据特点为出发点, 采用合适的插值方法, 并选择恰当的搜索域参数、输出参数等配置, 通常经过几次调整后, 可以得到一个比较满意的客观分析图像, 从而实现数据资料的客观分析图像展示。
利用现有的插值方法绘制海洋要素图像时, 我们发现在陆架区、近岸海域及陆架坡区有时会出现一些之前没有被关注到的“藕”状或“台阶”状结构假象。我们分析认为这是由于要素特征超出了现有插值方法的基本设置要求, 或者说, 在现有的插值方法设计中对于要素场空间分布的某些特征没有被充分考虑到。如本文图 2中盐跃层存在不同倾斜角, 然而现有的插值方法中的搜索域主轴却不能同时选择几个不同的倾斜角进行插值计算。对此, 我们在充分尊重数据的前提下, 提出了坐标变换改进的插值方法。该方法对数据进行深度坐标变换, 快速调整数据结构, 使其适应插值方法的设置要求, 有效地避免了插值得到的要素图像中出现“藕”状或“台阶”状假象, 解决了插值方法在海洋环境调查数据插值中的一个实际问题, 也是对现有插值方法的一种补充。同时, 这里三角网线性插值法和Kriging方法的联合使用, 即最大化地保留了原始数据信息, 又完好保留了数据边界且所绘图像等值线线条平滑, 实现了两种方法的优势互补。
王兴, 刘莹, 王春晖, 等, 2016. 海洋盐度分布的插值方法应用与对比研究. 海洋通报, 35(3): 324-330 |
尹维翰, 齐衍萍, 樊晓杰, 2012. 空间差值在渤海海水污染面积评估应用研究. 科技视界, (30): 12-24 |
尹维翰, 曹志敏, 蓝东兆, 等, 2007. 象山港颗粒有机碳的分布及其影响因子. 海洋环境科学, 26(6): 550—552, 567 |
孔令娜, 向南平, 2012. 基于ArcGIS的降水量空间插值方法研究. 测绘与空间地理信息, 35(3): 123-126 DOI:10.3969/j.issn.1672-5867.2012.03.038 |
刘琰琰, 2017. 气象要素插值的空间化精度提高方法研究. 气象科学, 37(2): 278-282 |
刘瑞民, 王学军, 郑一, 等, 2002. 地统计学在太湖水质研究中的应用. 环境科学学报, 22(2): 209-212 |
杜红娟, 刘九夫, 谢自银, 等, 2012. 基于网格划分的自然邻点法在降雨空间分布研究中的应用. 水利水电技术, 43(4): 23-25 |
李峋, 仵彦卿, 范海梅, 2009. 高维空间插值在海洋环境数据预处理中的应用. 海洋环境科学, 28(6): 729-733 |
李俊龙, 丁页, 刘喜惠, 等, 2015. 全国近岸海域水质空间插值算法精度分析. 中国环境监测, 31(2): 135-140 |
吴翠晴, 李楠, 王亚涛, 等, 2012. 空间插值方法在锦州湾海水富营养化评价中的应用. 水资源与水工程学报, 23(6): 116-119 |
张海平, 周星星, 代文, 2017. 空间插值方法的适用性分析初探. 地理与地理信息科学, 33(6): 14-18 |
陈欢欢, 李星, 丁秀文, 2007. Surfer 8. 0等值线绘制中的十二种插值方法. 工程地球物理学报, 4(1): 52-57 |
范银贵, 2002. 空间插值方法在绘制降水量等值线中的应用. 水利水电科技进展, 22(3): 48-50 |
国家技术监督局, 1991, 中华人民共和国国家标准海洋调查规范海洋调查资料处理. 国家技术监督局, GB/T 12763.7-1991
|
潘楚东, 于非, 张志欣, 等, 2010. LOESS四维客观分析在中国近海的应用. 海洋科学进展, 25(2): 149-159 |
Dirks K N, Hay J E, Stow C D, et al, 1998. High-resolution studies of rainfall on Norfolk Island: part II: interpolation of rainfall data. Journal of Hydrology, 208(3-4): 187-193 |
Jeffrey S J, Carter J O, Moodie K B, et al, 2001. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environmental Modelling & Software, 16(4): 309-330 |
Stohl A, Wotawa G, Seibert P, et al, 1995. Interpolation errors in wind fields as a function of spatial and temporal resolution and their impact on different types of kinematic trajectories. Journal of Applied Meteorology, 34(10): 2149-2165 |
 2020, Vol. 51
2020, Vol. 51