中国海洋湖沼学会主办。
文章信息
- 穆珊珊, 李海艳, 吴明柏. 2020.
- MU Shan-Shan, LI Hai-Yan, WU Ming-Bo. 2020.
- 基于Sentinel-1A的全球有效波高的反演研究
- INVERSION OF GLOBAL SIGNIFICANT WAVE HEIGHT BASED ON SENTINEL-1A
- 海洋与湖沼, 51(2): 235-247
- Oceanologia et Limnologia Sinica, 51(2): 235-247.
- http://dx.doi.org/10.11693/hyhz20190900177
文章历史
-
收稿日期:2019-09-21
收修改稿日期:2019-12-07
2. 中国科学院地理科学与资源研究所 北京 100101
2. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Science, Beijing 100101, China
海浪是海洋最明显的表面特征, 波长范围从几厘米到数百米, 波高范围从海洋表面的微小扰动到数十米, 对海洋工程、船舶设计、海上运输以及海洋污染的消散等都有很大的影响。因此, 通过有效的技术手段了解海浪的统计特性, 如有效波高、平均波周期等尤为重要。
自1978年发射Seasat1搭载合成孔径雷达(Synthetic Aperture Radar, SAR)开始, ERS-1/2、RADARSAT-1和ENVISAT、Sentinel-1持续运行, 星载SAR不断提供全球范围内实时动态的海面波浪信息, 凭借其间接的、大范围的测量方式和全天候、全天时、高分辨率的测量能力, 成为海浪信息获取的重要途径之一(Jackson et al, 2004)。利用SAR进行海浪统计参数的反演有两种常见的方式, 一种是通过SAR图像谱获取二维海浪方向波谱, 继而获取海浪统计参数。例如, 有效波高(Hs)可以表示为方向波谱的积分:
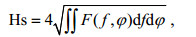 (1)
(1)其中, F(f, φ)表示二维海浪方向谱, f为频率, φ为方向。另一种方式是通过直接建立SAR图像与海浪参数之间的关系, 在无需反演得到海浪方向谱的情况下进行海浪参数反演。
第一种通过SAR图像谱获取海浪谱, 反演海浪参数的方式在海浪遥感应用中是很常见的。但海洋的SAR图像常常在方位方向显得十分模糊且导出的波谱容易发生畸变(Grieco et al, 2016; Stopa et al, 2017)。这是由于SAR特殊的成像机制——速度聚束调制引起的。受这一调制作用的影响, 海浪的随机运动会引起SAR后向散射回波信号的多普勒频移, 造成SAR不能对低于某一波长(即方位向截断波长)的波浪进行成像。在这种情况下, 海浪的成像过程中常表现出很强的非线性, 对SAR图像影响很大(Hasselmann et al, 1985; Jackson et al, 2004)。因此, 通过SAR图像推导二维海浪谱绝非一项简单的任务, 必须通过引入其他数值模式结果作为先验信息才有可能估计完整的二维波谱(Hasselmann et al, 1991; Hasselmann et al, 1996; Schulz-Stellenfleth et al, 2005)。或者利用SAR图像交叉谱计算得到海浪谱, 此计算虽不需要初猜信息, 且可以消除海浪传播方向180°模糊的问题, 但产生的海浪谱无法完全解析高频波, 即丢失短波信息, 多数情况下是涌浪部分的谱分量(Engen et al, 1995)。由此可见, 通过SAR图像谱获取海浪谱, 进一步获得Hs等海浪统计参数这一途径, 具有一定的困难性和局限性。
因此, 很多学者针对第二种方法, 即在不获取二维海浪谱的情况下反演海浪参数的方法进行了研究。Schulz-Stellenfleth等(2007)基于ERS2数据, 提出了一个经验二次模型CWAVE-ERS, 在不需要先验信息的条件下, 通过SAR图像直接获取海浪积分参数。Li等(2011)与Stopa等(2017)在CWAVE-ERS模型的基础上, 分别提出了针对ENVISAT ASAR数据的CWAVE- ENV模型以及针对S1A数据的CWAVE-S1A模型, 用于计算有效波高、平均周期等海浪参数。但由于上述CWAVE算法, 仅针对特定的SAR数据, 因此对于其他卫星数据的普适性不强(Stopa et al, 2017)。
除以上两种方法之外, 随着海浪参数反演研究的不断进步, 许多学者认识到方位向截断波长与海况条件之间具有强相关性, 可用于海浪统计参数反演的研究(Jackson et al, 1985; Kerbaol et al, 1998; Ren et al, 2016; Wang et al, 2012)。方位向截断波长为SAR数据所特有的海况参数, 可作为对SAR方位向分辨率的一种度量(Greico et al, 2016)。在假设线性波的情况下, 方位向截断波长可表示为(Lyzenga, 1986; Kerbaol et al, 1998):
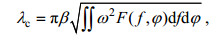 (2)
(2)其中, 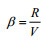
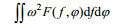
Beal等(1983)研究发现λc与Hs的平方根有经验依赖关系, 而且对于Hs在1—8m的范围内, 二者成正比关系。Marghany等(2002)依据λc与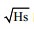
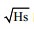
因此, 本文拟在相关有效波高反演研究的基础上进行拓展, 利用S1A二级波模式数据, 采用神经网络的技术手段建立有效波高与σ0、λc等SAR参数之间的联系, 旨在分析各参数对有效波高反演的影响。本次实验建立的神经网络模型, 除用于模型训练的欧洲中程天气预测中心(the European Centre for Medium-Range Weather Forecasts, ECMWF)模式数据外, 不需要额外模式数据作为先验信息, 且模型输入的SAR参数可在S1A二级WV数据中直接获取, 大大降低了数据存储内存, 减化了数据处理过程, 对于硬件条件受限的用户尤为重要。
1 数据源介绍本文采用了三种类型的数据, 分别为S1A卫星二级波模式数据、ECMWF再分析数据和美国国家数据浮标中心(National Data Buoy Center, NDBC)浮标数据。其中, S1A数据与ECMWF再分析数据进行时空匹配, 用于神经网络模型的训练, 独立测量的浮标数据用于神经网络训练结果的验证。
1.1 Sentinel-1A二级波模式数据Sentinel-1A卫星于2014年4月发射成功, 在太阳同步轨道运行, 高度(H)约为693km, 飞行速度约为7570m/s, 倾角98.18°, 重复周期为12d, 搭载了基于C波段的雷达成像系统。S1A卫星具有四种成像模式, 其中波模式(Wave Mode, WV)是S1A在大洋上的操作模式, 主要应用于海洋参数的获取。在此模式下, S1A沿卫星轨道每100km进行一次采集, 以23°(WV1)和36°(WV2)两个入射角交替工作, 在近距处获取一个图斑, 在远距处获取下一个图斑, 具有相同入射角的图斑间隔为200km, 空间分辨率为5m, 图斑大小约为20km×20km。
本研究使用的卫星数据为S1A二级WV海洋产品(L2 Ocean Product, OCN)中的海洋涌浪谱(Ocean Swell spectra, OSW)数据, 可通过ESA网站(https:// scihub.copernicus.eu/dhus/#/home)免费下载获取。该数据可提供σ0、NV、θ、skew、kurt、对数极坐标系下的海浪方向谱、λc、Hs等参数。但受到速度聚束调制作用的影响, 其测量的海浪Hs被严重低估, 且受方位向截断波长的影响较大, 仅可用于较低海况(Li et al, 2011)。如图 1所示, 我们将S1A二级数据提供的Hs以及根据公式(1)将S1A提供的海浪谱数据进行积分获得的Hs与ECMWF再分析数据提供的Hs进行了比较, 可以看出, 图 1a、b中散点基本分布在x=y直线下方, 表明S1A二级数据提供的以及通过海浪谱计算的Hs低于ECMWF再分析数据中的Hs。
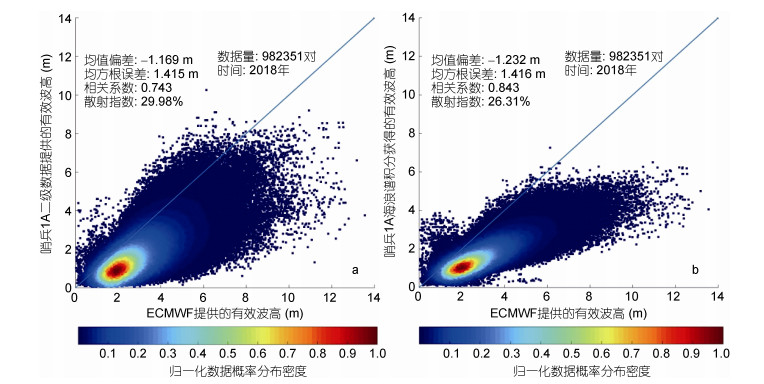 |
| 图 1 S1A二级波模式数据提供的Hs与ECMWF再分析数据提供的Hs的对比散点图 Fig. 1 Scatter plots of Hs provided by S1A level2 wave mode data and ECMWF reanalysis data 注: a: S1A二级波模式数据提供的Hs与ECMWF再分析数据提供的Hs的比较散点图; b:通过S1A二级波模式数据提供的海浪谱积分获得的Hs与ECMWF再分析数据提供的Hs的比较散点图; Hs:有效波高 |
为保证本研究实验结果不受船舶、海冰、溢油等影响, 选择雷达截面的归一化方差在1—2之间, 纬度在±60°, 时间为2018年1—12月的S1A数据作为实验数据。
1.2 ECMWF再分析数据由于本研究选用的S1A波模式数据通常为全球公海数据, 而在公海仅有少量浮标测量数据可用。考虑到神经网络对训练数据高准确度、广覆盖度的要求, 因此, 本研究同时选择ECMWF再分析数据ERA5与S1A数据进行时空匹配, 组成神经网络训练数据集。
ERA5是第五代ECMWF再分析数据集, 是ECMWF使用其预测模型和数据同化系统“重新分析”存档的观测结果, 用于创建描述大气、陆地表面和海洋最近历史的全球数据集, 可由ECMWF网站下载获得(http://www.ecmwf.int/)。本研究主要采用ERA5海浪数据中的有效波高数据, 其格网大小为0.5°×0.5°, 时间间隔为1h。本研究按照小于0.25°的空间窗口、小于30min的时间窗口对二者进行时空匹配, 共获得982351对匹配数据对, 其中328081对用于模型训练, 其余数据用于模型应用。
1.3 NDBC浮标数据为了对神经网络模型输出结果进行对比分析, 本文采用独立测量的具有海浪谱信息的浮标数据对其进行验证, 其数据可由NDBC网站下载获得(https://www.ndbc.noaa.gov/)。浮标多布放于北半球, 数据获取频率约为1次/h, 根据其频率测量范围分为两类: 0.03—0.4Hz, 离散为38个频率; 0.02—0.485Hz, 离散为47个频率。可根据公式(1), 将海浪谱进行积分获取有效波高。本研究将浮标数据和S1A数据按照小于0.5°的空间窗口和小于0.5h的时间窗口进行时空匹配, 获得400对数据用于模型验证。
2 研究方法本研究拟在Schulz-Stellenfleth等(2007)开发的利用ERS2 SAR数据σ0、NV及其乘积项(σ02、NV2、σ0×NV)共5个参数用于海浪参数反演的双参数模型基础上, 加入经纬度、λc等信息进行反演研究。同时, 为增加模型的计算效率, 本文将利用神经网络技术进行多元非线性回归, 用于描述SAR不同输入参数与有效波高之间的关系。首先将S1A数据与时空匹配后的ECWMF数据用于模型的训练, 然后利用独立的浮标数据对模型性能进行验证, 同时, 选取均值偏差(Bias)、均方根误差、散射指数、相关系数四个统计参数对模型性能进行定量评估。
2.1 神经网络的选取神经网络是一种方便而通用的预测结果的方法, 近年来被多次应用于遥感研究中。本研究基于MATLAB进行神经网络训练, 选用的BP(back propagation)神经网络, 是一种多层前馈神经网络, 包括输入层, 输出层和隐藏层。其主要特点是信号前向传递, 误差反向传播。当神经网络的输入和输出数据确定后, 可调整的只有隐藏层的神经元数目, 而优化隐藏层结点数, 成为神经网络训练的首要任务。实验表明, 如隐藏层结点数过少, 网络则不能具有必要的学习和信息处理能力。反之, 若过多, 不仅会增加网络结构的复杂性, 还会降低网络学习的速度。因此, 在神经网络模型测试过程, 可对隐藏层结点数进行
调整, 最终取最优结果来确定神经元数目(王小川等, 2013; Stopa et al, 2017)。本文在进行神经网络训练的实验中, 根据不同N_N模型输入参数的个数, 将隐藏层神经元个数设定为4—30之间, 发现其性能均在隐藏层神经元个数大于输入参数个数时有所提升, 且在大于20时趋于稳定, 但随着神经元数目增多, 训练时间也逐渐增加, 因此, 考虑到不同模型之间的对比, 本文将N_N模型的隐藏层神经元数目均定为20。
基于输入与输出参数之间非线性关系的考虑, 神经网络采用正切S型传递函数(tansig)隐藏神经元和线性传递函数(purelin)输出神经元。另外, 基于Levenberg-Marquardt反向传播算法(trainlm)是现阶段应用最广泛的优化算法, 可为非线性最小二乘问题提供解决方案, 本研究采用trainlm进行神经网络训练。最后, 使用均方误差(MSE)和回归分析评估其性能(王小川等, 2013)。
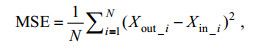 (3)
(3)其中, Xin _i表示N_N模型训练的输入数据, Xout _i表示N_N模型训练的输出数据, N表示数据量。
2.2 N_N模型建立为避免神经网络训练效果受到进行不同范围的Hs数据分层筛选等人为因素影响, 同时考虑到对全球范围内的有效波高反演的目的以及有效波高随季节明显变化的特性, 本文拟在2018年所有S1A数据以及时空匹配后的ECMWF的Hs数据中每个季节选择一个月份的数据(本文选择1、4、7、10月份的数据)作为训练数据, 同时拟采用常规神经网络模型训练方法, 在模型训练过程中将训练数据随机分为60%、20%、20%, 分别用于模型建立过程中的训练、测试和验证。
本文首先对2018年4个月训练数据的ECMWF的Hs数据的分布及其占2018年总Hs数据的比例分布进行了分析。1、4、7、10月份数据包括了全球范围内不同的海况, 且分别代表冬、春、夏、秋四个季节, 因此最终选择1、4、7、10月份的数据进行训练, 并将2018年其他月份数据作为独立的数据(应用数据)用于神经网络的应用, 不参与模型的训练。训练数据的Hs分布情况以及在2018年所有数据中的比例分布情况的柱状图, 分别如图 2a和b所示, 可以看出, 其主要Hs范围在1—4m, 且在2018年总数据中分布较均匀, 比例均在33%左右。
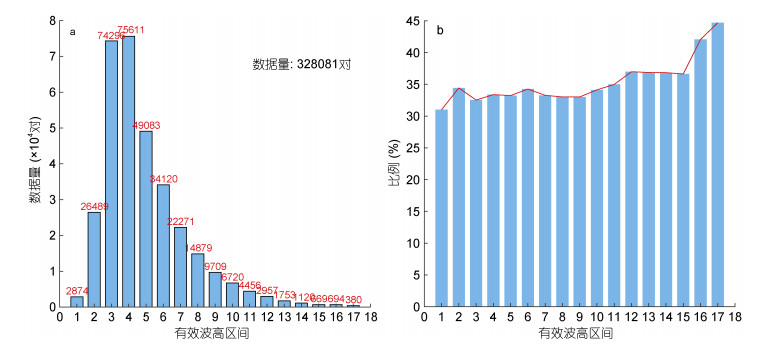 |
| 图 2 训练数据的Hs分布情况 Fig. 2 Hs distribution of training data 注: a:训练数据的Hs在每个区间内的数据量分布情况; b:训练数据的Hs与总数据在每个区间内的比例, 其中, 由于较低海况以及高海况的数据较少, 因此将Hs按照以下方式进行划分:横轴代表不同的Hs区间, 共17个, 1代表Hs < 1m; 2—15代表 1 < Hs≤8m, 间隔为0.5m; 16代表 8 < Hs≤9m; 17代表Hs > 9m |
本文选用σ0、NV、σ02、NV2、σ0×NV、λc、skew、kurt、lon、lat、β作为神经网络训练模型的输入参数, 通过改变输入参数的个数, 进行神经网络模型调整, 共建立14个N_N模型, 如表 1所示。
| 模型 | 模型输入参数 | 输出参数 | 输入参数个数(个) | 隐藏层节点数(个) |
| N_N 1 | lon, lat, σ0, NV | 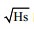
|
4 | 20 |
| N_N 2 | lon, lat, σ0, NV, λc | 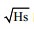 |
5 | 20 |
| N_N 3 | lon, lat, σ0, NV, σ02, σ0×NV, NV2 | 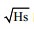 |
7 | 20 |
| N_N 4 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β | 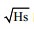 |
8 | 20 |
| N_N 5 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc | 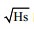 |
8 | 20 |
| N_N 6 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, β | 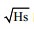 |
9 | 20 |
| N_N 7 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, skew | 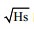 |
9 | 20 |
| N_N 8 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, kurt | 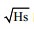 |
9 | 20 |
| N_N 9 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, skew, kurt | 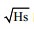 |
10 | 20 |
| N_N 10 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, skew | 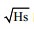 |
9 | 20 |
| N_N 11 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, kurt | 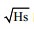 |
9 | 20 |
| N_N 12 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, skew, kurt | 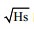 |
10 | 20 |
| N_N 13 | lon, lat, σ0, NV, λc, σ02, NV2, λc2, σ0×NV, σ0×λc, NV×λc | 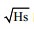 |
11 | 20 |
| N_N 14 | σ0, NV, σ02, σ0×NV, NV2, λc, skew | 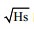 |
7 | 20 |
N_N模型输入参数中, σ0通常与风速和风向有关, 常用于风场反演算法中, 因此可表示海浪的短波信息(Horstmann et al, 2003; Li et al, 2011)。NV提供关于图像均匀性和海况的信息, 反映了由于SAR图像中的波浪而引起的回波强度调制(Stopa et al, 2017)。考虑到有效波高具有明显的纬向分布的特征, 因此在进行神经网络训练时, 加入经纬度信息, 增加输入与输出参数之间的空间对应性。λc反映SAR非线性成像机制, 与Hs具有很强的相关性(Beal et al, 1983; Shao et al, 2016)。另外, 有研究表明, 海表面的随机运动对SAR成像的影响取决于SAR卫星系统的表征参数β, β值越大, SAR成像海洋表面波的能力就越差, 因此, β信息可用于提供海表面运动的信息(Beal et al, 1983)。最后利用skew、kurt来考虑SAR图像重要的高阶特征信息(Stopa et al, 2017)。
本研究选用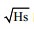
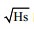
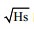
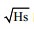
本研究对上述N_N模型反演得到的海浪有效波高, 进行对比分析, 选择Bias、RMSE、SI、CORR四种统计参数进行评价, 定义如下:
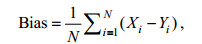 (4)
(4)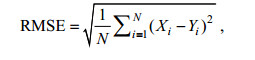 (5)
(5)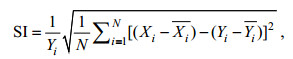 (6)
(6)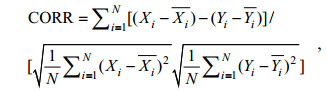 (7)
(7)其中, Xi表示N_N模型训练的结果, Yi表示ECMWF数据的反演结果, N表示时空匹配后的数据量, 公式(7)中横杠表示取均值。
3 结果分析为了更全面的对不同N_N模型的反演结果进行分析, 本研究分别从模式数据、独立测量的浮标数据以及不同环境条件下的模型性能分析三个方面对海浪有效波高反演结果进行了对比分析。
3.1 N_N模型反演结果与模式数据对比为评估上述14个神经网络模型的性能, 本研究对应用数据进行了有效波高的反演, 对其结果进行了统计分析。本节主要分析输出结果与进行时空配后的ECMWF数据之间的对比, 统计参数如表 2所示。
| 模型 | 模型输入参数 | Bias(m) | RMSE(m) | CORR | SI(%) |
| N_N 1 | lon, lat, σ0, NV | -0.017 | 0.654 | 0.832 | 24.38 |
| N_N 2 | lon, lat, σ0, NV, λc | -0.009 | 0.534 | 0.892 | 19.93 |
| N_N 3 | lon, lat, σ0, NV, σ02, σ0×NV, NV2 | -0.013 | 0.643 | 0.838 | 23.98 |
| N_N 4 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β | -0.010 | 0.557 | 0.882 | 20.77 |
| N_N 5 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc | -0.012 | 0.532 | 0.892 | 19.86 |
| N_N 6 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, β | -0.010 | 0.533 | 0.892 | 19.89 |
| N_N 7 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, skew | -0.011 | 0.535 | 0.891 | 19.97 |
| N_N 8 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, kurt | -0.011 | 0.539 | 0.889 | 20.11 |
| N_N 9 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, β, skew, kurt | -0.010 | 0.535 | 0.891 | 19.94 |
| N_N 10 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, skew | -0.010 | 0.502 | 0.905 | 18.74 |
| N_N 11 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, kurt | -0.012 | 0.510 | 0.902 | 19.02 |
| N_N 12 | lon, lat, σ0, NV, σ02, σ0×NV, NV2, λc, skew, kurt | -0.011 | 0.503 | 0.905 | 18.76 |
| N_N 13 | lon, lat, σ0, NV, λc, σ02, NV2, λc2, σ0×NV, σ0×λc, NV×λc | -0.009 | 0.531 | 0.893 | 19.80 |
| N_N 14 | σ0, NV, σ02, σ0×NV, NV2, λc, skew | -0.014 | 0.512 | 0.901 | 19.10 |
| 注: Bias:均值偏差; RMSE:均方根误差; CORR:相关系数; SI:散射指数 | |||||
根据表 2不同模型间的Bias、RMSE、CORR、SI四个统计参数对比可知:
1) N_N 2与N_N 1相比, 方位向截断波长的加入使神经网络模型的性能显著提高, 散射指数明显下降为19.93%, Bias与RMSE分别由-0.017m、0.654m降为-0.009m、0.534m, 相关系数由0.832提升至0.892, 这与Stopa等(2017)中的结果相近, 证明了方位向截断波长与有效波高之间的强相关性。
2) N_N3模型在N_N1模型的基础上, 加入σ02、NV2、σ0×NV三个参量, 使得模型的统计参数略有提升, 均方根误差的由0.654m降为0.643m, 以下模型均在N_N3基础上进行改进。
3) N_N4、N_N5模型分别加入β、λc参数, N_N6模型则同时加入β、λc参数, N_N5与N_N6的统计参数相差较小, N_N4与N_N5相比, RMSE由0.557m降为0.532m, 这可能是由于λc与β成比例, 且其包含除β信息外的更多信息的关系(Beal et al, 1983)。但N_N4与N_N3相比, 性能有明显提升, 相关系数由0.838升为0.882, 因此在方位向截断波长信息缺失或者不准确时, 可以选择β信息作为有效波高反演模型的输入参数。
4) N_N7、N_N8、N_N9与N_N10、N_N11、N_N12这两组模型分别在N_N4和N_N5的基础上依次加入skew、kurt、skew和kurt。通过分别对这两组模型进行分析, 可以看出, skew加入比kurt的加入, 对模型性能的改善更有优势, 而二者的同时加入与单独加入skew对模型的影响相近, 统计参数的差别均在千分之一数量级。另外, 在模型训练过程中, skew对模型的稳定性有所提升, 而kurt的单独加入会造成模型结果出现与ECMWF数据相差5m以上的奇异点。
5) N_N13是参照Schulz-Stellenfleth等(2007)的双参数模型, 在N_N5基础上加入方位向截断波长的乘积参数(λc2、σ0×λc、NV×λc)。研究表明, N_N13和N_N5统计参数之间的差别均在千分之一的数量级, RMSE下降了0.001m, 相关系数提升了0.001, 对模型的结果影响很小, 但输入参数却增加了8个。
6) N_N14在N_N10基础上去掉了经纬度信息, 旨在分析经纬度信息对有效波高反演的重要性。研究表明, N_N14模型较N_N10模型, RMSE提升0.01m, SI增大0.36%, N_N10模型的性能优于N_N14模型, 表明经纬度信息对有效波高的反演具有一定的影响, 但影响很小。
综上所述, 14个神经网络模型中, N_N10为最佳模型, 其性能最稳定, 相关系数最高达到0.905, SI与RMSE最低, 分别为18.74%、0.502m。
为了更加直观的对模型的性能进行分析, 本研究将N_N模型的输出结果与ECMWF数据的输出结果的对比散点图及二者之间的残差全球分布图展示如下, 由于篇幅限制, 本文仅对N_N5、N_N10模型的输出结果与ECMWF数据的对比散点图由图 3表示, 将N_N10模型与ECMWF数据的对比残差全球分布图由图 4表示。
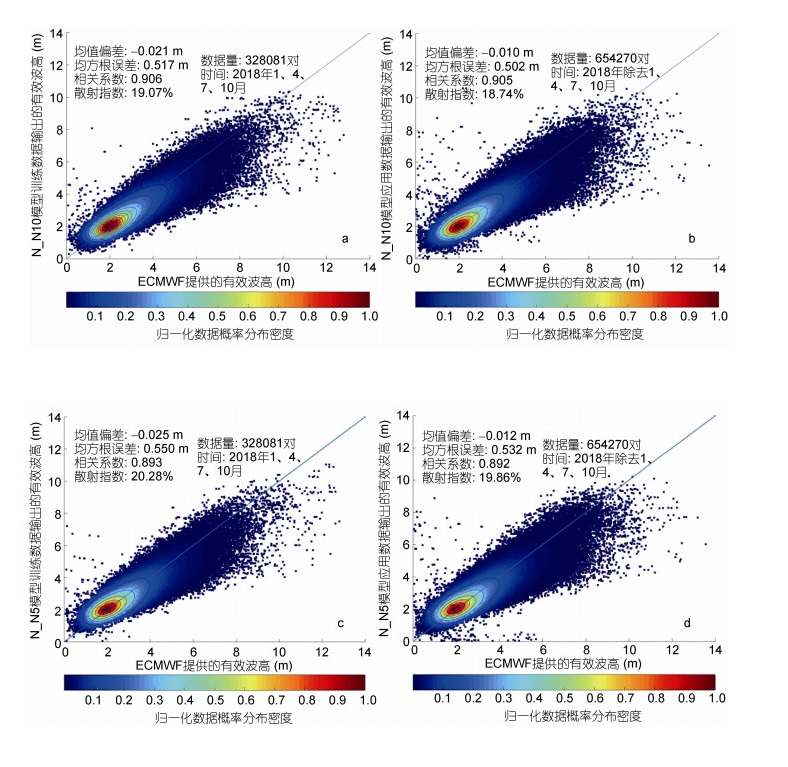 |
| 图 3 S1A数据通过神经网络模型得到的Hs与ECMWF再分析数据提供的Hs的对比散点图 Fig. 3 Scatter plots of Hs obtained from S1A data through N_N Model and ECMWF reanalysis data 注: a: N_N10训练数据的输出结果; b: N_N10应用数据的输出结果; c: N_N5训练数据的输出结果; d: N_N5应用数据的输出结果; 蓝色实线表示x=y |
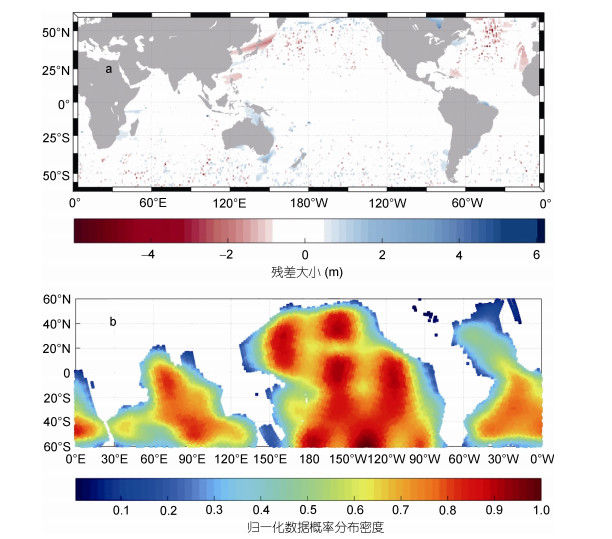 |
| 图 4 Hs的残差及S1A应用数据密度的全球分布图 Fig. 4 Global distribution map of Hs residuals and the density of S1A application data 注: a: S1A数据通过N_N10模型得到的Hs与ECMWF再分析数据提供的Hs的残差全球分布图; b: 2018年S1A应用数据全球分布密度图 |
通过与ECMWF数据相比, 由图 3a可知, N_N10模型训练结果较为理想, 相关系数接近0.91, SI为19.07%。图 3cN_N5模型与N_N10的散点图分布相似度极高, 且相关系数也接近0.9, 但其Bias、RMSE均低于N_N10模型。图 3b的应用效果也较好, Bias接近于零, RMSE为0.502m, SI低于20%。其数据点集中在1—4m之间, 且基本围绕在x=y左右, 与Stopa等(2017)中的结果类似。当Hs大于4m时, 随着训练数据点的减少, 训练效果也逐渐变差, 尤其当Hs大于10m时, 数据点基本在x=y以下, 这是由于在极端海况下, 数据点较少, 神经网络模型不能达到较好的学习效果造成的。
虽然图 3dN_N5模型的结果较图 3bN_N10模型稍差, 但二者的统计参数差别在百分之一的数量级, 均值偏差接近, 相关系数仅相差0.013。也就是说, 即使无法获取代表雷达截面高阶特征的skew、kurt时, 神经网络模型反演的Hs仍然可接受。
图 4a展示了S1A二级波模式数据通过N_N10模型反演得到的Hs与ECMWF模式数据提供的Hs之差的全球分布图。可以看出, 二者之间的残差整体在±1m, 南半球残差正值居多, 而北半球残差多为负值, 且中高纬度地区残差水平高于低纬度地区, 整体色调为白色, 沿海地区有少量的红色和蓝色。数据分析得到, 二者之间的残差小于二者的RMSE(0.502m)的数据占整体数据的90%左右, 而残差水平大于3倍的RMSE (HsN_N10-HsECMWF > 3*RMSE)的数据异常值仅为整体数据的0.1%, 异常值在全球分布且没有空间相关性, 这与Stopa等(2017)的结果类似。表明整体残差控制在理想的范围之内。由图 4b可知, 在太平洋海域, S1A数据最多, 沿海地区相对稀疏, 这是由于在一些沿海地区, SAR天线经常以其他模式(例如, 干涉宽幅模式)获取数据, 无法获得波模式数据造成的(Li et al, 2011)。通过对比图 4a、b还可以观察到, 残差值的大小与应用数据点的密度成正相关关系, 数据点密集区域, 残差为正值, 数据点稀疏的区域, 残差为负值, 这是由于训练数据点过少导致的神经网络模型不能达到较好的学习效果, 使得训练结果限制在一定范围内, 相反, 数据点过于密集的区域, 可能存在过拟合现象。由图 4a可以看出, 残差的高值分布区域, 一般为数据点比较少的区域, 证明了神经网络模型对训练数据的高要求。
3.2 N_N模型反演结果与浮标数据对比本节拟将N_N模型的反演结果与独立测量的浮标数据结果进行比较, 由于篇幅限制, 本文只将N_N10模型的与浮标数据的对比分析结果进行展示, 如图 5所示。
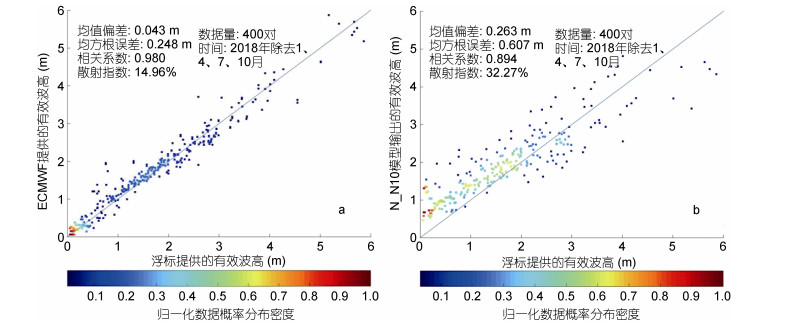 |
| 图 5 浮标数据提供的Hs与ECMWF再分析数据提供的Hs及S1A数据通过N_N10模型得到的Hs的对比散点图 Fig. 5 Scatter plots of Hs provided by buoy and Hs obtained from ECMWF reanalysis data and S1A data through N_N10 Model 注: a:浮标数据提供的Hs与ECMWF再分析数据提供的Hs比较结果; b:浮标数据提供的Hs与S1A数据通过N_N10模型得到的Hs的比较结果; 蓝色实线表示x=y |
为了更好的分析N_N10模型输出结果与浮标数据的差别, 本研究首先对浮标数据与时空匹配后的ECMWF模式数据进行对比, 见图 5a。由于N_N10模型是以ECMWF数据为基准进行训练的神经网络, 因此本文判断其结果应与ECMWF数据具有相似的趋势。
由图 5a可知, 浮标和ECMWF的有效波高整体上围绕着x=y直线, 相关系数高达0.980, 散射系数为14.96%, 这表明了ECMWF再分析数据的可靠性及其用于提供可靠海况信息的能力。当Hs < 2m时, 分布于x=y直线上方的数据点居多, 表明二者之间存在一个正偏差(HsECMWF-Hsbuoy), 数据点比较集中; 当Hs > 2m时, 数据点分布在x=y直线左右, 数据点相对较为离散。
图 5b中散点图分布趋势与图 5a类似, 当Hs < 2m时, 数据点基本分布于x=y直线上方, 当Hs > 2m时, 数据点则离散的分布于x=y直线两侧。与图 5a相比, 图 5b的数据点则更加离散, SI值更大, 为32.27%, 图 5a、b的Bias分别为0.043m和0.263m, 均为正值, 这是由Hs < 2m部分的数据所造成的。图 5b相关系数为0.894, 虽然没有图 5a相关性高, 但也达到了较好的结果, 且二者之间相似的分布趋势也进一步证明N_N10模型提供了可靠的Hs估计。
3.3 不同环境条件下N_N10模型的性能分析本节拟对不同SAR观测模式(WV1/2), 不同的λc以及不同海况下的N_N10模型的Hs反演情况进行分析, 以有效波高的大小表示海况的变化。不同条件下的统计参数变化如表 3所示。
| 参数 | 阈值 | 数据点个数(个) | Bias(m) | RMSE(m) | CORR | SI(%) |
| 全部数据 | 654270 | -0.010 | 0.502 | 0. 905 | 18.74 | |
| 入射角(θ) | 约23°(WV1) | 314717 | -0.008 | 0.487 | 0.909 | 18.19 |
| 约36°(WV2) | 339553 | -0.011 | 0.516 | 0.901 | 19.22 | |
| 有效波高(Hs) | Hs < 1m | 6393 | 0.351 | 0.601 | 0.077 | 57.17 |
| 1 < Hs < 4m | 564197 | 0.049 | 0.393 | 0.846 | 16.61 | |
| Hs > 8m | 1426 | -1.807 | 2.388 | 0.137 | 17.61 | |
| 方位向截断波长(λc) | λc > 500m | 1419 | 0.102 | 1.062 | 0.944 | 35.94 |
| 100 < λc≤300m | 575720 | -0.011 | 0.441 | 0.849 | 18.27 | |
| λc≤100m | 3112 | -0.061 | 0.407 | 0.418 | 32.93 |
由表 3对不同入射角、Hs、λc条件下的统计参数比较可知:
1) S1A卫星在WV模式下以23°(WV1)和36°(WV2)两个入射角交替工作, WV2模式的数据点较WV1的数据点略多, 但N_N10模型在WV2模式的反演结果比WV1稍差, RMSE相差0.029m, WV2的SI为19.22%, WV1的SI为18.19%, WV2的低性能是由于它的倾斜调制较弱, 信噪比较低, 在σ0和λc中产生较大噪声值的比率造成的(Stopa et al, 2017)。整体上N_N10模型在两种SAR观测模式下均取得了较好的反演结果。
2) 对于不同的Hs, N_N10模型性能具有明显差异。其中, 平稳海况(1 < Hs≤4m)下的数据点占总体数据的86%以上, N_N10模型的性能最佳, Bias、RMSE分别为0.049m、0.393m, 且SI低于17%, 表明了N_N10模型对于一般海况下有效波高反演的有效性。对于低海况(Hs < 1m)以及高海况(Hs > 8m), N_N10模型性能大幅降低, 相关系数均在0.15以下。分析可知, 针对低海况的情况, 一方面由于用于进行模型训练的低海况数据点较少, 神经网络的学习要求未达标, 另一方面, 当Hs < 1m时, 存在一些N_N10模型输出结果与ECMWF相差很大的数据点(由图 3可知)。而高海况下, 数据点更少, N_N10与N_N5模型均处于低估的状态。
3) 方位向截断波长表示为SAR图像谱在方位方向上受约束的程度, 当方位向截断波长较大时(如, λc > 500m), SAR图像谱将变得不清楚, 多数波谱成分将不可靠(Kerboal et al, 1998), 但N_N10模型在高λc条件下, 却取得了较好的结果, 相关系数高达0.944, Bias仅为0.102m, 而SI为35.94%表明数据较为离散。对于λc小于100m的情况, 其Bias接近于0, 但相关系数很低, 为0.418, 分析可知, 由于λc较小的情况下, 海面大多处于较为平稳的状态, 训练数据较少, 训练效果不佳导致相关系数降低。
图 6进一步对S1A的λc、N_N10模型输出的Hs、以及N_N10模型与ECMWF对比的残差全球分布进行展示, 从全球分布的角度, 分析三者之间的关系, 本研究选择春秋两个季节的数据进行分析, 以1°的经纬度窗口进行季度平均计算。
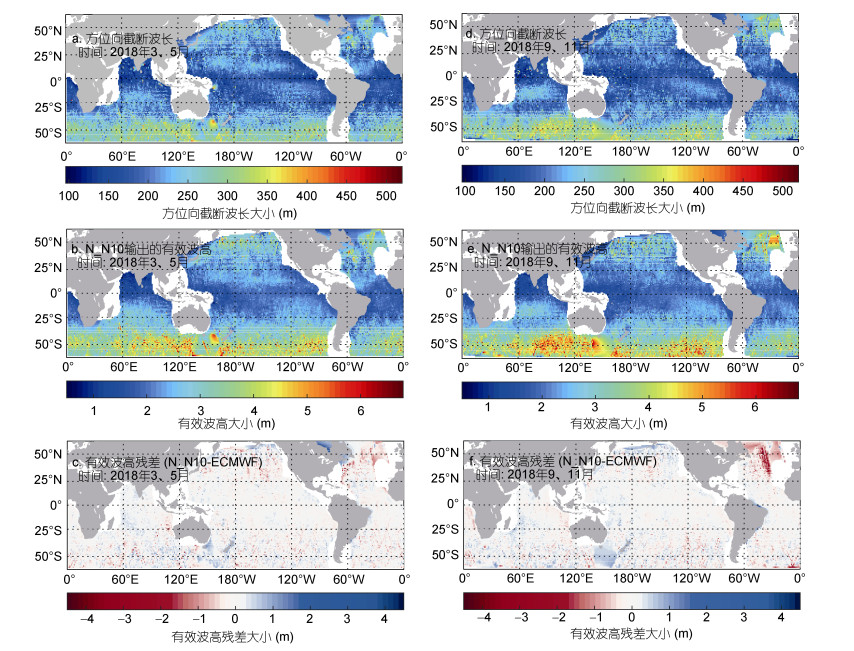 |
| 图 6 S1A数据的λc、N_N10模型输出的Hs及Hs残差的全球分布图 Fig. 6 Global distribution of λc, Hs obtained from S1A data through N_N10 Model and Hs residuals 注: a、d表示S1A数据的λc全球分布图; b、e表示S1A数据通过N_N10模型得到的Hs分布图; c、f表示N_N10模型输出的Hs以及ECMWF再分析数据提供的Hs对比的残差(HsN_N10-HsECMWF)分布情况; 以上数据均为季度平均的结果, 其中图a、b、c为春季, 时间为2018年三月、五月, 图d、e、f为秋季, 时间为2018年九月、十一月 |
从图 6a、b、d、e可知, λc与Hs均具有纬向分布的特征, 且二者具有明显正相关关系。春、秋两个季节, 南半球平均海浪有效波高均高于北半球, 尤其在30°—50°S, 平均Hs达到5m以上, 与λc分布一致, 秋季则更为明显。秋季时期北大西洋与南印度洋均出现了Hs高值区, Hs在5m左右, 此处λc也处于高值区, 而春季时期, 南印度洋、南太平洋与南大西洋Hs较秋季时期减小, 但也为高值区与相应的λc的全球分布情况一致, 这也表明λc可用于表示Hs的季节变化。从两个季节的平均残差分布图可知, N_N10模型整体性能良好, 其残差水平在沿岸地区高于大洋内部, 且随着λc与Hs的提高, 残差有增大的趋势, 且中高纬度地区的残差水平高于低纬度地区。
4 结论本文在Schulz-Stellenfleth等(2007)提出的双参数模型的基础上, 利用神经网络技术对2018年的S1A二级波模式数据进行了海浪有效波高的反演, 对具有不同输入参数的神经网络模型的性能进行了分析。为了更准确的进行全球范围的Hs反演, 本文在N_N模型中加入经纬度的信息。对模型反演结果, 除利用ECMWF再分析数据进行对比外, 还利用独立测量的浮标数据进行了验证, 初步得到以下结论:
1) 总体上, 14个N_N模型的反演结果与ECMWF数据相比, 均达到了可接受的训练结果, 相关系数均在0.8以上, 且大部分模型RMS控制在0.6m以内, 其中N_N10的性能最佳, 相关系数达到0.9以上, 散射指数在19%以内。
2) 通过表 2对14个模型性能的分析, 随着λc的加入, N_N模型的性能大幅提升, 相关系数达到0.88以上。其次, β参数的加入也会小幅度提高模型反演的准确度, 因此, 在λc缺失或者不准确时, 可选择β信息作为Hs反演模型的输入参数。
3) 浮标测量数据用于验证N_N模型算法, N_N10与浮标对比的RMS为0.607m, Bias为0.263m, 且相关系数达到了0.894, 表明将N_N10模型用于Hs的反演, 整体上达到了较好的结果。同时, 通过散点图可知, 当Hs < 2m时, N_N10模型、ECMWF均与浮标观测结果之间存在较小的正偏差; 当Hs > 2.5m时, 数据点的偏差趋于0, 但数据点相对较为离散, N_N10与浮标的散点图分布情况与ECMWF和浮标的对比散点图具有相似趋势, 也进一步表明N_N10模型提供了可靠的Hs估计。由于本研究用于评估的浮标数据仅有400对, 数量较少, 因此, 为了更好的确认N_N性能, 需要进行更密集的现场浮标测量。
4) 通过对不同入射角下N_N10模型的性能分析, 在入射角为36°(WV2)模式的反演结果比23°(WV1)较差, RMSE相差0.029m, WV1的SI控制在19%以内。但总体上N_N10模型在两种SAR观测模式下均取得了不错的反演结果。
5) 对于不同海况条件, N_N10模型性能具有明显差异。其中, 平稳海况(1 < Hs≤4m)下的数据居多, N_N10模型的性能最佳, Bias、RMSE分别为0.049m、0.393m, 且SI低于17%, 这表明了N_N10模型对于一般海况下有效波高反演的有效性。而对于低海况(Hs < 1m)以及高海况(Hs > 8m)的模型性能大幅降低, 相关系数均在0.15以下, 这是由于用于模型训练的低海况及高海况的数据点较少, 神经网络的学习要求未达标所造成, 但如果通过加入更大的反映所有海况下的数据集, 该模型性能将会有所改进。
6) 历史研究表明, 较大的λc, 会引起SAR图像谱, 在方位方向上变得十分模糊, 很难用于海浪参数的提取(Kerbaol et al, 1998)。但本研究通过N_N10模型进行Hs反演, 在高λc条件下, 却取得了较好的结果, 相关系数高达0.944。同时, 通过对S1A数据的λc以及N_N10模型反演的Hs进行春、秋两个季节的全球分布分析可知, λc与Hs的全球分布具有大致相同的纬向分布的特征, 表明λc还可用来表示Hs的季节变化。
7) 通过对N_N10与ECMWF的Hs残差全球分布图可知, N_N10模型在全球大部分海域达到了较好的反演效果, 但在沿岸地区的有效波高反演结果仍不理想, 远不及远海地区, 该问题与数据点的分布密度有关。因此, 通过加入包含更多沿岸数据的训练数据用于神经网络的训练, 可以完善N_N模型在全球范围内Hs反演的性能。
综上分析, 本研究建立的用于Hs反演的神经网络模型, 取得了较好的反演效果, 在全球范围内提供了可靠的海浪有效波高估计。尽管本研究仅限于S1A卫星, 但该方法还可应用于当前任何具有二级波模式数据的其他合成孔径雷达数据, 如ENVISAT、Sentinel 1B等。此外, 若在模型训练过程中考虑海浪的传播方向以及主波波长等信息, 模型性能将会有所改进(Stopa et al, 2017)。
致谢 本文使用的Sentinel 1A二级波模式数据由欧洲太空局(ESA)网站提供, ECMWF再分析数据集ERA5由ECMWF网站提供, 浮标数据由美国国家数据浮标中心(NDBC)网站下载, 在此表示感谢。
王小川, 史峰, 郁磊, 等. 2013. MATLAB神经网络43个案例分析. 北京: 北京航空航天大学出版社, 1-32
|
Beal R C, Tilley D G, Monaldo F M, 1983. Large-and small-scale spatial evolution of digitally processed ocean wave spectra from SEASAT synthetic aperture radar. Journal of Geophysical Research:Oceans, 88(C3): 1761-1778 DOI:10.1029/JC088iC03p01761 |
Engen G, Johnsen H, 1995. SAR-ocean wave inversion using image cross spectra. IEEE Transactions on Geoscience and Remote Sensing, 33(4): 1047-1056 DOI:10.1109/36.406690 |
Grieco G, Lin W, Migliaccio M et al, 2016. Dependency of the Sentinel-1 azimuth wavelength cut-off on significant wave height and wind speed. International Journal of Remote Sensing, 37(21): 5086-5104 DOI:10.1080/01431161.2016.1226525 |
Hasselmann K, Hasselmann S, 1991. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. Journal of Geophysical Research:Oceans, 96(C6): 10713-10729 DOI:10.1029/91JC00302 |
Hasselmann K, Raney R K, Plant W J et al, 1985. Theory of synthetic aperture radar ocean imaging:A MARSEN view. Journal of Geophysical Research:Oceans, 90(3): 4659-4686 |
Hasselmann S, Brüning C, Hasselmann K et al, 1996. An improved algorithm for the retrieval of ocean wave spectra from synthetic aperture radar image spectra. Journal of Geophysical Research:Oceans, 101(C7): 16615-16629 DOI:10.1029/96JC00798 |
Horstmann J, Schiller H, Schulz-Stellenfleth J et al, 2003. Global wind speed retrieval from sar. IEEE Transactions on Geoscience and Remote Sensing, 41(10): 2277-2286 DOI:10.1109/TGRS.2003.814658 |
Jackson C R, Apel J R, 2004. Synthetic aperture radar marine user's manual. U.S. Department of Commerce National Oceanic and Atmospheric Administration. http://sarusersmanual.com
|
Jackson F C, Walton W T, Baker P L, 1985. Aircraft and satellite measurement of ocean wave directional spectra using scanning-beam microwave radars. Journal of Geophysical Research:Oceans, 90(C1): 987-1004 DOI:10.1029/JC090iC01p00987 |
Kerbaol V, Chapron B, Vachon P W, 1998. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. Journal of Geophysical Research:Oceans, 103(C4): 7833-7846 DOI:10.1029/97JC01579 |
Li X M, Lehner S, Bruns T, 2011. Ocean wave integral parameter measurements using Envisat ASAR wave mode data. IEEE Transactions on Geoscience and Remote Sensing, 49(1): 155-174 |
Lyzenga D R, 1986. Numerical simulation of synthetic aperture radar image spectra for ocean waves. IEEE Transactions on Geoscience and Remote Sensing, GE-24(6): 863-872 DOI:10.1109/TGRS.1986.289701 |
Marghany M, Ibrahim Z, Van Genderen J, 2002. Azimuth cut-off model for significant wave height investigation along coastal water of Kuala Terengganu, Malaysia. International Journal of Applied Earth Observation and Geoinformation, 4(2): 147-160 DOI:10.1016/S0303-2434(02)00012-0 |
Ren L, Yang J S, Zheng G et al, 2015. Significant wave height estimation using azimuth cutoff of C-band RADARSAT-2 single-polarization SAR images. Acta Oceanologica Sinica, 34(12): 93-101 DOI:10.1007/s13131-015-0769-6 |
Schulz-Stellenfleth J, König T, Lehner S, 2007. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data. Journal of Geophysical Research:Oceans, 112(C3): C03019 |
Schulz-Stellenfleth J, Lehner S, Hoja D, 2005. A parametric scheme for the retrieval of two-dimensional ocean wave spectra from synthetic aperture radar look cross spectra. Journal of Geophysical Research:Oceans, 110(C5): C05004 DOI:10.1029/2004JC002822 |
Shao W Z, Zhang Z, Li X F et al, 2016. Ocean wave parameters retrieval from Sentinel-1 SAR imagery. Remote Sensing, 8(9): 707 DOI:10.3390/rs8090707 |
Stopa J E, Ardhuin F, Chapron B et al, 2015. Estimating wave orbital velocity through the azimuth cutoff from space-borne satellites. Journal of Geophysical Research:Oceans, 120(11): 7616-7634 DOI:10.1002/2015JC011275 |
Stopa J E, Mouche A, 2017. Significant wave heights from Sentinel-1 SAR:validation and applications. Journal of Geophysical Research:Oceans, 122(3): 1827-1848 DOI:10.1002/2016JC012364 |
Wang H, Zhu J H, Yang J S et al, 2012. A semiempirical algorithm for SAR wave height retrieval and its validation using Envisat ASAR wave mode data. Acta Oceanologica Sinica, 31(3): 59-66 DOI:10.1007/s13131-012-0206-z |
 2020, Vol. 51
2020, Vol. 51


