
中国海洋湖沼学会主办。
文章信息
- 陈娟, 李少峰, 曹安州, 宋金宝. 2020.
- CHEN Juan, LI Shao-Feng, CAO An-Zhou, SONG Jin-Bao. 2020.
- 北太平洋涡旋对基于细尺度参数化的海洋内部混合的影响
- INFLUENCE OF EDDY ON OCEAN INTERNAL MIXING IN NORTH PACIFIC BY FINE-SCALE PARAMETERIZATION
- 海洋与湖沼, 51(2): 248-257
- Oceanologia et Limnologia Sinica, 51(2): 248-257.
- http://dx.doi.org/10.11693/hyhz20191100211
文章历史
-
收稿日期:2019-11-11
收修改稿日期:2019-12-10
海洋中不同性质的海水在相邻区域彼此渗透, 形成性质均一的新的水团, 这一过程称为海水混合。海水混合包含分子混合、湍流混合和对流混合三种形式。通过海洋中的跨等密度面湍流混合, 进行海水间热量、盐量和动量的交换过程, 对海洋中不同尺度的运动都有重要影响, 因此关于湍流混合的研究意义重大。基于一维垂向对流扩散平衡方程, Munk(1966)指出, 为了维持深海的层结, 全球海洋的平均扩散率至少要达到10-4m2/s。但是Gregg(1987)和Ledwell等(1993)的研究发现扩散率在远离边界的大洋内区仅为10-5m2/s。之后的一些研究发现, 在粗糙的海底地形, 例如海山(Kunze et al, 1997)、峡谷(Carter et al, 2002)以及海脊(Klymak et al, 2004)等处混合明显增强, 扩散率可达10-4m2/s甚至更大。
前人的研究表明, 地形和海表风应力输入等对海洋内部混合产生较大的影响。在粗糙地形处, 内潮耗散强, 海洋内部混合增强(Kunze et al, 2006; Jing et al, 2011; Wu et al, 2011)。混合的另一个重要的能量来源是海表风应力的能量输入。研究发现, 风驱动的混合(Munk et al, 1998; Wunsch, 1998)和风产生的近惯性波(Alford, 2001)对全球能量平衡有着重要影响。上层海洋混合的季节变化受到海表风应力的影响较大, 变化幅度随水深增加而减小(Jing et al, 2010, 2011; Wu et al, 2011)。另外, 有研究发现卡特里娜飓风过后, 近惯性剪切升高从而增强了湍流混合(Jing et al, 2015)。随着Argo数据的积累, Wu等(2011)、Whalen等(2012)、Li等(2014)、Zhu等(2018)分别计算了南大洋、全球、西北太平洋、热带太平洋等海域的混合扩散率的空间分布, 加深了我们对海洋混合的认识。
根据Chelton等(2011)的统计结果, 中尺度涡旋在全球海洋中广泛存在。研究表明, 除地形外, 中尺度涡背景场也是影响内孤立波传播和变形的重要因素(Liao et al, 2012)。并且有研究表明涡旋对海洋内部混合产生了一定影响, Cheng等(2018)研究发现在4°—6°N存在一个比较大的跨等密度面混合扩散率, 而该位置的涡动能也达到最大值。Jing等(2013)研究夏威夷海时间序列(Hawaii Ocean Time series, HOT)的温盐深(Conductivity-Temperature-Depth, CTD)数据发现, 在300—600m水深上, 气旋涡对混合的影响不明显, 而反气旋涡明显增强了混合, 且混合的季节性变化在一定程度上受到反气旋涡的季节性变化的调节。Yang等(2017)通过对南海北部3个暖涡的研究发现, 涡旋边缘的混合扩散率比涡旋中心高5—7倍。本文利用Argo剖面观测资料, 从统计意义上研究海洋涡旋对不同深度的混合的影响以及涡旋的旋转方向、强度、与涡旋中心的距离对海洋内部混合的影响。
1 数据与方法 1.1 数据资料介绍本文选取了CMEMS提供的海表面高度异常(sea level anomaly, SLA)数据(http://marine.copernicus.eu/)进行海洋涡旋识别。该SLA数据是TOPEX/Poseidon、Jason-1、ERS-1和ERS-2等高度计的融合产品, 已经减去了20a(1993年1月—2012年12月)的平均海表面高度。文中选取数据的空间范围为10°—40°N、140°W—140°E, 时间范围为2016—2018年, 空间分辨率为1/4°×1/4°, 时间分辨率为1d。
本文使用的温盐数据来自中国Argo实时资料中心(http://www.argo.org.cn/)提供的Argo实测资料。该资料选取的时间和空间范围与上述海表面高度异常数据相同, 并对温盐数据剖面的分辨率和测量水深进行筛选, 共筛选出位于涡旋附近, 平均分辨率不大于10m以及水深不小于1200m的Argo剖面2064个。最后使用细尺度参数化方法来估算海洋内部混合的扩散系数, 进而评估海洋涡旋对跨等密度面混合的影响。特别地, 我们还使用了2014年3—10月在24°—36°N、132°—152°E区域观测的沿着涡旋轨迹的Argo数据(Xu et al, 2016, 2017)作为个例进行分析, 该数据同样可以从中国Argo实时资料中心进行下载。
1.2 涡旋识别方法Nencioli等人在2010年提出一种基于地转流异常场的向量几何算法(vector geometry, VG)探测海洋涡旋, 这种方法将涡旋直观的定义为一个区域, 在这个区域速度场表现为一个旋转流。也就是说, 该区域的特点是速度矢量围绕一个中心顺时针或者逆时针旋转。根据涡旋速度场的特性, VG方法探测的涡旋中心可以通过以下四个约束条件进行确定:
(1) 沿东西方向的速度分量v必须满足在远离涡旋中心两侧的符号相反, 随着距中心点的距离增大, v的值线性增加;
(2) 沿南北方向的速度分量u必须满足在远离涡旋中心两侧的符号相反, 随着距中心点的距离增大, u的值线性增加。速度分量u的旋转方向必须与v相同;
(3) 找到选定区域内速度的最小值点近似为涡旋中心;
(4) 近似涡旋中心点附近的速度矢量必须具有相同的旋转方向, 即两个相邻速度矢量的方向必须在同一个象限或相邻的两个象限内(通过南北和东西轴来定义四个象限:第一象限包括从东到北的方向, 第二象限包括从北到西的方向, 第三象限包括从西到南的方向, 第四象限包括从南到东的方向)。
约束条件中用到两个参数a和b:一个用于第一、第二和第四约束条件, 一个用于第三个约束条件。参数a确定了有多少个网格点用于检验沿着东西轴向速度v分量和沿着南北轴向速度u分量的增加情况。此外, 参数a也决定着绕涡旋中心的曲线(四条边界线), 沿该曲线可以观察速度矢量的方向变化。涡旋的旋转方向可以由v的东西向变化来确定, 如果通过中心后v的符号从负到正(由东向西), 那么则为反气旋式涡旋; 反之则为气旋式涡旋(以北半球为例, 南半球相反)。参数b用来确定局地速度最小值的分布区域(以网格点表示)。在算法中, 参数a和b的取值是弹性的, 以便用来设定涡旋检测的最小尺度, 并使算法可以适用于不同分辨率的网格(Dong et al, 2009)。参考Liu等(2012)和Ma等(2014), 本文选取a=3, b=2。
针对海洋涡旋探测, 除了本文用到的VG方法, 还有一些其他的方法, 如Okubo-Weiss(OW)方法等。Nencioli等(2010)的研究表明, VG方法比OW方法探测的结果具有更高的成功率以及更低的多余率, 因此本文采用VG方法探测研究区域的涡旋。
1.3 基于应变的细尺度参数化方法基于内波理论的细尺度参数化方法(Polzin et al, 1997; Kunze et al, 2006; Wu et al, 2011)将厘米尺度的湍流混合过程与大洋中的温盐及流速观测数据建立起联系。假设海洋内部10—100m的剪切或应变变化, 主要是由内波过程导致的, 通过非线性波-波相互作用, 将能量稳定地从大尺度传输到小尺度, 在这种尺度下, 由于剪切或对流不稳定性, 最终内波破碎并驱动海洋内部跨等密度面混合。
基于应变的细尺度参数化方法, 计算跨等密度面扩散系数K的表达式(Kunze et al, 2006)为:
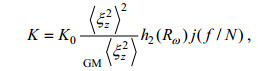 (1)
(1)其中, K0=0.5×10-5m2/s, < ξz2 >和GM < ξz2 > 分别代表观测和Garrett-Munk(GM; Garrett et al, 1979)模型得到的应变方差, h2(Rω)和j(f/N)分别为参数化方案中关于内波结构和纬度影响的修正项,
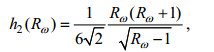 (2)
(2)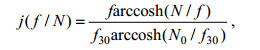 (3)
(3)其中, Rω表示剪切/应变方差比, N是浮力频率, N0=5.24×10-3rad/s, f为科里奥利频率, f30表示南北纬30°的科里奥利频率。由于Argo剖面缺少速度数据, 无法对Rω直接进行计算, 本文选取Rω=7(Jing et al, 2011; Zhu et al, 2018)。
本文将300—1200m深度上的剖面分割为300m长度的子剖面, 每段子剖面上的垂向应变ξz的计算公式为:
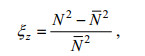 (4)
(4)其中, N2是由位势密度的垂直差分得到, 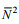
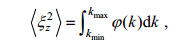 (5)
(5)同时, 为了避免对方差的低估, 垂直波数的积分上限最大波数kmax应满足 < ξz2 > ≤0.1, 从而得到最大波数kmax。
对于GM模型的应变方差GM < ξz2 > 的计算也采用相同的积分区间, 具体计算公式如公式(6)(Kunze et al, 2006):
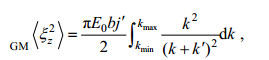 (6)
(6)其中, E0=6.3×10-5是一个无量纲常数, b=1300m表示温跃层的垂直尺度, j′=3表示参考模数, k′=πj′N/bN0表示与j′相对应的参考波数。
2 结果与分析利用VG方法共探测出2016—2018年期间北太平洋区域(10°—40°N/140°W—140°E)SLA≥5cm的涡旋, 共有2248个气旋涡, 1076个反气旋涡, 表明研究区域的气旋涡要远多于反气旋涡。图 1展示了2018年1月1日在研究区域探测出的涡旋, 图中标记的红色圆圈代表涡旋的中心位置, 从图中可以看出西北太平洋的涡旋明显要多于东北太平洋。我们共筛选出该区域在3a中所有符合条件的Argo剖面(平均分辨率不大于10m且水深不小于1200m)14580个, 并采用细尺度参数化方法计算300—1200m深度上的跨等密度面扩散系数, 即图 2所示, 为了方便绘图, 对扩散率K采用对数坐标即log10K。图中显示在西北太平洋有较高的扩散率, 可能是由于粗糙地形或风的近惯性能量输入的影响, 海洋涡旋对其也产生了一定的影响; 在太平洋东部, 扩散率整体较低, 但在夏威夷附近海域扩散率增大, 可能内潮的运动增强了局地的混合。上述结果表明该区域的扩散率水平分布与Zhu等(2018)的研究结果基本相符。查找出位于涡旋附近(剖面距涡心小于2倍涡旋半径)的Argo剖面2064个(图 3), 对这2064个剖面数据进行详细分析, 探讨海洋涡旋对海洋内部混合的影响。
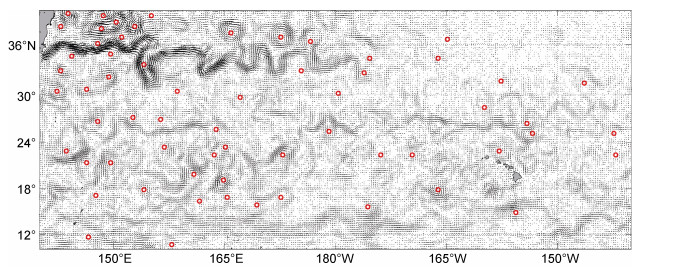 |
| 图 1 2018年1月1日在10°—40°N、140°W—140°E区域的涡旋分布 Fig. 1 Eddies distribution in the region of 10°—40°N/140°W—140°E on January 1, 2018 注:红色圆圈表示涡心的位置; 背景为地转流场 |
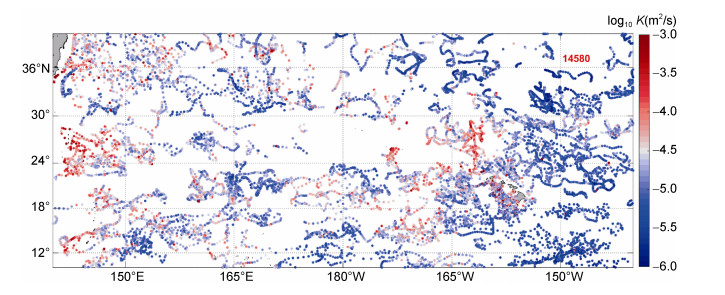 |
| 图 2 2016—2018年10°—40°N、140°W—140°E区域300—1200m深度垂直平均扩散率空间分布图 Fig. 2 The spatial distribution of the vertical average diffusivity at the depth of 300—1200m in the region of 10°—40°N / 140°W—140°E (2016—2018) |
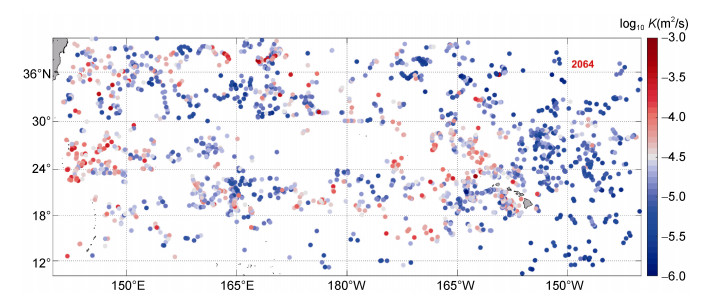 |
| 图 3 2016—2018年位于涡旋附近的Argo剖面计算的垂直平均扩散率空间分布图 Fig. 3 The spatial distribution of the vertical average diffusivity calculated by Argo profiles near the eddy (2016—2018) |
经过计算, 该区域平均扩散率为3.25×10-5m2/s, 在没有涡旋影响的情况下平均扩散率为3.24× 10-5m2/s, 在涡旋影响下的平均扩散率为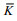
为了直观的观察距涡旋中心的距离对海洋内部混合的影响, 将2016—2018年10°—40°N、140°W—140°E区域位于涡旋附近Argo数据计算的垂直平均扩散率按相对涡旋中心的位置绘制在同一张图上, 并将气旋涡和反气旋涡分开研究, 如图 4所示。图 4展示了涡旋附近扩散率(log10K, 扩散率K的单位为m2/s)的变化, 图中不同颜色的点表示不同的扩散率值。图 4a中气旋涡附近共有1205个Argo剖面, 图 4b中反气旋涡附近有859个剖面。涡旋附近的扩散率平均值如表 1所示, 根据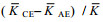
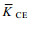
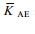
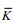
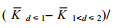
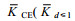
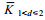
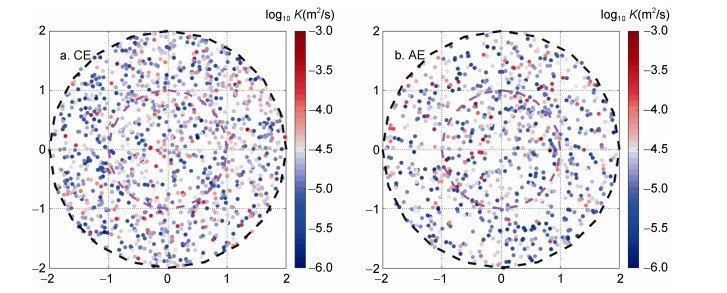 |
| 图 4 气旋涡(Cyclonic Eddy, CE, a)与反气旋涡(Anticyclonic Eddy, AE, b)附近的Argo相对涡旋中心的位置以及对应的垂直平均扩散率 Fig. 4 The position of Argo near cyclonic eddies (CE, a) and anticyclonic eddies (AE, b) relative to the eddy center and the corresponding vertical average diffusivity 注:紫红色和黑色虚线分别表示归一化半径为1和2的圆 |
| 涡旋类型 | 均值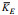
|
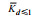
|
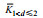
|
| 气旋涡 | 3.51×10-5 | 4.15×10-5 | 3.32×10-5 |
| 反气旋涡 | 3.32×10-5 | 3.43×10-5 | 3.27×10-5 |
注: 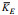 表示气旋涡或反气旋涡影响下的扩散率平均值; 表示气旋涡或反气旋涡影响下的扩散率平均值; 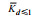 表示距涡心不大于涡半径的扩散率平均值; 表示距涡心不大于涡半径的扩散率平均值; 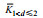 表示距涡心大于1个涡半径且不大于2个涡半径的扩散率平均值 表示距涡心大于1个涡半径且不大于2个涡半径的扩散率平均值 | |||
图 5表示扩散率在不同量级上的分布直方图, 图中的红色数字表示每个量级范围内的个数, 简单的计算发现90%的扩散率值在10-5.5—10-4m2/s范围内, 即两条紫红色虚线之间的范围, 图中蓝色虚线为平均扩散率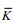
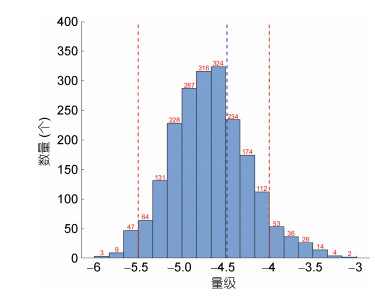 |
图 5 扩散率在不同量级的分布直方图 Fig. 5 The histogram of diffusivity distribution at various orders of magnitude 注:, 红色虚线之间的数量占总数的90%;蓝色虚线表示平均扩散率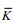
|
我们计算了2018年涡旋附近的扩散率垂直剖面, 计算深度为300—1200m, 每300m片段计算一个值。将每个剖面上的扩散率进行垂直平均, 研究涡旋对不同深度上的混合的影响以及涡旋的旋转方向、强度、距涡心的距离对海洋内部混合的影响。
表 2给出了在气旋涡和反气旋涡影响下不同深度的平均扩散率, 结果显示, 随着深度增加, 混合扩散率减小; 气旋涡对300—600m深度的混合影响不明显, 但明显增强了600—1200m深度上的混合, 且在600—900m深度上混合扩散率增大最为明显, 比无涡旋影响下的扩散率约大了18%;反气旋涡加强了300—600m以及600—900m深度上的混合, 分别比无涡旋情况下的扩散率值增大了3%和5%, 但它对900—1200m深度的混合没有明显的影响。
| 涡旋情况 | 平均扩散率 | ||
| 300—600m | 600—900m | 900—1200m | |
| 无涡旋 | 3.73×10-5 | 3.12×10-5 | 2.87×10-5 |
| 有涡旋 | 3.79×10-5 | 3.52×10-5 | 3.00×10-5 |
| 气旋涡 | 3.74×10-5 | 3.70×10-5 | 3.09×10-5 |
| 反气旋涡 | 3.84×10-5 | 3.27×10-5 | 2.87×10-5 |
表 2的结果与Jing等(2013)关于夏威夷海时间序列ALOHA观测站的研究结果比较一致, 但在细节上有所区别。Jing等研究结果显示, 在300—600m深度, 反气旋涡影响下的混合比无涡旋影响下的混合增强了53%, 但本文的结果仅增强了3%;在600—900m深度, 气旋涡影响下的混合比无涡旋影响下的混合增强了8%, 而本文中增强了18%。因为本文是对北太平洋(10°—40°N、140°W—140°E)的统计结果进行分析, 与Jing等(2013)在ALOHA观测站的研究区域相差较大, 研究结果存在一定差异也是可以理解的。
图 6展示了距涡旋中心的距离对扩散率的影响, 图中蓝色和红色实线分别表示分段线性和二次拟合结果, 虚线表示对应的95%置信区间。图中显示, 在距离涡心1个涡旋半径以内, 扩散率随着距离的增大没有显著变化; 而在1个涡旋半径以外, 扩散率随着距离的增大而微弱减小。
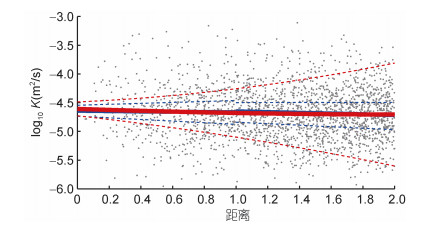 |
| 图 6 距涡心的距离对扩散率的影响 Fig. 6 The influence of distance from the eddy center on diapycnal diffusivity 注:灰色点表示基于Argo剖面计算的扩散率; 蓝色实线表示分段线性拟合结果; 红色实线表示二次拟合结果; 虚线表示对应的95%置信区间 |
我们用海表面高度异常SLA的数值大小来表示涡旋强度, 如图 7所示, 随着强度增大, 扩散率很明显呈现出增大的趋势, 图中曲线含义与图 6中相同, 拟合曲线主要在10-5—10-4m2/s范围内变化, 并且大部分剖面集中在0.05—0.6m涡旋强度范围内。拟合结果表明, 距涡心的距离对海洋内部混合的影响较小, 涡旋强度对其影响较大。
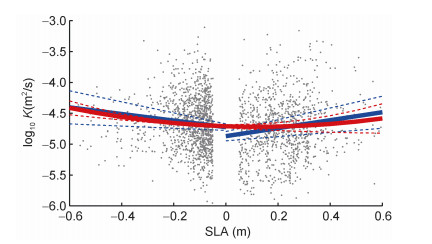 |
| 图 7 涡旋强度对扩散率的影响 Fig. 7 The influence of the intensity of the eddy on diapycnal diffusivity 注:灰色点表示基于Argo剖面计算的扩散率; 两条蓝色实线表示线性拟合结果; 红色实线表示二次拟合结果; 虚线表示对应的95%置信区间; 图中横坐标用海表面高度异常(sea level anomaly, SLA)的值表示涡旋强度 |
我们处理并分析了2014年3—10月所观测的沿着涡旋轨迹的Argo数据, 该数据主要分布在24°—36°N、132°—152°E区域。首先, 我们先利用VG方法探测出2014年3—10月该区域的海洋涡旋, 部分探测结果如图 8所示。图中显示VG方法探测出了该区域大部分的涡旋, 但是也会把个别涡旋边缘的点识别成涡心, 这是VG方法本身的缺陷导致的。
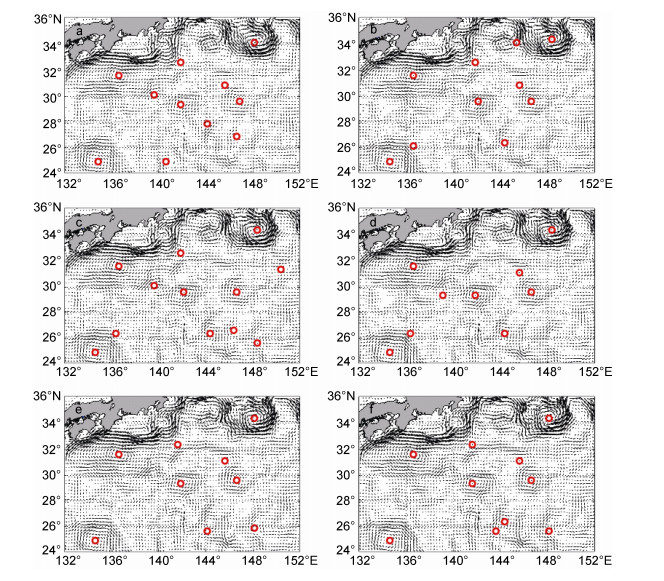 |
| 图 8 2014年4月1—6日在24°—36°N、132°—152°E区域的涡旋分布 Fig. 8 The eddy distribution in the region of 24°—36°N/ 132°—152°E from April 1 to 6, 2014, respectively 注:红色圆圈表示涡旋中心的位置; 背景为地转流场 |
统计结果显示, 在24°—36°N、132°—152°E区域探测出气旋涡附近的Argo剖面仅有31个, 而反气旋涡附近有400个, 说明当时Argo是投放在反气旋涡(暖涡)中, 并随着涡旋的运动来测量数据剖面。图 9中标注的绿色五角星即投放位置, 对照图 8发现对应的位置确实是一个反气旋涡。该区域涡旋影响下的平均扩散率为7.01×10-5m2/s, 对表 3中的数值进行计算发现在气旋涡影响下的扩散率是反气旋涡影响下的近3倍。由于此区域气旋涡与反气旋涡附近的剖面个数相差较大, 且气旋涡距离地形较近, 因此不能表明气旋涡对海洋内部混合的影响大于反气旋涡的影响。另外, 由于气旋涡附近剖面很少, 下文将不再分析气旋涡对混合的影响。反气旋涡影响下, 与涡心距离不大于涡半径的扩散率要比距离1—2个涡半径的值大24%。综上所述, 涡旋内部对混合的影响要明显大于涡旋外围产生的影响。
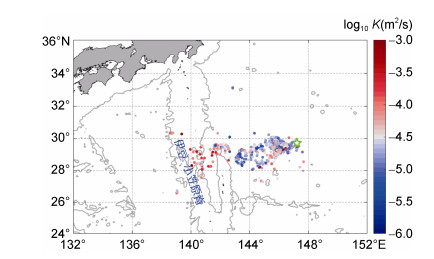 |
| 图 9 涡旋附近垂直平均扩散率空间分布(24°—36°N、132°—152°E) Fig. 9 The spatial distribution of vertical average diffusivity near the eddy (24°—36°N/132°—152 °E) 注:灰色线表示–3000m等深线, 绿色五角星表示Argo投放位置 |
| 涡旋类型 | 均值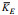
|
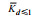
|
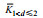
|
| 气旋涡 | 1.71×10–4 | 8.82×10–4 | 1.47×10–4 |
| 反气旋涡 | 6.23×10–5 | 7.10×10–5 | 5.62×10–5 |
与表 1的结果相比, 在24°—36°N、132°—152°E区域的扩散率比整个北太平洋区域(10°—40°N、140°W—140°E)的变化更明显, 平均扩散率也要高于整个北太平洋区域的平均值。Xu等(2017)的研究表明伊豆-小笠原脊(Izu-Ogasawara Ridge)的存在使得地形对混合影响较大, 增强了周围的海洋混合。
由于该个例是在同一个反气旋涡中观测得到的Argo剖面数据, 涡旋强度相差不大, 因此我们将只分析距涡心的距离对混合的影响。图 11展示了距涡旋中心的距离对扩散率的影响, 图中蓝色和红色实线分别表示分段线性和二次拟合结果, 虚线表示对应的95%置信区间。图中显示, 在距离涡心1个涡旋半径以内, 扩散率随着距离的增大没有显著变化; 而在1个涡旋半径以外, 扩散率随着距离的增大而微弱减小。综上所述, 个例分析结果与北太平洋的统计结果基本一致。
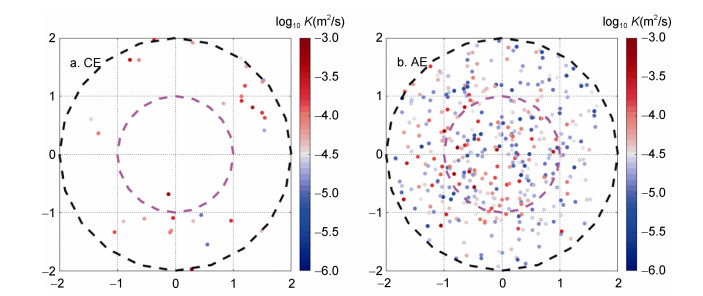 |
| 图 10 24°—36°N、132°—152°E区域气旋涡(a)与反气旋涡(b)附近的Argo相对涡旋中心的位置以及对应的垂直平均扩散率 Fig. 10 The position of Argo near cyclonic eddies (a) and anticyclonic eddies (b) relative to the eddy center and the corresponding vertical average diffusivity (24°—36°N/132°—152°E) 注:紫红色和黑色虚线分别表示归一化半径为1和2的圆 |
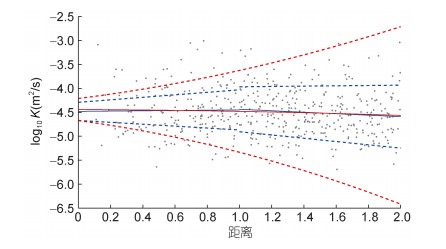 |
| 图 11 距涡心的距离对扩散率的影响 Fig. 11 The influence of distance from the eddy center on diapycnal diffusivity 注:灰色点:基于Argo剖面计算的扩散率; 蓝色实线:分段线性拟合结果; 红色实线:二次拟合结果; 虚线:对应的95%置信区间; 距离:归一化的距涡心的距离 |
本文基于VG方法利用2016—2018年的高度计资料进行涡旋识别, 并基于细尺度参数化方法利用Argo数据计算涡旋附近的扩散率, 分析了北太平洋(10°—40°N、140°W—140°E)区域涡旋对海洋内部混合的影响。另外还研究了2014年3—10月在24°—36°N、132°—152°E区域的涡旋对海洋内部混合的影响。经初步研究得到如下结论。
(1) 在涡旋影响下, 北太平洋区域在2016—2018年的平均扩散率比无涡旋影响情况下的值大6%, 结果显示涡旋对混合扩散率的影响较小。
(2) 在2016—2018年, 研究区域(10°—40°N、140°W—140°E)气旋涡的个数多于反气旋涡的个数。通过研究涡旋影响下不同深度的扩散率发现, 涡旋整体对600—900m深度上的混合影响最大; 气旋涡增强了600—1200m深度的混合, 对600—900m影响最大, 可达18%;反气旋涡明显增强了300—900m深度的混合, 对900—1200m的混合影响不明显。
(3) 拟合结果发现, 随着距涡心的距离增加, 涡旋外围的混合扩散率缓慢减小, 而涡旋内部的混合扩散率变化不明显; 随着涡旋强度的增大, 扩散率明显增大。表明距涡旋中心的距离对海洋内部混合的影响较小, 涡旋强度对内部混合的影响较大。另外, 统计结果表明, 北太平洋区域90%的扩散率值分布在10–5.5—10–4m2/s范围内。
本文主要是基于VG涡旋识别方法和细尺度参数化方案, 得出北太平洋3a中涡旋对混合产生的影响的统计结果。文章使用VG方法识别涡旋, 会将个别的涡旋边缘识别成涡心, 可能会对最终结果产生影响。我们使用基于应变的细尺度参数化方法计算混合扩散率, 细尺度方法是基于大洋内波GM谱提出的, 可能无法正确计算海洋涡旋影响下的跨等密度面扩散率, 这对于最后的结果可能也会产生一些影响。
致谢 感谢南京信息工程大学董昌明教授提供的涡旋识别方法的代码。感谢浙江大学刘聪博士在论文撰写过程中提供的建议与帮助。
Alford M H, 2001. Internal swell generation:the spatial distribution of energy flux from the wind to mixed layer near-inertial motions. Journal of Physical Oceanography, 31(8): 2359-2368 DOI:10.1175/1520-0485(2001)031<2359:ISGTSD>2.0.CO;2 |
Carter G S, Gregg M C, 2002. Intense, variable mixing near the head of Monterey submarine canyon. Journal of Physical Oceanography, 32(11): 3145-3165 DOI:10.1175/1520-0485(2002)032<3145:IVMNTH>2.0.CO;2 |
Chelton D B, Schlax M G, Samelson R M, 2011. Global observations of nonlinear mesoscale eddies. Progress in Oceanography, 91(2): 167-216 DOI:10.1016/j.pocean.2011.01.002 |
Cheng L Q, Gao G P, 2018. Evaluation of spatial distribution of turbulent mixing in the central Pacific. Journal of Oceanography, 74(5): 471-483 DOI:10.1007/s10872-018-0473-1 |
Dong C M, Mavor T, Nencioli F et al, 2009. An oceanic cyclonic eddy on the lee side of Lanai Island, Hawai'i. Journal of Geophysical Research:Oceans, 114(C10): C10008 DOI:10.1029/2009JC005346 |
Garrett C, Munk W, 1979. Internal waves in the ocean. Annual Review of Fluid Mechanics, 11: 339-369 DOI:10.1146/annurev.fl.11.010179.002011 |
Gregg M C, 1987. Diapycnal mixing in the thermocline:a review. Journal of Geophysical Research:Oceans, 92(C5): 5249-5286 DOI:10.1029/JC092iC05p05249 |
Jing Z, Chang P, Dimarco S F et al, 2015. Role of near-inertial internal waves in subthermocline diapycnal mixing in the northern gulf of Mexico. Journal of Physical Oceanography, 45(12): 3137-3154 DOI:10.1175/JPO-D-14-0227.1 |
Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress. Geophysical Research Letters, 37(23): L23604 |
Jing Z, Wu L X, 2013. Low-frequency modulation of turbulent diapycnal mixing by anticyclonic eddies inferred from the HOT time series. Journal of Physical Oceanography, 43(4): 824-835 DOI:10.1175/JPO-D-11-0150.1 |
Jing Z, Wu L X, Li L et al, 2011. Turbulent diapycnal mixing in the subtropical northwestern Pacific:spatial-seasonal variations and role of eddies. Journal of Geophysical Research:Oceans, 116(C10): C10028 DOI:10.1029/2011jc007142 |
Klymak J M, Moum J N, Nash J D et al, 2004. An estimate of tidal energy lost to turbulence at the Hawaiian Ridge. Journal of Physical Oceanography, 36(6): 1148-1164 |
Kunze E, Firing E, Hummon J M et al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553-1576 DOI:10.1175/JPO2926.1 |
Kunze E, Toole J M, 1997. Tidally driven vorticity, diurnal shear, and turbulence atop Fieberling Seamount. Journal of Physical Oceanography, 27(12): 2663-2693 DOI:10.1175/1520-0485(1997)027<2663:TDVDSA>2.0.CO;2 |
Ledwell J R, Watson A J, Law C S, 1993. Evidence for slow mixing across the pycnocline from an open-ocean tracer-release experiment. Nature, 364(6439): 701-703 DOI:10.1038/364701a0 |
Li Y, Xu Y S, 2014. Penetration depth of diapycnal mixing generated by wind stress and flow over topography in the northwestern Pacific. Journal of Geophysical Research:Oceans, 119(8): 5501-5514 DOI:10.1002/2013JC009681 |
Liao G H, Yang C H, Xu X H et al, 2012. Effects of mesoscale eddies on the internal solitary wave propagation. Acta Oceanologica Sinica, 31(5): 26-40 DOI:10.1007/s13131-012-0233-9 |
Liu Y, Dong C M, Guan Y P et al, 2012. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 68: 54-67 DOI:10.1016/j.dsr.2012.06.001 |
Ma L B, Wang Q, 2014. Mean properties of mesoscale eddies in the Kuroshio recirculation region. Chinese Journal of Oceanology and Limnology, 32(3): 681-702 DOI:10.1007/s00343-014-3029-2 |
Munk W H, 1966. Abyssal recipes. Deep Sea Research and Oceanographic Abstracts, 13(4): 707-730 DOI:10.1016/0011-7471(66)90602-4 |
Munk W, Wunsch C, 1998. Abyssal recipes Ⅱ:Energetics of tidal and wind mixing. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
Nencioli F, Dong C M, Dickey T et al, 2010. A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the southern California bight. Journal of Atmospheric and Oceanic Technology, 27(3): 564-579 DOI:10.1175/2009JTECHO725.1 |
Polzin K L, Toole J M, Ledwell J R et al, 1997. Spatial variability of turbulent mixing in the abyssal ocean. Science, 276(5309): 93-96 DOI:10.1126/science.276.5309.93 |
Whalen C B, Talley L D, Mackinnon J A, 2012. Spatial and temporal variability of global ocean mixing inferred from Argo profiles. Geophysical Research Letters, 39(18): L18612 DOI:10.1029/2012GL053196 |
Wu L X, Jing Z, Riser S et al, 2011. Seasonal and spatial variations of Southern Ocean diapycnal mixing from Argo profiling floats. Nature Geoscience, 4(6): 363-366 DOI:10.1038/ngeo1156 |
Wunsch C, 1998. The work done by the wind on the oceanic general circulation. Journal of Physical Oceanography, 28(11): 2332-2340 DOI:10.1175/1520-0485(1998)028<2332:TWDBTW>2.0.CO;2 |
Xu L X, Li P L, Xie S P et al, 2016. Observing mesoscale eddy effects on mode-water subduction and transport in the North Pacific. Nature Communications, 7: 10505 DOI:10.1038/ncomms10505 |
Xu L X, Xie S P, Jing Z et al, 2017. Observing subsurface changes of two anticyclonic eddies passing over the Izu-Ogasawara Ridge. Geophysical Research Letters, 44(4): 1857-1865 |
Yang Q X, Zhao W, Liang X F et al, 2017. Elevated mixing in the periphery of mesoscale eddies in the South China Sea. Journal of Physical Oceanography, 47(4): 895-907 DOI:10.1175/JPO-D-16-0256.1 |
Zhang Z G, Zhang Y, Wang W et al, 2013. Universal structure of mesoscale eddies in the ocean. Geophysical Research Letters, 40(14): 3677-3681 DOI:10.1002/grl.50736 |
Zhu Y C, Zhang R H, 2018. An Argo-derived background diffusivity parameterization for improved ocean simulations in the tropical pacific. Geophysical Research Letters, 45(3): 1509-1517 DOI:10.1002/2017GL076269 |
 2020, Vol. 51
2020, Vol. 51


