中国海洋湖沼学会主办。
文章信息
- 于定勇, 赵伟, 王逢雨, 王世林. 2020.
- YU Ding-Yong, ZHAO Wei, WANG Feng-Yu, Wang Shi-Lin. 2020.
- 不同布设间距下梯形台人工鱼礁体的水动力特性研究
- TRAPEZOID ARTIFICIAL REEFS IN DIFFERENT DEPLOYMENT SPACING: PHYSICAL AND NUMERICAL SIMULATIONS
- 海洋与湖沼, 51(2): 283-292
- Oceanologia et Limnologia Sinica, 51(2): 283-292.
- http://dx.doi.org/10.11693/hyhz20191000190
文章历史
-
收稿日期:2019-10-16
收修改稿日期:2019-12-11
人工鱼礁体通过将人工构造物投入海底后与波浪和水流相互作用改变附近的流场, 形成上升流或复杂尾流区而发挥作用。合理布放人工鱼礁体一方面可以促进水体循环, 改善海区水质状况, 另一方面可以增加渔获量, 是一种可持续的新型渔业生产模式。
早在1994年新加坡学者Chua等(1994)发现, 混凝土礁体在聚鱼的丰富度方面比轮胎礁体效果更佳, 并且在生产区域增强了生物资源。Granneman等(2015)则对比了加利福尼亚南部5组人工鱼礁体和天然鱼礁在集鱼效果方面的区别, 发现在聚集鱼类丰富度方面人工鱼礁体和天然鱼礁并没有显著差异, 但是人工鱼礁体提高了鱼类密度和生物复杂程度。借助计算机, 很多学者开始使用数值模拟技术研究人工鱼礁体的流场, 如马荍沣等(2018)发现在开口比较小时, 开口单礁体的流场效应优于实心单礁体。Liu等(2013)利用计算流体动力学(Computational Fluid Dynamics, CFD)方法模拟了开孔方形人工鱼礁体分别在横向(即垂直水流方向, 以下均简称为“横向”)、纵向(即平行水流方向, 以下均简称为“纵向”)及堆叠布置情况下的水流场, 其模拟结果表明, 随着布设间距的增大, 礁体的遮流效应逐渐减弱; 当横向布设间距大于2倍礁长时, 双礁体间的影响消失; 随着纵向布设间距的增大, 礁体缓流区的范围逐渐增大, 但增长幅度会有限制; 当纵向布设间距为4倍礁长时, 缓流区的最大长度为18.5倍的礁长; 当礁体堆叠布置时, 其堆叠高度的增大并不能实现更经济的集鱼效益。国内的庞运禧等(2017)通过数值方法模拟透空率为20%的箱型、梯形台、三棱体多孔空心人工鱼礁体在不同来流速度和布设工况下的流场过程, 结果表明同种模拟工况下人工鱼礁体以90°摆放时形成的上升流和背涡流规模强度达到最大; 同种摆放角度下, 梯形台礁体上升流强度最大。除了使用数值模拟方法, 在物理模型试验方面, Li等(2017)研究了5种不同来流速度和3种不同布置组合情况下圆管型人工鱼礁体周围的流场效应, 发现上升流和背涡流的强度和规模均随着礁体数量的增加而增强。崔勇等(2011)在研究组合方型人工鱼礁体在3种来流速度和4种布设间距条件下的流场效应发现:当布设间距为1倍礁长时, 上升流的影响面积最大; 当布设间距为1.5倍礁长时, 背涡流效果最好。刘洪生等(2009)通过风洞实验研究正方体、金字塔及三棱柱人工鱼礁体在3种来流速度、4种横向与4种纵向布设间距条件下的水流场, 发现礁体产生的上升流和背涡流的规模随着流速的增大逐渐增强; 相同来流速下, 同种空心礁体上升流和背涡流规模相对于实心礁体小; 当礁体布设间距为1-1.5倍礁长时, 流场效应差异显著, 且横向组合比纵向组合产生的流场效应更佳。刘同渝(2003)通过水槽和风洞实验研究了梯形台、半球型、三角锥体、堆叠式人工鱼礁体的流场效应, 发现水流经过鱼礁体时会在其两侧形成上升流和背涡流, 且上升流区范围约为鱼礁体的1/3, 背涡流距礁体渐远渐弱; 从流场效应看堆叠式礁体优于单礁体, 单礁体中梯形台人工鱼礁体较佳。
总结前人研究发现, 国内外学者主要研究了人工鱼礁在不同摆放方式下礁体周围流场形态随海流流速、礁体形状、礁体迎流角度等方面的变化, 对梯形台双礁体的流场效应、阻力系数随横向及纵向间距的变化情况尚缺乏研究, 因此, 本文通过物理模型实验和数值模拟研究梯形台双礁体水动力特性, 旨在探究礁体上升流规模、阻力系数随布设间距的变化规律, 为礁区布局方案的确定提供参考。
1 物模实验 1.1 模型制作开口比(φ)定义为鱼礁迎流面在垂直于水流方向上开口的投影面积与迎流面投影面积之比(邵万骏等, 2014)。数值模拟的模型为梯形台混凝土人工鱼礁体, 下底边长3m、上底边长1.8m、高2m、厚0.2m、开口比0.1, 糙率n实=0.014(郑延璇, 2014), 根据糙率相似准则, 当模型比尺λ=20时, 物模实验中礁体模型糙率为n模=n实/λ1/6=0.0085, 而有机玻璃的糙率为0.0070-0.0087, 利用有机玻璃制作礁体模型满足要求。采用厚度为0.01m有机玻璃板制作开口比为0.1的梯形台鱼礁模型, 如图 1所示。
 |
| 图 1 礁体模型 Fig. 1 The reef model |
物模实验在中国海洋大学水动力实验室循环水槽中进行。该水槽实验段尺寸长、宽、高分别为4、1.2、1m, 水槽可测流速范围0-1.2m/s, 稳定流速范围0-0.8m/s。水槽配有六分力仪传感器(量程0-50kg, 精度±0.3%), 可精确测量礁体在x轴方向的受力; 另外水槽配有小威龙Vectrino+点式流速仪(换能器到采样单元距离为5cm, 分辨率为0.01cm/s, 量程0-2m/s, 精度±0.5%), 可精确测量实验过程中礁体周围的流速情况。
1.3 实验方法实验开始前将礁体固定在直径为0.01m的螺杆上, 螺杆与六分力仪端相连接。实验测量的数据通过桥盒、应变仪等设备传输。礁体模型距离水槽出流口1.64m, 根据物模实验比尺λ=20, 数模计算域礁前12m对应的是距离水槽0.6m, 1.64m远大于0.6m, 因此模型距水槽出流口1.64m足够。模型底面与水槽底部相接近但不接触, 以水槽底部模拟海底, 假设模型不受缝隙水流影响(姜昭阳, 2009)。
D为两礁体之间的距离; L为礁体底面边长; A0B1等点是为标明礁体前后测量点位置而设置的坐标点。每次实验开始之前, 用流速仪测量距离第一个礁体模型迎流面前方0.6m处(即A0B1点)的流速, 使其稳定流速接近0.179m/s, 然后移动流速仪测量礁体前后A1B1、A2B1、A3B1、A4B1、A5B1、A6B1六个测点的流速, 待测点的流速测量值波动幅度较小时, 采集10s的流速数据后重复三次取平均值作为该测点的流速测量值。不同布设间距下测点位置如图 3所示。
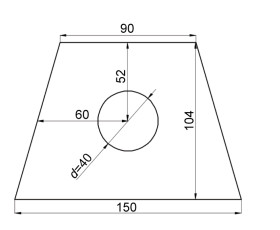 |
| 图 2 模型侧面示意图(单位: mm) Fig. 2 The side view of the model(unit: mm) |
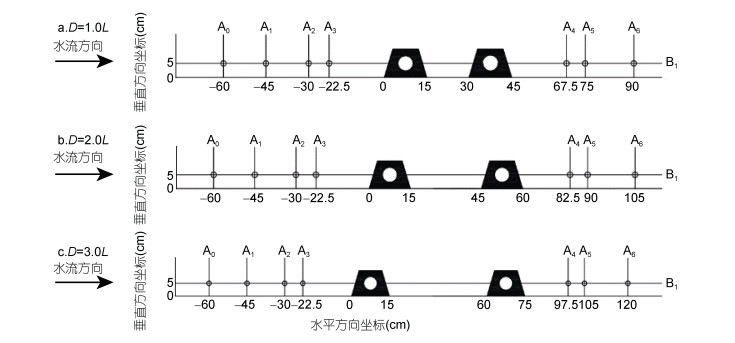 |
| 图 3 纵向布设间距下双礁体模型测点位置示意图 Fig. 3 The sketch map of measurement points position of double reefs with vertical disposal spaces 注: D:两礁体之间的距离; L:礁体底面边长; A0-A6等点:为标明礁体前后测量点位置而设置的坐标点 |
假设鱼礁体附近的流场为黏性不可压缩流体的湍流运动, 温度变化不大, 因此能量方程可以忽略。
连续方程:
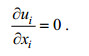 (1)
(1)动量方程:
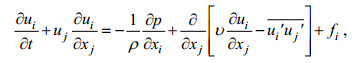 (2)
(2)式中, ui(i=1, 2, 3)分别为x、y、z方向的雷诺平均速度; ρ为流体密度; p为压强; υ为运动黏性系数; 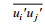
本文采用RNG κ-ε两方程湍流模型, 该模型可以更好地处理流线弯曲程度较大的及高应变率流动; 选用标准壁面函数法处理近壁区内及Re数较低的流动(郑延璇, 2014)。
湍动能κ方程:
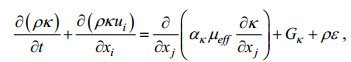 (3)
(3)湍流耗散率ε方程:
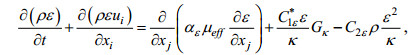 (4)
(4)其中, 有效黏性系数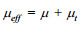
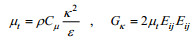
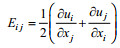
选取下底面为3m×3m、上底面为1.8m×1.8m、高为2m、开口比φ为0.1, 根据已有研究, 双礁体之间横向和纵向的影响范围不一样, 一般为横向2倍礁长, 纵向4倍礁长, 因此, 本文横向布设间距分别为0.5L、1.0L、1.5L和2.0L、纵向布设间距分别为0.5L、1.0L、2.0L、3.0L、4.0L的梯形台双礁体, 流速取为0.8m/s。礁体结构如图 4所示, 数值模拟计算区域如图 5所示。
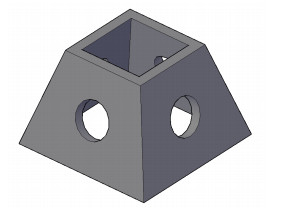 |
| 图 4 开口比为0.1的梯形台人工鱼礁体结构 Fig. 4 The sketch of trapezoidal artificial reef in opening ratio of 0.1 |
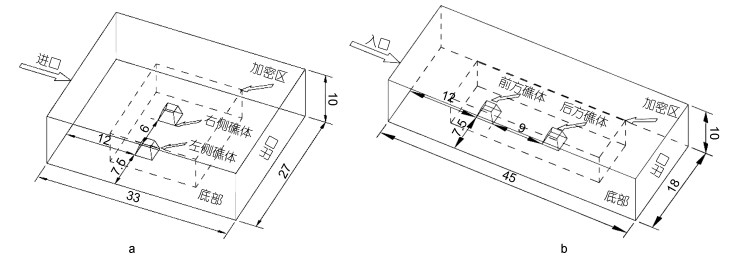 |
| 图 5 纵向布设间距为2.0L(a)和3.0L(b)的双礁体流场计算域示意图 Fig. 5 The computational domain sketch of double reefs with vertical disposal space of 2.0L(a) and 3.0L(b) |
初始边界条件设定:
(1) 进口边界设置为速度进口, 来流速度为0.8m/s, 进口边界处的湍动能κ和湍流耗散率ε值可根据湍流强度I和特征长度L粗略得到,
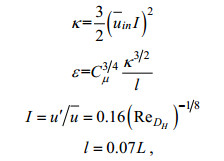 (5)
(5)式中, 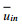
(2) 出口边界设置为自由出流;
(3) 计算域的两侧面设置为对称边界;
(4) 计算域的顶面设置为具有与入口水流相同速度的可移动壁面, 剪切力为零, 底面和鱼礁体表面设置为无滑移壁面。
2.4 模型可靠性验证 2.4.1 网格收敛性验证为了减小数值模拟过程中由于网格尺度所产生的误差, 以纵向布设间距为3.0L的双礁体为例, 计算域网格分别为0.900、0.700、0.500和0.300m, 同时参考大多数文献, 选择以前方礁体阻力系数作为网格收敛性验证的变量, 结果如表 1所示。
| 最大网格尺寸(m) | 网格单元数(×105个) | 前方礁体阻力系数 |
| 0.900 | 9.187 | 1.252 |
| 0.700 | 10.065 | 1.249 |
| 0.500 | 12.996 | 1.242 |
| 0.300 | 29.672 | 1.241 |
由表 1可得, 在计算域网格尺寸均为0.500m时, 前方礁体阻力系数值已经较为稳定, 网格收敛性较好。因此, 设置加密区长度为礁前3m, 礁后9m, 宽9m, 高9m, 考虑计算效率, 设置加密区网格尺寸为0.250m, 其收敛性仍符合要求。
基于上述数值模型, 模拟研究开口比为0.1、横向布设间距为0.5L、1.0L、1.5L、2.0L、横向布设间距为0.5L、1.0L、2.0L、3.0L、4.0L时双礁体的上升流规模、阻力系数随布设间距的变化情况。
2.4.2 实验验证将Fluent软件模拟得到的测点对应位置处的流速和前方礁体阻力系数值与物模实验结果进行对比, 如图 6和表 2所示。
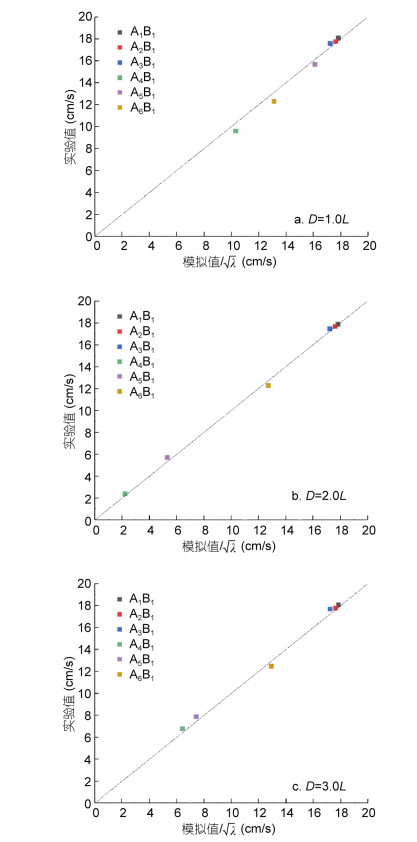 |
| 图 6 不同布设间距双礁体测点流速模拟值与实验值比较 Fig. 6 Comparison of the simulated and measured velocities of the measuring stations of the double reefs with vertical disposal spaces 注: λ表示模型比尺, λ=20; A1B1等点是为标明礁体前后测量点位置而设置的坐标点 |
| 布设间距 | 数值模拟值(N) | 物模实验值(N) | 相对误差(%) |
| 1.0L | 0.238 | 0.229 | 3.782 |
| 2.0L | 0.358 | 0.396 | 10.615 |
| 3.0L | 0.376 | 0.411 | 9.309 |
| 注: L表示礁体底面边长 | |||
由图 6可知, 纵向布设第一个礁体模型迎流面前方测点的流速模拟值与实验值相对误差较小, 相对误差较大的测点出现在靠近第二个礁体的背流面处, 其中当纵向布设间距为2.0L时, 由于礁体开口比面积较小, 礁后流场复杂且流速较小, 礁后第一个测点相对误差较大, 为9.90%, 其他测点的流速模拟值和实验值相对误差较小, 比较吻合。
由表 2可知, 当纵向布设间距为2.0L时, 由于造流电机频率、振动、螺杆发生绕流现象等因素的影响, 六分力仪采集的数据有一定的波动范围, 双礁体模型所受沿水流方向的阻力模拟值与实验值之间的相对误差较大, 约为10.62%, 其他布设间距下双礁体模型所受沿水流方向的阻力模拟值与实验值吻合较好。
由图 6和表 2可知, 本文数值模拟所得到的流速值、阻力值和实验值吻合较好, 说明本文数值模拟方法是可行的, 结果是可信的, 能够用于双礁体水动力特性的研究。
3 水动力特性研究 3.1 流场形态本文以上升流特性参数为指标判定双礁体流场效应的强与弱, 其中上升流定义为水流z方向(即垂直地面方向)速度与来流速度之比大于或等于5%的水域(黄远东等, 2012)。
由图 7及表 3可知, 每个礁体前方均会形成半圆形的缓流区, 两侧形成一定范围的急流区; 随着横向布设间距的增大, 礁体两侧急流区的范围增大。当横向布设间距为0.5L时, 双礁体阻水作用较强, 上升流最大高度约为礁高的3.28倍, 上升流水平跨度约为礁宽的8.14倍, 流场效应较佳; 随着横向布设间距的增大, 双礁体所形成的上升流规模逐渐减小, 而竖向最大速度分量变化幅度较小, 当横向布设间距大于1.5L时, 上升流规模趋于稳定。
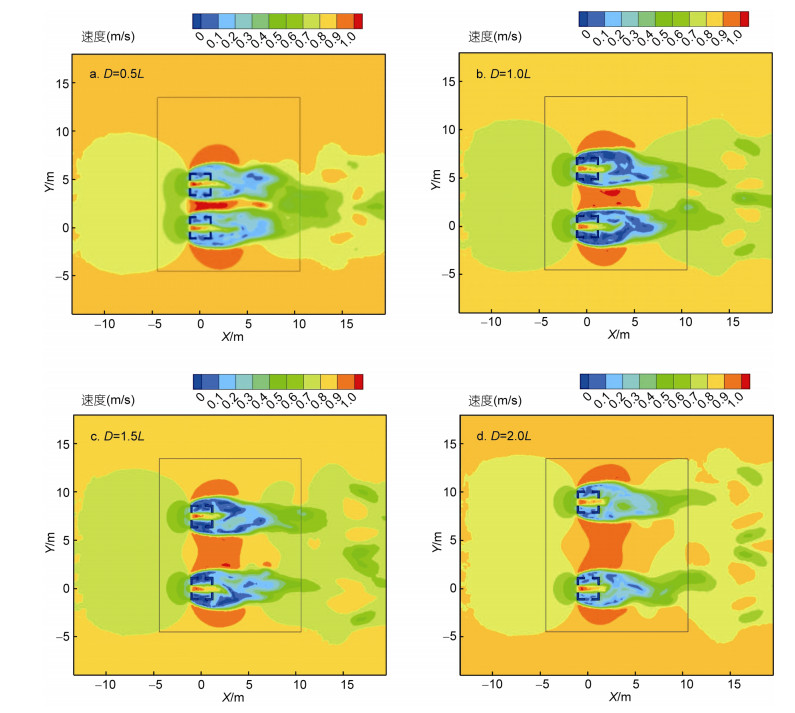 |
| 图 7 不同横向布设间距双礁体横向断面速度云图 Fig. 7 Velocity contour across transverse section of double reefs with different horizontal disposal spaces 注: X:水平方向距离; Y:垂直方向流速 |
| 布设间距 | 上升流最大高度/礁高 | 上升流水 平跨度/礁长 |
竖向最大速度 分量/来流速度 |
| 0.5L | 3.28 | 8.14 | 0.76 |
| 1.0L | 3.27 | 8.05 | 0.76 |
| 1.5L | 3.00 | 7.64 | 0.75 |
| 2.0L | 3.00 | 7.62 | 0.72 |
由图 8及表 4可知, 当纵向布设间距为0.5L和1.0L时, 由于双礁体距离较近, 后方礁体受前方礁体的遮流效应较明显, 其中空部分流速接近于0, 且后方礁体附近流速较小; 当纵向布设间距为2.0L、3.0L、4.0L时, 后方礁体中空部分流速增大, 且后方礁体上方急流区的范围也逐渐变广; 随着纵向布设间距的增大, 双礁体上升流最大高度先变化幅度较小后增大, 上升流水平跨度逐渐增大, 而竖向最大速度分量变化幅度不明显; 当纵向布设间距为4.0L时, 前方礁体的遮流效应较弱, 双礁体周围的流场效应较佳, 上升流规模较大, 其上升流最大高度约为礁高的3.23倍, 上升流水平跨度约为礁长的11.67倍。
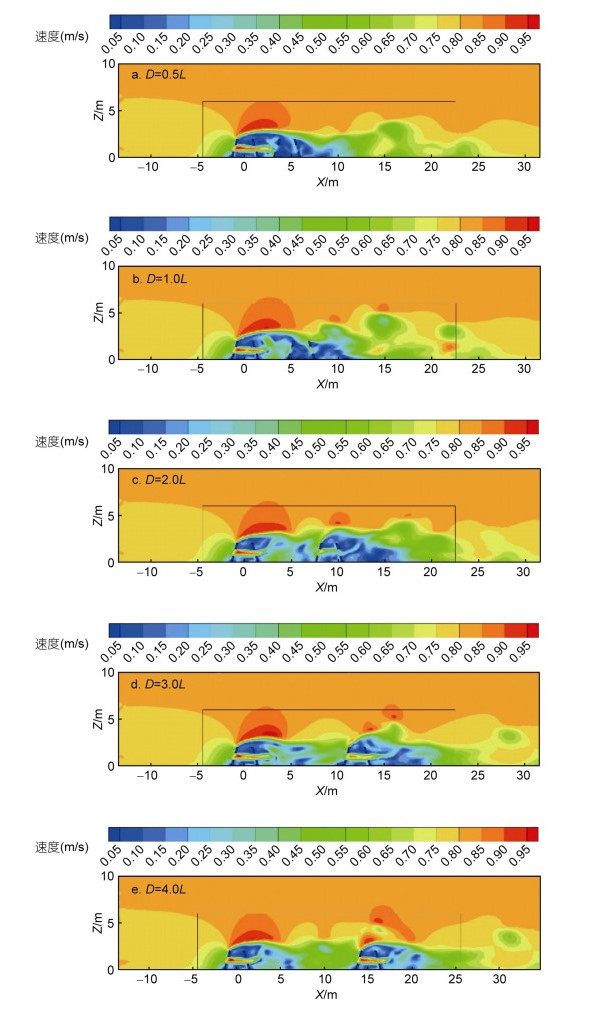 |
| 图 8 不同纵向布设间距双礁体纵向断面速度云图 Fig. 8 Velocity contour on transverse section of double reefs with different vertical disposal spaces 注: Z表示垂直于XY面方向上的距离 |
| 布设间距 | 上升流最大高度/礁高 | 上升流水 平跨度/礁长 |
竖向最大速度 分量/来流速度 |
| 0.5L | 2.93 | 8.45 | 0.75 |
| 1.0L | 2.95 | 8.74 | 0.68 |
| 2.0L | 2.95 | 10.08 | 0.76 |
| 3.0L | 2.94 | 10.74 | 0.75 |
| 4.0L | 3.23 | 11.67 | 0.74 |
由图 9可知, 左右两礁体阻力系数均随着横向布设间距的增大而逐渐较小; 当横向布设间距为0.5L时, 由于间距较近、礁体开口面积较小, 双礁体阻水作用显著, 因此, 当布设间距由0.5L增至1.0L时, 左侧与右侧礁体阻力系数下降幅度最明显, 大于其他布设间距变化的幅度。
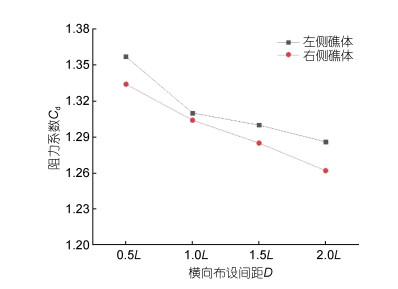 |
| 图 9 双礁体Cd与D的关系 Fig. 9 The relation between drag coefficient and horizontal disposal space |
为了更直观地表示双礁体阻力系数与横向布设间距的关系, 引入双礁体横向阻力影响系数kH(邓绍云等, 2014):双礁体平均阻力系数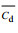
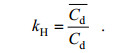 (6)
(6)通过计算得到双礁体横向阻力影响系数kH与横向布设间距的关系, 如图 10所示:
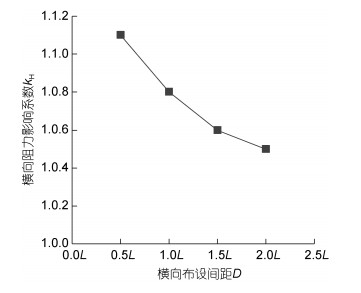 |
| 图 10 双礁体kH与D的关系 Fig. 10 The relation between kH and horizontal disposal space |
由图 10可知, 随着横向布设间距的增大, 双礁体横向阻力影响系数逐渐减小, 当横向布设间距大于1.5L时, 双礁体横向阻力影响系数减小幅度变缓, 表明横向布设间距对双礁体阻力系数的影响逐渐减小。
由图 11可知, 随着纵向布设间距的增大, 前方礁体的阻力系数变化幅度较小, 后方礁体的阻力系数逐渐增大; 当纵向布设间距小于2.0L时, 前后两礁体阻力系数相差较大, 表明后方礁体受前方礁体遮流效应影响较为严重, 尤其当纵向布设间距为0.5L时, 后方礁体阻力系数为负值, 表明后方礁体处于前方礁体后侧的负压区, 受吸力; 当纵向布设间距大于2.0L时, 后方礁体的阻力系数增速变缓且与前方礁体阻力系数相差较小, 表明前方礁体遮流效应减弱。
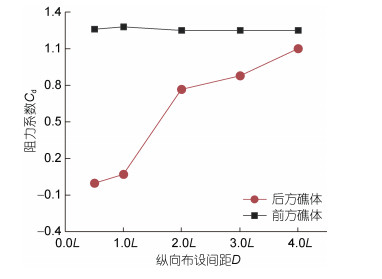 |
| 图 11 双礁体Cd与D的关系 Fig. 11 Relationship between drag coefficient and horizontal vertical disposal space |
为了更直观地表示双礁体阻力系数与纵向布设间距的关系, 引入双礁体双礁体遮流阻力影响系数kz(邓绍云等, 2014):双礁体总阻力系数与原单礁体阻力系数之比与1的差值。如公式(7)所示:
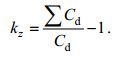 (7)
(7)由图 12可知, 随着纵向布设间距的增大, 双礁体纵向阻力影响系数逐渐增大; 当纵向布设间距为0.5L时, 遮流影响系数为负值, 表明后方礁体受吸力, 和前文结论一致; 当纵向布设间距大于2.0L时, 遮流阻力影响系数增幅较缓, 表明后方礁体受前方礁体遮流效应逐渐减弱。
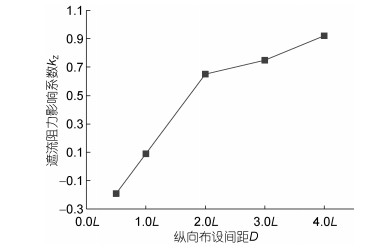 |
| 图 12 双礁体kz与D的关系 Fig. 12 Relationship between kz and vertical disposal space |
本文通过数值模拟计算得到的礁体周围测点流速及阻力值与同工况物模实验实测值吻合较好, 说明本文采用的数值模拟计算方法可行, 结论可靠。因此, 本文利用数值模拟研究了不同布设间距下梯形台人工鱼礁体的水动力场, 通过分析其上升流区规模、阻力系数随布设间距变化情况, 得到了如下结论:
(1) 在布设间距变化的情况下, 人工鱼礁体流场效应等方面的水动力特性具有一定的差异。随着横向布设间距的增大, 双礁体所形成的上升流规模逐渐减小, 当横向布设间距为0.5L时, 上升流规模较大, 流场效应较佳。
(2) 随着横向布设间距的增大, 双礁体阻力系数与横向阻力影响系数均逐渐减小, 表明双礁体阻力系数受横向布设间距的影响逐渐减弱。
(3) 随着纵向布设间距的增大, 双礁体所形成上升流规模逐渐增大, 当纵向布设间距为4.0L时, 上升流规模较大, 流场效应较佳。
(4) 随着纵向布设间距的增大, 前方礁体阻力系数变化幅度较小, 后方礁体阻力系数逐渐增大, 遮流阻力影响系数逐渐增大, 当纵向布设间距大于2.0L时, 遮流阻力影响系数增幅变缓, 表明后方礁体受前方礁体遮流效应逐渐减弱。
由此可见, 当横向布设间距为0.5L、纵向布设间距为4.0L时, 双礁体周围的流场效应较佳。研究结果可为礁区布局方案的确定提供参考。
马荍沣, 张瑞瑾, 席彦彬, 徐佳诺. 2018. 开口比变化对人工鱼礁流场效应影响的评价. 安徽农业科学, 46(5): 105-108 |
邓绍云, 宁东卫, 邱清华. 2014. 桩群绕流阻力特性. 郑州: 黄河水利出版社
|
刘同渝. 2003. 人工鱼礁的流态效应. 水产科技, (6): 43-44 |
刘洪生, 马翔, 章守宇, 等. 2009. 人工鱼礁流场效应的模型实验. 水产学报, 33(2): 229-236 |
邵万骏, 刘长根, 聂红涛, 等. 2014. 人工鱼礁的水动力学特性及流场效应分析. 水动力学研究与进展, 29(5): 580-585 |
郑延璇, 2014.人工鱼礁流场效应与物理稳定性研究.青岛: 中国海洋大学博士学位论文
|
庞运禧, 李芳成, 李尧. 2017. 同透空率下多孔人工鱼礁流场效应的三维数值模拟研究. 水资源与水工程学报, 28(2): 133-141 |
姜昭阳, 2009.人工鱼礁水动力学与数值模拟研究.青岛: 中国海洋大学博士学位论文
|
崔勇, 关长涛, 万荣, 等. 2011. 布设间距对人工鱼礁流场效应影响的数值模拟. 海洋湖沼通报, (2): 59-65 |
黄远东, 姜剑伟, 赵树夫. 2012. 方型人工鱼礁周围水流运动的数值模拟研究. 水资源与水工程学报, 23(3): 1-3 |
Chua C Y Y, Chou L M, 1994. The use of artificial reefs in enhancing fish communities in Singapore. Hydrobiologia, 285(1-3): 177-187 DOI:10.1007/BF00005665 |
Granneman J E, Steele M A, 2015. Effects of reef attributes on fish assemblage similarity between artificial and natural reefs. ICES Journal of Marine Science, 72(8): 2385-2397 DOI:10.1093/icesjms/fsv094 |
Li J, Zheng Z Y, Gong P H et al, 2017. Numerical simulation and PIV experimental study of the effect of flow fields around tube artificial reefs. Ocean Engineering, 134: 96-104 DOI:10.1016/j.oceaneng.2017.02.016 |
Liu T L, Su D T, 2013. Numerical analysis of the influence of reef arrangements on artificial reef flow fields. Ocean Engineering, 74: 81-89 DOI:10.1016/j.oceaneng.2013.09.006 |
 2020, Vol. 51
2020, Vol. 51

