
中国海洋湖沼学会主办。
文章信息
- 王宁, 侯一筠, 李水清, 莫冬雪, 刘泽, 李健. 2020.
- WANG Ning, HOU Yi-Jun, LI Shui-Qing, MO Dong-Xue, LIU Ze, LI Jian. 2020.
- 1979—2018年间山东半岛沿海台风浪危险性分布的数值模拟研究
- NUMERICAL SIMULATION OF THE HAZARD DISTRIBUTION OF TYPHOON WAVES IN 1979—2018
- 海洋与湖沼, 51(4): 861-868
- Oceanologia et Limnologia Sinica, 51(4): 861-868.
- http://dx.doi.org/10.11693/hyhz20191200263
文章历史
-
收稿日期:2019-12-18
收修改稿日期:2020-01-06
2. 中国科学院大学 北京 100049;
3. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 青岛 266237;
4. 中国科学院海洋大科学中心 青岛 266071;
5. 国家海洋局北海预报中心 青岛 266061
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Laboratory for Ocean and Climate Dynamics, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China;
4. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
5. North China Sea Marine Forecasting center of State Oceanic Administration, Qingdao 266061, China
山东半岛海域是海洋灾害频发区域之一, 每年都有不同程度的海洋灾害发生, 主要灾害为风暴潮和海浪灾害。山东受台风影响情况各年不等, 为了人民群众生命、财产安全, 台风浪的模拟预报及其危险分析具有重要的现实意义。
海浪数值预报经历了第一代到第三代的发展。第三代海浪模式SWAN(Simulation Waves Nearshore)更加适用于海岸、湖泊和河口等浅水区域。SWAN模式在我国海区的适用性研究是“九五”国家重点科技攻关方向, 研究人员将SWAN模式应用于我国不同海域, 对台风浪过程进行了模拟研究。徐福敏等(2004)对SWAN模型的适用性、数值特性、功能及局限性进行了阐述, 模拟了海安湾有效波高、波周期场, 并分析波与波之间非线性相互作用对波浪要素预报的影响, 对SWAN模型的应用前景和研究趋势进行了展望。孙瑞等(2013)利用SWAN模式模拟了莫拉菲台风的海浪场, 结果表明模式结果与实测值吻合良好。赵鑫等(2006)使用SWAN模型计算浙江沿海海域在“9711”台风下的波浪场分布, 结果表明, 有效波高实测值与计算值符合良好, 说明SWAN模型能够合理地反映浙东沿海的波浪场。杨德周等(2005)通过对SWAN模式的改进, 建立了适应于各种天气状况的渤海海浪数值预报模式, 模式结果与实测符合很好。史剑等(2011)采用NCEP再分析风场驱动海浪模式SWAN, 分别采用矩形网格和非结构三角网格对2000年12月黄渤海海域波浪场进行模拟, 并与海洋浮标观测数据作对比分析, 结果表明, 相对于矩形网格, 非结构三角网格模拟有效波高效果较好。邓兆青等(2007)利用SWAN模式对渤海海域的波浪进行了20a的数值计算, 模拟值与实测值符合的较好, 说明了SWAN模式适合渤海海域波浪的计算。蒋小平等(2007)应用海浪模式SWAN对Winnie(1997)引起的台风浪进行了模拟, 结果表明, SWAN在模拟较大尺度的海区时也能得到较好的模拟效果, 能较好地再现海浪的发展过程和合理地反映台风浪的分布。Wang等(2012)使用SWAN模式模拟了1985—2004年渤海的海浪场, 模拟结果与台站观测的有效波高的对比显示出良好的一致性。高松等(2018)利用数值模式SWAN构建了近30年山东省海域有效波高分布, 并进行近岸海浪强度等级划分并给出了危险性分布。李雪等(2018)利用SWAN模式对1960—2012年期间发生于山东沿海的50场台风进行模拟, 将模拟的有效波高与观测数据作了对比分析, 验证了模型在计算海域的适用性, 并绘制50年一遇和100年一遇的台风浪波高分布图。
上述研究表明, SWAN模式可以对我国海域的大浪特征进行较好的模拟。值得注意的是, 强风条件下近岸区域可以出现明显的增减水特性, 进而对波浪进行调制, 因此, 考虑浪-流-水位的耦合作用, 更为接近实际情形。Feng等(2016)将SWAN+ADCIRC耦合模式应用于台风“天兔”过境过程中波浪的模拟, 结果表明, 耦合模型模拟效果好于仅采用SWAN模式, 其结果与实测数据更加吻合。李绍武等(2016)运用SWAN与ADCIRC实时耦合模型对南玛都台风进行了模拟, 计算结果与实测资料吻合较好, 验证了模型在该区域内的合理性。Shih等(2018)利用ADCIRC+SWAN耦合模式模拟了台湾海域的124次台风过程, 并给出了台风浪危险图。本研究采用ADCIRC+SWAN耦合模式, 模拟山东半岛附近海域的台风过境期间的波浪有效波高(significant wave high, SWH)的特征分布, 给出山东半岛台风浪危险性等级评价。
1 资料与方法在本文的研究中, 利用ADCIRC和SWAN的耦合模式进行台风过程模拟, 风场采用Holland模型风场与美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)再分析数据风场组合的合成风场, 水深地形数据采用Etopo1数据(图 1a); 模式采用非结构三角网格, 网格覆盖范围117°—128°E, 30°—41°N, 共有95682个三角形网格, 49094个网格节点, 网格分辨率从开放海域边界的10km到山东半岛沿岸海岸线的500m不等(图 1b)。
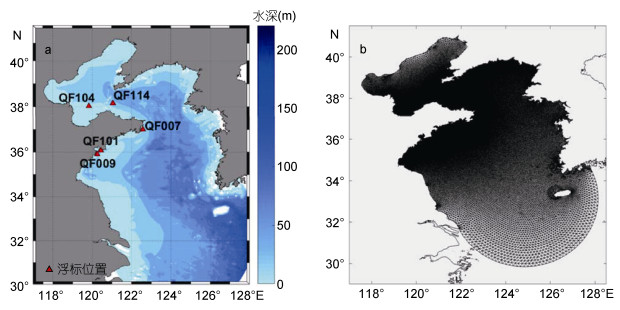 |
| 图 1 计算区域水深及浮标位置(a)和计算网格(b) Fig. 1 Bathymetry and Position of buoy(a) and unstructured grid of the computational domain(b) |
Holland参数模型(Holland, 1980)的表达式为:
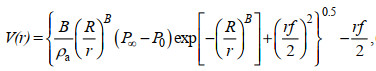 (1)
(1)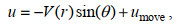 (2)
(2)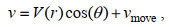 (3)
(3)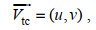 (4)
(4)其中, V表示模型计算的风速大小; u、v表示风速的纬向和经向分量; 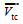
合成输入风场是由Holland模型风场与NCEP气候预报系统再分析(Climate Forecast System Reanalysis, CFSR)风场通过加权计算得到, 在台风中心附近Holland模型风场占较大的权重, 在台风的外围则是NCEP风场占据较大权重, 同时实现了合成输入风场从台风中心到外围的平滑过渡。合成输入风场 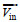
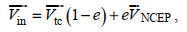 (5)
(5)其中, 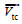
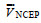
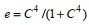
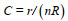
海浪模拟采用ADCIRC和SWAN的耦合模式。
ADCIRC模式是由美国学者开发, 适用于海洋、近岸及河口地区流场模拟的数值模型。模式垂向平均的连续方程表达式为:
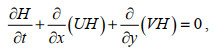 (6)
(6)其中, t表示时间, 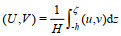
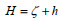
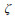
SWAN模式是由DELFT大学开发的第三代波浪数值模式。SWAN模式的控制方程为波作用平衡方程(Booij et al, 1999), 控制方程如下:
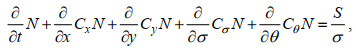 (7)
(7)其中, N为波作用量; σ为波的相对频率; θ为波向; S项为源汇项。式中左端第一项为波作用量的局地变化; 第二、三项为波作用量在地理空间上的传播, 其中Cx和Cy分别为波作用量在x和y方向上的传播速度; 第四项为由于水深和水流变化造成的相对频率变化, 其中Cσ为波作用量在频率空间中的传播速度; 第五项为水深和流产生的波浪折射, 其中Cθ为波作用量在波向空间中的传播速度。
模拟过程, ADCIRC的时间步长设置为1s, 以实现模型的稳定性, SWAN模式是无条件稳定的, 其时间步长设置为30min; 耦合间隔为10min, 即ADCIRC与SWAN每10min的计算交换一次信息。开放海域边界选取8个分潮K1(太阴太阳合成全日分潮)、K2(太阴太阳合成半日分潮)、M2(太阴主要半日分潮)、N2(太阴椭率主要半日分潮)、O1(太阴主要全日分潮)、P1(太阳主要全日分潮)、Q1(太阴椭率主要全日分潮)和S2(太阳主要半日分潮)作为边界潮位驱动, 模式提前2d开始计算, 每1h输出一次计算结果。
1.3 海浪等级划分及危险指数计算分别提取模拟的各例台风事件在研究区域网格点处的SWH的最大值, 然后再提取同一类台风事件的最大SWH, 并将每个类别的最大SWH划分为四个台风浪强度等级(高松等, 2018), 并为山东半岛近岸海域绘制台风浪强度分布图。当SWH小于1.3m时, 台风浪强度被视为一级(level 1);当SWH在1.3—2.5m之间时, 台风浪强度被视为二级(level 2);当SWH处于2.5—4m之间时, 该强度被视为三级(level 3);如果SWH在4m以上, 该台风浪强度则被视为四级(level 4)。
基于海浪模拟结果, 分别计算一、二、三、四级浪高的时间频率。根据公式(8)计算各点的海浪灾害危险指标HW:
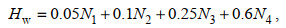 (8)
(8)式中, N1、N2、N3、N4分别为一、二、三、四级浪高的时间频率。通过归一化方法, 获得山东省沿海的海浪危险性指数, 并绘制危险性指数分布图。
2 模拟及结果验证根据中国气象局热带气旋资料中心的最佳路径数据集(tcdata.typhoon.org.cn)(Ying et al, 2014), 统计了1949—2018年间6—9月对山东半岛产生影响的72次台风过程, 并根据台风路径将台风事件分为6种类型(以下简称T1—T6, 如图 2所示)(温连杰等, 2016)。例如, 如果台风直接在山东半岛登陆, 则将其归为T1;如果台风路径在山东半岛东部海域北上, 则将其归为T2;等等。表 1列出了各种路径台风相应的发生情况, 并且在图 3中展示了T1—T6的台风轨迹。
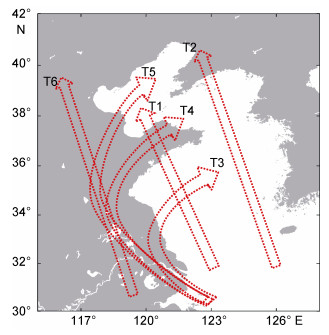 |
| 图 2 六种台风路径类型(T1—T6) Fig. 2 Six categories of typhoon tracks(T1—T6) |
| 台风类型 | 台风数量(次) | 模拟数量(次) |
| T1 | 12 | 4 |
| T2 | 17 | 10 |
| T3 | 27 | 12 |
| T4 | 4 | 2 |
| T5 | 7 | 4 |
| T6 | 5 | 4 |
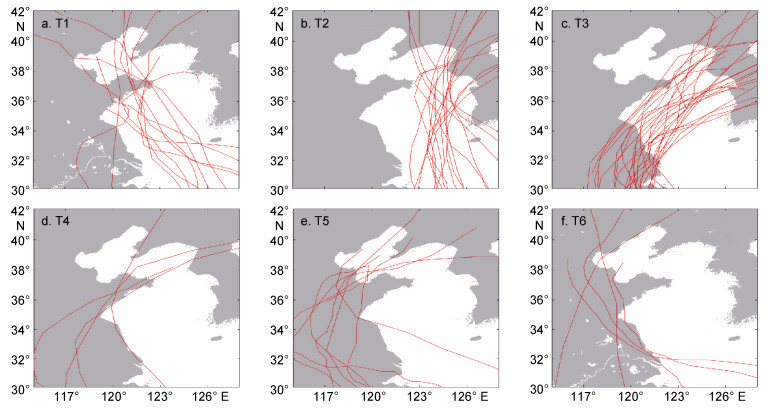 |
| 图 3 1949—2018年期间每一类台风的路径 Fig. 3 Typhoon tracks for each category during the period 1949—2018 |
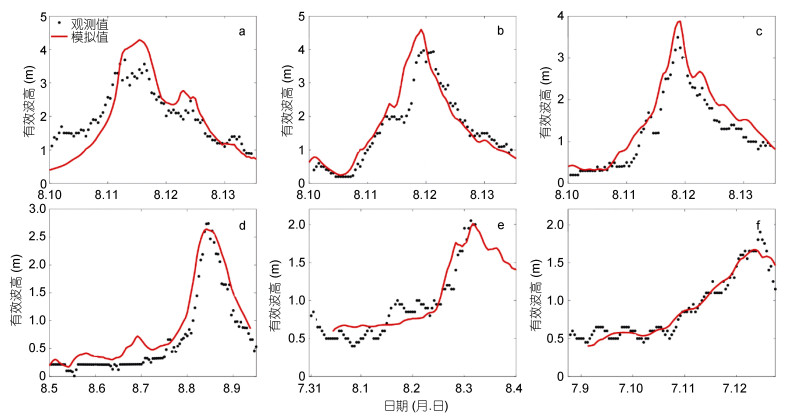
利用浮标实测数据, 对2011年台风“梅花”、2012年台风“达维”、2015台风“灿鸿”年及2019年台风“利奇马”的模式模拟结果的SWH进行验证。图 4显示模拟结果与实测数据匹配良好, 模式能够很好地再现台风过程。
 |
|
图 4 模拟结果与测量的有效波高的比较 Fig. 4 Comparison of the significant wave height(SWH) between model predictions and measurements 注: a、b、c分别表示“利奇马”期间QF101、QF104、QF114位置; d表示“梅花”期间QF114位置; e表示“达维”期间QF007位置; f表示“灿鸿”期间QF009位置 |
在回顾1949—2018年山东半岛周边各类的台风事件之后, 利用组合风场驱动耦合模式重现了模拟区域内的SWH。考虑风场资料时间的有限性, 选取了1979年之后的36次台风事件进行模拟(各类别的模拟数量在表 1给出), 用于SWH的分布分析研究。同时, 根据SWH的分布特征将山东半岛海域划分为五个区域(图 5中Ⅰ—Ⅴ)来进行危险性分析。
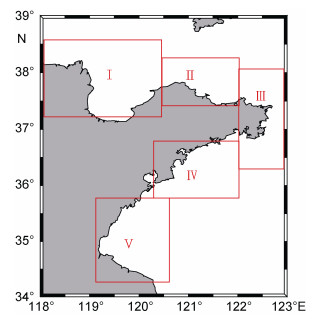 |
| 图 5 用于危险评价的区域(Ⅰ—Ⅴ)划分示意图 Fig. 5 Areas Ⅰ—Ⅴ divided for hazard assessment |
图 6展示了山东半岛近岸海域T1—T6类别的台风浪强度分布。蓝色、绿色、黄色、红色分别代表 1—4级台风浪强度(level 1、level 2、level 3和level 4)。如图 6a所示, T1类别的台风浪强度在区域Ⅰ西部和南部为一级、东北为二级; 区域Ⅱ西部处于二级, 东部达到三级; 区域Ⅲ最高, 达到四级强度; 区域Ⅳ东部处于三级, 西部处于二级强度; 区域Ⅴ台风浪强度主要为二级。图 6b显示了T2的台风浪在Ⅰ区和Ⅴ区主要处于二级强度; Ⅱ区和Ⅳ区主要处于三级强度; Ⅲ区海浪强度为四级; T3的台风影响作用较为平均, Ⅰ区西部和南部、Ⅱ区西南部和Ⅳ区西部为二级, 其余各处均为三级台风浪强度(图 6c)。
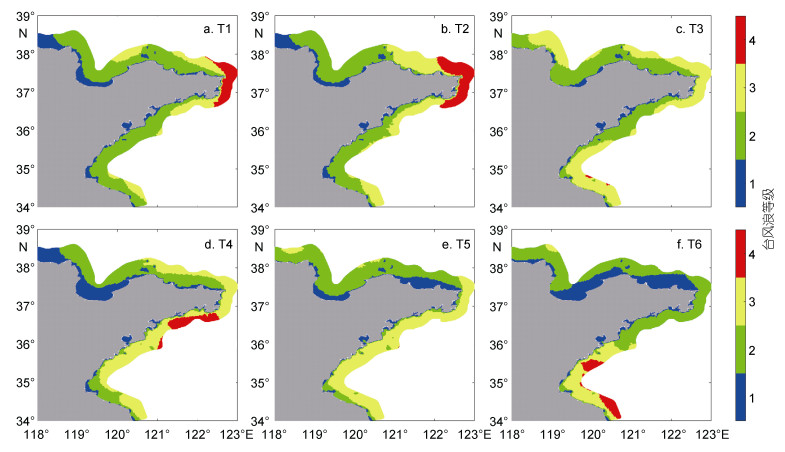 |
| 图 6 T1—T6对应的台风浪强度等级分布 Fig. 6 The distribution of the intensity of typhoon waves corresponding to T1—T6 |
图 6d展示了T4台风浪强度等级分布, Ⅰ区西部和南部莱州湾内较低处于一级, Ⅰ区中部、Ⅱ区西、南部和Ⅴ区西部近岸处于二级, Ⅲ区、Ⅳ区和Ⅴ区北部和南部达到三级, 在Ⅳ区东部达到最高的四级。对于T5的台风浪, 最高等级为三级, 出现在Ⅲ区、Ⅳ区、Ⅴ区的大部分区域, 而Ⅰ区和Ⅱ区多处于二级, Ⅰ区南部及Ⅱ区南部近岸区域为一级台风浪强度(图 6e)。T6的影响区域较小, 仅在Ⅴ区到达三级, 其余都低于三级, Ⅰ区大部分、Ⅲ区和Ⅳ区处于二级, 而Ⅰ区南部莱州湾和Ⅱ区东南则为一级强度。
采用相同的方法提取T1—T6类别中的最大SWH, 并绘制综合台风浪强度等级分布图(图 7), 可以看出, 在台风的影响下, 山东半岛近岸海域台风浪的强度等级都在二级以上。Ⅰ区大部分处于二级台风浪强度, Ⅰ区的中间部分区域、Ⅱ区、Ⅳ区西部以及Ⅴ区处于三级, 而Ⅳ区东部及Ⅲ区到达台风浪等级四级。
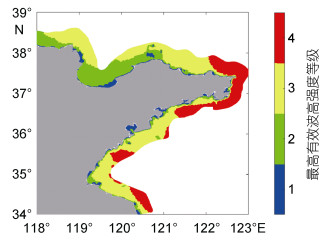 |
| 图 7 所有台风类别的最高有效波高强度等级分布 Fig. 7 Distribution of the intensity of maximum significant wave height for all typhoon categories |
结合统计的level 2—4的SWH的频数(该等级波高在输出结果中出现的次数, 同时也表示历时的小时数)分布图(图 8), 可以看出, 山东半岛海域波高处于level 4的台风浪仅出现于东部海域, 该区域是海浪危害最高的区域, 但台风浪历时较短, 最高在50h上下; 波高处于level 3的台风浪发生次数较level 4要高, 历时最高可达250h, 同样集中发生在东部海域; Level 2的台风浪历时最高可达700h以上, 是三个等级中发生最为频繁的, 且东部和南部海域历时均较长。
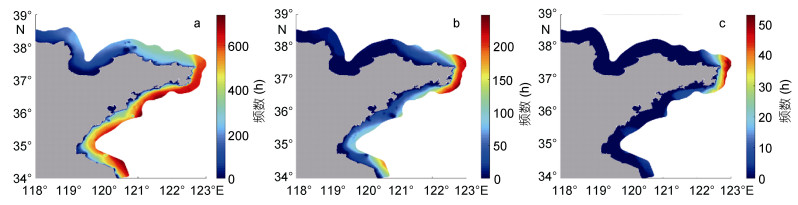 |
| 图 8 所有台风不同有效波高的频数分布 Fig. 8 The frequency distribution of different significant wave heights for all typhoon categories 注: a: SWH处于1.3—2.5m; b: SWH处于2.5—4.0m; c: SWH处于4.0m及以上 |
图 9展示了山东半岛台风浪危险性指数的分布, 由图可以看出, 山东半岛台风浪危险性南部要高于北部; 莱州湾(区域Ⅰ)台风浪危险性最小; 东部海域(区域Ⅲ)的危险性最高, 是最容易遭受台风浪危害的区域。高松等(2018)在其图 2b中给出了山东省海浪危险性指数分布, 本文结果与高松等的分布特征定性相似, 然而由于本文仅考虑台风引起的海浪危险性, 因此在数值上本文结果小于高松等的特征值, 特别是在山东半岛以北海域, 这些区域易受寒潮的影响。
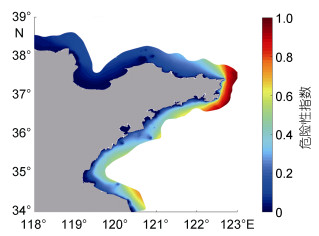 |
| 图 9 山东半岛海域台风浪危险性指数分布图 Fig. 9 Hazard index distribution map of typhoon waves in Shandong Peninsula |
采用耦合高分辨率非结构化网格风暴潮-波浪模式(ADCIRC+SWAN), 对山东半岛近岸海域的台风浪的危险性进行分析。模型以Holland模型风场与再分析风场的组合风场为驱动, 对1979—2018年的36次台风过程进行后报模拟。根据SWH的最大值范围划分为四级台风浪强度等级, 并统计2—4级发生的历时时长频数, 绘制了每种台风类别单独的台风浪强度等级图和综合台风浪强度等级图, 以及历时分布图和危险性指数分布图。
研究结果显示, 山东半岛东部海域(区域Ⅲ)危险性最高, 台风浪强度可以达到四级; 南部(区域Ⅳ、Ⅴ)危险性较高, 可以达到三级台风浪强度, 二级强度台风浪发生较为频繁; 北部(区域Ⅰ、Ⅱ)危险性最低, 台风浪强度低且历时短。整体而言, 山东半岛东部和南部较北部更易遭遇台风浪。
邓兆青, 周良明, 吴伦宇, 等. 2007. 渤海重现期波高的数值计算. 海洋湖沼通报, (S1): 8-14 |
史剑, 王璞, 钟中, 等. 2011. 两种网格下的SWAN模式对黄渤海海浪模拟比较. 海洋预报, 28(4): 48-57 DOI:10.3969/j.issn.1003-0239.2011.04.008 |
孙瑞, 侯一筠, 李健, 等. 2013. 南海北部一次台风浪过程的数值模拟. 海洋科学, 37(12): 76-83 |
李雪, 宋冲, 巩艺杰, 等. 2018. 山东沿海台风浪数值模拟与统计分析. 海洋湖沼通报, (1): 27-33 |
李绍武, 李松樵. 2016. 南玛都台风期间平潭湾风浪及风暴增水数值模拟. 水道港口, 37(3): 242-246 DOI:10.3969/j.issn.1005-8443.2016.03.007 |
杨德周, 尹宝树, 徐艳青, 等. 2005. SWAN浅水波浪模式在渤海的应用研究——Phillips线性增长比例系数的改进. 水科学进展, 16(5): 710-714 DOI:10.3321/j.issn:1001-6791.2005.05.017 |
赵鑫, 黄世昌. 2006. 浙东沿海"9711"台风波浪场数值模拟研究. 浙江水利科技, (3): 24-27 DOI:10.3969/j.issn.1008-701X.2006.03.008 |
徐福敏, 张长宽, 陶建峰. 2004. 浅水波浪数值模型SWAN的原理及应用综述. 水科学进展, 15(4): 538-542 DOI:10.3321/j.issn:1001-6791.2004.04.025 |
高松, 钟山, 李亚汝, 等. 2018. 山东省海洋自然灾害综合危险性评估研究. 海洋科学, 42(9): 55-63 |
蒋小平, 钟中, 张金善, 等. 2007. 台风Winnie(1997)影响下海浪的数值模拟研究. 热带气象学报, 23(4): 376-382 DOI:10.3969/j.issn.1004-4965.2007.04.008 |
温连杰, 刘桂艳, 刘清容, 等. 2016. 1960-2013年影响渤海的热带气旋特征分析. 海洋开发与管理, 33(8): 84-89 DOI:10.3969/j.issn.1005-9857.2016.08.018 |
Booij N, Ris R C, Holthuijsen L H, 1999. A third-generation wave model for coastal regions:1. Model description and validation. Journal of Geophysical Research:Oceans, 104(C4): 7649-7666 |
Feng X R, Yin B S, Yang D Z, 2016. Development of an unstructured-grid wave-current coupled model and its application. Ocean Modelling, 104: 213-225 DOI:10.1016/j.ocemod.2016.06.007 |
Holland G J, 1980. An analytic model of the wind and pressure profiles in hurricanes. Monthly Weather Review, 108(8): 1212-1218 DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 |
Shih H J, Chen H, Liang T Y et al, 2018. Generating potential risk maps for typhoon-induced waves along the coast of Taiwan. Ocean Engineering, 163: 1-14 DOI:10.1016/j.oceaneng.2018.05.045 |
Wang Z F, Wu K J, Zhou L M et al, 2012. Wave characteristics and extreme parameters in the Bohai Sea. China Ocean Engineering, 26(2): 341-350 DOI:10.1007/s13344-012-0026-0 |
Ying M, Zhang W, Yu H et al, 2014. An overview of the China meteorological administration tropical cyclone database. Journal of Atmospheric and Oceanic Technology, 31(2): 287-301 DOI:10.1175/JTECH-D-12-00119.1 |
 2020, Vol. 51
2020, Vol. 51


