
中国海洋湖沼学会主办。
文章信息
- 范守志, 付永涛. 2020.
- FAN Shou-Zhi, FU Yong-Tao. 2020.
- 岩石圈挠曲-弹性薄板小挠度弯曲的新方程
- A NEW FORMULA FOR LITHOSPHERE FLEXURE-ELASTIC THIN PLATE SMALL DEFLECTION BENDING
- 海洋与湖沼, 51(4): 869-874
- Oceanologia et Limnologia Sinica, 51(4): 869-874.
- http://dx.doi.org/10.11693/hyhz20191200280
文章历史
-
收稿日期:2019-12-27
收修改稿日期:2020-03-22
2. 中国科学院海洋大科学研究中心 青岛 266071;
3. 青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室 青岛 266237
2. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
3. Laboratory for Marine Geology, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China
自Vening Meinesz采用走航式三摆重力仪进行海洋重力测量和均衡学研究(Vening-Meinesz, 1948), 在20世纪50年代即已认识到岩石圈的弹性薄板模型是足够精确的(Gunn, 1949), 依据弹性力学薄板理论(Timoshenko, 1958)和岩石圈均衡响应理论(Jeffreys, 1945; Gunn, 1949), 伴随20世纪70、80年代至今的海洋和大陆岩石圈重力均衡和挠曲研究(Walcott, 1970; Watts et al, 1974; McNutt et al, 1978; Watts, 2001), 岩石圈在火山岛屿、俯冲带、挠曲盆地等处的挠曲变形可以用弹性薄板模型来近似研究的认识已经获得广泛的承认(Watts, 2001; Turcotte et al, 2014)。
目前岩石圈挠曲研究中采用的是克希霍夫(Kirchhoff)弹性薄板小挠度弯曲平衡方程(钱伟长等, 1956;柳春图等, 2001):
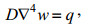 (1)
(1)其中, 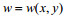
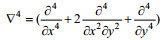
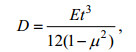 (2)
(2)其中, t是板的厚度, E是板材的杨氏模量, μ是泊松比(因下文中板的挠曲位移采用v, 本文用μ记泊松比)。
克希霍夫方程由于其数学形式上的简洁而被广泛应用, 但在推导过程中采用的各项假设中, 有一个关于薄板内垂向应力2σ的假设是
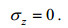 (3)
(3)它是基于克希霍夫薄板理论的一个主要假设——薄板的厚度比薄板的其它尺寸小, 可以把垂向应力忽略不计(钱伟长等, 1956), 它的物理意义是平行于板面的各个面在挠曲中不相互挤压。此项假设, 式(3), 不仅在物理上非常牵强, 而且在推导式(1)的过程中还与其它假设不相协调。因此假设式(3)是克希霍夫方程推导过程中的一个问题, 也是一个缺陷。
在岩石圈挠曲的研究中仍然采用这一假设, 并因为薄板表面垂向应力为0, 而且薄板相对很薄, 可以取垂向应力在薄板中都为0(特科特等, 1986; Turcotte et al, 2014)。但很难设想岩石圈在施加负载时其内部应力没有变化, 这一假设是许多学者不赞同的(金煜等, 2002)。可是鉴于克希霍夫方程数学上的简洁和国际惯例, 目前仍普遍接受采用这一假设得到的克希霍夫方程。
本文针对克希霍夫方程中的这一问题, 提供了一个不需要假设式(3)的推导过程, 建立了一个新的弹性薄板挠曲方程:
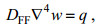 (4)
(4)其中DFF是新的挠曲刚度,
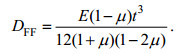 (5)
(5)但前人在建立式(1)中所用的其他5个假设, 即下文中式(6)、(9)、(12)、(26)及(35), 在本文建立式(4)的过程中仍保留使用, 但并不增加任何新的假设。
1 推导过程仍旧把直角坐标系O-xyz之原点取在板之中面内, 且中面选为xOy平面, z轴则垂直板面向下, 如图 1所示。
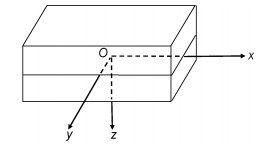 |
| 图 1 弹性薄板与坐标系 Fig. 1 The elastic thin plate and Coordinates |
板内任意一点(x, y, z)在挠曲时的位移记为(u, v, w)。一般而言, u, v及w均是(x, y, z)之函数。
采用z轴方向应变为0的假设
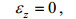 (6)
(6)则描述弹性体形变的几何方程(Cauchy方程)组
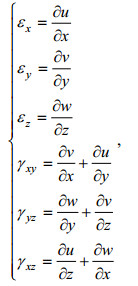 (7)
(7)其中, 第三式给出w与z无关, 仅是x与y的函数, 即有:
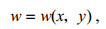 (8)
(8)采用假设
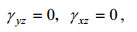 (9)
(9)可由式(7)之第五、第六式给出:
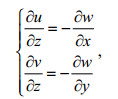 (10)
(10)将式(10)两边对z积分, 可得:
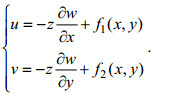 (11)
(11)采用假设(中面内各点无面内位移):
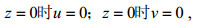 (12)
(12)得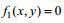
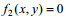
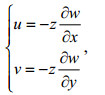 (13)
(13)将式(13)代入式(7), 就有
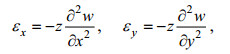 (14)
(14)及
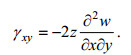 (15)
(15)依弹性体变形的物理方程(胡克定律), 有
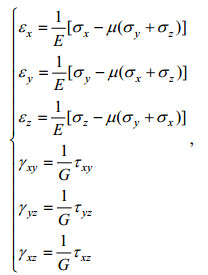 (16)
(16)其中, σx、σy、σz分别表示各个正应力, τxy、τyz、τxz分别表示各个剪应力, G是板材的切变弹性模量, 即
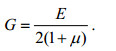 (17)
(17)现在, 本文摒弃假设式(3), 保留σz, 进行如下恒等变换。
首先由式(16)中第三式解出σz, 得到
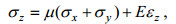 (18)
(18)将式(18)代入式(16)中第一、二式, 有
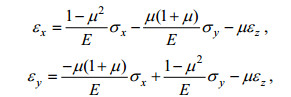
视此二式为σx及σy的二元一次代数方程, 求解有
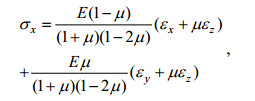 (19)
(19)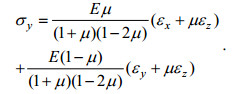 (20)
(20)现在, 引用假设式(6), 并注意到式(14), 此二式变为
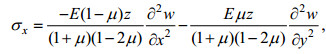 (21)
(21)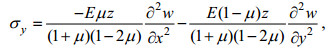 (22)
(22)又将式(15)及式(17)代入式(16)之第四式得到式(23), 待用。
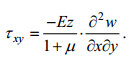 (23)
(23)依照弹性体的静力平衡方程组(Navier方程), 有
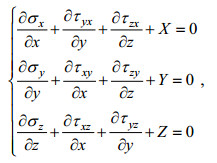 (24)
(24)及
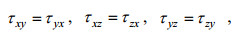 (25)
(25)其中, (X, Y, Z)是弹性体在(x, y, z)处的单位体积所受到的外力(如重力)。
仍旧采用假设
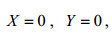 (26)
(26)则式(24)化为
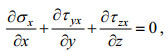 (27)
(27)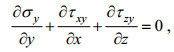 (28)
(28)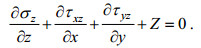 (29)
(29)注意到式(25), τxy= τyx, 则式(27)可写成
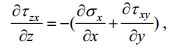 (30)
(30)将式(21)及(23)中的σx及τxy代入式(30)得到
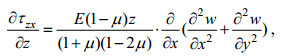 (31)
(31)同样, 将式(22)及(23)代入式(28)可得到
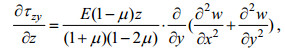 (32)
(32)将式(31)及(32)的两边对z积分, 并注意到式(8), 有
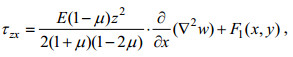 (33)
(33)及
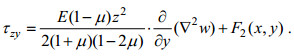 (34)
(34)这里,
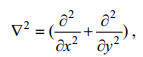 (35)
(35)而F1(x, y)及F2(x, y)是任意函数, 待定。
依旧采用克希霍夫方程推导中采用的假设:
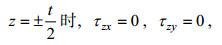 (36)
(36)即在板的上、下表面上无剪切应力, 则可由式(36)、(33)与(34)解出F1(x, y)及F2(x, y), 从而得出
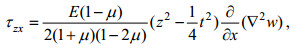 (37)
(37)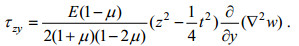 (38)
(38)根据式(25)、(37)、(38), 式(29)变成为
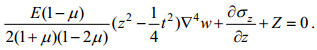 (39)
(39)如果弹性薄板受到的体力只有重力, 那么Z=ρg, 这里ρ是薄板的材料密度, 而g是重力加速度。但我们这里不做此限定, 而是一般地, 容许有可变体力
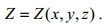 (40)
(40)为了由方程(39)推导出薄板挠曲的微分方程, 我们引入一个辅助量P如下:
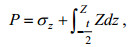 (41)
(41)于是,
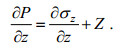 (42)
(42)仍用q1及q2记薄板顶面及底面上受到的横向载荷, 见图 2。
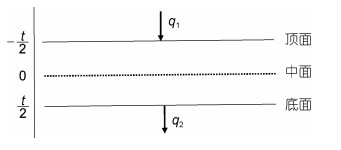 |
| 图 2 薄板顶面及底面的横向载荷 Fig. 2 Lateral load on the surfaces of elastic thin plate 注: q1、q2分别表示薄板顶面及底面上受到的横向载荷; t为薄板厚度 |
则有如下的边界条件成立(依惯例, 张应力为正):
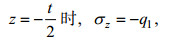 (43)
(43)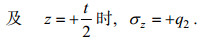 (44)
(44)仍旧用q表示薄板受到的横向总载荷, 即
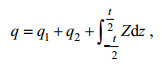 (45)
(45)则有如下边界公式成立:
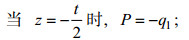 (46)
(46)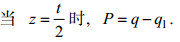 (47)
(47)将(42)式代入(39)式, 有
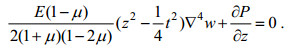 (48)
(48)将此式两边对z积分, 得到
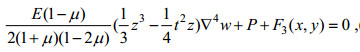 (49)
(49)由(46)及(49)可求出F3(x, y),
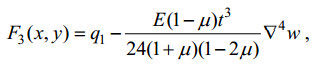
再将F3(x, y)代回(49), 有
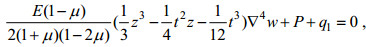 (50)
(50)将条件(47)代入式(50), 有
 (51)
(51)这就是弹性薄板小挠度弯曲中面微分方程。它是在没有采用假设(3)的情况下由弹性体几何方程、物理方程和静力平衡方程推导成立的。
为了与经典的克希霍夫方程(1)及(2)式相对照, 引入符号DFF代表新的挠曲刚度,
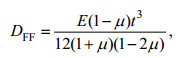 (52)
(52)则挠曲方程(51)可写成
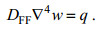 (53)
(53)这个结果显示新建立的方程(52)与克希霍夫方程(1)具有同等的数学简洁性。至于就数值影响而言, 试取泊松比μ=0.25, 则有
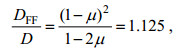 (54)
(54)对此, 新挠曲方程(52)中的挠曲刚度(因子DFF)要比经典克希霍夫挠曲方程的D值大12.5%。
2 讨论 2.1 本文推导的弹性薄板小挠度弯曲方程无需垂向应力为0的假设在弹性薄板小挠度弯曲方程的推导中假设垂直薄板方向的应力为0(钱伟长等, 1956), 鉴于薄板厚度相对很小, 而且获得的克希霍夫挠曲方程具有简介的数学形式, 至今仍是广泛采用的经典公式(柳春图等, 2001;刘人通, 2002)。但在本文的上述推导表明, 这个假设可以省去, 而且本文公式(43)及(44)还表明假设条件式(3)也并不成立。在岩石圈挠曲的研究中, 虽然很早就确认了岩石圈是在冰川、火山岛屿等负载的作用下发生挠曲的, 其挠曲可以近似地采用弹性薄板来拟合(Gunn, 1949; Walcott, 1970), 但在其挠曲方程的推导中仍继承了克希霍夫挠曲方程, 这就默认了垂向应力为0的假设, 并认为薄板的表面无应力、而且薄板厚度很薄, 因此可以假设薄板上下垂向应力均为0(特科特等, 1986; Turcotte et al., 2014)。也曾有人对岩石圈挠曲中采用垂向应力为0的假设提出疑问(金昱等, 2002), 但未解决该问题。而本文推导的岩石圈挠曲方程则不需要这一假设, 并且解决了这一问题。
2.2 在岩石圈挠曲研究中的应用在俯冲带海沟、大洋岛屿等相对简单的负载下, 可以直接采用岩石圈挠曲方程和海底地形来计算挠曲参数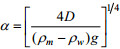
若采用本文推导的岩石圈挠曲新方程, 则由其挠曲刚度DFF之值得到的岩石圈弹性厚度值TFF与克希霍夫挠曲方程计算得到的弹性厚度值Te的关系式为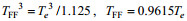
上述表明, 虽然本文推导的岩石圈挠曲新方程的挠曲刚度值DFF与“经典的”D值有明显的不同, 但从DFF及D值进一步计算的岩石圈有效弹性厚度值之间相差很小, 仅有不到4%的差别。但鉴于新挠曲方程无需垂向应力为0的假设, 这一假设在岩石圈动力学研究中是无法得到合理解释的, 采用新挠曲方程计算的TFF显然更合理, 而且只需将已有的岩石圈Te值做约4%的校正即可, 并不要求推翻已有的岩石圈Te研究中有关的方法。
实际上岩石圈有效弹性厚度是为了研究和比较岩石圈在不同构造背景(即不同应力状态和负载)下挠曲响应的参数, 进而分析其动力学性质, 在物质上是不存在的, 因此本文提出的岩石圈TFF值虽然比Te值更合理, 但不会在实际应用中给出显著不同的结论。
2.3 新挠曲方程有待于三维数值模拟或光弹性法实验的验证本文推导的弹性薄板小挠度弯曲的新方程在弹性力学中也可得到应用, 例如对于同样弹性模量的材料、同样负载、同样挠曲(或弯曲)的情况下, 本方程得到的材料厚度比相对经典克希霍夫方程得到的材料的厚度可以降低约4%。
与岩石圈挠曲中的应用不同, 本文推导的新挠曲方程可以通过三维数值模拟或光弹性法模拟(曾佐勋等, 1992)来验证, 分析垂向应力的影响, 这有待于业内专家的研究工作。
3 结论与岩石圈挠曲——弹性薄板小挠度弯曲中垂向应力为0的假设不同, 本文在不需要假设岩石圈垂向应力为0的假设, 推导了新的岩石圈-弹性薄板挠曲方程, 在数学形式上与经典的克希霍夫挠曲方程一样, 但新的挠曲刚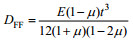
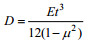
刘人通. 2002. 弹性力学. 西安: 西北工业大学出版社, 153-159
|
杨安, 付永涛, 李安春. 2016. 卡罗琳板块及其附近地区的岩石圈有效弹性厚度. 地球物理学报, 59(9): 3280-3290 |
金煜, 姜效典. 2002. 岩石圈动力学. 北京: 科学出版社, 72
|
柳春图, 蒋持平. 2001. 板壳断裂力学. 北京: 国防工业出版社, 16-22
|
钱伟长, 叶开沅. 1956. 弹性力学. 北京: 科学出版社, 253-260
|
特科特D L, 舒伯特G编著, 韩贝传等译, 1986.地球动力学-连续介质物理在地质问题上的应用.北京: 地震出版社, 102-124
|
曾佐勋, 刘立林. 1992. 构造模拟. 武汉: 中国地质大学出版社, 3
|
Forsyth D W, 1985. Subsurface loading and estimates of the flexural rigidity of continental lithosphere. Journal of Geophysical Research:Solid Earth, 90(B14): 12623-12632 DOI:10.1029/JB090iB14p12623 |
Gunn R, 1949. Isostasy:extended. The Journal of Geology, 57(3): 263-279 DOI:10.1086/625608 |
Jeffreys H, 1945. Types of isostatic adjustment. American Journal of Science, 243-A Daly: 352-359
|
Jin Y, McNutt M K, Zhu Y S, 1994. Evidence from gravity and topography data for folding of Tibet. Nature, 371(6499): 669-674 DOI:10.1038/371669a0 |
Kalnins L M, Watts A B, 2009. Spatial variations in effective elastic thickness in the Western Pacific Ocean and their implications for Mesozoic volcanism. Earth and Planetary Science Letters, 286(1-2): 89-100 DOI:10.1016/j.epsl.2009.06.018 |
McKenzie D P, Bowin C, 1976. The relationship between bathymetry and gravity in the Atlantic Ocean. Journal of Geophysical Research, 81(11): 1903-1915 DOI:10.1029/JB081i011p01903 |
McNutt M K, Parker R L, 1978. Isostasy in Australia and the evolution of the compensation mechanism. Science, 199(4330): 773-775 DOI:10.1126/science.199.4330.773 |
Pérez-Gussinyé M, Lowry A R, Watts A B et al, 2004. On the recovery of effective elastic thickness using spectral methods:Examples from synthetic data and from the Fennoscandian Shield. Journal of Geophysical Research:Solid Earth, 109(B10): B10409 |
Timoshenko S, 1958. Strength of Materials. Part Ⅱ. Advanced Theory and Problems. New York: D. Von Nostrand Co., 76-144
|
Turcotte D L, Schubert G, 2014. Geodynamics. Cambridge: Cambridge University Press, 131-162
|
Vening-Meinesz F A, 1948. Gravity Expeditions at Sea 1923-1938. IV. Complete Results with Isostatic Reduction, Interpretation on the Results. Delft: The Netherlands Geodetic Commission, 18-24
|
Walcott R I, 1970. Flexural rigidity, thickness, and viscosity of the lithosphere. Journal of Geophysical Research, 75(20): 3941-3954 DOI:10.1029/JB075i020p03941 |
Watts A B, 1978. An analysis of isostasy in the world's oceans 1.Hawaiian-Emperor Seamount Chain. Journal of Geophysical Research:Solid Earth, 83(B12): 5989-6004 DOI:10.1029/JB083iB12p05989 |
Watts A B, 2001. Isostasy and Flexure of the Lithosphere. Cambridge: Cambridge University Press, 87-221
|
Watts A B, Talwani M, 1974. Gravity anomalies seaward of deep-sea trenches and their tectonic implications. Geophysical Journal International Royal Astronomical Society, 36(1): 57-90 DOI:10.1111/j.1365-246X.1974.tb03626.x |
Yang A, Fu Y T, 2018. Estimates of effective elastic thickness at subduction zones. Journal of Geodynamics, 117: 75-87 DOI:10.1016/j.jog.2018.04.007 |
 2020, Vol. 51
2020, Vol. 51


