
中国海洋湖沼学会主办。
文章信息
- 杨兵, 侯一筠. 2020.
- YANG Bing, HOU Yi-Jun. 2020.
- 基于高分辨率风场的海洋近惯性能通量计算——时空特征及其影响因素
- WIND-GENERATED NEAR-INERTIAL ENERGY FLUX TO THE OCEANS——THE SPATIAL-TEMPORAL VARIATIONS AND IMPACT FACTORS
- 海洋与湖沼, 51(5): 978-990
- Oceanologia et Limnologia Sinica, 51(5): 978-990.
- http://dx.doi.org/10.11693/hyhz20200100018
文章历史
-
收稿日期:2020-01-15
收修改稿日期:2020-02-27
2. 中国科学院海洋环流与波动重点实验室 青岛 266071;
3. 中国科学院海洋大科学研究中心 青岛 266071;
4. 青岛海洋科学与技术试点国家实验室海洋动力过程与气候功能实验室 青岛 266237;
5. 中国科学院大学 北京 100049
2. CAS Key Laboratory of Ocean Circulation and Waves, Chinese Academy of Sciences, Qingdao 266071, China;
3. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
4. Laboratory for Ocean and Climate Dynamics, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China;
5. University of Chinese Academy of Sciences, Beijing 100049, China
近惯性运动是指频率接近局地惯性频率(f0)的海洋运动, 它是地球自转导致的海洋本征频率运动。近惯性运动的频率通常为1.0f0—1.2f0, 其水平和垂向尺度的量级分别为102km和102m, 其持续时间通常为5—10个局地惯性周期。近惯性运动的能量是海洋能量谱的重要组成部分, 它不仅是上层海洋混合的推动因素, 还是海洋内部混合的重要能量源(Jing et al, 2010), 因此是目前海洋内波和混合研究的核心内容之一。近惯性运动的生成机制包括大气风场、非线性波波相互作用、海底地形处的山后波和大尺度环流失去稳定后的地转适应过程(Yang et al, 2014; Alford et al, 2016)。目前的研究认为, 大气风场是近惯性运动最主要的能量源, 尤其是风场中快速变化的部分(Pollard, 1970; Alford et al, 2016; Yang et al, 2019)。准确估计风场向海洋的近惯性能通量有助于评估海洋内部混合的能量源, 对海洋能量收支和海洋混合研究有重要的科学意义。
维持全球海洋层化需要外界机械能带来的海洋内部混合, 海洋内部混合需要的机械能输入功率约为2.1TW(1TW=1012W), 其中天文潮向内潮的转化可以为海洋内部混合提供约1TW的能量(Egbert et al, 2000), 而风场被认为是该机械能的另一个重要来源(Munk et al, 1998; Carter et al, 2012)。风场向海浪和Ekman流输入的能量主要激发上层海洋的混合, 因此不能为海洋内部混合提供大量的能量(Wang et al, 2004a, b)。而风场向海洋输入的近惯性能量则可以通过近惯性内波的形式向海洋内部传播(Yang et al, 2015; 张骞等, 2019), 因此近惯性能量被认为是海洋内部混合的潜在能量源(Alford et al, 2016)。已有研究指出, 风场向全球海洋输入近惯性能量的功率在0.29—0.70TW之间(Alford, 2001, 2003; Watanabe et al, 2002; Furuichi et al, 2008; Simmon et al, 2012)。
中尺度涡旋是影响近惯性运动的重要因子, 其相对涡度场对近惯性运动存在显著影响。当中尺度涡旋存在时, 海洋的局地惯性频率(f0)被有效科氏频率(fe)取代, 即
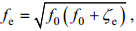 (1)
(1)其中, ζe为中尺度涡旋的涡度。在气旋涡中, 近惯性运动会发生频率“蓝移”, 即其频率偏移至略大于局地惯性频率, 此时近惯性能量会被气旋涡辐散出去。在反气旋涡中, 近惯性运动会发生频率“红移”, 即其频率会偏移至略小于局地惯性频率, 此时近惯性运动会被捕获在反气旋涡中从而持续较长时间(Kunze, 1985; D’Asaro, 1995; Klein et al, 2004; 梁辉, 2016)。
已有研究对近惯性能通量估计所用的风场资料时间分辨率为6h(Alford, 2001, 2003; Watanabe et al, 2002; Furuichi et al, 2008), 该时间分辨率对风场的近惯性频段刻画不足, 这导致估计的近惯性能通量不准确。而风场时间分辨率是影响海洋近惯性能通量的重要因子(Jiang et al, 2005; Rimac et al, 2013), 另外混合层厚度、模型参数的选取和海洋表面涡度等也是可能的影响因素。本文利用高时间分辨率风场资料、气候态月平均混合层厚度和高度计海面高度异常资料来更准确地估计风场向海洋的近惯性能通量, 并探讨混合层厚度、风场时间分辨率、经验衰减系数和中尺度涡旋涡度的作用。本文的结构如下:第一部分介绍所用的研究方法, 第二部分给出本文的计算结, 第三部分为讨论, 第四部分为结论。
1 研究方法风场向海洋近惯性能通量的估计需要风应力和混合层近惯性流数据。在实际观测中, 风应力和混合层流速的同步大范围观测很少, 这使得基于实测数据的近惯性能通量估计难以实现。本文利用CFSR再分析风场驱动混合层阻尼平板模型得到混合层近惯性流, 然后估计近惯性能通量。
1.1 风场的验证和风应力计算本文选用的风场资料为美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)发布的高分辨率CFSR(Climate Forecast System Reanalysis)再分析风场资料。该风场资料的时间分辨率为1h, 空间分辨率约为38 km。为验证CFSR风场资料的有效性, 选取美国国家浮标中心(NBDC)的浮标实测风场数据和CFSR风场资料作对比(图 1)。风场资料对比选用的浮标观测位于太平洋东部(34°15'53"N, 120°28'37"W), 浮标观测风场的时间范围为2000年。CFSR风场和实测风场的变化趋势基本一致, 但是CFSR风场对极值风速的刻画偏小。浮标实测风场和CFSR风场的散点图证实了这一点, CFSR风场是实测风场的84%左右。功率谱表明, CFSR资料对风场的近惯性频段变化也偏小, 对高频段的风场变化则偏小的更多。风场向海洋的近惯性能通量同风场的惯性频段变化密切相关, 鉴于CFSR风场比实测风场的谱密度小, 本文根据风场验证结果将CFSR风场放大1.19倍(1/0.84)后再用于估计近惯性能通量。
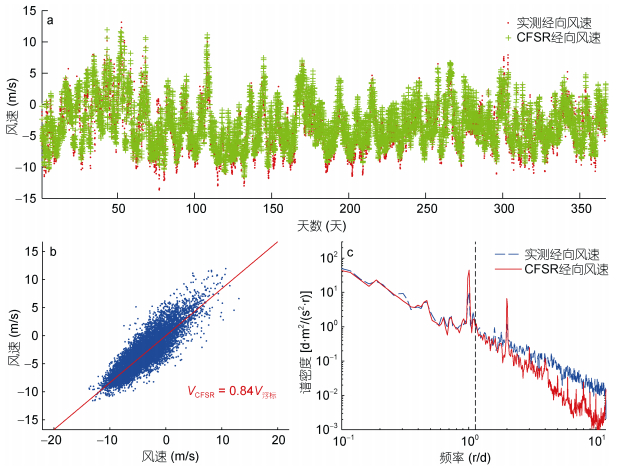 |
| 图 1 浮标实测和CFSR经向风速的时间序列(a)、散点图(b)和功率谱(c) Fig. 1 Time series (a), scatter plot (b) and power spectra (c) of buoy observed and CFSR wind 注: a横坐标为2000年的天数; VCFSR表示CFSR经向风速; V浮标表示浮标实测经向风速 |
风应力(τ)的计算采用参数化公式
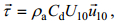 (2)
(2)其中,ρa为大气密度, Cd为拖曳系数, U10和u10分别为海面10m处的风速大小和风速矢量。大气密度通常取为1.25kg/m3。拖曳系数的计算使用经验公式
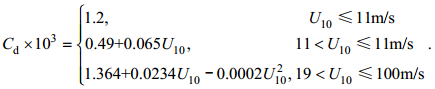 (3)
(3)该拖曳系数经验公式同时适用于低、中、高风速的情形(Oey et al, 2006)。
1.2 阻尼平板模型阻尼平板模型被广泛应用于混合层近惯性流的计算, 本文也采用该模型。该模型假设风应力均匀作用于整个海洋上混合层, 上混合层的运动满足
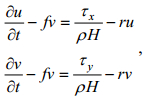 (4)
(4)其中, u、v为混合层流速, f为科氏频率, τx, τy为风应力, ρ=1024kg/m3为海水密度, H为混合层厚度, r为经验衰减系数, 用于参数化混合层底部混合和近惯性能量下传等过程引起的混合层近惯性能量损失。因为赤道附近海域的科氏频率较小, 阻尼平板模型在赤道附近并不适用, 本文将阻尼平板模型应用于赤道以南和以北5°以外的海域。海洋混合层厚度选用气候态月平均资料(Levitus et al, 1994)。阻尼平板模型的解包括近惯性流和Ekman流, 本文利用带通滤波得到提取模型输入结果中的近惯性流。由于f随纬度变化, 将r取为局地科氏频率f0的倍数是符合近惯性运动衰减规律的(Alford, 2001, 2003)。
1.3 近惯性能通量的计算风场向海洋混合层的近惯性能通量(Π)通过式(5)计算:
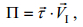 (5)
(5)其中, τ为大气风应力, 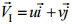
图 2给出了实测近惯性流速和模拟近惯性流速的对比, 以及实测和基于模拟得到的近惯性能通量和累积近惯性能量密度的对比。实测风场来自上文介绍的浮标观测风场数据, 该浮标观测位于太平洋东部, 浮标观测的时间范围为2000年。模拟的近惯性流和实测近惯性流在位相上契合很好, 但是在振幅上存在略微的偏差。模拟和实测的近惯性能通量和累积近惯性能量密度则十分接近, 这表明利用阻尼平板模型估计近惯性能通量是可行的。此处选取的经验衰减系数为r=0.25f0, 鉴于模拟和实测比较相符, 因此本文选取r=0.25f0来估计近惯性能通量。
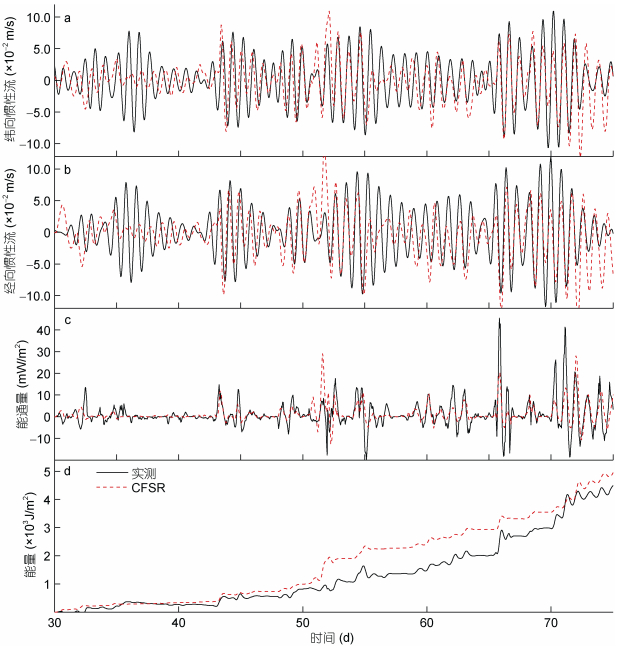 |
| 图 2 实测和模拟的纬向(a)和经向(b)近惯性流、近惯性能通量(c)和累积近惯性能量密度(d) Fig. 2 Time series of observed and modeled zonal (a) and meridional (b) near-inertial currents, near-inertial energy flux (c), and cumulative near-inertial energy density (d) 注:黑色实线为潜标实测结果, 红色虚线为阻尼平板模型的模拟结果。 |
近惯性能通量的估计和混合层厚度、风场时间分辨率、经验衰减系数以及科氏频率等有关。风场时间分辨率的影响通过将风场再取样为3h和6h时间分辨率来探究。模式验证和已有的研究表明, 经验衰减系数r取为0.25, 对海洋近惯性运动衰减的刻画较准确, 本文同时将r取为0.2f0和0.3f0来探究该因子的作用。海洋的有效科氏频率受中尺度涡旋涡度的影响, 此处通过AVISO海面高度异常资料计算中尺度涡旋的涡度ζe。然后, 利用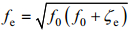
| 序号 | 经验衰减系数 r |
混合层厚度 | 风场分辨率(h) | 科氏参数 |
| 1 | 0.25f0 | 气候态 | 1 | f0 |
| 2 | 0.25f0 | *50m | 1 | f0 |
| 3 | 0.25f0 | 气候态 | *3 | f0 |
| 4 | 0.25f0 | 气候态 | *6 | f0 |
| 5 | *0.20f0 | 气候态 | 1 | f0 |
| 6 | *0.30f0 | 气候态 | 1 | f0 |
| 7 | *0.25fe | 气候态 | 1 | *fe |
| 注: *表示各个实验与对照实验配置不同的参数; f0表示海洋的局地惯性频率; fe表示有效科氏频率 | ||||
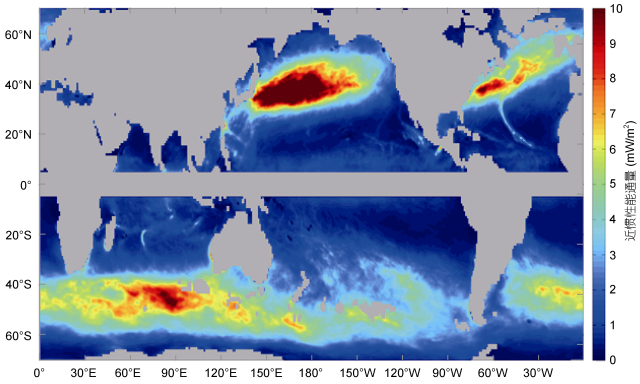
全球年平均近惯性能通量的空间分布见图 3。南、北半球的中纬度海洋是近惯性能通量最强的海域, 这说明中纬度西风带大气风场能够有效驱动混合层近惯性运动。在北半球, 太平洋和大西洋中纬度海盆西部是近惯性能通量最大的海域, 而且海盆西部的能通量显著大于海盆东部。在北大西洋的中纬度, 近惯性能通量的高值区主要集中在北美东部海域, 该海域混合层厚度偏小是其原因之一。北太平洋中纬度海盆西部的年平均近惯性能通量最大超过10mW/m2(1mW/m2=10-3W/m2), 而北大西洋中纬度海盆西部的能通量可以达到22mW/m2。在南半球, 整个南大洋的近惯性能通量都比较强, 而且在非洲东南部、澳洲南部和南美洲东南部海域存在能通量的极值。本研究得到的近惯性能通量空间分布特征和已有的研究结果(Jiang et al, 2005; Simmon et al, 2012; Rimac et al, 2013)基本一致, 但是本研究得到的年平均近惯性能通量中仍然可以看到热带气旋激发的近惯性能通量, 尤其是在北大西洋和印度洋。所以本文所用的1h时间分辨率风场资料可以分辨出热带气旋的风场, 这也使得本文的估计更加合理。
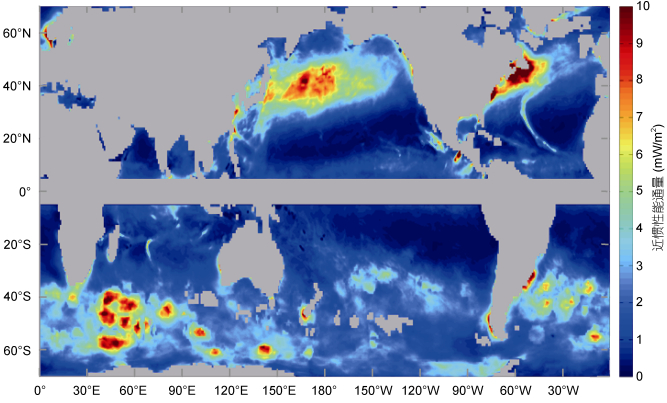 |
| 图 3 年平均近惯性能通量(单位: mW/m2; 1mW/m2=10-3W/m2) Fig. 3 Annual mean near-inertial energy flux (unit: mW/m2; 1mW/m2=10-3W/m2) |
近惯性能通量呈现显著的季节变化(图 4), 而且该季节变化在北半球和南半球的表现并不相同。在北半球, 近惯性能通量在北半球的冬季最强, 秋季次之, 春季和夏季则较弱。在南半球, 近惯性能通量在南半球的冬季和春季较强, 而在夏季和秋季较弱。该季节变化特征和前人的研究结果一致(Alford, 2001, 2003; Watanabe et al, 2002; Furuichi et al, 2008), 即近惯性能通量在各个半球的冬季较强, 而在夏季较弱。风场时间分辨率提高带来的提升是在各个半球的夏季, 热带气旋活动频繁, 其对近惯性能通量的贡献明显且被很好估计出来。虽然热带气旋引起的近惯性能通量持续时间较短(通常不超过1个月)、且覆盖范围较小(集中在热带气旋路径两侧), 但是季节平均的近惯性能通量表明, 其对全球近惯性能通量的贡献不容忽视(钱奇峰等, 2012)。季节平均近惯性能通量的空间分布表明, 北太平洋和北大西洋中纬度海盆西部、非洲东南部的南大洋是全球近惯性能通量最强的三个海域。
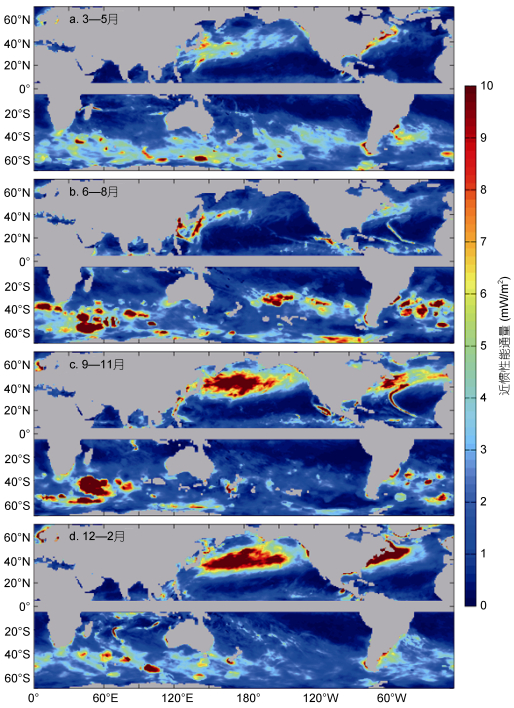 |
| 图 4 近惯性能通量的季节变化 Fig. 4 Seasonal variation of near-inertial energy flux |
纬向平均近惯性能通量的季节平均和年平均见图 5。年平均的近惯性能通量表明, 北半球中纬度是全球近惯性能通量最强的海域, 该海域从30°N一直持续到60°N, 该海域近惯性能通量超过3mW/m2。在南半球, 年平均近惯性能通量同样在中纬度最强, 其大致纬度范围为35°—60°S, 该海域近惯性能通量接近3mW/m2。年平均的近惯性能通量在42°N最强, 约为5mW/m2, 在南半球中纬度约为3mW/m2, 而在低纬度海域仅为1mW/m2左右。纬向平均的近惯性能通量在北半球存在显著的季节变化, 表现为秋季和冬季较强、春季和夏季较弱。在北半球中纬度, 春季和夏季的近惯性能通量不超过3mW/m2, 而在秋季和冬季最大值接近8mW/m2。北半球纬向平均近惯性能通量的极大值冬季出现在42°N, 秋季出现在45°N。而在南半球, 纬向平均近惯性能通量的季节变化则不显著, 仅在南半球冬季出现能通量的略微加强, 这说明南半球不同季节的近惯性能通量存在空间变化, 导致纬向平均后近惯性能通量的季节变化不显著。
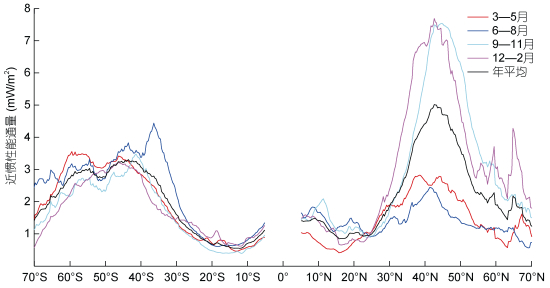 |
| 图 5 纬向平均近惯性能通量的季节平均和年平均 Fig. 5 Seasonal and annual mean of zonal mean near-inertial energy flux |
南、北半球和全球积分的近惯性能量输入功率见图 6。全球近惯性能量输入功率随月份变化, 且在4月份最小为0.47TW, 而在12月份最大为0.70TW。北半球近惯性能量输入功率在冬季和秋季超过0.2TW, 而在春季和夏季则小于0.2TW, 在12月达到最大值0.41TW。南半球近惯性能量输入功率则在大部分月份都超过0.3TW, 仅在10—12月不足0.3TW。在1—9月份, 南半球的能量输入功率大于北半球, 在10—12月份则反之。全球年平均近惯性能量输入功率约为0.56TW, 其中北半球和南半球贡献分别为0.22TW和0.34TW。北半球和南半球的平均近惯性能通量分别为2.02和1.90mW/m2, 全球平均的能通量为1.94mW/m2。南半球的平均能通量小于北半球, 而能量输入功率则大于北半球, 这是因为南半球海洋面积比北半球大。表 2总结了实验1得到的全球平均近惯性能量输入功率和近惯性能通量。
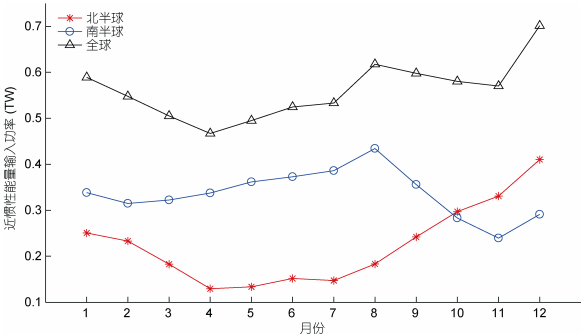 |
| 图 6 实验1得到的北半球、南半球和全球积分的近惯性能量输入功率 Fig. 6 The North Hemisphere, South Hemisphere, and global mean near-inertial power input obtained from the experiment 1 |
| 区域 | 总功率(TW) | 平均能通量(mW/m2) |
| 北半球 | 0.22 | 2.02 |
| 南半球 | 0.34 | 1.90 |
| 全球 | 0.56 | 1.94 |
在风速一定时, 混合层越深, 风场在混合层驱动的近惯性流就越弱, 近惯性能通量就越小; 反之亦然。在实际海洋中, 较强的风场通常激发较强的海洋混合, 因此强风和较厚的混合层往往伴随发生。为探究混合层厚度对近惯性能通量的影响, 此处将混合层厚度取为常数50m, 此时近惯性能通量的时空变化主要由风场的变化引起。
混合层厚度为常数时, 近惯性能通量的纬向变化减弱, 此时近惯性能通量在纬向大致呈带状分布, 尤其是在南大洋(图 7)。这说明混合层厚度的空间变化是中纬度近惯性能通量东西不对称的原因之一。在北半球中纬度, 海盆西部的近惯性能通量依旧强于海盆东部, 这意味着风场的纬向变化是北半球中纬度海盆近惯性能通量东西不对称的另一个原因。混合层为常数时, 北大西洋的近惯性能通量变得明显小于北太平洋, 这表明北太平洋的风场强于北大西洋。在实际海洋中(图 3和图 4), 北太平洋和北大西洋的近惯性能通量接近, 这意味着北大西洋的混合层厚度小于北太平洋。所以, 北太平洋和北大西洋中纬度海域近惯性能通量都很强是风场和混合层厚度共同作用的结果。混合层为常数时, 在南大洋, 风场在60°—110°E激发的近惯性能通量最强, 而在南太平洋激发的能通量最弱。由于南大洋风场的纬向变化较小, 因此混合层厚度对南大洋近惯性能通量的空间变化起主导作用。
 |
| 图 7 混合层厚度为50m时的年平均近惯性能通量 Fig. 7 Annual mean near-inertial energy flux with uniform mixed layer thickness of 50 m |
风场时间分辨率对近惯性能通量的影响主要取决于该时间分辨率能否有效地刻画风场在局地惯性频率附近的变化。近惯性运动的频率自赤道向两极逐渐变大, 即运动的周期逐渐减小。近惯性运动的周期T和纬度φ的关系为
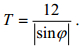 (6)
(6)式(6)计算得到的近惯性运动周期的单位为h。在低纬度海域, 局地惯性周期较大, 因此该海域近惯性能通量的计算对风场时间分辨率的要求相对较低。然而, 在高纬度海域, 局地惯性周期较小(例如南北纬60°处惯性周期约为13.86h), 此时近惯性能通量的计算对风场的时间分辨率要求相对较高。
将风场再取样为3h和6h分辨率时计算得到的年平均近惯性能通量和1h风场计算结果的绝对和相对变化分别见图 8和图 9。可以看出, 风场时间分辨率的降低导致近惯性能通量估计的降低, 尤其是在近惯性能通量较强的中纬度海洋。在中纬度海域, 3h风场计算的能通量比1h风场的结果偏小0.5—2.0mW/m2; 而6h风场计算的能通量比1h风场的结果偏小达1.0—4.0mW/m2。在北半球中纬度, 3h风场计算的近惯性能通量比1h风场的计算结果偏低5%—15%, 6h风场计算的近惯性能通量比小时风场的计算结果偏低20%—40%。在南大洋, 3h风场计算的近惯性能通量比1h风场的计算结果偏低15%—30%, 而6h风场计算的近惯性能通量比1h风场的计算结果偏低达到40%—60%。3h风场计算得到的全球近惯性能量输入功率为0.49TW, 比1h风场的结果偏低约13%;而6h风场计算的能量输入功率为0.39TW, 比1h风场的结果偏低达到30%。3h和6h风场计算得到的全球和南北半球近惯性能量输入功率以及平均能通量的具体信息见表 3。
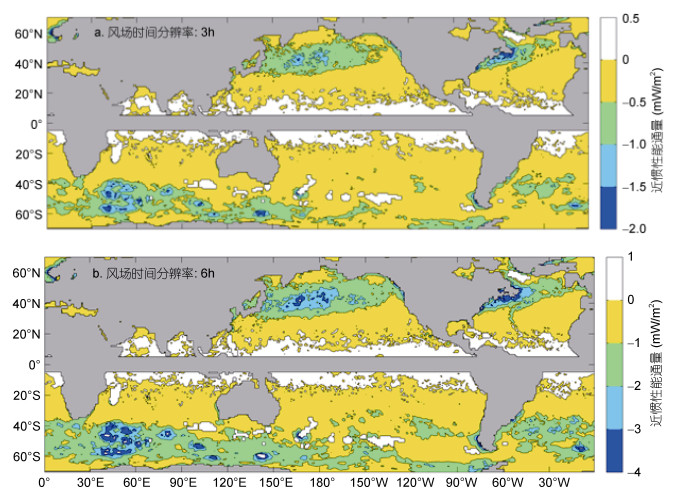 |
| 图 8 时间分辨率3h(a)和6h(b)风场同时间分辨率1h风场计算得到的年平均近惯性能通量的差值 Fig. 8 Difference of annual mean near-inertial energy flux in 3-hour (a), 6-hour (b) and 1-hour temporal resolution wind |
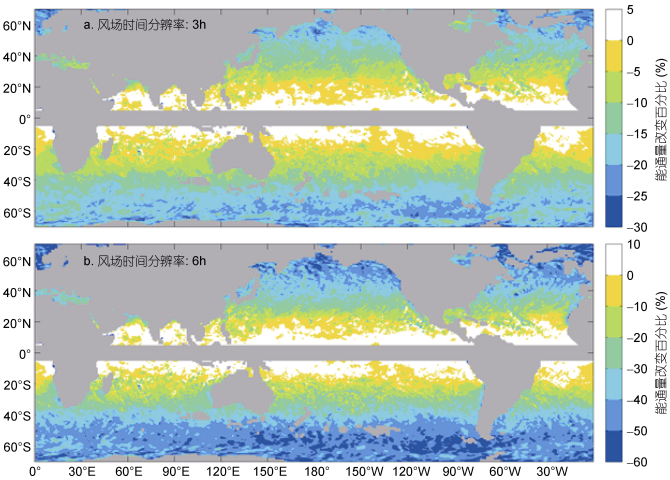 |
| 图 9 时间分辨率3h(a)和6h(b)风场相对时间分辨率1h风场计算得到的年平均近惯性能通量改变的百分比 Fig. 9 Relative difference of annual mean near-inertial energy flux in 3-hour (a), 6-hour (b) and 1-hour temporal resolution wind |
| 区域 | 总功率(TW) | 平均能通量(mW/m2) | |||
| 6h分辨率风场 | 3h分辨率风场 | 6h分辨率风场 | 3h分辨率风场 | ||
| 北半球 | 0.17 | 0.20 | 1.52 | 1.83 | |
| 南半球 | 0.22 | 0.29 | 1.27 | 1.66 | |
| 全球 | 0.39 | 0.49 | 1.36 | 1.72 | |
经验衰减系数r是决定混合层近惯性运动衰减的重要参数。图 10展示了r为0.2f0和0.3f0时的近惯性能通量同r为0.25f0时近惯性能通量的差值。可以看出, 较小的r会引起近惯性能通量的增强, 而较大的r会导致近惯性能通量的减弱。当经验衰减系数r为0.2f0时, 中纬度近惯性能通量增加约0.1—0.4mW/m2; 当经验衰减系数r为0.3f0时, 中纬度近惯性能通量降低约0.2—0.4mW/m2。当经验衰减系数r为0.2f0时, 全球近惯性能量输入功率为0.59TW, 比r为0.25f0时增大约5%;而当经验衰减系数r为0.3f0时, 全球近惯性能量输入功率为0.53TW, 比r为0.25f0时减小约5%。考虑到经验衰减系数的取值范围通常为0.2f0—0.3f0, 所以经验衰减系数对近惯性能量输入功率计算的影响较小。r为0.2f0和0.3f0时的近惯性能量输入功率和全球平均近惯性能通量见表 4。
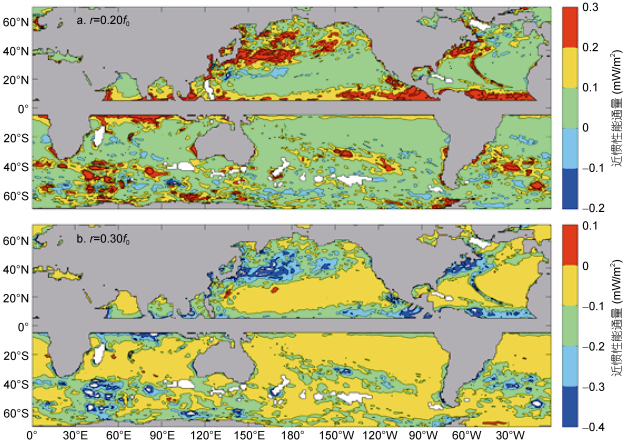 |
| 图 10 经验衰减系数r=0.2f0(a)和r=0.3f0(b)时的近惯性能通量同r=0.25f0时的近惯性能通量的差值 Fig. 10 Difference of near-inertial energy flux between experiments with r=0.2f0 (a), r=0.3f0 (b), and experiment with r=0.25f0 |
| 区域 | 总功率(TW) | 平均能通量(mW/m2) | |||
| 0.2f0 | 0.3f0 | 0.2f0 | 0.3f0 | ||
| 北半球 | 0.24 | 0.21 | 2.13 | 1.89 | |
| 南半球 | 0.35 | 0.32 | 1.97 | 1.80 | |
| 全球 | 0.59 | 0.53 | 2.03 | 1.84 | |
中尺度涡旋涡度的存在能够改变局地有效科氏频率, 而有效科氏频率决定风场和大气之间共振响应的频率, 进而影响近惯性能通量。值得注意的是, 中尺度涡旋的多发海域和近惯性能通量较强的海域都出现在中纬度地区, 这也是本文考虑中尺度涡旋涡度对近惯性能通量影响的原因。在中尺度涡旋频发的中纬度海域, 考虑中尺度涡旋涡度时, 计算得到的近惯性能通量同时存在增强与减弱(图 11)。在热带海域, 由于科氏频率非常小, 因此更容易受到中尺度涡旋涡度的影响, 进而改变近惯性能通量。中尺度涡旋的涡度能够改变近惯性能通量, 但其引起的近惯性能通量变化较小, 在中纬度海域仅为0.4—0.8mW/m2, 这比全球平均能通量小一个数量级。这和海洋中的相对涡度比行星涡度小1—2个数量级有关。考虑中尺度涡旋涡度时, 南半球近惯性能量输入功率减小0.01TW, 而北半球的近惯性能量输入功率则无变化, 因此中尺度涡旋涡度对近惯性能通量的影响可以忽略。考虑中尺度涡旋涡度时计算得到的全球近惯性能量输入功率和平均近惯性能通量见表 5。
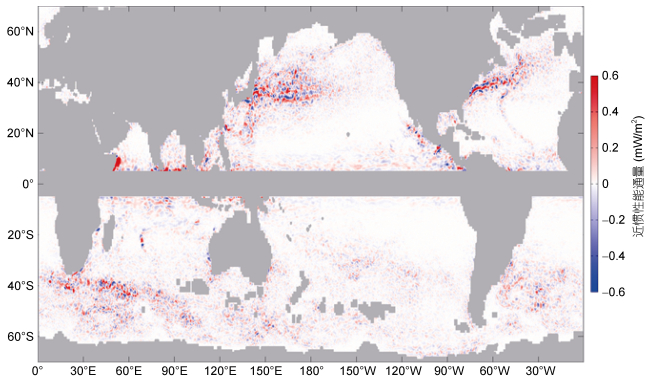 |
| 图 11 考虑与未考虑中尺度涡旋涡度计算得到的年平均近惯性能通量之差 Fig. 11 Difference of annual mean near-inertial energy flux with and without consideration of mesoscale eddy |
| 区域 | 总功率(TW) | 平均能通量(mW/m2) |
| 北半球 | 0.22 | 2.02 |
| 南半球 | 0.33 | 1.88 |
| 全球 | 0.55 | 1.93 |
本文的结果表明, 在影响近惯性能通量估计的因素中风场资料的时间分辨率是最重要的。本文所用风场的时间分辨率为1h, 因此该风场资料可以在高纬度海域也能较好的再现风场在局地惯性频段的变化。得益于风场资料的高时间分辨率, 本文计算的近惯性能通量覆盖70°N—70°S的海域, 该范围比之前研究者的覆盖范围要广(Alford, 2001)。
混合层厚度和风场的季节变化是决定近惯性能通量季节变化的主导因素。北半球冬季风场最强, 但冬季的近惯性能量输入和秋季接近, 其原因就是北半球中纬度冬季的混合层厚度较厚。北半球中纬度海盆混合层厚度和风场的纬向变化是海盆西部近惯性能通量高于海盆东部的原因。北大西洋海盆西部的近惯性能通量高值海域主要是混合层较浅导致的。由于南大洋风场的纬向变化较弱, 混合层厚度的纬向变化是近惯性能通量纬向变化的主要原因。
混合层近惯性流速的激发是海洋和风场之间共振响应的结果, 因此近惯性能通量的计算和风场资料中近惯性频段风速密切相关。当利用再取样为3h分辨率的风场时, 计算得到的全球近惯性能量输入功率降低13%;而采用6h分辨率风场时, 计算得到的全球近惯性能量输入功率的降低达到30%。该结果表明, 3h和6h分辨率的风场同1h分辨率风场相比对风场近惯性频段变化的刻画偏弱, 而且该现象在中高纬度尤为严重。因此, 风场时间分辨率是影响算近惯性能通量计算的重要因素。
经验衰减系数r的改变对近惯性能通量的影响表现为, r增大时近惯性能通量减小, 而r减小时近惯性能通量增加。但是当r从0.25f0变化到0.2f0和0.3f0时, 全球近惯性能量输入功率的变化仅为5%。考虑到r的取值范围通常为0.2f0—0.3f0, 因此经验衰减系数对全球近惯性能量输入功率估计的影响较小。另外, 中尺度涡旋的涡度仅仅能够改变局部海域近惯性能通量的空间变化, 但是对全球海洋的近惯性能量输入功率几乎没有影响。各个实验中得到的全球平均近惯性能通量和近惯性能量输入功率的汇总见表 6。
| 序号 | 变化参数 | 总功率(TW) | 平均能通量(mW/m2) | |||||
| 北半球 | 南半球 | 全球 | 北半球 | 南半球 | 全球 | |||
| 1 | 参照实验 | 0.22 | 0.34 | 0.56 | 2.02 | 1.90 | 1.94 | |
| 2 | 3h风场 | 0.20 | 0.29 | 0.49 | 1.83 | 1.66 | 1.72 | |
| 3 | 6h风场 | 0.17 | 0.22 | 0.39 | 1.52 | 1.27 | 1.36 | |
| 4 | r=0.2f0 | 0.24 | 0.35 | 0.59 | 2.13 | 1.97 | 2.03 | |
| 5 | r=0.3f0 | 0.21 | 0.32 | 0.53 | 1.89 | 1.80 | 1.84 | |
| 6 | f=fe | 0.22 | 0.33 | 0.55 | 2.02 | 1.88 | 1.93 | |
| 注: f表示科氏频率; r表示经验衰减系数 | ||||||||
本文基于高时间分辨率CFSR再分析风场、气候态海洋上混合层厚度和卫星高度计海面高度异常(Sea Level Anomaly, SLA)资料, 利用阻尼平板模型估计了全球风场向海洋输入近惯性能量的能通量和功率。本文所用风场的时间分辨率是目前可获取的再分析风场中最高的, 高时间分辨率有助于更准确的估计风场向海洋的近惯性能通量。本文给出了近惯性能通量的空间分布和时间变化特征, 并讨论了海洋上混合层厚度、风场时间分辨率、阻尼平板模型中的经验衰减系数和海洋中尺度涡旋涡度对近惯性能通量和能量输入功率估计的影响。
再分析风场和实测风场的时间序列和功率谱表明, CFSR风场资料对极值风速和风场高频段的刻画较实测风场偏小。本文根据CFSR风场和实测风场的统计特征, 将CFSR风场进行了加强。模型验证表明, 阻尼平板模型能够较好地模拟出风场驱动的混合层近惯性流, 且基于该模拟流速计算的风场近惯性能通量和实测结果基本一致。
风场向海洋的近惯性能通量在南、北半球的西风带海域最强, 尤其是南大洋。这说明西风带的风场能够有效的驱动海洋近惯性运动。近惯性能通量在各个半球的冬季最强, 夏季最弱, 这和西风带风场的季节变化是一致的。全球风场向海洋输入近惯性能量的功率为0.56TW, 其中北半球为0.22TW, 南半球为0.34TW。全球平均的近惯性能通量为1.94mW/m2, 其中北半球为2.02W/m2, 南半球为1.90mW/m2。
混合层厚度和风场的季节变化是决定近惯性能通量季节变化的主导因素, 而混合层厚度和风场的空间变化导致中纬度海域近惯性能通量的东西不对称。风场的时间分辨率对近惯性能通量的估计特别重要。当风场时间分辨率从1h变为3h时, 估计的近惯性能量输入功率降低13%;而当风场时间分辨率从1h变为6h时, 估计的近惯性能通量降低达到30%。阻尼平板模型中的经验衰减系数对近惯性能通量的影响较小。由于经验衰减系数的取值范围较小, 该参数变化引起的近惯性能通量改变不超过5%。中尺度涡旋的涡度能够一定程度上改变风场近惯性能通量在局部的空间结构, 但是对全球海洋近惯性能量输入功率几乎没有影响。
张骞, 廖光洪, 蔺飞龙, 等. 2019. 南海西北部上层海洋对台风"杜苏芮"的响应分析. 海洋学报, 41(7): 22-35 |
钱奇峰, 江静. 2012. 由热带气旋进入海洋近惯性运动能量的估计. 热带气象学报, 28(4): 471-477 |
梁辉, 郑洁, 田纪伟, 等. 2016. 南海西北陆坡区内潮与近惯性内波观测研究. 海洋学报, 38(11): 32-42 |
Alford M H, 2001. Internal swell generation:the spatial distribution of energy flux from the wind to mixed layer near-inertial motions. J Phys Oceanogr, 31(8): 2359-2368 DOI:10.1175/1520-0485(2001)031<2359:ISGTSD>2.0.CO;2 |
Alford M H, 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophys Res Lett, 30(8): 1424 |
Alford M H, MacKinnon J A, Simmons H L et al, 2016. Near-inertial internal gravity waves in the ocean. Annu Rev Mar Sci, 8: 95-123 DOI:10.1146/annurev-marine-010814-015746 |
Carter G S, Fringer O B, Zaron E D, 2012. Regional models of internal tides. Oceanography, 25(2): 56-65 DOI:10.5670/oceanog.2012.42 |
D'Asaro E A, 1995. Upper-ocean inertial currents forced by a strong storm, Part III:Interaction of inertial currents and mesoscale eddies. J Phys Oceanogr, 25(11): 2953-2958 DOI:10.1175/1520-0485(1995)025<2953:UOICFB>2.0.CO;2 |
Egbert G D, Ray R D, 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature, 405(6788): 775-778 DOI:10.1038/35015531 |
Furuichi N, Hibiya T, Niwa Y, 2008. Model-predicted distribution of wind-induced internal wave energy in the world's oceans. J Geophys Res, 113(C9): C09034 |
Jiang J, Lu Y Y, Perrie W, 2005. Estimating the energy flux from the wind to ocean inertial motions:the sensitivity to surface wind fields. Geophys Res Lett, 32(15): L15610 DOI:10.1029/2005GL023289 |
Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress. Geophys Res Lett, 37(23): L23604 |
Klein P, Lapeyre G, Large W G, 2004. Wind ringing of the ocean in presence of mesoscale eddies. Geophys Res Lett, 31(15): L15306 DOI:10.1029/2004GL020274 |
Kunze E, 1985. Near-inertial wave propagation in geostrophic shear. J Phys Oceanogr, 15(5): 544-565 DOI:10.1175/1520-0485(1985)015<0544:NIWPIG>2.0.CO;2 |
Levitus S, Boyer T P, 1994, World Ocean Atlas 1994, vol, 4, Temperature, Washington: NOAA Atlas, NESDIS
|
Munk W, Wunsch C, 1998. Abyssal recipes II:energetics of tidal and wind mixing. Deep Sea Res Part I:Oceanogr Res Pap, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
Oey L Y, Ezer T, Wang D P et al, 2006. Loop current warming by hurricane Wilma. Geophys Res Lett, 33(8): L08613 |
Pollard R T, 1970. On the generation by winds of inertial waves in the ocean. Deep Sea Res Oceanogr Abstr, 17(4): 795-812 DOI:10.1016/0011-7471(70)90042-2 |
Rimac A, Von Storch J S, Eden C et al, 2013. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophys Res Lett, 40(18): 4882-4886 DOI:10.1002/grl.50929 |
Simmons H L, Alford M H, 2012. Simulating the long-range swell of internal waves generated by ocean storms. Oceanography, 25(2): 30-41 DOI:10.5670/oceanog.2012.39 |
Wang W, Huang R X, 2004a. Wind energy input to the Ekman layer. J Phys Oceanogr, 34(5): 1267-1275 DOI:10.1175/1520-0485(2004)034<1267:WEITTE>2.0.CO;2 |
Wang W, Huang R X, 2004b. Wind energy input to the surface waves. J Phys Oceanogr, 34(5): 1276-1280 DOI:10.1175/1520-0485(2004)034<1276:WEITTS>2.0.CO;2 |
Watanabe M, Hibiya T, 2002. Global estimates of the wind-induced energy flux to inertial motions in the surface mixed layer. Geophys Res Lett, 29(8): 1239 |
Yang B, Hou Y J, 2014. Near-inertial waves in the wake of 2011 Typhoon Nesat in the northern South China Sea. Acta Oceanol Sin, 33(11): 102-111 DOI:10.1007/s13131-014-0559-6 |
Yang B, Hou Y J, Hu P, 2015. Observed near-inertial waves in the wake of typhoon Hagupit in the northern South China Sea. Chin J Oceanol Limnol, 33(5): 1265-1278 DOI:10.1007/s00343-015-4254-z |
Yang B, Hou Y J, Li M, 2019. Response of the western North Pacific subtropical ocean to the slow-moving super typhoon Nanmadol. J Oceanol Limnol, 37(3): 938-956 DOI:10.1007/s00343-019-8114-0 |
 2020, Vol. 51
2020, Vol. 51


