中国海洋湖沼学会主办。
文章信息
- 杜云飞, 张继才, 王道胜. 2020.
- DU Yun-Fei, ZHANG Ji-Cai, WANG Dao-Sheng. 2020.
- 杭州湾三维悬浮泥沙输运模型初始场的伴随法反演研究
- INVERSION OF INITIAL CONDITION OF A THREE-DIMENSIONAL SUSPENDED SEDIMENT TRANSPORT MODEL IN HANGZHOU BAY WITH AN ADJOINT METHOD
- 海洋与湖沼, 51(5): 1025-1042
- Oceanologia et Limnologia Sinica, 51(5): 1025-1042.
- http://dx.doi.org/10.11693/hyhz20191000189
文章历史
-
收稿日期:2019-10-15
收修改稿日期:2019-12-08
2. 中国地质大学(武汉)海洋学院 海洋地质资源湖北省重点实验室 武汉 430074;
3. 南方海洋科学与工程广东省实验室(广州) 广州 511458
2. College of Marine Science and Technology Hubei Key Laboratory of Marine Geological Resources, China University of Geosciences, Wuhan 430074, China;
3. Southern Marine Science and Engineering Guangdong Laboratory(Guangzhou), Guangzhou 511458, China
由于径流输入和局部泥沙再悬浮, 近岸、河口海域通常具有高悬浮泥沙浓度的特征(Yang et al, 2016)。杭州湾作为典型的强潮河口湾, 具有潮流急, 潮差大, 水体含沙量高的显著特征。大量悬浮泥沙的存在和大范围含沙量时间、空间变化的存在, 使杭州湾悬浮泥沙分布比较复杂(中国海湾志编纂委员会, 1992)。因此, 准确了解杭州湾海域悬浮泥沙的时空分布和输运规律, 不仅具有重要的科学价值, 还对杭州湾海域及近岸地区水质、地貌、生态环境、海岸工程、港口建设以及滩涂开发等具有重要意义。数值模拟具有成本低、预报性强、可移植性强、定量的特点, 可有效获取悬浮泥沙的时间和空间分布(Wang et al, 2018b), 从而弥补传统现场观测和卫星遥感观测的不足。因此, 悬沙输运模型已经成为研究泥沙输运的一个有力工具(Papanicolaou et al, 2008)。
随着对泥沙输运机制认知的深入以及科学计算能力的不断进步, 悬沙输运模型从一维发展到了三维。众多学者利用三维悬沙输运模型开展悬浮泥沙的研究工作(Normant, 2000; Dufois et al, 2014; Chen et al, 2015)。三维悬沙输运模型对初始场比较敏感(Wang et al, 2018a), 即悬浮泥沙浓度(suspended sediment concentration, SSC)在数值模拟初始时刻的空间分布直接影响数值模拟的精度, 初始场的空间分布与实际SSC的空间分布越接近, 相应的数值模拟精度越高, 反之则越低。因此, 对于短期的悬浮泥沙数值模拟而言, 初始场的准确给定至关重要(Lee et al, 2007; Yang et al, 2016)。到目前为止, 在悬浮泥沙输运的数值模拟中, 初始场的确定方法主要有四种: (1)假定在整个模型计算区域内为常数分布, 以模型运行稳定时的结果作为最终的模拟结果(Hu et al, 2009; Gourgue et al, 2013); (2)根据现场实测水文资料插值得到(曹振轶等, 2002; Du et al, 2010); (3)由经验、半经验的公式确定(Woolnough et al, 1995; Schwab et al, 2000); (4)用卫星遥感观测资料获得(Chen et al, 2010; Ramakrishnan et al, 2012; Yang et al, 2016)。前三种方法与实际SSC的空间分布偏差较大, 因而数值模拟的精度较差; 随着卫星遥感观测手段的不断发展, 初始场的确定更多依赖于卫星遥感数据及与之相关的反演方法和经验公式。卫星遥感反演方法虽然能够获取海洋表层大面积、连续的SSC, 但由于受到云覆盖或恶劣天气条件的限制, 卫星遥感数据存在不同程度的缺测, 这在一定程度上限制了卫星遥感方法的应用范围和准确度。
伴随同化方法是建立在严格的数学基础上的一种有效的四维变分同化技术, 它将所要解决的实际问题作为最小值问题来解决, 流体力学方程组及其初边值条件作为约束条件, 使得根据具体问题设计的代价函数达到最小(Sasaki, 1970)。伴随同化方法能够充分利用已有的观测资料, 实现观测资料和数值模型的有机结合, 得到更加符合实际的模拟结果, 并能对模型重要参数如初始场、边界条件等进行优化反演。目前为止, 伴随同化方法已广泛应用于海表温度数值模型(马继瑞等, 2002)、风暴潮预报模型(Peng et al, 2006)、海洋生态系统动力学模型(Wang et al, 2013)、海洋环流模型(Song et al, 2016)以及悬沙输运模型(Wang et al, 2018b)等海洋数值模型中初始场的优化反演, 并取得了良好的应用效果。基于此背景, 本文利用Wang等(2018a)构建的一个三维悬沙输运伴随同化模型, 针对模型初始场的优化反演进行一系列孪生实验和实际实验, 孪生实验验证伴随同化方法优化反演模型初始场的有效性并定量评估该模型数据同化的能力; 实际实验则根据孪生实验的结论同化杭州湾海域典型的小潮时期和大潮时期的GOCI卫星遥感资料所得表层SSC数据, 获得模型初始场的最优估计。
1 模型介绍 1.1 正向模型三维悬沙输运模型的控制方程(Wang et al, 2018a):
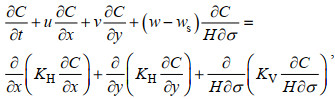 (1)
(1)其中, C是悬浮泥沙浓度, t是时间, x、y是水平坐标, σ是垂向坐标, H是包含静水深和海面起伏的总水深, u、v和w分别是x、y和σ方向的流速, ws为悬浮泥沙的沉降速度, KH和KV分别为水平扩散系数和垂向扩散系数。
初始条件:
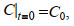 (2)
(2)其中, C0是初始场。
边界条件:
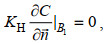 (3)
(3)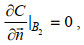 (4)
(4)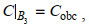 (5)
(5)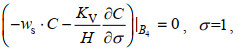 (6)
(6)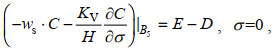 (7)
(7)其中, 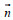
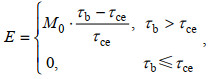 (8)
(8)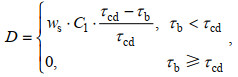 (9)
(9)其中, M0是再悬浮率, τb是底部剪切应力值, τce是侵蚀的临界剪切应力值, τcd是沉降的临界剪切应力值, C1是近海底处的悬浮泥沙浓度值。
正向模型的离散形式和求解方式详见Wang等(2018a), 此处不再赘述。
1.2 伴随模型定义如下的代价函数:
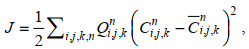 (10)
(10)其中, Ci, j, kn和Ci, j, kn分别是网格点(i, j, k)处第n时间步的SSC的模拟值和观测值。矩阵Q满足如下条件:
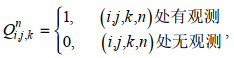 (11)
(11)根据拉格朗日乘子法, 引入伴随变量λ, 令拉格朗日函数关于各个变量和模型参数的梯度值为0, 可以推导出伴随模型以及代价函数关于初始场的梯度表达式, 具体的推导过程和差分格式详见Wang等(2018a), 此处不再赘述。
1.3 优化算法由伴随模型求得代价函数关于初始场的梯度后, 可以利用优化算法通过迭代获得最优初始场, 迭代公式可以表示为:
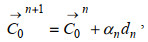 (12)
(12)其中, 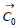
本文中, αn是正值, 一般取为常数, 但调整步长过大或过小都会对反演结果产生影响。调整步长过大时, 在极小值附近会造成约化代价函数“过调整”的问题, 产生“锯齿效应”; 调整步长过小时, 会造成收敛速度慢, 计算效率低的问题。与以往调整步长取为常数不同, 本文中调整步长依赖于初始场的空间分布, 取为空间分布的形式, 即将αn取为初始场的第n个迭代步迭代结果的3%(公式13), 这样能够保证迭代收敛的稳定性, 且不需要人为地凭经验给定调整步长, 可以避免由调整步长过大或者过小引起的上述问题, 同时避免需要反复调试才能获得最佳的调整步长, 提高了计算效率。
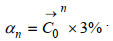 (13)
(13)确定dn有许多可供选择的优化算法, 本文选择并比较了其中的三种, 分别是最速下降法(the gradient descent algorithm, GD)、共轭梯度法(the conjugate gradient algorithm, CG)和有限记忆BFGS法(the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm, L-BFGS)。
在GD中, 搜索方向为代价函数关于模型初始场的负梯度方向:
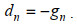 (14)
(14)在CG中, 搜索方向为共轭方向:
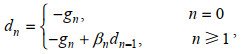 (15)
(15)其中, dn为搜索方向, gn为代价函数关于模型初始场的梯度方向, 根据βn的不同求法, CG又可以分为许多种类, 其中PRP、HS、LS方法的数值表现较好, 这三种方法中βn的计算公式如下:
(1) PRP方法(CG-PRP, Polak et al, 1969; Polyak, 1969):
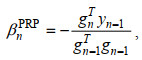 (16)
(16)(2) HS方法(CG-HS, Hestenes et al, 1952):
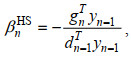 (17)
(17)(3) LS方法(CG-LS, Liu et al, 1991):
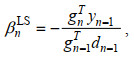 (18)
(18)其中, yn-1=gn-gn-1。
在L-BFGS中, 要求搜索方向满足(Liu et al, 1989):
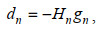 (19)
(19)其中,
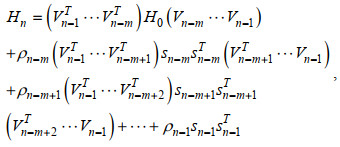 (20)
(20)方程中, ρn=1/snynT, Vn=1-ρnynsnT, sn=C0n+1-C0n=αndn, yn=gn+1-gn; m是矫正对的数量, 一般取值范围为3-7, 本文取为5(Alekseev et al, 2009)。
在初始场优化反演的迭代过程中, 迭代收敛标准可以有很多, 当达到某一收敛标准时迭代终止。收敛标准可以是最后两个迭代步的代价函数值充分接近或小于某个值, 也可以是最后两个迭代步的代价函数关于初始场的梯度值充分接近或小于某值等。本文的孪生实验中, 迭代收敛标准是最后两个迭代步的约化代价函数值之差的绝对值小于3.0×10-5, 且最大迭代步设置为200, 即:
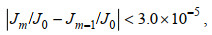 (21)
(21)实际实验中, 迭代收敛标准是最后两个迭代步的约化代价函数值之差的绝对值小于1.0×10-5, 且最大迭代步设置为500, 即:
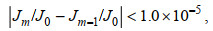 (22)
(22)其中, Jm、J0和Jm-1分别是最后一次迭代、第一次迭代和倒数第二次迭代后的代价函数值。
2 研究区域、模型设置及数据来源本文的研究区域为杭州湾海域(图 1), 经纬度范围为29.902°-30.904°N、120.602°-121.806°E。背景流场数据由FVCOM(Chen et al, 2003)计算得到, 与Wang等(2018b)相同。模型的水平分辨率为0.006°×0.006°; 垂向分为四层, 与输出背景流场数据的数值模型FVCOM一致。正向模型的时间步长为180s, 总的模拟时间是31h, 小潮时期数值模拟实验的初始时刻是2011年6月26日0:28, 结束时刻是2011年6月27日7:28, 大潮时期数值模拟实验的初始时刻是2015年3月24日0:28, 结束时刻是2015年3月25日7:28。河流流入开边界条件在小潮时期取为1.5×10-1kg/m3(中华人民共和国水利部, 2011), 在大潮时期取为1.0×10-1kg/m3(中华人民共和国水利部, 2015)。根据唐建华(2007)的研究, 一个潮周期内杭州湾海域絮凝的平均沉速的量级为10-4m/s, 因此沉降速度取为1.0×10-4m/s。参照Hu等(2009)在模拟杭州湾悬浮泥沙输运时再悬浮率的取值, 再悬浮率取为3.0×10-6m/s, 沉降和侵蚀的临界切应力均取为0.4N/m2。基于Wang等(2018a)中的尺度分析, 水平扩散系数取为80m2/s, 垂向扩散系数在小潮时期取为3.0×10-3m2/s, 在大潮时期取为3.0×10-2m2/s。以上模型参数的具体描述和取值如表 1所示。
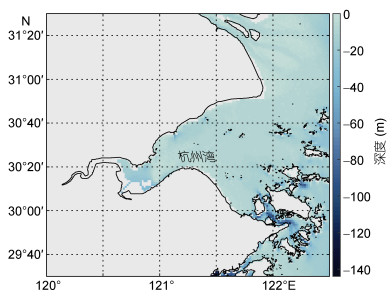 |
| 图 1 研究区域及水深 Fig. 1 Study area and the bathymetry |
| 参数 | 参数意义 | 参数取值 | ||
| 小潮时期 | 大潮时期 | |||
| Δt | 正向模型(伴随模型)的时间步长 | 180s | 180s | |
| Cobc | 河流流入开边界条件 | 1.5×10-1kg/m3 | 1.0×10-1kg/m3 | |
| ws | 沉降速度 | 1.0×10-4m/s | 1.0×10-4m/s | |
| M0 | 再悬浮率 | 3.0×10-6m/s | 3.0×10-6m/s | |
| τce | 侵蚀的临界切应力 | 0.4N/m2 | 0.4N/m2 | |
| τcd | 沉降的临界切应力 | 0.4N/m2 | 0.4N/m2 | |
| KH | 水平扩散系数 | 80m2/s | 80m2/s | |
| KV | 垂向扩散系数 | 3.0×10-3m2/s | 3.0×10-2m2/s | |
本文采用由静止水色卫星GOCI的观测数据反演所得SSC作为同化数据, 由He等(2013)提供。GOCI卫星能够对潮汐、赤潮、河流羽流、泥沙输运等短期的区域性海洋现象实现高时空分辨率的监测, 在水色遥感探测中具有很大的发展潜力(He et al, 2013)。GOCI数据的空间分辨率为500m, 时间分辨率为1h, 每天可以获得八幅观测图像(Ryu et al, 2011)。He等(2013)构建了一个大气校正算法和经验关系模型, 可以反演得到小潮时期和大潮时期长江口和杭州湾海域表层SSC, 该数据在Wang等(2018b)中有具体描述。
数据同化的有效性需要用未被同化的独立观测进行检验(Elbern et al, 2007)。因此, 在本文的孪生实验和实际实验中, 为了检验伴随同化方法优化反演模型初始场的有效性, 将随机选取10%的观测数据不参与同化而作为独立观测来检验数据同化的结果, 将这些观测数据称为“检验观测”(check observations, COs); 其余90%的观测数据参与同化, 称其为“被同化观测”(assimilated observations, AOs)。孪生实验和实际实验中观测数据的唯一区别是, 孪生实验中的观测数据是给定模型参数值运行正向模型生成的表层“观测”, 实际实验中的观测数据则是实际GOCI卫星遥感数据反演所得SSC。
3 孪生实验及结果分析 3.1 初始场的误差对模拟结果的影响初始场的不确定性是模型误差的主要来源之一。基于三维悬沙输运伴随同化模型, 以小潮时期为例, 利用初始时刻实测的GOCI卫星遥感观测数据经过水平空间插值获得表层SSC的初始场(图 2a), 插值方法采用MATLAB软件自带的自然邻近插值法(natural), 其余各层初始场由表层初始场线性插值得到, 插值公式与Wang等(2018b)中相同, 该插值公式是由SSC原位观测数据(杨旸等, 2008)线性拟合得到, 较好地体现了杭州湾SSC由表及底逐渐增大的特点。运行正向模型获得整个研究区域的SSC“观测值”, 每小时输出一次结果。
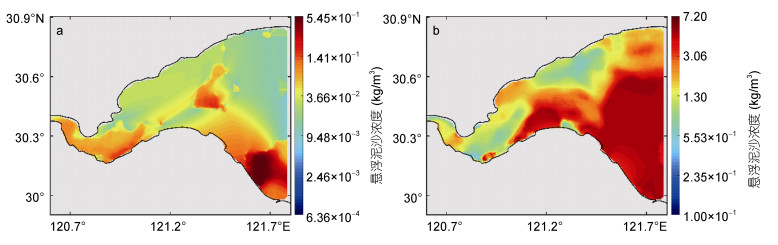 |
| 图 2 初始时刻实测的GOCI卫星遥感观测数据经过水平空间插值后所得表层悬浮泥沙浓度的初始场 Fig. 2 Initial field of the surface SSC obtained by horizontal spatial interpolation of GOCI satellite remote sensing observation data measured at initial time during neap tide 注: a:小潮时期; b:大潮时期 |
为了评估初始场的误差对模拟结果的影响, 对初始场分别添加最大不超过10%、20%、30%的随机相对误差, 计算公式如下:
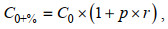 (23)
(23)其中, C0+%为添加随机误差后的初始场, C0为给定初始场, p为最大随机相对误差百分比, r为介于–1-1之间的随机数。
将垂向四层的SSC模拟值与观测值之间的相对误差分别进行水平和垂向空间平均后得到整个研究区域的SSC的平均相对误差(mean relative error, MRE)随模拟时间的变化情况(图 3)。可以看出, SSC模拟结果的MRE均随初始场误差的增大而增大; 随着模拟时间的增加, 模拟结果的MRE没有明显下降。这说明初始场对于三维悬沙输运模型是敏感参数, 初始场的给定越准确, 模拟结果的MRE越小, 反之, 则越大。因此, 对于三维悬沙输运模型而言, 尤其是短期的SSC数值模拟, 初始场的给定至关重要, 将直接影响SSC的模拟精度。
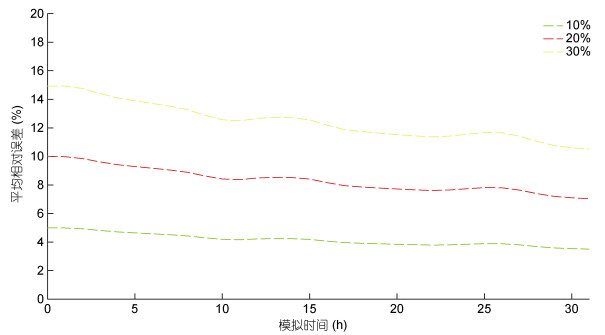 |
| 图 3 整个研究区域的SSC模拟值与观测值之间的平均相对误差随模拟时间的变化情况 Fig. 3 The change of mean relative errors of SSC between the simulation results and observations for the total study area with the model time increasing 注: 10%、20%和30%为初始场中添加的随机误差的最大百分比 |
本节探讨GD、CG-PRP、CG-HS、CG-LS和L-BFGS五种算法在三维悬沙输运伴随同化模型中优化反演初始场的表现。设计孪生实验TE11-E15, 以图 2a所示的初始场作为给定初始场, 初始场的初始猜测值取为给定初始场的水平空间平均值的一半, 即常数0.03325kg/m3, 其余模型参数均为默认值。从反演结果和误差分布(图 4)来看, 五种算法的反演结果与给定分布较为吻合, 利用GD、CG-PRP和CG-LS算法反演所得初始场的误差主要集中分布在杭州湾东侧湾口的海洋开边界处, 而在其余的大部分区域误差较小, 均取得了良好的反演效果; 然而利用CG-HS和L-BFGS算法反演所得初始场的误差在湾顶、湾口和南部的大部分区域都很大, 反演效果较差, 且CG-HS算法要比L-BFGS算法更差。从统计结果(图 5、表 2)来看, 五组实验中约化代价函数、SSC模拟结果与“观测数据”之间的平均绝对误差(mean absolute error, MAE)均有不同程度的下降, 可以定量说明数据同化的效果(Jin et al, 2015; Liu et al, 2017; Zong et al, 2018)。以约化代价函数为例, 实验TE15的约化代价函数下降速度最快, 但只下降了2个数量级; 实验TE11、TE12和TE14的约化代价函数下降速度相当, 均下降了3个数量级; 实验TE13的约化代价函数下降速度最慢, 在第3步已达到收敛准则, 迭代停止。此外, 代价函数关于初始场的梯度的L1范数、反演结果与给定分布之间的MRE两个统计量可以直观地说明初始场的反演效果。实验TE11、TE12和TE14中两个统计量分别经过171、181、181步均大幅度下降, 表明初始场的反演效果较好; 而实验TE13和TE15中反演结果的误差较大, 反演效果较差。综合以上分析, GD、CG-PRP和CG-LS三种算法反演初始场的效果相当, 但GD算法具有易于实现、迭代平稳易于控制、良好的可操作性等优点, 在本模型中具有很大的优势; L-BFGS算法的反演速率最快, 但最终的反演结果较差; CG-HS算法无论是反演速率还是反演结果都是最差的。以上数值实验的结论与Chen等(2013)和Zhang等(2015)的研究结论相似。因此, 本节之后的孪生实验和实际实验选用GD算法用于模型初始场的优化反演。
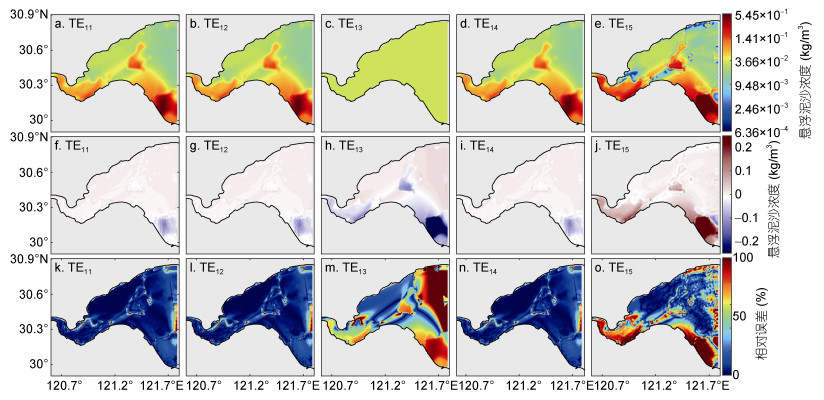 |
| 图 4 TE11-TE15中反演后的表层初始场(a-e)、反演后的表层初始场与给定初始场的误差(f-j)、反演后的表层初始场与给定初始场的相对误差(k-o)的空间分布 Fig. 4 The spatial distributions of the surface initial field after inversion in TE11-TE15 (a-e); the spatial distributions of errors between the surface initial field after inversion and the given initial field in TE11-TE15 (f-j); and the spatial distributions of relative errors between the surface initial field after inversion and the given initial field in TE11-TE15 (k-o) |
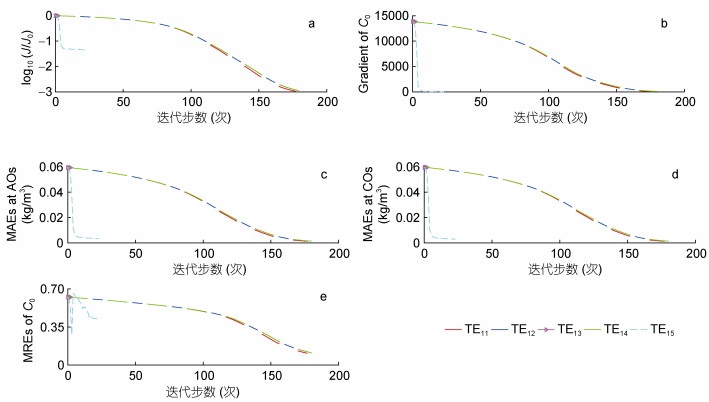 |
| 图 5 实验TE11-TE15中约化代价函数(log10(J/J0)) (a)、代价函数关于初始场的梯度的L1范数(Gradient of C0) (b)、SSC模拟结果与“被同化观测”(AOs)之间的平均绝对误差(MAEs at AOs) (c)、SSC模拟结果与“检验观测”(COs)之间的平均绝对误差(MAEs at COs) (d)、初始场的反演结果与给定分布之间的平均相对误差(MREs of C0) (e)随迭代步的变化 Fig. 5 The values of log(J/J0) versus the iteration steps (a); the variations of Gradient of C0 (b); the variations of MAEs at AOs (c); the variations of MAEs at COs (d); and the variations of MREs of C0 (e) in TE11-TE15 |
| 实验编号 | J/J0 | Gradient of C0 | MAEs at AOs(kg/m3) | MAEs at COs(kg/m3) | MREs of C0 | ||||||||||
| 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | ||||||||
| TE11 | 1.07×10-3 | 1.38×104 | 9.70×101 | 5.94×10-2 | 1.26×10-3 | 5.96×10-2 | 1.25×10-3 | 62.50% | 10.78% | ||||||
| TE12 | 1.12×10-3 | 1.38×104 | 1.14×102 | 5.94×10-2 | 1.37×10-3 | 5.96×10-2 | 1.36×10-3 | 62.50% | 11.24% | ||||||
| TE13 | 9.97×10-1 | 1.38×104 | 1.38×104 | 5.94×10-2 | 5.93×10-2 | 5.96×10-2 | 5.95×10-1 | 62.50% | 62.40% | ||||||
| TE14 | 1.13×10-3 | 1.38×104 | 1.17×102 | 5.94×10-2 | 1.39×10-3 | 5.96×10-2 | 1.38×10-3 | 62.50% | 11.30% | ||||||
| TE15 | 4.45×10-2 | 1.38×104 | 2.67×101 | 5.94×10-2 | 3.28×10-3 | 5.96×10-2 | 2.87×10-3 | 62.50% | 40.56% | ||||||
本节设计孪生实验TE21-TE23研究初始场的初始猜测值对反演结果的影响。初始场的初始猜测值分别取为给定初始场的水平空间平均值的1/2、给定初始场的水平空间平均值和给定初始场的水平空间平均值的3/2, 即常数0.03325、0.0665和0.09975kg/m3。从反演结果和误差分布(图 6)来看, 三组实验的反演结果相差不大, 反演结果与给定分布吻合良好, 相对误差在大部分区域均小于20%。从统计结果(图 7、表 3)来看, 三组实验中相关统计量均大幅度下降。其中, 约化代价函数均下降了至少3个数量级, 代价函数关于初始场的梯度的L1范数均至少下降了2个数量级, SSC模拟结果与观测之间的MAE均至少下降了1个数量级, 初始场的反演结果与给定分布之间的MRE均小于16%, 表明初始场的反演结果充分收敛到了“真实值”附近。本节数值实验结果表明, 初始场的反演效果受初始猜测值的影响较小, 初始场的“真实值”均能得到精确反演。因此, 本节之后的敏感性理想实验中初始猜测值均取为0.03325kg/m3。
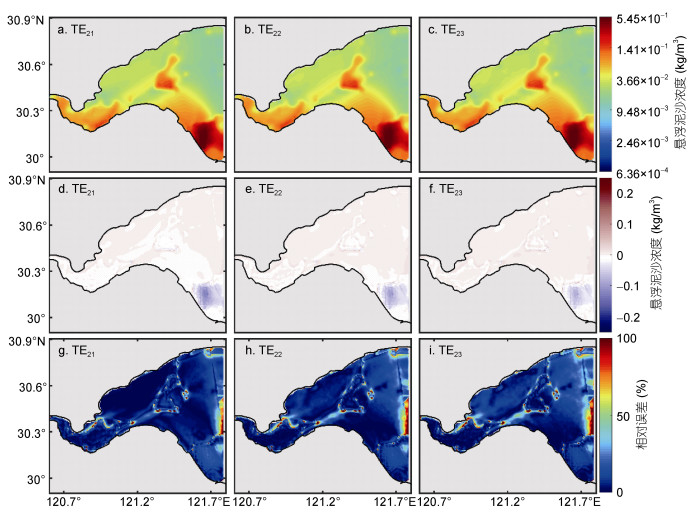 |
| 图 6 TE21-TE23中反演后的表层初始场(a-c)、反演后的表层初始场与给定初始场的误差(d-f)、反演后的表层初始场与给定初始场的相对误差(g-i)的空间分布 Fig. 6 The spatial distributions of the surface initial field after inversion in TE21-TE23 (a-c); the spatial distributions of errors between the surface initial field after inversion and the given initial field in TE21-TE23 (d-f); and the spatial distributions of relative errors between the surface initial field after inversion and the given initial field in TE21-TE23 (g-i) |
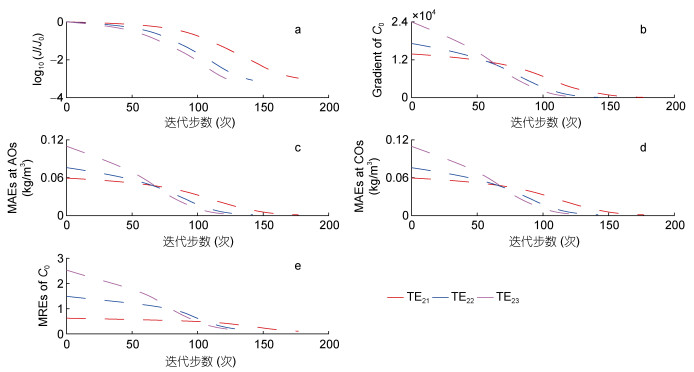 |
| 图 7 实验TE21-TE23中log10(J/J0) (a)、Gradient of C0 (b)、MAEs at AOs(c)、MAEs at COs (d)、MREs of C0(e)随迭代步的变化 Fig. 7 The values of log(J/J0) versus the iteration steps (a); the variations of Gradient of C0 (b); the variations of MAEs at AOs (c); the variations of MAEs at COs (d); and the variations of MREs of C0 (e) in TE21-TE23 |
| 实验编号 | J/J0 | Gradient of C0 | MAEs at AOs(kg/m3) | MAEs at COs(kg/m3) | MREs of C0 | |||||||
| 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | |||||
| TE21 | 1.07×10-3 | 1.38×104 | 9.70×101 | 5.94×10-2 | 1.26×10-3 | 5.96×10-2 | 1.25×10-3 | 62.50% | 10.78% | |||
| TE22 | 8.34×10-4 | 1.72×104 | 1.22×102 | 7.60×10-2 | 1.33×10-3 | 7.59×10-2 | 1.34×10-3 | 149% | 13.31% | |||
| TE23 | 6.23×10-4 | 2.40×104 | 1.42×102 | 1.10×10-1 | 1.44×10-3 | 1.10×10-1 | 1.46×10-3 | 253% | 15.64% | |||
在实际的卫星遥感观测中, 由于云覆盖或恶劣天气条件等因素的影响, 卫星遥感数据往往存在一定程度的缺失, 因此有必要讨论卫星遥感数据数量对初始场优化反演的影响。本节设计孪生实验TE31-TE34, 四组实验中“被同化观测”的数量依次随机减少1/10、1/4、1/2、3/4。从反演结果和误差分布(图 8)可以看出, 随着卫星数据数量的减少, 反演精度相差不大, 反演结果在大部分区域与给定分布吻合良好, 误差较大的区域主要集中在湾口的海洋开边界处。从统计结果(图 9、表 4)可以看出, 反演结果与给定分布之间的MRE分别为10.94%、10.82%、12.71%和13.62%, 依然取得了较高的反演精度, 实验TE34相比于实验TE31初始场的反演结果与给定分布之间的MRE只增大了2.68%, 相差不大。据此我们认为, 在目前的实验设置下, 卫星遥感数据数量对初始场的优化反演影响较小, 即便是分布稀疏或云覆盖现象较为严重, 依然能够取得良好的反演效果, 表明伴随同化方法是还原SSC空间分布的有效手段。
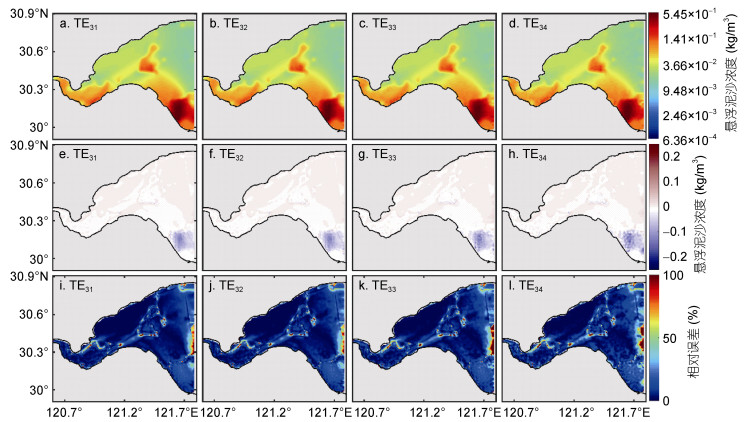 |
| 图 8 TE31-TE34中反演后的表层初始场(a-d)、反演后的表层初始场与给定初始场的误差(e-h)、反演后的表层初始场与给定初始场的相对误差(i-l)的空间分布 Fig. 8 The spatial distributions of the surface initial field after inversion in TE31-TE34 (a-d); the spatial distributions of errors between the surface initial field after inversion and the given initial field in TE31-TE34 (e-h); and the spatial distributions of relative errors between the surface initial field after inversion and the given initial field in TE31-TE34 (i-l) |
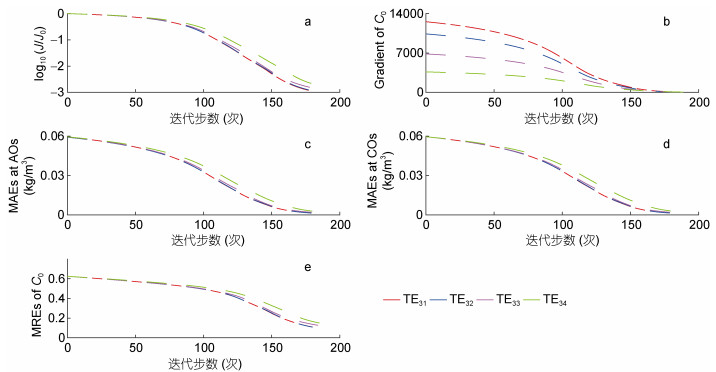 |
| 图 9 实验TE31-TE34中log10(J/J0) (a)、Gradient of C0 (b)、MAEs at AOs (c)、MAEs at COs (d)、MREs of C0(e)随迭代步的变化 Fig. 9 The values of log(J/J0) versus the iteration steps (a); the variations of Gradient of C0 (b); the variations of MAEs at AOs (c); the variations of MAEs at COs (d); and the variations of MREs of C0 (e) in TE31-TE34 |
| 实验编号 | J/J0 | Gradient of C0 | MAEs at AOs(kg/m3) | MAEs at COs(kg/m3) | MREs of C0 | |||||||
| 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | |||||
| TE31 | 1.11×10-3 | 1.26×104 | 9.09×101 | 5.94×10-2 | 1.30×10-3 | 5.96×10-2 | 1.29×10-3 | 62.50% | 10.94% | |||
| TE32 | 1.15×10-3 | 1.04×104 | 7.39×101 | 5.92×10-2 | 1.29×10-3 | 5.96×10-2 | 1.28×10-3 | 62.50% | 10.82% | |||
| TE33 | 1.35×10-3 | 6.83×103 | 7.42×101 | 5.94×10-2 | 1.63×10-3 | 5.96×10-2 | 1.63×10-3 | 62.50% | 12.71% | |||
| TE34 | 1.61×10-3 | 3.64×103 | 4.45×101 | 5.95×10-2 | 1.88×10-3 | 5.96×10-2 | 1.98×10-3 | 62.50% | 13.62% | |||
本节设计孪生实验TE41-TE44研究卫星遥感数据同化时间窗口的宽度对初始场优化反演的影响。SSC数值模拟的起始时刻是GOCI卫星遥感观测数据同化时间窗口的起始时刻, 同化窗口依次增大, 分别为1、2、3、4h, 即分别覆盖2次、3次、4次、5次的GOCI卫星遥感观测。从反演结果和误差分布(图 10)可以看出, 随着同化窗口的宽度的增大, 初始场的反演效果越来越好, 当同化窗口的宽度增加到3h, 在杭州湾中部和东南部两个误差相对较大的区域得到明显改善。从统计结果(图 11、表 5)可以看出, 四组实验的约化代价函数、代价函数关于初始场的梯度的L1范数以及模拟结果和观测之间的MAE分别经过200、200、194、191步均显著下降, 四组实验初始场的反演结果与给定分布之间的MRE分别为13.53%、10.03%、8.15%和8.73%, 即增大同化窗口的宽度可以有效改善反演结果。由此可见, 初始场的优化反演效果对同化窗口的宽度较为敏感, 当SSC数值模拟的起始时刻是GOCI卫星遥感观测数据同化窗口的起始时刻, 只需要至少3h的同化窗口即可得到改善效果明显的反演结果。因此, 对于SSC的数值模拟而言, 合理设置卫星遥感数据同化时间窗口的宽度可以有效提高初始场的优化反演效果。
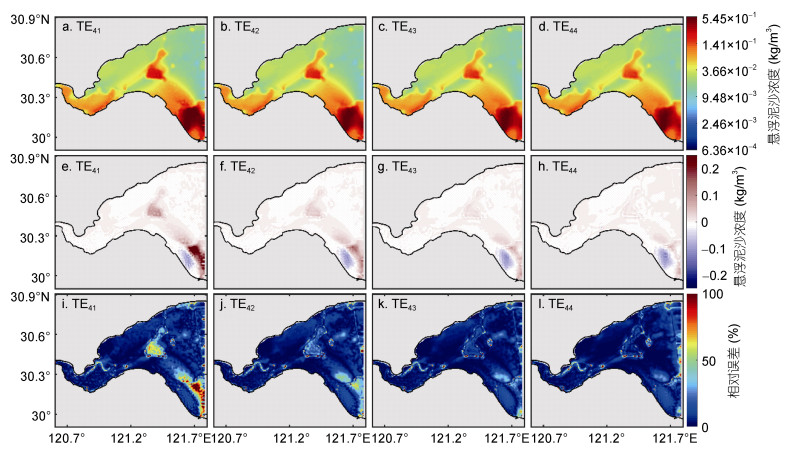 |
| 图 10 TE41-TE44中反演后的表层初始场(a-d)、反演后的表层初始场与给定初始场的误差(e-h)、反演后的表层初始场与给定初始场的相对误差(i-l)的空间分布 Fig. 10 The spatial distributions of the surface initial field after inversion in TE41-TE44 (a-d); the spatial distributions of errors between the surface initial field after inversion and the given initial field in TE41-TE44 (e-h); and the spatial distributions of relative errors between the surface initial field after inversion and the given initial field in TE41-TE44 (i-l) |
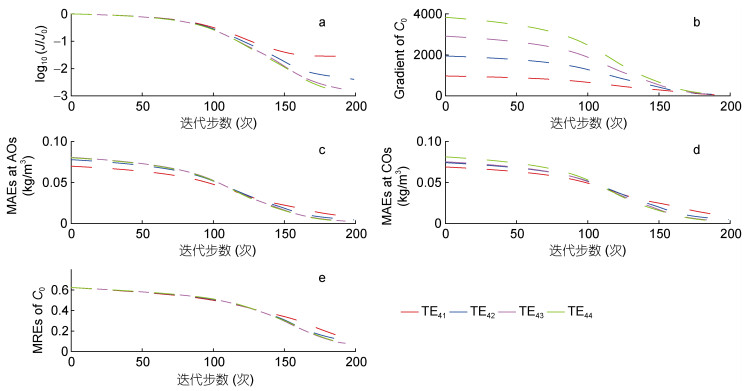 |
| 图 11 实验TE41-TE44中log10(J/J0) (a)、Gradient of C0 (b)、MAEs at AOs (c)、MAEs at COs (d)、MREs of C0(e)随迭代步的变化 Fig. 11 The values of log(J/J0) versus the iteration steps (a); the variations of Gradient of C0 (b); the variations of MAEs at AOs (c); the variations of MAEs at COs (d); and the variations of MREs of C0 (e) in TE41-TE44 |
| 实验编号 | J/J0 | Gradient of C0 | MAEs at AOs(kg/m3) | MAEs at COs(kg/m3) | MREs of C0 | |||||||||||
| 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | |||||||||
| TE41 | 2.76×10-3 | 9.71×102 | 3.21×101 | 6.99×10-2 | 8.71×10-3 | 6.90×10-2 | 9.93×10-3 | 62.50% | 13.53% | |||||||
| TE42 | 4.02×10-3 | 1.95×103 | 3.84×101 | 7.79×10-2 | 4.55×10-3 | 7.42×10-2 | 4.74×10-3 | 62.50% | 10.03% | |||||||
| TE43 | 1.74×10-3 | 2.91×103 | 3.95×101 | 8.06×10-2 | 2.91×10-3 | 7.53×10-2 | 3.02×10-3 | 62.50% | 8.15% | |||||||
| TE44 | 1.43×10-3 | 3.84×103 | 6.69×101 | 8.02×10-2 | 2.82×10-3 | 8.13×10-2 | 2.93×10-3 | 62.50% | 8.75% | |||||||
本文中背景水动力场是由FVCOM模拟生成, 用于驱动三维悬沙输运模型。由于背景流场的模拟结果与实际流场不可避免地存在误差, 因而三维悬沙输运模型的模拟精度会很大程度上依赖于背景水动力场的模拟精度(Mehta et al, 1989, Xie et al, 2009, Wang et al, 2018b), 因此有必要讨论背景水动力场的误差对初始场优化反演的影响。李丹(2016)利用FVCOM对长江口杭州湾海域的水动力场进行模拟, 将模拟结果与实测资料进行对比, 潮流流速误差的最大值在15%以内。Wang等(2018b)利用FVCOM对杭州湾海域水动力场的模拟结果显示, 模拟的潮流流速的相对误差大多不超过20%。因此, 本节设计孪生实验TE51-TE53, 三组实验中分别对背景水动力场中流速的三个分量u、v、w均添加最大不超过10%、20%和30%的随机误差, 误差添加方式与3.1节中相同。从反演结果和误差分布(图 12)来看, 三组实验中初始场的反演结果相差不大, 反演结果均与给定分布吻合良好。从统计结果(图 13、表 6)来看, 三组实验相关统计量分别经过179、179、180步都下降到了相同的数量级, 三组实验中反演结果与给定分布之间的MRE均小于12%。因此, 背景水动力场的误差对初始场优化反演的影响较小, 本文所采用的FVCOM模拟结果足以满足研究要求。
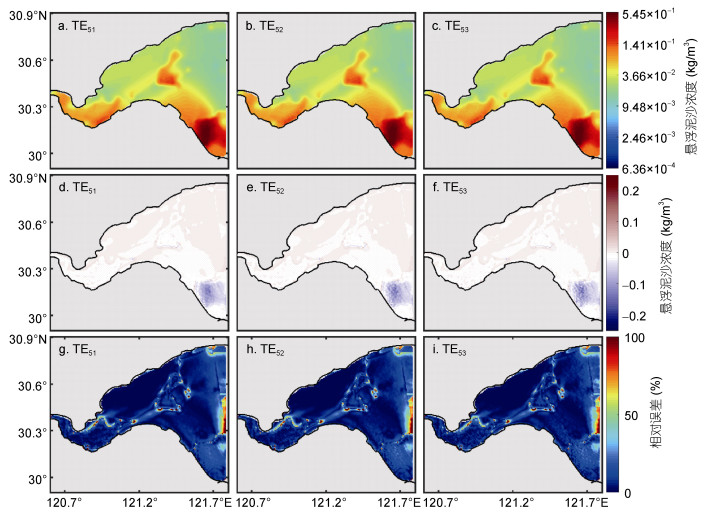 |
| 图 12 TE51-TE53中反演后的表层初始场(a-c)、反演后的表层初始场与给定初始场的误差(d-f)、反演后的表层初始场与给定初始场的相对误差(g-i)的空间分布 Fig. 12 The spatial distributions of the surface initial field after inversion in TE51-TE53 (a-c); the spatial distributions of errors between the surface initial field after inversion and the given initial field in TE51-TE53 (d-f); and the spatial distributions of relative errors between the surface initial field after inversion and the given initial field in TE51-TE53 (g-i) |
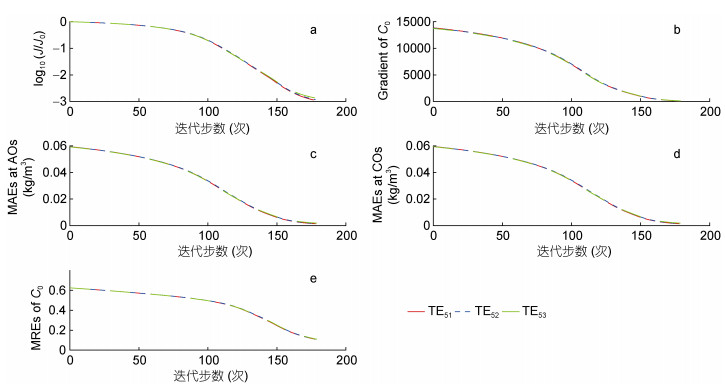 |
| 图 13 实验TE51-TE53中log10(J/J0) (a)、Gradient of C0(b)、MAEs at AOs (c)、MAEs at COs (d)、MREs of C0(e)随迭代步的变化 Fig. 13 The values of log(J/J0) versus the iteration steps (a); the variations of Gradient of C0 (b); the variations of MAEs at AOs (c); the variations of MAEs at COs (d); and the variations of MREs of C0 (e) in TE51-TE53 |
| 实验编号 | J/J0 | Gradient of C0 | MAEs at AOs(kg/m3) | MAEs at COs(kg/m3) | MREs of C0 | |||||||
| 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | 同化前 | 同化后 | |||||
| TE51 | 1.10×10-3 | 1.39×104 | 1.04×102 | 5.94×10-2 | 1.38×10-3 | 5.95×10-2 | 1.37×10-3 | 62.50% | 10.93% | |||
| TE52 | 1.17×10-3 | 1.38×104 | 1.11×102 | 5.93×10-2 | 1.58×10-3 | 5.95×10-2 | 1.57×10-3 | 62.50% | 11.03% | |||
| TE53 | 1.32×10-3 | 1.38×104 | 1.12×102 | 5.92×10-2 | 1.86×10-3 | 5.94×10-2 | 1.84×10-3 | 62.50% | 10.94% | |||
为了比较伴随同化方法和插值方法重构模型初始场的能力, 我们构建一个新的初始场(图 14a), 该初始场由图 2a所示初始场运行正向模型所得与实际GOCI卫星遥感观测时刻对应的“观测数据”也即3.1节中的“观测数据”经过时间平均后获得。利用新的初始场运行正向模型, 获得与实际观测数据一一对应的受云覆盖影响的“被同化观测”和“检验观测”用于本节的数据同化和初始场重构。在伴随同化方法中, 初始场的初始猜测值取为新的初始场的水平空间平均值的一半, 即常数0.0535kg/m3, 卫星遥感数据同化时间窗口的宽度设置为3h, 其余模型设置不变。在插值方法中, 分别利用双三次插值法、自然邻近插值法和最近邻点插值法插值数值模拟初始时刻的“观测数据”, 获得重构的初始场。从初始场的重构结果(图 14b-e)和误差分布(图 14f-m)可以看出, 伴随同化方法重构的初始场与给定分布最接近, 在绝大部分区域二者吻合良好, 很好地重现了SSC变化剧烈的区域, 且保持了很好的平滑性, 重构结果与给定分布之间的MRE只有11.53%;双三次插值法和自然邻近插值法重构初始场的效果较差, 虽然总体保持了与给定分布一致的空间变化规律, 但在杭州湾中西部、南部陆地边界处和中东部存在三个相对误差局部高值区, 插值结果对三处SSC的剧烈变化刻画不够细致; 最近邻点插值法重构的初始场与给定分布偏差最大, 在上述三个局部区域SSC均远高于给定初始场, 重构结果与给定分布之间的MRE高达46.95%, 且插值结果的平滑性较差, 与实际偏差较大。因此, 与传统的插值方法相比, 伴随同化方法是重构模型初始场更有效的手段。
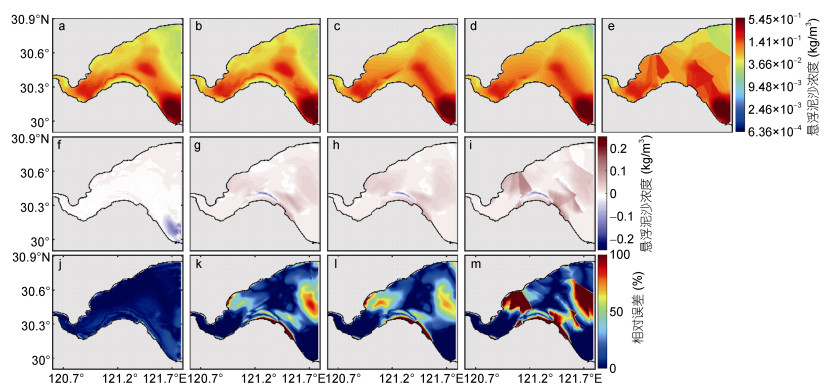 |
| 图 14 给定的(a)和重构的(b-e)表层初始场的空间分布; 重构的表层初始场与给定初始场的误差(f-i)以及相对误差(j-m)的空间分布 Fig. 14 The spatial distribution of the given surface initial field (a); the spatial distributions of initial field of the surface layer reconstructed by adjoint assimilation method, bicubic interpolation method, natural neighbor interpolation method, and nearest neighbor interpolation method (b-e); the spatial distributions of errors between the surface initial field of the reconstructed surface initial field and the given initial field (f-i); and the spatial distributions of relative errors of the reconstructed surface initial field and the given initial field (j-m) 注: b、f、j:伴随同化方法; c、g、k:双三次插值法; d、h、l:自然邻近插值法; e、i、m:最近邻点插值法的结果 |
实际实验中, 分别同化典型的小潮时期和大潮时期GOCI卫星遥感资料所得杭州湾海域表层SSC数据, 利用伴随同化方法对模型初始场进行优化反演。根据孪生实验的结论, 优化算法选用GD算法, 初始场的初始猜测值取为初始时刻实测的GOCI卫星遥感观测数据经过空间插值获得的SSC(图 2), 卫星遥感数据同化时间窗口的宽度设置为3h, 其余模型设置不变。从图 15可以看出, 实际初始场缺测严重, 在缺测区域优化反演后的初始场(图 16)与反演前的插值初始场(图 2)有很大不同。在小潮时期, 反演前的初始场的SSC高值区出现在杭州湾的西部、中部和东南部, 而反演后的初始场的SSC高值区出现在杭州湾的东南部及南部沿岸的大部分地区。在大潮时期, 反演前的初始场的SSC高值区出现在杭州湾的中南部、东部和东南部的大部分区域, 而反演后的初始场的SSC高值区出现在杭州湾的东南部及南部沿岸的大部分地区。无论是小潮时期还是大潮时期, 反演后的初始场的SSC均呈现出由南到北逐渐递减的趋势, 这与基于一个潮汐周期得到的杭州湾GOCI卫星遥感观测中SSC“北低南高”的分布特征相似(He et al, 2013; 江彬彬等, 2015; Liu et al, 2018), 显然优化反演后的初始场更符合实际, 证明了伴随同化方法优化模型初始场的有效性。从图 17可以看出, 优化模型初始场可以很大程度上提高SSC的模拟精度。小潮(大潮)时期, 经过260(102)步迭代, 满足收敛标准, 约化代价函数、代价函数关于初始场的梯度的L1范数均大幅下降并趋于平稳, “被同化观测”和模拟结果之间的MAE从8.72×10-2kg/m3(3.66kg/m3)下降到了2.72×10-2kg/m3 (7.25×10-1kg/m3), 下降了68.81%(80.19%); “检验观测”和模拟结果之间的MAE从9.02×10-2kg/m3(3.63kg/m3)下降到了2.88×10-2kg/m3 (7.39×10-1kg/m3), 下降了68.07%(79.64%)。可见, 反演后SSC的模拟结果和观测之间的误差大幅度降低, 模拟结果与观测更接近。以上结果表明, 初始场对SSC的模拟结果有重要的影响, 利用伴随同化方法可以获得模型的最优初始场, 从而很大程度上改善SSC的模拟结果。
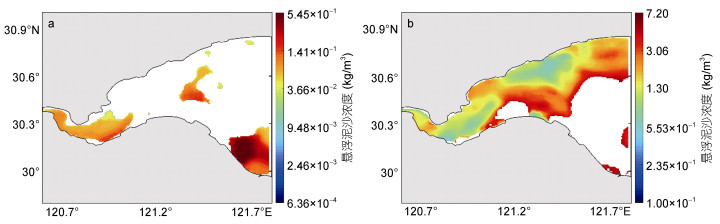 |
| 图 15 小潮(a)和大潮(b)时期实际初始场的空间分布 Fig. 15 The spatial distribution of actual initial field during neap tide (a) and spring tide(b) 注:白色区域代表数据缺失区域 |
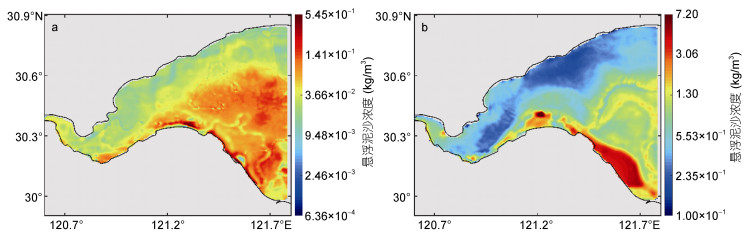 |
| 图 16 实际实验中, 小潮(a)和大潮(b)时期初始场的反演结果 Fig. 16 The inversion result of initial field during neap tide (a) and spring tide (b) in practical experiments |
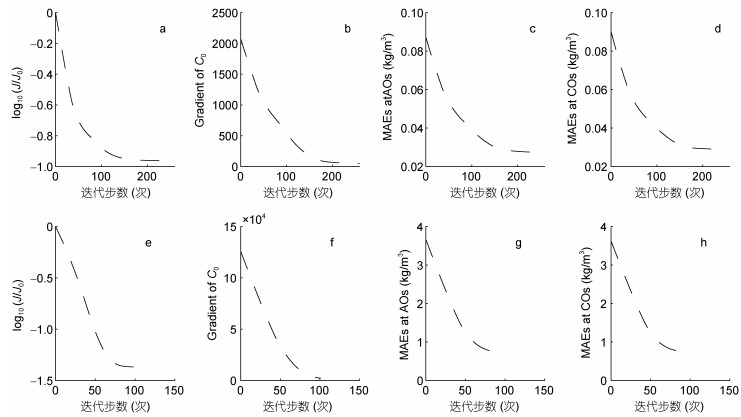 |
| 图 17 实际实验小潮时期的log10(J/J0)(a)、Gradient of C0(b)、MAEs at AOs(c)、MAEs at COs (d)随迭代步的变化; 实际实验大潮时期的log10(J/J0) (e)、Gradient of C0 (f)、MAEs at AOs (g)、MAEs at COs (h)随迭代步的变化 Fig. 17 The values of log(J/J0) (a, e), the variations of Gradient of C0 (b, f), the variations of MAEs at AOs (c, g), and the variations of MAEs at COs (d, h) during neap tide and spring tide in practical experiments |
根据以上分析, 实际初始场缺测严重时, 利用插值方法获得的初始场(图 2)不能体现杭州湾南部沿岸高SSC的特征, 且插值结果的平滑性较差。而利用伴随同化方法反演所得初始场在有观测区域与实际初始场较为一致, 且在初始场的观测数据缺测区域, 伴随同化方法的反演效果要更好, 很好地反演出了SSC“北低南高”的分布特征, 且总体上保持了很好的平滑性, 更符合实际。这是因为插值方法仅考虑了SSC的空间分布, 未考虑时间变化, 不能充分地利用观测资料, 因而不能较好地重现SSC的时空变化特征, 特别是在云覆盖较为严重的区域, 传统的插值方法往往是失效的, 模拟所得SSC与实际偏差较大; 而伴随同化方法既考虑SSC的空间分布, 又考虑其时间变化, 可以获得与实际观测更加接近的初始场, 因而模拟结果更接近观测值, 且更符合实际。
5 结论本文基于一个三维悬沙输运伴随同化模型, 通过一系列孪生实验和实际实验, 对模型初始场进行优化反演研究。
孪生实验中, 首先验证了三维悬沙输运模型对于初始场的相对敏感性, 引出了利用伴随同化方法优化初始场的必要性。其次, 探讨了初始场对于不同影响因素的相对敏感性, 包括优化算法、初始猜测值、卫星遥感数据数量、卫星遥感观测数据同化时间窗口的宽度和背景流场误差。结果表明, 在五种优化算法中, GD算法是最优的; 对本模型设置而言, 初始猜测值对反演效果影响较小, 初始场的“真实值”均能得到精确反演; 初始场对卫星遥感数据数量较不敏感, 即便是分布稀疏或云覆盖现象较为严重, 依然能够取得良好的反演效果; 初始场对同化窗口的宽度较为敏感, 合理设置同化窗口的宽度可以有效改善初始场的优化反演效果; 初始场对背景流场的误差较不敏感, 即便是30%的随机误差, 反演结果与给定分布之间的MRE依然小于12%。最后, 比较了伴随同化方法和插值方法重构模型初始场的能力。结果表明, 与传统的插值方法相比, 伴随同化方法是重构模型初始场更有效的手段。
实际实验中, 利用孪生实验的相关结论, 在杭州湾海域同化典型的小潮时期和大潮时期的GOCI卫星遥感资料所得表层SSC数据, 优化反演了模型初始场。结果表明, 无论是小潮时期还是大潮时期, 利用伴随同化方法均得到了更加符合实际的最优初始场, 使得SSC的数值模拟结果和实测数据更加接近。
该研究进一步证实了伴随同化方法优化模型初始场的有效性, 并为改进悬沙输运模型及其他海洋数值模型的初始化方案提供了一种有效的方法。未来我们将尝试同时同化更多、更长时间尺度的观测资料, 为悬沙输运的数值模拟提供更为精确的初始场。
马继瑞, 韩桂军, 李冬. 2002. 变分伴随数据同化在海表面温度预报中的应用研究. 海洋学报, 24(5): 1-7 |
中华人民共和国水利部. 2011. 中国河流泥沙公报-2011. 北京: 中国水利水电出版社, 64
|
中华人民共和国水利部. 2015. 中国河流泥沙公报-2014. 北京: 中国水利水电出版社, 68
|
中国海湾志编纂委员会. 1992. 中国海湾志(第五分册). 北京: 海洋出版社, 1-51
|
江彬彬, 张霄宇, 黄大松, 等. 2015. 基于GOCI的近岸高浓度悬浮泥沙遥感反演——以杭州湾及邻近海域为例. 浙江大学学报(理学版), 42(2): 213-220 |
李丹, 2016.长江口杭州湾潮流能资源评估.杭州: 浙江大学硕士学位论文, 36-37
|
杨旸, 高抒, 汪亚平. 2008. 杭州湾北部潮流深槽区细颗粒物质输运与再悬浮过程. 海洋学报, 30(2): 92-101 |
唐建华, 2007.长江口及其邻近海域黏性细颗粒泥沙絮凝特性研究.上海: 华东师范大学硕士学位论文, 54-57
|
曹振轶, 胡克林. 2002. 长江口二维非均匀悬沙数值模拟. 泥沙研究, (6): 66-73 |
Alekseev A K, Navon I M, Steward J L, 2009. Comparison of advanced large-scale minimization algorithms for the solution of inverse ill-posed problems. Optimization Methods and Software, 24(1): 63-87 DOI:10.1080/10556780802370746 |
Chen C, Liu H, Beardsley R C, 2003. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model:application to coastal ocean and estuaries. Journal of Atmospheric and Oceanic Technology, 20(1): 159-186 DOI:10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2 |
Chen H B, Miao C B, Lv X Q, 2013. Estimation of open boundary conditions for an internal tidal model with adjoint method:a comparative study on optimization methods. Mathematical Problems in Engineering: 802136 |
Chen W B, Liu W C, Hsu M H et al, 2015. Modeling investigation of suspended sediment transport in a tidal estuary using a three-dimensional model. Applied Mathematical Modelling, 39(9): 2570-2586 DOI:10.1016/j.apm.2014.11.006 |
Chen X L, Lu J Z, Cui T W et al, 2010. Coupling remote sensing retrieval with numerical simulation for SPM study-taking Bohai Sea in China as a case. International Journal of Applied Earth Observation and Geoinformation, 12(S2): S203-S211 |
Du P J, Ding P X, Hu K L, 2010. Simulation of three-dimensional cohesive sediment transport in Hangzhou Bay, China. Acta Oceanologica Sinica, 29(2): 98-106 DOI:10.1007/s13131-010-0028-9 |
Dufois F, Verney R, Le Hir P et al, 2014. Impact of winter storms on sediment erosion in the Rhone River prodelta and fate of sediment in the Gulf of Lions (North Western Mediterranean Sea). Continental Shelf Research, 72: 57-72 DOI:10.1016/j.csr.2013.11.004 |
Elbern H, Strunk A, Schmidt H et al, 2007. Emission rate and chemical state estimation by 4-dimensional variational inversion. Atmospheric Chemistry and Physics, 7(14): 3749-3769 DOI:10.5194/acp-7-3749-2007 |
Gourgue O, Baeyens W, Chen M S et al, 2013. A depth-averaged two-dimensional sediment transport model for environmental studies in the Scheldt Estuary and tidal river network. Journal of Marine Systems, 128: 27-39 DOI:10.1016/j.jmarsys.2013.03.014 |
He X Q, Bai Y, Pan D L et al, 2013. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sensing of Environment, 133: 225-239 DOI:10.1016/j.rse.2013.01.023 |
Hestenes M R, Stiefel E, 1952. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Bureau of Standards (United States), 49(6): 409-436 DOI:10.6028/jres.049.044 |
Hu K L, Ding P X, Wang Z B et al, 2009. A 2D/3D hydrodynamic and sediment transport model for the Yangtze Estuary, China. Journal of Marine Systems, 77(1-2): 114-136 DOI:10.1016/j.jmarsys.2008.11.014 |
Jin G Z, Liu Q, Lv X Q, 2015. Inversion study of vertical eddy viscosity coefficient based on an internal tidal model with the adjoint method. Mathematical Problems in Engineering: 915793 |
Lee C, Schwab D J, Beletsky D et al, 2007. Numerical modeling of mixed sediment resuspension, transport, and deposition during the March 1998 episodic events in southern Lake Michigan. Journal of Geophysical Research:Oceans, 112(C2): C02018 |
Liu D C, Nocedal J, 1989. On the limited memory BFGS method for large scale optimization. Mathematical Programming, 45(1-3): 503-528 DOI:10.1007/BF01589116 |
Liu J, Liu J H, He X Q et al, 2018. Diurnal dynamics and seasonal variations of total suspended particulate matter in highly turbid Hangzhou bay waters based on the geostationary ocean color imager. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 11(7): 2170-2180 DOI:10.1109/JSTARS.2018.2830335 |
Liu Y Z, Shen Y L, Lv X Q et al, 2017. Numeric modelling and risk assessment of pollutions in the Chinese Bohai Sea. Science China (Earth Sciences), 60(8): 1546-1557 DOI:10.1007/s11430-016-9062-y |
Liu Y, Storey C, 1991. Efficient generalized conjugate gradient algorithms, part 1:theory. Journal of Optimization Theory and Applications, 69(1): 129-137 DOI:10.1007/BF00940464 |
Mehta A J, Mcanally Jr W H, Hayter E J et al, 1989. Cohesive sediment transport. Ⅱ:application. Journal of Hydraulic Engineering, 115(8): 1094-1112 DOI:10.1061/(ASCE)0733-9429(1989)115:8(1094) |
Normant C L, 2000. Three-dimensional modelling of cohesive sediment transport in the Loire estuary. Hydrological Processes, 14(13): 2231-2243 DOI:10.1002/1099-1085(200009)14:13<2231::AID-HYP25>3.0.CO;2-# |
Papanicolaou A N, Elhakeem M, Krallis G et al, 2008. Sediment transport modeling review-current and future developments. Journal of Hydraulic Engineering, 134(1): 1-14 |
Partheniades E, 1965. Erosion and deposition of cohesive soils. Journal of the Hydraulics Division, 91(1): 105-139 |
Peng S Q, Xie L, 2006. Effect of determining initial conditions by four-dimensional variational data assimilation on storm surge forecasting. Ocean Modelling, 14(1-2): 1-18 DOI:10.1016/j.ocemod.2006.03.005 |
Polak E, Ribière G, 1969. Note sur la convergence de méthodes de directions conjuguées. Revue Française Information Recherche Opérationnelle, 3(16): 35-43 |
Polyak B T, 1969. The conjugate gradient method in extremal problems. USSR Computational Mathematics and Mathematical Physics, 9(4): 94-112 DOI:10.1016/0041-5553(69)90035-4 |
Ramakrishnan R, Rajawat A S, 2012. Simulation of suspended sediment transport initialized with satellite derived suspended sediment concentrations. Journal of Earth System Science, 121(5): 1201-1213 DOI:10.1007/s12040-012-0222-6 |
Ryu J H, Choi J K, Eom J et al, 2011. Temporal variation in Korean coastal waters using Geostationary Ocean Color Imager. Journal of Coastal Research, SI64: 1731-1735 |
Sasaki Y, 1970. Some basic formalisms in numerical variational analysis. Monthly Weather Review, 98(12): 875-883 DOI:10.1175/1520-0493(1970)098<0875:SBFINV>2.3.CO;2 |
Schwab D J, Beletsky D, Lou J, 2000. The 1998 coastal turbidity plume in lake Michigan. Estuarine, Coastal and Shelf Science, 50(1): 49-58 DOI:10.1006/ecss.1999.0531 |
Song H, Edwards C A, Moore A M et al, 2016. Data assimilation in a coupled physical-biogeochemical model of the California current system using an incremental lognormal 4-dimensional variational approach:Part 2-Joint physical and biological data assimilation twin experiments. Ocean Modelling, 106: 146-158 DOI:10.1016/j.ocemod.2016.09.003 |
Wang C H, Li X Y, Lv X Q, 2013. Numerical study on initial field of pollution in the Bohai Sea with an adjoint method. Mathematical Problems in Engineering: 104591 |
Wang D S, Cao A Z, Zhang J C et al, 2018a. A three-dimensional cohesive sediment transport model with data assimilation:model development, sensitivity analysis and parameter estimation. Estuarine, Coastal and Shelf Science, 206: 87-100 DOI:10.1016/j.ecss.2016.08.027 |
Wang D S, Zhang J C, He X Q et al, 2018b. Parameter estimation for a cohesive sediment transport model by assimilating satellite observations in the Hangzhou Bay:temporal variations and spatial distributions. Ocean Modelling, 121: 34-48 DOI:10.1016/j.ocemod.2017.11.007 |
Woolnough S J, Allen J R L, Wood W L, 1995. An exploratory numerical model of sediment deposition over tidal salt marshes. Estuarine, Coastal and Shelf Science, 41(5): 515-543 DOI:10.1016/0272-7714(95)90025-X |
Xie D F, Wang Z B, Gao S et al, 2009. Modeling the tidal channel morphodynamics in a macro-tidal embayment, Hangzhou Bay, China. Continental Shelf Research, 29(15): 1757-1767 DOI:10.1016/j.csr.2009.03.009 |
Yang X F, Mao Z H, Huang H Q et al, 2016. Using GOCI retrieval data to initialize and validate a sediment transport model for monitoring diurnal variation of SSC in Hangzhou Bay, China. Water, 8(3): 108 DOI:10.3390/w8030108 |
Zhang Q L, Gao Y Q, Lv X Q, 2015. Estimation of oceanic eddy viscosity profile and wind stress drag coefficient using adjoint method. Mathematical Problems in Engineering: 309525 |
Zong X L, Xu M J, Xu J L et al, 2018. Improvement of the ocean pollutant transport model by using the surface spline interpolation. Tellus A:Dynamic Meteorology and Oceanography, 70(1): 1-13 |
 2020, Vol. 51
2020, Vol. 51


