中国海洋湖沼学会主办。
文章信息
- 唐启邦, 欧素英, 蔡华阳, 杨清书. 2020.
- TANG Qi-Bang, OU Su-Ying, CAI Hua-Yang, YANG Qing-Shu. 2020.
- 珠江磨刀门河口水位与海平面、上游流量的联合分布关系异变研究
- ABRUPT VARIATION OF JOINT DISTIBUTION OF WATER LEVEL, SEA LEVEL, AND RIVER DISCHARGE IN THE MODAOMEN ESTUARY OF THE ZHUJIANG (PEARL) RIVER
- 海洋与湖沼, 51(5): 1080-1092
- Oceanologia et Limnologia Sinica, 51(5): 1080-1092.
- http://dx.doi.org/10.11693/hyhz20191000194
文章历史
-
收稿日期:2019-10-22
收修改稿日期:2020-01-15
2. 中山大学 海洋工程与技术学院河口海岸研究所 广州 510275;
3. 河口水利技术国家地方联合工程实验室 广州 510275;
4. 广东省海岸与岛礁工程技术研究中心 广州 510275
2. Institute of Estuarine and Coastal Research, School of Marine Engineering and Technology, Sun Yat-sen University, Guangzhou 510275, China;
3. State and Local Joint Engineering Laboratory of Estuarine Hydraulic Technology, Guangzhou 510275, China;
4. Guangdong Provincial Engineering Research Center of Coasts, Islands and Reefs, Guangzhou 510275, China
河口是陆海相互作用的过渡区域, 其水位变化一方面是径潮动力相互作用的直接结果, 既受自下而上的河口潮波、海平面上升等海洋动力的影响, 也受自上而下的上游径流作用(Cai et al, 2016, 2019a); 另一方面强人类活动引起的地形边界改变, 直接或间接导致河口三角洲水位、潮差、盐度等动力结构的变化, 引起河口沉积作用过程、化学及生态过程的调整改变, 进而对河口水资源规划、防洪、排涝等河口治理策略提出了新的挑战。作为我国人口集聚程度极大的珠江河口地区, 随着其经济的快速发展及城市规模的迅速扩张, 人类活动对河口环境的影响已远超环境自我修复能力, 导致河口环境急剧恶化。研究表明, 近几十年来珠江三角洲河道大规模无序挖砂、口门围垦、航道整治及上游水库建设等强人类活动导致河口三角洲的地形边界、水文环境已经发生明显异变, 如口门水道缩窄延长、河道下切、过水断面面积增大, 珠江来沙量显著减少, 三角洲内马口分流分沙比减少、三水分流分沙比增加等(陈子燊等, 2015; 倪培桐等, 2016; Wu et al, 2016; 陆永军等, 2019; Liu et al, 2019), 相同珠江流量条件下三角洲中上段的水位明显下降, 水位出现由缓慢上升转为急剧下降的异变等(蒋陈娟等, 2012); 而水位异变导致洪季河网区水位坡降变缓, 泄洪排涝效率降低, 枯季潮汐动力明显增强, 河口盐水入侵加剧(黄洪城等, 2014; Cai et al, 2019b)。珠江三角洲水文的自然演变规律在强人类活动干预下甚至出现自然过程难以达到的异变, 而河口水文过程及其规律是水资源管理利用的重要依据, 因此研究陆海相互作用下强人类活动对河口三角洲区水位变化的影响, 既是河口动力过程研究的热点问题, 也对探讨人类活动驱动下河口区域洪潮水位预报、水资源的高效利用以及河口治理等具有重要的现实意义, 为今后磨刀门河口的综合整治规划、有序开发航运资源、防洪排涝和调水压咸等迫切社会经济需求提供重要技术支撑。
近20年来, 众多研究者采用小波变换、理论解等不同的方法辨识河口地区不同时间尺度的水位变化及机制, 比如潮周期变化、水位的长期变化趋势、极端低水位及设计水位的变化等(欧素英等, 2004a; 欧素英等, 2004b; 蒋陈娟等, 2012; 陈子燊等, 2013, 蔡华阳等, 2018; 杨昊等, 2019; Yang et al, 2019a)。但如何从多因素共同影响下的水位变化中辨识出强人类活动的作用仍有待于进一步研究。近年来广泛应用于水文要素研究中的Copula联合概率分布方法, 在研究多边界联合约束下的水文要素分布上具有明显的优势(陈子燊等, 2015, 2018; 陈玲舫等, 2017; Bacopoulos, 2017; Liu et al, 2018)。本文尝试从概率统计分布角度, 采用Copula联合概率分布方法, 选取受强人类活动影响显著的珠江磨刀门河口为研究区域, 以珠江流量为上游边界, 下边界不考虑潮汐的短周期变化, 以河口月均海平面为月均态下海洋动力的综合驱动因子, 拟研究磨刀门月均水位与上下边界条件即三灶海平面(即平均海平面水位)和马口流量之间的联合依赖关系, 比较研究上游流量和外海海平面共同约束下强人类活动前后的水位概率分布特征及极端水位风险的变化过程, 对比研究其联合依赖关系异变, 进而定量计算强人类活动对水位变化的影响程度。
1 研究区域概况本文研究区域为珠江磨刀门河口, 包括西江干流水道-磨刀门水道(如图 1所示)。西北江水沙经思贤滘口分水分沙后, 约78%—84%的径流量通过西江干流水道进入西北江三角洲。磨刀门作为珠江八大口门中入海径流量和输沙量最大的河口, 约36%的珠江径流量通过磨刀门进入南海, 是珠江最重要的泄洪通道。磨刀门河口潮差较小, 口门三灶站多年平均潮差小于1m。因此, 磨刀门河口径流动力强而潮汐动力弱, 是典型的河优型河口。基于上游马口水文控制站1965—2016年的月均流量统计资料, 可得洪季(4—9月)历史最大流量为29000m3/s, 平均流量为10810m3/s; 枯季(10月—次年3月)历史最大流量为14500m3/s, 平均流量为3428m3/s; 年均历史最大流量为9978m3/s, 平均流量为7119m3/s。口门三灶站1965—2016年的月均海平面数据显示, 其洪季历史最大海平面为0.90m, 平均海平面为0.63m;枯季历史最大海平面为0.87m, 平均海平面为0.56m;年平均历史最大海平面为0.70m, 平均海平面为0.59m。
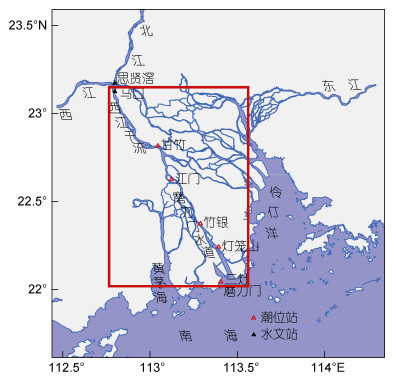 |
| 图 1 研究区域图 Fig. 1 Map of the study area |
从20世纪50年代开始, 磨刀门河口先后经历了联围筑闸、滩涂围垦、航道整治规划以及大规模的河道无序采砂等强人类活动。特别是20世纪90年代磨刀门完成口门整治后, 口门人为向海快速延伸约16km, 使得原本具有泄洪纳潮功能的宽阔内海湾消失, 河口环境转变为受人工导堤控制的河道, 口门迅速向海延伸, 延伸速度超越自然过程变化, 口门边界条件发生明显异变。西江上游流域方面, 建有大藤峡等骨干水源工程, 以西江龙滩及大藤峡等水库为骨干构建水资源调配体系, 直接改变磨刀门河口的来水来沙条件(张旭等, 2013)。而对磨刀门河口地形影响最为明显的是大规模、无序的河道采砂。根据调查分析(韩龙喜等, 2005), 1991—1994年(采砂高峰期)3年内从珠海大桥至竹银近口段仅24.4km的范围内, 共挖河沙2.4×107m3, 平均年挖砂量8×106m3; 1994—2000年6年内共挖砂1.92×107m3, 平均年挖砂量3.2×106m3; 1997年因在洪湾水道中段建“洪湾北保税区”, 需挖砂吹填, 从横州水道北口左侧河床采砂, 采砂量约为1×107m3。大规模挖砂以及航道整治引起磨刀门河口上游河段河床大幅度下切, 河床深泓平均下切0.59—2.25m, 河床冲淤演变趋势由原来淤积为主转变为显著冲刷(贾良文等, 2002)。自禁沙令颁布后, 2000年后河道采砂才逐渐减少。
2 数据与方法 2.1 数据及处理本文以1965—2016年的马口月均流量作为上游河流边界, 不考虑外海潮汐的短周期变化影响, 以三灶站的月均海平面为外海动力边界, 分别采用灯笼山、竹银、江门、甘竹站的月均水位序列进行联合依赖关系研究, 站位位置如图 1所示。根据人类活动历程(罗宪林等, 2002; 刘锋等, 2011; 袁菲等, 2018), 自1960年以来, 磨刀门河道整体上横断面平均河宽缩窄, 水深增加, 宽深比减小, 主槽断面面积增加; 20世纪80年代后期磨刀门开始大规模围垦整治, 直至20世纪90年代中期才基本结束。西北江水沙经思贤滘马口三水多年分流、分沙比大幅度变化发生在1993年, 其中洪季同多年变化一样, 也发生在1993年, 枯季比多年变化提早4年, 发生在1989年(胡德礼等, 2009)。基于此, 本文将1965—1985年划分为强人类活动前自然演变阶段, 2000—2016年作为强人类活动剧烈影响后阶段, 1985—2000年为相应的过渡阶段, 比较研究在马口流量和三灶海平面影响下磨刀门河口沿程各站水位对强人类活动的响应过程及演变规律。
2.2 Copula方法自然系统中水文事件大部分都是多因素共同影响作用的结果。Sklar(1959)提出Copula理论, 是研究多变量相关性及关联性的重要数学工具, 能够有效建立多变量之间的非线性关系, 且其边缘分布灵活, 形式不受边缘分布限制。目前Copula方法已被广泛应用于洪水、暴雨、干旱等多变量水文事件的联合概率分布研究(陈子燊等, 2013; Yang et al, 2019b)。
根据Sklar定理, 若F是一个p维随机变量X=(X1, …, XP)的累积分布函数, 其边缘分布是连续函数Fi(i=1, …, p), 则存在唯一一个Copula函数C, 使得:
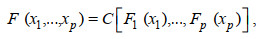 (1)
(1)式中, Copula函数C为一个多元分布函数, 其中每个变量的边缘概率分布是均匀的, 可捕捉不同变量之间的线性和非线性依赖关系。
基于Copula的条件概率分布函数, 可计算给定流量或(和)海平面条件下的水位条件概率, 即同时满足X1≤x1, X2≤x2的条件概率或同时满足X1≤x1, X2≤x2, X3≤x3三变量的条件概率分别为:
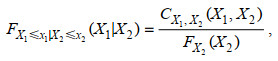 (2)
(2)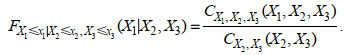 (3)
(3)一般来说, 如果x1出现超过某个极大值或低于某个极小值的极端情况时, 则事件x1可定义为危险或处于危险之中(Salvadori et al, 2004)。例如, 当河口沿程各站水位低于该站10%水位累积概率所对应的值时定义为低水位事件, 记为F(x1)low_WL≤10%, 类似的, 高水位事件定义为水位高于第90分位数所对应的水位值, 记为F(x1)high_WL≥90%。高水位及低水位事件的条件概率可由式(2)或(3)计算。
由于河口三角洲的月均水位既受到上游流量的影响, 同时也受到外海海平面变化的作用, 本文通过Copula函数来构建水位-海平面-流量的联合依赖关系模型, 不仅可以描述水位与海平面、流量的非线性依赖关系, 而且能够通过比较强人类活动前后联合依赖关系的变化, 从概率统计角度定量研究强人类活动对磨刀门河口沿程各站水位的影响程度。具体步骤为: 1)首先通过相关分析初步研究强人类活动影响下磨刀门河道沿程各站水位与海平面、流量的线性关系是否发生明显变化。2)确定强人类活动前后磨刀门河口沿程各站月均水位、马口流量及三灶海平面的最优概率分布, 即选择四种理论概率分布(即高斯分布、伽马分布、对数正态分布和威布尔分布)对各变量数据进行拟合, 采用卡方检验进行拟合优度比选, 确定最优边缘分布, 并初步研究人类活动前后单变量概率分布的变化。3)确定强人类活动前后磨刀门河口沿程各站月平均水位与上游流量、月平均海平面的最优Copula函数, 分析变量间相互依赖关系的变化。基于赤池信息量准则(Akaike information criterion, AIC), 从四个Copula函数即Gaussian函数和阿基米德Copula家族中Clayton、Gumbel和Frank函数中选择最优Copula函数来连接各变量, 构建双变量和三变量的联合分布模型, 比较分析人类活动前后两个阶段水位与流量、海平面之间联合依赖结构的变化。4)根据构建的水位与海平面、流量的联合依赖模型, 通过式(2)或(3)计算任意给定流量或(和)海平面条件下出现某个水位事件(特别是高水位及低水位事件)的条件概率。通过比较强人类活动前后相同条件概率所对应的水位事件的改变, 或同样水位事件所对应条件概率的变化, 定量分析强人类活动对水位的影响程度。
3 结果分析 3.1 人类活动前后月均水位与海平面、流量线性关系的变化强人类活动前(1965—1985年)和强人类活动后(2000—2016年)各站水位与三灶海平面及马口流量的相关系数如表 1所示。由表 1可见, 自甘竹至灯笼山段, 其月均水位与海平面的线性相关系数随距三灶站距离的缩小逐渐增大, 接近外海三灶的灯笼山站, 其相关系数最大。强人类活动后, 外海海平面对沿程各站水位的线性影响有所增强, 水位-海平面的线性相关系数较人类活动前均略有增加, 其中, 竹银站的增加幅度最大(由0.76增大到0.82)。反之, 上游马口流量对磨刀门沿程各站水位的影响在强人类活动影响后则有所减弱。其中, 甘竹和江门站水位-流量的线性相关系数分别由0.98、0.98分别减小至0.97、0.95, 上游流量影响强度略有减小, 但强人类活动后磨刀门水道的竹银和灯笼山站的水位-流量相关系数分别由0.94、0.74大幅减少为0.81、0.56, 即强人类活动影响下水位与马口流量的线性关系显著减弱。
| 关系 | 甘竹 | 江门 | 竹银 | 灯笼山 | |||||||
| 前 | 后 | 前 | 后 | 前 | 后 | 前 | 后 | ||||
| 水位-海平面 | 0.57 | 0.58 | 0.60 | 0.60 | 0.76 | 0.82 | 0.94 | 0.95 | |||
| 水位-流量 | 0.98 | 0.97 | 0.98 | 0.95 | 0.94 | 0.81 | 0.74 | 0.56 | |||
| 注:前/后分别代表强人类活动前/强人类活动后 | |||||||||||
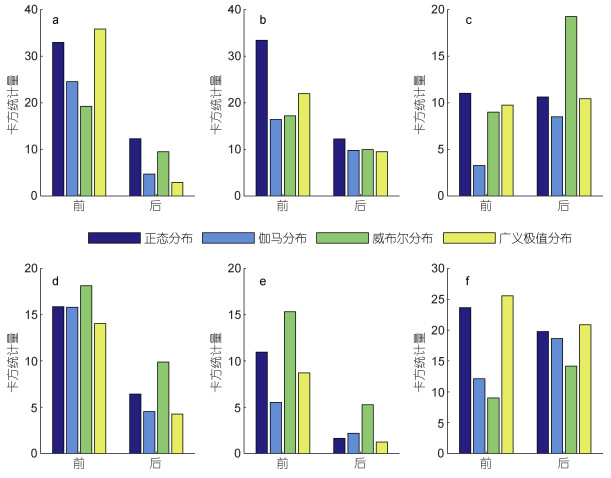
单变量边缘分布的卡方检验结果如图 2所示。各站月均水位的最优概率分布有所差异, 其中, 竹银站更倾向于伽马分布, 灯笼山站服从广义极值分布, 而马口流量更符合威布尔分布。采用图 2中各变量的最优概率分布, 可得强人类活动前后的累积频率分布曲线, 如图 3所示。受强人类活动影响后, 沿程各站低累积概率(< 0.18)所对应的水位有所增大(曲线右移), 反之, 高累积概率(> 0.18)所对应的水位有所减小(曲线左移)。对于海平面变化来说, 强人类活动影响后的概率密度分布曲线整体右移, 表明高水位事件概率明显增大, 海平面变化有较明显的上升趋势。对马口流量而言, 强人类活动前后的概率分布曲线形态比较一致, 但因思贤滘分流比的减小和上游流量峰值的降低, 平均流量所对应的概率有所增大, 而相同累积概率条件下所对应的流量有所降低(累积概率曲线整体左移)。由图 3可见拟合的边缘分布与观测数据吻合较好, 能够用于后续依赖关系的异变研究。
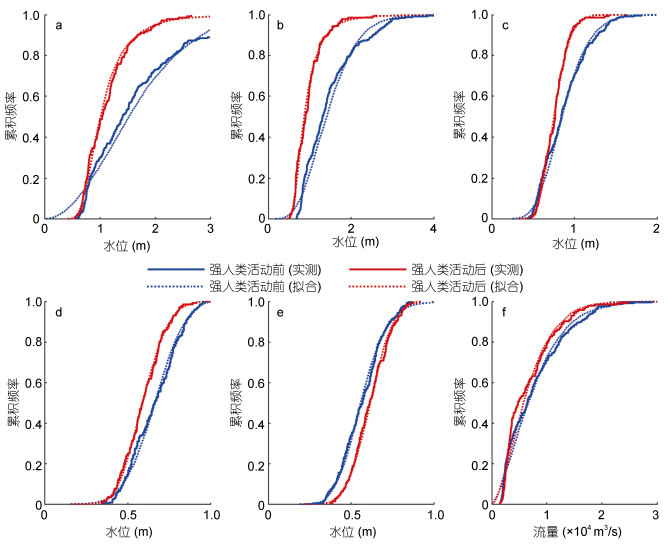 |
| 图 3 强人类活动前后磨刀门河口沿程各站变量边缘分布累积频率曲线 Fig. 3 Cumulative frequency curves of marginal distribution of different variables at stations along the Modaomen estuary before and after intensive human interventions |
由2.2节可知, 根据AIC准则选择最佳的Copula函数, 结果如表 2所示。选取AIC值最小的Gaussian函数作为水位-海平面和水位-流量的最佳拟合Copula联合分布函数用于后续依赖关系的异变研究。
| Coupla函数 | 强人类活动前的AIC | 强人类活动后的AIC | |||
| (水位-海平面) | (水位-流量) | (水位-海平面) | (水位-流量) | ||
| 甘竹站 | |||||
| Gaussian | -117.47 | -758.10 | -84.96 | -268.28 | |
| Clayton | 1096.96 | -441.00 | 553.20 | 119.20 | |
| Frank | -33.75 | -348.22 | -16.21 | -72.23 | |
| Gumbel | 2515.82 | -583.50 | 1366.50 | -107.93 | |
| 江门站 | |||||
| Gaussian | -143.82 | -789.77 | -102.28 | -234.81 | |
| Clayton | 905.81 | -457.61 | 330.09 | 236.18 | |
| Frank | -65.08 | -282.83 | -59.52 | -196.84 | |
| Gumbel | 2465.86 | -671.14 | 1190.77 | -21.05 | |
| 竹银站 | |||||
| Gaussian | -261.71 | -522.91 | -179.54 | -128.82 | |
| Clayton | 259.27 | -109.41 | -84.95 | 620.02 | |
| Frank | 8.25 | -399.65 | -133.01 | -84.47 | |
| Gumbel | 1515.63 | -133.92 | 639.24 | 714.78 | |
| 灯笼山站 | |||||
| Gaussian | -544.13 | -230.31 | -337.99 | -49.43 | |
| Clayton | -388.32 | 625.50 | -290.33 | 1026.14 | |
| Frank | -266.46 | -170.66 | -265.50 | 69.80 | |
| Gumbel | 10.24 | 1513.35 | -99.63 | 1512.11 | |
| 注:粗体代表拟合最好的Copula函数 | |||||
图 4和图 5分别给出各站强人类活动前后水位-海平面和水位-流量的联合累积频率关系曲线, 从中可以更直观的看出强人类活动影响下水位-海平面和水位-流量依赖关系异变情况。相同海平面影响下, 强人类活动影响后甘竹、竹银和灯笼山站的低水位-低海平面联合累积概率曲线明显抬升, 而高水位-高海平面事件则下降(图 4), 表明低海平面条件下发生低水位事件的联合累积概率明显提升, 发生低水位事件的风险增大, 反之, 高水位事件风险降低; 同流量条件下, 低水位-低流量变化不明显, 而强人类活动后甘竹至灯笼山站高水位-高流量的联合累积概率曲线显著下降(图 5)。这表明水位与海平面、流量的联合依赖关系发生明显改变, 低水位与海平面关系的敏感度增加, 而高水位与海平面关系的敏感度下降。低水位与流量关系的敏感度基本不变, 而高水位与海流量关系的敏感度明显下降。
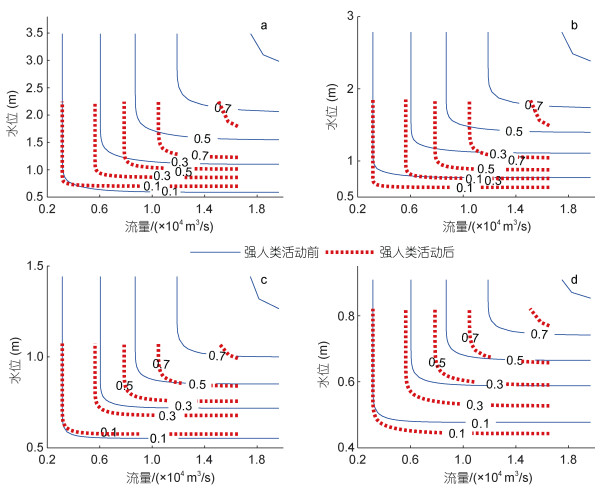 |
| 图 5 强人类活动前后流量-水位联合累积频率曲线 Fig. 5 Combined river discharge-water level recurrence frequency before and after intensive human interventions |
由3.1节可知, 海平面或流量和水位的线性相关性较强, 因此, 海平面或流量和水位同时出现的条件概率会存在一个阈值范围(即图 4、图 5中等值线弯曲处), 表明低水位条件仅匹配出现一定范围的低海平面或低流量, 相应地, 磨刀门河口沿程各站高水位出现时, 三灶站的海平面或马口站的流量也必定在某一个范围内变动, 大于或小于此海平面或流量范围的值基本不会出现。
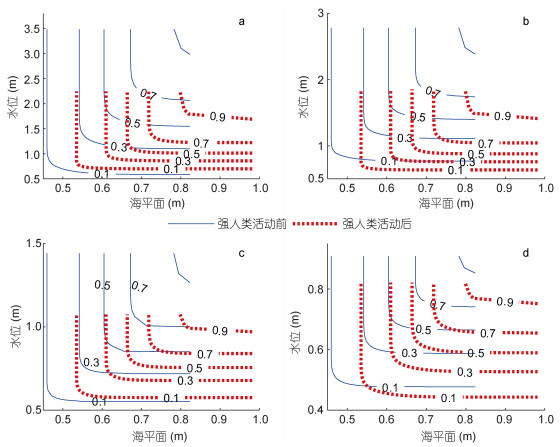
3.4 强人类活动前后月均水位异变的风险评估在给定海平面或流量概率事件的条件下, 基于构建的联合分布依赖模型可探讨水位事件发生的条件概率, 特别是极端水位事件发生的概率。采用式(2)计算极端海平面或流量条件下各站水位的条件概率, 即F(x2)low_(SL/D)≤10%和F(x2)high_(SL/D)≥90%, 同时计算海平面事件或流量事件影响下水位阈值的累积概率, 即高(F(x1)high_WT≥90%)和低(F(x1)low_WT≤10%)水位事件, 计算结果如图 6和图 7所示, 其中较小的数值意味着发生极端水位事件的风险较低的。图 6和7中两条实线(红、蓝)分别代表强人类活动前极端低海平面事件(对应累积概率小于10%的海平面阈值)和极端高海平面事件(对应累积概率大于90%的海平面阈值)条件下水位的累积概率, 而两条虚线(红, 蓝)对应强人类活动后极端海平面事件条件下的水位累积概率。两种条件分布曲线之间的概率差(即图中阴影区域)反映水位对海平面或流量变化敏感程度, 阴影区域面积的大小表明水位对海平面和流量的敏感性大小因位置(不同站位)和时段(强人类活动前后)的不同而有所差异。
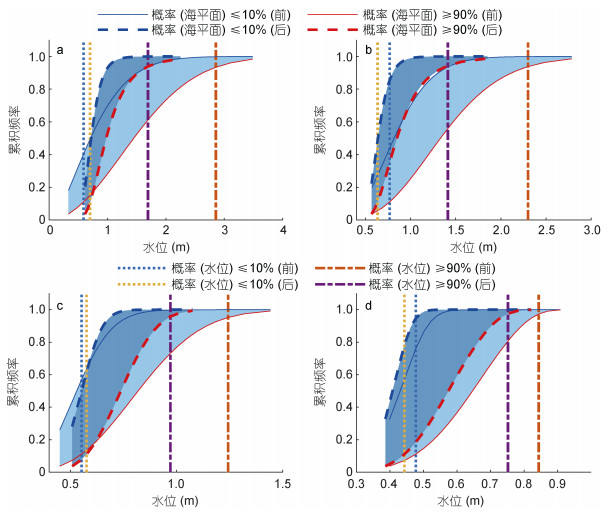 |
| 图 6 强人类活动前后海平面极端情况下的水位条件分布 Fig. 6 Conditional distribution of water level under extreme cases of sea level before and after intensive human interventions 注:蓝色区域表示概率差, 其面积大小表明流量与水位的敏感度, 浅蓝色是强人类活动前, 深蓝色是强人类活动后 |
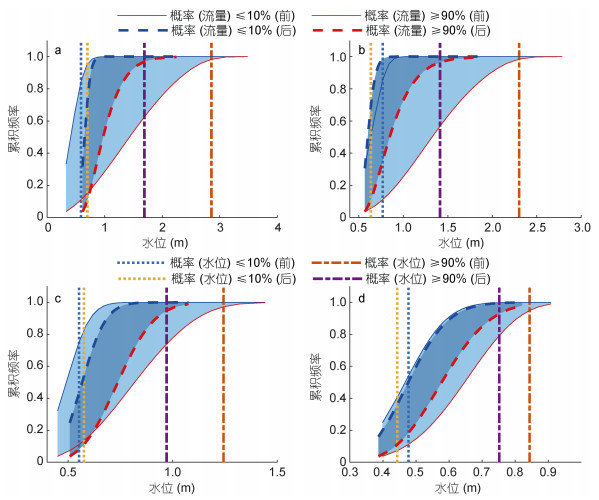 |
| 图 7 强人类活动前后流量极端情况下的水位条件分布 Fig. 7 Conditional distribution of water level under extreme cases of river discharge before and after intensive human interventions |
对于各站水位-海平面的依赖性(图 6), 强人类活动影响后概率差区域面积明显缩小, 表明各站月均水位对海平面的依赖性有所减弱。对于甘竹站(图 6a)水位与海平面的遭遇概率, 在高海平面(90%)条件下, 当累计频率大于0.18时, 水位曲线左移, 表明水位下降; 当累计频率小于0.18时, 水位曲线右移, 表明水位上升。而在低海平面(10%)条件下, 同样出现这种情况, 当累计频率大于0.5时, 水位曲线左移, 表明水位下降; 当累计频率小于0.5时, 水位曲线右移, 表明水位上升。三角洲中段的江门站(图 6b), 在同一海平面条件下, 强人类活动后水位曲线整体左移, 表明水位整体下降。三角洲中下段的竹银站(图 6c), 强人类活动后在高海平面(90%)条件下, 当累计频率大于0.18时, 水位曲线左移, 同概率下水位下降; 当累计频率小于0.18时, 水位曲线右移, 表明水位上升。而在低海平面(10%)条件下, 同样出现这种情况, 当累计频率大于0.6时, 水位曲线左移, 表明水位下降; 当累计频率小于0.6时, 水位曲线右移, 表明水位上升。三角洲下段的灯笼山站(图 6d), 在同一海平面条件下, 强人类活动后水位曲线整体左移, 表明水位整体下降。由此可见, 强人类活动影响后, 各站水位变化幅度变窄。其中甘竹站和竹银站在同一海平面概率下, 较高的累计频率对应的水位下降, 较低的累计频率对应的水位上升; 江门站和灯笼山站则整体水位下降。
类似的, 图 7显示强人类活动对磨刀门河口沿程各站水位-流量联合依赖关系影响。与水位-海平面联合依赖关系相同, 强人类活动影响后各站的概率差区域面积明显缩小, 表明各站月均水位对流量的依赖性均有所减弱。对于水位与流量的遭遇概率, 甘竹站(图 7a)在高流量(90%)条件下, 当累计频率大于0.18时, 水位曲线左移, 同条件概率下水位下降; 当累计频率小于0.18时, 水位曲线右移, 水位上升。而在低流量(10%)条件下, 水位曲线整体右移, 表明水位上升。三角洲中段的江门站(图 7b), 在同一海平面条件下, 强人类活动后水位曲线整体左移, 表明水位整体下降。三角洲中下段的竹银站(图 7c), 在高流量(90%)条件下, 当累计频率大于0.2时, 水位曲线左移, 表明水位下降; 当累计频率小于0.2时, 水位曲线右移, 表明水位上升。而在低流量(10%)条件下, 水位曲线整体右移, 表明水位整体抬升。三角洲下段的灯笼山站(图 7d), 在高流量(90%)条件下, 强人类活动后水位曲线整体左移, 表明水位整体下降; 在低流量(10%)条件下, 水位曲线整体右移, 表明水位整体抬升。可以看出, 各站在高流量(90%)条件下, 水位基本上呈下降趋势, 但甘竹站和竹银站在低累计频率下对应的水位上升; 而低流量(10%)条件下, 甘竹, 竹银和灯笼山站整体水位上升, 但江门站整体水位呈下降趋势。
前文已经分别分析了海平面或流量对水位的影响, 然而不同的极端水位事件可能是单因素影响, 也可能是海平面与流量共同作用引起的(如复合极低海平面和低流量事件), 即三角洲水位同时受海平面和流量的共同影响, 图 8即为磨刀门河口四个站点的月均水位、海平面和流量耦合条件下, 采用式(3)所计算的各站发生极端水位事件的条件概率。
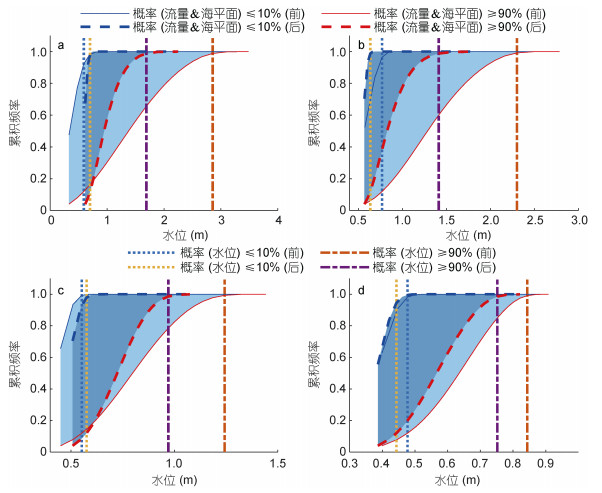 |
| 图 8 海平面和流量极端情况下的水位条件分布 Fig. 8 Conditional distribution of water level under extreme cases of sea level and river discharge |
由图 8可见, 在上、下边界的共同影响下, 三角洲大规模强人类活动之后, 各站概率差区域面积均有所减小, 表明各站水位对流量及海平面的敏感性均有不同程度的减弱。各站在高海平面和流量(90%)条件下, 水位基本上呈下降趋势, 但甘竹站和竹银站在低累积频率下(< 18%)对应的水位上升; 而低海平面和流量(10%)条件下, 甘竹站和竹银站整体水位上升, 但江门站和灯笼山站整体水位呈下降趋势。结合前文, 可以看出图 6中竹银、灯笼山站的图形与图 8中两站相对应的图形相似, 说明下游站位水位与海平面的依赖关系更加密切。而图 7中甘竹、江门站的图形与图 8中两站相对应的图形相似, 说明上游站位流量与水位的依赖关系更加密切。
给定遭遇概率下, 当水位不断增大到一定值时海平面或流量将达到一个极小值, 这个水位值定义为有效最大水位(刘曾美等, 2013)。为定量计算强人类活动的影响, 规定累计频率趋近于1时的水位为有效最大水位。计算给定不同海平面和流量遭遇概率下的有效最大水位, 结果如表 3所示。由表 3可见, 对于相同的水位与海平面、流量的遭遇概率, 强人类活动后其所对应的水位值较人类活动前有明显下降, 特别是在高海平面和高流量概率事件驱动下, 磨刀门河口沿程水位下降越为显著。如给定水位与海平面、流量的遭遇概率为0.9时, 甘竹站降幅最大, 下降了1.24m;江门站次之, 下降幅度为0.63m;竹银站和灯笼山站分别下降了0.25m、0.09m。当给定水位与海平面、流量的遭遇概率为0.5时, 甘竹站和江门站的水位降幅分别为0.88m和0.65m, 竹银站和灯笼山站降幅偏小, 分别下降了0.07m和0.06m;而当水位与海平面、流量的遭遇概率为0.1时, 甘竹站和江门站月平均水位分别下降了0.21m和0.26m, 竹银站略为上升0.05m, 灯笼山站下降0.01m。从遭遇概率的角度看, 低海平面和低流量条件下各站月平均水位的下降幅度明显小于高海平面和高流量条件下月平均水位的变幅。从空间上看, 上游站位月平均水位的下降幅度要明显大于下游站位。
| 潮位站 | 遭遇概率P | 强人类活动前水位(m) | 强人类活动后水位(m) | 差值(m) |
| 0.1 | 1.03 | 0.81 | -0.21 | |
| 甘竹站 | 0.5 | 2.15 | 1.27 | -0.88 |
| 0.9 | 3.49 | 2.25 | -1.24 | |
| 0.1 | 0.96 | 0.70 | -0.26 | |
| 江门站 | 0.5 | 1.73 | 1.08 | -0.65 |
| 0.9 | 2.49 | 1.85 | -0.63 | |
| 0.1 | 0.62 | 0.67 | 0.05 | |
| 竹银站 | 0.5 | 0.95 | 0.87 | -0.07 |
| 0.9 | 1.32 | 1.07 | -0.25 | |
| 0.1 | 0.54 | 0.53 | -0.01 | |
| 灯笼山站 | 0.5 | 0.74 | 0.68 | -0.06 |
| 0.9 | 0.91 | 0.82 | -0.09 |
从河口动力的角度来看, 河口水位受径潮相互作用影响, 同时也受强人类活动引起的地形边界改变影响。河口不同区段水位的主控因素有明显的洪枯季变化, 上游段枯季水位受径流和海平面共同控制, 洪季受径流控制; 下游段枯季水位受海平面控制, 而洪季水位主要受径流和海平面共同控制(蔡华阳等, 2018)。多年大规模的挖掘河床泥沙, 在很大程度上改变了河道河床演变的自然冲淤特性, 即磨刀门河道河床由总体缓慢淤积转变为大幅度冲刷。大规模采砂引起磨刀门河床河道大幅度下切和过水面积增大, 必将引起水位发生明显变化。由表 3可知, 近几十年来磨刀门河口的水位普遍下降, 表明挖砂已经使得水位变化由过去自然演变的缓慢上升转变为水位下降, 这是性质不同、方向不同的变化, 且在很长一段时间内不可恢复。因此, 未来河口三角洲水资源规划调用和河口治理都必须在新水位格局的基础上进行, 比如基于人类活动后阶段的Copula联合概率分布, 为引水口、排污口的位置, 防洪工程及堤防的极端水位设计、航道开发、防洪排涝等等提供新的设计水位参数。同时, 在不同强度的上下游边界驱动下, 强人类活动影响下河口三角洲系统内部不同概率水位变化的定量研究结果, 可为未来河口三角洲高效开发利用和治理比如综合整治规划、防洪排涝和调水压咸策略等用提供重要的基础参数。
4 结论本文选取受强人类活动(如大规模采砂及围垦等)影响显著的珠江磨刀门河口为主要研究区域, 根据人类活动历程将数据资料分成两个时段, 即强人类活动前(1965—1985年)和强人类活动后(2000—2016年), 在以马口站流量、三灶站海平面分别作为上游河流边界、外海边界的双边界驱动下, 分别对灯笼山、竹银、江门、甘竹站的水位序列在月均尺度上采用Copula方法研究水位与口外海平面、上游流量之间的联合分布依赖关系, 深入分析强人类活动对其联合分布依赖关系的影响, 指出强人类活动后磨刀门河口沿程水位与口外海平面、上游流量之间的依赖关系减弱, 主要结论如下:
1) 强人类活动后, 河道地形下切显著, 外海海平面对甘竹、竹银、灯笼山站月均水位的线性影响有所增强, 而上游马口流量对甘竹等站月平均水位的线性影响减弱, 竹银站和灯笼山站的水位-流量线性相关系数由强人类活动前的0.94、0.74分别减少为0.81、0.56。
2) 强人类活动前后月均水位、海平面和流量的概率分布特征变化明显。强人类活动后甘竹至灯笼山站水位概率密度曲线明显左移, 同概率的水位事件较强人类活动前明显降低, 同时高累级频率(>0.18)对应的水位下降, 低累级频率(<0.18)对应的水位上升; 三灶海平面概率密度曲线于强人类活动后右移, 同概率海平面呈上升趋势; 强人类活动前后流量的威布尔分布变化较小, 流量分布基本不受强人类活动影响, 但累计频率曲线整体左移, 表明流量整体下降。
3) 强人类活动后各站水位变化幅度变窄, 水位与海平面、流量的联合依赖关系发生明显改变, 低水位与海平面关系的敏感度增加, 而高水位与海平面关系的敏感度下降。低水位与流量关系的敏感度基本不变, 而高水位与海流量关系的敏感度明显下降。在相同海平面影响下, 强人类活动后发生低水位事件的风险增大, 反之, 高水位事件风险降低; 而在相同流量影响下, 强人类活动影响后低水位事件的风险基本不变, 而高水位事件的风险显著下降S。
4) 基于三变量联合概率分布分析, 与二元情况比较下发现下游站位水位与海平面的依赖关系更加密切, 而上游站位与流量的依赖关系更加密切。对于不同的水位与海平面、流量遭遇概率, 强人类活动后各站有效最大水位均有明显下降, 且遭遇概率越大, 相应的水位下降幅度越高, 遭遇概率为0.9时, 甘竹站月均有效最大水位下降幅度达到1.24m, 且上游站位的降幅大于下游站位。
刘锋, 田向平, 韩志远, 等. 2011. 近四十年西江磨刀门水道河床演变分析. 泥沙研究, (1): 45-50 |
刘曾美, 覃光华, 陈子燊, 等. 2013. 感潮河段水位与上游洪水和河口潮位的关联性研究. 水利学报, 44(11): 1278-1285 |
杨昊, 欧素英, 姚鹏, 等. 2019. 河口区斜压梯度对余水位的累积影响及其机制探讨. 海洋学报, 41(1): 21-31 |
张旭, 李敏, 郑冬燕. 2013. 珠江流域水资源配置总体格局. 人民珠江, 34(S1): 34-37 |
陆永军, 季荣耀, 王志力, 等. 2019. 珠江三角洲网河区低水位时空变化规律. 水科学进展, 30(6): 800-809 |
陈子燊, 刘曾美, 李志强, 2013.基于Copula函数的海岸增水高度与相应风速的遭遇概率分析.见: 热带海洋科学学术研讨会暨第八届广东海洋湖沼学会、第七届广东海洋学会会员代表大会论文及摘要汇编.广州: 广东省科学技术协会科技交流部, 7
|
陈子燊, 黄强, 刘曾美. 2015. 变化环境下西江北江枯水流量联合分布分析. 水科学进展, 26(1): 20-26 |
陈子燊, 曹深西. 2018. 洪峰流量与水位不同遭遇条件下的防洪设计. 中山大学学报(自然科学版), 57(4): 92-98 |
陈玲舫, 韩树宗, 车志伟, 等. 2017. 琼州海峡海口站近岸风暴增水概率风险分析. 海洋工程, 35(2): 115-122 |
欧素英, 杨清书. 2004a. 珠江三角洲网河区径流潮流相互作用分析. 海洋学报, 26(1): 125-131 |
欧素英, 陈子燊. 2004b. 小波变换在相对海平面变化研究中的应用. 地理科学, 24(3): 358-364 |
罗宪林, 杨清书, 贾良文, 等. 2002. 珠江三角洲网河河床演变. 广州: 中山大学出版社
|
胡德礼, 刘秋海, 吴超羽, 等. 2009. 基于DEM的西江磨刀门水道近40年来河床演变特征研究. 地理与地理信息科学, 25(2): 55-58, 62 |
袁菲, 何用, 吴门伍, 等. 2018. 近60年来珠江三角洲河床演变分析. 泥沙研究, 43(2): 40-46 |
贾良文, 杨清书, 钱海强, 等. 2002. 近几十年来西北江三角洲网河区顶点的河相关系. 地理科学, 22(1): 57-62 |
倪培桐, 闻平, 刘剑宇. 2016. 珠江三角洲水沙年际变化趋势分析. 人民珠江, 37(1): 19-24 |
黄洪城, 匡翠萍, 顾杰, 等. 2014. 河口咸潮入侵研究进展. 海洋科学, 38(9): 109-115 DOI:10.11759/hykx20130130002 |
蒋陈娟, 杨清书, 戴志军, 等. 2012. 近几十年来珠江三角洲网河水位时空变化及原因初探. 海洋学报, 34(1): 46-56 |
韩龙喜, 计红, 陆永军, 等. 2005. 河道采沙对珠江三角洲水情及水环境影响分析. 水科学进展, 16(5): 685-690 |
蔡华阳, 杨昊, 郭晓娟, 等. 2018. 珠江磨刀门河口径潮动力耦合条件下余水位的多时空尺度分析. 海洋学报, 40(7): 55-65 |
Bacopoulos P, 2017. Tide-surge historical assessment of extreme water levels for the St. Johns River:1928-2017. Journal of Hydrology, 553: 624-636 DOI:10.1016/j.jhydrol.2017.08.041 |
Cai H Y, Savenije H H G, Jiang C J et al, 2016. Analytical approach for determining the mean water level profile in an estuary with substantial fresh water discharge. Hydrology and Earth System Sciences, 20(3): 1177-1195 DOI:10.5194/hess-20-1177-2016 |
Cai H Y, Yang H, Liu J Y et al, 2019a. Quantifying the impacts of human interventions on relative mean sea level change in the Pearl River Delta, China. Ocean & Coastal Management, 173: 52-64 |
Cai H Y, Zhang X Y, Zhang M et al, 2019b. Impacts of Three Gorges Dam's operation on spatial-temporal patterns of tide-river dynamics in the Yangtze River estuary, China. Ocean Science, 15(3): 583-599 DOI:10.5194/os-15-583-2019 |
Liu F, Xie R Y, Luo X X et al, 2019. Stepwise adjustment of deltaic channels in response to human interventions and its hydrological implications for sustainable water managements in the Pearl River Delta, China. Journal of Hydrology, 573: 194-206 DOI:10.1016/j.jhydrol.2019.03.063 |
Liu Z Y, Chen X H, Liu F et al, 2018. Joint dependence between river water temperature, air temperature, and discharge in the Yangtze River:the role of the Three Gorges Dam. Journal of Geophysical Research:Atmospheres, 123(21): 11938-11951 DOI:10.1029/2018JD029078 |
Salvadori G, De Michele C, 2004. Frequency analysis via copulas:theoretical aspects and applications to hydrological events. Water Resources Research, 40(12): W12511 |
Sklar A, 1959. Fonctions de Répartition à n Dimensions et Leurs Marges. Paris: Publications de l'Institut de statistique de l'Uni-versité de Paris, 229-231
|
Wu Z Y, Saito Y, Zhao D N et al, 2016. Impact of human activities on subaqueous topographic change in Lingding Bay of the Pearl River estuary, China, during 1955-2013. Scientific Reports, 6(1): 37742 DOI:10.1038/srep37742 |
Yang L Z, Liu F, Gong W P et al, 2019a. Morphological response of Lingding Bay in the Pearl River Estuary to human intervention in recent decades. Ocean & Coastal Management, 176: 1-10 |
Yang X, Qian J, 2019b. Joint occurrence probability analysis of typhoon-induced storm surges and rainstorms using trivariate Archimedean copulas. Ocean Engineering, 171: 533-539 DOI:10.1016/j.oceaneng.2018.11.039 |
 2020, Vol. 51
2020, Vol. 51