中国海洋湖沼学会主办。
文章信息
- 戴娟娟, 袁野平, 宋浩宸. 2020.
- DAI Juan-Juan, YUAN Ye-Ping, SONG Hao-Chen. 2020.
- 利用旋转平台模拟双河口羽流相互作用的研究
- INVESTIGATION ON PLUME-TO-PLUME INTERACTION ON A LABORATORY-SCALE ROTATING TABLE
- 海洋与湖沼, 51(5): 1108-1117
- Oceanologia et Limnologia Sinica, 51(5): 1108-1117.
- http://dx.doi.org/10.11693/hyhz20191200248
文章历史
-
收稿日期:2019-12-04
收修改稿日期:2020-01-13
河口羽流(river plume)是河流淡水流出河口口门后在近岸区域形成的盐度较低的水体, 并发育特有的近岸流场, 一般会在河口附近形成一个向海突出的河口涡旋区(recirculating bulge), 并在其下游形成沿岸流。河口羽流是沿海系统陆地物质和土壤的重要来源, 也是近几十年来的研究热点。
关于单河口羽流结构以及羽流系统中淡水与盐水环境之间的混合情况, 前人早有研究。Yankovsky等(1997)通过理论推导出两个长度尺度hb和ys, 并认为其将直接影响大陆架的上层排放, 其中hb代表羽流平衡深度, ys代表羽流近海范围。他们还指出在hb < H且ys > 4Lr的情况下, 会出现具有循环涡旋结构的表面平流羽流, 其中H代表河口深度, Lr代表入流罗斯贝变形半径(Rossby radius of deformation)。在表面平流羽流中, 淡水流出河口后最初通过径向扩散(Garvine, 1987; Yuan et al, 2013), 随后由于受到科里奥利力(北半球)的作用而偏向右侧, 并且没有进一步接触底部(Yankovsky et al, 1997)。在低风及无环境流体的情况下, 它将形成两部分结构:停留在河口附近的循环涡旋区及向下游流动的沿岸流(Horner-Devine et al, 2006)。当河口涡旋区形成时, 大部分淡水在河口涡旋区中循环形成河口涡旋, 河口涡旋区将累积河流淡水流量的25%到75%, 而只有小部分淡水将通过沿岸流向下游输送(Fong et al, 2002; Avicola et al, 2003a, b; Horner-Devine et al, 2006; Chant et al, 2008)。在大规模的现场采样工作中, 前人已经观察到河口涡旋区的出现和沿岸流的相应减少。同时, 卫星观测也记录了河口涡旋区的不稳定性及其对沿海生态系统的影响(Horner-Devine et al, 2008)。王凯敏等(2012)将夏季长江冲淡水扩展分为3个阶段:第1阶段为射形流阶段, 长江径流直接冲入海并直达海底; 第2阶段为水舌形态扩展阶段, 冲淡水层的位置和运动受背景流场支配作用明显; 第3阶段为扩散阶段, 冲淡水先以较大团块, 后以逐渐变小的水块随背景流场运动。
针对长江冲淡水扩展区域出现的河口涡旋区现象, 张文静等(2014)对该现象开展正压不稳定机制研究, 主要讨论了快波过程(重力惯性波)和慢波过程(余流作用)对河口涡旋区的影响。他们的研究表明, 快波过程对河口涡旋区基本没影响, 而在河口涡旋从河口向口外运动的过程中, 由于水深加大, 慢波过程有利于河口涡旋区发展。浦泳修(2002)指出长江冲淡水的扩散形态与台湾暖流的强弱、离岸远近、离表面的深浅有关。乐肯堂(1984)等认为只有当径流量超过临界值时, 冲淡水才会发生转向, 而顾玉荷(1985)认为径流量越小, 外力越容易使其转向。赵保仁(1991)认为冬夏季风应力涡度的显著变化是改变长江冲淡水路径的原因。实际上, 长江冲淡水的发展是受到多因子共同影响的, 而不是某个因子单独作用造成的。羽流对陆架环流和生态系统健康的影响取决于羽流的稀释和运输过程, 其中稀释过程主要通过垂直混合来控制, 这增加了羽流的盐度并降低了河流携带物质的浓度, 羽流中的运输过程则主要由水平对流控制, 水平对流主要由羽流浮力驱动, 因此是通过混合作用驱动的(Horner-Devine et al, 2015)。
在自然环境下, 多河口的场景是很常见的:这包括一条有多个出口的河流, 如长江三角洲(Beardsley et al, 1985), 密西西比河(Wright et al, 1971)。更常见的情况是, 当来自不同流域且距离相近的多条河流在沿海海域相互作用时, 可能会出现重叠和聚结。例如, 由杜罗(Douro)和米尼奥(Minho)河流产生的西伊比利亚羽流(Western Iberian Buoyant Plume)(Mendes et al, 2016), 由波河及一系列自亚平宁山脉流出的较小河流形成的西部亚得里亚海沿岸流(Artegiani et al, 1995; Raicich, 1996), 从多条阿拉斯加沿海山脉小溪流中获取淡水的阿拉斯加沿岸流(Royer, 1982; Stabeno et al, 2004), 来自多条小山河的加利福尼亚州南部的沿岸流(Warrick et al, 2017)等等。针对由多个淡水入流形成的沿岸流情况, 前人也做了一些研究。Yuan等(2011)提出了一种技术用于区分来自不同水源的水团, 并将其应用于旋转平台上双羽流的演变过程。在旋转条件下, 入流的密度差异(Cenedese, 2012)、羽流的相互碰撞(Warrick et al, 2017)及羽流与环境水体间的混合(Cenedese et al, 2008)决定了两个浮力入流之间排列对齐的情况。
综上所述, 前人的大多数研究都集中在单河口羽流模式及双河口模型测算的羽流重叠结构上, 而关于多河口羽流与羽流相互作用三维结构的研究仍然较少。但是, 羽流多元互动的问题是一个具有社会和生态意义的问题。例如, 多河口场景下羽流的相互作用对河口涡旋体积的影响非常大, 其同时又与污染物的命运息息相关。羽流结构中的河口涡旋如果较大, 营养物和污染物可能会积聚在河口涡旋区部位, 那么被运送到下游的污染物就会变少, 反之更多的污染物将被运送到下游, 从而影响下游人类生存环境。同时, 其与有害藻华的存活、幼虫分散和种群连通性都息息相关。因此本文针对羽流与羽流之间的相互作用进一步开展实验, 在这项研究中, 我们提出了一种新技术来获得羽流的速度场及涡度场, 并模拟了旋转平台上双羽流系统的准三维结构。我们对不同入流速度下的双河口羽流流场演变过程和内部结构进行了一系列对比研究, 最终揭示在双河口环境下, 上游河流的入流如何影响下游河口涡旋的形成, 以及羽流与羽流相互作用情形下各个羽流的演变情况。
1 实验设置 1.1 实验装置与步骤本文的实验是在浙江大学地球流体力学实验室的半径为1.5m的旋转平台中进行的(图 1), 实验水槽的尺寸为3m×3m×0.5m, 转台系统由旋转实验台基座、平板、实验水槽、粒子图像测速(Partical Imagery Velocimetry: PIV)系统、仪器设备支架、供水系统等构成。整个转台系统在实验过程中呈逆时针旋转, 当旋转平台的底座平台等速运转时, 满负载变形率小于0.3mm, 台面平整度小于0.1mm。水槽侧面玻璃与底部玻璃保持严格垂直, 这用来确保光可以从侧面进入水槽。我们在水槽中使用透明亚克力板搭建有两个河口的海岸, 并用两个8cm×2cm的扩散器连接到海岸的后部, 以模拟两个相邻的河口, 这两个河口相隔48cm(中心到中心距离)。我们在水槽中填充了密度为ρa的盐水用来模拟海水, 河口区则用淡水模拟河流注入, 我们结合控制恒流泵为河口供应淡水及使用电动位移台控制河口闸门的方法, 来模拟河口河流在落潮或涨潮时的突然注入, 并将两种不同密度的流体(ρup和ρdown)分别以Qup和Qdown的流速由河口扩散器引入圆形水槽中。
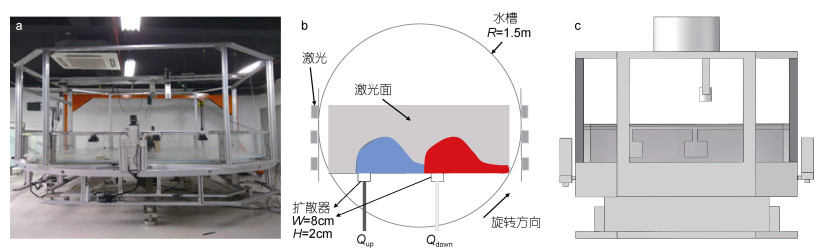 |
| 图 1 实验装置 Fig. 1 The experimental set-up 注:装置图显示的所有组件在实验过程中都随旋转平台逆时针旋转; a:实体图; b:俯视图, 其中蓝、红色分别表示上、下河口出流的河口羽流, 灰色表示激光面及相机拍摄视场; c:侧视图; Qup与Qdown分别表示上下游河口入流的流速, W与H分别表示河口闸门(入流)的宽度与高度; R表示平台半径 |
在我们的实验中, 我们使用PIV系统来可视化入流流动(Horner-Devine et al, 2006), 并应用分层PIV技术来获得准三维结构(Wang et al, 2017)。我们使用密度为1.04g/cm3, 直径为20μm的聚苯乙烯粒子作为PIV粒子, 并且将粒子密度设计为每32×32 pixel包括大约20个颗粒(Cowen et al, 1997)。我们将旋转平台两侧分布的六个激光器(每侧三个)调整到相同的水平位置以便照亮水槽平面, 并使用一台CCD相机以20帧/秒的帧率采集图像。该相机被安装在旋转平台的顶部, 距激光平面130cm, 相机正对激光平面拍摄, 采集的每个图像的物理宽度为120cm×73cm, 像素宽度为1092pixel×1200pixel, 本实验中每个像素约代表 0.061cm的长度。在每组实验的图像采集过程中, 我们首先在水体表面收集1200张图像(持续三个旋转周期), 这使我们能够观察到两个羽流早期相互作用的演变情况。随后系统自动转变为层模式, PIV相机和激光器自表面同步下移, 每次移动1cm并在该层连续收集150张图像, 共下移10次以获得每层(共11层)的速度场。我们假设系统在旋转三圈后是准稳态的(Horner-Devine et al, 2006), 故我们可以从每层获得的上游或下游入流产生的羽流速度场构建上游或下游羽流的准三维结构。
关于实验中可能出现的误差解释如下, 流体密度的变化通常是与折射率的变化相关联的, 而折射率的变化将扭曲入射激光路径, 从而导致粒子反射的光线和从染料发出的光线也扭曲, 使得图像模糊。针对该问题, 我们在实验前通过在配置淡水的水箱中加入异丙醇来精细匹配淡水和盐水的折射率(Horner-Devine et al, 2006)来解决。针对可能收集到无效及奇异值数据的问题, 在对不同阈值进行一系列测试后, 我们去除了每个像素下超过4.5倍标准差的速度数据, 在消除异常值的同时保证了不影响正常的羽流图。
1.2 特征参数及实验组别本实验对在上游流速改变情况下的双河口羽流演变情况进行了对比研究。在每组实验之前, 我们通过在水槽中装满盐水并旋转至少4h来实现流体的钢化(流体相对水槽保持静止)。根据均匀旋转时间来作为水槽流体达到钢性的时间阈值, 以1/(E1/2f)≈10min(Wedemeyer, 1964)来看, 这个时间已经足够长, 其中埃克曼数E=ν/fH02, 水黏度ν=1.01×10-6m2/s, 总水深H0=0.25m, 其中f代表科氏力参数。为了研究双河口羽流如何相互作用, 我们同时将两种浮力流体通过两个扩散器引入到环境盐水自由表面下方的水槽中, 并进行了九组实验。这其中包括四组通过恒流泵改变上游河口流速, 而下游河口流速Qdown保持不变且只在下游河口投放PIV粒子的羽流实验, 以及四次其他条件与前四组相同, 但改在上游河口投放PIV粒子的转台羽流实验。除此之外, 我们还进行了一组单一入流(Qup=0)的对照试验(表 1)。
| 粒子位置 | 实验编号 | T(s) | E | Qup (cm3/s) |
Qdown (cm3/s) |
G′up (m/s2) |
G′down (m/s2) |
W (cm) |
H (cm) |
Roup | Rodown | Frup | Frdown |
| 单河口 | 1 | 20 | 2.57×10-5 | -- | 50 | -- | 4.03 | 8 | 2 | -- | 0.62 | -- | 1.10 |
| 仅下游河口 | 2 | 20 | 2.57×10-5 | 25 | 50 | 4.03 | 4.08 | 8 | 2 | 0.31 | 0.62 | 0.55 | 1.10 |
| 3 | 20 | 2.57×10-5 | 50 | 50 | 4.03 | 4.11 | 8 | 2 | 0.62 | 0.62 | 1.10 | 1.10 | |
| 4 | 20 | 2.57×10-5 | 75 | 50 | 4.19 | 4.14 | 8 | 2 | 0.93 | 0.62 | 1.66 | 1.10 | |
| 5 | 20 | 2.57×10-5 | 100 | 50 | 3.9 | 4.05 | 8 | 2 | 1.24 | 0.62 | 2.24 | 1.10 | |
| 仅上游河口 | 6 | 20 | 2.57×10-5 | 25 | 50 | 3.84 | 3.81 | 8 | 2 | 0.31 | 0.62 | 0.56 | 1.13 |
| 7 | 20 | 2.57×10-5 | 50 | 50 | 3.81 | 3.86 | 8 | 2 | 0.62 | 0.62 | 1.13 | 1.12 | |
| 8 | 20 | 2.57×10-5 | 75 | 50 | 3.86 | 3.85 | 8 | 2 | 0.93 | 0.62 | 1.68 | 1.13 | |
| 9 | 20 | 2.57×10-5 | 100 | 50 | 3.9 | 3.82 | 8 | 2 | 1.24 | 0.62 | 2.24 | 1.13 | |
| 注: T表示旋转平台的旋转周期, E表示埃克曼数, Qup与Qdown分别表示上下游河口入流的流速, G′up与G′down分别表示上下游河口入流的约化重力, W与H分别表示河口闸门(入流)的宽度与高度, Roup及Rodown分别表示上下游河口入流的罗斯贝数, Frup及Frdown分别表示上下游河口入流的弗劳德数 | |||||||||||||
在我们的实验中, 旋转平台旋转周期T=20s, 扩散器(河口)宽度W=8cm, 高度H=2cm。我们根据每组实验各自的实验参数计算了其对应与羽流结构相关的参数(Fr, Ro)。我们将每对PIV实验都设计成具有相同的入流条件, 以独立地模拟来自上游和下游羽流之间的相互作用情况和入流的最终命运。然而, 由于实验的限制, 在两次独立的实验中不可能完全匹配g'up和g'down, 但每对实验中g'的差异非常小, 处于可以接受的误差范围内。为了研究上游产生的羽流对下游产生羽流的影响, 我们将上游河流的流量分别设计为下游入流流量的0.5, 1, 1.5和2倍。通过PIV系统, 我们预计将获得由上游河口和下游河口产生的每层羽流的速度场, 并据此得到羽流的准三维结构, 最终结合参数的变化分析上游羽流对下游羽流的影响。
2 实验结果分析 2.1 上游河口羽流对下游河口涡旋的抑制作用在河口开闸后, 淡水羽流开始从河口喷射出来。我们安排PIV相机在羽流的表面采集3个旋转周期(共1min)共1200张的图片。如图 2所示, 其展示了一组单羽流系统(Qdown=50cm3/s)下游羽流演变情况, 以及两组双羽流系统低上游和高上游入流流量条件下的下游羽流演变情况。从速度场中可以清晰分辨出典型羽流的两个主要组成部分, 即河口涡旋区和沿岸流区(Horner-Devine et al, 2015)。
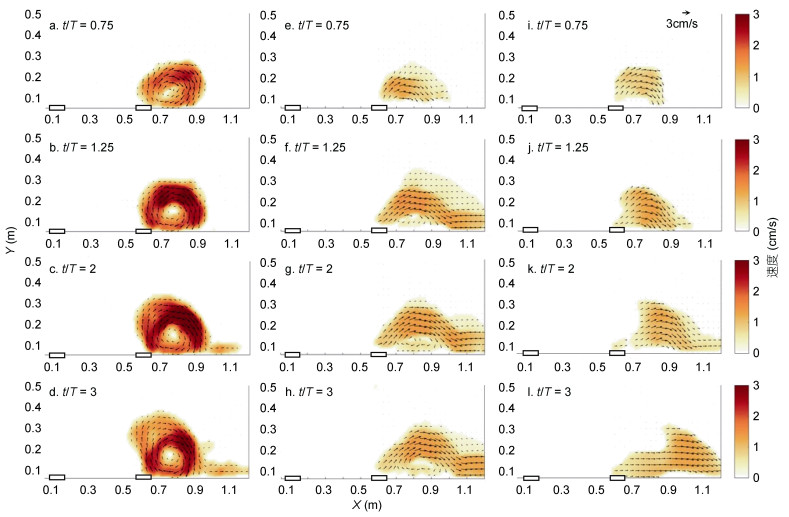 |
| 图 2 单羽流系统中(a-d)及双羽流系统中低上游入流流量(Qup=50cm3/s)下(e-h)及高上游入流流量(Qup=100cm3/s)下(i-l)下游(Qdown=50cm3/s)羽流的演变情况 Fig. 2 The evolution of downstream (Qdown=50cm3/s) plume with the presence of single plume system (a-d) and plume-to-plume interaction under low upstream river discharge (Qup=50cm3/s) (e-h) and high upstream river discharge (Qup=100cm3/s) conditions (i-l) 注:黑色箭头表示水平速度的方向及大小; 各分图左侧黑框表示上游河口, 其出流位置为X=0.1m, Y=0.05m, 右侧黑框表示下游河口, 其出流位置为X=0.58m, Y=0.05m; t表示旋转时间; T表示转台旋转周期 |
在单一河口入流(Qdown=50cm3/s)的条件下, 下游淡水流出后向右偏转, 并在河口打开后的一个旋转周期内重新接触到海岸(图 2a)。河口涡旋区呈现出一个反气旋涡旋和包围涡旋的地转射流结构(Horner-Devine et al, 2006; Chen, 2014; Yuan et al, 2018)。在第一个旋转周期结束时, 沿岸流开始形成。图 2b的河口涡旋与图 2a相比明显增大, 河口涡旋呈现反气旋旋转, 在接下来的两个旋转周期中, 从图 2c和图 2d中, 我们均可以观察到沿岸流的出现, 即水流从河口涡旋区的右侧位置脱离出来, 撞击海岸形成沿岸流。我们可以观察到沿岸流的宽度明显增加, 这是因为随着时间的变化, 越来越多的水流从河口涡旋区中脱离出来形成了沿岸流。我们同时发现涡旋面积也在逐渐增大(图 2c, d), 这说明这两种情况是同时发生的, 即河口涡旋区在其生长过程的某个时刻就会开始释放一部分水流, 而不是在其停止生长的时刻才开始形成沿岸流。在上游入流存在的情况下, 上游河口的羽流在出口的位置也会形成一个反气旋的河口涡旋区, 随着时间的推移, 该水团逐渐变大, 并伴随着沿岸流的出现。但由于下游河口的存在, 已经形成的沿岸流会被卷吸入下游羽流的河口涡旋区中, 最终从河口涡旋区中脱离出来, 撞击海岸形成沿岸流, 该入流条件下下游河口涡旋区的演变类似于前人对单河口羽流的实验研究(Horner-Devine et al, 2006)。然而, 在低上游入流流量(Qup=25cm3/s)和单一河口入流(Qup=0cm3/s)这两种情况下, 羽流的整体形状没有产生显著差异。当上游入流流量为50cm3/s时, 图 2e的河口涡旋与图 2a相比明显减小, 在一个旋转周期结束后, 图 2f中已经可以观察到沿岸流的出现, 其较前一种情况(图 2b)出现得更早。这说明随着上游入流流量的增加, 上游羽流形成的沿岸流对下游河口涡旋生长的抑制作用和沿岸迁移的促进作用都会显著增强。图 2h与图 2d相比沿岸流的厚度明显增加, 说明当上游羽流有更高的动量输入时, 将导致沿岸方向出现更强的沿岸流(Horner-Devine et al, 2006)。当上游入流流量较大(Qup=100cm3/s)时, 在第一个旋转周期期间, 由于上游沿岸流还未发展完全, 下游河口处的淡水离开河口后首先向离岸方向喷射, 然后向右偏转形成类圆状河口涡旋(图 2)。河口涡旋区的核心区域的速度变化几乎是线性的。在靠近海岸的一侧, 速度迅速降低到零, 而在离岸方向, 速度则是逐渐降低到零的。由于沿岸速度的这种不对称变化, 河口涡旋的形状并不是精确的圆形形状, 而是偏向海岸一侧。这与前人提出的惯性模型(Fong et al, 2002)以及实验室模拟实验(Horner-Devine et al, 2006)的结果保持一致。随后, 随着上游羽流形成的沿岸流到达下游河口涡旋区位置, 下游河口涡旋在沿岸方向上受到更强的动量输入的影响, 河口涡旋区变为类三角形状并且整体上被推移到离河口更远的位置(图 2k和图 2l)。这表明上游沿岸流向下游淡水输送了额外的沿岸动量, 因此下游河口出流方向也将不再与海岸保持垂直。这种羽流结构类似于Avicola等(2003a)讨论的入流与河口呈一定角度的情况, 这种情况在Horner-Devine等(2015)的文章中也有总结。
2.2 下游羽流河口涡旋区面积的时间变化我们将最大涡度的80%的等涡度线定义为羽流边缘轮廓, 这很好地指出了河口涡旋区的边界。我们计算了表面一分钟内, 在不同上游河流排放条件下下游羽流河口涡旋区域的面积变化。如图 3所示, 在所有情况下, 河口涡旋区的面积随时间不断增加, 这一点与前人的研究一致(Horner-Devine et al, 2006)。然而, 该面积增长速率在开始时较高, 并且在t=2T之后逐渐降低。值得注意的是, 该速率变化高度依赖于上游入流流量, 这一点也验证了Nof等(2001)关于河口涡旋区的理论预测, 即上游羽流产生的沿岸流可以为平衡下游羽流产生的沿岸流提供动量。因此, 特别是在上游入流流量等于或大于下游入流流量的情况下, 随着上游沿岸流的发展, 河口涡旋区的体积增长将开始放缓。在上游入流流量是下游入流流量的两倍的情况下, 第二次旋转周期后, 河口涡旋区面积的增长几乎停止。从旋转三周后的面积来看, 当Qup=0cm3/s时, 河口涡旋区的表面积将超过其他所有情况, 这是由于下游河口涡旋区没有受到上游的抑制作用所导致的。从2.1节我们讨论的结果来看, 随着上游河口的流量持续增加, 它对下游羽流的抑制作用将逐渐加强, 下游河口涡旋区面积本应当逐渐减少。但当Qup=75cm3/s时, 在三个旋转周期之后, 其下游羽流河口涡旋区的表面积甚至超过了Qup=50cm3/s的情况。我们猜测这种结果可能是由于Qup=75cm3/s情况下, 下游羽流形成的河口涡旋中卷吸了更多的上游入流, 这种卷吸效应甚至超过了上游羽流对其的抑制效果。当Qup=100cm3/s时, 羽流的面积在所有情况中处于最低水平, 造成这种情况的原因可能是上游羽流形成的沿岸流对下游河口涡旋区强烈的抑制作用已经超过了下游河口涡旋对上游入流的卷吸效应。
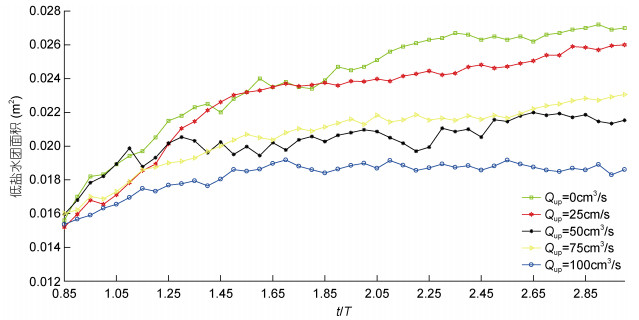 |
| 图 3 在不同的上游河流排放条件下下游河口涡旋区区域面积的时间序列 Fig. 3 Time series of the downstream bulge area under different upstream river discharge conditions |
在经过3T(旋转周期)的早期羽流演变之后, 河口涡旋将继续稳定增长到10T, 之后河口涡旋将在单羽流(Horner-Devine et al, 2006)或双羽流状况中变得不稳定(Yuan et al, 2011)。如图 2及图 3所示, PIV相机会在表面采集3T(1min)的图片, 随后我们让它配合激光进行同步下移来采集每一层羽流的图像, 相机会在每一层停留7.5s并采集150张图片, 一共下移10次共采集11层的图片。采集11层图片的总持续时间小于5T, 因此我们可以在在羽流变得不稳定之前完成观察。在河口涡旋稳定生长的阶段, 我们使用这种新颖的分层PIV技术单独研究每个羽流(分为上游河口和下游河口)的准三维结构(图 4, 5)。我们将每层获取到的涡度场进行150张平均并模拟羽流的准三维结构图, 同时我们在涡度场结构上叠加了水平速度箭头, 在旋转参考系下垂直速度很小, 故在本研究中忽略不计。之前的研究表明羽流的垂直结构对于羽流动力学的研究非常重要(Horner-Devine et al, 2006; Cenedese et al, 2008; Yuan et al, 2011), Yuan等(2011)使用光学方法研究了相同入流速度条件下两种羽流相互作用的情况, 但目前关于垂直结构的研究仍然非常少。我们认为这种分层PIV技术对不同入流速度条件下羽流相互作用的垂直结构的展示是一次重要的尝试(图 5a, b)。
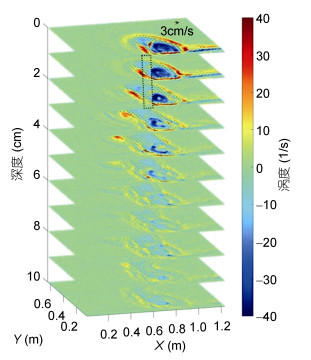 |
| 图 4 单羽流系统中由单一河口产生的羽状的准三维结构 Fig. 4 Quasi-3D structure of the plume generated by the downstream estuary 注: Z轴表示羽流的每一层; 黑色箭头表示速度的方向和大小; 图中虚线框比例并不代表河口真实比例(真实河口宽度为8cm, 高度为2cm), 仅表示下游河口所处位置(X=0.58m, Y=0.05m, 流量为Qdown=50cm3/s) |
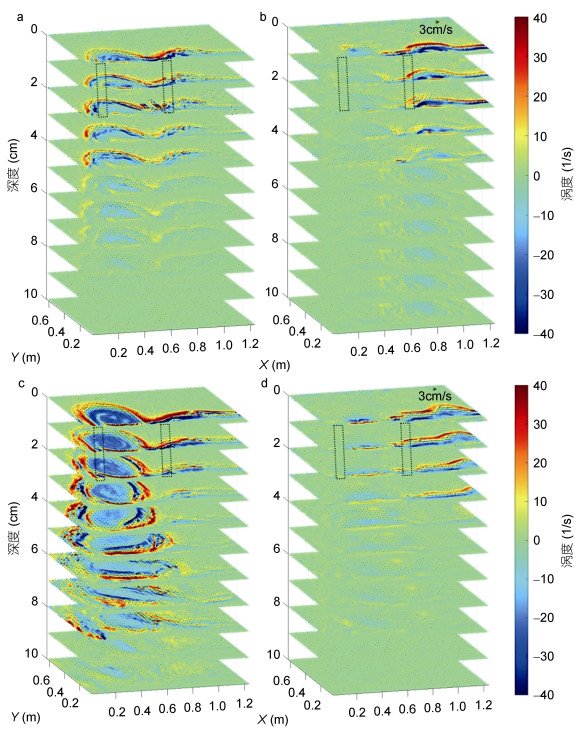 |
| 图 5 双羽流系统中低上游入流流量情况下由上游河口(a, c)和下游河口(b, d)产生的羽状的准三维结构 Fig. 5 Quasi-3D structure of the plume generated by the upstream estuary (a, c) and downstream estuary (b, d) 注:左侧黑色虚线框代表上游河口其出流位置为X=0.1m, Y=0.05m, 右侧黑色虚线框代表下游河口, 其出流位置为X=0.58m, Y=0.05m; a, b: Qdown=50cm3/s; c, d: Qup=100cm3/s |
需要指出的是, 随着河口涡旋在沿岸和离岸方向不断成长, 河口涡旋的演变是一个不稳定的过程(Nof et al, 2001; Horner-Devine et al, 2006)。下游羽流河口涡旋区的生长在受到抑制的同时并不会因上游羽流的存在而完全停止(参见2.1节的讨论), 而且每层的图像并不是同时拍摄的, 那么当我们在较下层(如在t≈8T)拍摄图像时, 表面处真实的河口涡旋其实已经比图中所示(图 4, 5)的河口涡旋(如在t≈3T)处大得多。因此我们最终得到的三维模型并不完全代表真实情况, 故将其称为准三维羽流结构。
我们按照统一的涡度标准来判断涡旋边界, 当上游入流不存在时(图 4), 据此标准, 下游河口涡旋的深度可以延伸到表面下方约6cm处。当上游入流流量很小(Qup=25cm3/s)时, 它对下游河口涡旋的影响很小。在这种情况下, 下游河口涡旋区的结构类似于单羽流的情况(图 4)。在Qup=50cm3/s情况下(图 5a, b), 即上下游入流流量相同的情况下, 如果上游羽流与下游羽流之间没有相互作用, 则下游河口形成的河口涡旋应与上游河口相同。但我们观察到上游河口形成的河口涡旋明显大于下游河口, 这也证明了下游羽流的成长受到了上游羽流的抑制。上游羽流的沿岸流并不是仅仅简单环绕在下游河口涡旋周围, 而是在类似于其自身河口涡旋的高度侵入下游河口涡旋区。在Qup=100cm3/s情况下, 下游原有河口涡旋被推向更下游位置, 在远离河口的位置形成另一个河口涡旋(图 5c, d)。
在垂直方向上, 我们可以观察到高上游入流流量条件下(图 5c, d)的下游河口涡旋深度比低上游入流流量条件(图 5a, b)更浅, 这一点为我们提供了一个关于双羽流河口涡旋垂直结构的新见解。一方面, 在水平对准情况下, 下游羽流被上游羽流通过环境水体完全隔离开来。因此, 在这种情况下, 跨岸物质输送是有限的。另一方面, 在垂直对准情况下, 上游羽流位于下游羽流的下方, 故三层结构(下游水体-上游水体-环境水体)间的垂直分层较弱, 这也会导致两个羽流之间以及羽流和环境水体之间的混合增强。我们的实验首次尝试研究了复杂情况下的羽状垂直结构, 我们希望该研究可以为如Kara Sea(Osadchiev et al, 2017), 西伊比利亚海岸(Mendes et al, 2016), 或智利中部海岸(Saldías et al, 2012)等短距离内有多条河流流出的现场观测数据提供相关解释。
3 结论我们通过对不同上游入流速度下的双河口羽流流场演变过程和内部结构进行了一系列对比研究, 最终揭示了在双河口环境下, 上游河流的排放如何影响下游河口涡旋的形成及羽流与羽流相互作用情形下各个羽流的演变。得出以下结论:
1) 上游河口的羽流在出口的位置会形成一个反气旋的河口涡旋, 随着时间的推移河口涡旋逐渐变大, 并伴随着沿岸流的出现, 但由于下游河口的存在, 已经形成的沿岸流会被卷吸入下游羽流的河口涡旋中, 最终从下游河口涡旋中脱离出来, 撞击沿岸形成沿岸流。随着上游入流流量的增加, 上游羽流形成的沿岸流对下游河口涡旋沿岸迁移的促进和离岸运输的抑制作用将更加显著;
2) 上游羽流产生的沿岸流可以为平衡下游羽流产生的沿岸流提供动量。因此, 特别是在上游入流流量等于或大于下游入流流量的情况下, 随着上游沿岸流的发展, 河口涡旋的体积增长也开始放缓。在上游入流流量是下游入流流量的两倍的情况下, 第二次旋转周期后河口涡旋区面积的增长几乎停止;
3) 当Qup=75cm3/s时, 在三个旋转周期之后, 下游羽流河口涡旋区的表面积甚至超过了Qup=50cm3/s的情况。我们猜测这可能是由于下游羽流河口涡旋区中卷吸了更多的上游流量, 这种卷吸效应甚至超过了上游羽流对其的抑制效果;
4) 上游羽流的沿岸流并不是简单地环绕在下游河口涡旋区周围, 而是在类似于其自身河口涡旋的高度侵入下游河口涡旋区。在上游入流流量较大的情况下, 下游原有河口涡旋被推向更下游位置, 在远离河口的位置形成另一个河口涡旋区。在垂直方向上, 我们可以观察到高上游入流流量条件下的下游河口涡旋区深度比低上游入流流量条件更浅。
本文讨论了在双河口情况下两个羽流将如何进行相互作用, 且首次尝试研究了复杂情况下的羽状垂向结构。但本文仅考虑了不同上游入流流量的这种情况, 实际上影响淡水羽流的扩散和混合过程的动力因素是多样且多变的。羽流区既会受到河流径流密度变化的影响, 例如河流当地降水量的变化及人类活动对当地河流密度造成的影响(如破坏植被造成水土流失, 河流密度变大); 又受地转偏向力的影响, 一方面地转偏向力会影响河流的流向, 另一方面不同纬度地区地转偏向力大小不同; 而且还受风场的影响, 风场的存在会影响羽流垂直方向的混合。上升流风使得淡水羽流向东北方向扩散, 由于风生混合的影响, 淡水羽流盐度在扩散过程中逐渐减弱。下降流风则使羽流局限在较窄的范围内并使羽流厚度增加。河口-陆架区的动力过程由于这些动力因素的共同作用变得异常复杂, 未来我们将对羽流多元互动等具有社会和生态意义的问题进行更加深入的研究, 这就包括我们对这些动力因素(入流密度, 科氏力, 风应力)对羽流的影响进一步开展研究并进行系统的理论分析, 以便将来能更好地应用于真实双河口环境中不同密度入流, 不同科氏力及风应力作用条件下双河口羽流的运动与归宿等研究中去。研究淡水羽流的动力机制对于河口泥沙输运和生态环境的变化趋势具有重要的理论意义和实用价值。
王凯敏, 熊学军, 郭炳火, 等. 2012. 2006-2007年长江冲淡水的扩展形态及季节变化. 海岸工程, 31(1): 46-54 |
乐肯堂. 1984. 长江冲淡水路径的初步研究Ⅰ.模式. 海洋与湖沼, 15(2): 157-167 |
张文静, 朱首贤, 阮鲲, 等. 2014. 长江口外低盐水团发展的正压不稳定机制分析. 解放军理工大学学报(自然科学版), 15(1): 80-87 |
赵保仁. 1991. 长江冲淡水的转向机制问题. 海洋学报, 13(5): 600-610 |
顾玉荷. 1985. 长江冲淡水转向原因的探讨. 海洋与湖沼, 16(5): 354-363 |
浦泳修. 2002. 夏季东海30°N断面的盐度分布类型. 东海海洋, 20(1): 1-13 |
Artegiani A, Paschini E, Russo A et al, 1995. The Adriatic Sea general circulation. Part Ⅰ:air-sea interactions and water mass structure. Journal of Physical Oceanography, 27(8): 1492-1514 |
Avicola G, Huq P, 2003a. The role of outflow geometry in the formation of the recirculating bulge region in coastal buoyant outflows. Journal of Marine Research, 61(4): 411-434 DOI:10.1357/002224003322384870 |
Avicola G, Huq P, 2003b. The characteristics of the recirculating bulge region in coastal buoyant outflows. Journal of Marine Research, 61(4): 435-463 DOI:10.1357/002224003322384889 |
Beardsley R C, Chapman D C, Brink K H et al, 1985. The Nantucket Shoals Flux Experiment (NSFE79). Part Ⅰ:a basic description of the current and temperature variability. Journal of Physical Oceanography, 15(6): 713-748 |
Cenedese C, 2012. Downwelling in basins subject to buoyancy loss. Journal of Physical Oceanography, 42(11): 1817-1833 DOI:10.1175/JPO-D-11-0114.1 |
Cenedese C, Lerczak J, 2008. Interaction and Stability of Two Buoyant Currents. Meeting of the Aps Division of Fluid Dynamics, American Physical Society.
|
Chant R J, Glenn S M, Hunter E et al, 2008. Bulge formation of a buoyant river outflow. Journal of Geophysical Research, 113(C1): C01017 |
Chen S N, 2014. Enhancement of alongshore freshwater transport in surface-advected river plumes by tides. Journal of Physical Oceanography, 44(11): 2951-2971 DOI:10.1175/JPO-D-14-0008.1 |
Cowen E A, Monismith S G, 1997. A hybrid digital particle tracking velocimetry technique. Experiments in Fluids, 22(3): 199-211 DOI:10.1007/s003480050038 |
Fong D A, Geyer W R, 2002. The alongshore transport of freshwater in a surface-trapped river plume. Journal of Physical Oceanography, 32(3): 957-972 |
Garvine R W, 1987. Estuary plumes and fronts in shelf waters:a layer model. Journal of Physical Oceanography, 17(11): 1877-1896 DOI:10.1175/1520-0485(1987)017<1877:EPAFIS>2.0.CO;2 |
Horner-Devine A R, Fong D A, Monismith S G, 2008. Evidence for the inherent unsteadiness of a river plume:satellite observations of the Niagara River discharge. Limnology and Oceanography, 53(6): 2731-2737 DOI:10.4319/lo.2008.53.6.2731 |
Horner-Devine A R, Fong D A, Monismith S G et al, 2006. Laboratory experiments simulating a coastal river inflow. Journal of Fluid Mechanics, 555: 203-232 DOI:10.1017/S0022112006008937 |
Horner-Devine A R, Hetland R D, MacDonald D G, 2015. Mixing and transport in coastal river plumes. Annual Review of Fluid Mechanics, 47: 569-594 DOI:10.1146/annurev-fluid-010313-141408 |
Mendes R, Sousa M C, deCastro M et al, 2016. New insights into the Western Iberian Buoyant Plume:Interaction between the Douro and Minho River plumes under winter conditions. Progress in Oceanography, 141: 30-43 DOI:10.1016/j.pocean.2015.11.006 |
Nof D, Pichevin T, 2001. The ballooning of outflows. Journal of Physical Oceanography, 31(10): 3045-3058 DOI:10.1175/1520-0485(2001)031<3045:TBOO>2.0.CO;2 |
Osadchiev A A, 2017. Spreading of the Amur River plume in the Amur Liman, Sakhalin Gulf, and the Strait of Tartary. Oceanology, 57(3): 376-382 DOI:10.1134/S0001437017020151 |
Raicich F, 1996. On the fresh balance of the Adriatic Sea. Journal of Marine Systems, 9(3-4): 305-319 DOI:10.1016/S0924-7963(96)00042-5 |
Royer T C, 1982. Coastal fresh water discharge in the Northeast Pacific. Journal of Geophysical Research, 87(C3): 2017-2021 DOI:10.1029/JC087iC03p02017 |
Saldías G S, Sobarzo M, Largier J et al, 2012. Seasonal variability of turbid river plumes off central Chile based on high-resolution MODIS imagery. Remote Sensing of Environment, 123: 220-233 DOI:10.1016/j.rse.2012.03.010 |
Stabeno P J, Bond N A, Hermann A J et al, 2004. Meteorology and oceanography of the Northern Gulf of Alaska. Continental Shelf Research, 24(7-8): 859-897 DOI:10.1016/j.csr.2004.02.007 |
Wang J H, Wang S Y, Chen X et al, 2017. Three-dimensional evolution of internal waves reflected from a submarine seamount. Physics of Fluids, 29(10): 106601 DOI:10.1063/1.4986167 |
Warrick J A, Farnsworth K L, 2017. Coastal river plumes:collisions and coalescence. Progress in Oceanography, 151: 245-260 DOI:10.1016/j.pocean.2016.11.008 |
Wedemeyer E H, 1964. The unsteady flow within a spinning cylinder. Journal of Fluid Mechanics, 20(3): 383-399 DOI:10.1017/S002211206400129X |
Wright L D, Coleman J M, 1971. Effluent expansion and interfacial mixing in the presence of a Salt Wedge, Mississippi River Delta. Journal of Geophysical Research, 76(36): 8649-8661 DOI:10.1029/JC076i036p08649 |
Yankovsky A E, Chapman D C, 1997. A simple theory for the fate of buoyant coastal discharges. Journal of Physical Oceanography, 27(7): 1386-1401 DOI:10.1175/1520-0485(1997)027<1386:ASTFTF>2.0.CO;2 |
Yuan Y P, Avener M E, Horner-Devine A R, 2011. A two-color optical method for determining layer thickness in two interacting buoyant plumes. Experiments in Fluids, 50(5): 1235-1245 DOI:10.1007/s00348-010-0969-y |
Yuan Y P, Horner-Devine A R, 2013. Laboratory investigation of the impact of lateral spreading on buoyancy flux in a river plume. Journal of Physical Oceanography, 43(12): 2588-2610 DOI:10.1175/JPO-D-12-0117.1 |
Yuan Y P, Horner-Devine A R, Avener M et al, 2018. The role of periodically varying discharge on river plume structure and transport. Continental Shelf Research, 158: 15-25 DOI:10.1016/j.csr.2018.02.009 |
 2020, Vol. 51
2020, Vol. 51


