
中国海洋湖沼学会主办。
文章信息
- 王鑫, 李大鸣, 白志刚, 齐占辉, 武贺. 2020.
- WANG Xin, LI Da-Ming, BAI Zhi-Gang, QI Zhan-Hui, WU He. 2020.
- 海岛周边波浪能资源精细化勘查与分布特征分析方法研究
- THE REFINED EXPLORATION AND ANALYSIS METHOD OF WAVE ENERGY RESOURCES AROUND ISLANDS
- 海洋与湖沼, 51(5): 1257-1266
- Oceanologia et Limnologia Sinica, 51(5): 1257-1266.
- http://dx.doi.org/10.11693/hyhz20190900178
文章历史
-
收稿日期:2019-09-22
收修改稿日期:2020-02-10
2. 国家海洋技术中心 天津 300112
2. National Ocean Technology Center, Tianjin 300112, China
迄今, 我国共开展了3次较大规模的波浪能资源勘查与评估(表 1, 王传崑等, 2009; 韩家新, 2015)。除大规模的波浪能资源勘查与评估研究外, 多位学者利用不同的数据和方法对中国特定海域的波浪能资源进行了分析。郑崇伟等(2014)利用模拟海浪数据、CCMP (cross-calibrated, multi-platform)风场资料, 对我国钓鱼岛、黄岩岛附近海域的波浪能、风能资源特征展开研究, 其研究表明, 钓鱼岛、黄岩岛海域可用波高(有效波高介于0.5—4m)、2kW/m以上波浪能流密度出现频率整体较高。李靖等(2011)也参照该方法评估了台湾周边海域的波浪能资源时空分布特征。张军等(2012)采用波浪模拟的方法, 较准确计算得出福建、浙江沿海海域波浪能资源分布状况, 并给出相应的分析和综合评价。另外, 蒋廷松(2013)也利用SWAN (simulating waves nearshore)数值模型结合实测波浪浮标数据对浙江近岸波浪能资源进行分析研究。周凯等(2013)、栗冬慧(2015)、刘首华等(2015)均利用SWAN模式模拟了山东半岛周边海域的波浪场, 并分析了山东波浪能资源时空分布特征。杨永增等(2005)在LAGFD-WAM海浪模式基础上建立球坐标系下MASNUM海浪数值模式, 以便进行全球或区域海浪数值模报。利用该高分辨率数值模式, 估算了渤黄东海波浪能流密度分布。刘秋林等(2015)从波浪能发电装置、波浪发电场选址工作需求出发, 利用第三代波浪模型对斋堂岛附近海域进行了数值模拟, 分析了当地的波浪条件并对蕴藏的波浪能资源, 并对目标位置的波浪资源进行了详细地计算和分析。史宏达等(2013, 2017)利用波浪数值模拟提出的联合分布法对波浪能资源评估方法进行了一定修正, 认为该方法对特定海域的波浪能资源评估更具有针对性, 且可为波浪能发电装置的研发服务。以Izadparast等(2011)为代表的多位国外学者, 结合波浪能装置能量获取方式和效能, 对区域波浪能资源的可开发量评价方法进行了研究。
| 资源类型 | 序数 | 实施年份 | 主持部门 | 勘查对象(区域) | 理论潜在量(104kW) |
| 波浪能 | 第一次 | 1986 | 水电部和海洋局 | 近岸海洋站连线 | 1284 |
| 第二次 | 2004 | 海洋局 | 中国近海离岸20km一线 | 1600 | |
| 第三次 | 2011 | 海洋局 | 渤、黄、东海建海海域 | 1046.7 |
综上所述, 我国对包括波浪能资源的勘查工作水平处于世界前列, 通过多个专项的实施, 已总体上摸清了我国管辖海域的波浪能资源储量及其时空分布状况。但受到水深地形比例尺及网格分辨率的限制, 评估对于特定小区域的刻画还不够精确, 尤其在波浪能资源丰富的海岛周围, 由于模型对该类岛屿进行了简化或删除, 无法准确刻画岛屿周边波浪的浅水变形、反射、绕射等波浪传播机制, 也难以准确刻画其波浪能资源的时空分布特征和变化规律。随着业内对波浪能开发利用需求的日益迫切, 对小区域波浪能资源的精细化勘查和分析提出了更高的要求。本文选择山东省威海市褚岛北部海域作为目标海域, 开展海岛周边波浪能资源精细化勘查与分布特征分析方法研究。
1 波浪能资源精细化勘查方法研究开展海岛周边小区域的波浪能资源精细化勘查, 需在掌握目标海域海洋环境条件概况的情况下有针对性地制定勘查方案。在缺少目标海域前期历史资料的情况下, 可通过搜集附近海域环境资料, 间接分析目标海域的环境条件概况, 为勘查方案制定提供参考依据。
1.1 历史资料分析褚岛位于山东省威海市孙家疃镇以北约3.7km处, 褚岛南北长0.82km, 平均宽度0.21km, 岛岸线长2.68km。褚岛地理位置如图 1。
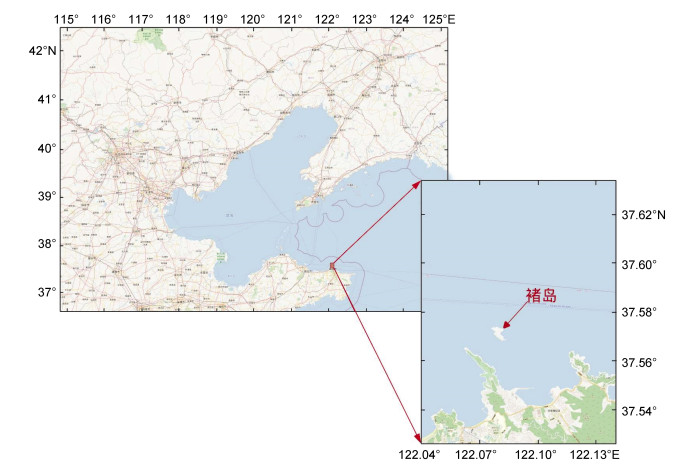 |
| 图 1 褚岛地理位置 Fig. 1 Geographic location of Chudao Island |
褚岛北部海域缺乏长期有效的波浪观测资料, 为给精细化勘查方案的设计提供参考依据, 本文分析褚岛以西距离约65km的烟台芝罘岛附近套子湾的海浪观测资料和褚岛以东60km的成山头海洋环境监测站20年的波浪历史观测资料, 对褚岛周边海域波浪特性进行间接分析(王鑫等, 2015a)。芝罘岛和成山头与褚岛的相对位置如图 2所示。
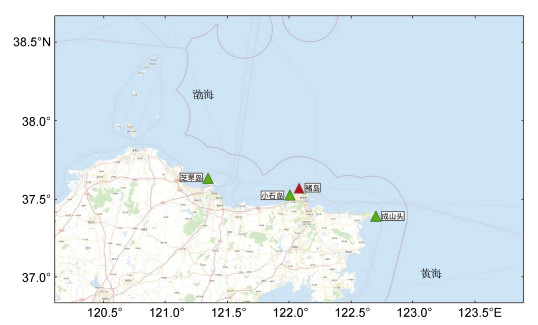 |
| 图 2 芝罘岛、小石岛与成山头的相对位置示意图 Fig. 2 Schematic diagram of relative position among Zhifu Island, Xiaoshi Island, and Cape of Chengshantou |
采用烟台套子湾(靠近芝罘岛)2012年1月1日至2012年2月29日(冬季)的波浪观测数据。根据统计, 该站冬季最大波高3.40m, 十分之一波高1.36m, 平均周期4.55s。对冬季该站十分之一波高分段进行频率统计(图 3)。
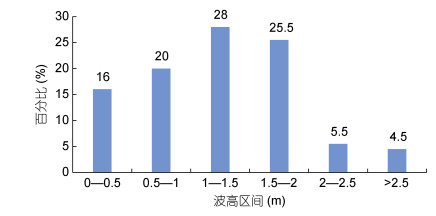 |
| 图 3 芝罘岛海域冬季1/10波高分段频率统计 Fig. 3 Frequency of 1/10 wave height section in Zhifu Island waters |
对成山头海洋环境监测站获得的1991—2010年20年的波浪观测资料进行的统计分析可以得到, 成山头以东海域多年平均的十分之一大波波高为1.81m, 十分之一大波周期为6.49s, 多年平均的有效波高为1.01m, 有效周期为5.67s, 图 4为多年统计的有效波高大于0.5m的天数。
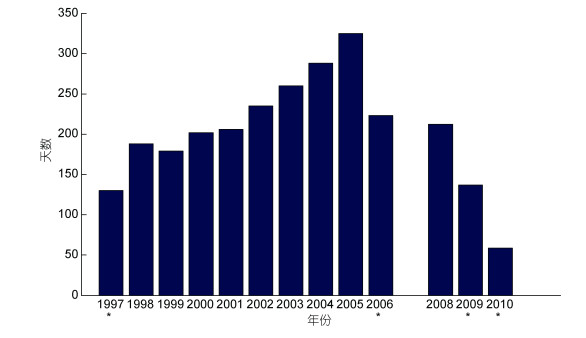 |
| 图 4 1997—2010年有效波高大于0.5m的天数 Fig. 4 The number of days with effective wave height greater than 0.5m during 1997—2010 注: *表示本年数据不完整; 未获得海洋站2007年全年电子版数据, 故未统计分析该年数据 |
通过对邻近海洋站波浪资料的分析, 可以推断褚岛海域冬季波浪能资源最佳, 常浪向、强浪向均为西北偏北等波浪的年季变化特点, 为褚岛北部海域波浪能资源的精细化勘查方案的制定提供重要的依据。
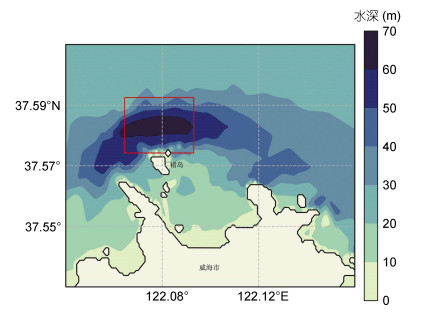
1.2 水深地形条件分析目标海域的水深条件同样是勘查方案设计制定的重要依据。由图 5可见, 褚岛以北约700—1200m之间存在一处海沟, 海沟呈东西向, 水深最深可达70m, 水深超过60m的区域大约500m宽, 2500m长。褚岛北部临岸区域地形陡峭, 水深变化剧烈, 岛北部离岸200m以外坡度趋于平缓。该海域等深线基本保持东西向, 海沟中部水深较深的地方相对较为平坦。剧烈的水深变化是海岛近岛处常有的情况, 对波浪在近岛海域的传播和波浪场的分布势必产生显著的影响, 这是制定海岛周边波浪能资源勘查方案过程中必须要考虑的因素。
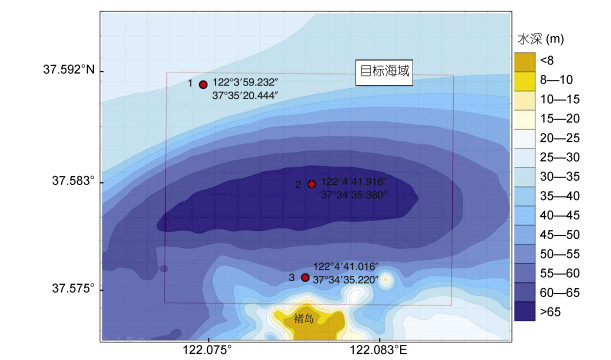 |
| 图 5 褚岛北部水深和测点布置图(红点位置) Fig. 5 The bathymetry of northern Chudao Island and deployment of the test points (red dots) |
对褚岛周边海域环境条件的分析可以初步分析推断:褚岛海域的全年最大波高出现在冬季, 且平均波高最大月也在冬季, 即该海域冬季波浪能资源最为丰富, 冬季以北浪向为主。同时, 由北侧开阔海域向南至岛, 有明显水深变化, 距岛1.2km处有东西向海沟, 近岛处水深快速变浅。据此, 研究制定精细化的观测勘查方案, 遵循以下原则:观测方案制定时应重点关注该海域冬季的波浪特性; 因海域水深变化会对波浪传播和消衰产生影响, 岸线的折射也会影响海域的波浪分布特征, 故在水深变化剧烈处和近岛测应加密观测。
在确定长期观测点前, 先设置短期试验测波点对观测点设置的合理性做进一步试验和验证。根据对目标海域历史资料和水深分布特征的分析, 共设置3个试验测波点:在海域冬季主浪向迎浪位置即目标海域的北测40m水深处布设一个试验测波点(试验点1);海域中部距岛1.2km的70m水深处为近岛最深的区域, 布设一个试验测波点(试验点2);近岛30m水深处, 水深变化最为剧烈的区域, 且岸线对波浪的反射对此区域的波浪影响最大, 设置一个试验测波点(试验点3), 如图 5所示。
对三个试验测试点为期一周的观测数据进行分析, 结果可见, 试验点1和试验点2的波浪特征较为一致, 而试验点3波浪特征与前两点有明显差异, 分析是由于岛岸线对波浪的折射造成的(图 6)。
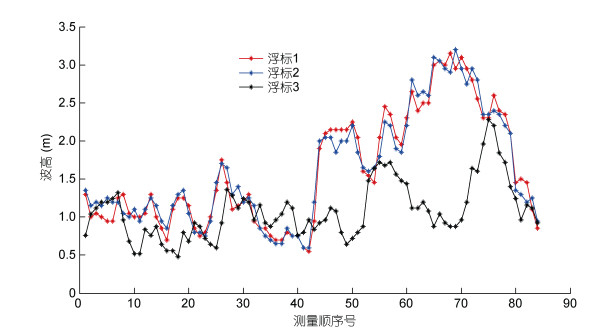 |
| 图 6 三个测试点有效波高数据比较 Fig. 6 Comparison of effective wave height data at the three test points |
在保证观测质量的基础上, 为降低观测成本, 同时降低观测过程中仪器设备丢失的风险, 确定观测方案为:在试验点1和试验点3的位置开展为期一年的连续观测, 试验点2设备回收; 在利用数值模型计算波浪能资源的过程中, 为提高计算精度, 需考虑海流的作用, 同时需要获得风要素数据, 可选择同时具有波浪、海流、风观测能力的综合多参数浮标或其他综合观测设备布放于试验点1的位置进行观测。
1.4 目标海域波浪场时空分布特征分析依据制定的精细化勘查方案, 开展为期1年的长期观测。采用观测时间为2015年1月24日到12月24日的连续观测数据对目标海域波高和波周期特性进行分析:最大波高6.30m, 周期7.50s。观测时段内, 平均有效波高0.62m, 周期4.16s, 平均波高0.42m, 周期3.94s。从2015年1—12月的有效波高变化可以看出, 波浪观测结果与利用周边海域资料分析的该海域波浪特征基本吻合, 波浪资源的季节变化显著, 冬半年波浪较大, 夏半年明显减弱(图 7)。在冬季(11、12、1月)平均有效波高可达1m以上, 经常有大的波高过程; 5—8月主要受夏季季风影响, 但由于褚岛所在海域以南紧邻广阔的大陆, 风浪无法成长, 有效波高基本在0.2—0.3m之间; 从9月底开始逐渐增强; 到了10月份, 开始经常出现有效波高超过2m的大的波浪过程。
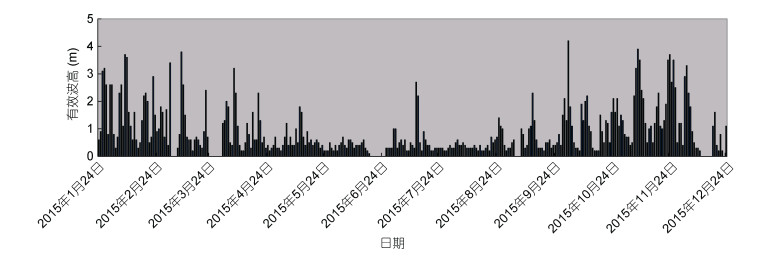 |
| 图 7 2015年1—12月的有效波高变化 Fig. 7 Variations of effective wave height from January to December in 2015 |
为分析目标海域的波浪能资源分布特征, 首先对观测获得目标海域全年的观测数据以主波向角度为基准进行分类, 并统计在各个波向下的有效波高平均值、波周期平均值、风速平均值及风向平均值。经过统计计算, 各个波向的出现频率及其对应的波要素见表 2。按照频率优先的原则, 选择出现频率高于5%的7种波况进行模拟计算并按照频率的高低对其进行排序。计算分析的7种代表波况及其波要素如表 3所示。
| 序号 | 波向 | 频率(%) | 有效波高(m) | 波浪周期(s) | 风速(m/s) | 风向(°) |
| 1 | W(348.75°—360°, 0°—11.25°) | 11.834 | 1.234 | 4.879 | 6.613 | 261.946 |
| 2 | WSW(11.25°—33.75°) | 13.493 | 1.137 | 4.837 | 5.907 | 245.811 |
| 3 | SW(33.75°—56.25°) | 15.388 | 0.672 | 4.303 | 4.122 | 179.470 |
| 4 | SSW(56.25°—78.75°) | 14.177 | 0.447 | 4.010 | 3.772 | 156.617 |
| 5 | S(78.75°—101.25°) | 15.954 | 0.349 | 3.784 | 3.701 | 154.241 |
| 6 | SSE(101.25°—123.75°) | 3.652 | 0.405 | 3.641 | 4.637 | 158.626 |
| 7 | SE(123.75°—146.25°) | 0 | ||||
| 8 | ESE(146.25°—168.75°) | 0 | ||||
| 9 | E(168.75°—191.25°) | 0 | ||||
| 10 | ENE(191.25°—213.75°) | 0 | ||||
| 11 | NE(213.75°—236.25°) | 0 | ||||
| 12 | NNE(236.25°—258.75°) | 0.762 | 0.395 | 3.192 | 6.730 | 190.205 |
| 13 | N(258.75°—281.25°) | 2.499 | 0.402 | 3.263 | 7.067 | 177.969 |
| 14 | NNW(281.25°—303.75°) | 2.089 | 0.444 | 3.723 | 4.959 | 213.187 |
| 15 | NW(303.75°—326.25°) | 11.228 | 0.621 | 3.988 | 5.339 | 230.951 |
| 16 | WNW(326.25°—348.75°) | 8.924 | 0.671 | 4.035 | 5.050 | 232.153 |
| 合计 | 100 |
| 波况编号 | 波向 | 频率(%) | 有效波高(m) | 波浪周期(s) | 风速(m/s) | 风向(°) |
| 1 | S | 15.954 | 0.349 | 3.784 | 3.701 | 154.241 |
| 2 | SW | 15.388 | 0.672 | 4.303 | 4.122 | 179.470 |
| 3 | SSW | 14.177 | 0.447 | 4.010 | 3.772 | 156.617 |
| 5 | W | 11.834 | 1.234 | 4.879 | 6.613 | 261.946 |
| 6 | NW | 11.228 | 0.621 | 3.988 | 5.339 | 230.951 |
| 7 | WNW | 8.924 | 0.671 | 4.035 | 5.050 | 232.153 |
| 合计 | 90.998 |
本文利用SWAN (simulating waves nearshore)计算统计出7种代表波况下的波浪能量, 进而利用计算结果对目标海域的波浪能资源分布特征进行分析(郑崇伟等, 2011, 2015)。
2.2.1 计算模型设置为提高模型的计算精度和计算效率, 设置了不同的运算域和网格尺度, 采用嵌套的方法分别进行计算。大模型的模拟范围为山东半岛近海北黄海海域(37°25′9″—37°51′32″N, 121°41′15″—122°35′31″E), 空间步长约为0.017°。小区域选取威海北部海岸线、褚岛及其北部海域为模型计算区域(37°31′50.35″—37°36′21.18″N, 122°3′3.05″— 122°8′36.36″E), 空间步长均为0.005°, 在褚岛北侧近岛处再加密计算网格; 模型东西向长8173m, 南北向最长为8359m。计算区域水深地形如图 8、图 9所示, 该区域最大水深70m。
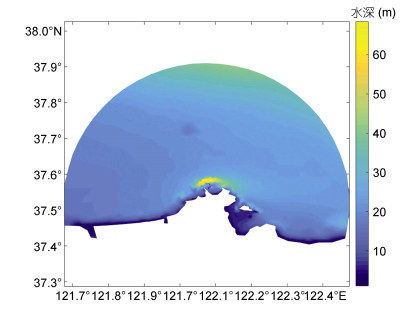 |
| 图 8 大区域模型计算域地形图(单位: m) Fig. 8 Topography of model computation domain of large area (unit: m) |
 |
| 图 9 小区域计算区域地形图(单位: m) Fig. 9 Topographic of computational domain of small area (unit: m) |
模型的频率离散采用Log对数分布, 最小频率f0取0.04, 频率数n取34;方向离散使用全方向离散, 满足技术要求所需达到的计算精度; 通过破碎参数γ值控制由水深引起的波浪破碎, 一般大量的现场观测和实验室模拟表明, γ值跟地形和波况有关, 在0.6—0.8之间随地形坡度而异, 本文采用默认值0.73作为破碎指标; 模型采用JONSWAP底摩擦耗散半经验公式计算底摩阻系数, 因目标海域以涌浪为主, 计算公式中常量系数定为0.038。此外, 考虑到在岛屿海域, 在剧烈变化的水深和复杂的岸线影响下造成的较大流速也将对波周期等要素产生影响, 本文在模型的边界条件中加入了潮流流场, 以更好地模拟岛屿周边波浪要素时空分布特征。
先使用研究区域的风场作为边界条件驱动大模型进行运算, 并输出小区域的波浪谱, 随后, 再利用输出的波浪谱, 以及风场条件驱动小模型运算, 得到更加细致的波浪场分布。
2.2.2 计算模型验证利用试验点1和试验3的实测波浪数据对模型的计算效果进行验证。验证参数为波高, 验证结果如图 10、图 11所示。经验证, 数值模型设置合理, 计算结果准确有效; 特别是近岸试验点3验证了改进的模型对近岛波浪折射、绕射模拟效果良好。
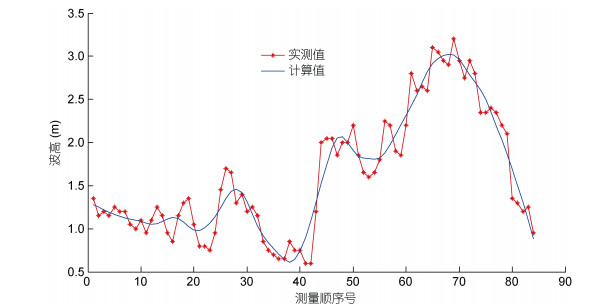 |
| 图 10 试验点1测波浮标数值模拟验证 Fig. 10 The numerical simulation verification of telemetering wave buoy at the test point 1 |
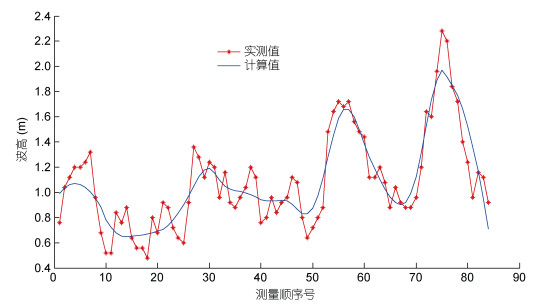 |
| 图 11 试验点3测波浮标数值模拟验证 Fig. 11 The numerical simulation verification of telemetering wave buoy at test point 3 |
本文使用SWAN模式计算得出波高和波周期, 通过“经验方法”计算目标海域的波浪能功率密度P。
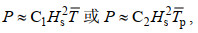 (1)
(1)其中, Hs是有效波高, T为平均周期, Tp是谱峰周期, C1、C2分别为两个经验参数, 一般取C1=0.42, C2=0.5。(侯一筠等, 1990, 1993; 王鑫等, 2008, 2015b)
2.2.4 代表波向波浪能功率密度计算对统计分析得出的出现频率最高的7种波况, 利用前述方法进行计算, 计算结果如表 4。以波况5为例, 其有效波高和波浪能功率密度空间分布如图 12。
| 波况编号 | 有效波高最大值(m) | 目标海域内波浪能分布特征 |
| 1 | 0.25 | 东侧和西侧波浪能功率密度相对最高, 最大值大约为120W/m; 绝大部分区域的波功率密度低于60W/m。 |
| 2 | 0.7 | 西侧波浪能功率密度相对最高, 最大值约为836W/m; 大部分区域的波浪能功率密度分布在200—800W/m。 |
| 3 | 0.46 | 波浪能集聚现象不明显, 最大值约为380W/m; 大部分区域的波功率值分布在100—350W/m。 |
| 4 | 1.12 | 西侧和北侧, 波浪能集聚现象明显, 波浪功率密度最大值约为2830W/m; 大部分区域的波功率值分布在1000—2800W/m。 |
| 5 | 1.28 | 西侧波浪能集聚现象明显, 波浪能功率密度最大值约为3500W/m; 大部分区域的波浪能功率密度分布在2500—3500W/m。 |
| 6 | 0.65 | 西北测波浪能最为集中; 大部分区域波浪能功率密度分布在600—670W/m。 |
| 7 | 0.67 | 西北测波浪能最为集中, 最大值约为810W/m; 大部分区域的波浪能功率密度分布在700—800W/m。 |
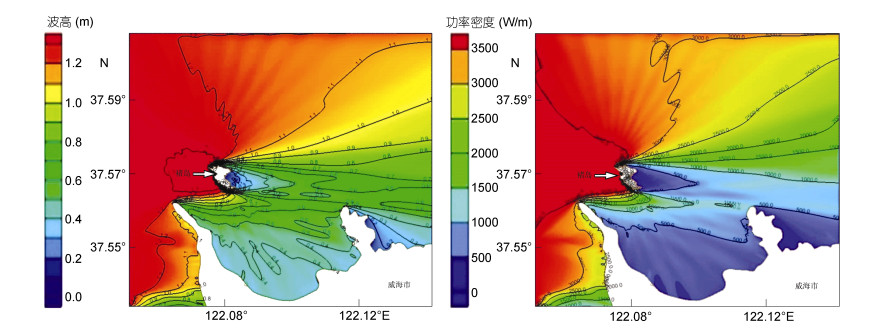 |
| 图 12 波况5有效波高(单位: m)和波浪能功率密度(单位: W/m)空间分布 Fig. 12 Spatial distribution of effective wave height (unit: m) and wave power (unit: W/m) |
7种波况的波浪方向都为偏西方向, 利用其计算分析褚岛及其周边海域波浪能功率密度, 由此可见, 由于远遥嘴和褚岛对波浪传播的阻挡, 在威海海岸线北部至褚岛之间和褚岛东侧海域, 主要受到波浪绕射的影响, 有效波高较小, 相应地波浪能功率密度也较低。在波况1、2、3、6、7五种波况下, 目标海域内的波浪能功率密度都不超过1000W/m, 在波况4和波况5两种波况下, 目标海域区域的波浪能功率密度超过2000W/m。计算各个波况频率在参与计算的波况总频率中的占比, 可以得到各个波况的频率加权系数(表 5)。
| 波况编号 | 波浪方向 | 出现频率(%) | 频率加权系数 |
| 1 | S | 15.954 | 0.1753 |
| 2 | SW | 15.388 | 0.1691 |
| 3 | SSW | 14.177 | 0.1558 |
| 4 | WSW | 13.493 | 0.1483 |
| 5 | W | 11.834 | 0.1300 |
| 6 | NW | 11.228 | 0.1234 |
| 7 | WNW | 8.924 | 0.0981 |
| 合计 | 90.998 | 1.0000 |
按照表 5中的频率加权系数, 可以得到目标海域内7种波况的频率加权平均波功率分布, 计算结果代表了目标海域内全年不同波向上的波浪能量分布情况(图 13)。综合分析各波况的计算结果可见:目标海域的波浪能受季风和海岛及大陆岸线的影响明显, 而受到水深梯度变化的影响不明显; 波浪能蕴藏量的时空分布特征总体表现为冬季强夏季弱, 冬季在西侧多会出现波浪能集聚, 西部强东部弱, 且为自西向东递减; 西北向是波浪能功率密度最大的区域, 波浪能功率密度值大于1200W/m; 在褚岛的东侧海域, 波浪能功率密度较小, 均小于400W/m。
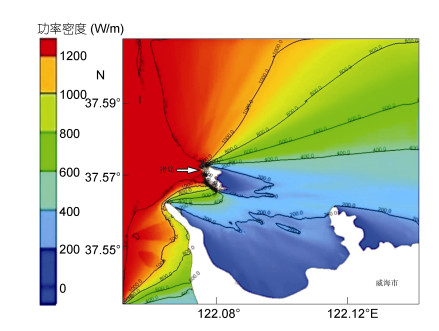 |
| 图 13 目标海域各波向波浪能量分布图(单位: W/m) Fig. 13 Wave energy distribution in each wave direction in targeted sea area (unit: W/m) |
对小区域波浪能资源的勘查, 往往是作为波浪能电站建设前期的评估和选址工作而开展, 其方法和要求有别于以往大范围普查, 特别是海岛周边复杂的地形和动力环境条件, 对勘查工作提出了更高的要求。为实现对海岛周边海域的精细化勘查, 本文对传统勘查方法进行了有益的改进:首先搜集历史数据掌握海域的资源条件概况, 结合对波浪要素分布进行的动力学理论分析, 有针对性地制定勘查方案, 观测点和观测周期在水动力复杂区域均进行加密; 进行长期观测前, 先对观测点设置的合理性进行短期的试验验证, 根据试验结果对勘查方案进行优化, 一是调整代表性不强的观测点位置, 二是在保证勘查结果满足计算分析精度要求的前提下, 合并或减少观测点, 从而减少观测设备的投入, 即可有效降低长期观测期间设备丢失和损坏的概率, 从而降低勘查成本, 这一勘查方案制定流程和勘查方法不仅适用于波浪能电站建设等海洋工程的前期选址和评估工作, 在其他海上观测工作中也具有借鉴和应用价值。
与追求某几个特定波况下波浪能电站的高效获能相比, 波浪能电站的设计与建造者更关注电站全年的发电量。对于海岛周边小区域波浪能资源分布特征的分析, 应建立在长期精细化勘查的基础上, 综合全面分析目标海域波浪能资源的时空分布特征, 以保证电站建成后实现预期的年发电量指标要求。本文将统计学方法和数值模拟方法相结合, 从对各波向的统计分析入手, 得出目标海域的主要波向及其对应的波参量, 进而定量地计算得出了目标海域全年在各主要波向上波浪能量分布, 并以此从总体上分析目标海域波浪能量时空分布特征, 分析结果对于波浪能电站建设前期评估和选址具有很高参考价值。本文研究的方法对于应用俘获能量效果受波向影响明显的波浪能开发利用技术或波浪能阵列的波浪能电站设计尤其适用。此外, 利用类似的方法, 对全年波周期和波高在各值域的出现概率进行统计, 进而分析计算目标海域全年波浪能量集中的波周期和波高区间, 对于波浪能电站能量俘获装置的设计优化同样具有较高的指导价值。
王鑫, 王兵振, 武贺, 等. 2015b. 利用波浪谱理论计算我国近岸波浪能方法研究. 海洋通报, 34(3): 316-319 |
王鑫, 侯一筠. 2008. 风浪频谱的成长模型Ⅰ.谱参量随风区的增长关系. 海洋与湖沼, 39(5): 433-438 |
王鑫, 韩林生, 朱锐, 等. 2015a. 海上试验场对近岸波浪数值模式研究工作的支撑作用分析. 海洋通报, 34(5): 547-550 |
王传崑, 卢苇. 2009. 海洋能资源分析方法及储量评估. 北京: 海洋出版社, 85-95
|
史宏达, 马哲, 梁丙臣, 等. 2013. 波浪能资源评估方法研究——以担杆岛为例. 中国海洋大学学报(自然科学版), 43(7): 89-93 |
史宏达, 曲娜, 曹飞飞, 等. 2017. 振荡浮子波能发电装置浮子运动性能的试验研究. 中国海洋大学学报, 47(6): 124-130, 145 |
刘首华, 杨忠良, 岳心阳, 等. 2015. 山东省周边海域波浪能资源评估. 海洋学报, 37(7): 108-122 |
刘秋林, 张永良, 梁森栋. 2015. 斋堂岛海域波浪能资源的数值模拟研究. 水力发电学报, 34(11): 148-156 |
杨永增, 乔方利, 赵伟, 等. 2005. 球坐标系下MASNUM海浪数值模式的建立及其应用. 海洋学报(中文版), (02): 1-7 |
李靖, 周林, 郑崇伟等, 2011.台湾海峡及其邻近海域波浪能资源评估.见: 中国可再生能源学会2011年学术年会论文集.北京: 中国可再生能源学会, 37-40
|
张军, 许金电, 郭小钢. 2012. 福建沿海海域波浪能资源分析与评价. 台湾海峡, 31(1): 130-135 |
周凯, 汪睿. 2013. 山东半岛近海波浪能资源状况初步分析. 水力发电, 39(11): 94-99 |
郑崇伟, 李崇银. 2015. 中国南海岛礁建设:重点岛礁的风候、波候特征分析. 中国海洋大学学报(自然科学版), 46(9): 1-6 |
郑崇伟, 郑宇艳, 陈洪春. 2011. 基于SWAN模式的近10年南海北部波浪能资源研究. 亚热带资源与环境学报, 6(2): 54-59 |
郑崇伟, 游小宝, 潘静, 等. 2014. 钓鱼岛、黄岩岛海域风能及波浪能开发环境分析. 海洋预报, 31(1): 49-57 |
侯一筠, 王涛. 1993. 风浪频谱中的特征量. 海洋与湖沼, 24(2): 126-131 |
侯一筠, 文圣常. 1990. 三参量的风浪频谱. 海洋与湖沼, 21(6): 495-504 |
栗冬慧, 2015.山东半岛蓝黄两区海域风能、波浪能资源数值评估.青岛: 中国海洋大学硕士学位论文, 41-47
|
蒋廷松, 2013.浙江省海域的波浪数值模拟与波浪能资源分析.杭州: 浙江工业大学硕士学位论文, 33-45
|
韩家新. 2015. 中国近海海洋:海洋可再生能源. 北京: 海洋出版社, 35-67
|
Izadparast A H, Niedzwecki J M, 2011. Estimating the potential of ocean wave power resources. Ocean Engineering, 38(1): 177-185 |
 2020, Vol. 51
2020, Vol. 51


