
中国海洋湖沼学会主办。
文章信息
- 孙丹译, 李爽. 2020.
- SUN Dan-Yi, LI Shuang. 2020.
- 基于大涡模拟耦合模式的小尺度海气相互作用研究
- LARGE EDDY SIMULATION COUPLING MODEL FOR SMALL-SCALE AIR-SEA INTERACTION
- 海洋与湖沼, 51(6): 1310-1319
- Oceanologia et Limnologia Sinica, 51(6): 1310-1319.
- http://dx.doi.org/10.11693/hyhz20191200277
文章历史
-
收稿日期:2019-12-26
收修改稿日期:2020-01-28
大气和海洋是地球系统中的两个重要组成部分, 它们之间的相互作用是地球气候系统的关键调节因素之一, 而单一的大气或海洋模式无法完整描述此过程, 所以海气耦合模式被提出并得到快速发展, 其发展经历了从全球到区域的过程, 其中全球海气耦合模式主要用于研究大尺度海气相互作用, 然而全球模式的分辨率无法准确描述中小尺度海气相互作用, 因此区域海气耦合模式凭借其较高的分辨率, 能够对海气相互作用进行更细致的研究, 其广泛应用于数值模拟、预报和区域气候变化动力降尺度研究(Peng et al, 2012)。海气通量则是海气相互作用中的一个重要研究课题(陈烈庭, 1991), 所以在全球或区域的海气耦合模式中考虑海气通量的变化对深入研究海气相互作用具有重要意义。Zhou等(2000)将海气淡水通量的交换引入耦合模式Global-Ocean-Atmosphere- Land-System-model(GOALS)成功地控制了气候漂移现象(Neelin et al, 1992;陈克明等, 1997)。海气界面处的动量通量也叫风应力, 是海气相互作用研究的重点之一, 也是海气耦合模式中的一个重要参数(冯兴如等, 2018)。Ma等(2010)在海气耦合模式FOAM中通过控制变量证明风应力对气候的重要影响。Zhou等(2015)将AGCM模式和一个混合层海洋模式耦合用以探究海气耦合对大西洋多年代际振荡的影响。
区域海气耦合模式的关键技术是在系统质量和能量守恒的前提下实现高效的海气参数的交互传递, 现如今耦合模式普遍采用“耦合器”技术(Coupler), 而另一个技术难题是侧边界条件的处理, 对于侧边界的处理直接影响模拟结果(Peng et al, 2012)。上述这些海气耦合模式对于处理海气之间的质量、动量和能量的交换问题通常是依靠经典参数化方案, 而且模式的空间分辨率并不能准确描述小尺度的海气相互作用。2001年海气相互作用耦合边界层低风速实验(The Coupled Boundary Layers and Air-Sea Interaction- Low Winds, CBLAST-Low)项目在沿海部署了一套观测系统用以提供海气数据, 取得了很好的观测结果(Austin et al, 2002; Vickers et al, 2006; Edson et al, 2007)。但是相对于观测系统造价昂贵以及单点观测所带来结果特殊性的特点, 数值模拟作为一种新兴的研究方式近年来发展迅速。因为大气和海洋中的湍流时刻影响着海气通量的交换, 所以模式需要充分考虑湍流作用。以往的湍流模式大多是雷诺平均模式(Reynolds Average Navier-Stokes, RANS), Peng等(2012)中介绍的区域海气耦合模式大都使用RANS方法, 而大涡模拟(Large Eddy Simulation, LES)与RANS不同, 其原理是基于尺度的分离:在模拟中直接计算大尺度的脉动, 对于小尺度的湍流效应则采用参数化的方案(Smagorinsky, 1963; Deardorff, 1970), 因为其较为精确且节省计算成本的特性, 已经成为大气和海洋领域中研究湍流的一种成熟方法。Esau(2014)采用并行大涡模拟模式(The Parallelized Large-Eddy Simulation Model, PALM), 研究了大气边界层(Atmospheric Boundary Layer, ABL)与海洋混合层(Oceanic Mixed Layer, OML)之间在无剪切对流情况下的湍流相互作用。
湍流作为大气和海洋中显著的动力过程, 是影响海气通量的重要因素。大涡模拟允许湍流场的三维实现, 可以用湍流动能平衡方程中的耗散项、剪切项和传输项等来刻画湍流过程, 这是大尺度模式和大多数实验研究所不能实现的(Maronga et al, 2015)。所以在湍流尺度运用大涡模拟来探究风速对海气通量的影响和对深入了解海气相互作用过程具有重要的意义。为此本文在Esau(2014)的基础上引入风速, 用大涡模拟海气耦合模式探究风速对海气通量和海洋湍流动能收支各项分布的影响。
1 模式简介 1.1 PALM简介PALM是由德国汉诺威莱布尼茨大学开发的用于大气和海洋边界层的一种湍流分解大涡模拟模式, 已应用于各种大气和海洋边界层的模拟超过15年(Huq et al, 2019)。经过优化, PALM可用于大规模并行计算机架构, 这也是它能进行模式耦合的技术基础, 关于PALM的详细介绍可见https://palm.muk.uni-hannover.de/trac/wiki。
本文使用的模式基于Boussinesq近似的非流体静力学, 对经过滤波的不可压缩的Navier-Stokes方程进行求解。下面的方程组通过对离散笛卡尔网格体积上的控制方程求平均值, 可以隐式地实现分辨尺度和次网格尺度湍流模式(Sub-grid Scale, SGS)的分离, 其中SGS的建立是基于Deardorff(1980)提出的方法, 但是为了方便起见, 这里使用了方程的连续形式。PALM中有六个预测量:速度场的三个变量(u, v, w)位势温度(θ), 湿度(q)(海洋中是盐度(s))和次网格动能(e), 其基本方程为:
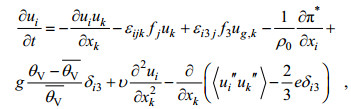 (1)
(1) (2)
(2) (3)
(3)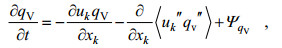 (4)
(4)其中, i, j, k ∈ { 1, 2, 3 }, t是时间, ui是速度分量(u1=u, u2=v, u3=w), 坐标xi(x1 = x, x2 = y, x3 = z), ε是列维-奇维塔符号, fi = (0, 2Ω cos (ϕ), 2Ω sin (ϕ))是科氏力参数, ρ0是密度, π*是修改后的扰动压力, g是重力加速度, θV是位势温度, v是运动黏度, δi3克罗内克符号, e是次网格湍流动能, LV蒸发潜热, cp是恒压干燥空气的比热容, qV是湿度, ΨqV是湿度的源/汇项, Π是温度和位势温度之间的转换公式, 双撇号表示SGS, 上划线表示水平平均, 尖括号表示SGS通量。
在海洋模式中:将公式(1)中的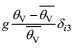
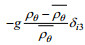
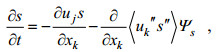 (5)
(5)其中, s是盐度, 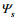
根据公式(1)可得水平平均的SGS-TKE方程(Skyllingstad et al, 2000)为:
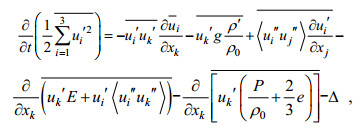 (6)
(6)其中:
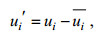 (7)
(7)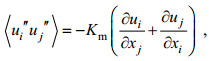 (8)
(8)P是压强, Km是次网格涡粘系数。公式(6)中等号右边各项依次是:速度剪切项、浮力项、次网格耗散项、湍流动能传输项、压力项和耗散项。下文中湍流动能收支的耗散项包含了次网格耗散, 而湍流动能传输项包含了次网格湍流动能传输。
1.2 海气耦合模式简介为了研究ABL和OML中湍流过程之间的相互作用, PALM组开发了一种海气耦合模式。这种耦合模式是通过两个大涡模拟(一个大气和一个海洋)之间在海面上的变量实时在线交换实现的。海洋和大气之间的通量守恒要求根据水的密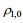
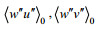
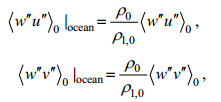 (9)
(9)由于海水蒸发导致海面冷却, 海洋的热通量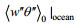
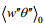
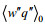
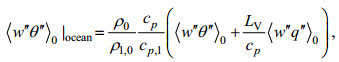 (10)
(10)这里cp, l是水在恒压下的比热容。由于盐不能蒸发, 海水的蒸发会导致海水含盐量的增加, 这一过程由Steinhorn(1991)通过一种在海面的负(向下)盐度通量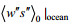
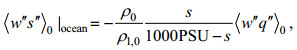 (11)
(11)PSU(Practical Salinity Units)表示盐度的标准, 为无单位量纲。将海面位温θ0和水平速度分量uo和vo作为表面边界条件传递到大气中:
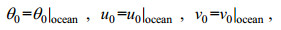 (12)
(12)大气和海洋的时间步长是单独设置的, 不要求相等, 然后以用户指定的频率执行耦合, 目前, 该耦合要求大气和海洋的水平域的大小相等, 而耦合则是通过海面数据的双向双线性插值实现的。此外, 在大气和海洋中, 由于模式稳定时间的不同, 即动能输出达到稳定的时间不同, 可以为大气和海洋先执行非耦合的前驱运行, 然后再进行耦合的重新启动运行, 这可以减少计算量, 也是本文所使用的方法。
1.3 模式设置本文的模式设置中大气部分的网格数是100× 100×60(x, y, z), 网格大小是1m×1m×5m;海洋部分的网格数是100×100×100(x, y, z), 网格大小是1m×1m× 1m。本文中PALM海气耦合分为两个部分:前驱运行和耦合运行, 两者的设置大致相同, 时间步长方案均采用三阶Runge-Kutta方法, 侧边界条件均是周期性边界条件, 大气(海洋)模式中的下(上)边界采用自由滑移边界条件, 大气模式的表面温度是270.6K, 温度梯度是0.015K/m, 海洋模式的温度是272.65K, 盐度是34.8, 纬度设置为45°N。本文不考虑海洋分层和海洋背景流; 前驱运行中大气模式依靠风速输入启动, 海洋模式则是在运行初始加入一个微小扰动用于模式启动, 具体表现是在海表面以热通量的形式输入模式, 该扰动不会影响模拟结果。前驱运行中大气模式的运行时间是7200s, 海洋模式则是40000s;耦合运行的时间均是86400s, 耦合步长均是30s。这样设置的原因是大气和海洋的时间尺度不一致且海洋的响应时间比大气慢, 所以在模式前驱运行中的稳定时间海洋比大气长很多。本文通过设置三种地转风速度(5m/s, 10m/s, 15m/s)来探究其对海气通量及海洋湍流动能收支的影响。
1.4 模式验证Esau(2014)运用大涡模拟海气耦合模式探究ABL与OML之间的湍流相互作用, 然而他并没有考虑风速对海气湍流相互作用的影响, 为此本文在Easu(2014)的基础上引入风速, 使用耦合模式探究风速对海气相互作用的影响。在此之前, 本文先重复Easu(2014)的结果, 来证明该耦合模式在海气相互作用研究中的可行性。
耦合模式初始设置:网格数128×128×64(x, y, z), 网格大小25m×25m×10m(大气), 25m×25m×5m(海洋)。将ABL中位温的初始垂直梯度设为0.015K/m, 初始相对湿度为0%(干燥空气)。OML的初始温度和盐度剖面来自Esau(2014):海面温度为275.65K, 盐度为34.8, 大气边界层表面温度为270.6K, 耦合模拟时间为22h。湍流是由ABL中40—90m层和OML中-40—90m层规定的速度场中的弱扰动引起的, 其中湍流数据每60s采样一次, 二维数据每5min采样一次。
图 1显示了温度、净热通量、动量通量在最后一小时的时间平均剖面, 虚线是Esau(2014)的结果, 实线是耦合模式运行结果。在图 1中, 两者温度值的分布相差不大, 净热通量和动量通量的分布也大致相同, 本文将两者的差异归结为以下几点:
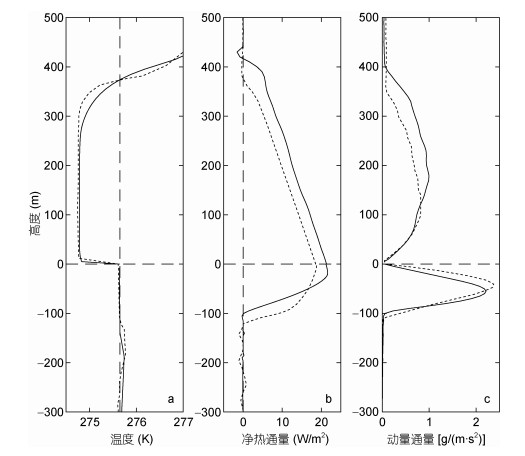 |
| 图 1 温度、净热通量和动量通量的垂向分布 Fig. 1 Vertical distribution of temperature, net heat flux, and momentum flux 注:实线:模式运行的结果; 虚线: Esau(2014)的结果 |
(1) 模式直接取Esau (2014)文献中的温盐初始剖面, 并没有得到其原始数据, 所以导致结果存在微小偏差。
(2) 模式版本经过更新换代。
(3) 关于耦合模式中前驱运行的细节文献中没有详细说明, 可能模式输入存在些许偏差。
2 模拟结果 2.1 风速和流速耦合模式由前驱运行在大气和海洋部分中产生稳定的湍流, 之后再进行耦合, 考虑到耦合模式有一个启动过程, 将垂向动能进行水平平均得到图 2, 横坐标是时间, 纵坐标是高度, 在图 2中大气部分从模式启动开始就一直稳定, 而海洋需要响应时间, 所以从图 2中可以看到整体模式稳定时间在耦合开始1h后。
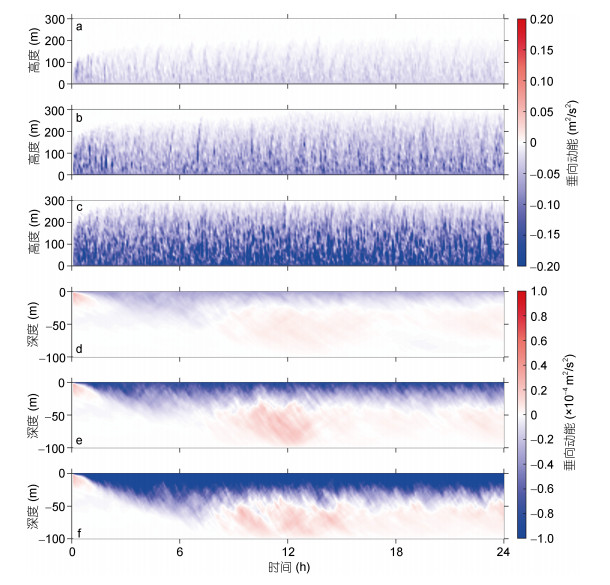 |
| 图 2 垂向动能时间序列 Fig. 2 Time series of vertical momentum 注: a—c:大气的垂向动能; d—f:海洋的垂向动能; a, d:风速5m/s; b, e:风速10m/s; c, f:风速15m/s |
地转风速为5m/s时, 大气的垂向动能在0—150m的区域内变化明显, 其最值约为-0.05m2/s2, 相应的海洋受风速影响的深度约为20m, 垂向动能的最值约为在-2×10-5m2/s2。地转风速为10m/s时, 大气受风速影响的高度约为250m, 垂向动能的最值约为-0.1m2/s2; 海洋受风速影响的深度为25m, 垂向动能的最值在-5×10-5m2/s2。地转风速为15m/s时, 大气受风速影响的高度增大为300m, 垂向动能的最值为-0.2m2/s2; 海洋受风速影响的深度约为35m, 垂向动能的最值为-1×10-4m2/s2。
除了垂向动能的时间变化外, 本文还关注了大气海洋中速度分量在垂向上的变化, 将数据进行时间平均后得到大气风速和海洋流速垂向剖面图 3。图 3中实线表示u方向, 虚线表示v方向, 红线表示风速为5 m/s, 蓝线表示风速为10 m/s, 黑线表示风速为15m/s; 为了便于展示, 本文将海洋的流速数值放大100倍。
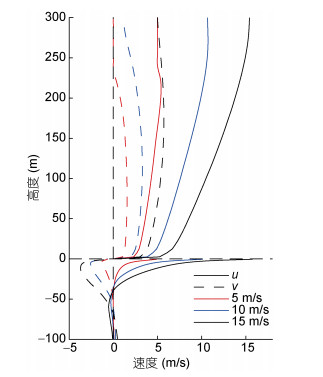 |
| 图 3 速度剖面图 Fig. 3 Velocity profile 注:实线表示u, 虚线表示v; 为了便于展示, 将实际海洋流速数值×102后绘制此图 |
图 3展示了耦合模式中大气和海洋中速度分量的分布。由于模式中只在u方向添加地转风, 所以在图 3中海洋中v方向流速从0开始。随着风速的增加, 海洋流速逐渐增大且呈现向下延伸的趋势, 并在-50m左右迅速减小。
2.2 海气通量PALM中的海气耦合是ABL和OML之间的耦合, 耦合是通过一个大气-海洋界面来保存每个网格单元内的质量(湿度、盐度)、动量和热量的湍流通量。ABL在OML的顶部边界提供了通量, 而OML在ABL的底部边界提供了速度和温度。
通过模式所得数据对其进行时间平均得到图 4:
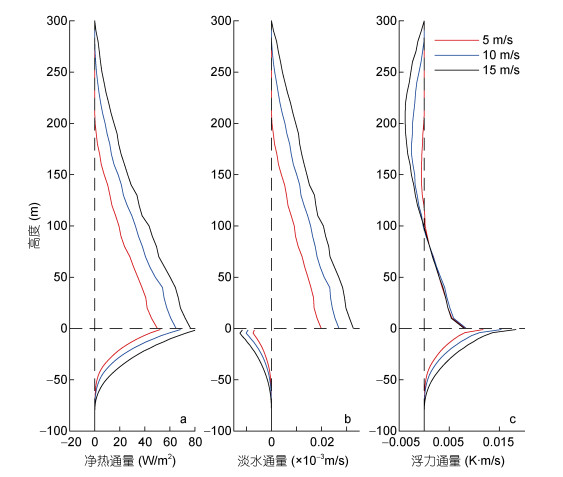 |
| 图 4 净热通量、淡水通量和浮力通量的垂向剖面图 Fig. 4 Vertical profiles for net heat flux, fresh water flux and buoyancy flux 注: a:大气和海洋的净热通量; b:大气的淡水通量, 海洋中用盐度通量代替; c:大气和海洋的浮力通量, 图中所示的海洋浮力通量值是实际值×103 |
由图 4可以直观的看到不同风速下海气通量的垂向变化。在海气界面处, 风速越大, 大气中的净热通量和淡水通量也相应增大, 而浮力通量变化不大; 海洋中则是净热通量和浮力通量增大, 盐度通量为负表示海面蒸发加剧。而且随着风速的增大, 各通量在海洋中向下传递的距离越大; 而在大气中, 净热通量和淡水通量也相应变大, 浮力通量在0—100m变化不大, 在100—300m变化明显。
本文取大气10m处和水下2m处的通量值进行对比得到图 5。图 5a中:海气的净热通量随风速增大而增大, 且随着海气之间相互传递热通量, 两者关系呈正相关; 图 5b中:随着风速增大, 海面受热蒸发加剧, 导致大气淡水通量增大, 而海洋盐度通量(负)增大。
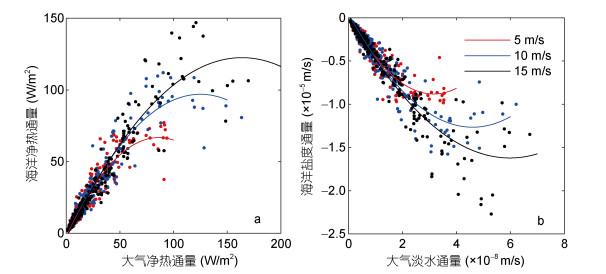 |
| 图 5 不同风速下大气海洋的净热通量, 淡水通量(盐度通量)的关系图 Fig. 5 The relationship between net heat flux and fresh water flux (salinity flux) of the atmosphere and ocean at different wind speeds 注:大气的净热通量和淡水通量取10m处的值; 海洋的净热通量和盐度通量取-2m处的值; 实线:通量的趋势 |
图 6展示了海洋湍流动能收支情况, 根据公式(6)本文用红线表示速度剪切项, 绿线表示湍流动能传输项, 蓝线表示压力项, 粉线表示浮力项, 黑线表示耗散项, 为了便于展示将各项数值×106。左图为三个风速下的海洋湍流动能收支情况, 右图均为左图-35—0m处的局部放大图。
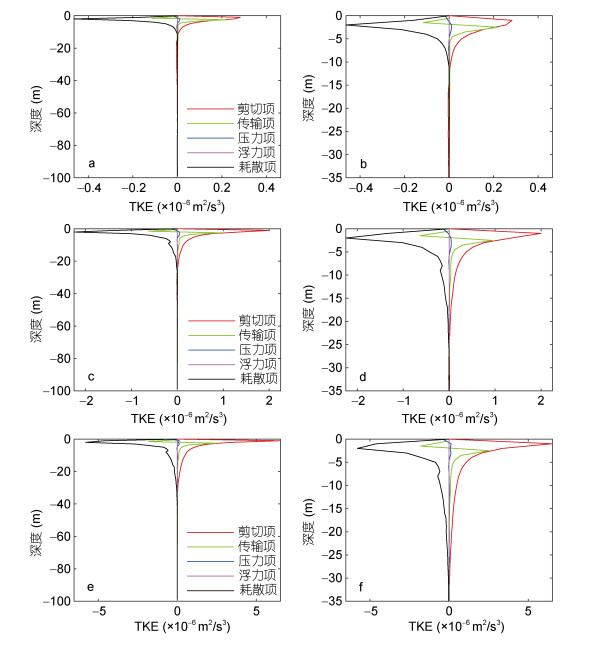 |
| 图 6 湍流动能收支 Fig. 6 The TKE budget 注: a: 5m/s时海洋湍流动能收支, b是a的区域放大图; c: 105m/s时海洋湍流动能收支, d是c的区域放大图; e: 155m/s时海洋湍流动能收支, f是e的区域放大图; TKE: Turbulence Kinetic Energy, 湍流动能 |
从图 6a, 6c, 6e可以发现海洋湍流动能收支各项分别在-15、-25、-35m处迅速减小, 说明不同风速所能影响海洋的深度随风速增加而加深。在图 6b中, 剪切项与湍流动能传输项的值在近海面处差别不大, 耗散项的值最大可以到达-4.5×10-7m2/s3; 在图 6d中, 剪切项与耗散项在近海面处的值达到最大且两项大致持平, 最值大约为2×10-6m2/s3; 在图 6f中, 剪切项、传输项和耗散项达到最大值, 最值约为5× 10-6m2/s3。随着风速的增加, 近海面处的剪切与传输必然增大, 导致向下传递的距离越远, 所产生的耗散也相应增大, 且随着深度加深逐渐减弱。
3 讨论 3.1 耦合模式与非耦合模式的差别前文分析了耦合模式的结果, 在耦合模式中海洋是依靠大气风速驱动, 而在非耦合模式中海洋是依靠固定的动量通量输入驱动。图 7展示了地转风为105m/s情况下, 海气耦合与非耦合模式的垂向流速在u, v两个方向的时间序列。图 7a和c分别表示耦合模式下的垂向流速在u方向和v方向的时间序列; 图 7b和d分别表示非耦合模式下的垂向流速在u方向和v方向的时间序列。
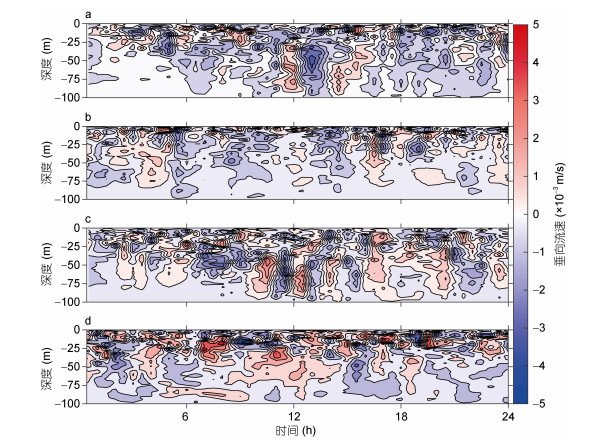 |
| 图 7 垂向流速时间序列 Fig. 7 Time series of vertical velocity 注: a:耦合模式下u方向垂向流速时间序列; b:非耦合模式下u方向垂向流速时间序列; c:耦合模式下v方向垂向流速时间序列; d:非耦合模式下v方向垂向流速时间序列 |
通过比较得知:在整个模式运行期间, 耦合模式海洋部分受风速影响较深, 而非耦合模式流速变化巨大的区域大多集中在靠近海面的地方。
图 8展示了经过时间平均后不同深度(-5、-15、-30、-40m)的垂向流速水平截面。从中可以发现耦合模式与非耦合模式从水下5m到水下30m区域中的垂向流速分布大致相同, 而在水下40m处时, 非耦合模式的垂向流速减弱明显, 这也说明了在耦合模式下, 受到大气持续影响, 能量向下传递的距离更远。
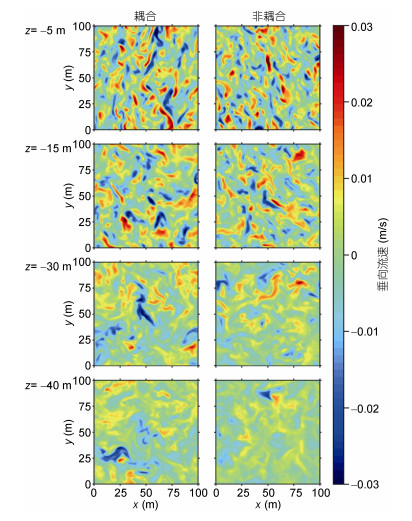 |
| 图 8 垂向流速水平截面 Fig. 8 Horizontal section of vertical velocity 注: x:水平u方向坐标; y:水平v方向坐标; z:垂直方向坐标 |
图 9展示了耦合模式与非耦合模式的海洋湍流动能收支情况, 实线表示耦合模式, 虚线表示非耦合模式的结果, 从中可以发现二者趋势大致相同, 但是非耦合模式的湍流动能收支各项略小于耦合模式, 且相较于耦合模式在-25m处趋于0, 非耦合模式趋于0的深度较浅, 这也符合图 7和图 8显示的耦合模式下海洋受风速影响区域较深的结果。
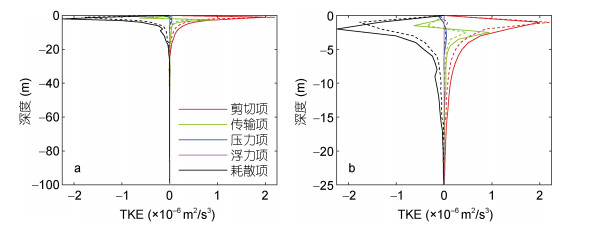 |
| 图 9 湍流动能收支对比 Fig. 9 Comparison of TKE budget 注: a:耦合模式与非耦合模式的海洋湍流动能收支图, b是a的区域放大图, 其中实线表示耦合模式结果, 虚线表示非耦合模式结果 |
海洋混合层受风速影响存在两个重要湍流过程:波浪破碎和Langmuir环流。波浪破碎在海面附近产生大量的小尺度湍流, 而由风驱动的表面流切变与Stokes漂移的相互作用产生Langmuir环流, 这两者对于海洋混合层有较大影响。Noh等(2004)对海洋混合层进行了波浪破碎和Langmuir环流的大涡模拟, 揭示了波流相互作用在海洋混合层垂向混合过程中的重要作用。Li等(2013)使用大涡模拟研究两者在海表边界层中的作用, 模式结果与从CBLAST站点湍流测量分析得出的结论一致。波浪破碎与Langmuir环流均发生在海气边界上, 影响海气通量交换, 未来的工作重点便是在耦合模式中加入波浪破碎和Langmuir环流, 考虑波流相互作用对海气通量交换的影响。
4 结论本文为探究小尺度海气相互作用, 使用大涡模拟海气耦合模式, 设置了5、10和15m/s三种地转风速度, 展示了不同风速下海气通量和OML湍流动能收支各项的分布结果, 并且对比分析了耦合模式与非耦合模式的差别。主要结论如下:
(1) 随着风速的增加, 垂向动能在大气和海洋中的分布呈现纵向加深的趋势; 净热通量在海气界面处进行交换, 在海洋中随着深度的增加而减小, 受到风速的影响, 随风速的增大而增加。海洋受热加剧海水蒸发, 从而持续向大气输送水汽导致海洋盐度通量的增大。大气的浮力通量在100—300m随风速增大而减小, 而海洋的浮力通量随风速增大而增加。
(2) 海洋混合层中湍流动能收支也响应风速的变化, 其中剪切项、耗散项和传输项随着风速的增大而增加, 且在区域-35—0m变化明显, 由于海洋模式受到大气风速的驱动, 所以在近海表面各项达到最大值, 之后随着深度逐渐减弱。
(3) 非耦合模式中海洋依靠定值的动量通量输入驱动, 从而导致非耦合模式中流速在靠近海面的区域变化明显, 之后向下迅速减弱; 而耦合模式中海洋依靠大气模式的风速持续驱动, 所以其流速分布显示在海表面处较大, 而随着深度缓慢减弱。湍流动能收支的结果表明耦合模式各项略大于非耦合模式。
对于大尺度的海气耦合模式不能解释小尺度海气相互作用的问题, 本文通过大涡模拟在湍流尺度展示了海气通量和海洋湍流动能收支情况, 为完善海气耦合模式提供新的方法。随着现今计算机技术的发展, 耦合模式所用的计算资源与非耦合模式相差不大, 而且耦合模式相比非耦合模式, 充分考虑海洋和大气的协同作用, 使得结果更趋近于真实情况。
冯兴如, 李水清, 尹宝树. 2018. 海气动量通量研究综述. 海洋科学, 42(10): 103-109 DOI:10.11759/hykx20180725001 |
陈克明, 金向泽, 张学洪. 1997. 关于海气耦合模式气候漂移及敏感性的一点探讨. 海洋学报, 19(2): 38-51 |
陈烈庭. 1991. 海气相互作用. 地球科学进展, 6(5): 76-77 |
Austin T C, Edson J B, McGillis W R et al, 2002. A network-based telemetry architecture developed for the Martha's Vineyard Coastal Observatory. IEEE Journal of Oceanic Engineering, 27(2): 228-234 DOI:10.1109/JOE.2002.1002477 |
Deardorff J W, 1970. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. Journal of Fluid Mechanics, 41(2): 453-480 DOI:10.1017/S0022112070000691 |
Deardorff J W, 1980. Stratocumulus-capped mixed layers derived from a three-dimensional model. Boundary-Layer Meteorology, 18(4): 495-527 DOI:10.1007/BF00119502 |
Edson J, Crawford T, Crescenti J et al, 2007. The coupled boundary layers and air-sea transfer experiment in low winds. Bulletin of the American Meteorological Society, 88(3): 341-356 DOI:10.1175/bams-88-3-341 |
Esau I, 2014. Indirect air-sea interactions simulated with a coupled turbulence-resolving model. Ocean Dynamics, 64(5): 689-705 DOI:10.1007/s10236-014-0712-y |
Huq S, De Roo F, Raasch S et al, 2019. Vertically nested LES for high-resolution simulation of the surface layer in PALM (version 5.0). Geoscientific Model Development, 12(6): 2523-2538 DOI:10.5194/gmd-12-2523-2019 |
Li S, Li M, Gerbi G P et al, 2013. Roles of breaking waves and Langmuir circulation in the surface boundary layer of a coastal ocean. Journal of Geophysical Research:Oceans, 118(10): 5173-5187 DOI:10.1002/jgrc.20387 |
Ma H, Wu L X, Li C, 2010. The role of southern high latitude wind stress in global climate. Advances in Atmospheric Sciences, 27(2): 371-381 DOI:10.1007/s00376-009-9047-x |
Maronga B, Gryschka M, Heinze R et al, 2015. The parallelized large-eddy simulation model (PALM) version 4.0 for atmospheric and oceanic flows:model formulation, recent developments, and future perspectives. Geoscientific Model Development, 8(8): 2515-2551 DOI:10.5194/gmd-8-2515-2015 |
Neelin J D, Latif M, Allaart M A F et al, 1992. Tropical air-sea interaction in general circulation models. Climate Dynamics, 7(2): 73-104 DOI:10.1007/BF00209610 |
Noh Y, Min H S, Raasch S, 2004. Large eddy simulation of the ocean mixed layer:the effects of wave breaking and Langmuir circulation. Journal of Physical Oceanography, 34(4): 720-735 DOI:10.1175/1520-0485(2004)034<0720:LESOTO>2.0.CO;2 |
Peng S Q, Liu D L, Sun Z B et al, 2012. Recent advances in regional air-sea coupled models. Science China Earth Sciences, 55(9): 1391-1405 DOI:10.1007/s11430-012-4386-3 |
Skyllingstad E D, Smyth W D, Crawford G B, 2000. Resonant wind-driven mixing in the ocean boundary layer. Journal of Physical Oceanography, 30(8): 1866-1890 DOI:10.1175/1520-0485(2000)030<1866:RWDMIT>2.0.CO;2 |
Smagorinsky J, 1963. General circulation experiments with the primitive equations:I.The basic experiment. Monthly Weather Review, 91(3): 99-164 DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
Steinhorn I, 1991. Salt flux and evaporation. Journal of Physical Oceanography, 21(11): 1681-1683 DOI:10.1175/1520-0485(1991)021<1681:SFAE>2.0.CO;2 |
Vickers D, Mahrt L, 2006. Evaluation of the air-sea bulk formula and sea-surface temperature variability from observations. Journal of Geophysical Research:Oceans, 111(C5): C05002 DOI:10.1029/2005JC003323 |
Zhou T J, Zhang X H, Yu Y Q et al, 2000. Response of IAP/LASG GOALS model to the coupling of air-sea fresh water exchange. Advances in Atmospheric Sciences, 17(3): 473-486 DOI:10.1007/s00376-000-0037-2 |
Zhou X M, Li S L, Luo F F et al, 2015. Air-sea coupling enhances the east Asian winter climate response to the Atlantic Multidecadal Oscillation. Advances in Atmospheric Sciences, 32(12): 1647-1659 DOI:10.1007/s00376-015-5030-x |
 2020, Vol. 51
2020, Vol. 51


