中国海洋湖沼学会主办。
文章信息
- 贾美军, 姚宇, 何天城, 郭辉群. 2020.
- JIA Mei-Jun, YAO Yu, HE Tian-Cheng, GUO Hui-Qun. 2020.
- 大糙率礁面影响下珊瑚礁海岸附近规则波演化及爬高试验研究
- A FLUME STUDY OF REGULAR WAVE TRANSFORMATION AND RUN-UP AROUND REEF COASTS WITH LARGE SURFACE ROUGHNESS
- 海洋与湖沼, 51(6): 1344-1349
- Oceanologia et Limnologia Sinica, 51(6): 1344-1349.
- http://dx.doi.org/10.11693/hyhz20200100022
文章历史
-
收稿日期:2020-01-16
收修改稿日期:2020-05-12
2. 水沙科学与水灾害防治湖南省重点实验室 长沙 410114
2. Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hunan Province, Changsha 410114, China
珊瑚礁作为一种独特的生物海岸地貌形态, 主要由靠近外海的礁前斜坡和与海岸相连的水平礁坪组成。当波浪由远海传播至珊瑚礁面, 由于礁前斜坡处地形的急剧变化, 波浪发生浅水变形作用, 波形变陡, 波高增大, 在礁缘附近发生波浪破碎, 破碎在礁坪上持续一段距离后重新生成稳定的波浪向海岸传播(姚宇, 2019)。珊瑚礁礁面糙率比沙质岸滩高出1-2个数量级(Lowe et al, 2005), 重新生成的波浪由于摩擦而持续衰减, 到达海岸线附近的波浪几乎可以忽略不计, 因此珊瑚礁是保护海岸线的天然屏障。同时, 相关研究表明, 波浪在珊瑚礁地形上发生浅化作用和破碎的同时, 波浪能量分别向高频和低频区间转移, 导致礁坪上的波谱变宽, (Brander et al, 2004)。
目前, 国内外有关波浪与珊瑚礁地形相互作用问题的物理模型试验研究中, 珊瑚礁礁面大多采用概化的光滑材料制成。文献中仅有Quiroga等(2013)通过在概化的珊瑚礁光滑表面添加均匀长方体木条来模拟粗糙工况, 研究了礁面糙率对孤立波沿礁的传播、破碎、能量衰减以及在礁坪上产生涌波的影响。Buckley等(2016)在物理模型试验中采用在礁面上布置均匀小方块体的方法来模拟礁面粗糙度, 探讨了粗糙礁面对波浪增水的影响。陈洪洲等(2018)通过在礁坪上涂抹粗化剂来模拟粗糙的珊瑚礁面, 研究了珊瑚礁粗糙表面对波浪非线性特征的影响。Yao等(2018)和姚宇等(2019)采用不同排列和密度的圆柱体阵列来模拟不同礁面粗糙度, 分别研究了礁面糙率影响下珊瑚礁海岸附近孤立波和不规则波的传播变形以及在礁后岸滩上爬高的变化规律。
从目前国内外的研究现状可知, 以往的试验研究中并没有分析粗糙礁面存在下珊瑚礁海岸附近规则波的运动和礁后岸滩爬高的规律。因此本文拟通过波浪水槽试验, 采用Yao等(2018)使用的圆柱体阵列来模拟礁面的粗糙度, 重点探讨大糙率礁面影响下高频波的产生以及波浪的反射、透射以及能量的衰减规律。本文的成果可为进一步研究珊瑚礁海岸附近基础设施的防灾减灾问题提供一定的理论参考。
1 试验设置本物理模型试验在长沙理工大学水沙科学与水灾害防治重点实验室小波浪水槽中进行, 水槽长×宽×高分别为40m×0.5m×0.8m, 如图 1a所示。水槽的一端设置有推板式造波机, 另一端布置坡度为1: 8的礁后岸滩斜坡。参考Hench等(2008)现场观测的原型, 采用重力相似准则, 选取几何比尺1︰20设计概化珊瑚岸礁模型。珊瑚礁模型采用厚度1cm的PVC板搭接而成(图 1b):礁前斜坡采用坡度为1: 6的斜面模拟并设置在距离造波机27.2m处, 斜坡后接长度为8m、距水槽底高度为0.35m的水平平台模拟礁坪, 整个物理模型宽度与水槽宽度保持一致。为了保证试验结果的精确性, 用玻璃胶密封模型与水槽的间隙。
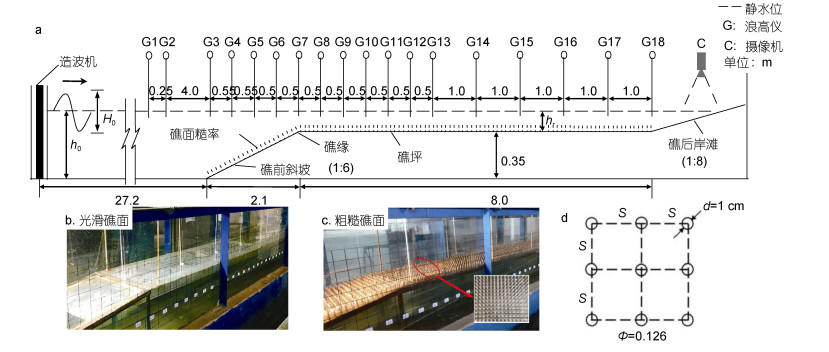 |
| 图 1 试验设置 Fig. 1 The experimental setup 注: a:总体布置图; b:光滑礁面; c:粗糙礁面; d:糙率单元的排列方式; d:圆柱体的直径; S:圆柱体之间的间距; ϕ:珊瑚礁表面粗糙度 |
本试验参考Yao等(2018)使用的圆柱体木条阵列模拟生长鹿角珊瑚的珊瑚礁礁面, 整个粗糙礁面由礁前斜坡和礁坪组成, 总长10.1m(图 1c)。单个糙率单元(圆柱体木条)直径d为1cm, 高为3.5cm, 固定于PVC板上预制的孔深为1cm的孔洞中, 故礁坪表面的实际物理糙率高度为2.5cm, 根据试验比尺原型糙率高度为50cm, 与Lowe等(2005)现场观测相符合。木条阵列采用串联的方式排列, 糙率元素间距S为2.5cm, 如图 1d所示。珊瑚礁表面粗糙度ϕ由柱体的分布密度来表示, 即控制体中圆柱体木条体积VS占控制体总体积V的比例, ϕ=VSV, 对于本试验设置为ϕ=0.126。
本试验共采用18个电阻式浪高仪(G1-G18)来测量自由液面的沿礁变化, 具体位置如图 1所示。其中, G1-G2设置在礁前斜坡离岸一侧, 用于分离珊瑚礁模型前的入射波和由礁体造成的向外海传播的反射波; G3-G6设在礁前斜坡上, 用来记录由于斜坡上的浅水效应引起的波形变化过程; G7-G18布置在礁坪上, 用于监测波浪从礁缘到海岸线的传播变形过程。在试验过程中, 所有浪高仪同步采集数据, 采样频率设为50Hz。为保证水槽中的波浪场达到相对稳定的状态, 采样时长为自造波机启动后连续8min。同时, 在岸滩上方布置1个高速相机记录波浪爬坡的全过程, 波浪在礁后岸滩上的爬高由斜坡上带有刻度的薄片来测定。
试验对光滑礁面(ϕ = 0)和粗糙礁面(ϕ = 0.126), 分别测试了2个礁坪水深(hr = 0.05, 0.10)、3个波浪周期(T = 1, 1.5, 2)和5个入射波高(H0 = 0.04, 0.06, 0.08, 0.10, 0.12)共计30种组合的规则波工况。根据相似准则和前述的几何比尺1︰20(相应的时间比尺为1︰4.5), 得到岸礁原型的礁坪宽度为160m, 相关波浪要素为hr=1-2m, H0=0.8- 2.4m, T=4.5-9s, 与现场报道(Hench et al, 2008)的波况范围符合。
2 结果与分析 2.1 高频波的沿礁变化与台阶式地形类似, 波浪由深海传播至浅水礁坪的过程中, 由于礁前斜坡地形的剧烈变化, 发生浅水变形, 产生高频波。高次谐波可采用快速傅里叶变换方法(Fast Fourier Transform, FFT)对所测量的液面时间序列进行谐波分析得到。图 2和图 3分别展示了两种礁坪水深(hr=0.05m和hr=0.10m)下典型波况(H0 = 0.08m, T = 1.5s)与光滑和粗糙礁面作用时总波幅(at)以及一到五阶各次谐波振幅(a1-a5)的变化规律。
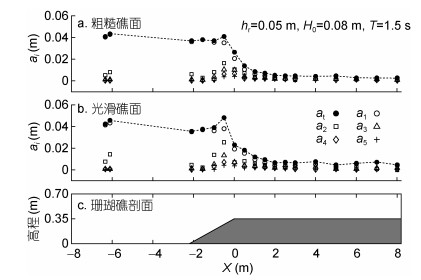 |
| 图 2 光滑和粗糙礁面存在下礁坪水深hr = 0.05m, 入射波高H0 = 0.08m, 波浪周期T = 1.5s时谐波振幅的沿礁变化 Fig. 2 Variation in harmonic wave amplitude across both the smooth and rough reef profiles under hr = 0.05m, H0 = 0.08m, T = 1.5s |
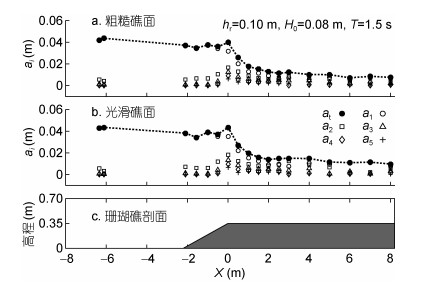 |
| 图 3 光滑和粗糙礁面存在下hr = 0.10m, H0 = 0.08m, T = 1.5s时谐波振幅的沿礁变化 Fig. 3 Variation in harmonic wave amplitude across both the smooth and rough reef profiles under hr = 0.10m, H0 = 0.08m, and T = 1.5s |
图 2和图 3表明总波幅at沿光滑礁面和粗糙礁面变化趋势基本一致:由于波浪在礁前斜坡上的浅化作用, 波形变陡, at达到最大, 波浪在礁缘外海一侧破碎; 波浪在破碎带内能量消耗迅速, 因此at沿程急剧减小, 直到破碎过程结束后, at在礁坪上逐渐保持不变(重新生成了行进波)。当礁面从光滑变为粗糙时, 沿礁耗损的波能更多, 总波幅有所降低。同时, 波浪与礁前斜坡相互作用, 入射波的能量明显由1阶主频波向2-5阶高次谐波转移, 各次谐波的波幅(a1-a5)沿礁逐渐增加, 并在波浪破碎点处达到最大值, 此处二次谐波振幅(a2)约为主频波幅(a1)的一半。在破碎带内, a1由于能量剧烈耗散迅速降低, 而2-5阶高次谐波波幅(a2-a5)仅略微减小。在破碎结束后的礁坪再生波带中, 高次谐波特别是二次谐波的波幅在礁坪透射波中仍然是相当重要的成分。同时, 对比图 2和图 3发现, 礁坪水深增大时, 礁坪上的总波幅和各次谐波的波幅均增加, 这是因为水深增大减弱了礁坪上由于波浪破碎和底部摩擦损耗的能量。对于任意hr, 相对于光滑礁面, 粗糙礁面的存在降低了礁坪上主频波和二次谐波, 对更高阶波的影响不显著。
2.2 透射系数、反射系数和能量耗散系数 2.2.1 计算方法波浪与结构物相互作用时的波浪反射和透射特征分别可以采用反射系数KR和透射系数KT来表述, 其表达式为
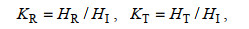 (1)
(1)式中, HI和HR分别为结构物外海侧入射和反射波高, HT为结构物后方的透射波高。对于本试验, 水槽中形成了不完全驻波, 这是由于波浪在造波机、礁前斜坡和礁后岸滩间发生了多重反射造成。本文基于在G1和G2处测得的波面时间序列, 通过两点法(Goda, 2000)分离得到HI和HR后计算KR。通常计算HT时, 选取的是礁坪上透射波中主频波的波高, 而本文3.1节结果分析说明:礁坪上透射波成分中除了主频波存在外, 高次谐波也有很大比重, 因此本文在计算KT时, 需要同时考虑主频波和高次谐波。此外, 对于珊瑚礁地形, 由于入射波和透射波在外海和礁坪上传播时水深(波速)不同, 因此公式(1)定义的KT不再适用, 需要根据透射波和入射波能量流的比值来重新定义(姚宇等, 2017)
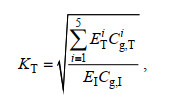 (2)
(2)式中, ETi和EI分别为礁坪上第i阶透射谐波(精确到5阶)和外海侧入射波的能量密度; Cg, Ti和Cg, I分别表示礁坪上第i阶透射谐波(精确到5阶)和外海侧入射波的波群速度; 入射波能流EICIg可运用能量守恒原理由深水波能流E0C0g进行换算, 根据线性波理论:深水波能密度为E0 = ρgH02/8, 其中深水波高H0由入射波高HI推算, 深水波群速度为C0g = gT/4π。透射波总能流的计算方法为:首先对礁坪G18位置测得的自由液面时间序列运用快速傅里叶变换分析得出能量谱, 然后对各次谐波对应的能量密度ETi和波群速度Cg, Ti的乘积求和得到, 其中各次谐波的Cg, Ti可通过色散关系求解。对于反射系数, 由于入射波和反射波在外海端传播时水深(波速)相同, 采用公式(1)波高的方法和类似于公式(2)能量流的方法定义是一致的。计算出KR和KT以后, 珊瑚礁海岸波浪能量耗散系数KD可由垂直于海岸线的方向能量流的守恒计算得到
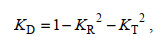 (3)
(3)图 4展示了在光滑和粗糙礁面情况下KR、KT和KD随礁坪相对水深(hr/H0)的变化关系。图 4a中KR值均小于0.2, 大部分工况在0.1以下, 表明珊瑚礁地形对波浪的反射作用较小; 同时KR值随着hr/H0增加无明显规律, 数据离散程度较大, 该现象主要是因为波浪在水槽中发生了前述的多重反射造成, 类似于Bragg共振引起的反射系数的震荡(Yao et al, 2012)。图 4b表明KT随着hr/H0的增大呈线性增长趋势, 这是由于礁坪波浪破碎和礁床的摩阻均受水深控制, 礁坪水深越大, 破碎强度和底部摩擦损耗越小, 透射波能量越大。对比光滑和粗糙礁面两种情况发现:在相同的hr/H0下, 粗糙礁面下的透射系数KT明显小于光滑礁面下的KT值。考虑到前述KR较小(KR2小于5%), 采用式(3)计算KD时, 可以忽略KR的影响, KD主要受到KT的影响, 故图 4c中两种礁面的能量耗散系数KD均随着hr/H0的增大而减小, 相同hr/H0下, 粗糙礁面的KD值相对于光滑礁面均显著增加, 平均增加了8%;对于光滑礁面而言, 当hr/H0 < 0.4时, KD值接近于1, 说明当hr非常小时, 入射波的能量可通过波浪在礁坪上的破碎和礁坪底部的摩阻全部耗散, 礁坪上剩余的波浪能可以忽略不计; 对于粗糙礁面由于底部摩擦的增强, 大约在hr/H0 < 1.5时便能达到KD=1。
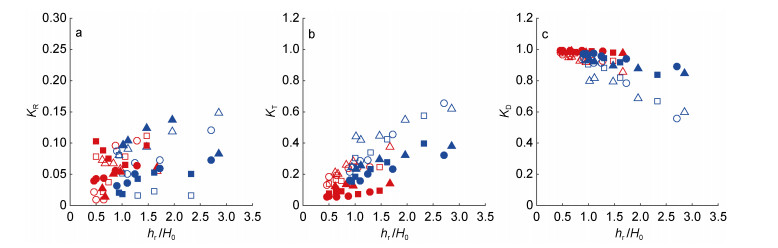 |
| 图 4 反射系数(KR, a)、透射系数(KT, b)和能量耗散系数(KD, c)随礁坪相对水深(hr/H0)的变化 Fig. 4 Variations of reflection coefficient (KR, a), transmission coefficient (KT, b), and energy dissipation coefficient (KD, c) with relative reef-flat submergence (hr/H0) 注:实心: ϕ 0.126, 空心: ϕ 0;红色: hr = 0.05m, 蓝色: hr = 0.1m;圆形: T = 1s, 正方形: T = 1.5s, 三角形: T = 2s |
对于传统的平底海岸, 美国海岸工程手册采用经验公式(4)预测发生破碎的规则波爬高
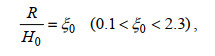 (4)
(4)式中, R为波浪岸滩爬高, ξ0为破碎相似参数, 定义为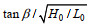
图 5a展示了本试验中R/H0随ξ0之间的变化关系, 结果表明: R/H0随ξ0呈线性变化关系, 并在低礁坪水位或者粗糙礁面下的R/H0值显著低于高水位或者光滑礁面时的值, 但结果较为离散, 因此公式(4)并不适用于珊瑚礁地形, 需要进一步改进。相对礁坪水深(hr/H0)常常被用来描述礁坪上水动力学问题(姚宇, 2019), 本文2.2.2节的结果同样表明hr/H0能较好的描述礁坪的透射波及其能量衰减, 因此图 5b展示了本试验R/H0随hr/H0之间的变化关系, 发现R/H0随hr/H0的增大呈增大趋势, 且粗糙礁面下的R/H0值显著低于光滑礁面时的值。但观察图 5b可发现单独使用hr/H0来描述结果仍然较为离散, 因此本文基于公式(4)的幂函数形式, 同时考虑ξ0和hr/H0作为输入参数, 并考虑礁面粗糙度ϕ的变化, 提出下述同时可以预测本试验中光滑和粗糙礁面的岸滩爬高公式:
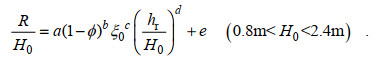 (5)
(5)
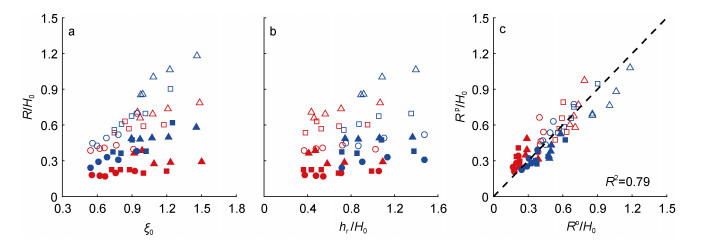 |
| 图 5 无量纲礁后岸滩爬高(R/H0)随破碎相似系数(ξ0)(a)以及随相对礁坪水深(hr/H0)(b)的变化, 无量纲岸滩爬高实测值(Ro/H0)与预测值(Rp/H0)的对比情况(c) Fig. 5 Variation of the normalized wave run-up on the back-reef beach (R/H0) with the surf similarity parameter (ξ0)(a); and with relative reef-flat submergence (hr/H0)(b), and measured normalized wave run-up on the back-reef beach (Ro/H0) v.s. predicted normalized wave run-up on the back-reef beach (Rp/H0) based on Eq. (5)(c) 注:实心: ϕ 0.126, 空心: ϕ 0;红色: hr = 0.05m, 蓝色: hr = 0.1m;圆形: T = 1s, 正方形: T = 1.5s, 三角形: T = 2s |
基于本试验数据通过回归分析得到公式(5)中的参数a=0.64, b = 5.83, c=0.85, d=0.20, e=0.06, 拟合精度为R2 = 0.79, 表明式(5)可以较好地预测本试验中规则波在不同礁面粗糙度影响下岸滩的爬高。值得说明的是公式(5)根据本试验的测试仅考虑了入射波特征参数和礁面糙率的影响, 进一步对其的改进可以加入其他的礁形参数(礁坪宽度, 礁前斜坡坡度)的影响以及考虑泻湖和/或防浪建筑物的存在, 其在更极端的波况下的适用性问题, 也待进一步研究。
3 结论本文通过在波浪水槽中进行一系列物理模型试验研究了大糙率礁面下珊瑚礁海岸附近波浪演化和爬高的变化规律。实验测试了一系列的规则波工况, 采用了圆柱体阵列来模拟礁面的粗糙度。结果分析表明:波浪在礁前斜坡处因浅化作用产生高次谐波, 且二次谐波是礁坪透射波的重要成分, 粗糙礁面削弱了礁坪上的主频波和二次谐波, 而对更高阶波的影响不显著。相对礁坪水深是表征礁坪上波浪透射的重要参数, 海岸附近的透射波因礁面糙率的存在而显著减小, 而礁前反射波则与礁面糙率无明显关系, 在测试的范围内粗糙礁面使入射波浪能沿礁的衰减相对于礁面光滑平均增加8%。礁后岸滩爬高随着透射波高的增大而增长并受到波浪周期和礁坪水深的影响, 最后拟合了本文试验条件下珊瑚礁大糙率礁面预测规则波爬高的关系式。
陈洪洲, 毕春伟, 高俊亮. 2018. 波浪在珊瑚岸礁礁坪上传播变形的数值研究. 水科学进展, 29(2): 252-259 |
姚宇. 2019. 珊瑚礁海岸水动力学问题研究综述. 水科学进展, 30(1): 139-152 |
姚宇, 张起铭, 蒋昌波. 2019. 礁面糙率变化下珊瑚礁海岸附近波浪传播变形试验. 科学通报, 64(9): 977-985 |
姚宇, 唐政江, 杜睿超, 等. 2017. 潮汐流影响下珊瑚岛礁附近波浪传播变形和增水试验. 水科学进展, 28(4): 614-621 |
Brander R W, Kench P S, Hart D, 2004. Spatial and temporal variations in wave characteristics across a reef platform, Warraber Island, Torres Strait, Australia. Marine Geology, 207(1-4): 169-184 DOI:10.1016/j.margeo.2004.03.014 |
Buckley M L, Lowe R J, Hansen J E et al, 2016. Wave setup over a fringing reef with large bottom roughness. Journal of Physical Oceanography, 46(8): 2317-2333 DOI:10.1175/JPO-D-15-0148.1 |
Goda Y, 2000. Random Seas and Design of Maritime Structures. Singapore: World Scientific Press, 356-361
|
Hench J L, Leichter J J, Monismith S G, 2008. Episodic circulation and exchange in a wave-driven coral reef and lagoon system. Limnology and Oceanography, 53(6): 2681-2694 DOI:10.4319/lo.2008.53.6.2681 |
Lowe R J, Falter J L, Bandet M D et al, 2005. Spectral wave dissipation over a barrier reef. Journal of Geophysical Research, 110(C4): C04001 DOI:10.1029/2004JC002711 |
Quiroga P D, Cheung K F, 2013. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs. Coastal Engineering, 80: 35-48 DOI:10.1016/j.coastaleng.2013.05.002 |
Yao Y, He F, Tang Z J et al, 2018. A study of tsunami-like solitary wave transformation and run-up over fringing reefs. Ocean Engineering, 149: 142-155 DOI:10.1016/j.oceaneng.2017.12.020 |
Yao Y, Huang Z H, Monismith S G et al, 2012. 1DH Boussinesq modeling of wave transformation over fringing reefs. Ocean Engineering, 47: 30-42 DOI:10.1016/j.oceaneng.2012.03.010 |
 2020, Vol. 51
2020, Vol. 51


