中国海洋湖沼学会主办。
文章信息
- 陈子飞, 于非, 王建丰, 南峰, 任强, 孙凡. 2021.
- CHEN Zi-Fei, YU Fei, WANG Jian-Feng, NAN Feng, REN Qiang, SUN Fan. 2021.
- 吕宋海峡不同湍流估算方法的应用对比研究
- COMPARATIVE STUDY ON THE APPLICATION OF DIFFETENT TURBULENCE ESTIMATION METHODS IN LUZON STRAIT
- 海洋与湖沼, 52(1): 27-38
- Oceanologia et Limnologia Sinica, 52(1): 27-38.
- http://dx.doi.org/10.11693/hyhz20200300086
文章历史
-
收稿日期:2020-03-23
收修改稿日期:2020-07-06
2. 中国科学院大学 北京 100049;
3. 中国科学院 海洋环流与波动重点实验室 青岛 266071;
4. 中国科学院海洋大科学研究中心 青岛 266071;
5. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 青岛 266237
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. CAS Key Laboratory of Ocean Circulation and Waves, Chinese Academy of Sciences, Qingdao 266071, China;
4. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
5. Marine Dynamic Process and Climate Function Laboratory, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China
海洋中湍流混合过程控制海洋中的动量、质量以及热量的输运, 对海水的温度、盐度、营养盐等的时空分布与变化有重要的影响(Munk et al, 1998)。研究湍流混合, 能够有效量化垂向输送过程, 提高海洋和气候模式的模-拟和预测能力, 对全球气候和海洋环境及生态系统的变异具有重要的意义(Wunsch et al, 2004)。
虽然湍流混合是海洋能量从大尺度到小尺度直至耗散的串级过程中至关重要的一环(范植松, 2002), 但由于湍流混合直接观测技术难度大、成本高, 很大程度限制了全球混合时空分布及机制研究。但温、盐、流水文资料不管从时间分布还是空间分布上均已有丰富的积累。目前已发展多种基于水文资料估算海洋湍流混合的方法。
Thorpe (1977)提出利用温、盐资料对水体翻转尺度进行量化, 通过翻转尺度捕捉能量级串过程, 进而估算耗散率的方法。Thompson等(2007)通过三年的温盐资料, 基于Thorpe尺度方法估算Drake海峡1000 m以浅的跨密度扩散率, 发现混合分布与近惯性波、中尺度涡以及双扩散活动相关。Jing等(2010)基于Thorpe尺度方法估算西北太平洋跨密度混合的季节性变率, 发现受风应力影响上层海洋的跨密度混合具有明显的季节性变率, 幅度随深度增加而减小。然而, Thorpe尺度方法容易受到仪器采样频率和噪声的影响, 对观测数据的准确度要求较高, 存在较大的不确定性(Galbraith et al, 1996)。由于内波破碎是海洋内部湍流混合的重要能量来源, 所以基于内波间相互作用和中纬度大洋内波场GM普适谱理论, 学者们提出了Gregg-Henyey-Polzin (GHP)细尺度参数化方法(Henyey et al, 1986; Gregg, 1989; Polzin et al, 1995)。该方法在之后的研究中得到广泛的应用和发展, 并促进全球混合分布特征的认识。Waterhouse等(2014)收集全球已用的水文观测数据, 利用GHP参数化方法研究全球的混合分布形态, 发现1000 m以浅扩散率量级是10–5 m2/s, 1000 m以深扩散率是10–4 m2/s。这与Munk (1966)提出需要10–4量级的深海跨密度扩散率维持深海层结是相一致的。近些年来, 许多研究者们尝试提出更加简洁的参数化方案。MacKinnon等(2003)通过研究陆架海内波场的剪切与能量通量, 提出MacKinnon and Gregg (MG)参数化方案, 并很好地应用在新英格兰陆架区域。Van der Lee等(2011)发现在波罗的海观测到的耗散率与剪切和层结成比例, MG参数化方法可以很好地估算当地的耗散率。虽然MG参数化的提出是基于陆架海研究, 但近期已有研究将其应用到开阔大洋。Liang等(2018)研究开阔大洋混合发现MG参数化能够较好地估算底地形粗糙站位的湍动能耗散率。
虽然以上三种湍流估算方法已有广泛的应用, 但目前为止还缺少对这三种方法应用比较工作。因此, 为了比较这些湍流混合方法的应用效果, 我们在吕宋海峡附近开展了微结构湍流和水文观测调查。吕宋海峡是南海与太平洋连接的通道, 在吕宋海峡由潮地形相互作用生成大量的内波, 携带大量的能量通量传播进入南海, 进而引发湍流混合(Tian et al, 2003; Jan et al, 2007)。此外, 观测表明大约有2 Sv的北太平洋的底层水通过吕宋海峡进入南海, 然后通过南海混合上涌到中间层, 返回到北太平洋(Tian et al, 2006)。所以, 这项比较工作不仅能够完善对不同参数化方法的比较, 也可以促进对吕宋海峡湍流混合空间分布特征的认识。
1 数据和方法 1.1 数据为了对比研究湍流混合参数化方法, 2018年6月和2019年7月在吕宋海峡附近开展了湍流混合观测调查。共收集23个站位的微结构湍流观测剖面和相应的23站水文观测剖面。直接湍流混合观测数据采用一种新型的自由下降微结构湍流剖面仪(expendable vertical microstructure profiler, XMP)。XMP头部安装一种可抛弃式剪切探头, 自由下降到设定深度经触发熔断后, 抛弃剪切探头, 然后靠浮力回到海面。温盐数据采用Seabird 9–11 Plus CTD (conductivity–temperature–depth), 分辨率为24 Hz, 温度精度为0.001℃, 电导率精度为0.0003 S/m。流速与剪切数据来源于2台300 kHz的lowered acoustic doppler current profilers (LADCP)。LADCP被固定在采水器上, 随CTD911plus一起下放, 采样频率为1 Hz, 层间距设置为10 m。在本文中我们利用同步观测的微结构湍流及温、盐、流数据, 开展湍流混合参数化方案比较研究, 站位图分布见图 1。
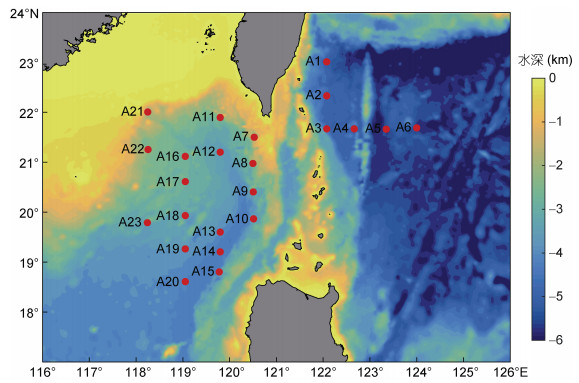 |
| 图 1 吕宋海峡地形和观测站位图 Fig. 1 The bathymetry of Luzon Strait and observation sites |
海洋内部的湍动能耗散率(ε)和密度扩散率(Kρ)是研究海洋混合分布特征及其影响因子的重要参数。利用微结构剪切信号, 在各项同性假设下, 湍动能耗散率εOB的计算公式:
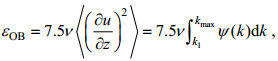 (1)
(1)式中, ν表示运动学分子粘性系数, 〈〉表示空间平均, u表示水平速度分量, z表示垂向坐标, Ψ(k)表示剪切谱, 采用6 m速度剪切剖面计算得到, k表示垂向波数。
由于湍流的高非线性和混沌特性, 目前对其精确描述是不可能的。我们近似认为微结构剪切计算得到的结果是海洋内部真实的湍动能耗散率。图 2是XMP观测的垂向剪切谱, 对剪切谱积分得到湍动能耗散率。积分下限(k1)设置为1 m–1; 积分上限(kmax)设置为以下值的最小值(Shang et al, 2017a): a.仪器振动破坏剪切信号的最低频率; b.剪切探头的空间分辨率(150 m–1); c. antialiasing filter的截止频率; d.通过Nasmyth谱计算得到90%剪切方差的波数k90 (Lueck, 2016)。
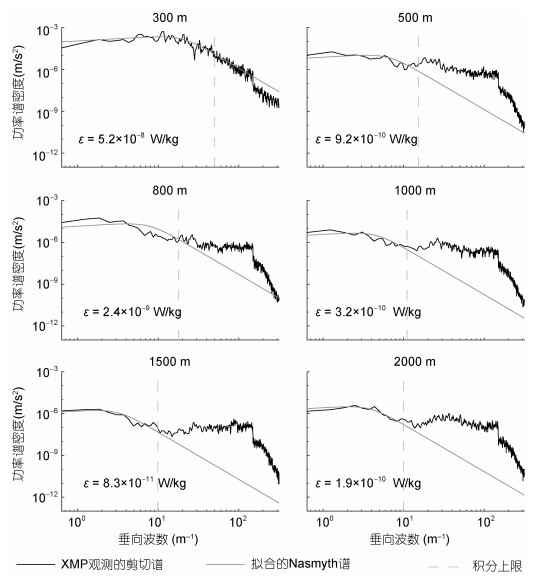 |
| 图 2 A9站抛弃式微结构湍流剖面仪的速度剪切谱 Fig. 2 Spectrum of shear observed from XMP (expendable vertical microstructure profiler) at site A9 注: ε:湍动能耗散率 |
Henyey等(1986)基于内波间相互作用理论, 通过ray-tracing方程预测内波从大尺度向小尺度湍流的能量转换率。Gregg等在1989年首次利用观测数据, 通过速度垂向剪切、浮力频率和大洋内波GM谱建立内波耗散参数化方法估算海洋混合, 内波作用的耗散率结果与Henyey模型预测结果一致, 该方案表明可以用细尺度海洋数据资料来估算微尺度混合。由于内波间非线性波波相互作用, 能量从大尺度向小尺度传播, 剪切方差逐渐增大到内波破碎发生湍流混合为止。内波破碎耗散的能量近似与从大尺度向小尺度的转换能量相等(Polzin et al, 1995; Gregg et al, 2003)。在之后的研究, 参数化方法得到进一步改进, 通过增加纬度依赖项和剪切应变方差率Rw, 分别来表征纬度变化和内波场的纵横比对混合强度的影响(Gregg et al, 2003; Kunze et al, 2006; Polzin et al, 2014), 耗散率可以参数化:
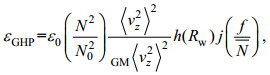 (2)
(2)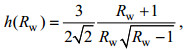 (3)
(3) (4)
(4)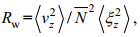 (5)
(5)式中, ε0=4.7×10–10 W/kg, f30=f(30°) f表示科氏频率, N表示浮力频率, N表示平均浮力频率, N0=5.2×10–3 rad/s, 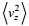

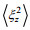
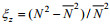
计算剪切方差和应变方差, 首先将LADCP数据处理成10 m分辨率标准网格的剪切数据, CTD数据处理成2 m分辨率标准网格的温盐密数据(Kunze et al, 2006); 其次, 将每个剖面从底部向上分成320 m长的一系列片段, 每个片段与相邻片段重叠160 m, 对每个片段的剪切和应变做谱分析, 得到速度剪切谱
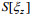
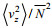
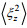
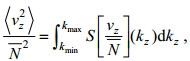 (6)
(6)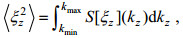 (7)
(7)
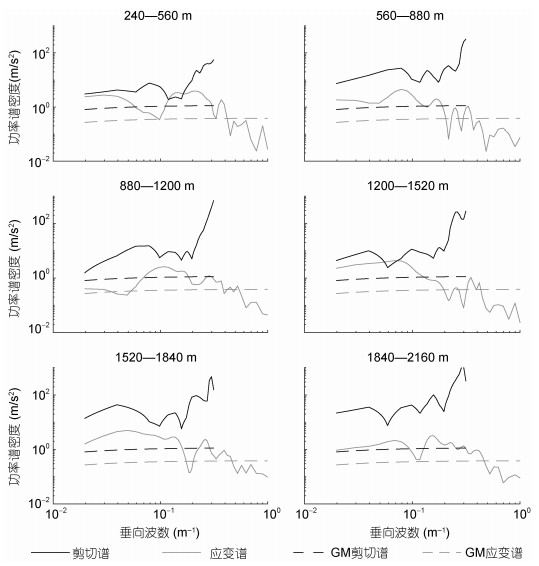 |
| 图 3 A9站位中六个片段深度内的LADCP剪切谱及CTD应变谱 Fig. 3 Spectrum of shear from Lowered Acoustic Doppler Current Profilers (LADCP) and spectrum of strain from conductivity–temperature–depth (CTD) at site A9 |
值得注意的是, 这里对谱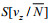
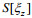
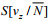
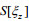
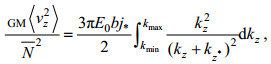 (8)
(8)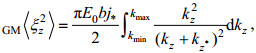 (9)
(9)式中, 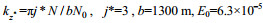
MG参数化方法是由MacKinnon等(2003)尝试将Henyey的ray-tracing能量传输模型引用到陆架区域而提出的新的混合参数化方案。其假定大尺度剪切主要来自于近惯性波和半日潮波, 能量密度与层结强弱成比例, 内波场中的水平波数是个常量。在这些假定下, 该方法估算的英格兰陆架的耗散率总体分布上与观测耗散率保持一致。MG参数化方法通过剪切和层结, 耗散率可以参数化为:
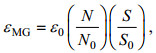 (10)
(10)式中, 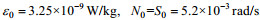
计算剪切和浮力频率前, 首先将LADCP数据处理成10 m分辨率标准网格的剪切数据, CTD数据处理成10 m分辨率标准网格的温盐密数据。然后, 将每个剖面从底部向上分成320 m长的一系列片段, 每个片段与相邻片段重叠160 m, 最后计算每个片段的剪切和和浮力频率的均值。
1.2.4 Thorpe尺度方法Thorpe尺度是基于水体翻转估算混合强弱的方法。Thorpe (1977)对水体翻转的尺度进行量化, 提出Thorpe尺度的概念。定义为:密度剖面上翻转水体内的水质点在重新排序成稳定密度剖面后所移动距离的均方根, 即:
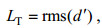 (11)
(11)式中, LT为Thorpe尺度, 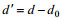
Thorpe尺度是Ozmidov尺度的一种很好的近似。Ozmidov尺度LO指在稳定层结的湍流中水体翻转可形成的各向同性湍流的垂向最大尺度, 即:
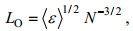 (12)
(12)Dillon(1982)研究表明LT和LO的关系为LO/LT=0.8, 所以通过Thorpe尺度可求得耗散率εThorpe:
 (13)
(13)24 Hz采样频率的密度剖面计算Thorpe尺度时, 需要去除由仪器噪声和盐度尖峰导致的虚假水体翻转, 适当进行滤波, 将高频的毛刺滤除。首先对质控后的密度数据进行重新排序, 然后计算Thorpe位移, 再利用Thorpe位移之和等于0, 即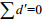
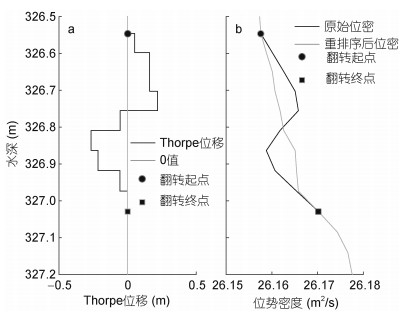 |
| 图 4 A9站位Thorpe位移与密度翻转 Fig. 4 The Thorpe displacement and density overturn at site A9 |
受海气间相互作用影响, 混合层内水体的性质变化较大。而混合层以深, 由于稳定的海洋动力过程, 水体的性质相对稳定。因此, 各站位数据处理过程中均去除混合层内的数据。另外, 观测中2000 m以深的数据相对较少, 如Argo数据主要是对上层2000 m的温盐观测。所以, 在本文中我们主要比较80—2160 m范围内的参数化结果。
2 结果 2.1 湍动能耗散率的水平分布比较为了研究三种方法估算耗散率在水平分布上的应用, 我们对80—2160 m的耗散率做垂向平均, 得到吕宋海峡耗散率的水平分布(图 5)。图 5a是XMP湍流剖面仪观测得到的耗散率的水平分布。在吕宋海峡120.5°E断面上, 平均耗散率为4.7×10–9 W/kg; 吕宋海峡断面以外, 平均耗散率为1.4×10–9 W/kg。其中, 吕宋海峡以东的平均耗散率为2.3×10–9 W/kg; 吕宋海峡以西的平均耗散率为1.0×10–9 W/kg。吕宋海峡断面上的平均耗散率是吕宋海峡以外区域的3.3倍, 是吕宋海峡东侧平均耗散率的2.0倍, 是吕宋海峡西侧的4.7倍。结果表明吕宋海峡断面上的耗散率最大, 向东西两侧呈递减趋势, 吕宋海峡东侧耗散率要高于西侧耗散率。另外, 也可以发现北部要比南部的耗散大, 从北向南有递减趋势。
 |
| 图 5 80—2160 m平均湍动能耗散率的水平分布比较 Fig. 5 Horizontal distribution comparison of mean dissipation rate in 80—2160 m 注: a: XMP观测的耗散率; b: Gregg-Henyey-Polzin(GHP)参数化方法估算的耗散率; c: Mackinnon and Gregg (MG)参数化方法估算的耗散率; d: Thorpe尺度方法估算的耗散率 |
接下来, 我们得到GHP参数化方法估算吕宋海峡平均耗散率的水平分布(图 5b)。结果显示吕宋海峡120.5°E断面上, 平均耗散率为3.2×10–9 W/kg; 吕宋海峡以外, 平均耗散率为1.2 ×10–9 W/kg。吕宋海峡以东的平均耗散率为1.9×10–9 W/kg; 吕宋海峡以西的平均耗散率为0.8×10–9 W/kg。估算结果与观测结果相比, 吕宋海峡断面上估算的耗散率是观测的68%;吕宋海峡东侧, 估算值是观测值的82%, 吕宋海峡西侧, 估算值是观测值的80%。基于GHP参数化估算耗散率水平分布的结果与XMP观测结果相比较, 我们发现GHP参数化结果要偏弱, 如吕宋海峡断面上的平均耗散率是吕宋海峡以外区域的2.8倍(小于XMP观测的结果3.3, 见图 5a)。
同样, 我们得到MG参数化方法估算吕宋海峡平均耗散率的水平分布(图 5c)。在吕宋海峡断面上, 平均耗散率为1.9×10–9 W/kg; 吕宋海峡断面以外, 平均耗散率为1.6×10–9 W/kg。吕宋海峡以东的平均耗散率为1.6×10–9 W/kg, 以西的平均耗散率为1.5×10–9 W/kg。MG参数化估算的结果在吕宋海峡断面及其东侧要比GHP参数化结果更弱些, MG方法估算值分别是观测值的41%和70%。然而, 在估算吕宋海峡西侧的平均耗散率的水平分布比观测结果偏大, 高出0.5×10–9 W/kg。表明MG参数化估算的耗散率在水平分布上与观测结果相比较, 呈现不一致性, 吕宋海峡及其东侧估算值要偏低, 而吕宋海峡西侧估算值要偏高。
最后, 我们给出基于Thorpe尺度方法估算吕宋海峡平均耗散率的水平分布(图 5d)。计算显示在吕宋海峡断面上, 平均耗散率为1.1×10–9 W/kg; 吕宋海峡断面以外, 平均耗散率为3.2×10–9 W/kg。吕宋海峡以东的平均耗散率为2.7×10–9 W/kg, 以西的平均耗散率为3.5×10–9 W/kg。Thorpe尺度估算吕宋海峡断面的耗散率与观测结果相比, 观测结果是估算结果的4.2倍。而在吕宋海峡断面东西两侧, 估算值分别是观测值的1.2和3.5倍。结果表明, 在水平分布上Thorpe尺度估算的耗散率与观测结果相比较, 吕宋海峡断面估算结果较低, 吕宋海峡东西两侧估算结果较高。
应用三种方法估算吕宋海峡的耗散率, 我们在水平分布上对估算结果和观测结果进行了比较。发现GHP参数化估算结果虽然略低于观测值, 但与观测的结果最接近。MG参数化方法估算吕宋海峡西侧耗散率要比观测值高, 但估算结果总体上和观测结果是一致的。Thorpe尺度估算的结果与观测结果存在较大差异, 在吕宋海峡断面上估计值小于实际值, 而吕宋海峡东西两侧均高于实际值, 尤其在吕宋海峡西侧, 估算的偏差更大。
2.2 湍动能耗散率的垂向分布比较为了探索三种方法估算耗散率在垂向分布上的应用, 我们将各站位计算的耗散率沿着经向对纬向做平均, 比较了三种方法估算的耗散率与微结构剖面仪观测的耗散率在垂向上的分布(图 6)。图 6a是XMP湍流剖面仪观测的耗散率的垂向分布。我们发现, 1200 m以浅耗散率呈现出东西方向的不均一性。吕宋海峡120.5°E断面及其以东1200 m以浅的耗散率可达O(10–8)W/kg, 吕宋海峡西侧1200 m以浅的耗散率比东侧耗散率要小, 量级在10–9 W/kg。另外, 垂向分布结果显示1200 m以深的耗散率逐渐递减, 且东西方向上呈现出均一性, 耗散率在10–10 W/kg。根据以上结果的分布特征, 我们将垂向分布分为A、B、C三个区域进行研究, 分别为吕宋海峡断面西侧1200 m以浅、吕宋海峡断面及其东侧1200 m以浅和吕宋海峡1200 m以深区域(图 6a)。计算结果显示, A区域平均耗散率为1.4×10–9 W/kg; B区域平均耗散率为4.3×10–9 W/kg; C区域平均耗散率为0.5×10–9 W/kg。
 |
| 图 6 湍动能耗散率的垂向分布比较 Fig. 6 Comparison in vertical distribution of dissipation rate 注: a: XMP微结构湍流剖面仪观测的耗散率; b: GHP参数化方法估算的耗散率; c: MG参数化方法估算的耗散率; d: Thorpe尺度方法估算的耗散率; A、B、C分别表示为吕宋海峡断面西侧1200 m以浅、吕宋海峡断面及其东侧1200 m以浅和吕宋海峡1200 m以深区域 |
接下来, 我们比较GHP参数化方法估算的耗散率与XMP湍流剖面仪观测耗散率的垂向分布(图 6b)。GHP参数化方法估算A、B、C区域平均耗散率分别为1.3×10–9 W/kg、3.4×10–9 W/kg、0.4×10–9 W/kg。在A区域, 估算值是观测值的86%;在B区域, 估算值是观测值的78%;在C区域, 估算值是观测值的68%。另外, GHP参数化估算结果显示B区域耗散率比A区域耗散率高, C区域的耗散率在东西向呈现均一性。结果表明, 虽然GHP参数化估算结果要偏低于XMP观测结果, 但估算结果与观测结果在垂向分布上具有相同的分布特征。
同样, 我们得到MG参数化方法估算耗散率的垂向分布(图 6c)。在A、B、C三个区域估算的平均耗散率分别为2.4×10–9 W/kg、2.6×10–9 W/kg、0.4×10–9 W/kg。我们发现MG参数化估算的耗散率在A区域比观测结果高, 估算值是观测值的1.6倍, 这与该方法估算耗散率的水平分布在西侧大于观测值是一样的。但在B和C区域, 估算结果要低于观测结果, 观测值是估计值的1.7和1.3倍。结果表明MG参数化方法估算的耗散率与观测的耗散率在垂向分布上总体是相似的, 但在吕宋海峡西侧1200 m以浅估算的耗散率要偏高。
最后, 我们得到Thorpe尺度方法估算耗散率的垂向分布(图 6d)。计算结果显示, 在A、B、C三个区域平均耗散率分别为7.1×10–9 W/kg、2.4×10–9 W/kg、0.7×10–9 W/kg。Thorpe尺度方法估算结果与观测结果相比较, A区域的估算结果比观测结果高出3.8倍, C区域的估算结果高出观测结果0.4倍。但在B区域, 观测结果高出估算结果0.9倍。结果表明, 在A、B、C三个区域, 估算结果与观测结果的垂向分布特征不对应, A区域的偏差最明显。
我们应用三种方法估算了吕宋海峡的湍动能耗散率的垂向分布。发现GHP参数化结果偏低于XMP湍流剖面仪观测结果, 但其垂向分布与观测的垂向分布最为一致。MG参数化结果与观测结果在垂向分布形态上基本相同, 能够较好地估算1200 m以深的湍流混合, 但在估算吕宋海峡西侧的上层区域偏大; Thorpe方法与观测结果在垂向分布上相比较, 估算结果与观测结果相差较大。
3 湍流混合参数化方案比较上节应用三种方法估算吕宋海峡耗散率的水平分布和垂向分布, 并与观测结果进行了初步的比较。接下来, 进一步对三种方法估算的结果进行统计比较。对吕宋海峡所有观测站点的耗散率做水平平均, 得到XMP湍流剖面仪观测和三种方法估算吕宋海峡耗散率的垂向结构(图 7)。图中绿色实线是XMP观测结果, 灰色阴影代表 95% bootstrap检验的置信区间。结果表明GHP与MG参数化估算结果均落在置信区间内, 能较好地估算实际值。Thorpe尺度结果显示600 m以浅估算结果相对较差, 共计33%的结果落在置信区间之外。
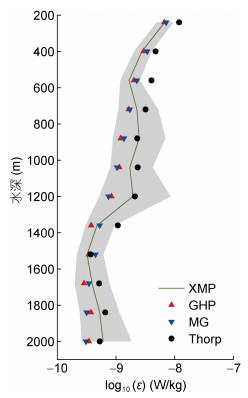 |
| 图 7 吕宋海峡湍动能耗散率的垂向结构 Fig. 7 Vertical structure of dissipation rate in Luzon Strait 注:绿线: XMP湍流剖面仪观测的耗散率; 红色上三角: GHP参数化方法估算的耗散率; 蓝色三角: MG参数化方法估算的耗散率; 黑色点: Thorpe尺度方法估算的耗散率; 灰色阴影: 95%bootstrap检验置信区间 |
接下来, 我们对三种方法估算的结果进行统计, 评估它们在吕宋海峡的应用情况(图 8)。首先, 我们定义一个统计比较因子α, α=|log10(εe/εo)|, εe代表估算值, εo代表观测值, 即估算结果与观测结果的比值取以10为底的对数的绝对值, α越接近于0, 估算值与观测值差异越小。如α≤1, 表示估算值与观测值差异在1个量级内。然后, 我们将结果分为α≤log102、1og102 < α≤1和1 < α≤2进行统计比较。图 8a—c分别是GHP参数化、MG参数化、Thorpe尺度结果与XMP观测结果的比较。结果表明GHP参数化和MG参数化的结果紧密分布在黑色实线附近, Thorpe尺度结果相对比较离散。进一步, 我们对估算结果离散情况进行统计, 给出统计直方图(图 8d)。结果表明对于GHP参数化、MG参数化、Thorpe尺度方法, 比较因子小于等于log102的结果(α≤log102)分别为71%、58%和30%, 比较因子大于1og102且小于1的(1og102 < α≤1)分别为28%、39%和48%, 比较因子大于1且小于2(1 < α≤2)的分别为2%、3%和21%。GHP参数化和MG参数化的比较因子小于等1的结果分别占98%和97%, 而Thorpe尺度方法估算的结果仅占78%, 且还有1%的估算结果的比较因子大于2。另一方面, MG参数化方法估算的结果在比较因子等于1og102范围内的要比GHP参数化方法少13%。从统计上说明, 三种混合参数化方案在吕宋海峡的应用中, GHP参数化方法与MG参数化方案都要优于Thorpe尺度方法, GHP参数化方案优于MG参数化方案。
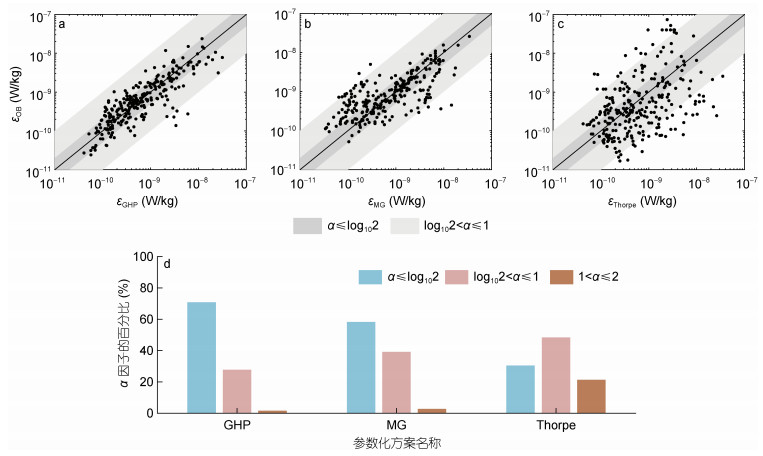 |
图 8 湍流混合参数化方案比较 Fig. 8 Comparison of turbulent mixing parameterizations 注: a: GHP参数化方法与XMP观测耗散率的比较; b: MG参数化方法与XMP观测耗散率比较; c: Thorpe尺度方法与XMP观测耗散率比较; d:比较因子α的统计直方图;  分别为GHP、MG、Thorpe尺度方法计算的耗散率 分别为GHP、MG、Thorpe尺度方法计算的耗散率 |
XMP湍流剖面仪观测结果表明, 吕宋海峡东西两侧1200 m以浅的耗散率具有空间分布的不均一性, 东侧强, 西侧弱。另外, 吕宋海峡北部的耗散率要比南部的大, 从北向南有递减趋势。本文观测结果与以往研究存在一定差异, 以往研究表明吕宋海峡是南海内波生成源区, 将向南海输入大量的能量并促进南海混合, 跨密度混合率可以达到10–3 m2/s, 比北太平洋平坦地形处的混合率高2个量级(Tian et al, 2003, 2009)。本文观测差异一方面可能是由于在调查期间吕宋海峡东侧观测站点正位于一个反气旋涡位置, 受反气旋涡影响, 海洋内部会捕获更多近惯性能量, 增强内部混合(Kunze et al, 1985; Jing et al, 2011)。另一方面, 强西边界流区, 跨密度扩散率可以高达10–3 m2/s(Yang et al, 2014), 由于吕宋东侧站点位存在强的水平与垂向剪切, 强背景流场会向小尺度持续输入能量, 促进该区域的上层混合增强。
通过GHP参数化方法估算吕宋海峡耗散率, 我们发现估算结果与XMP微结构湍流剖面仪观测结果的水平分布和垂向分布呈现出相同的分布特征。同时也发现GHP参数化估算的结果总体上要偏弱于观测的结果。由于在GHP参数化方法在计算剪切应变率时, 平滑的剪切谱去除线性拟合可能会低估10%—20%的方差(Kunze et al, 2006), 导致估算值略低于实际观测结果。但是, 统计表明基于GHP参数化方法估算的与观测差异在2倍以内的结果占71%, 在1个量级以内的结果占98%, 是三种方法中最好的方法, 能够很好地应用在吕宋海峡的湍流混合估算中。
通过水平分布和垂向分布比较, 我们发现在吕宋海峡西侧1200 m以浅MG参数化方法估算的耗散率要高于XMP微结构湍流剖面仪观测结果, 但其估算结果与观测结果总体上具有相同的分布特征。统计也表明基于MG参数化方法估算的与观测的差异在2倍以内的结果占58%, 1个量级以内的占97%。所以, 在估算吕宋海峡的湍流混合时, MG参数化方法要略差于GHP参数化方法, 这与前人给出MG参数化方法较好地估算上层湍流耗散率是不同的(周宇等, 2015; Shang et al, 2017b; Liang et al, 2018)。GHP参数化方法和MG参数化方法都是依据Henyey等建立的ray-tracing能量传输模型, 所不同的在于对模型中变量处理方式不同。GHP参数方法假定内波场是稳定的(或随时间变化缓慢), 内波破碎的引起的能量耗散近似等于内波从大尺度向小尺度传播的能量。所以总的内波场能量就仅取决于波数谱密度的能级(Polzin et al, 1995)。MG参数化方法更适用于耗散率同时与剪切和层结成比例的动力过程(MacKinnon et al, 2003), 当耗散率更依赖于剪切强弱时, MG方法在估算耗散率可能就会出现较大误差。在吕宋海峡附近, 由于水深普遍大于2000 m(图 1), 且存在大量内波生成, 伴随着波波间非线性相互作用引起的内波破碎可能更适用于基于大洋内波谱建立的GHP参数化方法。
Thorpe尺度方法在估算吕宋海峡湍流混合时结果较差。估算吕宋海峡东侧和西侧耗散率的水平分布时, 估算值高于观测值, 吕宋海峡断面上估算值低于观测值。估算耗散率的垂向分布时, 吕宋海峡西侧明显高于观测值。仅有78%的估算结果与观测结果差异在1个量级内, 且有1%的结果差异高出2个量级。相较于基于剪切与层结参数估算耗散率的GHP参数化和MG参数化方法, Thorpe尺度方法在估算耗散率的效果较差。由于Thorpe方法是基于水体重力不稳定而引发的密度翻转计算耗散率, 对仪器的精确度、采样率、下降速度都有较高的要求。因此, Thorpe尺度方法在估算湍流混合时可能存在很大的偏差。除此之外, Thorpe尺度在使用时更建议采用自由下降的剖面仪, 而不是有缆下放式的仪器。因为船在海水作用下的摇摆可能会引起传感器响应的一系列误差问题。如采用Argo浮标观测温盐数据识别水体翻转, 结果可能会更好些。
本文通过23个站点的自由下降湍流微尺度剖面仪观测到的夏季吕宋海峡附近海区的湍动能耗散率, 首次综合地对现今广泛使用的三种湍流混合估算方法进行比较研究, 评估了它们的适用性。分析表明GHP估算方法最优, MG参数化方法其次, Thorpe尺度方法相对GHP和MG参数化方法较差。由于吕宋海峡区域具有复杂的海洋动力过程和各种地形特征, 该海区的混合分布特征在一定程度上可以近似作为全球混合分布的缩影。因此该海区的混合参数化方案的深入认识将会对应用参数化方案研究全球混合有很大帮助。但由于海洋内部混合过程比较复杂, 每一种估算方法都有其最适用的动力条件。所以, 今后还需开展参数化方法动力条件适用性工作, 研究其原因机制。
范植松. 2002. 海洋内部混合研究基础. 北京: 海洋出版社
|
周宇, 陈桂英, 尚晓东, 等. 2015. 南海中部上层海洋湍流混合的空间分布特征及参数化模型. 海洋学报, 37(5): 24-33 DOI:10.3969/j.issn.0253-4193.2015.05.003 |
Dillon T M, 1982. Vertical overturns:A comparison of Thorpe and Ozmidov length scales. Journal of Geophysical Research:Oceans, 87(C12): 9601-9613 DOI:10.1029/JC087iC12p09601 |
Galbraith P S, Kelley D E, 1996. Identifying overturns in CTD profiles. Journal of Atmospheric and Oceanic Technology, 13(3): 688-702 DOI:10.1175/1520-0426(1996)013<0688:IOICP>2.0.CO;2 |
Garrett C, Munk W, 1972. Space-Time scales of internal waves. Geophysical Fluid Dynamics, 3(3): 225-264 DOI:10.1080/03091927208236082 |
Garrett C, Munk W, 1975. Space-time scales of internal waves:A progress report. Journal of Geophysical Research, 80(3): 291-297 DOI:10.1029/JC080i003p00291 |
Gregg M C, 1989. Scaling turbulent dissipation in the thermocline. Journal of Geophysical Research:Oceans, 94(C7): 9686-9698 DOI:10.1029/JC094iC07p09686 |
Gregg M C, Kunze E, 1991. Shear and strain in Santa Monica Basin. Journal of Geophysical Research:Oceans, 96(C9): 16709-16719 DOI:10.1029/91jc01385 |
Gregg M C, Sanford T B, Winkel D P, 2003. Reduced mixing from the breaking of internal waves in equatorial waters. Nature, 422(6931): 513-515 DOI:10.1038/nature01507 |
Henyey F S, Wright J, Flatté S M, 1986. Energy and action flow through the internal wave field:An eikonal approach. Journal of Geophysical Research:Oceans, 91(C7): 8487-8495 DOI:10.1029/JC091iC07p08487 |
Jan S, Chen C S, Wang J et al, 2007. Generation of diurnal K1 internal tide in the Luzon Strait and its influence on surface tide in the South China Sea. Journal of Geophysical Research:Oceans, 112(C6): C06019 DOI:10.1029/2006JC004003 |
Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress. Geophysical Research Letters, 37(23): L23604 DOI:10.1029/2010gl045418 |
Jing Z, Wu L X, Liu C Y et al, 2011. Turbulent diapycnal mixing in the subtropical northwestern Pasific:Spatial-seasonal variations and role of eddies. Journal of Geophysical Research DOI:10.1029/2011JC007142 |
Kunze E, 1985. Near-inertial wave propagation in Geostrophic Shear. Journal of Physical Oceanography, 15: 544-565 DOI:10.1175/1520-0485(1985)015<0544:NIWPIG>2.0.CO;2 |
Kunze E, Firing E, Hummon J M et al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553-1576 DOI:10.1175/JPO2926.1 |
Liang C R, Shang X D, Qi Y F et al, 2018. Assessment of fine-scale parameterizations at low latitudes of the North Pacific. Scientific Report, 8: 10281 DOI:10.1038/s41598-018-28554-z |
Lueck R, 2016. Calculating the rate of dissipation of turbulent kinetic energy. Rockland Scientific International Tech, Note TN-028, https://rocklandscientific.com/support/knowledge-base/technical-notes/
|
MacKinnon J A, Gregg M C, 2003. Mixing on the late-summer New England shelf-Solibores, shear, and stratification. Journal of Physical Oceanography, 33(7): 1476-1492 DOI:10.1175/1520-0485(2003)033<1476:MOTLNE>2.0.CO;2 |
Munk W H, 1966. Abyssal recipes. Deep Sea Research and Oceanographic Abstracts, 13(4): 707-730 DOI:10.1016/0011-7471(66)90602-4 |
Munk W, Wunsch C, 1998. Abyssal recipes Ⅱ:Energetics of tidal and wind mixing. Deep Sea Research Part I:Oceanographic Research Papers, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
Polzin K L, Garabato A C N, Huussen T N et al, 2014. Finescale parameterizations of turbulent dissipation. Journal of Geophysical Research:Oceans, 119(2): 1383-1419 DOI:10.1002/2013JC008979 |
Polzin K L, Toole J M, Schmitt R W, 1995. Finescale parameterizations of turbulent dissipation. Journal of Physical Oceanography, 25(3): 306-328 DOI:10.1175/1520-0485(1995)025<0306:FPOTD>2.0.CO;2 |
Shang X D, Qi Y F, Chen G Y et al, 2017a. An expendable microstructure profiler for deep ocean measurements. Journal of Atmospheric and Oceanic Technology, 34(1): 153-165 DOI:10.1175/JTECH-D-16-0083.1 |
Shang X D, Liang C R, Chen G Y, 2017b. Spatial distribution of turbulent mixing in the upper ocean of the South China Sea. Ocean Science, 13(3): 503-519 DOI:10.5194/os-13-503-2017 |
Thompson A F, Gille S T, MacKinnon J A et al, 2007. Spatial and temporal patterns of small-scale mixing in Drake Passage. Journal of Physical Oceanography, 37(3): 572-592 DOI:10.1175/JPO3021.1 |
Thorpe S A, 1977. Turbulence and mixing in a Scottish loch. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 286(1334): 125-181 DOI:10.1098/rsta.1977.0112 |
Tian J W, Yang Q X, Liang X F et al, 2006. Observation of Luzon Strait transport. Geophysical Research Letters, 33(19): L19607 DOI:10.1029/2006GL026272 |
Tian J W, Yang Q X, Zhao W, 2009. Enhanced diapycnal mixing in the South China Sea. Journal of Physical Oceanography, 39(12): 31931-3203 DOI:10.1175/2009JPO3899.1 |
Tian J W, Zhou L, Zhang X Q et al, 2003. Estimates of M2 internal tide energy fluxes along the margin of Northwestern Pacific using TOPEX/POSEIDON altimeter data. Geophysical Research Letters, 30(17): 1889 DOI:10.1029/2003GL018008 |
Van der Lee E M, Umlauf L, 2011. Internal wave mixing in the Baltic Sea:Near-inertial waves in the absence of tides. Journal of Geophysical Research:Oceans, 116(48): C10016 DOI:10.1029/2011JC007072 |
Waterhouse A F, MacKinnon J A, Nash J D et al, 2014. Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. Journal of Physical Oceanography, 44(7): 1854-1872 DOI:10.1175/JPO-D-13-0104.1 |
Wunsch C, Ferrari R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annual Review of Fluid Mechanics, 36: 281-314 DOI:10.1146/annurev.fluid.36.050802.122121 |
Yang Q X, Zhao W, Li M et al, 2014. Spatial structure of turbulent mixing in the Northwestern Pacific Ocean. Journal of Physical Oceanography, 44(8): 2235-2247 DOI:10.1175/JPO-D-13-0148.1 |
 2021, Vol. 52
2021, Vol. 52


