
中国海洋湖沼学会主办。
文章信息
- 李朝, 侯一筠, 李水清, 李健. 2021.
- LI Zhao, HOU Yi-Jun, LI Shui-Qing, LI Jian. 2021.
- 两类典型台风路径影响下的黄、渤海海浪场特征研究
- CHARACTERISTICS OF WAVE FIELD IN THE YELLOW SEA AND THE BOHAI SEA UNDER THE INFLUENCE OF TWO TYPICAL TYPHOONS
- 海洋与湖沼, 52(1): 51-65
- Oceanologia et Limnologia Sinica, 52(1): 51-65.
- http://dx.doi.org/10.11693/hyhz20200300089
文章历史
-
收稿日期:2020-03-24
收修改稿日期:2020-05-17
2. 中国科学院大学 北京 100049;
3. 中国科学院海洋大科学研究中心 青岛 266071;
4. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 青岛 266237;
5. 国家海洋局北海预报中心 青岛 266061
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
4. Laboratory for Ocean and Climate Dynamics, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China;
5. North China Sea Marine Forecasting center of State Oceanic Administration, Qingdao 266061, China
热带气旋是形成于热带或者副热带洋面上的低压气旋性涡旋, 根据中国气象局的定义, 底层中心附近最大风力达到12级及以上的热带气旋的被称为台风(张锐锐, 2007)。海浪通常指风引起的海面波动, 台风引起的海浪(台风浪)能摧毁沿岸的建筑、防护工程等并造成渔业、水产养殖等巨大损失(李雪等, 2018; 冯兴如等, 2018)。黄、渤海沿岸各地是我国受台风侵略较严重的区域之一, 根据自然资源部发布的《中国海洋灾害公报》, 由台风引起的海浪、风暴潮等海洋灾害近些年来对黄海和渤海沿岸的人民群众的生命财产安全造成极大威胁, 相关经济损失巨大, 仅在2014—2018年这5年间在山东一省的引起的直接损失就高达5.29亿元(http://www.mnr.gov.cn/sj/sjfw/hy/gbgg/zghyzhgb/)。1909号超强台风“利奇马”于2019年8月10日1时45分在浙江省温岭市登陆, 并于8月11日20时50分二次登陆山东省青岛市, “利奇马”为2019年登陆我国最强的台风, 导致我国沿海地区受灾严重, 其中受灾人数共1402.4万人, 并造成了515.3亿元的直接经济损失(http://news.weather.com.cn/2019/08/3228731.shtml)。1109号超强台风“梅花”在2011年7月28日14时生成, 并于8月8日18时30分在朝鲜沿海登陆, 该台风使得我国受灾人数达364.98万人, 且导致31.28亿元的直接经济损失(http://news.weather.com.cn/1443798.shtml)。因此研究黄、渤海区域的台风浪分布和传播特征对灾害预警和防控决策具有实际应用意义。
台风浪特征近些年来得到了广泛研究, 台风浪的成长过程与波-波非线性相互作用密切相关(Young, 2006; Xu et al, 2017; Wang et al, 2019a)。陈晓斌等(2013)研究了“梅花”台风在我国东部相关海域的台风浪场空间结构, 发现台风中心区域为较大的涌浪, 且台风外围区域的风浪场波高与涌浪场波高的分布特征相反。韩树宗等(2013)则发现在东中国海浅水区域的台风浪有效波高最大值分布与水深分布一致, 并呈现从西北到东南方向水越深波高越大的特点。邹文峰等(2012)研究了从东海向黄、渤海传播的台风浪发现, 波高在以涌浪为主时并未达到最大。刘彬贤等(2019)利用风-浪关系方程对渤海区域几个浮标站的风-浪关系进行了拟合, 发现订正后的效果较好。He等(2016)则发现黄、渤海的有效波高与平均波周期在四个季节的空间分布上均呈现出由西北向东南、由近海向深海递增的特征。Kim等(2017)研究了台风“赫拔”在黄、东海造成的涌浪的发生与传播过程, 发现周期较长的涌浪由于受海底地形影响易发生折射。
台风“利奇马”在菲律宾以东的西太平洋海面生成并沿西北方向在浙江登陆北上, 这种台风路径属于“提前登陆型”; 台风“梅花”在菲律宾以东的西太平洋海面生成后先沿西北向移动, 由黄海边界传入, 这种台风路径属于典型的“外海入侵型”。本文研究了两类典型路径的台风过程(如图 1所示):台风“利奇马”、台风“梅花”在黄、渤海区域引起的海浪场的空间分布特征及风-浪成长关系, 对今后黄、渤海沿岸各省份进行海浪的模拟观测以及防灾预警有着重要的意义。
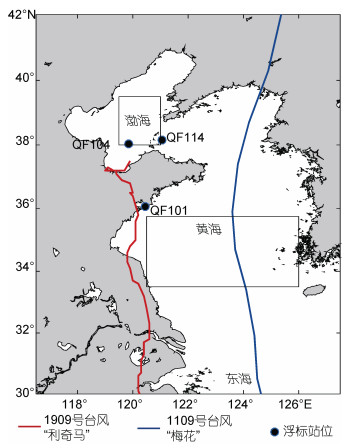 |
| 图 1 1909号台风“利奇马”(红线)和1109号台风“梅花”(蓝线)移动路径及各浮标站位(黑点) Fig. 1 Tracks of No.1909 typhoon Lekima (red line) and No.1109 typhoon Muifa (blue line) with buoy stations (black dots) 注:方框所框选区域代表研究台风浪成长特性的区域 |
使用精准的风场资料进行台风浪的研究是极为重要的。柳婧等(2019)通过对中国近海区域的ASCAT(Advanced SCATterometer)卫星风场资料和ERA-Interim(European Centre for Medium-Range Weather Forecasts Interim Reanalysis)再分析风场资料进行质量评估, 发现ASCAT风场风速精度较优, 但其不具有ERA-Interim风场在时间和空间的连续性。Lv等(2014)和Wang等(2019b)认为在渤海区域, 如果使用ERA-Interim风场数据则会低估了渤海区域的风速和风应力。Rivas等(2019)研究则发现, ERA5风场资料的风速、风应力旋度等均优于ERA-Interim风场资料。综合前人研究考虑, 本文选择较优的ERA5风场进行台风浪的研究评估。ERA5是欧洲中期天气预报中心(European Center for Medium-Range Weather forecasts, ECMWF)发布的第五代全球气象再分析产品。该产品覆盖时间从1979年至今, 其时间分辨率为1 h, 大气再分析数据水平分辨率为0.25°×0.25°, 海洋再分析数据水平分辨率为0.5°×0.5°, 提供了距离海面10 m高度的经向风和纬向风以及海浪的有效波高、波周期等资料。下载地址为https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview。
1.2 方法在利用ERA5数据资料与浮标观测资料进行匹配时, 采用均方根误差(RMSE)、平均绝对误差(MAE)和相关系数(COR)这三个误差衡量指标进行考量, 相应公式如下:
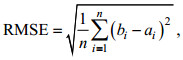 (1)
(1)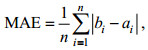 (2)
(2)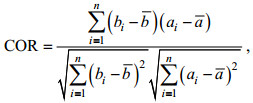 (3)
(3)其中, a代表浮标的观测资料, b为ERA5数据资料。
1.3 研究区域图 1中“利奇马”和“梅花”台风的中心移动路径是采用中央气象台台风网的路径信息数据(http://typhoon.nmc.cn/web.html)绘制的。此次两个台风的台风浪研究时间为: “利奇马”台风(2019年8月10日0:00—8月13日11:00), “梅花”台风(2011年8月6日0:00—8月9日11:00), 所有时间均为北京时间。QF101(水深: 9.09 m, 浅水区域)、QF104(水深: 17.85 m, 深水区域)和QF114(水深: 27.98 m, 深水区域)为风速和波高的浮标观测站位(深、浅水区域判定依据此处水深/波长是否大于0.5)。渤海所划方框区域(38.0°—39.5°N, 119.5°—121.0°E)和黄海所划方框区域(33.5°—35.75°N, 120.5°—126.0°E)为研究台风浪成长特性的区域。
2 ERA5数据资料评价 2.1 风速图 2、图 3给出了“利奇马”台风、“梅花”台风期间, 在QF101、QF104、QF114三个浮标站位的ERA5风场的风速与浮标实测风速的对比, 可以发现ERA5风场的风速与实测风速的吻合度很高, 相应站位风速的均方根误差均不超过2.5 m/s, 其中台风“利奇马”期间在QF101的ERA5风速均方根误差最小, 而台风“梅花”期间在QF104的ERA5风速的均方根误差最小。两个台风期间在各浮标站位风速的相关系数均在0.80以上, 平均绝对误差不超过2.0 m/s, 说明ERA5风场是可靠的(表 1)。
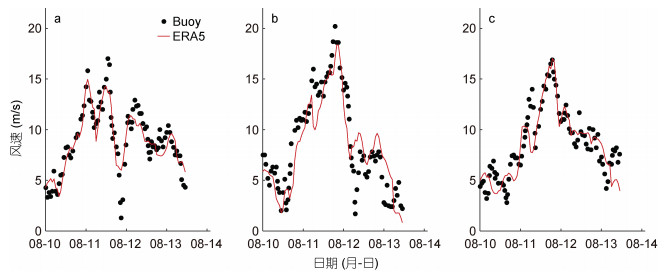 |
| 图 2 台风“利奇马”期间(2019年)ERA5风速与实测数据(Buoy)在QF101(a)、QF104(b)和QF114(c)站位的对比 Fig. 2 Comparison between wind speed of ERA5 with the measured data (Buoy) at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Lekima in 2019 |
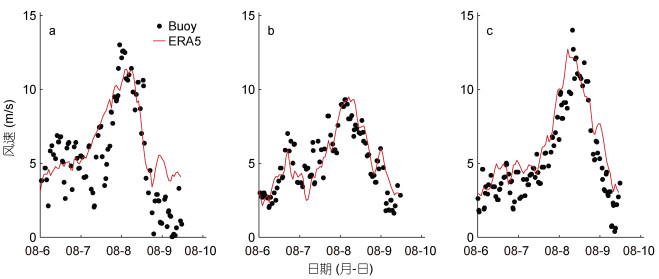 |
| 图 3 台风“梅花”期间(2011年)ERA5风速与实测数据(Buoy)在QF101(a)、QF104(b)和QF114(c)站位的对比 Fig. 3 Comparison between wind speed of ERA5 with the measured data (Buoy) at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Muifa in 2011 |
| 台风名称 | 均方根误差(m/s) | 平均绝对误差(m/s) | 相关系数 | ||||||||
| QF101 | QF104 | QF114 | QF101 | QF104 | QF114 | QF101 | QF104 | QF114 | |||
| 利奇马 | 1.3859 | 2.4099 | 1.7789 | 1.1242 | 1.9369 | 1.3755 | 0.9097 | 0.8727 | 0.8626 | ||
| 梅花 | 2.1457 | 1.0610 | 1.5774 | 1.6720 | 0.8505 | 1.3131 | 0.8052 | 0.8622 | 0.9144 | ||
可以从图 4、图 5可以看出, 两个台风的ERA5的有效波高与浮标实测数据在三个浮标站位均比较吻合, 不过两个台风在QF114站位ERA5的有效波高的最大值都偏低, 对应该站位的ERA5的有效波高的均方根误差较大, 而该站位的风速对比结果良好。这表明ERA5的模式的结果在深水区的模拟结果可能偏低, 这与前人的研究结论一致。尽管如此, ERA5的模拟结果还是很好的再现了各个站位有效波高的时间变化特征, 如表 2所示, 两个台风在各站位有效波高的相关系数均在0.89以上, 平均绝对误差不超过0.23 m, 表明ERA5模拟结果基本可靠。
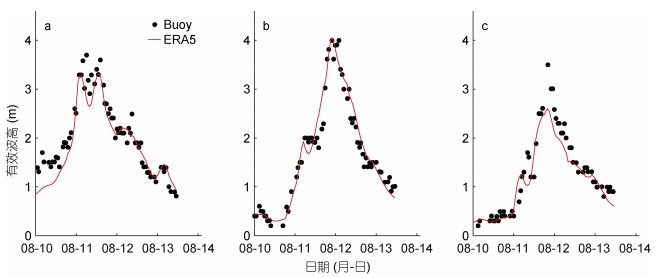 |
| 图 4 台风“利奇马”期间(2019年)ERA5有效波高与实测数据(Buoy)在QF101(a)、QF104(b)和QF114(c)站位的对比 Fig. 4 Comparison between significant wave height of ERA5 with the measured data (Buoy) at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Lekima in 2019 |
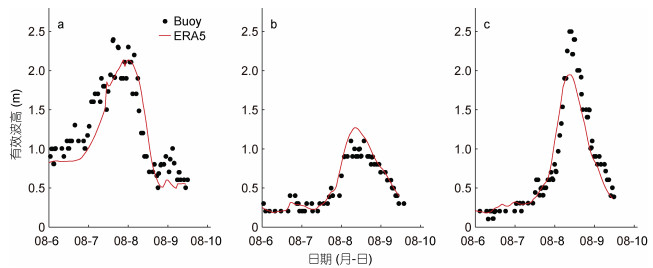 |
| 图 5 台风“梅花”期间(2011年)ERA5有效波高与实测数据(Buoy)在QF101(a)、QF104(b)和QF114(c)站位的对比 Fig. 5 Comparison between significant wave height of ERA5 with the measured data (Buoy) at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Muifa in 2011 |
| 台风名称 | 均方根误差(m) | 平均绝对误差(m) | 相关系数 | ||||||||
| QF101 | QF104 | QF114 | QF101 | QF104 | QF114 | QF101 | QF104 | QF114 | |||
| 利奇马 | 0.2915 | 0.2313 | 0.2888 | 0.2264 | 0.1739 | 0.2023 | 0.9442 | 0.9792 | 0.9615 | ||
| 梅花 | 0.2721 | 0.1169 | 0.2084 | 0.2282 | 0.0775 | 0.1435 | 0.8917 | 0.9732 | 0.9595 | ||
通过上述浮标对比结果表明, ERA5的风、浪模拟结果基本可靠, 可以用来研究台风“利奇马”和“梅花”期间的风-浪特征。
3 台风风场与海浪场的关系 3.1 空间分布特征图 6、图 7分别给出了台风“利奇马”、台风“梅花”在黄、渤海区域的ERA5风场与海浪场的空间分布, 图中列出了风速、风向与海浪有效波高、波平均周期与波向等特征要素, 同时此处及后文的台风路径从ERA5产品获得, 以保证台风风场的研究一致。分别取了台风在黄海与东海交界附近、黄海中部区域附近、渤海附近、出渤海这四个时间点作为分析(具体时刻为, 台风“利奇马”(2019年8月11日0时、8月11日12时、8月12日2时、8月13日11时), 台风“梅花”(2011年8月7日6时、8月7日22时、8月8日12时, 8月8日22时))。可以看到, 两个台风引起的海浪的有效波高分布存在明显的差异, 其中台风“利奇马”在山东、江苏沿岸海域和渤海区产生了较强的波浪, 而台风“梅花”在朝鲜半岛沿海区域产生了较大的波高值; 波高的分布与风速的分布特征基本一致, 台风风速关于移动路径存在不对称性, 台风移动方向右侧风速偏大。海浪周期的分布与风速和有效波高的分布关系不大, 两个台风中心附近海域均产生较大周期的海浪; 值得注意的是, 台风“利奇马”和台风“梅花”在进入黄、渤海之前, 在山东半岛“头部”沿海区域和黄、渤海交界区域存在较大的周期的海浪, 这是由于台风在远区产生的大浪过程传播至此, 涌浪的传播速度要明显大于台风的移动速度; 另外台风“利奇马”在黄、东海交界区持续存在较大周期的海浪, 这应该是受附近的1910号台风“罗莎”的影响导致。波向与风向之间存在着显著的偏差, 波向相对于风向偏于台风移动方向位置, 这表明台风浪是风浪和涌浪的混合形式, 下文将对风浪和涌浪的成分特征进行细致分析。
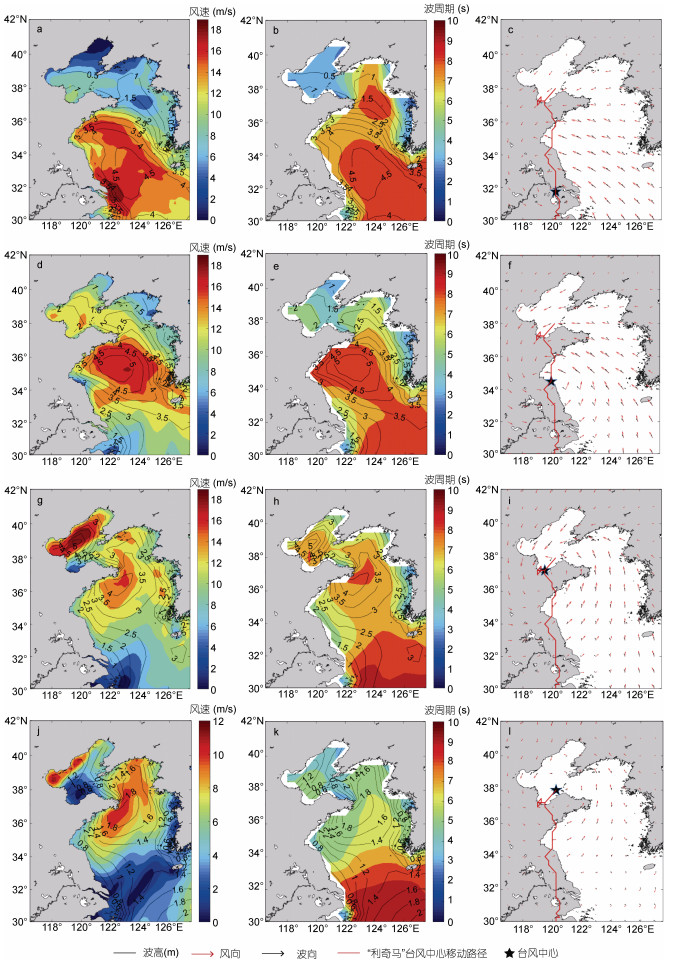 |
| 图 6 台风“利奇马”期间风速与波高(a、d、g、j)、波周期与波高(b、e、h、k)、风向与波向(c、f、i、l)的空间分布 Fig. 6 Spatial distribution of wind speeds with significant wave height (a, d, g, j), wave period with significant wave height (b, e, h, k), and wind direction with wave direction (c, f, i, l) during typhoon Lekima 注: a、d、g、j为风速与波高(等值线, 单位: m)分布; b、e、h、k为波周期与波高(等值线, 单位: m)分布; c、f、i、l为风向(红箭头)和波向(黑箭头)分布, 风向、波向的箭头长度代表其数值大小; a、b、c的时间为2019年8月11日0时, d、e、f的时间为8月11日12时, g、h、i的时间为8月12日2时, j、k、l的时间为8月13日11时 |
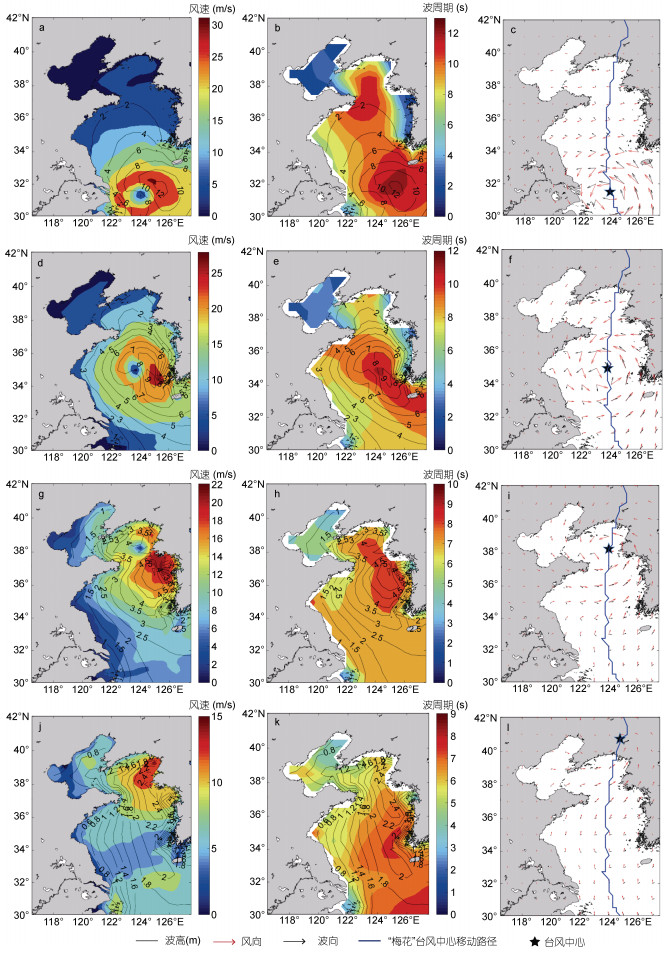 |
| 图 7 台风“梅花”期间风速与波高(a、d、g、j)、波周期与波高(b、e、h、k)、风向与波向(c、f、i、l)的空间分布 Fig. 7 Spatial distribution of wind speeds with significant wave height (a, d, g, j), wave period with significant wave height (b, e, h, k), and wind direction with wave direction (c, f, i, l) during typhoon Muifa 注: a、d、g、j为风速与波高(等值线, 单位: m)分布; b、e、h、k为波周期与波高(等值线, 单位: m)分布; c、f、i、l为风向(红箭头)和波向(黑箭头)分布, 风向、波向的箭头长度代表其数值大小, 蓝线代表“梅花”台风中心移动路径, 黑色五角星代表对应时刻的台风中心; a、b、c的时间为2011年8月7日6时, d、e、f的时间为8月7日22时, g、h、i的时间为8月8日12时, j、k、l的时间为8月8日22时 |
台风浪一般是以风浪和涌浪的混合形式存在(Li et al, 2012; 陈汉宝等, 2013), 其中风浪是指台风过境期间由局地强风驱动引起的, 涌浪是台风过境前在远区形成的海浪传播至此。ERA5提供了风浪和涌浪的有效波高数据, 它基于海浪谱的二维谱方法对风浪和涌浪进行分离(ECMWF, 2016; Hersbach et al, 2018; Bruno et al, 2020)。图 8、图 9分别给出了“利奇马”、“梅花”台风期间在山东沿岸海域3个浮标站位产生的风浪有效波高、涌浪有效波高与混合浪有效波高。可以看到两个台风过程的海浪成分特征在黄海的QF101站位存在明显的差异, 对于台风“利奇马”, 在海浪成长期主要以风浪占优, 而台风“梅花”以涌浪为主, 值得注意的是, 风浪增长的同时, 涌浪也呈现一定的成长, 这是由于台风期间存在强烈的波-波非线性相互作用, 风浪可以向涌浪进一步传递能量(Young, 2006; Xu et al, 2017; Wang et al, 2019a), 后文将结合海浪的无因次关系对海浪成长特性做进一步分析。在渤海的两个站位(QF104, QF114), 两个台风过程的海浪成长期以风浪为主, 先行涌浪特征不明显(波高小于0.3 m), 这是由于山东半岛的阻隔作用; 在海浪消衰期, 对应着局地风速的衰减, 海浪以涌浪为主, 海浪衰减相对于风速过程明显偏缓。
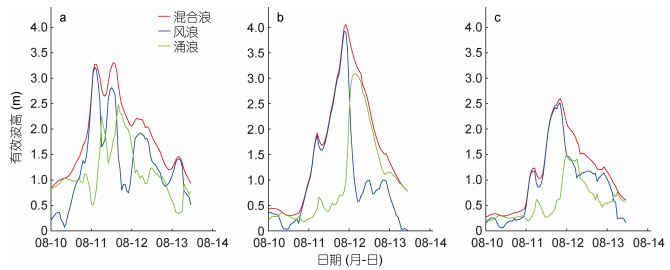 |
| 图 8 台风“利奇马”期间(2019年)在QF101(a)、QF104(b)和QF114(c)站位的混合浪、风浪、涌浪的有效波高 Fig. 8 Significant wave height of combined wind waves and swell, wind waves, and swell at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Lekima in 2019 |
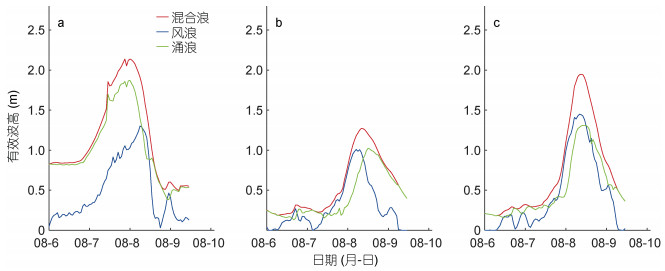 |
| 图 9 台风“梅花”期间(2011)在QF101(a)、QF104(b)和QF114(c)站位的混合浪、风浪、涌浪的有效波高 Fig. 9 Significant wave height of combined wind waves and swell, wind waves and swell at buoy stations QF101(a), QF104(b), and QF114(c) during typhoon Muifa in 2011 |
图 10和图 11给出了台风“利奇马”、台风“梅花”的混合浪、风浪和涌浪的有效波高空间分布图。整体上看, 两个台风进入黄海前, 存在一个明显的从黄海向渤海的“涌浪舌”。台风“利奇马”引起的沿岸大浪主要对应风浪, 而台风梅花移动方向右侧风浪明显占优, 左侧有明显的涌浪特征。具体来看台风“利奇马”在黄、渤海区域的海浪场情况, 在2019年8月11日0时左右, 台风“利奇马”从东海附近区域进入黄海附近区域, 在黄海区域引起了较大的风浪和较小的涌浪; 而到了8月11日12时, 此时台风“利奇马”从陆地进入黄海区域, 此时黄海和渤海区域均产生了风浪, 渤海区域涌浪很小; 到了8月12日2时, 台风“利奇马”进入渤海区域, 黄、渤海区域呈现风浪与涌浪互相混合但风浪为主的状态; 最后8月13日11时, 台风“利奇马”减弱为弱气旋过程, 黄、渤海区域则出现风浪与涌浪互相混合但主要以涌浪为主的海浪(此时海浪还受到附近1910号台风“罗莎”的影响)。可以发现, 大部分时间山东沿岸区域的风浪均大于涌浪。对于台风“梅花”, 具体从图 11来看, 2011年8月7日6时左右台风“梅花”逐渐靠近东、黄海交界区域, 此时虽然黄、渤海区域的海浪主要以风浪为主, 但显然涌浪的影响范围较风浪广; 8月7日22时, 台风“梅花”进入黄海中部海域, 8月8日12时台风“梅花”开始影响渤海区域, 从8月7日22时到8月8日12时这段时间黄、渤海尤其山东沿岸海域呈现风浪与涌浪相混合的状态, 但海浪仍是风浪为主。8月8日22时, 此时台风“梅花”已经登陆, 可以明显发现黄、渤海区域的海浪主要是涌浪。
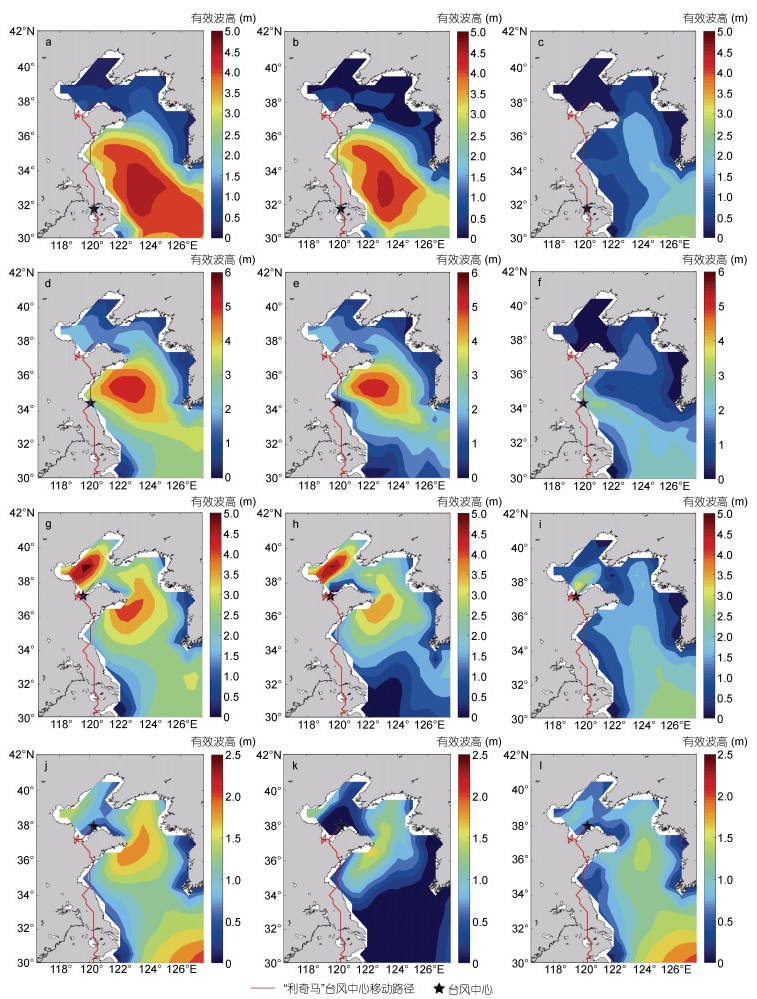 |
| 图 10 台风“利奇马”期间混合浪(a、d、g、j)、风浪(b、e、h、k)、涌浪(c、f、i、l)场的有效波高空间分布 Fig. 10 Spatial distribution of combined wind waves and swell (a, d, g, j), wind waves (b, e, h, k) and swell (c, f, i, l) during typhoon Lekima 注: a、d、g、j为混合浪场的有效波高分布; b、e、h、k为风浪场的有效波高分布; c、f、i、l为涌浪场的有效波高分布; a、b、c的时间为2019年8月11日0时, d、e、f的时间为8月11日12时, g、h、i的时间为8月12日2时, j、k、l的时间为8月13日11时 |
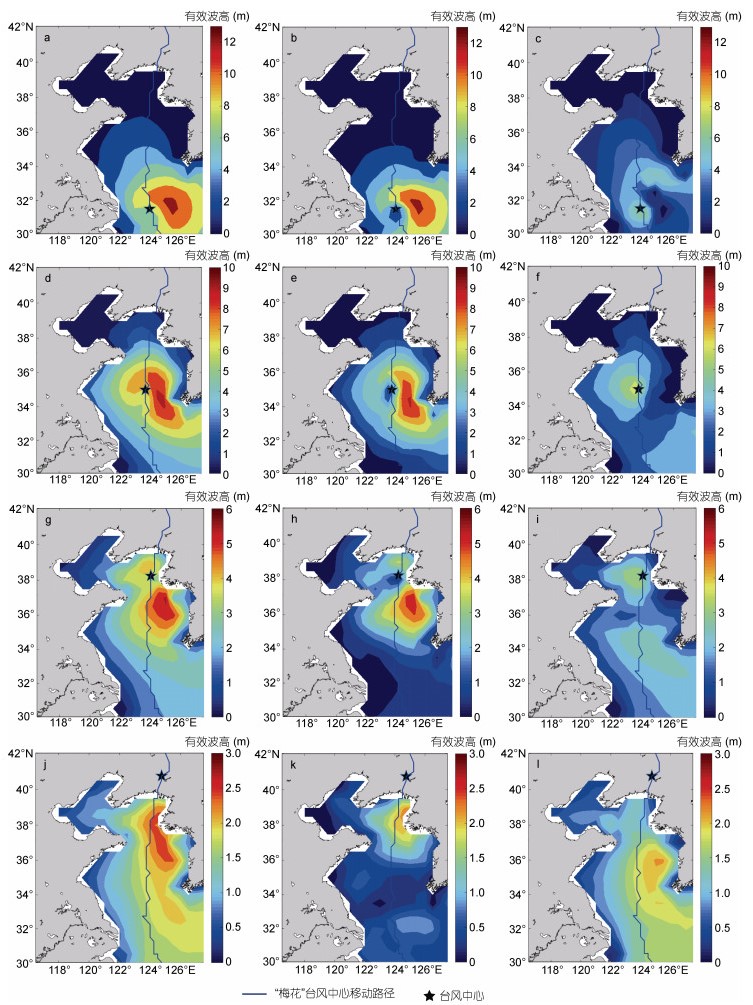 |
| 图 11 台风“梅花”期间混合浪(a、d、g、j)、风浪(b、e、h、k)、涌浪(c、f、i、l)场的有效波高空间分布 Fig. 11 Spatial distribution of combined wind waves and swell (a, d, g, j), wind waves (b, e, h, k) and swell (c, f, i, l) during typhoon Muifa 注: a、b、c的时间为2011年8月7日6时, d、e、f的时间为8月7日22时, g、h、i的时间为8月8日12时, j、k、l的时间为8月8日22时 |
在风的强迫作用下, 风浪的周期和波高并不是相互独立的, 而是在波-波相互作用下存在内在联系, 前人研究发现, 风浪无因次波高和无因次周期存在显著的相关性, 目前已经提出了诸多模型关系(Hasselmann et al, 1976; Kahma, 1981; Zakharov et al, 1983; Donelan et al, 1985; Dobson et al, 1989; Wen et al, 1989; Ewans et al, 1990; Babanin et al, 1998; Hsu et al, 2017), 这些模型可概括表示为:
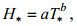 (4)
(4)其中a、b为所求参数(幂律系数); 无因次波高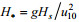
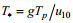
本文将选取两个台风期间的海浪数据进行无因次分析, 以检验风浪成长过程中的波-波相互作用特性。值得注意的是, 上述式(4)仅在深水条件下适用, 因此本文选择了黄、渤海的深水区域(水深d和海浪波长Lp满足关系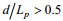 )进行探究, 其中
)进行探究, 其中 取自图 1所划黑框区域内的深水区域的数据, 保证了模型的适用性和计算的准确性。水深数据从海洋通用水深测量图(General Bathymetric Chart of the Oceans, GEBCO)数据集(https://www.gebco.net/)获得, 其分辨率高达15arc-seconds。
取自图 1所划黑框区域内的深水区域的数据, 保证了模型的适用性和计算的准确性。水深数据从海洋通用水深测量图(General Bathymetric Chart of the Oceans, GEBCO)数据集(https://www.gebco.net/)获得, 其分辨率高达15arc-seconds。
将两个台风在黄、渤海区的无因次过程分别进行描述, 如图 12、13所示(双对数坐标绘制)。
 |
| 图 12 台风“利奇马”期间黄海(a)、渤海(b)区域的无因次波高、周期的散点图和拟合曲线 Fig. 12 Scatter diagrams and fitted curves of dimensionless wave height with dimensionless wave period in the Yellow Sea (a) and the Bohai Sea (b) during typhoon Lekima |
 |
| 图 13 台风“梅花”期间黄海(a)、渤海(b)区域的无因次波高、周期的散点图和拟合曲线 Fig. 13 Scatter diagrams and fitted curves of dimensionless wave height with dimensionless wave period in the Yellow Sea (a) and the Bohai Sea (b) during typhoon Muifa |
台风“利奇马”期间黄海区域的无因次风-浪关系可表示为:
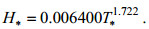 (5)
(5)台风“利奇马”期间渤海区域的无因次风-浪关系可表示为:
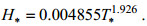 (6)
(6)台风“梅花”期间黄海区域的无因次风-浪关系可表示为:
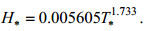 (7)
(7)台风“梅花”期间渤海区域的无因次风-浪关系可表示为:
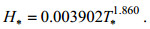 (8)
(8)从图 12、13可以看到Hsu模型比较吻合上边界值, Zakharov模型则较为吻合下边界值, Donelan模型和本文拟合模型则更接近黄、渤海区域的真实情况(拟合模型的可决系数R2(拟合优度)在黄、渤海区域分别为, 台风“利奇马”: 0.8587、0.9598;台风“梅花”: 0.7341、0.8893, 说明拟合模型较佳)。从拟合的关系模型不难发现, 台风“利奇马”期间黄、渤海区域的幂律系数a、b值与台风“梅花”接近, 整体来说, 两个台风的无因次关系较为一致。对比来看, 幂律系数b在黄海区域明显小于渤海区域, 该系数能反应波浪的成长阶段, 系数值越小, 波浪成长越充分(Badulin et al, 2012)。因此, 可以推论黄海的风浪成长更为充分, 这与黄海开阔的海区对应的长风区特性有关。下面将对结合波高关于风速的变化对风浪成长关系做进一步分析。
通过台风浪的空间分布特征发现海浪的有效波高与风速的变化几乎一致, 有效波高与风速之间具有较高的相关性, 已有研究表明两者之间呈二次多项式关系(Carter, 1982; Taylor et al, 2001; Andreas et al, 2007; Emeis et al, 2009; 王晨迪等, 2017; 王小丹等, 2019), 可表示为:
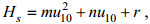 (9)
(9)其中, m、n、r为待求系数(二次多项式系数)。
图 14、15给出了两个台风期间海浪的有效波高Hs与风速u10的风-浪关系。
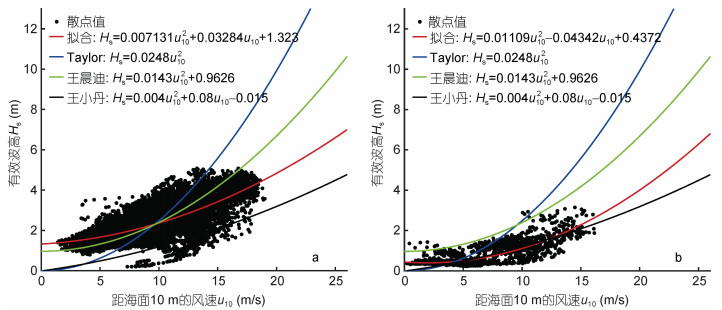 |
| 图 14 台风“利奇马”期间黄海(a)、渤海(b)区域的有效波高、风速的散点图和拟合曲线 Fig. 14 Scatter diagrams and fitted curves of significant wave height with wind speed in the Yellow Sea (a) and the Bohai Sea (b) during typhoon Lekima |
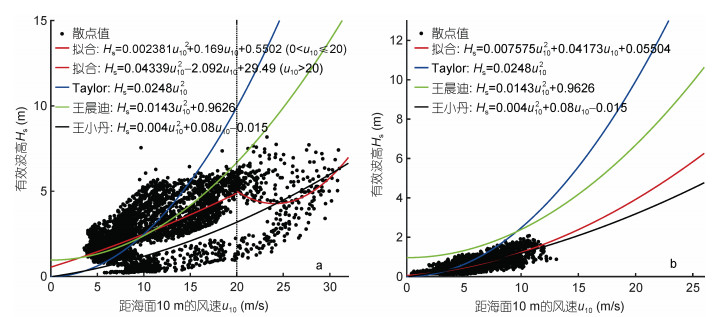 |
| 图 15 台风“梅花”期间黄海(a)、渤海(b)区域的有效波高、风速的散点图和拟合曲线 Fig. 15 Scatter diagrams and fitted curves of significant wave height with wind speed in the Yellow Sea (a) and the Bohai Sea (b) during typhoon Muifa |
台风“利奇马”期间黄海区域的海浪有效波高与风速的风-浪关系模型为:
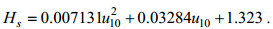 (10)
(10)台风“利奇马”期间渤海区域的海浪有效波高与风速的风-浪关系模型为:
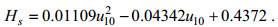 (11)
(11)台风“梅花”期间黄海区域的海浪有效波高与风速的风-浪关系模型为:
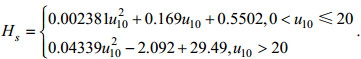 (12)
(12)台风“梅花”期间渤海区域的海浪有效波高与风速的风-浪关系模型为:
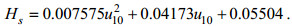 (13)
(13)由图 14、15可以看到, Taylor等、王晨迪等的模型较为高估了有效波高, 而王小丹等的模型则较为低估了有效波高, 本文拟合的风-浪模型则更适合黄、渤海区域。总体来看, 两个台风过程的有效波高与风速关系模型中, 台风“利奇马”的台风浪成长特性与台风“梅花”基本一致, 而两者在黄海区域的台风浪成长较在渤海区域都更为充分(需要区别注意的是, 台风“利奇马”期间的风速普遍低于20 m/s, 而台风“梅花”期间的存在风速超过20 m/s的情形, 从拟合关系来看, 这一高风速情形下的波高随风速的成长变化趋势变缓, 这可能是由于风区的限制导致), 这与前面的无因次分析结果基本一致。上述结果表明, 台风浪的成长特性主要与区域有关, 与台风过程关系不明显。
4 结论本文首先评估了ERA5产品的质量, 研究表明ERA5产品的风速和有效波高与浮标实测资料是吻合的。然后基于ERA5数据对1909号台风“利奇马”和1109号台风“梅花”(两类典型不同移动路径的台风)在黄海和渤海区域的海浪场特征和风-浪成长关系进行研究, 得到了以下结论:
(1) 两个台风引起的台风浪的有效波高分布差异较大, 波高的分布和风速分布基本相同, 台风移动路径右侧风速偏大; 海浪的风速、有效波高与周期之间的分布关系不大, 台风中心附近区域均形成了较大周期的海浪; 风向与波向之间存在一定偏差, 波向相对风向偏于台风移动方向。
(2) 分析台风浪各成分的空间分布发现, 一个从黄海向渤海的“涌浪舌”在两个台风进入黄海之前便存在; 台风“利奇马”导致的沿岸海浪以风浪为主; 台风“梅花”的移动方向左侧主要表现为涌浪特征, 右侧则以风浪为主。
(3) 台风浪的无因次波高与无因次周期呈现幂律关系, 台风浪的有效波高与风速呈二次多项式函数关系; 两个台风路径下的台风浪的成长特性较为一致, 台风浪的成长特性主要与所处区域的水深、地形有关, 体现为台风浪在黄海区域较渤海区域成长更为充分。
王小丹, 赵文静. 2019. 基于ERA-Interim再分析资料的南沙海域风、浪场特征分析. 海洋预报, 36(2): 30-37 |
王晨迪, 费建芳, 丁菊丽, 等. 2017. 海气界面动量通量算法的改进. 热带气象学报, 33(5): 627-636 |
冯兴如, 杨德周, 尹宝树, 等. 2018. 中国浙江和福建海域台风浪变化特征和趋势. 海洋与湖沼, 49(2): 233-241 |
刘彬贤, 史得道, 杨炳栋. 2019. 渤海海域风浪特征相关性分析. 中国航海, 42(2): 97-100 |
李雪, 宋冲, 巩艺杰, 等. 2018. 山东沿海台风浪数值模拟与统计分析. 海洋湖沼通报, (1): 27-33 |
邹文峰, 李艳阳, 张宁川. 2012. 中国内海台风浪传播和演化过程数值模拟. 水道港口, 33(2): 93-100 DOI:10.3969/j.issn.1005-8443.2012.02.001 |
张锐锐. 2007. 热带气旋新划分等级标准及相关术语. 中国科技术语, 9(2): 56 DOI:10.3969/j.issn.1673-8578.2007.02.016 |
陈汉宝, 刘海源, 徐亚男, 等. 2013. 风浪与涌浪相互影响的实验. 天津大学学报(自然科学与工程技术版), 46(12): 1122-1126 |
陈晓斌, 周林, 史文丽, 等. 2013. 台风"梅花"风浪场和涌浪场特征分析. 海洋科学进展, 31(1): 22-30 DOI:10.3969/j.issn.1671-6647.2013.01.003 |
柳婧, 宋晓姜, 王彰贵. 2019. 中国近海ASCAT和ERA-Interim风场资料的评估. 海洋预报, 36(1): 10-19 |
韩树宗, 史玉姣. 2013. 东中国海台风浪分布特征研究. 中国海洋大学学报, 43(10): 1-7 |
Andreas E L, Wang S, 2007. Predicting significant wave height off the northeast coast of the United States. Ocean Engineering, 34(8-9): 1328-1335 DOI:10.1016/j.oceaneng.2006.08.004 |
Babanin A V, Soloviev Y P, 1998. Field investigation of transformation of the wind wave frequency spectrum with fetch and the stage of development. Journal of Physical Oceanography, 28(4): 563-576 DOI:10.1175/1520-0485(1998)028<0563:FIOTOT>2.0.CO;2 |
Badulin S I, Grigorieva V G, 2012. On discriminating swell and wind-driven seas in Voluntary Observing Ship data. Journal of Geophysical Research:Oceans, 117(C11): C00J29 |
Bruno M F, Molfetta M G, Totaro V et al, 2020. Performance assessment of ERA5 wave data in a swell dominated region. Journal of Marine Science and Engineering, 8(3): 214 DOI:10.3390/jmse8030214 |
Carter D J T, 1982. Prediction of wave height and period for a constant wind velocity using the JONSWAP results. Ocean Engineering, 9(1): 17-33 DOI:10.1016/0029-8018(82)90042-7 |
Dobson F, Perrie W, Toulany B, 1989. On the deep-water fetch laws for wind-generated surface gravity waves. Atmosphere-Ocean, 27(1): 210-236 DOI:10.1080/07055900.1989.9649334 |
Donelan M A, Hamilton J, Hui W H, 1985. Directional spectra of wind-generated ocean waves. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 315(1534): 509-562 DOI:10.1098/rsta.1985.0054 |
ECMWF, 2016. IFS Documention-Cy43r1 Operational implementation 22 Nov 2016 Part VⅡ: ECMWF Wave Model. Reading: ECMWF Shinfield Park
|
Emeis S, Türk M, 2009. Wind-driven wave heights in the German Bight. Ocean Dynamics, 59(3): 463-475 DOI:10.1007/s10236-008-0178-x |
Ewans K C, Kibblewhite A C, 1990. An examination of fetch-limited wave growth off the west coast of New Zealand by a comparison with the JONSWAP results. Journal of Physical Oceanography, 20(9): 1278-1296 DOI:10.1175/1520-0485(1990)020<1278:AEOFLW>2.0.CO;2 |
Hasselmann K, Ross D B, Müller P et al, 1976. A parametric wave prediction model. Journal of Physical Oceanography, 6(2): 200-228 DOI:10.1175/1520-0485(1976)006<0200:APWPM>2.0.CO;2 |
He H L, Xu Y, 2016. Wind-wave hindcast in the Yellow Sea and the Bohai Sea from the year 1988 to 2002. Acta Oceanologica Sinica, 35(3): 46-53 DOI:10.1007/s13131-015-0786-5 |
Hersbach H, de Rosnay P, Bel B et al, 2018. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP, ERA Report Series. Reading: ECMWF Shinfield Park
|
Hsu S A, He Y J, Shen H, 2017. Buoy measurements of wind-wave relations during hurricane Matthew in 2016. Journal of Physical Oceanography, 47(10): 2603-2609 DOI:10.1175/JPO-D-16-0280.1 |
Kahma K K, 1981. A study of the growth of the wave spectrum with fetch. Journal of Physical Oceanography, 11(11): 1503-1515 DOI:10.1175/1520-0485(1981)011<1503:ASOTGO>2.0.CO;2 |
Kim K O, Yuk J H, Jung K T et al, 2017. Swell propagation caused by typhoon passage to the Yellow and East China Seas. Journal of Coastal Research, 79(sp1): 144-148 |
Li S Q, Zhao D L, 2012. Comparison of spectral partitioning techniques for wind wave and swell. Marine Science Bulletin, 14(2): 24-36 |
Lv X C, Yuan D K, Ma X D et al, 2014. Wave characteristics analysis in Bohai Sea based on ECMWF wind field. Ocean Engineering, 91: 159-171 DOI:10.1016/j.oceaneng.2014.09.010 |
Rivas M B, Stoffelen A, 2019. Characterizing ERA-interim and ERA5 surface wind biases using ASCAT. Ocean Science, 15(3): 831-852 DOI:10.5194/os-15-831-2019 |
Taylor P K, Yelland M J, 2001. The dependence of sea surface roughness on the height and steepness of the waves. Journal of Physical Oceanography, 31(2): 572-590 DOI:10.1175/1520-0485(2001)031<0572:TDOSSR>2.0.CO;2 |
Toba Y, 1973. Local balance in the air-sea boundary processes Ⅱ:Partition of wind stress to waves and current. Journal of the Oceanographical Society of Japan, 29(2): 70-75 |
Wang N, Hou Y J, Li S Q et al, 2019a. Numerical simulation and preliminary analysis of typhoon waves during three typhoons in the Yellow Sea and East China Sea. Journal of Oceanology and Limnology, 37(6): 1805-1816 DOI:10.1007/s00343-019-8260-4 |
Wang Y P, Liu Y L, Mao X Y et al, 2019b. Long-term variation of storm surge-associated waves in the Bohai Sea. Journal of Oceanology and Limnology, 37(6): 1868-1878 DOI:10.1007/s00343-019-8257-z |
Wen S C, Zhang D C, Guo P F et al, 1989. Parameters in wind-wave frequency spectra and their bearings on spectrum forms and growth. Acta Oceanologica Sinica, 8(1): 15-39 |
Xu Y, He H L, Song J B et al, 2017. Observations and modeling of typhoon waves in the South China Sea. Journal of Physical Oceanography, 47(6): 1307-1324 DOI:10.1175/JPO-D-16-0174.1 |
Young I R, 2006. Directional spectra of hurricane wind waves. Journal of Geophysical Research:Oceans, 111(C8): C08020 |
Zakharov V E, Zaslavsky M M, 1983. Dependence of the wave parameters on the wind velocity, the duration of its action and the fetch in the weak-turbulence theory of wind waves. Izvestia Akademii nauk SSSR. Fizika atmosfery i okeana, 19(4): 406-415
|
 2021, Vol. 52
2021, Vol. 52


