中国海洋湖沼学会主办。
文章信息
- 温昌麒, 朱君, 蔡锋, 王立辉, 戚洪帅, 刘建辉, 雷刚, 赵绍华. 2021.
- WEN Chang-Qi, ZHU Jun, CAI Feng, WANG Li-Hui, QI Hong-Shuai, LIU Jian-Hui, LEI Gang, ZHAO Shao-Hua. 2021.
- 海滩修复工程影响下的低能海岸波浪能量时空分布特征研究
- SPATIAL AND TEMPORAL DISTRIBUTION OF WAVE ENERGY ON LOW ENERGY COASTS UNDER THE EFFECT OF BEACH RESTORATION PROJECT
- 海洋与湖沼, 52(1): 75-85
- Oceanologia et Limnologia Sinica, 52(1): 75-85.
- http://dx.doi.org/10.11693/hyhz20200300104
文章历史
-
收稿日期:2020-03-31
收修改稿日期:2020-05-12
2. 福建省海洋生态保护与修复重点实验室 厦门 361005;
3. 福州大学 土木工程学院 福州 350108
2. Fujian Provincial Key Laboratory of Marine Ecological Conservation and Restoration, Xiamen 361005, China;
3. School of Civil Engineering, Fuzhou University, Fuzhou 350108, China
波浪是塑造海岸地貌的主要动力因素, 波浪能量分布变化将导致海岸地形地貌发生显著变化。目前关于波浪能量的研究主要通过数值模拟分析其时空变化特征。Rusu等(2009)应用WAM(WAve Modelling project)和SWAN(Simulating Wave Nearshore)数学模型对葡萄牙近岸海域波浪场进行了数值模拟, 分析了该海域波浪能量分布状况; 刘劲等(2012)基于SWAN建立了铁山湾海域风浪数学模型, 研究了不同风要素组合作用下该海域波浪特征; Mirzaei等(2014)利用WAVEWATCH III模型模拟并分析了1979—2009年马来西亚半岛东海域波浪能季节变化与空间分布特点; 朱君等(2017)利用SWAN模拟并分析了厦门湾波浪能量的时空变化特征; 邱文博等(2019)基于SWAN和WAVEWATCH III两个模型对广东珠江口海域波浪场进行了嵌套数值模拟, 分析了该海域波浪要素的时空变化特征。以上关于波浪能量时空变化特征的研究大多针对中能或高能海域, 而聚焦于低能海域的波浪能量分析研究匮乏。此外关于波浪能量人为干预再分配的研究亦有不少, 但主要集中在波浪能量的削弱上(赵桂侠等, 2017; Pranzini et al, 2018; Wang et al, 2018), Daly等(2014)发现对于岬湾型海岸波浪折射使得波浪能量辐散, 致使近岸波浪能量将被削弱; Zhu等(2019)研究了防波堤对于波浪能量的削减作用。对于通过人为干预增加局部海域波浪能量的研究较为少见, 通过合理的海滩修复设计来提高低能海岸波浪能量的研究更为匮乏。
本文以钦州湾茅尾海为例, 基于SWAN模型对该海域波浪场进行了周年数值模拟, 详细分析了茅尾海低能海滩波浪能量的时空分布特征。在此基础上探讨了该海域主要的波浪能量输入与耗散过程, 以及海滩修复前后波浪能量的分布变化差异, 研究成果可为弱动力环境下进行的海滩修复工程提供一定的科学依据。
1 研究区概况茅尾海位于广西壮族自治区钦州市, 东靠北海市, 西侧与防城港市相邻(图 1)(吴良, 2013)。该海域位于钦州湾顶部的一个内湾, 东、西、北三面由陆地环绕, 南侧与钦州湾相通, 是一个半封闭天然海湾(郭雅琼等, 2016)。为便于描述, 将茅尾海所在的海域称为“湾内”, 茅尾海口门之外的海域称为“湾外”。研究区湾内以风浪为主, 湾外涌浪难以传入, 水动力条件较弱。茅尾海平均有效波高不足0.2 m, 当风速达8 m/s时, 有效波高仅0.35 m(李树华等, 1993), 符合Jackson等(2002)中关于低能海岸的定义(正常天气条件下有效波高 < 0.25 m; 风速为8.0 m/s时有效波高 < 0.5 m)。
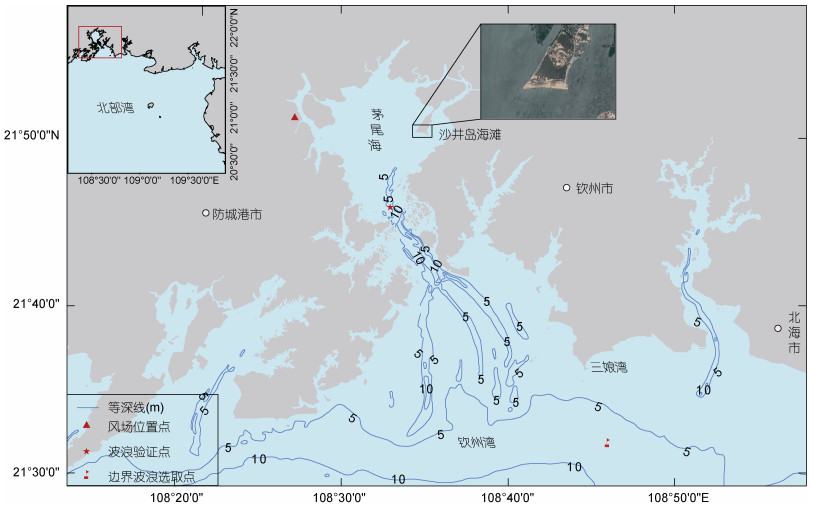 |
| 图 1 研究区位置图 Fig. 1 Map of study area |
茅尾海由于波浪动力较弱, 泥质颗粒易沉积, 砂泥分界线高程较高, 因此该海域海滩修复难度较大, 修复后的海滩易发生泥化。提高修复岸段波浪能量成为在该海域保障修复海滩质量的关键。茅尾海沙井岛人工海滩位于茅尾海东北部, 其修复过程中采取了人工岬头设计和水深疏浚措施来提高修复岸段的波浪能量, 海滩修复后岸线形态由尖角型变为岬头型, 长度约1.2 km, 干滩平均宽度为95 m, 滩肩高程(平均海平面, Mean Sea Level, MSL)为3.26 m, 施工滩面坡度为1:20。海滩前沿清淤面积约10 km2, 平均清淤深度为2.5 m左右(图 2)。为便于标识, 图 2及后续空间分布图像采用转换后的平面坐标。
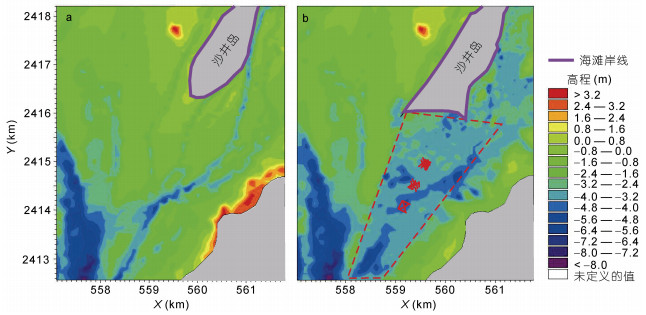 |
| 图 2 海滩修复前后岸线(紫色实线)及水深变化对比 Fig. 2 Comparison of shoreline and water depth changes before and after beach restoration 注: a:海滩修复前; b:海滩修复后; 水深基面为当地平均海平面; 横(纵)坐标是经(纬)度由高斯克吕投影得到的平面坐标, X对应经度, Y对应纬度, 余同 |
SWAN模型是基于第三代海浪模式开发的波浪模型(Booij et al, 1999; Ris et al, 1999), 可全面模拟近岸波浪传播过程中的折射、绕射、白帽、浅化、底摩擦等物理过程。目前, 该模型在近海海域波浪数值模拟研究中得到广泛的运用(张宏伟等, 2008; 滕陈轲敏等, 2019), 本次采用的SWAN版本为41.01A版。
SWAN模型中以作用量密度N建立平衡方程。作用量密度的变化率可以用作用量平衡方程(SWAN Team, 2006)表示为:
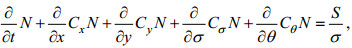 (1)
(1)式中, N为作用量密度, t为时间, x、y为平面坐标; σ、θ分别为频率和方向; 方程左边第一项表示作用量密度随时间的变化率; 第二项和第三项表示作用量密度在几何空间的传播变化率(Cx和Cy); 第四项表示流和水深引起的频移(Cσ); 第五项表示由流和水深引起的折射和变浅作用(Cθ); 方程右边S表示波能的源汇项, 其具体描述为:
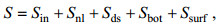 (2)
(2)式中, Sin代表风输入的能量, Snl代表波与波之间的非线性相互作用引起的能量损耗, Sds代表白帽引起的能量损耗, Sbot代表底摩擦引起的能量损耗, Ssurf代表由于水深变化引起的波浪破碎产生的能量损耗。
2.2 模型设置模型周年波浪计算起止时间为2015年1月1日0:00—2015年12月31日23:00, 模型波浪验证计算时间为2019年1月10日0:00—2019年1月23日23:00;模型采用非结构网格(三角形), 网格数为57326个, 网格节点数为30787个; 网格间距从外海向近岸逐渐减小(图 3a), 最大网格间距为1744.3 m, 最小网格间距为7.2 m; 模型使用的水深数据采用的是近岸实测与大范围海图资料, 所有水深数据统一至当地平均海平面。茅尾海平均水深约为4.1 m, 最大水深位于口门航道处约为39.5 m(图 3b)。
 |
| 图 3 模型计算网格(a)和水深(b) Fig. 3 The computation grid (a) and water depth (b) |
模型中主要参数设置包括: (1)波浪开边界采用JONSWAP谱, 谱峰升高因子取3.3; (2)第三代海浪模式选用风生浪指数型增长的KOMEN公式; (3)底摩擦计算选用Hasselmann的经验公式; (4)开启三波相互作用, 关闭白帽破碎和波浪反射; (5)其余参数均采用SWAN模型默认设置。
2.2.1 风场数据本研究将美国气象环境预报中心(National Centers for Environmental Prediction, NCEP)再分析风场作为SWAN模型的驱动场, NCEP再分析风场(Kanamitsu et al, 2002)是由NCEP和美国国家大气研究中心(National Center for Atmospheric Research, NCAR)联合制作的, 空间分辨率为2.5°×2.5°, 时间分辨率为6 h。NCEP风场具有很高的精度和时空分辨率, 被广泛用作模拟风浪过程的驱动场(闻斌等, 2008; 郑崇伟等, 2011)。选取的风场位置见图 1, 研究区常风向为N向、出现频率为20%;次常风向为偏SW向、出现频率为8.5%(图 4a)。风场资料为海平面10 m处的风场数据, 因模型区域较小, 模型中使用空间一致的风场资料, 并插值成时间间隔为1 h的数据。
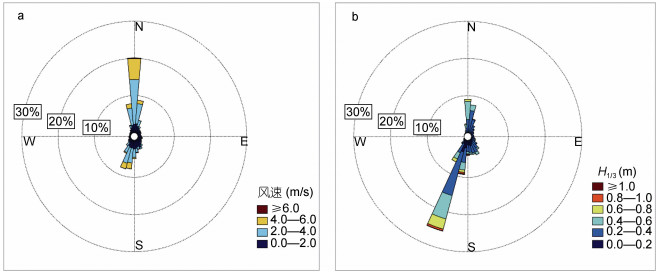 |
| 图 4 研究区风场(a)和边界波浪玫瑰(b)图 Fig. 4 Wind field (a) and wave rose illustration (b) of the study area |
波浪模拟开边界采用MIKE全球波浪模型再分析波浪数据(https://www.metocean- on-demand.com/), 该波浪数据覆盖了全球大部分海域, 时间从1980年至今, 时间间隔为1 h。提取对应边界位置波浪要素(图 1), 研究区外海主波向为SSW向, 出现频率为25%。次波向为N向, 出现频率约10%(图 4b)。
2.3 模型验证为验证研究区海域波浪模型的有效性, 本文利用自然资源部第三海洋研究所的实测资料进行验证, 观测位置为21.78°N, 108.55°E(图 1), 验证段时间为2019年1月15日13:00—2019年1月20日14:00, 时间间隔为1 h。验证结果表明(图 5), 实测有效波高与模拟有效波高的相关系数为85.59%, 均方根误差为6.06%。总体上看, 模拟结果与观测结果较为一致, 两者吻合性较好。仅在2019年1月19—20日, 由于实测有效波高较小(小于0.1 m), 波向较为杂乱, 导致该时间段模型难以验证。
 |
| 图 5 实测波浪与模拟波浪对比 Fig. 5 Comparison of measured and simulated waves 注: a:有效波高; b:主波向 |
为进一步分析茅尾海海域波浪分布情况, 本节基于上述验证后的模型, 对研究区海域进行了为期1 a波浪数值模拟, 对模拟结果进行统计并绘制了该海域年平均、夏季平均和冬季平均有效波高分布图(图 6)。总体来看, 受口门众多岛屿的阻隔, 湾外波浪仅能传播至茅尾海口门处, 波浪在向湾内传播过程中显著减小, 使得茅尾海内的有效波高整体相对较小。
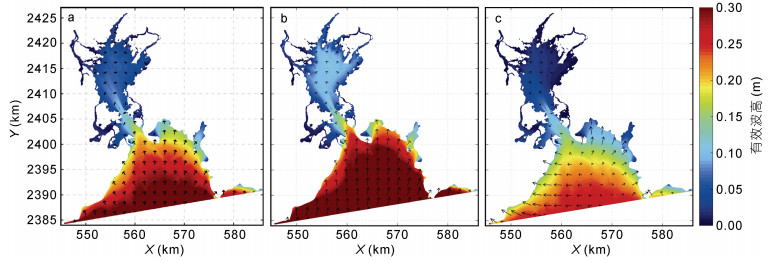 |
| 图 6 茅尾海海域有效波高分布 Fig. 6 Distribution of significant wave height in the Maowei Sea 注: a:年平均; b:夏季平均; c:冬季平均 |
研究区海域全年平均浪向主要集中在偏S向, 年平均波高分布整体上由湾外向湾内依次递减; 湾外由于水深较大且面向开阔的北部湾海域, 受到来自南海的涌浪影响, 有效波高相对较大, 年平均有效波高最高可达0.3 m左右(图 6a); 波浪传播过程中受地形起伏影响, 至茅尾海口门处, 有效波高衰减至0.15—0.2 m, 由于口门狭窄且两侧岛屿众多, 只有有限的波浪能够通过口门传进茅尾海内; 湾内水深较浅且水道较多, 受底摩擦影响, 波高继续减小至0.1 m以下; 海滩前沿波浪以当地风生浪为主, 但由于风区较短产生的波浪能量有限, 因此滩面前沿海域年平均有效波高相对较小, 约0.05 m。
由于茅尾海海域波浪具有季节性变化特点, 故本文选取夏、冬两季有效波高进行对比, 分析茅尾海海域的波浪季节性变化特征。夏季受SW季风影响, 该海域波浪主要来自偏SW向, 湾外平均有效波高约0.4 m(图 6b)。波浪从外海传播至口门外侧由于受到折射、绕射及底摩擦等因素的影响, 有效波高逐渐衰减, 入射波向发生偏转, 斜向射入茅尾海内, 至口门内侧有效波高仅有0.15 m左右。但是由于夏季风速较大, 湾内将产生较大风浪, 滩面前沿海域平均有效波高约0.1 m。冬季该海域风向为偏N向, 但风力较弱(图 4)。湾外依旧主要受外海波浪影响(图 6c), 有效波高最大约0.25 m; 相较于夏季, 湾内波浪明显减小, 平均有效波高不足0.05 m, 波向较为杂乱。
4 讨论 4.1 茅尾海海域波浪能量输入耗散过程波浪在近岸传播过程中, 波能的主要输入项为风能输入, 主要的耗散项为底摩擦耗散、水深变化引起的波浪破碎产生的耗散、白帽引起的耗散以及波与波之间的非线性相互作用引起的能量耗散(SWAN Team, 2006)。波浪能量的输入和耗散过程决定了海域有效波高的时空分布, 本节将通过分析茅尾海波浪能量的输入和耗散过程来探讨茅尾海有效波高分布时空分布差异的机理。本研究区由于水深较浅, 故可忽略四波相互作用引起的能量耗散, 同时由于常年波高较小, 白帽破碎引起的能量损失也较小, 因此本文暂不讨论这两项。
对于波浪能量的输入而言, 风能输入能量时空分布不均, 研究区海域夏季风能输入能量远远大于冬季(图 7)。湾内和湾外能量分布差异较大, 湾外面向开阔海域, 水深较大, 风生浪的过程中风成长受阻较小, 年平均风能输入为7×10–7 W/m2, 夏季和冬季平均风能输入分别为9.2×10–7 W/m2和5.5×10–7 W/m2。湾内形状似布袋, 内宽外窄, 水深不足4 m, 该环境不利于风能的输入, 年平均风能输入仅为3.5×10–7 W/m2, 夏季和冬季平均风能输入分别为7×10–7 W/m2和1×10–7 W/m2。无论湾内还是湾外, 夏季平均风能输入都要比冬季大的多, 因此夏季的平均有效波高要明显高于冬季(图 6)。
 |
| 图 7 风能输入能量分布 Fig. 7 Distribution of wind input energy 注: a:年平均; b:夏季平均; c:冬季平均 |
就波浪能量耗散项来说, 研究区海域总能量耗散分布呈湾外密集, 湾内稀疏的特点(图 8), 其中以底摩擦耗散为主, 该耗散项占比95%以上, 其余两项不足5%。这是因为在浅水海域中, 底摩擦引起的耗散占主导, 水深越浅处底摩阻系数越大, 波浪传播过程中波浪能量就越容易受其影响而发生衰减。湾外水深变化较大, 航道两侧存在相对浅水区, 波浪从外海深水区传播至此处因底摩擦突增而发生严重耗散, 从而形成能量耗散密集区。深水航道至湾内口门处属于深水区, 底摩擦耗散对于波浪能量影响较小, 为能量耗散稀疏区。造成上述差异的主要原因是由于水深变化导致的(王道龙等, 2010)。由于湾内波浪能量远低于湾外, 湾内各耗散项所能引起的波浪耗散量相应降低, 主要集中在水深变化显著区域。海滩前沿海域因水深变化不大, 底摩擦耗散较小, 年平均总耗散能量仅1×10–7 W/m2(图 9)。其余两能量耗散项(浅水变形和三波相互作用)占比极小, 分布零星, 主要发生在湾内外水深变浅区域(图 10—11)。同时可以看出夏季的各耗散量均大于冬季, 底摩擦引起的耗散尤为突出, 这主要是因为该海域夏季能量输入远大于冬季, 使得波浪传播过程中更容易受到底摩擦的影响, 由此引起的耗散量也就相应增多。
 |
| 图 8 总耗散能量分布 Fig. 8 Distribution of total energy dissipation 注: a:年平均; b:夏季平均; c:冬季平均 |
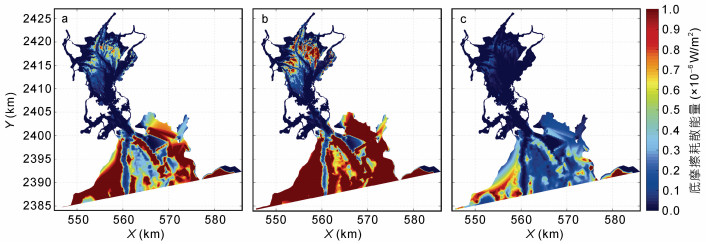 |
| 图 9 底摩擦耗散能量分布 Fig. 9 Distribution of bottom friction dissipation 注: a:年平均; b:夏季平均; c:冬季平均 |
 |
| 图 10 浅水变形耗散能量分布 Fig. 10 Distribution of surf breaking dissipation 注: a:年平均; b:夏季平均; c:冬季平均 |
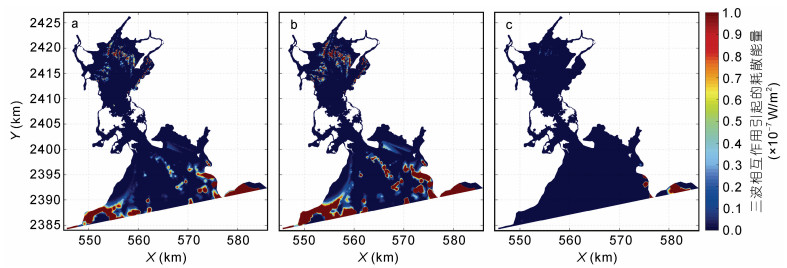 |
| 图 11 三波相互作用引起的耗散能量分布 Fig. 11 Distribution of dissipation due to triads 注: a:年平均; b:夏季平均; c:冬季平均 |
茅尾海海滩修复后, 岸线形态和临近水深均发生了显著变化, 本文采用海滩修复前的岸线水深进一步模拟了海滩修复前的波浪场分布(海滩修复前的岸线水深见图 2a), 通过对比海滩修复前后滩面前沿波浪能量分布变化来研究弱动力环境下的海滩修复工程对低能海滩波浪能量再分配的影响。
为便于分析海滩修复对滩面波浪能量的影响, 在海滩前沿纵向和横向方向上各选取5个点(图 12)来对比有效波高的变化。同时计算表征波浪能量的能流密度Pw(Hagerman, 2003)(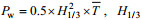
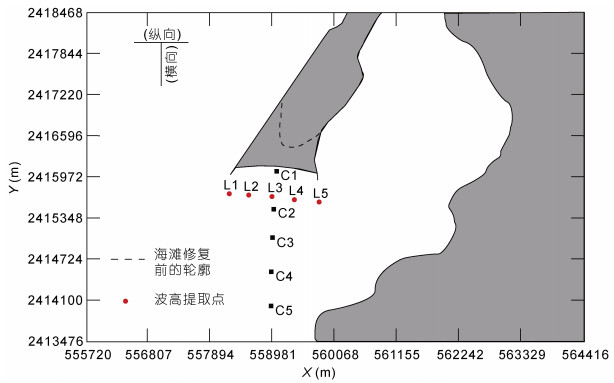 |
| 图 12 横、纵向波高对比点位置 Fig. 12 The location of horizontal and vertical wave height contrast points |
沿纵向断面, 海滩修复前, 有效波高在海滩前沿同一轴线上分布不均(图 13), 海滩西侧略大于东部, 其中西侧L1点波高为0.0430 m, 而东侧L5点为0.0389 m, 呈西向东递减趋势, 这主要是因为该海域常风向为SW向, 西侧的风区更长, 输入能量更多。海滩修复后, 波高依然为西侧大, 东侧小, 但该轴线上的波高均有所增加, L1—L5各点年平均有效波高为0.050 m。有效波高在海滩修复后平均增加23.7%, 波能增加百分比平均高达63.0%(表 1)。
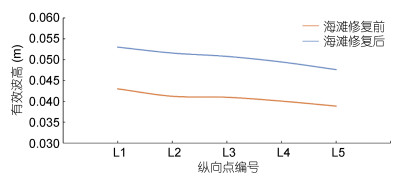 |
| 图 13 纵向有效波高对比 Fig. 13 Comparison in vertical wave height |
| 纵向点 | 海滩修复前 | 海滩修复后 | 增加百分比 | ||||||||
| 有效波高(m) | 平均周期(s) | 有效波高(m) | 平均周期(s) | 有效波高(%) | 波浪能量(%) | ||||||
| L1 | 0.0430 | 0.9745 | 0.0532 | 1.0071 | 23.7 | 58.2 | |||||
| L2 | 0.0412 | 0.9652 | 0.0516 | 1.0363 | 25.1 | 68.2 | |||||
| L3 | 0.0410 | 0.9729 | 0.0508 | 1.0439 | 23.9 | 64.8 | |||||
| L4 | 0.0401 | 0.9741 | 0.0494 | 1.0427 | 23.4 | 63.1 | |||||
| L5 | 0.0389 | 0.9643 | 0.0476 | 1.0328 | 22.5 | 60.7 | |||||
横向上, 海滩修复前后有效波高在滩面前沿变化差异显著(图 14)。修复前由海向陆有效波高整体呈现先逐渐减小后逐渐增加的趋势; 而海滩修复后海滩前沿水深较深且分布均一, 波浪从C5点传至C1点过程中能量损失较小, 故有效波高值近乎相同, 平均约0.052 m。海滩修复后, 横向上最大波高增加约13.9%, 最大波能增加约43.8%;随着离岸距离的增加波浪能量增加百分比逐渐降低, 海滩修复对于波浪能量的增加效果也随之下降(表 2)。由此可知, 海滩修复工程虽能提升波能, 但其影响范围有限, 仅在局部有效, 越靠近海滩前沿, 作用效果越显著。海滩修复后滩面波浪能量的增加主要有两个原因:一是茅尾海海滩修复采用了突出岬头设计, 波浪在向沙滩传播过程中, 波浪发生折射, 波向发生偏转, 逐渐向岬头辅聚, 从而有效提升了滩面前沿波浪能量(水燕等, 2010; 吴月勇等, 2017); 二是水深疏浚降低了底摩擦对波浪的影响, 导致能量耗散减少, 传播至滩面前沿波浪能量相对增加(夏波等, 2006; 付博新等, 2016)。以上分析说明在低能海岸进行海滩修复时, 通过合理的海滩修复设计(如聚能岬头和水深疏浚)能够增加局部海域的波浪能量。
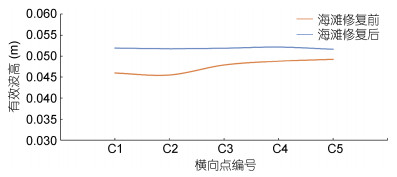 |
| 图 14 横向有效波高对比 Fig. 14 Comparison in horizontal wave height |
| 横向点 | 海滩修复前 | 海滩修复后 | 增加百分比 | ||||||||
| 有效波高(m) | 平均周期(s) | 有效波高(m) | 平均周期(s) | 有效波高(%) | 波浪能量(%) | ||||||
| C1 | 0.0460 | 0.9292 | 0.0519 | 1.0457 | 13.1 | 43.8 | |||||
| C2 | 0.0455 | 0.9865 | 0.0518 | 1.0433 | 13.9 | 37.1 | |||||
| C3 | 0.0479 | 1.0126 | 0.0519 | 1.0379 | 8.5 | 20.6 | |||||
| C4 | 0.0488 | 1.0056 | 0.0522 | 1.0288 | 6.9 | 17.0 | |||||
| C5 | 0.0493 | 0.9901 | 0.0517 | 1.0143 | 4.9 | 12.6 | |||||
本文基于SWAN模型对茅尾海海域波浪场进行了为期1 a的数值模拟, 通过与实测数据进行对比, 验证了模型的可靠性。根据模型输出结果分析了正常天气条件下研究区海域波浪场时空分布特征, 讨论了该海域波浪能量的输入耗散过程, 以及海滩修复对波浪能量空间分布的影响。得到如下结论:
(1) 研究区海域全年平均有效波高较小且季节性变化明显, 夏季有效波高明显大于冬季, 夏季波浪以偏SW向浪为主, 冬季波向分布杂乱。湾内外波浪分布不均, 湾外波高约0.2—0.4 m, 波浪由于受到口门处众多岛屿的阻隔, 难以传播进湾内, 湾内主要以风生浪为主, 湾内波高仅约0.05—0.15 m。
(2) 研究区海域全年能量耗散过程主要以底摩擦引起的波浪能量耗散为主, 其余耗散项占比极小, 可忽略不计。夏季波能输入量和耗散量均大于冬季, 波能耗散在空间上分布不均, 存在波能耗散密集区和稀疏区, 造成此差异的主要原因是由于水深变化导致的。
(3) 海滩修复后滩面前沿纵向轴线上分布点波高平均增加23.7%, 波能增加63.0%;横向轴线上分布点波高增加值随离岸距离变大而逐渐减小, 最大波高增加百分比为13.9%, 最大波能增加百分比为43.8%。波浪能量的增加与突出岬头引起的波浪能量辅聚以及水深疏浚导致的能量耗散减少有关。由此说明在低能海岸进行海滩修复是可行的, 可通过采取清淤疏浚、设计聚能岬头等手段来有效提升局部区域波浪能量。
科学的海滩修复设计对于低能海滩局部海域波浪能量有较为明显的提升效果, 但实际海滩修复工程中波浪能量的再分配程度和多种因素有关, 如岬头突出程度、修复海滩滩面坡度等。具体的波浪能量增强效果和各影响因素之间的非线性关系需通过理想数值模型试验开展更深入研究。同时需要指出, 本研究模型计算时未考虑潮汐过程对波浪的影响, 虽然不影响本研究的主要结论, 但为了提高近岸波浪数值模拟的精度, 今后应进一步开展波流耦合的研究。
王道龙, 华锋, 江志辉. 2010. SWAN近岸海浪模式在辽东湾的应用. 海洋科学进展, 28(3): 285-291 DOI:10.3969/j.issn.1671-6647.2010.03.002 |
水燕, 荣传亚, 王震. 2010. 天津临港工业区开挖航道对港外波浪传播的影响. 水运工程, (9): 31-35 DOI:10.3969/j.issn.1002-4972.2010.09.007 |
付博新, 刘林. 2016. 漳州南太武海滩泥化综合整治. 水运工程, (10): 50-56 DOI:10.3969/j.issn.1002-4972.2016.10.010 |
朱君, 蔡锋, 戚洪帅, 等. 2017. 基于数值模拟的厦门湾波浪特征研究. 应用海洋学学报, 36(3): 341-348 DOI:10.3969/J.ISSN.2095-4972.2017.03.006 |
刘劲, 官志鑫, 邓斌, 等. 2012. 铁山湾海域风浪数值模拟研究. 交通科学与工程, 28(2): 84-89, 106 DOI:10.3969/j.issn.1674-599X.2012.02.014 |
李树华, 黎广钊. 1993. 中国海湾志(第十二分册·广西海湾). 北京: 海洋出版社, 144
|
吴良. 2013. 钦州港发展港航物流业的思路及对策措施. 中国港口, (4): 47-49 DOI:10.3969/j.issn.1006-124X.2013.04.031 |
吴月勇, 陈国平, 高晨晨, 等. 2017. 航道开挖对波浪传播影响的试验研究. 水运工程, (5): 92-97 DOI:10.3969/j.issn.1002-4972.2017.05.017 |
邱文博, 张永合, 胡轶群, 等. 2019. 珠江口附近海域波浪场的数值计算与特征分析. 海洋湖沼通报, (4): 14-21 |
张宏伟, 康海贵. 2008. SWAN波浪模型在黄河三角洲海域的应用. 水运工程, (12): 24-28 DOI:10.3969/j.issn.1002-4972.2008.12.007 |
郑崇伟, 郑宇艳, 陈洪春. 2011. 基于SWAN模式的近10年南海北部波浪能资源研究. 亚热带资源与环境学报, 6(2): 54-59 DOI:10.3969/j.issn.1673-7105.2011.02.010 |
闻斌, 汪鹏, 万雷, 等. 2008. 中国近海海域台风浪模拟试验. 海洋通报, 27(3): 1-6 DOI:10.3969/j.issn.1001-6392.2008.03.001 |
赵桂侠, 张晨, 张赫, 等. 2017. 人工岛布置方式对周围海域水动力及水交换影响研究. 水力发电学报, (2): 18-28 |
夏波, 张庆河, 杨华. 2006. 水动力时空变化对近岸风浪演化的影响——以渤海湾西南岸为例. 海洋通报, 25(5): 1-8 |
郭雅琼, 马进荣, 邹国良, 等. 2016. 钦州湾湾口填海对茅尾海水交换能力的影响. 水运工程, (6): 84-92, 124 |
滕陈轲敏, 岳显昌, 吴雄斌, 等. 2019. 风场对SWAN模式在台湾海峡后报结果的影响. 海洋学报, 41(5): 59-69 |
Booij N, Ris R C, Holthuijsen L H, 1999. A third-generation wave model for coastal regions:1. Model description and validation. Journal of Geophysical Research:Oceans, 104(C4): 7649-7666 |
Daly C J, Bryan K R, Winter C, 2014. Wave energy distribution and morphological development in and around the shadow zone of an embayed beach. Coastal Engineering, 93: 40-54 |
Hagerman G, 2003. Guidelines for preliminary estimation of power production by offshore wave energy devices. USA: Electric Power Research Institute. http://oceanenergy.epri.com/attachments/wave/reports/001_wec_power_production.pdf
|
Jackson N L, Nordstrom K F, Eliot I et al, 2002. 'Low energy' sandy beaches in marine and estuarine environments:a review. Geomorphology, 48(1-3): 147-162 |
Kanamitsu M, Ebisuzaki W, Woollen J et al, 2002. NCEP-DOE AMIP-Ⅱ reanalysis (R-2). Bulletin of the American Meteorological Society, 83(11): 1631-1644 |
Mirzaei A, Tangang F, Juneng L, 2014. Wave energy potential along the east coast of Peninsular Malaysia. Energy, 68: 722-734 |
Pranzini E, Rossi L, Lami G et al, 2018. Reshaping beach morphology by modifying offshore breakwaters. Ocean & Coastal Management, 154: 168-177 |
Ris R C, Holthuijsen L H, Booij N, 1999. A third-generation wave model for coastal regions:2. Verification. Journal of Geophysical Research:Oceans, 104(C4): 7667-7681 |
Rusu E, Soares C G, 2009. Numerical modelling to estimate the spatial distribution of the wave energy in the Portuguese nearshore. Renewable Energy, 34(6): 1501-1516 |
SWAN Team, 2006. SWAN User Manual. Delft: Delft University of Technology, 9-94
|
Wang X Y, Liu Y, Liang B C, 2018. Analysis of oblique wave interaction with a comb-type caisson breakwater. Journal of Ocean University of China, 17(2): 281-290 |
Zhu J, Cai F, Shi F Y et al, 2019. Beach response to breakwater layouts of drainage pipe outlets during beach nourishment. Estuarine, Coastal and Shelf Science, 228: 106354 |
 2021, Vol. 52
2021, Vol. 52


