中国海洋湖沼学会主办。
文章信息
- 贺芊菡, 孙翁杰, 刘必林, 孔祥洪, 林龙山. 2021.
- HE Qian-Han, SUN Weng-Jie, LIU Bi-Lin, KONG Xiang-Hong, LIN Long-Shan. 2021.
- 基于计算机视觉的头足类角质颚特征研究Ⅱ:形态学参数测量
- MORPHOLOGICAL STUDY OF CEPHALOPOD BEAK BASED ON COMPUTER VISION Ⅱ: MORPHOLOGICAL PARAMETER MEASUREMENT
- 海洋与湖沼, 52(1): 252-259
- Oceanologia et Limnologia Sinica, 52(1): 252-259.
- http://dx.doi.org/10.11693/hyhz20200300075
文章历史
-
收稿日期:2020-03-15
收修改稿日期:2020-06-26
2. 上海海洋大学信息学院 上海 201306;
3. 大洋渔业资源可持续开发教育部重点实验室 上海 201306;
4. 国家远洋渔业工程技术研究中心 上海海洋大学 上海 201306;
5. 农业农村部大洋渔业开发重点实验室 上海 201306;
6. 农业农村部大洋渔业资源环境科学观测实验站 上海 201306;
7. 自然资源部第三海洋研究所 厦门 361005
2. College of Information Technology, Shanghai Ocean University, Shanghai 201306, China;
3. The Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China;
4. National Distant-water Fisheries Engineering Research Center, Shanghai Ocean University, Shanghai 201306, China;
5. Key Laboratory of Oceanic Fisheries Exploration, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
6. Scientific Observing and Experimental Station of Oceanic Fishery Resources, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
7. Third Institute of Oceanography, Ministry of Natural Resources, Xiamen 361005, China
头足类角质颚形态结构稳定、耐腐蚀、储藏信息丰富(刘必林等, 2009), 广泛用于种群判别、种类鉴定、摄食生态等方面研究(刘必林等, 2015, 2016; Liu et al, 2019; 林静远等, 2020)。基于游标卡尺的手动径向测量法是获取角质颚形态参数的传统方法(方舟等, 2014; 陈楠桦等, 2018), 而利用计算机视觉进行角质颚形态参数测定是一种新方法, 具有准确、快捷方便的特性。为了避免人为测量造成的误差, 提高研究耳石日轮的准确性, 国外已有学者研究开发了耳石日轮自动识别和分析程序(Fowler, 1989; Rypel, 2008), 但是对于角质颚的相关研究在国内外却鲜有报道。文章根据角质颚三视图获取的角质颚特征点及空间坐标系从计算机视觉角度估算角质颚形态学参数, 并与传统的方法进行比较, 以评估基于计算机视觉测量角质形态的准确性、优越性, 为头足类角质颚参数的测量提供新方法。
1 材料与方法 1.1 材料实验样本为2019年1—2月在印度洋海域进行渔业资源调查时所获得的10尾个体大小相近的鸢乌贼Sthenoteuthis oualaniensis, 采集海域为61°02′E—61°35′E, 17°04′N—17°18′N。样本经冷冻保存后带回实验室提取角质颚并进行形态学测定。
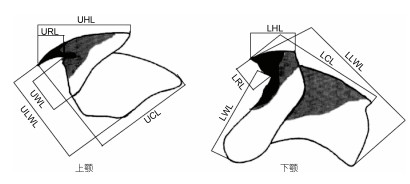
1.2 角质颚的手动测量利用游标卡尺对角质颚wwwwww形态参数进行手动测量(方舟等, 2014)(图 1):上头盖长(upper hood length, UHL)、上脊突长(upper crest length, UCL)、上喙长(upper rostrum length, URL)、上翼长(upper wing length, UWL)、上侧壁长(upper lateral wall length, ULWL); 以及下头盖长(lower hood length, LHL)、下脊突长(lower crest length, LCL)、下喙长(lower rostrum length, LRL)、下翼长(lower wing length, LWL)、下侧壁长(lower lateral wall length, LLWL)。游标卡尺的精度为0.02 mm。每个角质颚样本分别重复测量十次进行分析。
1.3 角质颚计算机视觉测量(1) 利用自制拍摄装置对每个角质颚进行三视图获取, 对所得三视图进行轮廓的提取, 分别得到上、下颚三视图的边缘轮廓图。
(2) 根据得到的边缘轮廓图提取上、下颚的特征点(薛延学等, 2004), 获取上、下颚各10个特征点位置及其空间坐标。
(3) 依据空间坐标计算空间距离(徐阳, 2019), 获取角质颚各形态学参数, 计算机精度与像素精度和亚像素有关, 本文计算机精度为0.001 mm。
(4) 每个角质颚样本调整位置和角度拍摄十组不同三视图重复步骤(2)、(3)。
(5) 十个角质颚样本重复以上步骤。
以上步骤均通过MATLAB软件编程完成。
1.4 数据分析(1) 异常值检验。采用格拉布斯检验对以上两种方法得到的每个角质颚样本形态学参数进行正态分布异常值检验, 剔除异常值, 其计算公式如下(潘仁瑾, 1996):
 (1)
(1)式中, xi是每个样品每次测定值, x是每个样本十次测定值的算术平均值, S为样本标准差, 显著水平为0.05。
(2) 准确度计算。利用绝对误差e和相对误差er比较两种方法测量值的准确度, 计算公式如下(钱政等, 2008):
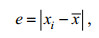 (2)
(2)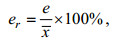 (3)
(3)式中, xi是各样品每次测定值, x是每个样本十次测定值的算术平均值。
为了方便比较两种方法的测量结果, 本研究采取平均绝对误差e和平均相对误差er进行分析, 计算公式如下:
 (4)
(4)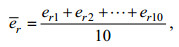 (5)
(5)式中, e1, e2, …, e10表示每个样本每次测量结果的绝对误差, er1, er2, …, er10表示每个样本每次测量结果的相对误差。
绝对误差是反映测量值偏离真值的大小, 误差单位和测量值单位相同, 绝对误差越小表明测量值偏离真值越少, 准确度越高(黄红珍, 2003)。而相对误差更能反映测量的可信程度, 表明测量值与准确值的逼近程度, 代表绝对误差在真值中所占的百分率, 本研究中采用相对误差为5%的标准进行评价, 相对误差越小则代表测量值偏离真值越少, 准确度越高(孙炳全, 1998)。
(3) 精密度计算。利用标准差S和离散系数C.V比较两种方法测量值的精密度, 计算公式如下(成正维, 2004; 王超, 2010):
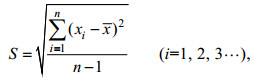 (6)
(6) (7)
(7)式中, xi为各样品的每次测量值, n为样本容量, x为每个样本十次测量结果的算术平均值, S为样本标准差。
标准差反映测量值的离散程度, 与测量值单位相同, 标准差越小, 表示数据越聚集于真实值附近, 精密度越高, 反之标准差越大则表示数据越分散, 精密度越小; 离散系数越大, 离散程度越大, 表明数据的平均数代表性差, 即数据远离平均值, 精密度较低; 反之则表示离散程度越小, 数据的平均数代表性高, 精密度较高(马立富, 2005)。
2 结果 2.1 格拉布斯检验格拉布斯检验结果表明, 手动测量与计算机视觉测量的7号角质颚样本数据TUHL, UCL > T表, 故而判断7号角质颚样本数据属于异常数据, 将其剔除(表 1, 表 2)。
| 序号 | UHL | UCL | URL | ULWL | UWL | LHL | LCL | LRL | LLWL | LWL |
| 1 | 0.12 | 0.34 | 1.85 | 2.26 | 0.15 | 0.08 | 0.44 | 0.03 | 0.06 | 1.18 |
| 2 | 0.19 | 0.30 | 0.06 | 1.46 | 0.46 | 1.21 | 0.87 | 0.85 | 0.01 | 0.90 |
| 3 | 0.13 | 0.91 | 0.87 | 0.34 | 0.23 | 0.64 | 0.62 | 1.18 | 0.90 | 0.35 |
| 4 | 0.28 | 0.04 | 0.84 | 0.04 | 0.79 | 0.18 | 0.48 | 0.78 | 0.66 | 0.15 |
| 5 | 0.97 | 1.02 | 0.63 | 0.72 | 0.76 | 0.44 | 1.05 | 0.77 | 1.92 | 1.15 |
| 6 | 0.82 | 0.40 | 0.26 | 0.30 | 0.67 | 0.25 | 0.23 | 0.85 | 0.68 | 0.02 |
| 7 | 2.44 | 2.36 | 1.42 | 0.92 | 1.88 | 1.64 | 2.20 | 1.95 | 1.76 | 1.96 |
| 8 | 1.04 | 0.90 | 0.82 | 0.33 | 1.39 | 1.11 | 0.92 | 0.89 | 0.11 | 0.35 |
| 9 | 0.33 | 0.46 | 0.61 | 0.04 | 0.28 | 1.46 | 0.72 | 0.42 | 0.36 | 0.66 |
| 10 | 0.22 | 0.32 | 0.72 | 0.03 | 1.21 | 0.83 | 0.12 | 0.34 | 0.53 | 0.92 |
| 序号 | UHL | UCL | URL | ULWL | UWL | LHL | LCL | LRL | LLWL | LWL |
| 1 | 0.12 | 0.33 | 0.53 | 1.68 | 0.15 | 0.68 | 0.49 | 0.16 | 0.64 | 0.27 |
| 2 | 0.07 | 0.06 | 0.04 | 1.17 | 0.49 | 0.46 | 0.54 | 0.02 | 0.68 | 2.34 |
| 3 | 0.36 | 0.68 | 0.07 | 0.64 | 0.50 | 0.41 | 0.95 | 1.56 | 1.13 | 0.20 |
| 4 | 0.23 | 0.20 | 0.45 | 0.07 | 0.25 | 0.06 | 0.23 | 0.16 | 0.27 | 0.55 |
| 5 | 0.88 | 0.81 | 1.36 | 0.88 | 0.83 | 0.30 | 0.44 | 0.94 | 0.15 | 0.70 |
| 6 | 0.21 | 0.09 | 0.58 | 0.40 | 2.07 | 0.06 | 0.32 | 1.18 | 0.91 | 1.05 |
| 7 | 2.67 | 2.71 | 2.11 | 1.79 | 1.69 | 2.26 | 1.50 | 1.06 | 1.33 | 0.85 |
| 8 | 0.86 | 0.51 | 0.72 | 0.35 | 0.12 | 1.63 | 1.76 | 1.64 | 0.97 | 0.65 |
| 9 | 0.16 | 0.13 | 0.60 | 0.21 | 0.41 | 0.48 | 1.21 | 0.47 | 0.27 | 0.37 |
| 10 | 0.21 | 0.25 | 0.96 | 0.14 | 0.57 | 0.02 | 0.58 | 0.36 | 1.76 | 0.39 |
将每个样本分别进行了十次手动测量和计算机视觉测量的角质颚形态学参数数据的算术平均值进行列表, 结果如表 3、表 4所示。
| 参数(mm) | UHL | UCL | URL | ULWL | UWL | LHL | LCL | LRL | LLWL | LWL |
| 1 | 19.70 | 25.28 | 9.61 | 26.81 | 6.53 | 5.85 | 12.71 | 6.73 | 17.00 | 12.74 |
| 2 | 19.53 | 23.57 | 7.21 | 12.63 | 6.05 | 4.87 | 10.91 | 6.02 | 16.85 | 9.74 |
| 3 | 19.68 | 22.00 | 5.95 | 16.67 | 6.23 | 6.48 | 11.25 | 5.76 | 14.02 | 10.53 |
| 4 | 20.68 | 24.50 | 5.98 | 17.78 | 5.79 | 6.08 | 12.76 | 7.33 | 18.86 | 10.81 |
| 5 | 17.66 | 21.70 | 6.27 | 15.32 | 5.81 | 5.53 | 10.67 | 6.09 | 10.88 | 9.38 |
| 6 | 18.02 | 23.32 | 6.77 | 16.84 | 6.94 | 5.70 | 11.78 | 7.38 | 14.69 | 11.08 |
| 7 | 17.50 | 22.02 | 6.01 | 16.71 | 5.32 | 4.95 | 10.85 | 5.99 | 17.15 | 10.53 |
| 8 | 20.79 | 25.58 | 6.29 | 18.11 | 6.19 | 7.19 | 13.09 | 7.04 | 17.92 | 11.99 |
| 9 | 20.53 | 25.23 | 8.09 | 17.82 | 7.36 | 5.20 | 11.93 | 6.43 | 18.47 | 9.70 |
| 注:表中每个数据是每个样本经过十次测量所得的算术平均值 | ||||||||||
| 参数(mm) | UHL | UCL | URL | ULWL | UWL | LHL | LCL | LRL | LLWL | LWL |
| 1 | 20.152 | 23.115 | 7.235 | 23.245 | 5.780 | 6.198 | 12.686 | 6.276 | 17.611 | 12.231 |
| 2 | 20.295 | 23.869 | 6.663 | 15.529 | 7.027 | 6.298 | 11.686 | 6.078 | 17.512 | 8.449 |
| 3 | 19.450 | 22.133 | 6.705 | 16.976 | 5.107 | 6.321 | 11.294 | 7.696 | 16.420 | 12.123 |
| 4 | 21.224 | 24.635 | 6.079 | 18.507 | 6.573 | 6.543 | 12.437 | 6.267 | 18.508 | 12.642 |
| 5 | 17.884 | 21.760 | 5.009 | 16.322 | 4.462 | 6.651 | 11.782 | 5.141 | 18.811 | 10.814 |
| 6 | 19.885 | 23.799 | 5.920 | 17.610 | 4.085 | 6.540 | 11.898 | 4.893 | 16.956 | 13.354 |
| 7 | 17.949 | 22.594 | 5.766 | 17.766 | 6.326 | 5.768 | 10.516 | 4.424 | 21.539 | 10.885 |
| 8 | 20.026 | 23.672 | 5.903 | 19.288 | 6.886 | 6.732 | 13.375 | 6.584 | 18.514 | 12.370 |
| 9 | 19.878 | 23.341 | 7.744 | 18.311 | 7.194 | 6.521 | 12.768 | 6.476 | 23.469 | 12.407 |
| 注:表中每个数据是每个样本经过十次测量所得的算术平均值 | ||||||||||
将十个样本所测数据都进行平均绝对误差、平均相对误差、标准差以及离散系数的计算, 将1号样本作为案例列出行平均绝对误差、平均相对误差、标准差以离散系数的计算结果如表 5所示, 进行分析。
| 参数 | 手动测量数据 | 计算机视觉测量数据 | |||||||
| 平均绝对误差 (mm) |
平均相对误差 (%) |
标准差 (mm) |
C.V.1 (%) |
平均绝对误差 (mm) |
平均相对误差 (%) |
标准差 (mm) |
C.V.2 (%) |
||
| UHL | 0.34 | 1.64 | 0.44 | 2.09 | 0.262 | 1.291 | 0.329 | 1.621 | |
| UCL | 0.27 | 1.08 | 0.34 | 1.39 | 0.355 | 1.482 | 0.448 | 1.871 | |
| URL | 0.18 | 2.75 | 0.23 | 3.59 | 0.085 | 1.386 | 0.109 | 1.777 | |
| ULWL | 0.44 | 2.57 | 0.63 | 3.71 | 0.324 | 1.693 | 0.379 | 1.979 | |
| UWL | 0.17 | 2.80 | 0.24 | 4.09 | 0.106 | 1.847 | 0.139 | 2.419 | |
| LHL | 0.18 | 3.39 | 0.22 | 4.12 | 0.100 | 1.807 | 0.127 | 2.300 | |
| LCL | 0.43 | 2.43 | 0.53 | 2.97 | 0.111 | 2.377 | 0.156 | 0.855 | |
| LRL | 0.21 | 3.75 | 0.27 | 4.75 | 0.078 | 1.508 | 0.114 | 2.199 | |
| LLWL | 0.44 | 3.64 | 0.51 | 4.22 | 0.159 | 1.255 | 0.200 | 1.585 | |
| LWL | 0.31 | 3.22 | 0.39 | 4.11 | 0.101 | 0.934 | 0.134 | 1.238 | |
| 注:由于两种方法精度不同, 所以测量结果有效数字不同。C.V.1表示手动测量的离散系数, C.V.2表示计算机视觉测量的离散系数 | |||||||||
比较分析显示, 除了形态学参数UCL之外, 其余形态学参数的平均绝对误差和平均相对误差均为计算机视觉测量结果小于手动测量结果(图 2, 图 3), 且分析平均相对误差可知手动测量与计算机视觉测量结果均小于5%(图 3), 因此测量结果均准确可靠, 但计算机视觉测量的角质颚形态学参数结果偏离真值的程度更小, 准确度更高。
 |
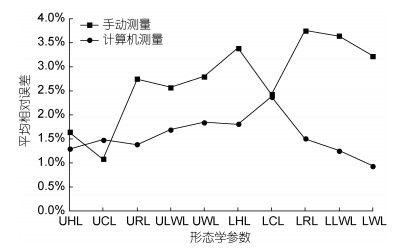
| 图 2 手动测量与计算机视觉测量各特征值的平均绝度误差比较 Fig. 2 Comparison of mean absolute error between manual measurement and computer vision measurement |
 |
| 图 3 手动测量与计算机视觉测量各特征值的平均相对误差 Fig. 3 Comparison of average relative error between manual measurement and computer vision measurement |
比较分析显示, 除了形态学参数UCL之外, 其余形态学参数的标准差和离散系数均为计算机视觉测量结果小于手动测量结果(图 4, 图 5), 表明计算机视觉测量的角质颚形态学参数的结果离散程度更小, 测量结果更加聚集于真实值附近, 精密度更高。
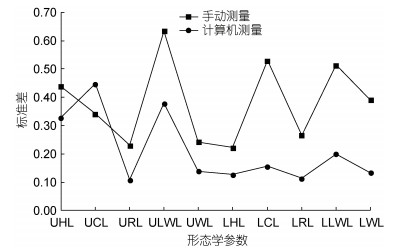 |
| 图 4 手动测量与计算机视觉测量各特征值的标准差比较 Fig. 4 Comparison of standard deviation between manual measurement and computer vision measurement |
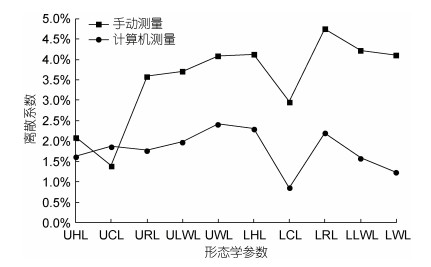 |
| 图 5 手动测量与计算机视觉测量各特征值的离散系数比较 Fig. 5 Comparison of discrete coefficients between manual measurement and computer vision measurement |
准确度是指观测值或估计值与真值的接近程度, 由于任何测定都不可避免的带有误差, 因此通过测定不能获得真值, 只能获得近似真值, 当误差较小时, 多次平行测定的平均值接近于真值(贺仁睦, 2000)。本文也将每个样本进行十次测量的算术平均值作为近似真值进行分析, 通过分析两种方法对每个样本进行十次测量所得的形态学参数的算数平均值(表 3, 表 4)以及平均绝对误差和平均相对误差(表 5)可知, 两种测量方法的算术平均值相差较小, 两种方法的平均相对误差都小于5%, 按照统计学的评价标准(周明昌, 2004), 两种方法的测量结果都是准确可靠的(张红川, 2012)。分析比较两组数据的平均绝对误差(表 5, 图 2)以及平均相对误差(表 5, 图 3)可知, 除形态学参数UCL外, 利用计算机视觉进行角质颚形态学参数的测量结果的平均绝对误差和平均相对误差更小, 计算机视觉测得的数据结果更加逼近真值, 偏离真值的程度更小, 准确度更高(曹毓等, 2011)。
综上所述, 基于计算机视觉和游标卡尺手动测量角质颚形态参数的方法都是准确可行的, 所获取的数据均准确可靠, 可供研究使用(朱朝晖等, 2006), 但是计算机视觉测量所得的角质颚形态学参数的结果偏离真值程度更小, 准确度更高。因此, 建议计算机视觉可以作为一种新的角质颚形态参数测量方法推广运用。
3.2 精密度分析精密度是指在同一条件下进行测定, 多次重复测定值之间的彼此相符合的程度, 往往用标准差以及离散系数来量度。当数据的离散程度越大时, 数据越分散, 数据的标准差和离散系数越大, 精密度越小(McHorney et al, 1992)。分析两种方法测量结果的标准差(表 5, 图 4)以及离散系数(表 5, 图 5), 除形态学参数UCL外, 计算机视觉的测量结果的标准差和离散系数都更小, 表明计算机视觉进行多次重复测定所测的结果更加聚集在真实值附近, 离散程度更小, 精密度更高(赵恒等, 2003; 余少雄, 2016)。
综上所述, 利用计算机视觉进行角质颚形态参数的提取不仅准确可靠, 而且离散程度更小, 所测结果更加聚集于真实值附近, 精密度更高。因此, 将头足类角质颚形态学的研究与计算机视觉相结合不仅是将角质颚的研究变得自动化, 更是提供一种新的更为准确精密的研究方法。
3.3 误差分析研究进行异常值检验时, 7号样本的检验结果为异常数据进行了剔除, 其原因可能由于7号样品的头足类个体与其他样本个体之间差异较大, 导致角质颚样本出现差异(陈子越等, 2019), 故而角质颚形态学参数与其他样本不同。依据算术平均值分析可知, 两种方法所得结果的算术平均值从十分位上开始出现差异, 其原因是手动测量时存在人为误差, 无法准确测量到每一个特征点的位置, 因而使得所测结果与计算机标定各特征点计算的结果出现了差异。形态学参数UCL的平均绝对误差、平均相对误差、标准差和离散系数的计算机视觉测量结果大于手动径向测量结果可能有以下四种原因: (1)畸变:所有依靠光学成像的照相机都会产生一定程度的畸变(贾谊等, 2013)。已经畸变的图进行计算机视觉的测定会造成误差, 导致计算机视觉测量的准确度和精密度降低。(2)透视:由于成像时近大远小的原理, 且角质颚侧壁透明度较高等因素, 拍摄时角质颚的两侧边缘无法重合, 导致两侧边缘错开, 在进行计算机视觉测定时会产生误差。(3)拍摄视角:拍摄角质颚角度不同或者角质颚摆放出现偏差, 会导致获得的三视图错开, 从而产生误差, 降低计算机视觉拍摄的准确度和精密度。(4)特征点位置:由于角质颚侧壁透明度较高且拍摄时上脊突的特征点刚好与载物台面重合, 进行计算机视觉测定时无法区分映像和载物台面, 导致对于形态学参数UCL的提取出现偏差。
综上所述, 计算机视觉测量角质颚形态学参数相较传统手动测量法准确度、精密度更高(王平等, 2003)。但是计算机视觉在进行角质颚形态学参数测量时还存在一些问题, 需要改进编程算法, 使其更加准确精密。
4 结论基于以上分析, 不难看出基于计算机视觉的角质颚形态学参数提取是一种全新的方法, 对于头足类角质颚的研究将更加趋向自动化与信息化, 提取角质颚形态学参数也会变得更加精确、更加科学(郭超, 2017; 帅晓华, 2019)。但是由于编程的不完全成熟, 考虑特征点的选取方面不够完善等, 会促使角质颚形态学参数测量过程中出现一些误差, 造成某些参数的精密度不够高, 离散程度偏大。因此, 在今后的研究中还需要进一步完善改进编程算法, 使得测量的角质颚形态学参数更为准确与精密。此外, 角质颚照片拍摄的清晰度对研究结果也会造成影响。因此, 在利用计算机视觉对角质颚形态学参数进行测量时, 往往还需要保证获得的角质颚图片达到一定的要求, 使得图片噪音较小, 以便准确的选定特征点。文章的研究表明了计算机视觉在头足类角质颚中研究前景可期, 期待未来会有越来越多的学者将计算机视觉与角质颚的研究相结合, 这不仅可以提高研究结果的准确性与精密性, 而且还可以大大缩短研究所需的时间。
马立富. 2005. 试析影响因子的精确性和模糊性. 淮北煤炭师范学院学报, 26(3): 73-75 DOI:10.3969/j.issn.2095-0691.2005.03.021 |
王平, 李吉芳, 于小平. 2003. 精密度、准确度、精确度的分析. 广西物理, 24(3): 37-38 |
王超. 2010. 离散系数的一种改进方法. 统计与咨询, (3): 49-50 |
方舟, 陈新军, 陆化杰, 等. 2014. 头足类角质颚研究进展Ⅰ——形态、结构与生长. 海洋渔业, 36(1): 78-89 DOI:10.3969/j.issn.1004-2490.2014.01.013 |
帅晓华. 2019. 基于计算机视觉的茶叶色泽检测研究. 农机化研究, 41(6): 209-213 DOI:10.3969/j.issn.1003-188X.2019.06.039 |
成正维. 2004. 一元线性问题中的实验标准差. 大学物理, 23(6): 35-36, 53 |
朱朝晖, 李涛. 2006. 测向定位技术准确度及误差校正. 信息技术, 15(8): 89-90, 95 |
刘必林, 陈新军. 2009. 头足类角质颚的研究进展. 水产学报, 33(1): 157-164 |
刘必林, 陈新军, 方舟, 等. 2015. 基于角质颚长度的头足类种类判别. 海洋与湖沼, 46(6): 1365-1372 |
刘必林, 林静远, 陈新军, 等. 2016. 西北太平洋柔鱼角质颚微结构及其生长纹周期性研究. 海洋与湖沼, 47(4): 821-827 |
孙炳全. 1998. 大学物理实验教学中不确定度的评定方法. 物理实验, 18(6): 26-27 |
余少雄. 2016. 实验室生化检测系统精密度评价. 国际检验医学杂志, 37(11): 1541-1542 |
张红川, 2012.电能质量测量准确度影响因素分析及实验研究.河北: 华北电力大学硕士学位论文, 8-10
|
陈子越, 陆化杰, 童玉和, 等. 2019. 个体差异对西沙群岛海域鸢乌贼角质颚外部形态变化的影响. 水产学报, 43(12): 2501-2510 |
陈楠桦, 梁仁杰, 白义, 等. 2018. 基于几何形态测量学的四种滨螺形态差异与系统发生关系研究. 海洋与湖沼, 49(6): 1365-1374 |
林静远, 刘必林, 金宵. 2020. 头足类角质颚的色素沉积机制. 水产学报, 44(5): 777-783 |
周明昌. 2004. 检测与计量. 北京: 化学工业出版社, 53
|
赵恒, 杨万海. 2003. 模糊K-Modes聚类精确度分析. 计算机工程, 29(12): 27-28, 175 |
贺仁睦. 2000. 电力系统动态仿真准确度的探究. 电网技术, 24(12): 1-4 |
贾谊, 许建辉. 2013. 平面定机拍摄中镜头畸变对动作技术分析结果的影响及修正. 河北体育学院学报, 27(2): 83-87, 92 |
钱政, 王中宇, 刘桂礼. 2008. 测试误差分析与数据处理. 北京: 北京航空航天大学出版社, 46
|
徐阳, 2019.基于计算机视觉的桥梁结构局部损伤识别方法研究.哈尔滨: 哈尔滨工业大学博士学位论文, 9-11
|
郭超, 2017.柔性鱼体目标检测与跟踪技术研究.哈尔滨: 哈尔滨工业大学硕士学位论文, 7-9
|
黄红珍. 2003. 近似数简单运算的误差分析. 计量与测试技术, 30(1): 30-31 |
曹毓, 冯莹, 雷兵, 等. 2011. 逆透视映射公式的误差分析及准确度验证. 光子学报, 40(12): 1833-1838 |
雷晓平. 2011. 浅谈可疑数据的取舍方法——格拉布斯法. 河南建材, 12(2): 163 |
潘仁瑾. 1996. 单次测量值的检验采用格拉布斯准则检验论证. 宇航计测技术, 16(3): 12-14 |
薛延学, 张二虎, 吴学毅. 2004. 基于计算机视觉的印刷包装品缺陷检测系统. 包装工程, 25(5): 185-187 |
Fowler A J, 1989. Description, interpretation and use of the microstructure of otoliths from juvenile butterflyfishes (Family Chaetodontidae). Marine Biology, 102(2): 167-181 |
Liu B L, Jin Y, Chen X J et al, 2019. High individual variability in beak stable isotopes of jumbo squid off Peruvian Exclusive Economic Zone (EEZ) waters in the analysis of migratory and foraging ecology. Journal of Ocean University of China, 18(1): 232-238 |
McHorney C A, Ware Jr J E, Rogers W et al, 1992. The validity and relative precision of MOS short-and long-form health status scales and Dartmouth COOP charts. Results from the medical outcomes study. Medical Care, 30(5 Suppl): MS253-MS265 |
Rypel A L, 2008. An inexpensive image analysis system for fish otoliths. North American Journal of Fisheries Management, 28(1): 193-197 |
 2021, Vol. 52
2021, Vol. 52