中国海洋湖沼学会主办。
文章信息
- 叶潇潇, 游景皓, 宋金宝. 2021.
- YE Xiao-Xiao, YOU Jing-Hao, SONG Jin-Bao. 2021.
- 实验室造波条件对内孤立波发展影响的直接数值模拟
- DIRECT NUMERICAL SIMULATION OF THE EFFECT OF LABORATORY WAVE-MAKING CONDITIONS ON THE DEVELOPMENT INTERNAL SOLITARY WAVES
- 海洋与湖沼, 52(3): 573-583
- Oceanologia et Limnologia Sinica, 52(3): 573-583.
- http://dx.doi.org/10.11693/hyhz20200600157
文章历史
-
收稿日期:2020-06-01
收修改稿日期:2020-07-13
2. 四川大学水力学与山区河流开发保护国家重点实验室 成都 610065
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China
内波是发生在密度稳定分层的流体内部的一种波动, 而内孤立波是一种特殊的内波。内孤立波频繁地发生在海洋中, 在世界海洋的许多大陆边缘斜坡上都曾观测到内孤立波痕迹(Filonov et al, 2000; Azevedo et al, 2006; Vázquez et al, 2008)。内孤立波具有强垂向流和水平流, 受大陆或近岸斜坡影响的内孤立波会浅化、破碎, 并造成强烈的湍流混合(Forgia et al, 2018), 进而影响温度(Leichter et al, 1996; Davis et al, 2011; Walter et al, 2012)、氧气和营养物质的空间分布(Leichter et al, 1996; Omand et al, 2011; Walter et al, 2014)。
内孤立波对于结构物具有潜在的破坏性。在非线性效应和频散效应的平衡作用下, 在传播过程中, 内孤立波的波形和速度可以保持数百公里不变(Grue et al, 2000; Grimshaw et al, 2002)。在中国南海(South China Sea, SCS)曾记录到振幅最大为170 m的内孤立波, 且上、下层之间的水平速度差超过3.4 m/s (Warn-Varnas et al, 2010)。正是由于内孤立波具有振幅尺度大、能量集中的特点, 其引起流场和密度场的迅速变化可能对海洋工程的结构物以及水下潜体造成严重威胁(邹丽等, 2020)。由此可见, 内孤立波研究在海洋工程、海洋观测等方面具有十分重要的应用意义。因此研究不同造波条件下生成的内孤立波运动的流场特征具有重要的学术意义和实际应用价值。
在Chen等(2007)的实验室实验中, 内孤立波是在水闸两侧流体界面高度不同的坍塌机制下生成的(由水闸划分为左侧环境区和右侧扰动区)。目前在内孤立波的实验室研究过程中, 在分层水体制取方面, 要配制出质量高的稳定的分层水体, 需保证流入水槽流体运动的平稳性及均匀性, 使得配制过程要耗用很长的时间, 而且试验成功率低, 需经多次重新配制才能达到要求(徐鑫哲, 2012)。此外, 由实验仪器收集到的信息也往往比较有限, 即使使用了高频相机和超声波测试仪, 依然难以得出流场内部精确的密度、涡度的时空变化。
数值模拟是一种可以获得精确的流场内部变化信息的有效方法。对内孤立波的数值模拟研究基本都是从数值求解Navier-Stokes (N-S)方程入手, 根据求解N-S方程的方法可进一步分为: (1)直接求解N-S方程(直接数值模拟方法, direct numerical simulation, DNS); (2)求解雷诺平均的N-S方程(reynolds-averaged Navier-Stokes simulation, RANS) (Vlasenko et al, 2002; Lin et al, 2012); (3)求解空间滤波的N-S方程(大涡数值模拟法, large-eddy simulation, LES) (沈治等, 2009)。然而, RANS的模拟方法只能提供湍流的平均信息, 在模拟结果中, 上凸型内孤立波基本不呈现涡旋结构, 这与实验室实验结果不符。LES的模拟方法适用于研究运动尺度较大的湍流。目前有关直接数值模拟方法的内孤立波研究相对较少, 理论上来说, 直接数值模拟方法能够更好地模拟出内孤立波发展和传播过程中的细微结构, 如因断裂形成的湍流涡旋结构。
本文参考Chen等(2007)重力塌陷激发内孤立波的水槽实验, 构建了重力塌陷激发内孤立波的数学模型。根据Druzhinin等(2015)的密度跃迁公式计算初始密度场。以Boussinesq假定下的N-S方程组及盐分对流扩散方程作为控制方程, 并采用有限差分法进行离散, 实现了重力塌陷造波方式下形成的内孤立波运动的数值模拟。通过与Chen等(2007)的实验结果对比, 验证了本文方法的有效性, 而后本文进一步与Lin等(2012)对比不同数值模拟方法下呈现的涡旋结构。之后, 通过改变造波参数, 即流体密度差、上下层水深比和台阶深度(水闸两侧初始密度界面的高度差), 对一系列算例进行数值模拟, 得到流场的密度界面、涡旋结构、涡度等的时空演化结果, 比较不同造波条件对内波后续发展过程中的波型、涡度、水平速度、流场动能和特征波长的影响。
1 数学模型本文参考Chen等(2007)重力崩塌激发内孤立波的水槽实验, 构建了含有斜坡、重流体、轻流体等的数学模型, 如图 1所示。模型设置为: 在H × L的水箱中(H为水箱高度、L为水箱长度), 设置左右两侧不同初始密度界面高度的两层流体, 其中上层流体密度ρ1, 下层流体密度ρ2, 左侧环境区域的上层流体水深H1, 右侧扰动区域的上层流体水深h1, H2、h2为对应的下层流体水深, 其中H1+H2=h1+h2=H, H2=h2-η0, η0为台阶深度。扰动区长度Lp=0.3 m, 斜坡长度Ls=1.882 m。Lw为波长, a为波高。两种流体的运动黏度均为v。计算时的各算例参数设置参见表 1, 时间步长Δt=0.005Δx, 盐分施密特数(salt Schmidt number) Scs为100。
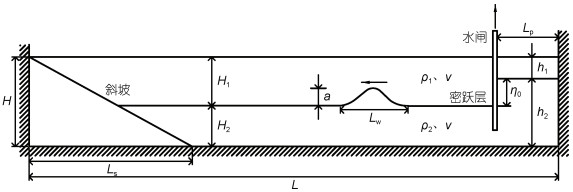 |
| 图 1 模型示意图 Fig. 1 Schematic of the model 注: H: 水箱高度; L: 水箱长度; Ls: 斜坡长度; Lp: 扰动区长度; H1: 左侧环境区域的上层流体水深; H2: 左侧环境区域的下层流体水深; h1: 右侧扰动区域的上层流体水深; h2: 右侧扰动区域的下层流体水深; a: 波高; Lw: 波长; ρ1: 上层流体密度; ρ2: 下层流体密度; v: 流体运动黏度; η0: 台阶深度 |
| 工况编号 | H(m) | L(m) | H1(m) | H2(m) | h1(m) | η0(m) | ρ1(kg/m3) | ρ2(kg/m3) | 计算网格数 | Δx | Re |
| Chen1 | 0.4 | 12 | 0.3 | 0.1 | 0.1 | 0.2 | 999 | 1030 | 3000×100 | 0.02 | 31602 |
| Chen2 | 0.4 | 12 | 0.1 | 0.3 | 0.15 | -0.05 | 999 | 1030 | 3000×100 | 0.01 | 31602 |
| Lin | 0.4 | 6 | 0.1 | 0.3 | 0.05 | 0.05 | 999 | 1030 | 3000×100 | 0.01 | 31602 |
| 工况1 | 0.2 | 3 | 0.16 | 0.04 | 0.12 | 0.04 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 工况2 | 0.2 | 3 | 0.16 | 0.04 | 0.08 | 0.08 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 工况3 | 0.2 | 3 | 0.16 | 0.04 | 0.04 | 0.12 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 工况4 | 0.2 | 3 | 0.14 | 0.06 | 0.10 | 0.04 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 工况5 | 0.2 | 3 | 0.12 | 0.08 | 0.08 | 0.04 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 工况6 | 0.2 | 3 | 0.16 | 0.04 | 0.12 | 0.04 | 999 | 1010 | 1500×100 | 0.01 | 18825 |
| 工况7 | 0.2 | 3 | 0.16 | 0.04 | 0.12 | 0.04 | 999 | 1020 | 1500×100 | 0.01 | 26010 |
| 工况8 | 0.2 | 3 | 0.08 | 0.12 | 0.04 | 0.04 | 999 | 1030 | 1500×100 | 0.01 | 31602 |
| 注: 除Chen1、Chen2外, 均不设置斜坡; H: 水箱高度; L: 水箱长度; H1: 左侧环境区域的上层流体水深; H2: 左侧环境区域的下层流体水深; h1: 右侧扰动区域的上层流体水深; η0: 台阶深度; 2: 上层流体密度; 2: 下层流体密度; Δx: 网格尺寸; Re: 雷诺数(Reynolds number) | |||||||||||
本文以不可压缩N-S方程组(连续性方程及动量守恒方程)和对流扩散方程为控制方程, 三个方程分别为:
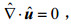 (1)
(1)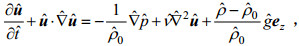 (2)
(2)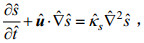 (3)
(3)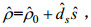 (4)
(4)其中, 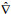
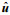
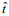
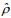
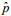
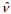
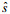
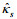
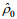
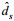
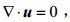 (5)
(5)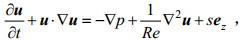 (6)
(6)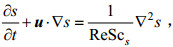 (7)
(7)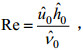 (8)
(8)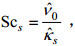 (9)
(9)| 参数名称 | 有量纲形式 | 无量纲形式 |
| 长度 | 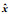 |
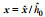 |
| 速度 | 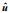 |
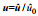 |
| 时间 | 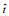 |
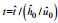 |
| 密度 | 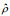 |
 |
| 黏度 | 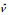 |
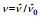 |
| 压力 | 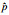 |
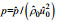 |
| 盐度 | 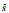 |
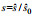 |
| 梯度 | 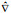 |
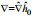 |
注: x=(x, y); u=(u, v); 下标0表示特征物理量, 如特征长度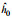 | ||
其中, 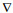
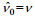
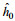
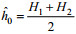
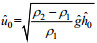
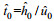
控制方程中的盐分对流扩散方程用迎风紧致差分格式(upwinding combined compact difference, UCCD)离散(Yu et al, 2019)。N-S方程, 利用二阶显式Adams-Bashforth法离散时间项, 二阶迎风格式离散对流项, 以二阶中心差分格式离散黏性扩散项, 压力项通过超松弛迭代法(successive over relaxation method, SOR)求解(Yu et al, 2019)。
1.2 初始及边界条件本文采用了密跃层假设(Druzhinin et al, 2015), 认为流体间的密度是按双曲正切函数变化。相对于简单的线性分层, 双曲正切函数具有阶跃突变的特点, 这与实际海洋中的密跃情况相接近。本文设置计算流体的初始盐度分布如下:
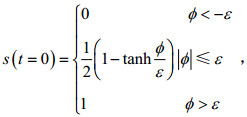 (10)
(10)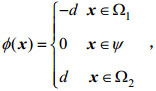 (11)
(11)式中, s(t=0)为初始盐度; ϕ为网格点到密跃层中间界面ψ的符号距离函数(王德军等, 2003); Ω1、Ω2分别为上层流体和下层流体; x=(x, y)为网格点; d为任意网格点到密跃层中间界面的最短距离, 最短距离沿法线方向; ε为密跃层厚度。初始密度可通过式(12)计算:
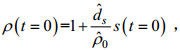 (12)
(12)式中, ρ(t=0)为初始密度, 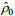
对于速度边界条件, 在顶底及两侧界面处均使用了自由滑移边界条件(free-slip boundary condition)。以顶部为例:
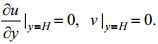 (13)
(13)对于盐度边界条件, 在界面处均使用了无通量条件。
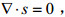 (14)
(14)采用浸入边界法, 求解斜坡边界处的速度及盐分浓度变化。通过在动量方程中添加虚拟力F, 用以反映不规则地形对流体的作用力:
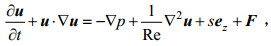 (15)
(15)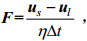 (16)
(16)其中, us为固体速度, us=0, ul为流体速度, η为固体在网格单元中的体积分数, Δt为模拟时的迭代时间间隔。
2 模型检验为检验本文数值方法的有效性, 将本文模拟结果和前人的实验(Chen et al, 2007)及模拟结果(Lin et al, 2012)进行比较。
本文与Chen等(2007)实验结果进行了两方面的比对, 分别为界面波形的演化过程和定点波动时间序列。图 2为界面波形的演化过程, 图 2a为Chen等(2007)实验的结果, 图 2b为本文的模拟结果。由图 2可以看出, 实验与模拟方式之间最明显的差异是: 在实验水槽内填充阶段引入了厚度较小的水闸, 以便在左右两侧流体区域之间产生不同的分层。实验中水闸的去除会引起垂直剪切应力, 并将力传递到与其直接接触的流体。但考虑到水闸的厚度较小, 其所产生的干扰应是相当有限的。图 2证实, 在去除水闸不久后, 扰动区附近模拟得到的密度界面便与通过实验观察到的染料的空间分布非常吻合: 在无量纲时间t=3.5, 最初放置在扰动区内的较重的流体开始呈现出内孤立波的典型形状; 在t=6.22至t=10.5, 内孤立波向左传播, 同时保留其形状; 在t=6.22至t=15, 在实验和模拟中, 均存在界面尾随内波。
 |
| 图 2 界面波形的演化过程 Fig. 2 Evolution of the interface waveforms 注: a: Chen等(2007)实验结果; b: 本文模拟结果(表 1中工况Chen1, 实际距离10.75—12 m), t表示无量纲时间 |
总体而言, 本文的直接数值模拟结果与Chen等(2007)实验结果所得的流场界面波形具有较好的一致性。
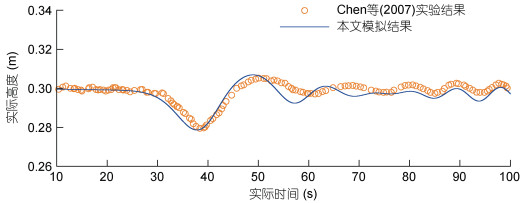
图 3为定点波动时间序列对比图, 参照实验选取定点为(8.7 m, 0.3 m)。结果表明, 本文模拟的定点波动较实验结果波动幅度更大。但总体而言, 本文模拟结果的定点波动与实验结果较为吻合, 能够基本体现定点的波动特征。图 3从微元层面反映了稳定传播的下凹型内孤立波(h1>H1, H1<H2)。
本文与Lin等(2012)的RANS模拟结果进行了界面涡旋结构对比。如图 4所示, 在扰动区水体刚开始下落时, 本文与Lin等(2012)模拟结果中的密度界面位移变化基本一致。随着时间的推移, 两种模拟方法开始有所区别: 在Lin等(2012)模拟结果中, 上凸型内波基本不呈现涡旋结构, 这与实验室实验结果不符; 本文模拟结果则呈现了因断裂形成湍流涡旋结构的详细过程, 这为后续对比内孤立波的起涡能力提供了充分条件。
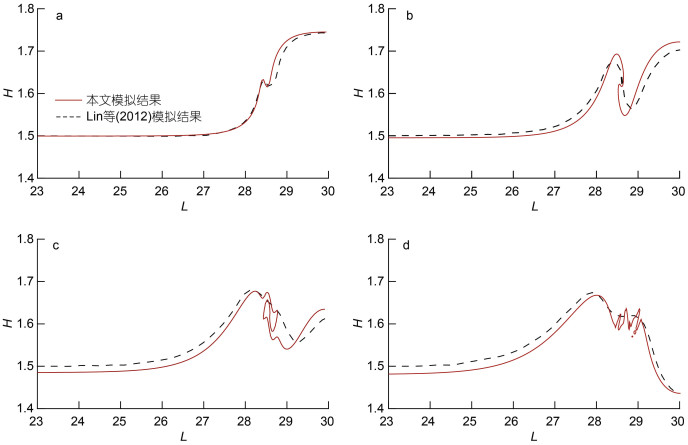 |
| 图 4 本文模拟结果(表 1中工况Lin)与Lin等(2012)模拟结果的界面涡旋结构对比 Fig. 4 Comparison of interface vortex structure between the simulation results of this paper (Case Lin in Tab.1) and those by Lin et al (2012) 注: a: t=0.14; b: t=0.27; c: t=0.41; d: t=0.54; H表示无量纲高度, L表示无量纲水平距离 |
综上, 对验证算例的模拟结果表明, 本文所采用的直接模拟数值模型有效地模拟了重力塌陷式内孤立波的波动变化过程, 相比于Lin等(2012)的RANS模拟结果呈现出更为明显的涡旋结构。
3 模拟结果分析为研究造波条件对重力塌陷式内孤立波发展的影响, 本文设计了8组算例(工况1—工况8), 各算例的主要参数参见表 1。由于本文主要考虑的是造波条件对内孤立波后续发展过程中的波型、涡度、振幅和水平速度的影响, 而根据验证算例和Chen等(2007)实验可知, 如果斜坡与扰动区距离较远, 在内孤立波没有传递到斜坡之前, 斜坡的影响基本可以忽略, 因此本文没有在这些算例中加入斜坡。
工况1、工况2、工况3的H1相同, η0不同, 可研究台阶深度η0对内孤立波发展的影响。工况1、工况6、工况7可研究流体密度差对内孤立波发展的影响。工况1、工况4、工况5、工况8可研究环境区上下层水深比(H1/H2)对内孤立波发展的影响, 四个算例的η0相同, 且均设置为H1>h1, 即初始波型为上凸型。其中工况1、工况4、工况5设置为H1>H2; 工况8设置为H1<H2, 可研究初始波型为上凸型内孤立波的反转现象。
3.1 流场涡度涡度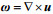
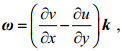 (17)
(17)其中, k为z方向单位长度分量。
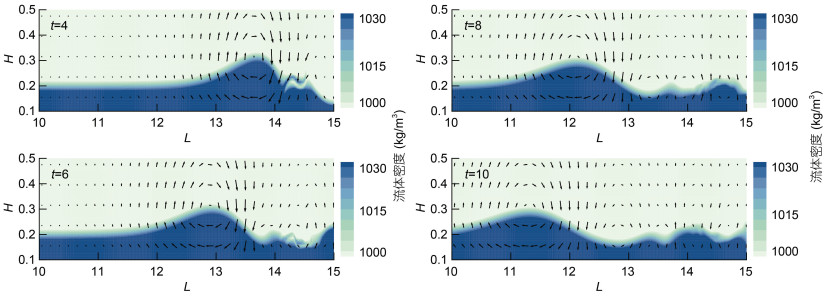
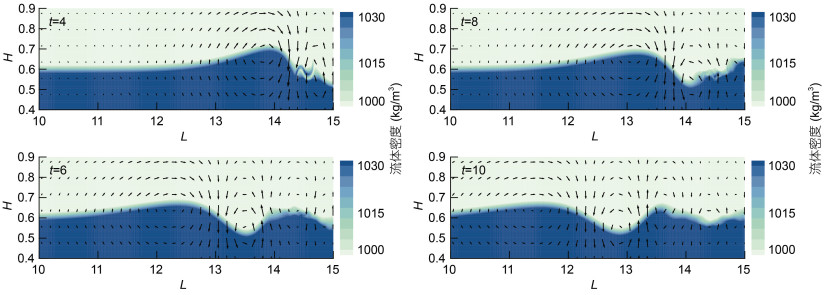
在研究过程中发现流体密度差对无量纲速度几乎没有影响, 因此本节将不给出工况6、工况7流场涡度对比图。图 5a、5b、5c为不同台阶深度的流场涡度时间演化的对比图。结果表明, 台阶深度η0对流场涡度的影响较为显著。在无量纲时间t=2.5时, 工况3几乎没有出现正涡度, 在之后的时间t=3.5至t=5.5, 工况1、工况2均表现出正涡度先增大后衰减的过程, 工况3的衰减过程则相对不明显。这表明台阶深度越大, 对尾部的湍流振荡影响越显著, 湍流振荡越剧烈, 且振荡持续时间相对越长。除此之外, 台阶深度越大, 产生的内孤立波波高越大, 内孤立波传播的平均速度越大。
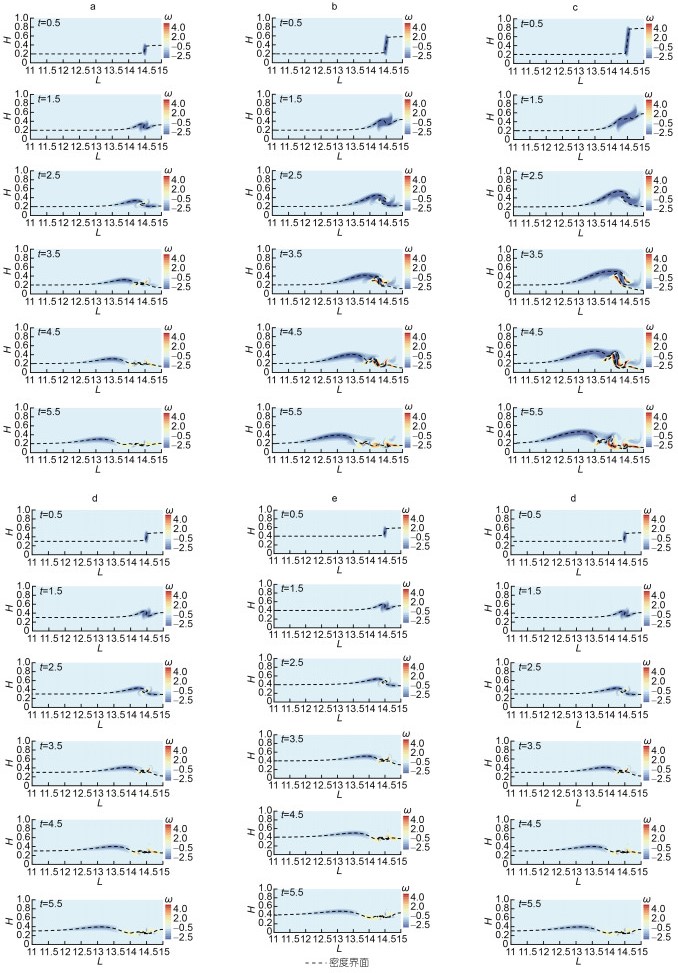 |
| 图 5 不同算例流场涡度的时间演化 Fig. 5 Time evolution of the flow field vorticity in different cases 注: H表示无量纲高度, L表示无量纲水平距离, ω表示涡度, 方向向上为正; a: 工况1; b: 工况2; c: 工况3; d: 工况4; e: 工况5; f: 工况8 |
图 5a、5d、5e为不同环境区上下层水深比(H1/H2)的流场涡度时间演化的对比图。结果表明, 上下层水深比(H1/H2)对流场涡度的影响较小。在t=2.5时, 3个算例均开始出现正涡度, 在之后的时间t=3.5至t=5.5, 工况5的负涡度衰减的更快, 且正涡度相对工况1、工况4更明显。这表明在H1>h1的条件下, 上下层水深比(H1/H2)越小, 前部波衰减的相对更快, 尾部的湍流振荡相对更剧烈。
图 5a、5f为不同水层条件下(分别为稳定和不稳定的内孤立波)的流场涡度时间演化的对比图。结果表明, 工况8的负涡度衰减的更快, 且正涡度相对工况1数值更大。这定性地表明了不稳定内孤立波在向前传播的过程中, 存在能量的向后部传递。
3.2 最大水平速度图 6为不同算例的流场最大水平速度
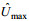
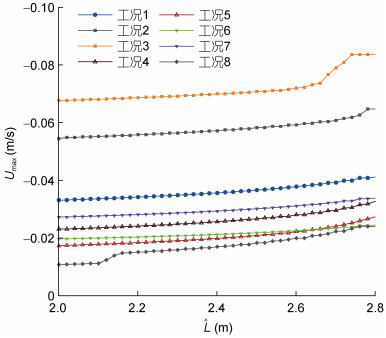 |
图 6 不同算例流场最大水平速度随水平位置的变化 Fig. 6 Change of maximum horizontal velocity of flow field with horizontal position
注: 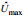 : 最大水平速度; : 最大水平速度; 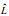 : 水平位置 : 水平位置 |
(1) 增大流体密度差, 流场最大水平速度将随之增大;
(2) 随着台阶深度的增大, 流场最大水平速度将随之增大; 台阶深度较大的算例(工况3)初始会有一段最大水平速度保持不变的阶段, 这可能是因为增大台阶深度会加长初始水体顺时针涡流运动的持续时间;
(3) 在水层条件h1<H1, H1>H2下, 产生稳定的上凸型内孤立波, 随着上下层水深比的增大, 流场最大水平速度将随之增大;
(4) 在水层条件h1<H1, H1<H2下, 产生不稳定的内孤立波, 在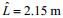
由于不稳定内孤立波的前部上凸型内孤立波处为顺时针涡流, 后部下凹型内孤立波处为逆时针涡流。这表明在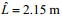
图 7为不同算例的最大波高Hmax随时间t的变化, 两者均为无量纲形式, 其中Hmax为内孤立波运动状态趋于稳定时, 流场内的最大波高。由图可知, 最大波高的变化过程可大致分为三个阶段: 第一阶段为快速衰减阶段, 在这一阶段, 由于两侧水体的密度交互作用, 水体倾覆, 最大波高快速衰减; 第二阶段为振荡阶段, 在这一阶段, 水体倾覆运动基本完成, 密度界面形成稳定的前部高程波, 但由于尾随界面振荡的存在, 表现出最大波高下降再升高的反复现象, 但总体趋势是呈相对快速衰减; 第三阶段为缓慢衰减阶段, 达到一定时间后, 前部波以较为稳定的状态向左传播, 由于能量耗散, 内孤立波波高逐渐缓慢减小。对比各算例结果可知:
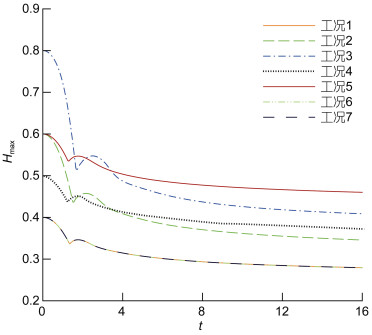 |
| 图 7 不同算例最大波高Hmax的时间演化 Fig. 7 Time evolution of the maximum wave height in different cases |
(1) 流体密度差对最大波高基本没有影响;
(2) 随着台阶深度的增大, 最大波高第二阶段的反复现象越明显, 即振荡越剧烈;
(3) 在台阶深度一定, 且产生稳定内孤立波的水层条件下(h1<H1, H1>H2), 内孤立波表现出极为相似的波高变化。
根据上述的内孤立波传播特点, 本文选取无量纲时间t=9—10内的界面波动振幅的平均值作为内孤立波的振幅Aw。计算公式如下:
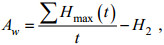 (18)
(18)图 8为内孤立波的振幅Aw随各项造波参数的变化曲线。结果表明: 台阶深度对内孤立波的振幅影响显著, 上下层水深比对振幅影响相对较小, 流体密度差对振幅基本不产生影响。
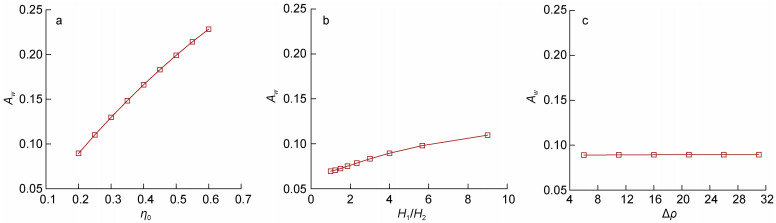 |
| 图 8 振幅Aw随各项造波参数的变化曲线 Fig. 8 The variation curves of amplitude with various wave-forming parameters 注: η0=h2-H2: 台阶深度; H1/H2: 上下层水深比; Δρ=ρ2-ρ1: 流体密度差 |
图 9为工况1流场界面内孤立波的演化过程。稳定的内孤立波在传播过程中, 其前部内孤立波处的顺时针涡流始终维持较大速度, 这表明能量集中在前部波内。图 10为工况8流场界面内孤立波波型反转的演化过程。与图 9对比, 可清楚观察到工况8的内孤立波在传播过程中发生波型不稳定转换的现象:
(1) 在H1>h1的条件下, 工况8内孤立波的初始波型表现为上凸型。随着时间的递进, 前部的上凸型内孤立波振幅逐渐减小, 反之, 其后部的下凹型内孤立波振幅逐渐增大;
(2) 不稳定的内孤立波在传播过程中, 前部上凸型内孤立波处的顺时针涡流速度逐渐减小; 反之, 后部的下凹型内孤立波处的逆时针涡流速度逐渐增大。这证实了不稳定内孤立波在传播过程中会发生内部能量传递, 能量由前部上凸型内孤立波, 逐渐传递到后部下凹型内孤立波。
以上均是定性判断了内孤立波运动过程中的能量变化, 下面将通过给出内孤立波动能的定量计算, 分析内孤立波运动过程中的能量变化。
图 11为稳定内孤立波(工况1)与不稳定内孤立波(工况8)的流场动能水平分布对比图。其中, Ekr为不同水平位置处的流体动能占整个流场动能的比例, 计算公式如下:
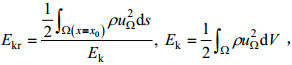 (19)
(19)
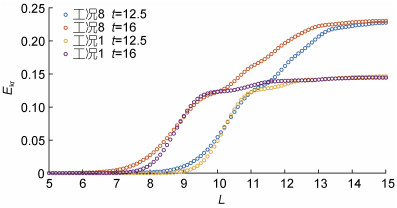 |
| 图 11 不同时间的流场动能的水平分布 Fig. 11 Horizontal distribution of kinetic energy in flow field at different times 注: Ekr: 不同水平位置处的流体动能占整个流场动能的比例; L: 无量纲水平距离; t: 无量纲时间 |
其中, ρ为微元的密度, uΩ为微元的速度, x0为微元的水平位置, dV为微元的体积, ds为微元的剖面积(二维时可认为是高度dy), Ω为计算域。
结果表明, 在无量纲时间t=12.5至t=16的这段时间内, 稳定内孤立波(工况1)的流场动能水平分布形态基本不发生改变, 第一个转折点处判断为前部波波峰位置; 不稳定内孤立波(工况8)的流场动能水平分布形态发生明显改变, 对比t=12.5与t=16的第一个转折点处的动能占比, 可看到随时间的推移, 前部流体动能占比减小。这表明在不稳定内孤立波在向前传播的过程中, 存在能量的向后部传递。除此之外, 工况8的后部动能占比明显大于工况1, 这可能是由于工况8的上下层水深比接近1, 不稳定内孤立波在主波后方产生了连续的内波波列, 造成能量分散。
4 结论本文通过建立重力塌陷激发内孤立波运动的数值模型, 采用直接模拟数值方法, 研究了不同造波条件对内孤立波发展的影响, 结果表明:
(1) 通过直接数值模拟方法得到的流场界面呈现更为明显的涡旋结构。此外, 从定性和定量的角度, 证实了不稳定内孤立波传播过程中存在能量的向后传递。
(2) 增大台阶深度、流体密度差、上下层水深比, 流场最大水平速度都将随之增大, 其中台阶深度的影响最为显著。
(3) 对于相同的台阶深度, 初始涡流保持相同, 但是随着上下层水深比的减小, 其强度明显下降; 台阶深度对初始涡流的垂直结构的影响要大于上下层水深比。
(4) 台阶深度对内孤立波的振幅影响显著, 上下层水深比对振幅影响相对较小, 流体密度差对振幅基本不产生影响。
邹丽, 马鑫宇, 李振浩, 等. 2020. 分层流体孤立子模型的实验重现及流场分析. 哈尔滨工程大学学报, 41(2): 263-270 |
沈治, 李宇鹏, 崔桂香, 等. 2009. 稳定分层湍流的大涡模拟. 中国科学G辑: 物理学力学天文学, 39(10): 1503-1513 |
王德军, 唐云, 于洪川, 等. 2003. 水平集方法与距离函数. 应用数学和力学, 08: 839-848 DOI:10.3321/j.issn:1000-0887.2003.08.011 |
徐鑫哲, 2012. 内波生成机理及二维内波数值水槽模型研究. 哈尔滨: 哈尔滨工程大学硕士学位论文
|
Azevedo A, da Silva J C B, New A L, 2006. On the generation and propagation of internal solitary waves in the southern Bay of Biscay. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 53(6): 927-941 DOI:10.1016/j.dsr.2006.01.013 |
Chen C Y, Hsu J R C, Chen C W et al, 2007. Generation of internal solitary wave by gravity collapses. Journal of Marine Science and Technology, 15(1): 1-7 |
Davis K A, Monismith S G, 2011. The modification of bottom boundary layer turbulence and mixing by internal waves shoaling on a barrier reef. Journal of Physical Oceanography, 41(11): 2223-2241 DOI:10.1175/2011JPO4344.1583 |
Druzhinin O A, Ostrovsky L A, 2015. Dynamics of turbulence under the effect of stratification and internal waves. Nonlinear Processes in Geophysics, 22(3): 337-348 DOI:10.5194/npg-22-337-2015 |
Filonov A E, Trasviña A, 2000. Internal waves on the continental shelf of the gulf of Tehuantepec, Mexico. Estuarine, Coastal and Shelf Science, 50(4): 531-548 DOI:10.1006/ecss.1999.0583 |
Forgia G L, Tokyay T, Adduce C et al, 2018. Numerical investigation of breaking internal solitary waves. Physical Review Fluids, 3(10): 104801 DOI:10.1103/PhysRevFluids.3.104801 |
Grimshaw R, Pelinovsky E, Poloukhina O, 2002. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlinear Processes in Geophysics, 9(3-4): 221-235 |
Grue J, Jensen A, Rusås P O et al, 2000. Breaking and broadening of internal solitary waves. Journal of Fluid Mechanics, 413: 181-127 DOI:10.1017/S0022112000008648 |
He Z G, Zhao L, Hu P et al, 2018. Investigations of dynamic behaviors of lock-exchange turbidity currents down a slope based on direct numerical simulation. Advances in Water Resources, 119: 164-177 DOI:10.1016/j.advwatres.2018.07.008 |
Leichter J J, Wing S R, Miller S L et al, 1996. Pulsed delivery of subthermocline water to Conch Reef (Florida Keys) by internal tidal bores. Limnology and Oceanography, 41(7): 1490-1501 DOI:10.4319/lo.1996.41.7.1490 |
Lin Z H, Song J B, 2012. Numerical studies of internal solitary wave generation and evolution by gravity collapse. Journal of Hydrodynamics, 24(4): 541-553 DOI:10.1016/S1001-6058(11)60276-X |
Omand M M, Leichter J J, Franks P J S et al, 2011. Physical and biological processes underlying the sudden surface appearance of a red tide in the nearshore. Limnology and Oceanography, 56(3): 787-801 DOI:10.4319/lo.2011.56.3.0787 |
Vázquez A, Bruno M, Izquierdo A et al, 2008. Meteorologically forced subinertial flows and internal wave generation at the main sill of the Strait of Gibraltar. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 55(10): 1277-1283 DOI:10.1016/j.dsr.2008.05.008 |
Vlasenko V, Hutter K, 2002. Numerical Experiments on the breaking of solitary internal waves over a slope-shelf topography. Journal of Physical Oceanography, 32(6): 1779-1793 DOI:10.1175/1520-0485(2002)032<1779:NEOTBO>2.0.CO;2 |
Walter R K, Woodson C B, Arthur R S et al, 2012. Nearshore internal bores and turbulent mixing in southern Monterey Bay. Journal of Geophysical Research: Oceans, 117(C7): C07017 |
Walter R K, Woodson C B, Leary P R et al, 2014. Connecting wind-driven upwelling and offshore stratification to nearshore internal bores and oxygen variability. Journal of Geophysical Research: Oceans, 119(6): 3517-3534 DOI:10.1002/2014JC009998 |
Warn-Varnas A, Hawkins J, Lamb K G et al, 2010. Solitary wave generation dynamics at Luzon Strait. Ocean Modelling, 31(1-2): 9-27 DOI:10.1016/j.ocemod.2009.08.002 |
Yu C H, Zhao L, Wen H L et al, 2019. Numerical study of turbidity current over a three-dimensional seafloor. Communications in Computational Physics, 25(4): 1177-1212 |
 2021, Vol. 52
2021, Vol. 52