中国海洋湖沼学会主办。
文章信息
- 刘秀青, 张杰, 杨俊钢, 曹蕾. 2021.
- LIU Xiu-Qing, ZHANG Jie, YANG Jun-Gang, CAO Lei. 2021.
- 基于卫星测高与卫星测温的表层流产品生成方法应用评估
- APPLICATION EVALUATION OF SURFACE CURRENTS PRODUCT GENERATION METHOD BASED ON SATELLITE ALTIMETRY AND SATELLITE TEMPERATURE MEASUREMENT
- 海洋与湖沼, 52(3): 593-600
- Oceanologia et Limnologia Sinica, 52(3): 593-600.
- http://dx.doi.org/10.11693/hyhz20200600169
文章历史
-
收稿日期:2020-06-19
收修改稿日期:2020-08-30
2. 自然资源部海洋遥测技术创新中心 青岛 266061
2. Ocean Telemetry Technology Innovation Center, MNR, Qingdao 266061, China
表层流对海洋物质输送、气候变化等方面具有重要影响, 提高其精度和分辨率对于相关应用领域至关重要。然而目前尚没有直接获取海洋流场信息的遥感测量任务, 因此, 使用多源卫星遥感是间接获取海流的重要途径。
通过卫星测高数据反演表层流是迄今为止研究海洋表层流变化的最常用手段。因为在大洋内部和赤道以外区域地转平衡占据主导作用, 这意味着表层流可以从海面高度梯度获得, 但高度计观测系统存在不足: 只能在有限时空尺度上重建表层流动的地转分量(Yu et al, 1995, 2013; 邱云等, 2005)。为了获得更加真实的表层流信息, 可以利用风场估算Ekman流(Lagerloef et al, 1999), 并添加到地转流中(刘巍等, 2012; 安玉柱等, 2012; Rio et al, 2014; 赵新华, 2016), 结合风场资料和绝对动力地形在当前仍然是计算表层流的主要方法。此外, 一些学者提出了一种基于准线性和稳态物理诊断表层流的算法, 利用不同卫星数据分别估算地转分量、Ekman分量和浮力分量, 结果表明该算法能更好地捕获海流(Bonjean et al, 2002; Sikhakolli et al, 2013)。
近年来, 海表面温度数据量大大增加, 其时间变化与表层流的平流有关, 能够为表层流提供重要信息, 因此, 将卫星测高与卫星测温结合来估算洋流已成为一个全新领域。许多学者已经使用各种方法研究了高度测量和海表面温度数据的组合使用, 且已经取得巨大成果。在过去几十年中, 提出了许多新的表层流反演方法: 最大相关系数(maximum cross correlation, MCC)方法、表面准地转(surface quasigeostrophy, SQG)理论以及反演热量守恒方程。MCC方法在连续热图像之间计算局部相关性来估计偏移和局部运动(Bowen et al, 2002; 郭洪涛, 2012), 该方法受使用窗口大小的限制, 所得速度场空间分辨率更低; 此外, 当海温空间变异性较弱时, 也无法检索任何信息。基于MCC方法的不足, 已经提出了从单个海表面温度(sea surface temperature, SST)图像诊断表层流的新方法, 即表面准地转(surface quasigeostrophy, SQG)理论(Isern-Fontanet et al, 2006, 2020; González-Haro et al, 2014)。另一种全新的方法是通过反演热量守恒方程来估计表层流速度。Piterbarg(2009)首次通过结合SST和模式输出结果(背景速度场)来估算表层流, 该方法被证明可有效地改善背景速度场(简称PIT09)。在PIT09工作基础上, Rio等(2016)研究了应用经典方法从SST图像中提取表层流信息的可行性(讨论已知强迫情况), 结果表明该方法显著改善了背景流场, 改进达到了30%—35%, 并且速度的经向分量获得明显改进, SST观测能够在短时空尺度上提供重要信息, 而这些非地转信息高度计无法提供。在热量守恒方程中, 强迫项难以准确测量, Rio等(2018)进一步考虑了未知强迫的解决方案, 计算了全球海洋6年表层流速度, 结果表明结合两颗卫星高度计导出速度和微波SST数据获得的精度等于或高于4颗高度计获得的精度, 这强调了组合高度测量和海表面温度改善全球表层流的巨大潜力(简称RIO18)。最近, Ciani等(2019)进一步将该方法应用于地中海区域, 生成了2012—2016年每日无间隔高分辨率(1/24°)表层流, 通过与其他表层流估算值比较, 表明该方法可以改善局部表层流, 且经向分量和盆地西部具有更好的改进。由此可知, 将卫星测高与卫星测温结合在改善表层流方面具有巨大潜能。在流场实际应用中, 不仅需要获取大中尺度分量, 在亚中尺度上(涡旋、锋和细丝), 流场的表征也至关重要。事实上, 在相对较小尺度上也存在活跃的可变信号, 而常规方法只能在较大时空尺度上获取流场信息。为了更精确地认识海洋表面运动, 本文研究了引入高分辨率海表面温度对高度计导出流场的改进效果。
本文通过增加热量守恒方程约束, 引入卫星测温数据, 在地转流基础上生成全球海洋表层流产品, 并利用漂流浮标数据评估了产品质量; 此外, 本论文讨论了方法的适用性, 给出了在海表面温度梯度较小区域流速计算结果异常问题的解决办法; 并通过流速矢量沿等温线切向与法向的分解实验分析了方法改进流速的本质, 结果表明本文方法在不改变沿等温线的切向流速分量的前提下沿等温线的法向流速分量得到了改进, 方法能充分利用海表面温度信息提取流场特征信息, 这对获取高精度海表面流场具有理论研究价值。数据在第1节中描述, 第2节介绍了表层流生成方法, 第3节给出了方法适用性分析, 实验结果在第4节给出, 主要结论见第5节。
1 数据本文使用两类数据: 用于表层流生成的遥感产品和用于产品质量评估的漂流浮标数据, 其中遥感产品包括地转流场产品和海表温度产品。
作为表层流背景速度的地转流场产品来自AVISO(archiving, validation and interpretation of satellite oceanographic data), 其空间分辨率为1/4°× 1/4°, 时间分辨率为1 d, 使用两种不同产品: 仅两个高度计计算的"twosat"产品和所有可用高度计计算的"allsat"产品。海温数据来自遥感系统(remote sensing systems, REMSS)提供的空间分辨率为25 km以及时间分辨率为1 d的全球MW SST产品。
从表面漂流浮标数据装配中心(surface drifter data assembly center, SD‐DAC)下载6 h时间分辨率的2018年浮标数据, 获得15 m深度海表流速, 数据经过滤潮汐、日平均等处理。
2 方法通过增加热量守恒方程约束, 利用卫星测温产品, 在地转流(ubck, vbck)基础上生成表层流产品(uopt, vopt)是可行的方法。本文基于PIT09方法, 考虑到强迫项难以精确计算, 故对其进行了简化。
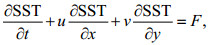 (1)
(1)式中, SST为海表面温度; u和v分别是纬向和经向表层流速度; x和y分别表示纬向和经向方向; F为强迫项。
强迫项包括热通量、垂直平流、夹带速度和扩散, 这些分量难以准确测量, 因此, 定义背景强迫项Fbck来粗略近似F。优化速度计算公式如下:
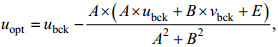 (2)
(2)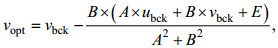 (3)
(3)式中, uopt、vopt分别表示优化速度的纬向和经向分量; ubck、vbck分别表示背景速度的纬向和经向分量;
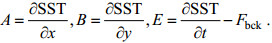 (4)
(4)假设影响SST时间变化的强迫场具有不同时空尺度特征, 其中SST时间变化的大空间尺度主要是由海气强迫和热通量引起, 小尺度变化是受平流影响。假设可忽略小尺度平流项, 则背景强迫项Fbck可以通过提取SST时间变化的大尺度分量来近似。
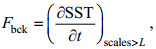 (5)
(5)式中, scales为空间尺度; L为滤波尺度; 这里L取500 km。
由公式(2)—(5)可知, 优化速度的计算主要取决于以下几个方面: 海表面温度的时空变化、背景强迫场Fbck和背景速度。
3 方法适用性分析 3.1 沿等温线切向与法向的流速分析根据RIO18论文可知, 该方法在温度梯度明显的区域改进效果较好, 因此以某涡旋为例, 给出方法改进流速的详细分析。已知初始流速矢量(u, v), 其沿等温线的法向分量为(ut, vt), 切向分量为(us, vs), 然后对该初始流速进行重构, 将法向分量扩大5倍且切向分量扩大1.5倍, 获得重构流速矢量uvnew=(5ut+1.5us, 5vt+1.5vs)。重构流速及其沿等温线切向与法向的分解如图 1a和图 1b所示。基于本文方法引入海温获得的优化流速如图 1c所示, 实验结果表明流速的法向分量明显被修正, 而切向分量无变化。根据图 1可以得出: 该方法对沿等温线的法向流速分量有约束, 但对于切向流速分量无明显改进效果。
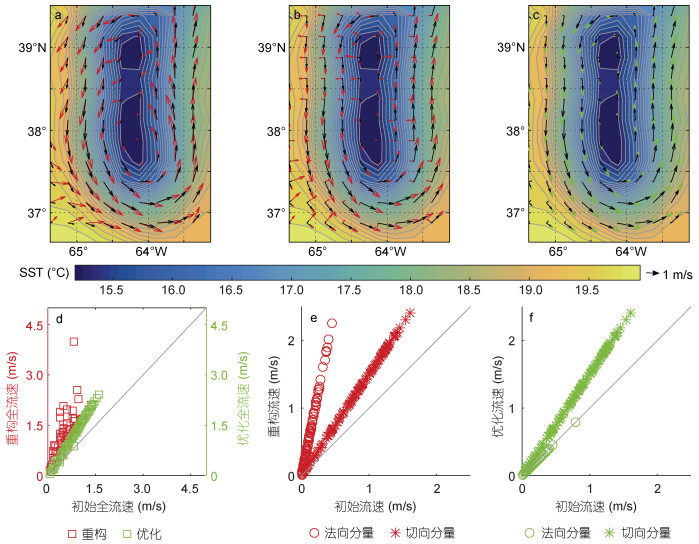 |
| 图 1 流速矢量沿等温线切向与法向的分解 Fig. 1 Decomposition of velocity vector along tangent and normal directions along isotherms 注: a: 初始流速(黑色)与重构流速(红色); b: 初始流速(黑色)与重构流速(红色)沿等温线切向与法向的分解; c: 初始流速(黑色)与优化流速(绿色)沿等温线切向与法向的分解; 三种颜色的矢量箭头共用一个比例尺; SST: 海表面温度 |
基于本文方法, 优化速度在海表面温度梯度(sea surface temperature gradient, SSTG)较小区域存在流速异常的问题。2018年1月2日湾流区域流场如图 2所示, 背景速度存在不合理的流场结构, 流速矢量跨越温度锋面, 优化速度在温度梯度较大区域获得明显改进(白框区域)。因此, 需要分析该方法的适用性。
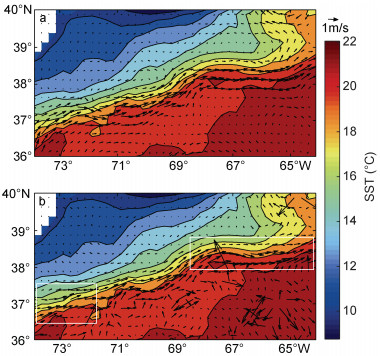 |
| 图 2 2018年1月2日湾流区域流场 Fig. 2 The current field in the gulfstream region on January 2, 2018 注: a: "twosat"背景速度; b: 优化速度; SST表示来自MW SST产品的海表面温度; 白色方框: 优化速度获得明显改善的区域 |
根据优化速度计算公式可知, 优化场是否能够获得改进在一定程度上取决于SSTG, 因此, 期望通过约束SSTG的取值范围进一步修正优化场。首先将背景速度、优化速度、SSTG与浮标数据进行时空匹配。然后设置SSTG阈值, 当SSTG小于该阈值时, 则去除相应的匹配数据点。最后针对剩余数据对分别计算背景速度、优化速度与浮标速度的均方根误差(root mean square error, RMSE), 得到RMSE随SSTG最小阈值变化的图像(图 3)。针对全球统计结果得出该方法的适用条件: 对于速度的纬向分量, 当SSTG < 2.0× 10-5℃/m时, 优化场不做修改, 保持背景场状态; 对于速度的经向分量, 当SSTG < 1.2×10-5℃/m时, 优化场不做修改, 保持背景场状态。
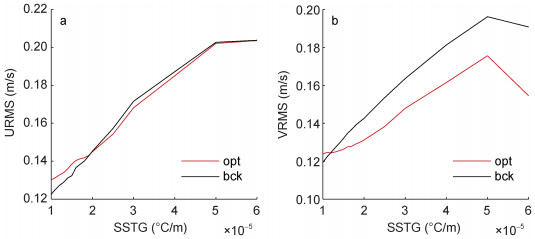 |
| 图 3 "twosat"背景速度、优化速度与浮标速度的均方根随SSTG最小阈值的变化 Fig. 3 The root mean square of "twosat" background velocities, optimized velocities, and buoy velocities changes with the minimum threshold of SSTG 注: a: 纬向分量; b: 经向分量; bck: 背景速度; opt: 优化速度; SSTG: 海表面温度梯度; URMS: 纬向速度分量的均方根; VRMS: 经向速度分量的均方根 |
基于"twosat"产品和MW SST产品, 根据以上方法, 生成2018年每日无间隔1/4°的全球海洋表层流产品。
4.1 定性区域评估为了评估方法的性能, 以黑潮区域涡旋为案例分析优化速度的改进效果。黑潮区域涡旋丰富, 在2018年3月24日黑潮附近发现了一个气旋涡。在"twosat"背景速度场中(图 4a), 由于受到高度计轨道距离和数量的限制, 获得的中尺度信号存在较大误差, 流速矢量跨越温度锋面(白框区域), 这与环流规律不符。在"allsat"速度场中(图 4c), 受益于高度计数量的增加, 解决了这种问题。通过将MW SST信息引入"twosat"背景速度, 获得的优化速度与"allsat"速度场相一致并且与温度锋面方向更加一致(图 4b)。
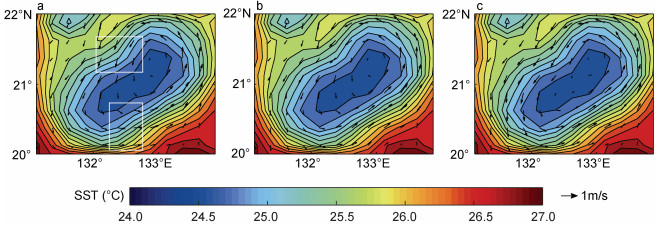 |
| 图 4 2018年3月24日黑潮区域气旋涡 Fig. 4 The eddy in the Kuroshio region on March 24, 2018 注: a: "twosat"背景速度; b: "twosat"背景速度和MW SST组合的优化速度; c: "allsat"速度场; SST来自MW SST产品; 白色方框: "twosat"背景速度误差较大区域 |
在本节中, 针对生成的2018年优化速度进行质量评估, 验证数据集采用对应时段的现场浮标测量数据(MW SST产品使用了日模型进行校正, 所有海温值相当于10 m左右深度的基础海温, 我们期望优化速度代表 10 m深度的速度, 因此漂流浮标15 m深度速度可作为参考数据集)。首先, 以浮标数据为基准, 背景速度与优化速度与之进行时空匹配。然后, 统计均方根误差(ERMS)、偏差(Sb)和相关系数(RCOR)。最后, 绘制均方根、相关系数和改进百分比随SSTG变化的图像(图 5)。改进百分比RI采用下式计算:
 (6)
(6)
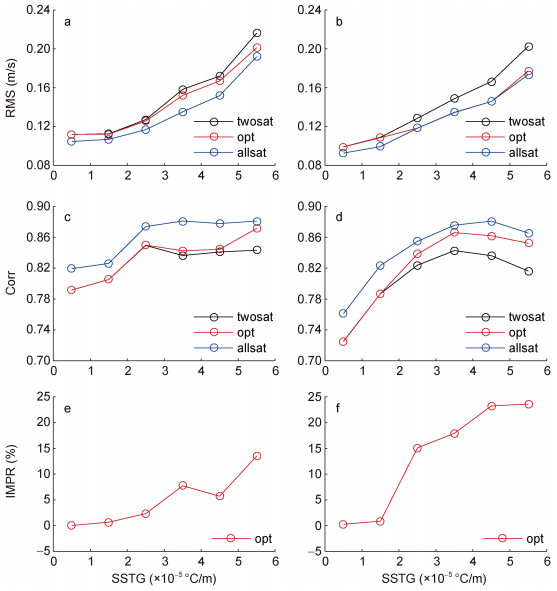 |
| 图 5 "twosat"背景速度、优化(opt)速度、"allsat"背景速度与浮标速度的均方根(RMS)、相关系数(Corr)和改进百分比(IMPR)随不同SSTG区间的变化 Fig. 5 The root mean square(RMS), correlation coefficient(Corr), and improvement percentage(IMPR) of "twosat" background velocities, optimized velocities, "allsat" background velocities, and buoy velocities change with different SSTG intervals 注: a、c、e: 纬向分量; b、d、f: 经向分量 |
式中, ERMS-opt表示优化速度与浮标速度的均方根; ERMS-bck表示背景速度与浮标速度的均方根。
本文分别针对全球、南极绕极流区域(35°—65°S, 0°—360°E)和黑潮延伸体区域(30°—40°N, 140°—180°E)给出了定量比较结果, 这三个区域的数据匹配个数分别为24843、10134和1344。就全球而言, 获得了"twosat"背景场、优化场、"allsat"速度场与浮标匹配的数据对, 保留SSTG满足适用条件的数据对, 不论经向分量还是纬向分量, 优化流较"twosat"地转流在各项指标均有所改进, 尤其是BIAS, 甚至优于"allsat"地转流(表 1)。由表 2和表 3可知, 在南极绕极流和黑潮延伸体这类强温度梯度区域, 优化场改进效果更加明显。
| 变量类型 | 统计量 | "twosat" 背景场 |
"twosat"+MW SST |
"allsat" 背景场 |
| 纬向分量 | 均方根误差(m/s) | 0.145 | 0.144 | 0.132 |
| 偏差(m/s) | 0.021 | 0.019 | 0.020 | |
| 相关系数 | 0.845 | 0.846 | 0.877 | |
| 经向分量 | 均方根误差(m/s) | 0.132 | 0.124 | 0.120 |
| 偏差(m/s) | 0.008 | 0.007 | 0.009 | |
| 相关系数 | 0.821 | 0.831 | 0.857 |
| 变量类型 | 统计量 | "twosat" 背景场 |
"twosat"+MW SST |
"allsat" 背景场 |
| 纬向分量 | 均方根误差(m/s) | 0.148 | 0.145 | 0.132 |
| 偏差(m/s) | 0.037 | 0.040 | 0.033 | |
| 相关系数 | 0.852 | 0.858 | 0.881 | |
| 经向分量 | 均方根误差(m/s) | 0.134 | 0.121 | 0.120 |
| 偏差(m/s) | 0.022 | 0.018 | 0.022 | |
| 相关系数 | 0.866 | 0.885 | 0.893 |
| 变量类型 | 统计量 | "twosat" 背景场 |
"twosat"+MW SST |
"allsat" 背景场 |
| 纬向分量 | 均方根误差(m/s) | 0.181 | 0.178 | 0.158 |
| 偏差(m/s) | -0.006 | 0.002 | 0.001 | |
| 相关系数 | 0.816 | 0.821 | 0.852 | |
| 经向分量 | 均方根误差(m/s) | 0.152 | 0.141 | 0.137 |
| 偏差(m/s) | -0.002 | -0.002 | 0.001 | |
| 相关系数 | 0.774 | 0.786 | 0.818 |
由图 5可知, 与"twosat"背景速度相比, 引入MW SST生成的优化速度获得明显改善。以1×10-5℃/m为间隔, 针对不同SSTG区间, 统计"twosat"背景速度、优化速度和"allsat"背景速度与浮标速度的均方根、相关系数和改进百分比。对于经向分量, 当SSTG > 2.0×10-5℃/m时, 优化速度的均方根小于背景速度, 相关系数大于背景速度, 并且可获得15%—24%的改善, 表明该方法在强SSTG区域可有效地改善经向分量。对于纬向分量, 当SSTG > 2.0×10-5℃/m时, 获得较小改进。在SSTG不明显的区域, 因优化速度保持背景速度, 因此没有改进。与经向分量相比, 纬向分量的校正效果不好, 可能因为等温线在全球大洋呈纬向分布, 经向温度梯度的量值与精度显著于纬向梯度, 因此对经向流速的改进效果更加明显。
与"twosat"背景速度相比, 在所有SSTG区间, "allsat"背景速度精度更高(随着高度计数量增加, 流场空间分辨率提高, 这为使用"allsat"产品检验优化场提供了理论依据)。对于速度的经向分量, 当SSTG > 2.0×10-5 ℃/m时, 基于"twosat"和MW SST的优化速度更接近"allsat"背景速度, 这表明该方法在强SSTG区域可弥补测高资料的不足。对于速度的纬向分量, 优化速度的精度小于"allsat"背景速度。
5 结论本文以卫星测高反演的地转流为背景数据, 利用可逐日覆盖全球的卫星测温数据, 评估了表层流生成方法。流速获得改进主要是由于相比背景速度SST具有更高的时空分辨率, 然而, 受制于SST输入数据集的时空分辨率和强迫项的粗略估算, 方法的改进主要是地转分量。主要结论如下:
(1) 本文方法在不改变沿等温线的切向流速分量的前提下, 沿等温线的法向流速分量得到了改进, 方法能充分利用海表温度信息提取流场特征信息。
(2) 方法不适用于海表面温度梯度较小区域, 在梯度较大区域可获得明显改进。
(3) 在该项研究中, 优化流场能更好地刻画海面海流变化, 证明结合卫星测高与卫星测温可改善海洋表层流动。
(4) 在海表面温度梯度较大区域, 增加SST观测能够弥补测高资料的不足。
刘巍, 张韧, 王辉赞, 等. 2012. 基于卫星遥感资料的海洋表层流场反演与估算. 地球物理学进展, 27(5): 1989-1994 |
安玉柱, 张韧, 王辉赞, 等. 2012. 基于卫星遥感数据的全球表层流场反演重构. 海洋通报, 31(1): 1-8 |
邱云, 胡建宇. 2005. 利用卫星高度计资料分析热带大西洋表层环流的季节性变化. 海洋通报, 24(4): 8-16, 72 DOI:10.3969/j.issn.1001-6392.2005.04.002 |
赵新华, 2016. 基于卫星测高数据的全球海洋流场产品研究与黑潮监测应用. 青岛: 国家海洋局第一海洋研究所硕士学位论文, 13
|
郭洪涛, 2012. 利用卫星资料反演表面海流的研究. 南京: 南京师范大学博士学位论文, 58
|
Bonjean F, Lagerloef G S E, 2002. Diagnostic model and analysis of the surface currents in the Tropical Pacific Ocean. Journal of Physical Oceanography, 32(10): 2938-2954 DOI:10.1175/1520-0485(2002)032<2938:DMAAOT>2.0.CO;2 |
Bowen M M, Emery W J, Wilkin J L et al, 2002. Extracting multiyear surface currents from sequential thermal imagery using the maximum cross-correlation technique. Journal of Atmospheric and Oceanic Technology, 19(10): 1665-1676 DOI:10.1175/1520-0426(2002)019<1665:EMSCFS>2.0.CO;2 |
Ciani D, Rio M H, Menna M et al, 2019. A synergetic approach for the space-based sea surface currents retrieval in the Mediterranean Sea. Remote Sensing, 11(11): 1285 DOI:10.3390/rs11111285 |
González-Haro C, Isern-Fontanet J, 2014. Global ocean current reconstruction from altimetric and microwave SST measurements. Journal of Geophysical Research: Oceans, 119(6): 3378-3391 DOI:10.1002/2013JC009728 |
Isern-Fontanet J, Chapron B, Lapeyre G et al, 2006. Potential use of microwave sea surface temperatures for the estimation of ocean currents. Geophysical Research Letters, 33(24): L24608 DOI:10.1029/2006GL027801 |
Isern-Fontanet J, García-Ladona E, Jiménez-Madrid J A et al, 2020. Real-time reconstruction of surface velocities from satellite observations in the Alboran Sea. Remote Sensing, 12(4): 724 DOI:10.3390/rs12040724 |
Lagerloef G S E, Mitchum G T, Lukas R B et al, 1999. Tropical Pacific near-surface currents estimated from altimeter, wind, and drifter data. Journal of Geophysical Research: Oceans, 104(C10): 23313-23326 DOI:10.1029/1999JC900197 |
Piterbarg L I, 2009. A simple method for computing velocities from tracer observations and a model output. Applied Mathematical Modelling, 33(9): 3693-3704 DOI:10.1016/j.apm.2008.12.006 |
Rio M H, Mulet S, Picot N, 2014. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophysical Research Letters, 41(24): 8918-8925 DOI:10.1002/2014GL061773 |
Rio M H, Santoleri R, Bourdalle-Badie R et al, 2016. Improving the altimeter-derived surface currents using high-resolution sea surface temperature data: a feasibility study based on model outputs. Journal of Atmospheric and Oceanic Technology, 33(12): 2769-2784 DOI:10.1175/JTECH-D-16-0017.1 |
Rio M H, Santoleri R, 2018. Improved global surface currents from the merging of altimetry and Sea Surface Temperature data. Remote Sensing of Environment, 216: 770-785 DOI:10.1016/j.rse.2018.06.003 |
Sikhakolli R, Sharma R, Kumar R et al, 2013. Improved determination of Indian Ocean surface currents using satellite data. Remote Sensing Letters, 4(4): 335-343 DOI:10.1080/2150704X.2012.730643 |
Yu Y Y, Emery W J, Leben R R, 1995. Satellite altimeter derived geostrophic currents in the western tropical Pacific during 1992-1993 and their validation with drifting buoy trajectories. Journal of Geophysical Research: Oceans, 100(C12): 25069-25085 DOI:10.1029/95JC02146 |
Yu Y, Wang L F, Li Z W et al, 2013. Geostrophic current estimation using altimeter data at ground track crossovers in the northwest Pacific Ocean. Frontiers of Earth Science, 7(4): 447-455 DOI:10.1007/s11707-013-0380-0 |
 2021, Vol. 52
2021, Vol. 52


