2021, Vol. 52
表1(Table 1)
基于神经网络的印度洋长鳍金枪鱼(Thunnus alalunga)时空分布与海洋环境关系研究
http://dx.doi.org/10.11693/hyhz20210100003
中国海洋湖沼学会主办。
中国海洋湖沼学会主办。
文章信息
- 程懿麒, 张俊波, 汪金涛, 雷林. 2021.
- CHENG Yi-Qi, ZHANG Jun-Bo, WANG Jin-Tao, LEI Lin. 2021.
- 基于神经网络的印度洋长鳍金枪鱼(Thunnus alalunga)时空分布与海洋环境关系研究
- STUDY ON THE RELATIONSHIP BETWEEN TEMPORAL-SPATIAL DISTRIBUTION OF INDIAN OCEAN ALBACORE(THUNNUS ALALUNGA) AND MARINE ENVIRONMENT BASED ON NEURAL NETWORK
- 海洋与湖沼, 52(4): 960-970
- Oceanologia et Limnologia Sinica, 52(4): 960-970.
- http://dx.doi.org/10.11693/hyhz20210100003
文章历史
-
收稿日期：2021-01-05
收修改稿日期：2021-03-15
引用本文
程懿麒, 张俊波, 汪金涛, 雷林. 2021. 基于神经网络的印度洋长鳍金枪鱼(Thunnus alalunga)时空分布与海洋环境关系研究[J]. 海洋与湖沼, 52(4): 960-970
CHENG Yi-Qi, ZHANG Jun-Bo, WANG Jin-Tao, LEI Lin. 2021. STUDY ON THE RELATIONSHIP BETWEEN TEMPORAL-SPATIAL DISTRIBUTION OF INDIAN OCEAN ALBACORE(THUNNUS ALALUNGA) AND MARINE ENVIRONMENT BASED ON NEURAL NETWORK[J]. Oceanologia et Limnologia Sinica, 52(4): 960-970.
基于神经网络的印度洋长鳍金枪鱼(Thunnus alalunga)时空分布与海洋环境关系研究
1. 上海海洋大学海洋科学学院 上海 201306;
2. 农业农村部大洋渔业开发重点实验室 上海 201306;
3. 国家远洋渔业工程技术研究中心 上海 201306;
4. 大洋渔业资源可持续开发教育部重点实验室 上海 201306;
5. 农业农村部大洋渔业资源环境科学观测实验站 上海 201306
2. 农业农村部大洋渔业开发重点实验室 上海 201306;
3. 国家远洋渔业工程技术研究中心 上海 201306;
4. 大洋渔业资源可持续开发教育部重点实验室 上海 201306;
5. 农业农村部大洋渔业资源环境科学观测实验站 上海 201306
摘要：长鳍金枪鱼（Thunnus alalunga）是主要的经济性金枪鱼鱼种之一，其空间分布与环境因子存在着密切联系。利用2012—2019年印度洋长鳍金枪鱼生产数据和海洋环境数据，包括海表面温度（sea surface temperature，SST）、叶绿素浓度（chlorophyll a，chl a）和海表面盐度（sea surface salinity，SSS）构建印度洋长鳍金枪鱼时空分布神经网络模型。以空间（经度，纬度）、环境因子（SST，chl a，SSS）为解释变量，局部渔获量为因变量，变化隐含层节点数，构建了18个BP空间分布模型，并采用10×10交叉验证模型稳定性，以均方误差（mean square error，MSE）、平均相对方差（average relative variance，ARV）以及拟合优度（R2）作为不同模型精度与稳定性的评判标准，最终选取5-18-1（隐含层节点18）模型为最佳模型，其平均MSE值为0.022 32，平均ARV值为0.511。利用最优模型预测结果与同期实际捕捞产量进行叠加对比发现两者具有一致性。环境因子敏感性分析表明海表温度显著影响印度洋长鳍金枪鱼渔场分布，其贡献率达到0.2。印度洋长鳍金枪鱼高精度BP神经网络时空分布模型为其资源的可持续开发与动态管理提供了一种新思路。
关键词：长鳍金枪鱼 印度洋 渔场预报 BP神经网络 时空分布
STUDY ON THE RELATIONSHIP BETWEEN TEMPORAL-SPATIAL DISTRIBUTION OF INDIAN OCEAN ALBACORE(THUNNUS ALALUNGA) AND MARINE ENVIRONMENT BASED ON NEURAL NETWORK
1. College of Marine Sciences of Shanghai Ocean University Shanghai 201306, China;
2. Key Laboratory of Oceanic Fisheries Exploration, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
3. National Engineering Research Center for Oceanic Fisheries, Shanghai Ocean University, Shanghai 201306, China;
4. Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai Ocean University, Shanghai 201306, China;
5. Scientific Observing and Experimental Station of Oceanic Fishery Resources, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China
2. Key Laboratory of Oceanic Fisheries Exploration, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
3. National Engineering Research Center for Oceanic Fisheries, Shanghai Ocean University, Shanghai 201306, China;
4. Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai Ocean University, Shanghai 201306, China;
5. Scientific Observing and Experimental Station of Oceanic Fishery Resources, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China
Abstract: Albacore (Thunnus alalunga) is one of the main economic tuna species, and its spatial distribution is closely related to environmental factors. In this research, BP artificial neural network method was applied, with which a neural network model was established based on the production data and environmental data of T. alalunga from 2012 to 2019. The output factor was the normalized fishing production data, and the input factors were spatial factors (including longitude and latitude), marine environmental factors, including sea surface temperature (SST), chlorophyll-a concentration, (chl a), and sea surface salinity (SSS), from which 18 BP neural network models were run using 10×10 cross-validation model stability, mean square error (MSE), average relative variance (ARV), and goodness of fit (R2) as the judgement of accuracy and stability of different models. Finally, Model 5-18-1 (hidden layer node 18) was chosen as the best model; its average MSE value is 0.022 32, and average ARV value is 0.511. The optimal model prediction results and the actual catch data during the same period were superimposed and compared, showing consistent results. Meanwhile, sensitivity analysis of environmental factors showed that SST significantly affected the distribution of T. alalunga fisheries in the Indian Ocean, with a contribution rate of 0.2. The high-precision BP neural network temporal-spatial distribution model of T. alalunga provides a new idea for the sustainable development and dynamic management of the resources.
Key words:
Albacore tuna Indian Ocean fishing ground forecast BP neural network temporal-spatial distribution
长鳍金枪鱼(Thunnus alalunga)是主要的经济性金枪鱼鱼种之一, 在太平洋、大西洋和印度洋均有分布(Chen et al, 2005; 官文江等, 2018)。印度洋海域是世界上重要的金枪鱼生产海区, 主要的捕捞国家和地区包括日本、韩国以及我国台湾省, 我国大陆在该海区的捕捞产量也在逐步上升(朱江峰等, 2014; 马璐璐等, 2018)。20世纪80年代中期, 我国台湾省主要在南印度洋海域采用流刺网对其进行捕捞, 印度洋长鳍金枪鱼产量达到历史上一个主要的高峰时期。1992年公海流刺网渔业被禁止, 长鳍金枪鱼渔获量在1993年下降到20 000 t, 随后因延绳钓渔业的发展, 渔获量逐步上升, 于2001年达到渔获量44 000 t (Lee et al, 2014)。自20世纪50年代以来, 印度洋长鳍金枪鱼产量一直呈上升趋势。近几年, 随着热带金枪鱼资源的衰退, 我国延绳钓渔业将长鳍金枪鱼作为资源对象进行开发, 长鳍金枪鱼渔获量在不断提升。因此, 跟踪、掌握印度洋长鳍金枪鱼资源分布状况有利于我国金枪鱼渔业发展(朱江峰等, 2014)。
长鳍金枪鱼时空分布与海洋环境因子密切相关(Chen et al, 2005)。近年来, 海洋遥感和计算机技术等的广泛应用, 鱼类分布和渔场预测研究也进入了新的发展阶段。如官文江等(2018)对影响印度洋长鳍金枪鱼资源评估的因素进行了分析; 闫敏等(2015)使用GAM模型研究南太平洋长鳍金枪鱼渔场与时空及环境因子存在的关系; 范江涛等(2011)等结合次表层水温等要素, 并按照季度构建南太平洋长鳍金枪鱼综合适应性指数。研究长鳍金枪鱼渔时空分布的相关模型也较多, 如栖息地指数(habitat suitability index, HSI)模型(范江涛等, 2011; 马孟磊等, 2017)、贝叶斯概率(Bayesian analysis, BA)模型(崔雪森等, 2015; 周为峰等, 2018)、广义加性模型(Generalized Additive Model, GAM)(牛明香等, 2012; 闫敏等, 2015)、支持向量机(support vector machine, SVM)(崔雪森等, 2016)、范例推理(Case-based reasoning, CBR)(张月霞等, 2009; 牛明香等, 2012)等方法。印度洋长鳍金枪鱼资源的时空分布研究通常分为基于单一环境因子(Lehodey et al, 1997; 郭爱等, 2005; 方舟等, 2013)和基于多环境因子(叶泰豪等, 2012; 唐浩等, 2013), 但由于渔业信息本身的模糊性、复杂性和不精确性(苏奋振等, 2003), 自变量与因变量之间的关系难以描述, 在实际模型构建中, 寻找和确定数学关系很容易陷入过拟合而降低模型的泛化能力(Lucas, 2004; Pan et al, 2007), 具有一定的局限性。
人工神经网络方法并不要求渔业数据满足任何假设, 也不需要分析鱼类对于环境条件的响应函数和各环境条件之间的相互关系, 它具有很好的自主学习能力和很强的泛化和容错能力(Demuth et al, 2014), 自20世纪90年代以来, 人工神经网络在国内外渐渐被大量应用于海洋及水产领域(Hawing et al, 1996; Chen et al, 1999; Hanson et al, 2006; 吴风霞等, 2009), 尤其是鱼类空间分布预测方面(Brosse et al, 1999; 汪金涛等, 2014; Wang et al, 2018)。毛江美等(2016)选用BP人工神经网络算法构建了南太平洋长鳍金枪鱼预报模型; 陈洋洋等(2017)基于BP神经网络构建了个中西太平洋鲣鱼渔场模型, 均取得了较好的效果。
本文选取2012—2019年长鳍金枪鱼渔获数据, 结合海洋环境数据, 包括海表温度(sea surface temperature, SST)、叶绿素浓度(chlorophyll a concentration, chl a)和海表面盐度(sea surface salinity, SSS)建立BP神经网络模型, 探索其时空分布与环境因子之间关系, 为印度洋长鳍金枪鱼延绳钓渔业生产及其管理保护提供参考。
1 材料与方法 1.1 材料来源印度洋长鳍金枪鱼生产数据来源于印度洋金枪鱼委员会(Indian Ocean Tuna Commission, IOTC) (https://www.iotc.org/), 时间范围为2012—2019年, 空间范围为20°E—135°E, 15°N—45°S, 渔业生产数据包括作业时间(年, 月)、位置(经度, 纬度)、放钩数和渔获重量等(图 1)。时间分辨率为月, 空间分辨率为5° × 5°。
 |
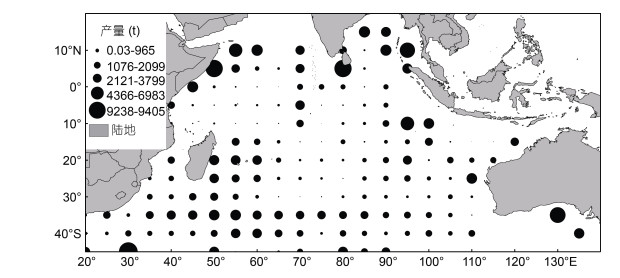| 图 1 印度洋长鳍金枪鱼2012—2019年累计产量分布图 Fig. 1 Distribution of cumulative production of albacore tuna in the Indian Ocean from 2012 to 2019 |
SST、chl a和SSS被认为是影响长鳍金枪鱼渔场分布的重要环境因子(Laurs et al, 1984; 奈须敬二, 1995; Zainuddin et al, 2008), 因此从美国国家海洋和大气管理局数据库(http://oceanwatch.pifsc.noaa.gov/las/servlets/dataset)下载SST、chl a和SSS, 时间分辨率为月, 空间分辨率为1° × 1°, 按空间平均法融合渔业与环境数据(Wang et al, 2018)。选用月分辨率下单个网格内的捕捞量数据表示长鳍金枪鱼局部资源丰度指标(local abundance, LA)。
将各影响因子和目标变量分别采取最大-最小标准化方法(也称特征缩放法)进行归一化(Wang et al, 2018), 消除由于数据因量级不同造成的, 同时剔除异常值和缺失值, 最后得到5 834条数据。
1.2 神经网络空间分布模型神经网络模型的输入层包括经度(Lon)、纬度(Lat)、环境因子(SST, chl a, SSS), 输出层为LA, 隐含层为1层, 结点数从3至20进行逐步增加, 构建不同方案的印度洋长鳍金枪鱼时空分布模型(图 2)。选取均方误差(mean square error, MSE)和平均相对方差(average relative variance, ARV)评价神经网络模型精度。
(1)
 |
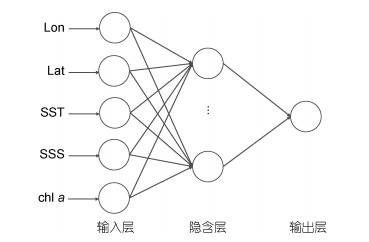| 图 2 神经网络结构示意图 Fig. 2 Schematic diagram of neural network structure |
式(1)中, n表示数据共有n条, Catch为捕捞量, LApredict为模型计算得出的LA数值, Catchactual表示Catch的实际值。MSE越小, 说明模型预测的结果与真实值越接近, 即模型的预测精度高。
(2)式(2)中, n表示数据共有n条, Catch为捕捞量, LApredict为模型计算得出的LA数值, Catchactual表示Catch的实际值, Catchaverage为实际Catch的平均值。同样, ARV越小, 说明模型预测的结果与真实值越接近, 即模型的预测精度高。
一般来说, 交叉验证的目的有三个: (1) 从有限的学习数据中获取尽可能多的有效信息; (2) 从多个方向开始学习样本, 有效的避免陷入局部最小值; (3) 在一定程度上避免过拟合问题(韩萌等, 2008)。因此, 使用交叉验证评价神经网络模型的稳定性。在每次循环时, 将样本按70% (4 083条)和30% (1 751条)的比例随机分为训练样本和测试样本, 模型训练结束后, 利用测试样本计算模型精度指标。此循环进行100次得到MSE、ARV、R2的分布, 再计算每个模型的最小拟合残差值, 通过对比每个模型的不同评价指标选取最优模型。
1.3 模型解释神经网路模型输入变量的解释方法主要有“权重法”和“敏感性分析法”。权重法是将单个变量的权重平方和除以所有变量的权重平方和, 得到输入变量的贡献率(Özesmi et al, 1999)。敏感性分析法是在最优模型基础上, 将要分析的变量按一定步长从其最小值到最大值逐渐变化, 其余变量可设定为其均值、中位数、最大值或最小值, 构建模拟样本, 来预测解释变量与因变量之间的关系(Gevrey et al, 2003; Olden et al, 2004; Wang et al, 2018)。本研究采用这两种方法解释SST、SSS和chl a等环境因子与长鳍金枪鱼分布之间的关系。
1.4 空间分布模式图绘制利用最优模型模型预报2012—2019年各月空间分布LA, 以0.1为步长划分10个等级, 并叠加同期实际生产作业数据, 绘制长鳍金枪鱼空间分布模式图。
2 研究结果 2.1 神经网络空间分布模型精度构建了隐含层节点数不同(3个到20个逐个递增)的18个神经网络模型, 分别基于4 083和1 751个数据集训练和验证了18个神经网络模型。根据MSE和ARV的交叉验证结果, 模型15 (隐含层节点17)、模型16 (隐含层节点18)和模型17 (隐含层节点19)的三个模型的MSE值和ARV值相对较小, 且出现最低平均值。因此最佳结构方案的神经网络模型分别设置为5 : 17 : 1、5 : 18 : 1和5 : 19 : 1。其中5 : 18 : 1表示神经网络的输入层、隐藏层和输出层中的神经元数量分别为5、18和1 (图 3a, 3b)。结合交叉验证运行的R2值分别根据隐含层节点数量的增加显著提升, 模型15 (隐含层节点17)、模型16 (隐含层节点18)和模型17 (隐含层节点19)的平均R2分别为0.159、0.166和0.157。
 |
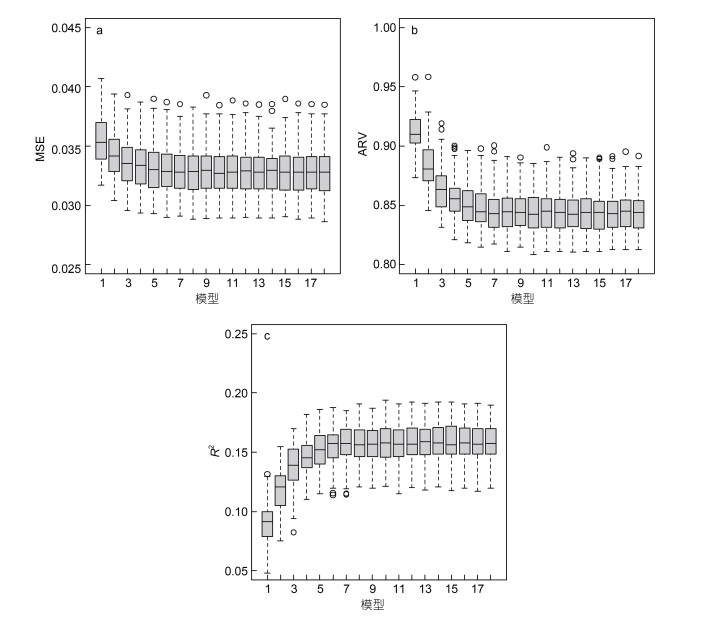| 图 3 神经网络模型不同评价方法评价结果 Fig. 3 Evaluation results of different evaluation methods of neural network model 注: a. MSE评价方法结果; b. ARV评价方法结果; c. R2评价结果 |
计算了每个模型的最小拟合残差值, 在对交叉验证的结果进行求平均, 得到不同模型的最小拟合残差结果(表 1), 模型13 (隐含层节点15)、模型16 (隐含层节点18)和模型15 (隐含层节点17)的最小拟合残差分别为0.028 5、0.023 3、0.242 0。
表 1 神经网络模型最小拟合残差结果 Tab. 1 The minimum residual results of neural network model
| 模型 | 模型结构 | 最小拟合残差值 | 模型 | 模型结构 | 最小拟合残差值 |
| 模型1 | 5-3-1 | 0.058 1 | 模型10 | 5-12-1 | 0.035 1 |
| 模型2 | 5-4-1 | 0.059 3 | 模型11 | 5-13-1 | 0.032 9 |
| 模型3 | 5-5-1 | 0.049 0 | 模型12 | 5-14-1 | 0.035 0 |
| 模型4 | 5-6-1 | 0.043 4 | 模型13 | 5-15-1 | 0.030 4 |
| 模型5 | 5-7-1 | 0.043 1 | 模型14 | 5-16-1 | 0.029 5 |
| 模型6 | 5-8-1 | 0.044 3 | 模型15 | 5-17-1 | 0.028 6 |
| 模型7 | 5-9-1 | 0.045 0 | 模型16 | 5-18-1 | 0.023 3 |
| 模型8 | 5-10-1 | 0.039 9 | 模型17 | 5-19-1 | 0.024 2 |
| 模型9 | 5-11-1 | 0.039 2 | 模型18 | 5-20-1 | 0.030 9 |
结合MSE值、ARV值、R2值和最小拟合残差结果, 从三个模型的选择性能最佳的神经网络模型, 选取模型16 (隐含层节点18)的5-18-1模型作为本文的最终模型, 并使用模型16对2012—2019年的渔业资源丰度进行预测。
2.2 长鳍金枪鱼时空分布影响因子神经网络模型在各层之间的权重连接情况中, 线的粗细表示各因子所占权重的大小(图 4a)。模型16的输入层最高贡献率排名依次为: 纬度(Lat)、经度(Lon)、海表面温度(SST)、叶绿素浓度(chl a)、海表面盐度(SSS) (图 4b)。
 |
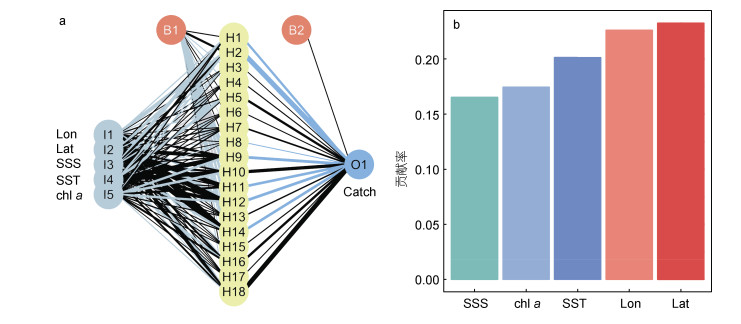| 图 4 模型16(5-18-11)的神经网络模型解释图 Fig. 4 Explanation of the neural network Model 16 (5-18-11) |
分别对环境因子(SST、SSS和chl a)设定步长, 其余输入因子取中位数作为固定值, 通过模型16进行环境因子的敏感性分析(图 5)。模型判断SST适宜范围(LA值大于0.6)在17—31 ℃, 从17 ℃开始, 预测的LA值显著增加, 当至20—21 ℃时获得最高预测LA值。随着SST再增加, 预测LA值有所减少, 但在27 ℃开始, LA值又开始增加, 并于29 ℃获得最高预测LA值; SSS适宜范围在34.5—35.5, 从33.5开始增加; chl a适宜范围在0.080—0.223 mg/m3。
 |
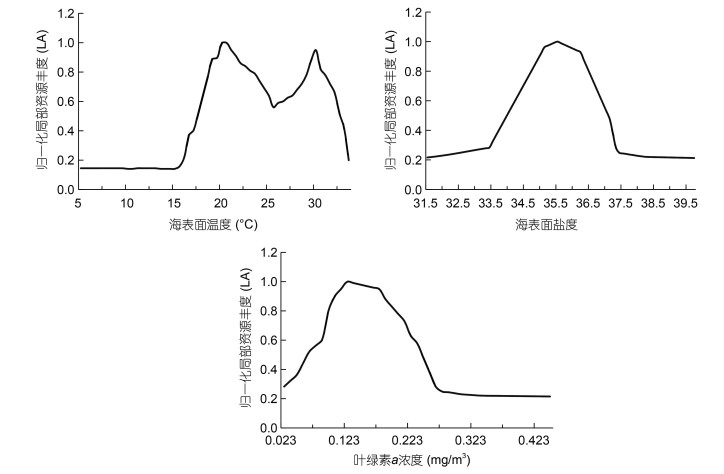| 图 5 长鳍金枪鱼时空分布与环境因子敏感性分析 Fig. 5 Sensitivity analysis of temporal-spatial distribution of T. alalunga and environment factors |
利用最优模型预测了2012—2019年长鳍金枪鱼的空间分布, 并与实际渔获量进行叠加, 以对比预报结果和实际产量分布的吻合程度。总体来看, 最优模型渔场的长鳍金枪鱼局部资源丰度(LA)分布可主要分为四个区域: 低LA区域(预测LA值在0.1—0.4之间), 中LA区域(预测LA值在0.4—0.6之间), 高LA区域(预测LA值在0.6—0.8之间), LA峰值区域(预测LA值在0.8—1.0之间)。
预测LA整体分布区域为5°N—40°S, 30°E—110°E海区, 与实际渔获量分布区域(图 1)较为吻合, 不同年份不同月份的中高低LA分布有所不同。各年高LA区域与整体渔获量分布较为吻合, 分布范围略大于实际高产量范围。通过计算每个区域的LA值(预测值)与中心点原始产量数据(实际值)的MSE和ARV, 量化整体的模型预测结果(表 2)。
表 2 2012—2019年长鳍金枪鱼时空分布预测结果 Tab. 2 Prediction results of the temporal and spatial distribution of T. alalunga from 2012 to 2019
| 年份 | MSE | ARV |
| 2012 | 0.022 43 | 0.582 |
| 2013 | 0.021 61 | 0.506 |
| 2014 | 0.022 82 | 0.768 |
| 2015 | 0.022 41 | 0.727 |
| 2016 | 0.022 81 | 0.575 |
| 2017 | 0.022 61 | 0.272 |
| 2018 | 0.020 96 | 0.255 |
| 2019 | 0.022 88 | 0.411 |
其中, 2012年峰值LA区域在9月至12月较为集中(附录图1)。10月的匹配度最佳, 分布区域为0°—30°S, 60°E—100°E海区, 在其他月份的峰值LA区域较为分散, MSE值为0.022 43, ARV值为0.582。
2013年峰值LA区域在6月和8月较为集中, 分布区域为0°—30°S, 50°E—70°E海区, 3月、9月、11月的匹配度也相对较高, 在1月分布区域较少(附录图2), MSE值为0.021 61, ARV值为0.506。
2014年整体峰值区域较为分散, 在3月和12月相对集中, 分布区域为0°—30°S, 50°E—70°E海区, 但对应实际的产量较低, 2014年存在实际产量明显低于其他年份的情况, LA峰值区域同样在1月份分布较少(图 6a), MSE值为0.022 82, ARV值为0.768。
 |
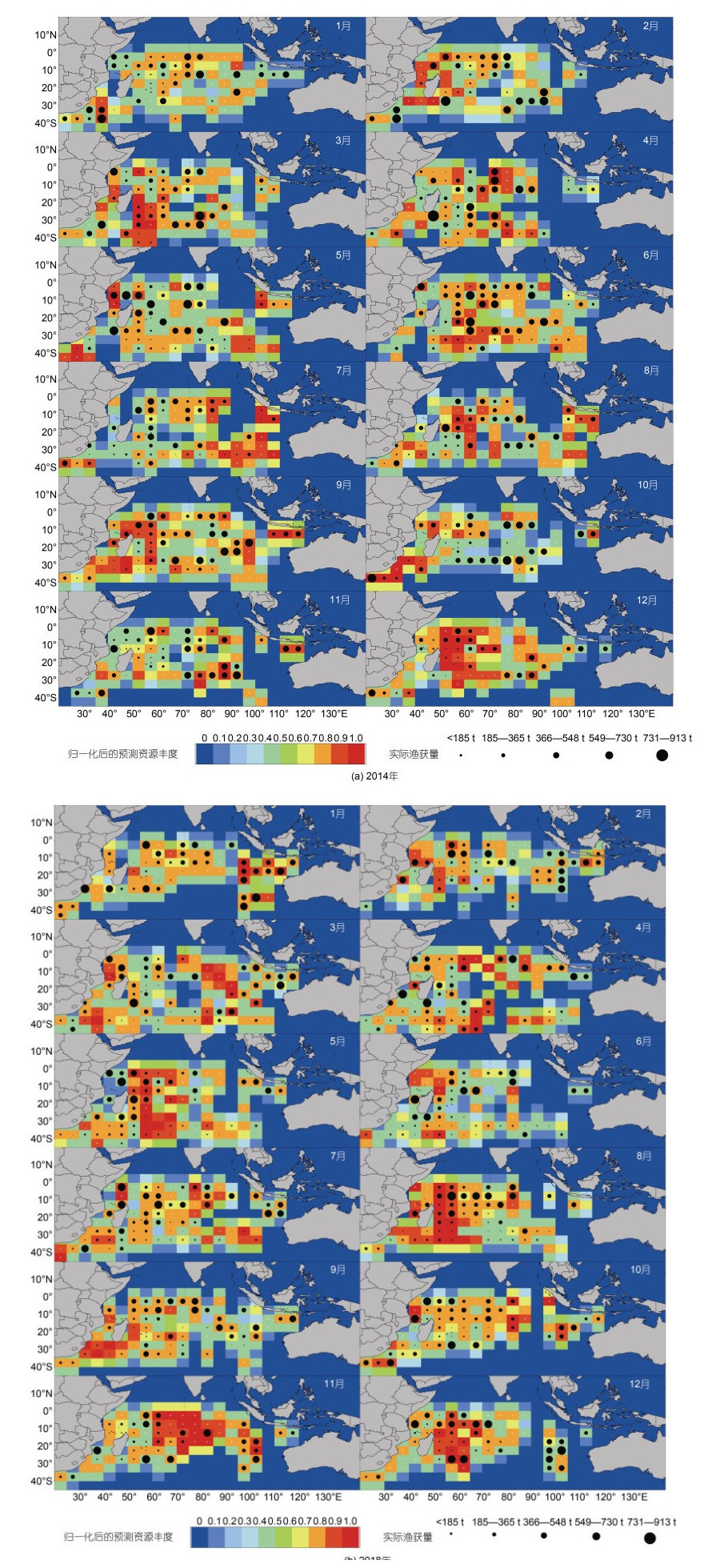| 图 6 模型16 (5-18-11)对2014年(a)和2018年(b)的渔业生产数据预测叠加图 Fig. 6 Model 16 (5-18-11) forecast overlay of production data in 2014 (a) and 2018 (b) |
2015年的峰值区域在3、4、10、12月较为集中, 12月范围最广, 分布区域为0°—40°S, 60°—100°E海区。1、5、11月的分布较少, 其中5月的LA值与实际产量值的匹配度较差(附录图3), MSE值为0.022 41, ARV值为0.727。
2016年的峰值区域在10月至12月较为集中, 10月范围最广, 分布区域为0°—30°S, 40°E—70°E海区, 其余月份分布较为分散, 在2月、5月的分布较少(附录图4), MSE值为0.022 81, ARV值为0.575。
2017年峰值区域整体较为分散, 高峰值月份(8、10、12月)均呈现带状分布, 7月和4月的高峰值区域与实际产量匹配度较差, 1月至3月和11月的分布较少(附录图5), MSE值为0.022 61, ARV值为0.272。
2018年整体预测区域较广, 且每月峰值区域分布面积高于其他年份, 2018年的峰值区域在5月、8月、11月、12月较为集中, 其中12月的匹配度相对较高, 主要集中在0°—30°S, 55°—70°E海区(图 6b), MSE值为0.020 96, ARV值为0.255。
2019年峰值区域在3月和12月匹配度和集中度较高, 分布区域为0°—15°S, 40°—60°E海区, 4月至9月的峰值区域分布较为分散, 在11月的分布较少(附录图6), MSE值为0.022 88, ARV值为0.411。
3 讨论 3.1 神经网络模型渔场预测结果本研究在以最优神经网络模型进行预测的基础上, 以2012—2019年的真实渔获数据对印度洋长鳍金枪鱼分布进行验证。整体上实际捕捞产量分布与预测分布较为一致, 预测高的LA区域很好对应实际高产量区域, 定量结果表明, 预测结果平均MSE值在0.022 32, 平均ARV值在0.511, 模型预测结果良好(表 2, 图 6)。2018年整体预测结果好于其他年份, 其ARV值显著低于其他年份, 2014年预测结果较差, ARV值高于其他年份(表 2, 图 6)。此精度达到进一步分析探索的要求(Wang et al, 2018)。
3.2 长鳍金枪鱼时空分布与环境因子关系印度洋长鳍金枪鱼局部资源丰度与SST、SSS和chl a均存在显著关系, 其中贡献值最高为SST(图 4b)。先前有部分研究得到太平洋海域中的长鳍金枪鱼资源丰度变化与温度随季节变化不明显(范江涛等, 2011; 闫敏等, 2015; 王震等, 2017), 这些研究的地理区域靠近热带, 且范围较小, 从而SST的季节变化较小。而本研究中敏感性分析发现LA值随SST增加变化明显(图 5)。因为印度洋海域区域较大, 纬度纵跨温带和热带区域, 温度随季节变化明显, 从而造成了不同季节的月份存在较为明显的预测差异。樊伟等(2007)指出, 长鳍金枪鱼渔获量随SST变化, 在20 ℃和29 ℃的海域附近呈双峰型, 与本文21 ℃与29 ℃左右峰值区域基本相同。高LA区域横跨17.5—32 ℃区域, 峰值LA区域所在SST范围为19.5—23 ℃区域以及28—30.5 ℃区域(图 5)。
海表温度直接或间接地影响渔场的分布、洄游的路线等(龙华, 2005; Sundermeyer et al, 2006; Wang et al, 2009; 苏艳莉, 2015)。在进行长鳍金枪鱼的时空分布与环境因子的研究中, 一般都选用海表温度作为环境因子之一(郭爱等, 2009; 杨胜龙等, 2010; Lan et al, 2012; 储宇航等, 2016)。叶泰豪等(2012)的研究发现, 海表温度对长鳍金枪鱼分布有显著影响, 海表温度同样是表层海水中未成熟的长鳍金枪鱼个体单位捕捞努力量(CPUE)的一个重要预测因子, 而长鳍金枪鱼幼体鱼的生长也与温带水域有关, 其表层有大量捕食对象。长鳍金枪鱼成年鱼主要分布在亚热带和热带水域, 其水域温度适宜产卵(张嘉容, 2020)。本文最优预报模型结构的解释, 以及海表面温度(SST)在模型中影响程度的结论与其他学者的研究结果基本上是一致的。但模型也存在局部集中高估问题, 可能是由于解释变量不足, 因此在今后的研究中, 须添加其他海洋环境因素, 如不同深度水温(郭刚刚等, 2016), 溶解氧等增强模型的容错率和泛用性。
海表盐度贡献率低, 对长鳍金枪鱼分布影响较小, 其最适宜范围在34.5—35.5, 与蒋汉凌(2014)、范永超等(2017)和张亚男等(2020)研究结果一致。另外, 不同深度盐度可以通过溶解气体、海流等其他环境因素对长鳍金枪鱼渔场分布造成间接影响(张嘉容, 2020), 日后可进一步考虑。
叶绿素a浓度通常影响长鳍金枪鱼的食物链, 从而间接影响长鳍金枪鱼渔场的分布(Sagarminaga et al, 2014), 本文叶绿素a浓度的贡献率仅次于海表温度, 最适宜范围为0.08—0.223 mg/m3, 略小于张亚男等(2020)HSI模型中的结果(0.03—0.22 mg/m3), 其中除11月份(0.03—0.06 mg/m3)外, 与本文结果相同。对应以往研究总结的叶绿素a浓度为影响长鳍金枪鱼分布的重要原因(闫敏等, 2015)。
3.3 长鳍金枪鱼时空分布规律总体来看, 不同年份MSE变化趋势与ARV相同(表 2, 图 7)。每年下半年(9—12月)的高值LA区域较为集中, 易形成良好渔场, 其余月份相对分散(图 6)。一旦发生海流、水团、温跃层等未知因素的季节性变化, 极易造成渔场年间显著变化, 预测难度增加, 与部分学者研究得到的结果相同(马璐璐等, 2018; 张亚男等, 2020), 本研究的3月、5月、11月为季节过渡月, 由于环境数据变化较大, 模型不稳定, 从而造成了部分年份高, 部分年份低的情况。张亚男等(2020)构建的印度洋长鳍金枪鱼栖息地指数模型中提出, 11月的最适温度分布在25—27 ℃, 而SST敏感性分析结果(图 5)中, 该段区域的LA值相对低于其他高LA区域的温度范围, 对应了图 6中部分年份11月份预测结果较差的现象。各年模型预测的渔场区域较为集中, 交叉各年重叠区域得到模型预测的渔业资源丰度最高的区域集中在0°—30°, 50°E—70°E的印度洋海域。
 |
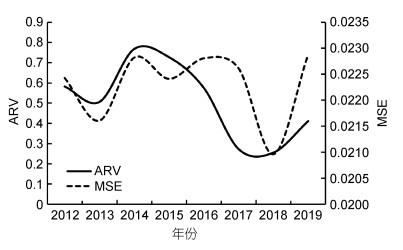| 图 7 2012—2019年长鳍金枪鱼时空分布预测结果 Fig. 7 Prediction results of the temporal and spatial distribution of T. alalunga from 2012 to 2019 |
本研究在季节的过渡月份的预测结果存在误差, 原因可能源自: (1) 渔业依赖数据(fishery-dependent data)自身分布不均匀特性; (2) 缺少其他生态环境因子。未来可从数据抽样技术, 获取更丰富的环境因子等入手进一步提高模型精度。
4 结论充分理解印度洋长鳍金枪鱼渔业资源丰度时空分布, 将有助于减少捕捞船队对于鱼群的搜索时间和与搜索成本, 以及预测资源如何应对捕捞策略和管理的可能变化至关重要(Lehodey et al, 1997)。本文研究与先前研究不同之处在于BP神经网络模型中的应用, 以探索印度洋长鳍金枪鱼的空间分布与栖息地海洋特征之间的关系。环境变量和资源丰度存在非线性关系, 构建的分布模型复杂。本研究描述了神经网络模型的构建、训练、验证、解释和预测的全过程, 提供了BP神经网络模型在渔业资源分布中的应用范例。模型预测效果与其他机器学习方法的横向比较有待进一步研究。
电子附件材料:
参考文献
马孟磊, 陈新军, 陈作志, 等. 2017. 南太平洋长鳍金枪鱼栖息地指数模型的比较研究. 广东海洋大学学报, 37(3): 59-66 DOI:10.3969/j.issn.1673-9159.2017.03.009 |
马璐璐, 朱江峰, 耿喆, 等. 2018. 运用生物量动态模型评估印度洋长鳍金枪鱼资源. 上海海洋大学学报, 27(2): 259-264 |
王震, 陈新军, 雷林. 2017. 东太平洋长鳍金枪鱼栖息地指数模型的比较. 广东海洋大学学报, 37(1): 58-64 DOI:10.3969/j.issn.1673-9159.2017.01.010 |
牛明香, 李显森, 徐玉成. 2012. 基于广义可加模型和案例推理的东南太平洋智利竹筴鱼中心渔场预报. 海洋环境科学, 31(1): 30-33 DOI:10.3969/j.issn.1007-6336.2012.01.007 |
毛江美, 陈新军, 余景. 2016. 基于神经网络的南太平洋长鳍金枪鱼渔场预报. 海洋学报, 38(10): 34-43 DOI:10.3969/j.issn.0253-4193.2016.10.004 |
方舟, 陈新军, 李建华, 等. 2013. 阿根廷专属经济区内鱿钓渔场分布及其与表温关系. 上海海洋大学学报, 22(1): 134-140 |
龙华. 2005. 温度对鱼类生存的影响. 中山大学学报(自然科学版), 44(S1): 254-257 |
叶泰豪, 冯波, 颜云榕, 等. 2012. 中西太平洋鲣渔场与温盐垂直结构关系的研究. 海洋湖沼通报, (1): 49-55 DOI:10.3969/j.issn.1003-6482.2012.01.007 |
朱江峰, 戴小杰, 官文江. 2014. 印度洋长鳍金枪鱼资源评估. 渔业科学进展, 35(1): 1-8 DOI:10.3969/j.issn.1000-7075.2014.01.001 |
闫敏, 张衡, 伍玉梅, 等. 2015. 基于GAM模型研究时空及环境因子对南太平洋长鳍金枪鱼渔场的影响. 大连海洋大学学报, 30(6): 681-685 |
苏奋振, 周成虎, 杜云艳, 等. 2003. 海洋渔业资源地理信息系统应用的时空问题. 应用生态学报, 14(9): 1569-1572 DOI:10.3321/j.issn:1001-9332.2003.09.036 |
苏艳莉. 2015. 环境温度对鱼类的影响及预防研究. 农技服务, 32(7): 191-192, 181 DOI:10.3969/j.issn.1004-8421.2015.07.150 |
杨胜龙, 周甦芳, 周为峰, 等. 2010. 基于Argo数据的中西太平洋鲣渔获量与水温、表层盐度关系的初步研究. 大连水产学院学报, 25(1): 34-40 DOI:10.3969/j.issn.1000-9957.2010.01.007 |
吴风霞, 李纯厚, 戴明. 2009. 人工神经网络在海洋科学中的应用. 南方水产, 5(1): 75-80 DOI:10.3969/j.issn.1673-2227.2009.01.013 |
汪金涛, 高峰, 雷林, 等. 2014. 基于神经网络的东南太平洋茎柔鱼渔场预报模型的建立及解释. 海洋渔业, 36(2): 131-137 DOI:10.3969/j.issn.1004-2490.2014.02.006 |
张月霞, 丘仲锋, 伍玉梅, 等. 2009. 基于案例推理的东海区鲐鱼中心渔场预报. 海洋科学, 33(6): 8-11 |
张亚男, 官文江, 李阳东. 2020. 印度洋长鳍金枪鱼栖息地指数模型的构建与验证. 上海海洋大学学报, 29(2): 268-279 |
张嘉容, 2020. 南太平洋长鳍金枪鱼栖息地预测模型建构研究. 上海: 上海海洋大学硕士学位论文
|
陈洋洋, 陈新军, 郭立新, 等. 2017. 基于BP神经网络的中西太平洋鲣鱼渔场预报模型构建与比较. 广东海洋大学学报, 37(6): 65-73 DOI:10.3969/j.issn.1673-9159.2017.06.011 |
范永超, 戴小杰, 朱江峰, 等. 2017. 南太平洋长鳍金枪鱼延绳钓渔业CPUE标准化. 海洋湖沼通报, (1): 122-132 |
范江涛, 陈新军, 钱卫国, 等. 2011. 南太平洋长鳍金枪鱼渔场预报模型研究. 广东海洋大学学报, 31(6): 61-67 DOI:10.3969/j.issn.1673-9159.2011.06.010 |
奈须敬二. 1995. 金枪鱼类的渔场环境. 齐鲁渔业, (3): 45 |
周为峰, 黎安舟, 纪世建, 等. 2018. 基于贝叶斯分类器的南海黄鳍金枪鱼渔场预报模型. 海洋湖沼通报, (1): 116-122 |
官文江, 朱江峰, 高峰. 2018. 印度洋长鳍金枪鱼资源评估的影响因素分析. 中国水产科学, 25(5): 1102-1114 |
郭爱, 陈新军. 2005. ENSO与中西太平洋金枪鱼围网资源丰度及其渔场变动的关系. 海洋渔业, 27(4): 338-342 DOI:10.3969/j.issn.1004-2490.2005.04.015 |
郭爱, 陈新军. 2009. 利用水温垂直结构研究中西太平洋鲣鱼栖息地指数. 海洋渔业, 31(1): 1-9 DOI:10.3969/j.issn.1004-2490.2009.01.001 |
郭刚刚, 张胜茂, 樊伟, 等. 2016. 南太平洋长鳍金枪鱼垂直活动水层空间分析. 南方水产科学, 12(5): 123-130 DOI:10.3969/j.issn.2095-0780.2016.05.016 |
唐浩, 许柳雄, 陈新军, 等. 2013. 基于GAM模型研究时空及环境因子对中西太平洋鲣鱼渔场的影响. 海洋环境科学, 32(4): 518-522 |
崔雪森, 唐峰华, 张衡, 等. 2015. 基于朴素贝叶斯的西北太平洋柔鱼渔场预报模型的建立. 中国海洋大学学报, 45(2): 37-43 |
崔雪森, 唐峰华, 周为峰, 等. 2016. 基于支持向量机的西北太平洋柔鱼渔场预报模型构建. 南方水产科学, 12(5): 1-7 DOI:10.3969/j.issn.2095-0780.2016.05.001 |
蒋汉凌, 2014. 南太平洋长鳍金枪鱼渔场与环境因素关系的研究. 上海: 上海海洋大学硕士学位论文
|
韩萌, 丁剑. 2008. 基于交叉验证的BP算法的改进与实现. 计算机工程与设计, 29(14): 3738-3739, 3742 |
储宇航, 戴小杰, 田思泉, 等. 2016. 南太平洋延绳钓长鳍金枪鱼生物学组成及其与栖息环境关系. 海洋渔业, 38(2): 130-139 DOI:10.3969/j.issn.1004-2490.2016.02.003 |
樊伟, 张晶, 周为峰. 2007. 南太平洋长鳍金枪鱼延绳钓渔场与海水表层温度的关系分析. 大连水产学院学报, 22(5): 366-371 DOI:10.3969/j.issn.1000-9957.2007.05.010 |
Brosse S, Guegan J F, Tourenq J N et al, 1999. The use of artificial neural networks to assess fish abundance and spatial occupancy in the littoral zone of a mesotrophic lake. Ecological Modelling, 120(2/3): 299-311 |
Chen I C, Lee P F, Tzeng W N, 2005. Distribution of albacore (Thunnus alalunga) in the Indian Ocean and its relation to environmental factors. Fisheries Oceanography, 14(1): 71-80 DOI:10.1111/j.1365-2419.2004.00322.x |
Chen D C, Ware D M, 1999. A neural network model for forecasting fish stock recruitment. Canadian Journal of Fisheries and Aquatic Sciences, 56(12): 2385-2396 DOI:10.1139/f99-178 |
Gevrey M, Dimopoulos I, Lek S, 2003. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecological Modelling, 160(3): 249-264 DOI:10.1016/S0304-3800(02)00257-0 |
Demuth H B, Beale M H, De Jess O et al, 2014. Neural network design. Stillwater: Oklahoma State University
|
Hanson P J, Vaughan D S, Narayan S, 2006. Forecasting annual harvests of Atlantic and Gulf menhaden. North American Journal of Fisheries Management, 26(3): 753-764 DOI:10.1577/M04-096.1 |
Hawing K, Aoki I, Komatsu T et al, 1996. Forecasting for the catch of Jack mackerels in the Komekami set net by a neural network. Bulletin of the Japanese Society of Fisheries Oceanography, 60(2): 136-142 |
Lan K W, Kawamura H, Lee M A et al, 2012. Relationship between albacore (Thunnus alalunga) fishing grounds in the Indian Ocean and the thermal environment revealed by cloud-free microwave sea surface temperature. Fisheries Research, 113(1): 1-7 DOI:10.1016/j.fishres.2011.08.017 |
Laurs R M, Fiedler P C, Montgomery D R, 1984. Albacore tuna catch distributions relative to environmental features observed from satellites. Deep Sea Research Part A. Oceanographic Research Papers, 31(9): 1085-1099 |
Lee L K, Hsu C C, Chang F C, 2014. Albacore (Thunnus alalunga) CPUE trend from Indian Core Albacore Areas based on Taiwanese longline catch and effort statistics dating from 1980 to 2013. IOTC-2014-WPTmT05-19l
|
Lehodey P, Bertignac M, Hampton J et al, 1997. El Niño Southern Oscillation and tuna in the western Pacific. Nature, 389(6652): 715-718 DOI:10.1038/39575 |
Lucas P, 2004. Bayesian analysis, pattern analysis, and data mining in health care. Current Opinion in Critical Care, 10(5): 399-403 DOI:10.1097/01.ccx.0000141546.74590.d6 |
Olden J D, Joy M K, Death R G, 2004. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecological Modelling, 178(3/4): 389-397 |
Özesmi S L, Özesmi U, 1999. An artificial neural network approach to spatial habitat modelling with interspecific interaction. Ecological Modelling, 116(1): 15-31 DOI:10.1016/S0304-3800(98)00149-5 |
Pan R, Yang Q, Pan S J, 2007. Mining competent case bases for case-based reasoning. Artificial Intelligence, 171(16/17): 1039-1068 |
Sagarminaga Y, Arrizabalaga H, 2014. Relationship of Northeast Atlantic albacore juveniles with surface thermal and chlorophyll-a fronts. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 107: 54-63 DOI:10.1016/j.dsr2.2013.11.006 |
Sundermeyer M A, Rothschild B J, Robinson A R, 2006. Assessment of environmental correlates with the distribution of fish stocks using a spatially explicit model. Ecological Modelling, 197(1/2): 116-132 |
Wang J T, Chen X J, Staples K W et al, 2018. The skipjack tuna fishery in the west-central Pacific Ocean: applying neural networks to detect habitat preferences. Fisheries Science, 84(2): 309-321 DOI:10.1007/s12562-017-1161-6 |
Wang N, Xu X L, Kestemont P, 2009. Effect of temperature and feeding frequency on growth performances, feed efficiency and body composition of pikeperch juveniles (Sander lucioperca). Aquaculture, 289(1/2): 70-73 |
Zainuddin M, Saitoh K, SAITOH S I, 2008. Albacore (Thunnus alalunga) fishing ground in relation to oceanographic conditions in the western North Pacific Ocean using remotely sensed satellite data. Fisheries Oceanography, 17(2): 61-73 DOI:10.1111/j.1365-2419.2008.00461.x |