
中国海洋湖沼学会主办。
文章信息
- 乔梦甜, 陈娟, 曹安州, 宋金宝. 2021.
- QIAO Meng-Tian, CHEN Juan, CAO An-Zhou, SONG Jin-Bao. 2021.
- 吕宋海峡及周边海域湍流混合的时空分布特征研究
- SPATIAL AND TEMPORAL DISTRIBUTION OF TURBULENT MIXING IN THE LUZON STRAIT AND NEARBY SEA
- 海洋与湖沼, 52(5): 1115-1124
- Oceanologia et Limnologia Sinica, 52(5): 1115-1124.
- http://dx.doi.org/10.11693/hyhz20210100009
文章历史
-
收稿日期:2021-01-11
收修改稿日期:2021-04-12
湍流混合影响着海洋的水体交换、物质输运和能量输运, 因此对于湍流混合的时空分布特征及影响因素的研究尤为重要。海洋内部混合的主要机制是内波破碎, 海洋内波的产生主要来自以下两种物理过程(Wunsch et al, 2004; 管守德, 2014): 其一是海表面风场激发的近惯性波, 向温跃层乃至海洋深层辐射; 其二是正压潮流经变化的海底地形时激发的内潮。根据Munk等(1998)的估计, 维持全球海洋的层结大约需要2.1 TW的能量, 其中的0.9 TW与内潮直接相关, 全球的风生近惯性能量约为0.3—1.5 TW(Alford, 2001, 2003; Watanabe et al, 2002; Jiang et al, 2005; Furuichi et al, 2008; Simmons et al, 2012; Rimac et al, 2013)。
内潮是具有天文潮频率的内波, 主要通过正压潮与地形的作用产生, 并将正压能量转移到斜压场能量。高模态内潮在源地耗散, 低模态内潮能够传播到较远海区。内潮在传播过程中发生破碎, 使能量得到重新分配, 从大尺度串级到更小尺度上, 从而导致湍流混合增强(Egbert et al, 2000; St Laurent et al, 2002; Legg et al, 2006)。
风输入海洋中的能量中有一部分在海洋上层很浅的区域内耗散, 并不能为深层混合提供能量(Zhai et al, 2009), 剩下的能量以近惯性内波的形式向深处传播。由于近惯性内波存在很强的剪切, 可以将自身的能量通过剪切不稳定机制转化为小尺度湍流运动的能量, 从而成为海洋内部混合的重要能量来源。通过分析锚定浮标资料, Alford等(2007)发现近惯性内波可以一直向下传播到海底区域。
由于潮汐和海表面风应力存在不同时间尺度上的变化, 可以推测混合也应表现出相应的时间变化。理解混合的时间变化特征及其影响机制对于改进气候模式对大洋环流变化的模拟和预测能力具有十分重要的作用。但到目前为止, 对混合在季节和更长时间尺度上的低频变化特征的认识还十分有限。Jing等(2010)通过分析137°E断面上的历史观测资料, 发现在海洋上层1 500 m范围内, 混合存在明显的季节变化, 并且这种季节变化与海表面风应力的季节变化具有较好的相关性。在副热带西北太平洋处的观测也表明混合的季节变化与风的作用密切相关(Jing et al, 2011), 但是该处混合的季节变化只存在于上层600 m。Whalen等(2018)通过研究30°—45°N区域的混合, 发现混合扩散率在2 000 m的整个深度上都存在季节性循环, 且这种循环与风输入的近惯性能通量的季节性循环相关。因此, 在不同海区, 风应力及其影响深度有很大差异, 其他海域混合强度与风输入的近惯性能通量之间的关系尚需进一步研究。
南海是西太平洋重要的边缘海, 拥有宽广的大陆架和深度超过3 000 m的中央海盆, 通过吕宋海峡与西太平洋相通。特殊的地形条件赋予了南海多尺度的海洋动力过程, 因此, 南海具有湍流混合强烈的特征(Tian et al, 2009; Liu et al, 2012; Yang et al, 2014), 也是湍流混合研究的热点区域。Tian等(2009)研究了沿21°N断面的湍流混合分布, 发现南海1 000 m水深以下的混合比太平洋大2个数量级。Lozovatsky等(2013)研究了南海北部有限区域湍流耗散的空间结构和时间变异性。Yang等(2014)认为南海陆架处的湍流强度大于陆坡处。Yang等(2016)发现在南海北部的湍流混合扩散率高达O(10-3 m2/s)。近年来, 有关南海和吕宋海峡的内潮能量及耗散也有不少相关的数值模拟工作, Wang等(2016)考虑了局地和远处传来的内潮的影响, 发现台湾东北地区的混合扩散系数比南海北部大陆架的混合扩散系数大1—2个数量级; Xu等(2016)发现沿台湾东北部大陆坡产生的M2内潮能量强于南海陆坡和俄勒冈陆架等其他区域; Chang等(2019)通过数值实验发现, 台湾东北部地形陡峭处的M2内潮能量更高, 垂向混合也越强。Cao等(2019)频谱分析的结果表明, 南海北部的剪切由近惯性波和全日内潮主导。除了由内潮维持之外, 南海的强混合还可能与黑潮入侵和中尺度涡旋等因素有关(Kunze et al, 2006; Jing et al, 2013; 陈娟等, 2020)。
本文基于1992—2002年的温盐深仪(conductivity-temperature-depth, CTD)现场观测资料与2012—2016年的Argo数据, 利用细尺度参数化方法研究了12°—30°N、115°—129°E区域内的湍流混合时空分布特征及其影响因素, 其中包含南海、吕宋海峡和菲律宾海三个具有代表性的海洋地形环境, 并探讨了地形粗糙度、内潮和风输入的近惯性能通量对海洋湍流混合的影响。
1 数据与方法 1.1 数据资料本文选取数据的空间范围均为12°—30°N、115°—129°E(图 1), 用到了温盐数据、地形数据和风场数据, 具体介绍如下:
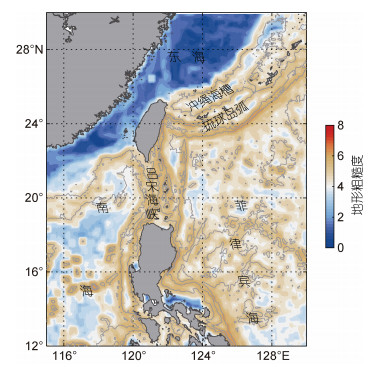 |
| 图 1 研究区域的地形粗糙度(单位: m2; 以10为底的对数坐标) Fig. 1 The topographic roughness of the region 注: 灰色实线为等深线, 只作辅助标注, 不作具体描述 |
温盐数据来自美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA, https://www.nodc.noaa.gov/)提供的CTD数据及中国Argo实时资料中心(http://www.argo.org.cn/)提供的Argo实测资料, 用于计算湍流混合扩散率。本文选取了1992—2002年(其中缺乏1999年数据)、垂向分辨率小于10 m、观测深度大于1 000 m的CTD数据, 和2012—2016年、垂向分辨率小于10 m、观测深度大于600 m的Argo数据。选取的CTD和Argo数据的剖面位置如图 2a和图 2b所示。地形数据使用的是ETOPO1数据(https://ngdc.noaa.gov/mgg/global/global.html), 分辨率为1′×1′, 用于计算地形粗糙度。本文定义的地形粗糙度(图 1)为1/3°×1/3°网格区域内地形高度的方差(Kunze et al, 2006)。
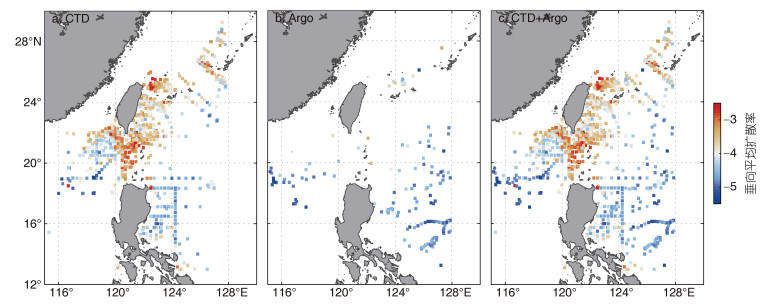 |
| 图 2 基于CTD (a)、Argo (b)以及CTD和Argo (c)数据的垂向平均扩散率(单位: m2/s; 以10为底的对数坐标)空间分布 Fig. 2 The depth-averaged diffusivity (unit: m2/s; logarithmic scale) based on (a) CTD data, (b) Argo data, and (c) CTD+Argo data |
风场资料为美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)发布的高分辨率CFSR (Climate Forecast System Reanalysis, https://rda.ucar.edu/)再分析风场资料, 时间分辨率为6 h, 空间分辨率约为38 km, 选取时间范围同CTD温盐数据, 用于计算风输入的近惯性能通量。
1.2 细尺度参数化方法在过去的几十年里, 发展了大量的经验的、统计的以及理论的模型将细尺度O(10—100 m)上的由内波引起的垂向剪切和应变与耗散速率以及扩散系数联系起来。最基本的观点就是内波间的弱非线性相互作用将能量从大尺度不断地向小尺度传播, 最终引起内波的破碎, 并引发湍流混合。Gregg(1989)最早将细尺度参数化方法用于细尺度流速观测资料, 经过诸多学者们的多次研究改进, Kunze等(2006)提出了基于应变的细尺度参数化方法计算海洋内部混合扩散系数, 其表达式为
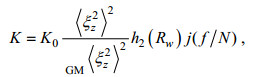 (1)
(1)其中, K0=5×10-6 m2/s; 〈ξz2〉2代表观测得到的细尺度上的应变方差; GM〈ξz2〉2是GM应变谱的方差(Gregg et al, 1991); h2(Rω)和j(f/N)分别为参数化方案中关于内波结构和纬度影响的修正项。
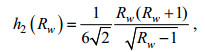 (2)
(2)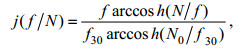 (3)
(3)其中, Rw表示剪切应变方差比, 可以通过流速和位势密度计算, 但由于流速剖面资料相对温盐资料来说更为匮乏, 难以直接估算, 在西北太平洋通常直接设定为常数7 (Kunze et al, 2006); 对于GM谱, GMRw=3; N是浮力频率; N0=5.2×10-3 rad/s; f为科里奥利频率; f30为南北纬30°的科里奥利频率。
在混合层与季节性温跃层的影响下, 基于细尺度参数化方法计算的混合扩散系数有很大的误差, 因此本文只采用300 m以深的剖面数据, 将每个CTD站点和Argo浮标的剖面资料划分为一系列300 m长的子剖面, 对每个300 m的子剖面计算湍流混合系数, 每段子剖面上的垂向应变的计算公式为
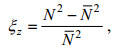 (4)
(4)其中, 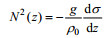
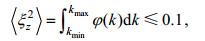 (5)
(5)从而得到最大波数kmax, 然后在同样的波束区间计算GM应变方差
 (6)
(6)其中, E0=6.3×10-5是无量纲能量; b=1 300 m是温跃层的垂向尺度; j*=3是参考模态; k*=(πj*N)/(bN0)是参考波数(Gregg et al, 1991)。
细尺度参数化方案是发展中的参数化方案, 该方案适用于开阔大洋(Kunze et al, 2006), 而不适用于发生在大陆架、峡谷的混合, 也不适用于孤立波, 水跃, 双扩散等其他机制引发的混合, 以及内波直接破碎引起的混合(李颖, 2015)。
1.3 内潮体力计算为探讨内潮对混合的影响, 本文计算了该区域内的内潮体力, 根据Baines(1982)和Bai等(2014), 内潮体力F的计算公式为
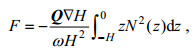 (7)
(7)其中, ω为潮汐角频率; z为垂向坐标, 海表面z=0, 且向上为正; N(z)为局地浮力频率; Q为正压潮流, Q=(Qx, Qy)=(uH, vh), u和v为正压潮流的纬向分量和经向分量, H为局地水深。
正压潮数据来自俄勒冈州立大学潮汐反演软件(OTIS7.1, 由Egbert等于2002年开发, http://volkov.oce.orst.edu/tides/otis.html), 水平分辨率为1/4°; 用于计算浮力频率N的温盐数据来自NOAA的国家海洋数据中心海洋气象实验室的海洋气候态数据集产品WOA13数据(https://www.nodc.noaa.gov/OC5/woa13/woa13data.html), 并插值到每10 m一层, 水深数据同样使用ETOPO1地形数据。
1.4 风输入近惯性能通量的计算方法风场向海洋输入的近惯性能通量为
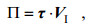 (8)
(8)其中, τ为风应力; VI=(u, v)为混合层近惯性流速。本文采用Pollard-Millard平板模型计算混合层近惯性流速(Pollard et al, 1970; Pollard, 1980; D’Asaro, 1985; Alford, 2001, 2003; Cao et al, 2018)。通过输入风应力、设置混合层厚度和衰减系数, 平板模型可以模拟混合层对风应力的近惯性流速响应。平板模型的控制方程为
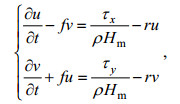 (9)
(9)其中, u和v分别是东西和南北方向上的流速分量; t是时间; f是科氏参数; τx和τy分别是东西和南北方向上的风应力; ρ是海水密度, 本文取1 023 kg/m3; Hm是混合层厚度(本文统一取50 m); r是衰减系数。风应力的计算公式为
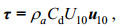 (10)
(10)其中, ρa是空气密度, 本文取为1.29 kg/m3; U10和u10分别代表海面10 m处的风速大小和风速矢量; Cd是风应力拖曳系数(Oey et al, 2006):
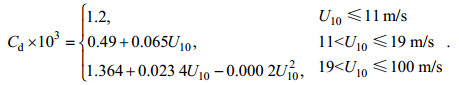 (11)
(11)本文采用Alford(2003)提出的谱方法对平板模型进行求解。在谱方法中, 衰减系数r不是一个常数, 而是随频率σ变化的函数:
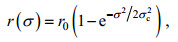 (12)
(12)其中, r0=0.15f, σc=f/2(Alford, 2003)。
2 结果 2.1 吕宋海峡及周边海域垂向混合的空间分布本文共筛选出符合要求的CTD站点剖面1 439个(图 2a), Argo浮标剖面167个(图 2b); 基于细尺度参数化方法, 从300 m起, 每300 m片段为一个子剖面, 计算混合扩散率; 将每个剖面的计算结果进行垂向平均, 得到吕宋海峡及周边海域垂向混合的空间分布, 如图 2所示。从整体上看, 基于CTD数据估算的混合扩散率与基于Argo数据估算的混合扩散率在空间分布上具有很高的一致性: 混合扩散率在吕宋海峡最高, 尤其是121°E处, 可达4×10-3 m2/s, 比同纬度的南海及菲律宾海均高出1—2个量级, 即在21°N附近的断面上, 海洋内部混合呈现明显的东西向差异。此外, 在东海陆坡、冲绳海槽以及中国台湾东部沿岸也具有较强的混合, 特别是在东海陆坡处, 混合强度与吕宋海峡相当。
南海海域在18°—22.5°N范围内呈现纬度越高, 混合越强的特征, 南海北部陆坡处的混合扩散率约为3×10-4 m2/s, 比南海中央海盆高1—2个量级。菲律宾海在吕宋岛东部近岸处的混合强于离岸处的混合, 与南海不同的是, 菲律宾海的混合在纬向上并没有明显的空间变异性。尽管CTD(图 2a)和Argo(图 2b)数据的观测年份不同, 但结果均显示17°—20°N的南海和菲律宾海的混合差别不大, 平均垂向混合扩散率均在3×10-5 m2/s左右。
图 3是基于CTD数据计算的300—2 700 m, 每个300 m子剖面的混合扩散率。结果显示, 吕宋海峡及东海陆坡处从海洋上层到近底层的整个深度都具有强烈的混合, 在300—600 m最强, 混合扩散率高达3×10-3 m2/s, 而菲律宾海的混合随深度加深而增强。Tian等(2009)研究了沿21°N断面的湍流混合分布, 发现南海1 000 m水深以下的混合比太平洋大2个数量级, 由于本文使用的观测数据在21°N断面较少, 无法再次验证Tian等(2009)的结果, 但本文发现在22°N断面上, 南海900 m水深以下的混合与菲律宾海相差不大, 这种差异可能与内潮强度的空间分布有关。
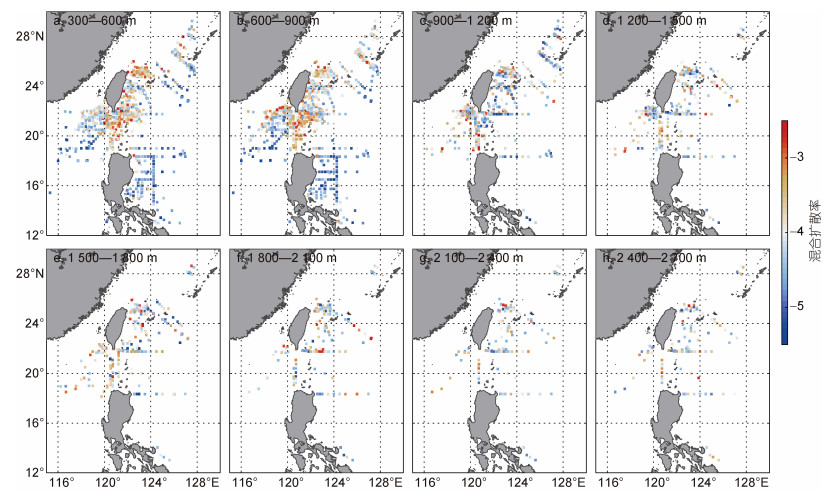 |
| 图 3 300—2 700 m深度的每个300 m子剖面的混合扩散率(单位: m2/s; 以10为底的对数坐标) Fig. 3 The depth-averaged diffusivity (unit: m2/s; logarithmic scale) for sections from 300 to 2700 m |
本文选取CTD观测数据较多的1992—2002年分析研究区域海洋内部混合扩散率的年际和季节变化特征。如图 4所示, 该区域内混合扩散率整体呈现出吕宋海峡和东海陆坡处混合最强, 南海北部及菲律宾海混合较弱的特征, 其年际变化并不显著。并且, 吕宋海峡和东海陆坡处一年四季都维持着较强的混合(图 5)。
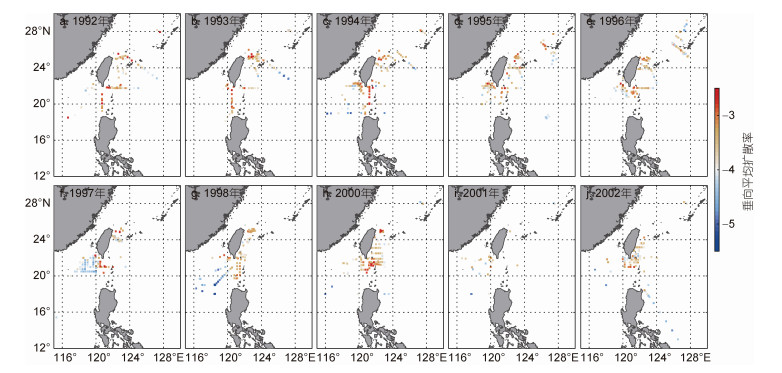 |
| 图 4 1992—2002年垂向平均扩散率(单位: m2/s; 以10为底的对数坐标)空间分布 Fig. 4 The depth-averaged diffusivity (unit: m2/s; logarithmic scale) in1992—2002 |
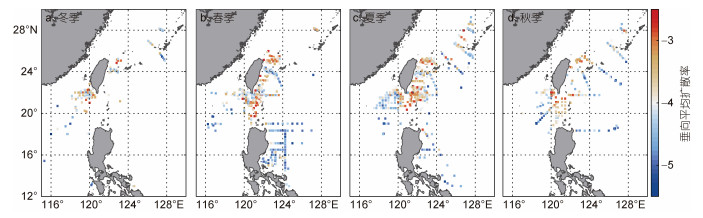 |
| 图 5 冬季(12—2月) (a)、春季(3—5月) (b)、夏季(6—8月) (c)以及秋季(9—11月) (d)的垂向平均扩散率(单位: m2/s; 以10为底的对数坐标)空间分布 Fig. 5 The depth-averaged diffusivity (unit: m2/s; logarithmic scale) in winter (December to February) (a), spring (March to May) (b), summer (June to August) (c) and autumn (September to November) (d) |
本文将基于CTD数据计算的300—600 m剖面的湍流混合扩散率与其对应时间、对应位置的风输入的近惯性能通量进行线性拟合(图 6), 相关系数为0.078 9, 即风输入的近惯性能通量与300—600 m剖面的湍流混合扩散率没有良好的相关性。细尺度参数化方案适用于混合层以下深度, 因此本文采用了同时刻的海洋上层300—600 m的混合扩散率, 而风生近惯性内波只有部分可以传到300 m以深, 且传播具有一定滞后性。由于数据和参数化方案的局限, 风对于海洋上层300 m的作用也未可知。因此, 风输入的近惯性能通量对湍流混合的影响还需要日后进一步研究。
 |
| 图 6 混合扩散率(K)和风输入的近惯性能通量的线性拟合 Fig. 6 Linear regression between depth-averaged diffusivity rates (K) and energy flux from the winds 注: 黄色实线为两者拟合的直线; 上虚线为10K, 下虚线为1/10K; r为相关系数 |
如图 7所示, 从时间上看, 风输入的近惯性能通量呈现冬季(12—2月)和春季(3—5月)较弱, 夏季(6—8月)和秋季(9—11月)较强的特征, 从空间上看, 呈现菲律宾海较强, 南海较弱的特征。该区域受大风过程影响较多, 几乎每年6—10月都会有台风经过, 因此在夏季和秋季风输入的近惯性能通量最强。Whalen等(2018)发现30°—45°N区域的混合扩散率在2 000 m的整个深度上都存在季节性循环, 且这种循环与风输入的近惯性能通量的季节性循环相关。本文使用的CTD数据缺少在大风天气下的观测, 而本文的研究区域多受台风过程的影响, 因此计算的混合扩散率也没有呈现明显的季节变化特征(图 5), 无法再次验证该区域内混合的季节变异性与风输入的近惯性能通量的相关性。
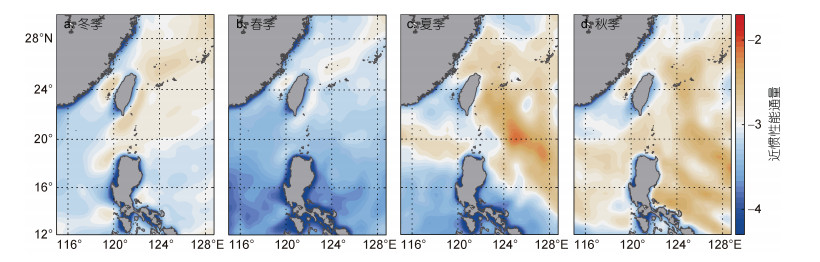 |
| 图 7 冬季(12—2月) (a)、春季(3—5月) (b)、夏季(6—8月) (c)及秋季(9—11月) (d)的风输入的近惯性能通量(单位: W/m2; 以10为底的对数坐标)空间分布图 Fig. 7 Maps of near-inertial wind energy flux (unit: W/m2; logarithmic scale) in winter (December to February) (a), spring (March to May) (b), summer (June to August) (c) and autumn (September to November) (d) |
本文基于ETOPO1的海底地形数据计算地形粗糙度, 如图 1所示, 可见该研究区域内地形变化复杂, 从南海北部陆架的平坦地形到陆坡的粗糙地形, 再到相对平缓的中央海盆, 南海是典型的半封闭型边缘海, 而吕宋海峡是连接南海与太平洋的重要通道, 吕宋海峡有南北走向的山脊, 海山以及深水海槽等显著地形, 吕宋海峡南北陆坡陡峭, 水深变化剧烈, 地形粗糙度高达106 m2。同样地, 东海陆坡和琉球岛弧一带地形粗糙度高于106 m2, 而在菲律宾海地形粗糙度在104—105 m2之间。
图 8为海洋湍流混合扩散率和对应地理位置上地形粗糙度的散点图, 可以看到, 扩散率与地形粗糙度呈正相关, 相关系数为0.221 9, 特别是在吕宋海峡、东海陆坡以及琉球岛弧等地形粗糙度大的地方(图 1), 混合扩散率的值也更高(图 2)。
 |
| 图 8 混合扩散率(K)和地形粗糙度的线性拟合 Fig. 8 Linear regression between depth-averaged diffusivity rates (K) and roughness 注: 黄色实线为两者拟合的直线; 上虚线为10K, 下虚线为1/10K, r为相关系数 |
正压潮流经变化的海底地形时激发的内潮是内波的主要来源之一。根据前人的研究, 南海海盆和部分陆架陆坡区域内, 内潮以全日分潮K1和O1为主, 半日分潮M2次之(Guo et al, 2012; Zhao, 2014; Cao et al, 2017), 因此本文利用公式(8)计算了一个完整潮汐周期内的M2、K1、O1分潮的最大内潮体力, 计算结果如图 9所示。结果显示, 内潮体力高值区主要集中在吕宋海峡、台湾岛东北的东海陆坡、琉球岛弧一带以及南海北部陆坡, 内潮体力高值区(图 9)基本与混合扩散率高值区(图 2)相对应。在吕宋海峡, 全日分潮K1、O1及半日分潮M2的体力都很强, 对局地的混合都有贡献。但在东海陆坡以及琉球岛弧的M2分潮体力最大, 远大于K1和O1内潮的体力, 这表明此处的强混合应当主要是由M2分潮引起的, 与前人基于数值模拟的内潮能量及耗散的空间分布基本一致(Wang et al, 2016; Xu et al, 2016; Chang et al, 2019)。
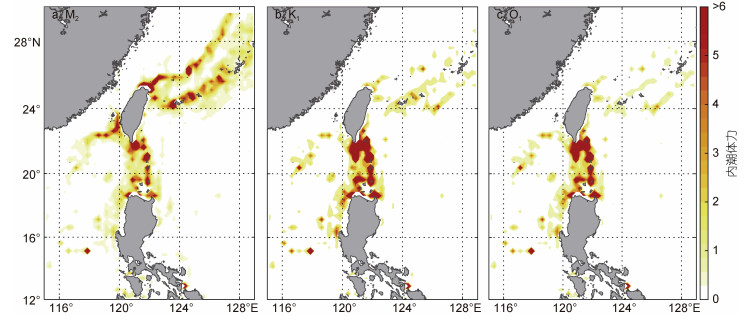 |
| 图 9 M2 (a)、K1 (b)、O1 (b)分潮在一个潮汐周期内的最大内潮体力(单位: m2/s2)分布图 Fig. 9 The maximum depth-integrated internal tide-generating body force (unit: m2/s2) over a complete tidal cycle due to the M2 (a), K1 (b) and O1 (c) tidal constituent |
本文的结果显示, 吕宋海峡、东海陆坡、南海北部以及菲律宾海湍流混合的空间变异性主要与内潮有关(图 9), 与地形粗糙度有一定相关性, 而与风输入的近惯性能通量没有良好的相关性, 且没有发现明显的年际和季节变化。
吕宋海峡几乎在整个深度上都存在强烈的混合, 扩散率高达4×10-3 m2/s左右, 引起强混合的主要原因是内潮(图 9), K1、O1及M2内潮明显增强了局地的混合; 另外还与吕宋海峡复杂的海底地形密切相关, 包括两条平行的南北走向的山脊和海山等显著地形, 李颖(2015)指出粗糙的海底地形对海洋内部混合的影响可至距离海底3 300 m远, 因此吕宋海峡的强混合存在于整个水深。以往的研究关于南海和吕宋海峡居多, 除此之外, 本文还发现了靠近台湾东北的东海陆坡处和冲绳海槽也具有强混合的特征, 混合强度与吕宋海峡相当, 根据本文的研究结果, 认为导致东海陆坡处和冲绳海槽强混合的原因也是内潮(图 9), 其中M2分潮贡献最大。
南海北部陆坡处的混合扩散率较高, 比南海中央海盆高1—2个数量级, 其原因可能是: 一是南海北部陆坡处是内潮产生的一个源地(图 9), 高模态的内潮在源地附近破碎导致强混合, 低模态的内潮在传播过程中与背景场的内波发生非线性作用, 同时发生破碎也会导致较强的湍流混合(Polzin et al, 1997; Lien et al, 2001); 二是从吕宋海峡传来的内潮遇到南海北部陆坡的超临界地形发生破碎(St. Laurent et al, 2003), 为该区域的强混合提供了能量来源, 而南海中央海盆地势相对平坦, 因此, 南海北部陆坡处的混合强于南海中央海盆。但本文的研究发现南海北部陆坡处垂向平均的混合扩散率为3×10-4 m2/s左右, 低于Yang等(2016)所提到的10-3 m2/s。Tian等(2009)研究了沿21°N断面的湍流混合分布, 发现南海1 000 m水深以下的混合比太平洋大2个数量级, 但本文发现在22°N断面上, 南海的混合与菲律宾海相差不大, 猜测这种差异可能s与内潮强度的空间分布有关(Guo et al, 2020)。此外, 菲律宾海在吕宋岛东部近岸处的混合要比离岸处的混合更强, 这可能是西边界流的剪切不稳定性导致了混合增强。在南海中央海盆和离岸的菲律宾海地形平坦, 混合较弱, 扩散率与海洋混合的背景值一致(Munk et al, 1998), 为O(10-5 m2/s)。
4 结论本文利用1992—2002年的CTD和2012—2016年的Argo温盐数据, 使用基于应变的细尺度参数化方法计算了吕宋海峡及周边海域(12°—30°N, 115°—129°E)的混合扩散率, 得到该区域垂向混合的时空分布特征, 并通过计算地形粗糙度、内潮体力以及风输入的近惯性能通量, 分析对混合的影响。主要有以下几点结论:
(1) 从空间来看, 吕宋海峡混合扩散率高达4×10-3 m2/s, 造成强混合的原因主要是K1、O1及M2分潮的贡献, 海峡南北陆坡陡峭, 深度变化剧烈, 是南海内潮的一个源地, 内潮在传播过程中与地形发生作用导致内波的破碎, 进而导致混合增强; 靠近台湾东北的东海陆坡处混合强度与吕宋海峡相当, 东海陆坡—冲绳海槽—琉球岛弧构成了特殊的地形环境, 东海陆坡及琉球岛弧也是内潮产生源地, 且主要是半日分潮M2的贡献(Xu et al, 2016; Chang et al, 2019), 但基于CTD及Argo数据计算的台湾东北部的混合扩散系数比Wang等(2016)基于数值模拟的结果略高, 差距在一个量级内; 在18°—22.5°N的南海海域呈现纬度越高, 混合越强, 南海北部陆坡的混合扩散率比南海中央海盆高1—2个量级, 主要与内潮的空间分布以及地形有关; 在南海中央海盆和离岸的菲律宾海的内潮生成较弱, 混合水平也较弱, 扩散率在O(10-5 m2/s)。该区域内混合的空间分布特征与内潮体力的空间分布几乎一致, 混合扩散率与地形粗糙度有一定相关性, 但与风输入的近惯性能量没有良好的相关性, 因此内潮是影响该区域混合的主要因素。
(2) 从时间来看, 无论是南海、吕宋海峡还是菲律宾海, 垂向混合的年际变化和季节变化都不明显, 由于此研究区域内受台风影响较多, 而本文使用的CTD数据缺少大风天气下的观测, 没有明确的证据表明此研究区域内的混合与风输入的近惯性能量有相似的时间变异性, 还有待后续更深入的研究。
李颖, 2015. 基于细尺度参数化的西北太平洋和南大洋的湍流混合研究. 青岛: 中国科学院研究生院(海洋研究所)博士学位论文, 42-43
|
陈娟, 李少峰, 曹安州, 等. 2020. 北太平洋涡旋对基于细尺度参数化的海洋内部混合的影响. 海洋与湖沼, 51(2): 248-257 |
荆钊, 2012. 中尺度涡和风应力影响下的跨等密度面湍流混合低频变异. 青岛: 中国海洋大学硕士学位论文, 15-17
|
管守德, 2014. 南海北部近惯性振荡研究. 青岛: 中国海洋大学博士学位论文, 10-11
|
Alford M H, 2001. Internal swell generation: the spatial distribution of energy flux from the wind to mixed layer near-inertial motions. Journal of Physical Oceanography, 31(8): 2359-2368 DOI:10.1175/1520-0485(2001)031<2359:ISGTSD>2.0.CO;2 |
Alford M H, 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophysical Research Letters, 30(8): 1424 |
Alford M H, Mackinnon J A, Zhao Z X et al, 2007. Internal waves across the Pacific. Geophysical Research Letters, 34(24): L24601 DOI:10.1029/2007GL031566 |
Baines P G, 1982. On internal tide generation models. Deep Sea Research Part A. Oceanographic Research Papers, 29(3): 307-338 DOI:10.1016/0198-0149(82)90098-X |
Bai X L, Liu Z Y, Li X F et al, 2014. Generation sites of internal solitary waves in the southern Taiwan Strait revealed by MODIS true-colour image observations. International Journal of Remote Sensing, 35(11-12): 4086-4098 DOI:10.1080/01431161.2014.916453 |
Cao A Z, Guo Z, Lv X Q et al, 2017. Coherent and incoherent features, seasonal behaviors and spatial variations of internal tides in the northern South China Sea. Journal of Marine Systems, 172: 75-83 DOI:10.1016/j.jmarsys.2017.03.005 |
Cao A Z, Guo Z, Song J B et al, 2018. Near-inertial waves and their underlying mechanisms based on the South China Sea internal wave experiment (2010-2011). Journal of Geophysical Research: Oceans, 123(7): 5026-5040 DOI:10.1029/2018JC013753 |
Cao A Z, Guo Z, Wang S Y et al, 2019. Upper ocean shear in the northern South China Sea. Journal of Oceanography, 75(6): 525-539 DOI:10.1007/s10872-019-00520-x |
Chang H, Xu Z H, Yin B S et al, 2019. Generation and propagation of M2 internal tides modulated by the Kuroshio northeast of Taiwan. Journal of Geophysical Research: Oceans, 124(4): 2728-2749 DOI:10.1029/2018JC014228 |
D'Asaro E A, 1985. The energy flux from the wind to near-inertial motions in the surface mixed layer. Journal of Physical Oceanography, 15(8): 1043-1059 DOI:10.1175/1520-0485(1985)015<1043:TEFFTW>2.0.CO;2 |
Egbert G D, Ray R D, 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature, 405(6788): 775-778 DOI:10.1038/35015531 |
Furuichi N, Hibiya T, Niwa Y, 2008. Model-predicted distribution of wind-induced internal wave energy in the world's oceans. Journal of Geophysical Research: Oceans, 113(C9): C09034 |
Gregg M C, 1989. Scaling turbulent dissipation in the thermocline. Journal of Geophysical Research: Oceans, 94(C7): 9686-9698 DOI:10.1029/JC094iC07p09686 |
Guo Z, Cao A Z, Lv X Q et al, 2020. Impact of multiple tidal forcing on the simulation of the M2 internal tides in the northern South China Sea. Ocean Dynamics, 70(2): 187-198 DOI:10.1007/s10236-019-01324-9 |
Guo P, Fang W D, Liu C J et al, 2012. Seasonal characteristics of internal tides on the continental shelf in the northern South China Sea. Journal of Geophysical Research: Oceans, 117(C4): C04023 |
Gregg M C, Kunze E, 1991. Shear and strain in Santa Monica basin. Journal of Geophysical Research: Oceans, 96(C9): 16709-16719 DOI:10.1029/91JC01385 |
Jiang J, Lu Y Y, Perrie W, 2005. Estimating the energy flux from the wind to ocean inertial motions: the sensitivity to surface wind fields. Geophysical Research Letters, 32(15): L15610 DOI:10.1029/2005GL023289 |
Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern pacific stirred by wind stress. Geophysical Research Letters, 37(23): L23604 |
Jing Z, Wu L X, 2013. Low-frequency modulation of turbulent diapycnal mixing by anticyclonic eddies inferred from the HOT time series. Journal of Physical Oceanography, 43(4): 824-835 DOI:10.1175/JPO-D-11-0150.1 |
Jing Z, Wu L X, Li L et al, 2011. Turbulent diapycnal mixing in the subtropical northwestern pacific: spatial-seasonal variations and role of eddies. Journal of Geophysical Research: Oceans, 116(C10): C10028 DOI:10.1029/2011JC007142 |
Kunze E, Firing E, Hummon J M et al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553-1576 DOI:10.1175/JPO2926.1 |
Liu Y, Dong C M, Guan Y P et al, 2012. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 68: 54-67 DOI:10.1016/j.dsr.2012.06.001 |
Lien R C, Gregg M C, 2001. Observations of turbulence in a tidal beam and across a coastal ridge. Journal of Geophysical Research: Oceans, 106(C3): 4575-4591 DOI:10.1029/2000JC000351 |
Legg S, Huijts K M H, 2006. Preliminary simulations of internal waves and mixing generated by finite amplitude tidal flow over isolated topography. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 53(1-2): 140-156 DOI:10.1016/j.dsr2.2005.09.014 |
Lozovatsky I, Liu Z Y, Fernando H J S et al, 2013. The TKE dissipation rate in the northern South China Sea. Ocean Dynamics, 63(11-12): 1189-1201 DOI:10.1007/s10236-013-0656-7 |
Munk W, Wunsch C, 1998. Abyssal recipes Ⅱ: Energetics of tidal and wind mixing. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
Oey L Y, Ezer T, Wang D P et al, 2006. Loop current warming by hurricane Wilma. Geophysical Research Letters, 33(8): L08613 |
Pollard R T, 1980. Properties of near-surface inertial oscillations. Journal of Physical Oceanography, 10(3): 385-398 DOI:10.1175/1520-0485(1980)010<0385:PONSIO>2.0.CO;2 |
Pollard R T, Millard Jr R C, 1970. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Research and Oceanographic Abstracts, 17(4): 813-821 DOI:10.1016/0011-7471(70)90043-4 |
Polzin K L, Toole J M, Ledwell J R et al, 1997. Spatial variability of turbulent mixing in the abyssal ocean. Science, 276(5309): 93-96 |
Rimac A, Von Storch J S, Eden C et al, 2013. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophysical Research Letters, 40(18): 4882-4886 DOI:10.1002/grl.50929 |
Simmons H L, Alford M H, 2012. Simulating the long-range swell of internal waves generated by ocean storms. Oceanography, 25(2): 30-41 DOI:10.5670/oceanog.2012.39 |
St Laurent L, Garrett C, 2002. The role of internal tides in mixing the deep ocean. Journal of Physical Oceanography, 32(10): 2882-2899 DOI:10.1175/1520-0485(2002)032<2882:TROITI>2.0.CO;2 |
St Laurent L, Stringer S, Garrett C et al, 2003. The generation of internal tides at abrupt topography. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 50(8): 987-1003 DOI:10.1016/S0967-0637(03)00096-7 |
Tian J W, Yang Q X, Zhao W, 2009. Enhanced diapycnal mixing in the South China Sea. Journal of Physical Oceanography, 39(12): 3191-3203 DOI:10.1175/2009JPO3899.1 |
Wunsch C, Ferrari R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annual Review of Fluid Mechanics, 36: 281-314 DOI:10.1146/annurev.fluid.36.050802.122121 |
Watanabe M, Hibiya T, 2002. Global estimates of the wind-induced energy flux to inertial motions in the surface mixed layer. Geophysical Research Letters, 29(8): 64 |
Whalen C B, Mackinnon J A, Talley L D, 2018. Large-scale impacts of the mesoscale environment on mixing from wind-driven internal waves. Nature Geoscience, 11(11): 842-847 DOI:10.1038/s41561-018-0213-6 |
Wang X W, Peng S Q, Liu Z Y et al, 2016. Tidal mixing in the south china sea: an estimate based on the internal tide energetics. Journal of Physical Oceanography, 46(1): 107-124 DOI:10.1175/JPO-D-15-0082.1 |
Xu Z H, Liu K, Yin B S et al, 2016. Long-range propagation and associated variability of internal tides in the South China Sea. Journal of Geophysical Research: Oceans, 121(11): 8268-8286 DOI:10.1002/2016JC012105 |
Yang Q X, Tian J W, Zhao W et al, 2014. Observations of turbulence on the shelf and slope of northern South China Sea. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 87: 43-52 DOI:10.1016/j.dsr.2014.02.006 |
Yang Q X, Zhao W, Liang X F et al, 2016. Three-dimensional distribution of turbulent mixing in the South China Sea. Journal of Physical Oceanography, 46(3): 769-788 DOI:10.1175/JPO-D-14-0220.1 |
Zhao Z X, 2014. Internal tide radiation from the Luzon Strait. Journal of Geophysical Research: Oceans, 119(8): 5434-5448 DOI:10.1002/2014JC010014 |
Zhai X M, Greatbatch R J, Eden C et al, 2009. On the loss of wind-induced near-inertial energy to turbulent mixing in the upper ocean. Journal of Physical Oceanography, 39(11): 3040-3045 DOI:10.1175/2009JPO4259.1 |
 2021, Vol. 52
2021, Vol. 52


