
中国海洋湖沼学会主办。
文章信息
- 栗小东, 王晶, 杨春蕙, 王迎宾. 2021.
- LI Xiao-Dong, WANG Jing, YANG Chun-Hui, WANG Ying-Bin. 2021.
- 基于两种机器学习方法分析东海北部海域三疣梭子蟹(Portunus trituberculatus)时空分布
- SPATIOTEMPORAL DISTRIBUTION OF PORTUNUS TRITUBERCULATUS IN THE NORTHERN EAST CHINA SEA BASED ON TWO MACHINE LEARNING METHODS
- 海洋与湖沼, 52(5): 1284-1292
- Oceanologia et Limnologia Sinica, 52(5): 1284-1292.
- http://dx.doi.org/10.11693/hyhz20210200050
文章历史
-
收稿日期:2021-02-11
收修改稿日期:2021-04-18
三疣梭子蟹(Portunus trituberculatus)隶属于十足目(Decapoda)、梭子蟹科(Portunidae)、梭子蟹属(Portunus) (俞存根, 2011), 头胸甲呈梭形(宋海棠, 2012), 因背部的三个疣状突起而得名, 其属于广温广盐生态类群(俞存根等, 2005), 广泛分布于中国的四大海区, 是东海海域重要的优势种和渔业捕捞对象之一, 具有重要的经济价值和生态价值。目前, 国内外关于三疣梭子蟹的研究报道有很多, 主要包括生物学特征(袁伟等, 2016; 叶婷, 2017)、营养生态位(丛旭日, 2015)、渔具选择性(张洪亮, 2011)以及增殖容量估算(徐雪等, 2019)和补充量预测(高丽, 2020)等方面。随着近海渔船吨位和功率的不断增大, 捕捞强度也随之增加, 对三疣梭子蟹资源造成了巨大的压力。为了保护三疣梭子蟹资源, 实现可持续利用, 2017年, 经农业农村部批准, 浙江省组织开展了浙北渔场梭子蟹限额捕捞试点工作(陈森, 2017)。实行限额捕捞是保护三疣梭子蟹资源的有效途径, 而准确了解三疣梭子蟹的资源分布状况和资源量对限额捕捞工作的开展具有重要意义。
三疣梭子蟹作为一种大型底层蟹类, 其分布易受到温度、盐度等一系列海洋环境因子的影响(徐勇等, 2015; 吴强等, 2016; 卢衎尔等, 2019), 蟹类的时空分布及其与环境因子之间的关系也是当前渔业研究的热点问题(丁朋朋等, 2019)。物种分布模型(SDMs)是研究物种分布与环境因子之间关系的一种重要方法, 它以生态位理论为基础, 将物种分布信息和相应的环境信息进行关联, 探究两者之间的关系, 进而利用这种关系对目标研究区域的物种分布进行预测(李国庆等, 2013; 许仲林等, 2015)。传统的SDMs大多使用基于回归的方法, 如广义线性模型(GLM)、广义可加模型(GAM)等(郑波等, 2008; 武胜男等, 2019; 马金等, 2020), 随着计算机技术和人工智能的发展, 机器学习方法也逐渐被应用于SDMs中, 且因为其可以识别物种分布和环境因子之间的复杂关系、能够更加准确地预测物种分布等优点而受到人们的广泛关注。在渔业领域, 机器学习方法已经被广泛地用于鱼类丰度和分布预测(Baran et al, 1996; Lek et al, 1996; Maravelias et al, 2003; Li et al, 2017)、种群鉴定(Haralabous et al, 1996)、CPUE标准化(杨胜龙等, 2015)以及资源分布与环境因子之间关系的探究(栾静等, 2018; Luan et al, 2018)等方面。
本研究采用梯度提升回归树(GBRT)和支持向量机(SVM)这两种机器学习方法, 对东海北部海域三疣梭子蟹的时空分布及其与环境因子之间的关系进行了分析, 筛选了影响三疣梭子蟹分布的主要环境因子, 对两种模型的拟合性能和预测性能进行了比较, 并利用最佳模型对三疣梭子蟹的分布进行了预测。研究结果预期可为三疣梭子蟹资源分布及资源量预测新方法的探索提供一定的技术参考。
1 材料与方法 1.1 数据来源三疣梭子蟹资源量数据来源于2006年8月, 2007年1月、5月、11月在东海北部海域的底拖网调查。调查海域范围为121°75′—124°25′E、29°75′—31°35′N, 共设置20个调查站位(图 1)。调查所用的船只为主发动机功率为184 kW的单拖渔船, 调查网具为桁杆虾拖网, 桁杆长度为30 m, 囊袋为7只, 拖曳航速为2节, 每站位拖行1 h。同时对每个站位的底层海水温度(SBT)、底层海水盐度(SBS)以及水深等环境因子进行测定和记录。表 1为调查所得的三疣梭子蟹渔获量以及环境因子的季节变化情况。
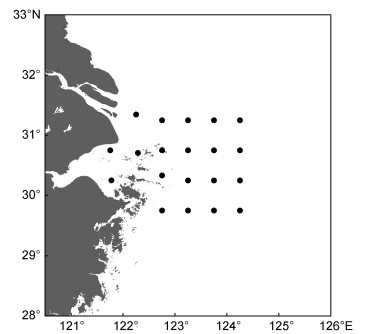 |
| 图 1 东海北部海域渔业资源采样站位分布 Fig. 1 Distribution of sampling stations for fishery resources in the northern part of the East China Sea |
| 调查变量 | 春季(5月) | 夏季(8月) | 秋季(11月) | 冬季(1月) |
| 三疣梭子蟹渔获量(g) | 13—28 867 | 785—67 528 | 45—806 857 | 0—154 234 |
| 底层海水温度(SBT) (℃) | 16.04—18.24 | 16.67—27.39 | 20.25—21.69 | 12.28—16.86 |
| 底层海水盐度(SBS) | 30.53—34.28 | 30.88—34.48 | 31.57—34.19 | 32.97—34.34 |
| 水深(m) | 9—82 | 3—59 | 17—58 | 11—44 |
| pH | 8.02—8.49 | 8.09—8.49 | 7.89—8.24 | 7.80—7.97 |
| 叶绿素a浓度(μg/L) | 0.31—3.98 | 0.45—3.05 | 0.34—1.34 | 0.38—1.4 |
梯度提升回归树(GBRT)和支持向量机(SVM)是两种机器学习方法, GBRT是一种由Friedman(2001)提出的迭代决策树算法, 其通过不断生成新的决策树来拟合前一棵树的误差, 进而获得更加准确的预测结果; SVM是一种由Cortes等(1995)提出的一种有监督学习模型, 具有泛化能力好、适用于非线性和高维问题等优点。
梯度提升回归树(GBRT) GBRT是一种以回归决策树为弱学习器的集成学习模型, 结合了提升法和梯度下降法两种思想, 提升法的目的是结合多棵决策树来共同进行决策, 梯度下降法是使用损失函数的负梯度在当前模型的值作为提升树中残差的近似值, 以此来拟合回归决策树(Friedman, 2001)。GBRT的构建过程主要有以下三个步骤: (1) 初始化决策树, 估计一个使得损失函数最小化的常数来构建一个只有一个根节点的树; (2) 不断提升迭代; (3) 经过若干次的提升法迭代过程之后, 输出最终的模型(赵卫东等, 2018)。
支持向量机(SVM) SVM是机器学习中一种常用的分类和回归模型, 其目的是在多维空间中找到一个能将全部样本单元分成两类的最优平面(丁世飞等, 2011), 这一平面应当使两类中距离最近的点的间距尽可能地大, 这时在间距边界上的点称为支持向量, 间距中间的平面称为分隔超平面(卡巴科弗, 2013)。SVM通过一个特定的核函数将样本单元投射到高维空间, 常用的核函数有线性核函数、多项式核函数、径向基核函数以及Sigmoid核函数等(杨云等, 2020), 渔业中三疣梭子蟹的分布与环境因子之间的关系多为非线性关系, 而径向基核函数是一种非线性投影, 可以灵活地识别变量之间的非线性关系, 故本研究中建立SVM模型使用的核函数为径向基核函数。
1.3 模型拟合及预测三疣梭子蟹作为一种大型底层游泳动物, 其分布与底层海洋环境有较强关联, 故选取水深(WD)、底温(SBT)、底盐(SBS)、pH以及叶绿素a浓度(Chlorophyll a concentration, chl a)作为环境因子, 选择季节作为时间因子, 共6个因子作为解释变量。为了减少数据的异质性, 避免异常值和零值的影响(Jongman et al, 1995; Brosse et al, 2002), 将单位网次渔获量Y进行对数转换得到ln(Y+1), 作为响应变量。使用方差膨胀因子(VIF)对解释变量进行多重共线性检验(Kabacoff, 2011), 以此来筛选上述可以加入到模型中的因子, 设置VIF的阈值为3, 即认为VIF > 3的因子存在多重共线性问题, 建模时不予考虑。
在拟合模型时, 采用逐步回归的方法将因子代入模型中, 使用方差解释率来检验模型的拟合效果, 方差解释率越高, 表明模型的拟合效果越好; 在逐步添加因子的过程中, 当方差解释率不再增大时, 停止添加因子, 此时即为最佳模型, 方差解释率由以下公式计算:
 (1)
(1)式中, Var(residual)表示残差方差, Var(y)表示原始数据方差。
使用交叉验证法来评估模型的预测性能(Franklin, 2010), 将总体数据分为训练数据和验证数据, 训练数据用于建模, 验证数据用于评估模型的预测性能。本研究随机抽取总体数据中80%的数据作为训练数据, 20%的数据作为验证数据。交叉验证过程重复模拟10 000次, 将均方根误差(RMSE) (Hyndman et al, 2006)和决定系数(R2)作为评估模型预测性能的指标, RMSE的计算公式如下:
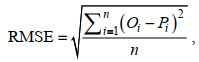 (2)
(2)式中, n为交叉验证中数据的数量, Oi和Pi分别表示观测值和预测值。
ΔR2即模型拟合与模型预测的R2的差值作为检验模型过拟合程度的指标, ΔR2越小, 过拟合程度越小; RMSE和R2的标准误差作为衡量模型稳定性的指标, 标准误差越小, 模型越稳定(Segurado et al, 2004)。
以上两种模型的构建和验证过程均在R 3.6.3软件中实现, 其中GBRT模型由“gbm”包构建, SVM模型由“e1071”包构建。
1.4 预测分布根据各季节的环境因子调查数据, 以0.05°× 0.05°为分辨率对所研究海域进行网格划分, 记录每个网格中心点所对应的坐标, 使用克里金插值法对各网格中心点的环境因子数据进行插值, 比较两种模型的预测性能, 挑选出最优的预测模型, 将插值获得的环境因子数据代入模型中, 以此来预测不同季节三疣梭子蟹的分布状况, 使用ocean data view软件绘制三疣梭子蟹资源分布图。
2 结果 2.1 因子筛选与模型拟合使用VIF对环境因子进行多重共线性检验, 结果显示各环境因子之间VIF值均小于3, 表明环境因子之间不存在多重共线性问题, 均可以作为解释变量加入模型中。表 2列出了两种模型的最佳拟合结果, 其中包括各模型逐步添加因子的顺序、逐步添加过程中模型累计方差解释率的变化情况以及各因子对模型的贡献率。
| 模型 | 加入的因子 | 累计方差解释率(%) | 贡献率(%) |
| 梯度提升回归树(GBRT) | SBS | 59.1 | 59.1 |
| +season | 70.4 | 11.3 | |
| +SBT | 79.2 | 8.8 | |
| +pH | 85.5 | 6.3 | |
| 支持向量机(SVM) | SBS | 33.7 | 33.7 |
| +season | 47.9 | 14.2 | |
| +pH | 75.2 | 27.2 | |
| 注: SBS表示底层海水盐度, season表示调查季节, SBT表示底层海水温度 | |||
GBRT模型累计方差解释率为85.5%, 包括底层盐度、季节、底层温度以及pH共四个因子, 其中底层盐度的贡献率最大, 为59.1%, 其次是季节、底层温度和pH, 分别为11.3%、8.8%、6.3%; SVM模型累计方差解释率为75.2%, 包括底层盐度、季节以及pH共三个因子, 其中底层盐度和pH的贡献率较大, 分别为33.7%和27.2%, 季节的贡献率较小, 为14.2% (表 2)。两种模型相比, SVM模型的累计方差解释率较低, GBRT模型的累计方差解释率较高, 表明GBRT模型的拟合效果较好。两种模型筛选出的解释变量均包含底层盐度、季节和pH, 且每个模型中底层盐度的贡献率均为最高, 表明底层盐度是影响三疣梭子蟹分布的主要因子, 其次为季节和pH。
2.2 资源密度与解释变量关系在GBRT模型中, 底层盐度在31—33时三疣梭子蟹资源密度较为稳定, 高于33时波动较为明显, 且在高于34时也呈现出急速下降的趋势。夏季的资源密度明显高于其他三个季节(图 2)。底层海水温度在15—21 ℃之间三疣梭子蟹资源密度波动较大, 随着温度的升高呈现先下降后上升再下降的趋势, 21—25 ℃之间较为稳定。pH在7.9—8.0之间三疣梭子蟹资源密度波动较大, 呈现先下降后上升的趋势, 8.0—8.4之间波动较小(图 2)。在SVM模型中, 随着底层海水盐度的升高, 三疣梭子蟹资源密度先呈现缓慢上升的趋势, 盐度超过33.5时急剧下降, 后又快速上升。夏季的资源密度明显高于其他三个季节。pH在7.8—7.9之间三疣梭子蟹资源密度呈现下降趋势, 8.0—8.4之间呈现波动上升的趋势(图 3)。
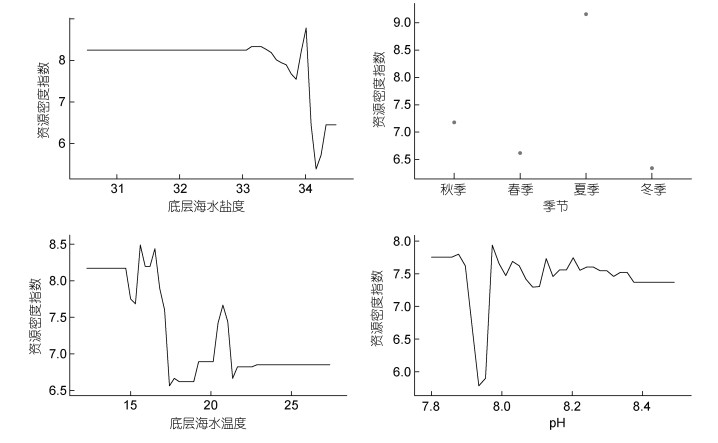 |
| 图 2 GBRT最优模型因子对三疣梭子蟹资源密度影响的分析图 Fig. 2 Effects of factors selected from the optimal gradient boosting regression tree model on the resource density of P. trituberculatus |
 |
| 图 3 SVM最优模型因子对三疣梭子蟹资源密度影响的分析图 Fig. 3 Effects of factors selected from the optimal support vector machine model on the resource density of P. trituberculatus |
两种模型所识别的底层海水盐度与三疣梭子蟹资源密度之间的关系基本一致, 均在盐度为34左右时表现出急剧下降的趋势; 所识别的pH与三疣梭子蟹资源密度之间的关系也基本一致, 均在pH为7.95附近存在一个资源密度的低值点。
2.3 模型预测性能检验从交叉验证结果(表 3)可知, GBRT模型的R2较大且RMSE较小, 表明GBRT模型的预测性能相对优于SVM模型; 从ΔR2的值可以看出, 两种模型的过拟合情况差别不大; 从R2和RMSE的标准误的值可以看出, 两种模型的稳定性差别不大, 但GBRT模型的稳定性略微优于SVM模型。综合以上各种指标, GBRT模型的整体表现相对优于SVM模型。
| 模型 | 均方根误差RMSE | 决定系数R2 | 决定系数的差值ΔR2 | 均方根误差的标准误 | 决定系数R2的标准误 |
| 梯度提升回归树(GBRT) | 0.16 | 0.36 | 0.51 | 0.44 | 0.16 |
| 支持向量机(SVM) | 0.17 | 0.31 | 0.48 | 0.45 | 0.18 |
使用两种模型中预测性能更好的GBRT模型对东海北部海域各季节三疣梭子蟹的资源分布进行预测。结果显示, 各季节三疣梭子蟹的资源分布具有一定差异, 整体上夏季的资源密度高于其他三个季节, 夏季和秋季三疣梭子蟹平均资源密度分别为35.2和28.7 kg/km2, 春季和冬季平均资源密度分别为20.9和16.4 kg/km2; 春季东北部海域资源密度较高, 夏季和秋季整个海域资源密度较为均匀, 冬季北部海域资源密度明显高于南部; 空间上, 各季节所调查海域的东南部均存在一个三疣梭子蟹资源密度的相对低值区(图 4)。
 |
| 图 4 各季节三疣梭子蟹资源分布预测图 Fig. 4 Forecast distribution of P. trituberculatus resources in different seasons 注: a. 春季; b. 夏季; c. 秋季; d. 冬季 |
本研究结果显示, GBRT模型的拟合效果相对优于SVM模型, 这可能与模型本身的结构以及所容纳的解释变量数量有关。GBRT模型属于集成学习模型, 而SVM模型属于单一结构模型, 且GBRT模型所容纳的解释变量数量要多于SVM模型。GBRT模型是在决策树模型的基础上引入了提升法(boosting)的思想(王磊等, 2019), 通过不断生成新的树来拟合前一棵树的误差, 使得最终的拟合效果更好; SVM模型是通过使用核方法将数据投影到高维空间, 利用高维空间中的超平面来分离数据, 从而使它对于非线性数据有很强的处理能力(孙亮等, 2017)。两种模型的基本结构和原理有很大的差异, 这也是其拟合效果不同的主要原因。
两种模型相比, GBRT模型比SVM模型所解释的三疣梭子蟹资源量和环境因子之间的非线性关系更加复杂, 这与模型本身的原理有很重要的关系, GBRT模型和随机森林模型等基于树的模型能够识别因子间的交互效应(Li et al, 2015), 使其能够更加充分地解释资源量与环境因子之间的关系。
从模型预测的角度来看, GBRT模型无论是预测性能还是稳定性都要略优于SVM模型, 这也展示出了集成学习算法在预测准确度上的优势, 即在单个模型的基础上, 通过提升迭代来不断优化模型, 使得最终的输出要优于单个模型。但同时, GBRT模型的过拟合现象也较为严重, 这与GBRT模型所使用的boosting方法有一定的关系, 使用boosting方法从训练集中提取信息来训练模型时更加激进, 容易受到噪声的影响, 进而导致过拟合。
两种模型虽然同属于机器学习方法, 但是模型的原理以及结构都有一定的差异, 从模型的理论基础来看, GBRT模型是基于树的模型, 而SVM模型以统计学习理论和解析几何为基础。从模型的主要结构来看, SVM模型属于单一结构模型, 而GBRT模型属于集成学习模型。根据本研究结果, 集成学习模型无论是从拟合效果还是预测性能都要优于单一结构的模型, 这对于今后研究中模型的选择具有一定的参考价值。
3.2 三疣梭子蟹分布与解释变量之间的关系东海北部海域三疣梭子蟹的资源分布具有明显的季节变化特征, 季节是一个综合性的因子, 不同季节之间包括温度、海流以及河口冲淡水等都有很大的差异, 这也间接地造成了不同季节海水温度和盐度的变化。三疣梭子蟹作为一种大型底栖的肉食性蟹类, 外界环境的变化不仅会影响它本身的生态习性, 如产卵、索饵等, 也会影响其饵料生物的生长(徐勇, 2014)。此外, 季节所导致的环境变化也是三疣梭子蟹产生洄游行为的主要因素, 三疣梭子蟹不断向最适合于自己生存的海域洄游, 进而使得不同季节之间研究海域资源分布有明显的不同。
两种模型的拟合结果均显示底层海水盐度(SBS)为影响三疣梭子蟹分布的一个重要环境因子, 这可能与三疣梭子蟹的生活史有一定关系, 三疣梭子蟹在生长发育的不同阶段对盐度的要求不同, 处于产卵和幼体生长阶段时需要低盐环境, 而进行索饵和越冬时更喜欢高盐度环境(宋海棠, 2012)。夏季是三疣梭子蟹产卵的高峰期, 而东海北部海域又处于长江和钱塘江两个大型河口交汇处, 夏季河水流量较大, 其海水盐度受到大量河流冲淡水的影响有所降低, 适合三疣梭子蟹产卵以及幼体的生长, 因此大量成熟的雌蟹在该海域产卵, 使得资源密度较高(图5b); 冬季时河水流量减少, 海水盐度也有所升高, 当年生的补充群体可能在此进行越冬(图5d)。GBRT模型拟合结果显示, 底层海水温度(SBT)对三疣梭子蟹的分布也有一定的影响, 很多研究都表明水温会影响三疣梭子蟹的分布(宋海棠等, 1989; 袁伟等, 2016), 当水温低于10 ℃时, 三疣梭子蟹甚至会进入休眠状态(宋海棠, 2012), 郑元甲等(2003)的研究认为, 水温是影响三疣梭子蟹洄游分布的主要原因。本研究结果显示当底层水温超过21 ℃时, 三疣梭子蟹资源密度处于较低的状态, 说明水温过高的环境并不适合三疣梭子蟹生存, 三疣梭子蟹是温水种, 但是水温过高反而会对它产生一种制约的作用。pH作为一个衡量水体酸碱度的指标, 会影响甲壳动物的呼吸作用和免疫力(林小涛等, 2000)。GBRT模型和SVM模型的拟合结果均显示, 当pH为7.95时存在一个三疣梭子蟹资源密度的低点, 说明当pH为7.95时, 可能会对三疣梭子蟹的呼吸作用和免疫力产生不利的影响, 进而导致资源密度的下降。
利用GBRT模型对东海北部海域三疣梭子蟹资源的分布状况进行预测, 结果显示夏季的资源量整体上要高于其他三个季节, 可能是因为夏季是三疣梭子蟹产卵的高峰期, 很多性成熟的雌蟹从深海区洄游到近海产卵, 使得近海资源密度较高, 而秋季时三疣梭子蟹的补充群体数量逐渐增多, 补充量大于死亡量, 资源密度也会有所增加(宋海棠, 2012)。四个季节的资源预测分布图均显示在所研究海域的东南部存在一个资源密度的低值区, 可能是因为该海域的环境状况不适合三疣梭子蟹生存, 这还需要进一步的研究。
4 结论本研究运用两种机器学习方法对东海北部海域三疣梭子蟹资源时空分布及其与环境因子之间的关系进行了分析, 筛选出了季节、SBS以及SBT等是影响三疣梭子蟹资源分布的重要因子。虽然不同模型之间的拟合效果有所不同, 但所反映出的因子对三疣梭子蟹资源分布的影响趋势大致相符, 说明该研究的结果相对比较可靠。两种模型最终的预测性能都不是特别高, 这可能与实验所用的数据量较少有一定的关系, 相关研究表明数据量对模型的预测性能有非常显著的影响(Luan et al, 2020), 此外, 海洋中可能存在一些对三疣梭子蟹生活史有显著影响的环境因子但在本研究中并未被采集到, 如底质类型(Luan et al, 2018), 这也值得接下来做进一步的探索和研究。
丁世飞, 齐丙娟, 谭红艳. 2011. 支持向量机理论与算法研究综述. 电子科技大学学报, 40(1): 2-10 |
丁朋朋, 高春霞, 田思泉, 等. 2019. 浙江南部近海蟹类群落结构及其与环境因子的关系. 海洋渔业, 41(6): 652-662 DOI:10.3969/j.issn.1004-2490.2019.06.002 |
马金, 黄金玲, 陈锦辉, 等. 2020. 基于GAM的长江口鱼类资源时空分布及影响因素. 水产学报, 44(6): 958-968 |
王磊, 王晓东. 2019. 机器学习算法导论. 北京: 清华大学出版社, 62
|
卡巴科弗R I编著, 高涛, 肖楠, 陈钢译. 2013. R语言实战. 北京: 人民邮电出版社, 442
|
卢衎尔, 张洪亮, 朱文斌, 等. 2019. 浙江近海春、夏季蟹类群落结构及其与环境因子的关系. 水生生物学报, 43(3): 612-622 |
叶婷, 2017. 浙江海域三疣梭子蟹生物学特征分析及放流容量的确定. 舟山: 浙江海洋大学硕士学位论文, 17
|
丛旭日, 2015. 莱州湾蟹类群落结构以及三疣梭子蟹营养生态位的研究. 上海: 上海海洋大学硕士学位论文, 10
|
许仲林, 彭焕华, 彭守璋. 2015. 物种分布模型的发展及评价方法. 生态学报, 35(2): 557-567 |
孙亮, 黄倩. 2017. 实用机器学习. 北京: 人民邮电出版社, 47
|
李国庆, 刘长成, 刘玉国, 等. 2013. 物种分布模型理论研究进展. 生态学报, 33(16): 4827-4835 |
杨云, 段宗涛. 2020. 机器学习算法与应用. 北京: 清华大学出版社, 53
|
杨胜龙, 张禹, 张衡, 等. 2015. 不同模型在渔业CPUE标准化中的比较分析. 农业工程学报, 31(21): 259-264 DOI:10.11975/j.issn.1002-6819.2015.21.034 |
吴强, 王俊, 陈瑞盛, 等. 2016. 莱州湾三疣梭子蟹的生物学特征、时空分布及环境因子的影响. 应用生态学报, 27(6): 1993-2001 |
宋海棠. 2012. 东海经济虾蟹类渔业生物学. 北京: 海洋出版社, 75
|
宋海棠, 丁耀平, 许源剑. 1989. 浙北近海三疣梭子蟹洄游分布和群体组成特征. 海洋通报, 8(1): 66-74 |
张洪亮, 2011. 浙江梭子蟹笼渔具的选择性研究. 舟山: 浙江海洋大学硕士学位论文, 33
|
陈森. 2017. 渔业限额捕捞制度试点工作稳步推进. 中国水产, (11): 7 |
武胜男, 陈新军, 刘祝楠. 2019. 基于GAM的西北太平洋日本鲭资源丰度预测模型建立. 海洋学报, 41(8): 36-42 DOI:10.3969/j.issn.0253-4193.2019.08.005 |
林小涛, 张秋明, 许忠能, 等. 2000. 虾蟹类呼吸代谢研究进展. 水产学报, 24(6): 575-580 |
郑波, 陈新军, 李纲. 2008. GLM和GAM模型研究东黄海鲐资源渔场与环境因子的关系. 水产学报, 32(3): 379-386 |
郑元甲, 陈雪忠, 程家骅, 等. 2003. 东海大陆架生物资源与环境. 上海: 上海科学技术出版社, 742-764
|
赵卫东, 董亮. 2018. 机器学习. 北京: 人民邮电出版社, 53
|
俞存根. 2011. 舟山渔场渔业生态学. 北京: 科学出版社, 47
|
俞存根, 宋海棠, 姚光展. 2005. 东海蟹类群落结构特征的研究. 海洋与湖沼, 36(3): 213-220 DOI:10.3321/j.issn:0029-814X.2005.03.004 |
袁伟, 金显仕, 单秀娟. 2016. 长江口及毗邻海域三疣梭子蟹种群生物学特征及与环境的关系. 水产科学, 35(2): 105-110 |
徐勇, 2014. 长江口无脊椎动物时空变化特征及其与环境因子的关系. 青岛: 中国科学院研究生院(海洋研究所)硕士学位论文, 79-81
|
徐勇, 线薇微, 李文龙. 2015. 2009-2011年秋季长江口无脊椎动物群落特征及其与环境因子的关系. 中国水产科学, 22(3): 478-487 |
徐雪, 唐伟尧, 王迎宾. 2019. 舟山渔场及长江口渔场临近海域三疣梭子蟹增殖容量估算. 南方水产科学, 15(3): 126-132 |
栾静, 张崇良, 徐宾铎, 等. 2018. 海州湾双斑蟳栖息分布特征与环境因子的关系. 水产学报, 42(6): 889-901 |
高丽, 2020. 基于主要海洋环境因子的浙江北部海域三疣梭子蟹补充量预测分析. 舟山: 浙江海洋大学硕士学位论文, 17
|
Baran P, Lek S, Delacoste M et al, 1996. Stochastic models that predict trout population density or biomass on a mesohabitat scale. Hydrobiologia, 337(1/3): 1-9 |
Brosse S, Lek S, 2002. Relationships between environmental characteristics and the density of age-0 Eurasian perch Perca fluviatilis in the littoral zone of a lake: a nonlinear approach. Transactions of the American Fisheries Society, 131(6): 1033-1043 DOI:10.1577/1548-8659(2002)131<1033:RBECAT>2.0.CO;2 |
Cortes C, Vapnik V, 1995. Support-vector networks. Machine Learning, 20(3): 273-297 |
Franklin J, 2010. Mapping Species Distributions: Spatial Inference and Prediction. Cambridge: Cambridge University Press, 76
|
Friedman J H, 2001. Greedy function approximation: a gradient boosting machine. The Annals of Statistics, 29(5): 1189-1232 DOI:10.1214/aos/1013203450 |
Haralabous J, Georgakarakos S, 1996. Artificial neural networks as a tool for species identification of fish schools. ICES Journal of Marine Science, 53(2): 173-180 DOI:10.1006/jmsc.1996.0019 |
Hyndman R J, Koehler A B, 2006. Another look at measures of forecast accuracy. International Journal of Forecasting, 22(4): 679-688 DOI:10.1016/j.ijforecast.2006.03.001 |
Jongman R H G, Ter Braak C J F, Tongeren O F R, 1995. Data Analysis in Community and Landscape Ecology. Cambridge: Cambridge University Press, 119
|
Kabacoff R I, 2011. R in Action: Data Analysis and Graphics with R. Shelter Island: Manning Publications, 1-474
|
Lek S, Belaud A, Baran P et al, 1996. Role of some environmental variables in trout abundance models using neural networks. Aquatic Living Resources, 9(1): 23-29 DOI:10.1051/alr:1996004 |
Li Z G, Wan R, Ye Z J et al, 2017. Use of random forests and support vector machines to improve annual egg production estimation. Fisheries Science, 83: 1-11 DOI:10.1007/s12562-016-1033-5 |
Li Z G, Ye Z J, Wan R et al, 2015. Model selection between traditional and popular methods for standardizing catch rates of target species: a case study of Japanese Spanish mackerel in the gillnet fishery. Fisheries Research, 161: 312-319 |
Luan J, Zhang C L, Xu B D et al, 2018. Modelling the spatial distribution of three Portunidae crabs in Haizhou Bay, China. PLoS One, 13(11): e0207457 DOI:10.1371/journal.pone.0207457 |
Luan J, Zhang C L, Xu B D et al, 2020. The predictive performances of random forest models with limited sample size and different species traits. Fisheries Research, 227: 105534 DOI:10.1016/j.fishres.2020.105534 |
Maravelias C D, Haralabous J, Papaconstantinou C, 2003. Predicting demersal fish species distributions in the Mediterranean Sea using artificial neural networks. Marine Ecology Progress Series, 255: 249-258 DOI:10.3354/meps255249 |
Segurado P, Araújo M B, 2004. An evaluation of methods for modelling species distributions. Journal of Biogeography, 31(10): 1555-1568 DOI:10.1111/j.1365-2699.2004.01076.x |
 2021, Vol. 52
2021, Vol. 52


