
中国海洋湖沼学会主办。
文章信息
- 闫晓梅, 张林林, 庞重光. 2022.
- YAN Xiao-Mei, ZHANG Lin-Lin, PANG Chong-Guang. 2022.
- 黑潮延伸体区跨等密度面湍流混合的次季节变化
- SUBSEASONAL VARIATION OF TURBULENT DIAPYCNAL MIXING IN THE KUROSHIO EXTENSION REGION
- 海洋与湖沼, 53(1): 33-48
- Oceanologia et Limnologia Sinica, 53(1): 33-48.
- http://dx.doi.org/10.11693/hyhz20210700153
文章历史
-
收稿日期:2021-07-05
收修改稿日期:2021-08-27
2. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 山东青岛 266237;
3. 中国科学院海洋大科学研究中心 山东青岛 266071
2. Laboratory for Ocean Dynamics and Climate, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China;
3. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qindao 266071, China
跨等密度面湍流混合控制着海洋中的热量和淡水输运, 对全球热盐环流和气候变化都有重要影响(Munk et al, 1998)。西北太平洋的海洋环境复杂, 存在西边界强流黑潮及其延伸体、大量的风生近惯性能量输入(Alford, 2001)以及丰富的中尺度涡(Chelton et al, 2011), 而西边界流区是发生强混合的关键海区(Jing et al, 2014; Nagai et al, 2021)。因此, 研究黑潮延伸体区跨等密度面湍流混合的变化规律及其影响机理, 对于加深我们对混合的认识, 进而改进数值模式, 理解海洋环流的变化及其在气候系统中的作用具有重要作用。
海洋内部的湍流混合主要由内波破碎导致, 而内波场的能量主要源自潮汐和海表面风应力(Munk et al, 1998; Wunsch et al, 2004)。已有研究表明, 维持深海层结大约需2 TW的能量, 其中风生近惯性能量提供了大约0.5~1.4 TW (Watanabe et al, 2002; Alford, 2003; Jiang et al, 2005)。然而, 目前对于风生近惯性内波的穿透深度及其对温跃层以深的跨等密度面湍流混合的贡献仍存在争议。例如, Furuichi等(2008)和Zhai等(2009)的数值研究结果显示, 风输入到混合层中的70%~85%的近惯性能量在150或200 m以上就耗散掉了; Alford等(2012)通过分析东北太平洋Papa站的潜标资料发现12%~33%的风生近惯性能量能够下传800 m; 而Jing等(2014)利用2005年1月黑潮延伸体区的潜标观测资料估算得到45%~62%的风生近惯性能量能够进入温跃层为深海混合提供能量。
在风生近惯性能量的影响下, 西北太平洋跨等密度面湍流混合呈现显著的季节变化, 秋冬季较强而春夏季较弱(Jing et al, 2010, 2011, 2016; Whalen et al, 2012; 闫晓梅等, 2014; Li et al, 2014; Inoue et al, 2017; Hu et al, 2020)。同时, 已有研究表明海表面风场还有明显的次季节(10~90 d)变化(祝从文等, 2019; Whitt et al, 2019)。Jing等(2015)在墨西哥湾北部观测发现这里2006年1月份的湍流混合强度是2005年11~12月的3倍, 并将湍流混合的这一次季节变化归因于风生近惯性能量的次季节变化。但是在西北太平洋, 除了季节变化, 目前对于该海区跨等密度面湍流混合在更小时间尺度上的变化(如次季节变化)及其影响机制的研究较少。
此外, 通过分析混合强度和风生近惯性能量季节变化之间的相关关系, 一些研究表明西北太平洋的风生近惯性能量能够下传600~1 800 m (Jing et al, 2010; 闫晓梅等, 2014; Li et al, 2014)。但是, 由于缺乏流速观测, 这些研究未能直接给出风生近惯性内波的垂向传播特征, 因此, 对于影响湍流混合低频变化机制的认识仍不完善。本文将利用黑潮延伸体区的一个长期潜标观测资料, 基于细尺度参数化方法, 研究该海区跨等密度面湍流混合的次季节变化及其影响机制。
1 数据与方法 1.1 数据黑潮延伸体系统研究(Kuroshio extension study system, KESS)于2004~2006年布放了一系列锚系潜标, 其中最南端的K7在144.5 E, 32.5 N (图 1), 该潜标配置了一个多普勒流速剖面仪(acoustic doppler current profiler, ADCP)、一个系缆式剖面仪(McLane moored profiler, MMP)以及四个海流计(current meter, CM)。如图 1b所示, 一个ADCP设置在250 m处, 向上发射信号, 其采样时间间隔是1 h, 垂向间隔是8 m, 垂向共44层, 本文采用的是KESS提供的0~250 m标准网格化流速数据, 其时空分辨率是10 m×1 h; MMP观测250~1 500 m的流速、温度和盐度, 每15 h完成一次剖面观测, 但在2005年1月, 变为每2 h完成一次剖面, 测得数据的垂向分辨率为2 m; 四个海流计分别设置在1 500, 2 000, 3 500和5 000 m, 每15 min观测一次水平流速。以上数据及其详细介绍和处理过程都可从KESS主页(https://uskess.whoi.edu/overview/dataproducts/)获得。本文主要采用K7潜标数据质量最高的2004年6~9月期间的流速和水文观测资料, 分析跨等密度面湍流混合的次季节变化以及近惯性内波的影响, 同时利用MMP在2005年1月的高分辨率数据进行比较和验证。
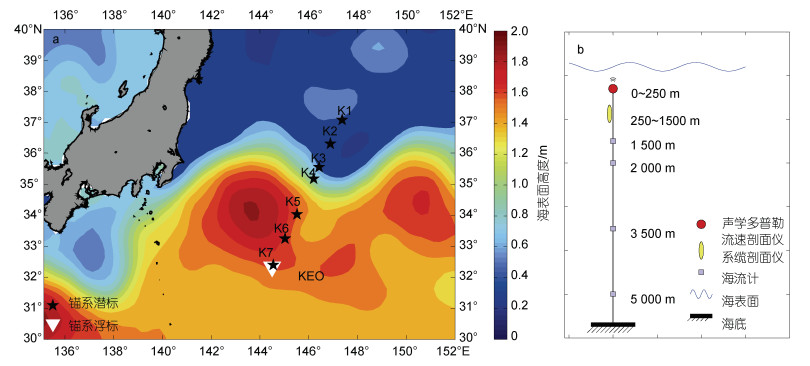 |
| 图 1 黑潮延伸体区2004年6月至2005年1月平均海表面高度及KESS潜标和KEO浮标站位分布(a)以及K7潜标的仪器设置示意图(b) Fig. 1 The mean sea surface height from June 2004 to January 2005 in the Kuroshio Extension region and the locations of KESS and KEO moorings (a), and schematic of the K7 mooring (b) 注: KESS表示黑潮延伸体研究(Kuroshio extension study system); KEO表示Kuroshio extension observatory |
美国国家海洋和大气管理中心/太平洋海洋环境实验室于2004年6月在K7附近布放了一个锚系浮标KEO (Kuroshio extension observatory, 图 1), 提供了每10 min一次的海表面风速。此外, 本文还采用了Levitus94全球月平均混合层深度(空间分辨率0.5°×0.5°), 日本气象厅提供的每6 h的台风路径资料, 美国国家环境预报中心提供的每小时的再分析海表面风应力资料(空间分辨率约0.3°×0.3°), 以及法国多源卫星高度计融合项目AVISO (archiving, validation, and interpretation of satellite oceanographic)提供的每天的海表面高度异常(sea level anomaly, SLA)(空间分辨率0.25°×0.25°)。基于SLA数据, 可根据地转平衡计算地转涡度:
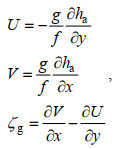 (1)
(1)其中, U和V分别是纬向和经向流速; ζg是地转涡度; ha是卫星高度计观测的SLA; g是重力加速度; f是科氏参数。
1.2 近惯性信号提取方法对于ADCP和海流计观测的水平流速, 可通过0.85f0~1.15f0 (f0是局地科氏频率)带通滤波直接获得近惯性流速信号, 且稍微改变滤波带宽, 如改为0.80f0~1.20f0, 对结果影响很小。但是, 对于MMP观测的水平流速, 由于其采样间隔是15 h, 约为局地惯性周期(22.3 h)的2/3, 因此惯性频率信号会发生混叠。参考Ray等(1997)和Sun等(2016)计算得到惯性频率f0被混叠到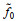
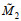
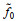
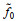
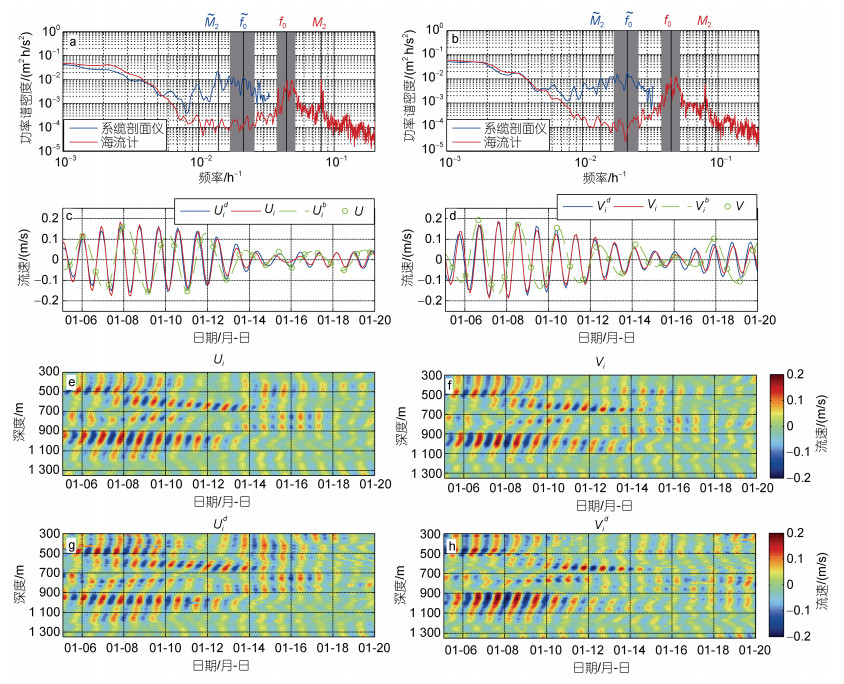 |
图 2 海流计和系缆剖面仪观测的1 500 m附近流速的频谱(a~b), 利用系缆剖面仪观测的1 000 m处的流速进行去混叠过程中得到的不同的流速时间序列(c~d), 以及基于系缆剖面仪观测的取2 h (e~f)和15 h (g~h)采样周期得到的近惯性流速的时间-深度分布 Fig. 2 Frequency spectrum of velocity near 1 500 m from current meter and moored profiler measurements (a~b), comparisons among different time series of velocity during de-aliasing (c~d), and the time-depth distribution of near-inertial velocity derived from moored profiler that are sampled every 2 h (e~f) and subsampled every 15 h (g~h)
注: a~b中海流计和系缆剖面仪的采样周期分别是15 min和15 h, 惯性频率f0和半日潮频率M2分别混叠到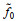 和 和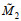 , 阴影区域表示滤波带宽; 左列是纬向流U的结果, 右列是经向流V的结果; c和d中U和V是采样间隔为15 h的原始流速, Uib和Vib是围绕混叠频率 , 阴影区域表示滤波带宽; 左列是纬向流U的结果, 右列是经向流V的结果; c和d中U和V是采样间隔为15 h的原始流速, Uib和Vib是围绕混叠频率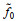 做带通滤波得到的流速, Uid和Vid是去混叠的近惯性流速, Ui和Vi是利用2 h采样周期观测直接得到的近惯性流速 做带通滤波得到的流速, Uid和Vid是去混叠的近惯性流速, Ui和Vi是利用2 h采样周期观测直接得到的近惯性流速 |
如前所述, K7站位的MMP数据在2005年1月的时间分辨率约为2 h, 可以很好地分辨近惯性信号, 这为我们验证以上提取近惯性信号的方法提供了条件。图 2c和图 2d比较了采用去混叠法和直接带通滤波法得到的近惯性流速, 可以看到两者有很好的一致性。在300~1 350 m, 两种方法得到的纬向(经向)近惯性流速方差一致为2.7×10-3 m2/s2 (2.7×10-3 m2/s2), 约为两者之间均方根误差5.16×10-4 m2/s2 (5.67×10-5 m2/s2)的5倍(图 2e, 2h), 这与Rainville等(2014)得到的结果一致。由此, 采用去混叠的方法得到了2004年6~9月期间300~1 500 m的近惯性水平流速(ui, vi), 进一步估算近惯性动能如下:
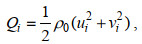 (2)
(2)其中, ρ0=1 025 kg/m3是海水密度。
1.3 细尺度参数化方法本文还利用MMP观测的温度、盐度和流速数据, 采用细尺度参数化方法估算了跨等密度面湍流混合率(Polzin et al, 1995; Gregg et al, 2003; Kunze et al, 2006)。根据Gregg等(2003)和Kunze等(2006), 湍流耗散率可由细尺度O (10~100 m)上的应变和剪切估算如下:
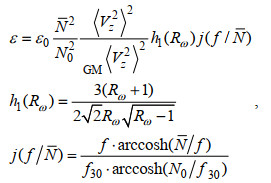 (3)
(3)其中, 是耗散率; h1(Rω)和j(f/N)是分别针对内波结构和纬度影响的修正系数; ε0=6.73×10-10 m2/s3; N0=5.2×10-3 rad/s; N是垂直平均的浮力频率; GM〈VZ2〉是依据GM谱模型得到的剪切方差(Gregg et al, 1991; Kunze et al, 1992); 〈VZ2〉是观测的剪切方差; f是局地科氏频率; f30=f (30°)是纬度为30°处的科氏频率; R是剪切应变方差比:
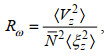 (4)
(4)其中, 〈ξZ2〉是应变方差。
计算耗散率的步骤基本如Kunze等(2006)和Jing等(2014)所用, 先将每个垂向剖面划分为300 m的子剖面, 并取150 m重叠, 在每个子剖面中, 由浮力频率计算应变ξZ=(N2-N2)/N2, 其中N2通过对位势密度剖面进行一阶差分得到而其垂向平均N2由二次拟合得到(Polzin et al, 1995), 将去掉线性趋势的速度剪切利用平均浮力频率N2进行正则化; 再利用傅里叶变换得到剪切和应变谱Φ (k), 并对其进行积分, 选取最小积分波数kmin=2π/150 rad/m, 而为了避免由于谱饱和而导致低估耗散率, 取最大积分波数kmax满足如下条件(Gargett, 1990):
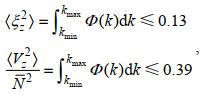 (5)
(5)得到kmax=2π/16 rad/m; 然后在相同的波数区间计算GM剪切谱:
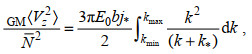 (6)
(6)其中, E0=6.3×10-5; b=1 300 m; j*=3, k* = (πj*N)/(bN0) (Gregg et al, 1991)。得到耗散率ε后, 扩散系数可根据关系式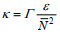
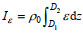
细尺度参数化方法已被成功应用于全球海洋混合研究中, 而前人研究结果显示该参数化方法估算结果的不确定度在2倍之内(Polzin et al, 1995; Gregg et al, 2003)。
1.4 风生近惯性能量计算方法结合KEO风速资料与ADCP表层流速数据, 可直接计算风输入到混合层的近惯性能量如下:
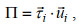 (7)
(7)其中, 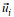
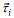
此外, 我们还基于风应力资料, 采用Pollard等(1970)提出的Slab模型间接估算风生近惯性能量如下:
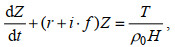 (8)
(8)其中, Z = u + i · v是混合层流速, T = τx + i · τy是海表面风应力, f是局地科氏参数, r=r0(1-e-σ2/2σc2)是衰减系数(Alford, 2003), 其中σ是角频率, 根据Alford(2001, 2003), 取r0=0.15f, σc = f / 2, H是混合层深度, 采用Levitus94月平均值。通过求解方程(8)可得风生近惯性能量
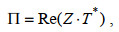 (9)
(9)其中, T*是T的共轭。
2 结果与讨论 2.1 跨等密度面湍流混合的次季节变化Jing等(2014)研究结果表明, 在K7站位处, 300~1 350 m的跨等密度面湍流混合存在明显的季节变化, 2004年冬季的平均耗散率约为夏季的3倍, 而本文进一步发现这里的混合也存在明显的逐月变化即次季节变化。如图 3所示, 300~1 350 m垂向平均的耗散率在8月份最强(2.7×10-9 m2/s3)而在9月份最弱(1.0×10-9 m2/s3), 8月份的平均耗散率与6月、7月、9月平均耗散率的比值R0分别为1.6、2.1、2.7, 扩散系数的结果与此一致。
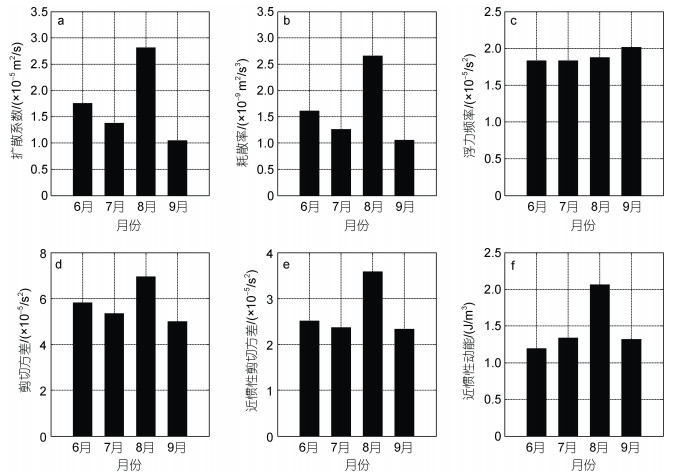 |
| 图 3 基于系缆式剖面仪观测的且取300~1 350 m垂向平均的跨等密度面扩散系数(a)、耗散率(b)、浮力频率(c)、剪切方差(d)、近惯性剪切方差(e)、近惯性动能(f)的月平均分布 Fig. 3 Monthly distributions based on the moored profiler measurements and the average within 300~1 350 m of (a) diapycnal diffusivity, (b) dissipation rate, (c) squared buoyancy frequency, (d) shear variance, (d) near-inertial shear variance, and (e) near-inertial kinetic energy |
考虑到与真实的耗散率εreal相比, 利用细尺度参数化方法估算得到的耗散率εobs的不确定度约为2倍(Polzin et al, 1995; Gregg et al, 2003)。因此, 以上我们看到的次季节变化是个真实的物理现象还是仅仅由随机误差导致需要进一步验证。这里我们采用Jing等(2013)的方法, 以8月份的平均耗散率εobs与其他月份εobs之间的比值R作为检验统计量, 对混合的次季节变化信号进行假设检验。原假设是耗散率不存在逐月变化, 每个月耗散率的数学期望相同; 而备择假设是耗散率存在逐月变化, 8月份耗散率的数学期望要比其他月份大。假定εobs在区间[0.5εreal, 2εreal]上均匀分布, 则R的概率密度函数可由Monte Carlo方法模拟得到, 结果显示, R > R0的概率不足1% (图 4)。这意味着, 在1%显著性水平下, 可以拒绝原假设。因此, 以上观测到的耗散率的次季节变化是可信的。
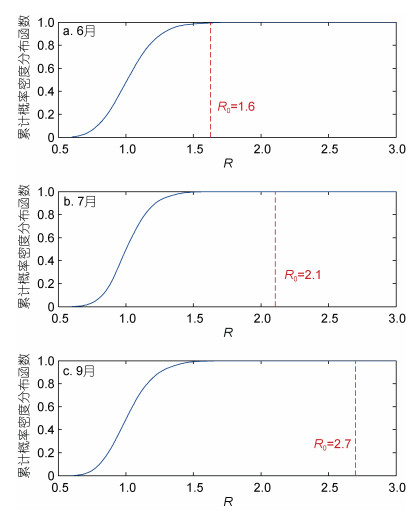 |
| 图 4 假设8月平均耗散率与6月(a)、7月(b)、9月(c)平均耗散率之间没有明显差异时, 检验统计量R的累计概率密度分布函数 Fig. 4 Distribution function of cumulative probability density of R in assumption of no significant difference in average dissipation rates of August from those of June (a), July (b), and September (c) 注: R0表示8月份与其他月份平均耗散率的比值 |
背景层结N2和剪切方差S2都能影响跨等密度面湍流混合的强度变化。Jing等(2015)在墨西哥湾北部发现扩散系数和浮力频率之间存在弱相关关系。但是, 在K7站位, 背景层结在2004年6~9月不存在明显的次季节变化, 8月份的平均N2仅比6~7月(9月)强(弱) 2% (7%) (图 3c), 而且耗散率ε和N2之间也没有明显的相关关系(图 5)。因此, K7处的跨等密度面湍流混合的次季节变化与背景层结无关。
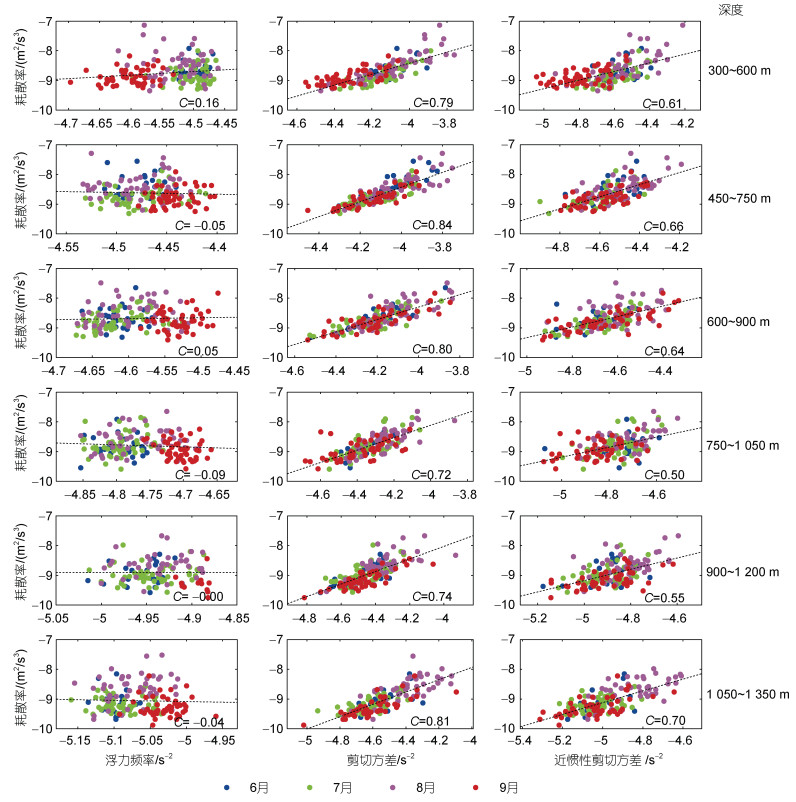 |
| 图 5 2004年6~9月不同深度的浮力频率(左)、剪切方差(中)、近惯性剪切方差(右)和耗散率的关系 Fig. 5 Scatterplots of squared buoyancy frequency (left panel), shear variance (middle panel), and near-inertial shear variance (right panel) vs dissipation rate at different depth segments from Junes to September 2004 注: 所有变量均是取对数log10后的结果; 虚线表示两个变量的线性拟合; C表示相关系数 |
不同于背景层结, 流速的剪切方差S2和近惯性剪切方差Si2都有明显的次季节变化, 且与耗散率和扩散系数的变化位相一致(图 3)。特别的, 在300~1 350 m, 耗散率ε随着S2和Si2增大而增强, ε与S2 (Si2)的相关系数在0.72~0.84 (0.50~0.70)之间(图 5), 且所有相关系数都超过95%显著性水平。图 6进一步比较了不同月份300~1 350 m垂向平均的背景层结和流速剪切与耗散率的相关关系, 可以看到8月份的S2和Si2与耗散率ε的相关最强, 相关系数分别为0.86和0.81, 也远远超过95%显著性水平。Jing等(2014)也发现在K7处, 2005年1月的耗散率与近惯性剪切方差明显相关, 指出近惯性内波在调制湍流混合中起着重要作用。因此, 以上结果意味着这里的近惯性内波对湍流混合的次季节变化也有重要影响, 而且近惯性内波的影响在8月份最强。
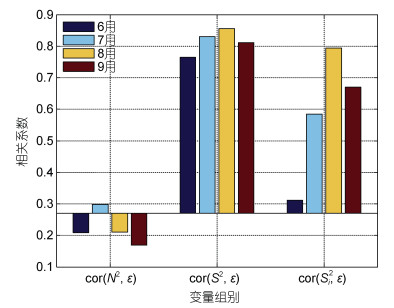 |
| 图 6 2004年6~9月300~1 350 m垂向平均的浮力频率N2 (左)、剪切方差S2 (中)、近惯性剪切方差Si2 (右)和耗散率的相关系数 Fig. 6 Correlation coefficients between the depth-averaged (300~1 350 m) dissipation rate and the buoyancy frequency (left), shear variance (middle), and near-inertial shear variance (right) in June to September, 2004 注: 柱状图的基值为95%显著性水平 |
通过分析流速剪切uz+i·vz的频率-波数谱, 可以进一步探究近惯性内波的能量来源。图 7a显示了2004年6~9月MMP观测的水平流速(15 h采样间隔)的频率-波数谱, 可以看到谱峰落在第四象限混叠惯性频率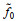
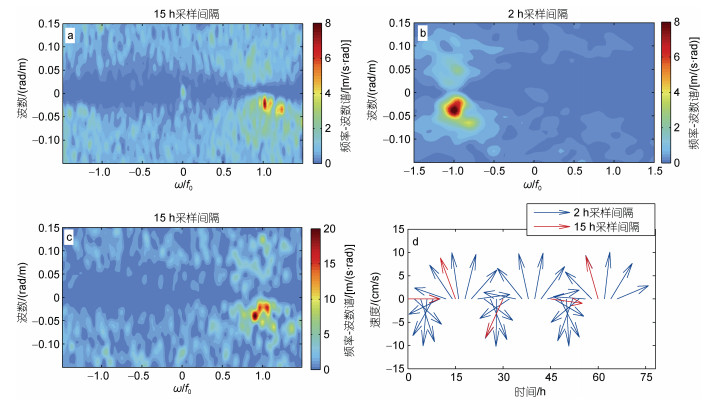 |
图 7 基于系缆式剖面仪观测的2004年6~9月采样间隔为15 h (a)、2005年1月采样间隔为2 h (b)和15 h (c)得到的流速剪切的频率-波数谱以及周期为22.3 h随时间顺时针旋转的惯性流速的概念图(d) Fig. 7 The frequency-wavenumber spectra of complex velocity shear, calculated with moored profiler measurements from June to September 2004 that were sampled every 15 h (a), and during January 2005 that were sampled every 2 h (b) and 15 h (c), and the schematic plot (d) showing the inertial velocity of clockwise rotation with a period of 22.3 h in sampling interval
注: a~c中横坐标是由局地惯性频率f0或混叠惯性频率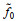 标准化的频率, ω表示频率; d中以2 h为采样间隔的流速为顺时针旋转(蓝线), 以15 h为采样间隔的流速变为逆时针旋转(红线) 标准化的频率, ω表示频率; d中以2 h为采样间隔的流速为顺时针旋转(蓝线), 以15 h为采样间隔的流速变为逆时针旋转(红线) |
进一步, 我们分析了每个月平均的近惯性流速剪切的旋转垂向波数谱(图 8), 结果发现, 当波数小于0.04 rad/m, 即波长大于150 m时, 随深度顺时针旋转的分量约是逆时针旋转分量的2倍以上, 意味着下传能量强于上传能量, 这与图 7所示的频率-波数谱一致。特别的, 在8月份, 顺时针旋转分量最强且其主导作用最为明显, 在垂直尺度大于120 m, 即波数小于0.05 rad/m处, 下传分量强度约是上传分量的4倍。以上结果表明近惯性内波的能量主要是向下传播的, 而这些下传的能量很可能是来源于海表面的风生近惯性能量, 这将在后文中做进一步的分析。
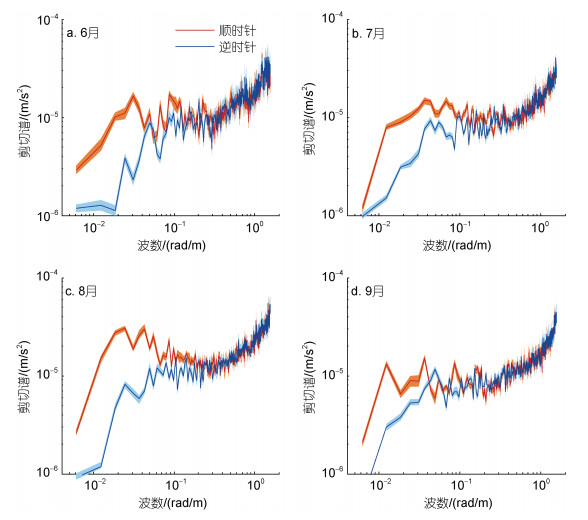 |
| 图 8 近惯性流速剪切的月平均旋转垂直波数谱 Fig. 8 The mean rotary vertical wavenumber spectra of near-inertial velocity shear in June (a), July (b), August (c), and September (d) 注: 红线(蓝线)为随深度增加顺时针(逆时针)旋转的分量; 阴影区域是基于bootstrap法计算的90%置信区间 |
一般地, 风向海洋中输入近惯性能量主要是在风暴过境期间(D’Asaro, 1985)。在2004年6~9月, 有6个台风经过研究海区(图 9), 其中6月底至7月初发生的“婷婷”、7月底发生的“南川”和8月发生的“暹芭”在K7处输入海洋的近惯性能量较强, 超过4×10-3 W/m2; 相反地, 8月初经过的“玛瑙”由于风力较弱, 在K7处无明显增强的风生近惯性能量, 而8月底9月初发生的“桑达”由于距离K7较远输入的近惯性能量也较小, 仅2×10-3 W/m2 (图 10a)。值得注意的是, 8月中旬K7处有很强的风生近惯性能量, 最强达到8×10-3 W/m-2, 此时虽然台风“鲇鱼”过境, 但其中心距离K7站位约2 000 km, 风力也较弱, 因此对K7处的近惯性流不会产生直接影响。进一步基于再分析风应力资料, 利用Slab模型得到了8月13~16日风生近惯性能量的水平分布(图 11), 结果发现, 在8月14日, K7站位及其西北侧的局地风都向海洋输入了很强的近惯性能量, 在8月15日达到最强, 到了8月16日, 尽管台风“鲇鱼”的边缘掠过K7, 但对K7处近惯性能量的影响很小。总之, 8月中旬K7处的风生近惯性能量增强是局地风导致, 与台风“鲇鱼”无关。对于月平均的风生近惯性能量, 也是8月份最强(1.6×10-3 W/m2), 9月份最弱(0.5×10-3 W/m2), 其次季节变化的位相与近惯性剪切方差及湍流混合一致。这一结果进一步说明了风生近惯性能量对调制跨等密度面湍流混合的次季节变化起着重要作用。
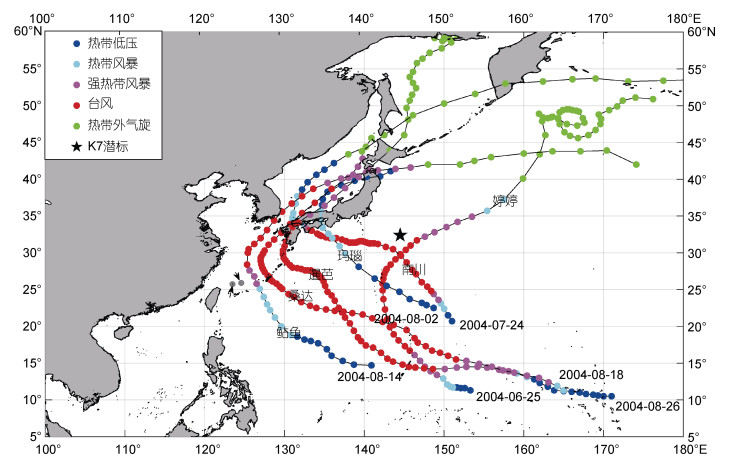 |
| 图 9 热带气旋每6 h的移动轨迹 Fig. 9 The storm tracks every 6 h with different colors denoting their development stages |
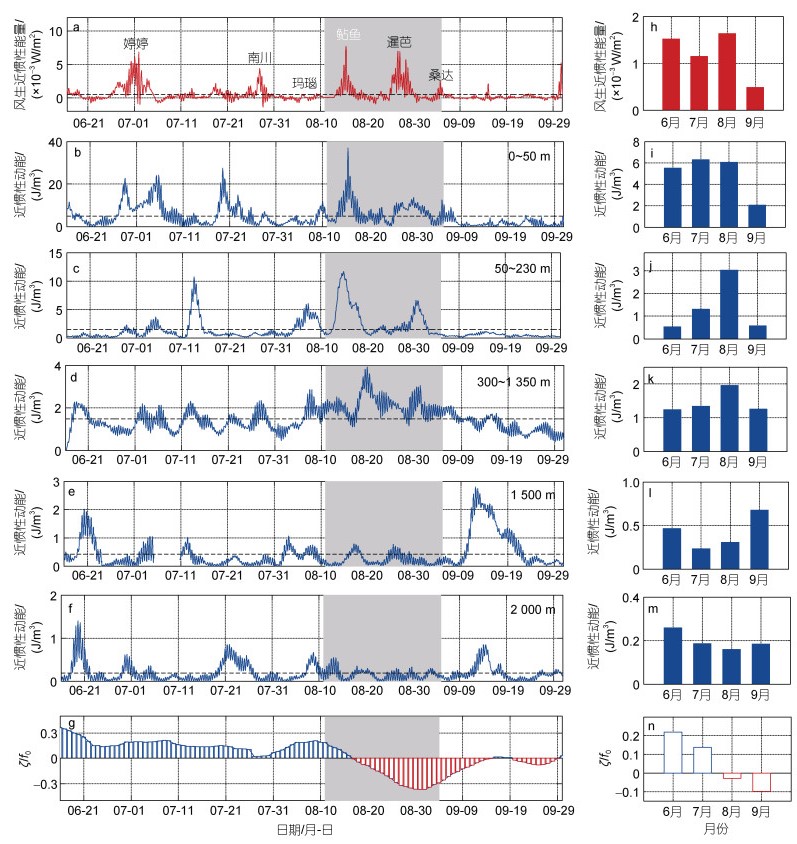 |
| 图 10 基于直接观测计算的风生近惯性能量(a, h)以及近惯性动能(b~f, i~m)和地转涡度(g, n)的时间序列 Fig. 10 Time series of wind-induced near inertial energy (a, h), near-inertial kinetic energy (b~f, i~m), as well as the geostrophic vorticity (g, n) 注: b: 0~50 m垂向平均; c: 50~230 m垂向平均; d: 300~1 350 m垂向平均; e: 1 500 m处; f: 2 000 m处; i~m: 是相应的月平均时间序列; g和n中的地转涡度ζ由局地惯性频率f0进行了标准化, 蓝色和红色分别表示正涡度和负涡度; 30 m以浅、300~1 350 m、1 500及2 000 m处的近惯性动能分别是基于ADCP、MMP和两个海流计的观测计算得到的; 阴影区域表示估算能量通量的时间段 |
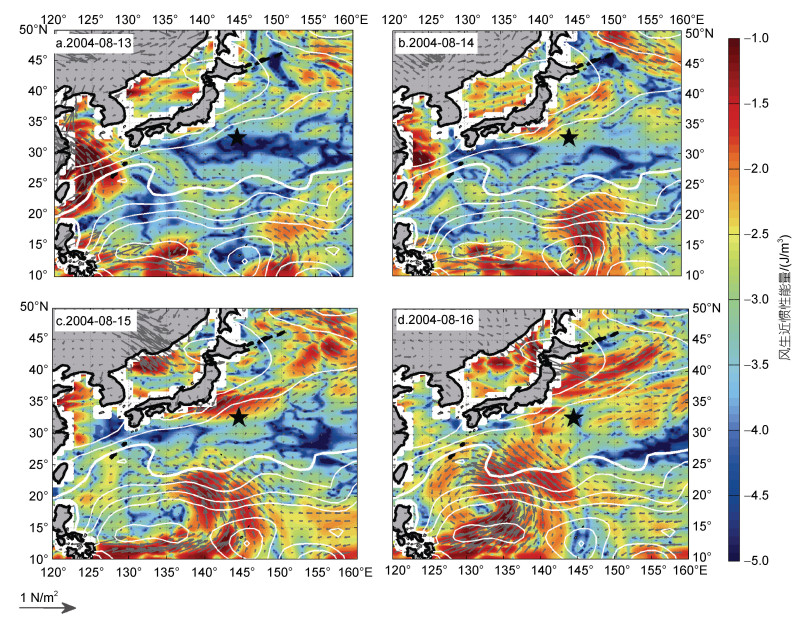 |
| 图 11 基于Slab模型计算的风生近惯性能量(颜色)和再分析风应力(箭头)的水平分布 Fig. 11 Horizontal distribution of wind-induced near-inertial energy (color) and wind stress (arrows) 注: 风生近惯性能量是取对数log10的结果; 黑色星号表示K7潜标站位; 白线表示8月平均混合层深度, 其间隔为5 m; 白色粗线为15 m等值线 |
伴随着每个强风生近惯性能量事件, 混合层中的近惯性动能也增强, 特别是对应于8月中旬最强的风生近惯性能量, 表层0~50 m的近惯性动能也达到最强35 J/m3 (图 10)。但是, 如图 10所示, 风生近惯性能量与表层近惯性动能的变化幅度也有所差异, 例如台风“暹芭和“婷婷”过境时, 风输入的近惯性能量大小相当, 但是50 m以浅的近惯性动能在“暹芭”期间仅是“婷婷”期间的1/2 (图 10b); 而在7月19日前后, 无台风发生且风生近惯性能量较弱, 但表层的近惯性动能却与台风“婷婷”经过时相当。相应的, 对于表层近惯性动能的次季节变化, 6~8月的大小相当, 且7月最强, 也与风生近惯性能量的变化位相不同。这些差异可能是由于台风的水平结构、路径以及局地风场和背景流等因素的不同导致(Alford et al, 2016)。
与表层的近惯性动能相比, 深层的近惯性动能明显减弱。在2004年6~9月期间, 50~230、300~1 350、1 500、2 000 m的平均近惯性动能分别为1.5、1.5、0.4、0.1 J/m3, 分别是表层0~50 m平均近惯性动能的30%、30%、8%、2%, 意味着大部分的风生近惯性能量在表层就耗散掉了。但对于8月中旬表层的强近惯性动能峰值, 也明显存在于次表层50~230 m, 至8月20日出现在了300~1 350 m垂向平均的近惯性动能时间序列中, 而在1 500和2 000 m处消失, 这直观地显示了近惯性能量的下传(图 10b~10f)。对于月平均的近惯性动能, 50~230和300~1 350 m处都是在8月最强, 而1 500和2 000 m处都是在9月最强。另外值得注意的是, 伴随着这个近惯性动能的下传, 地转相对涡度在8月中旬由正变负, 这一结果符合Kunze (1985)的理论, 即背景涡度ζg能够将内波的频率下限f0变为有效频率feff=f0+ζg/2, 因此负涡度区将捕获固有频率小于feff的近惯性内波, 促进近惯性能量下传。Martínez-Marrero等(2019)基于观测也发现在弱风环境下, 反气旋涡中也会存在很强的近惯性内波及湍流混合。因此, 对于8月份增强的近惯性剪切, 除了较强的风生近惯性能量输入, 负涡度也起了一定作用。
图 12显示了2004年8~9月近惯性动能随深度的变化, 可以看到伴随着表层近惯性流增强, 次表层100~150 m处也存在一个明显的近惯性动能极大值。Chen等(2013)也曾在台风“浣熊”经过南海西北部时发现类似现象, 他们指出近惯性动能的表层峰值主要由第一斜压模态主导, 而次表层峰值是由高阶垂直模态决定。进一步通过将傅里叶变换的流速针对正负波数进行分离, 可得到近惯性流速的上传和下传信号。图 12b~12c显示了近惯性动能及其下传分量的深度-时间分布, 其中对于流速, 我们进行了wentzel- kramers-brillouin (WKB)近似以消除层结的影响(Alford et al, 2012)。从中可以明显看到一个很强的近惯性内波波包从8月14日的300 m处下传, 至9月4日到达1 300 m, 下传速度约为5.5×10-4 m/s, 在此期间平均下传的近惯性动能约为1.61 J/m3, 超过上传动能的3倍。
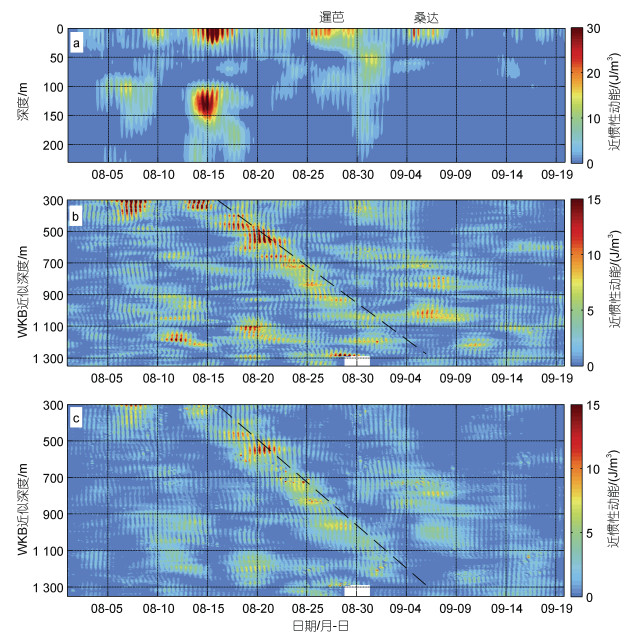 |
| 图 12 230 m以浅的近惯性动能(a)以及300~1 350 m处Wentzel-Kramers-Brillouin (WKB)修正后的总近惯性动能(b)及其下传分量(c) Fig. 12 Time-depth distribution of near-inertial kinetic energy in the upper 230 m (a), and the total (b) and downward-propagating near-inertial kinetic energy (c) within 300~1 350 m, being WKB-scaled 注: 黑色虚线表示近惯性内波波包下传; b和c的空白处表示无数据 |
针对图 12中的强近惯性内波波包, 我们进一步分析了其下传期间即8月11日至9月4日的垂向能量通量。根据Leaman (1976)和Jaimes等(2010), 垂向能量通量可计算如下:
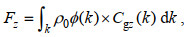 (10)
(10)其中, k是垂直波数, ϕ是近惯性流速的波数谱, Cgz是垂直群速度, 参考Rossby等(1976)可估算如下:
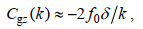 (11)
(11)其中, δ是观测到的惯性频率fobs与局地科氏频率f0之间的差异。
为了得到fobs, 我们对ADCP观测的0~230 m处8月11日至9月4日的流速进行了谱分析, 结果如图 13a所示。可以看到, 谱值在近惯性频段明显增大, fobs在0~230 m的平均值为0.267 rad/h, 比f0小5%。因此, 对于上传和下传的能量, 分别设置δ为-0.05和0.05。
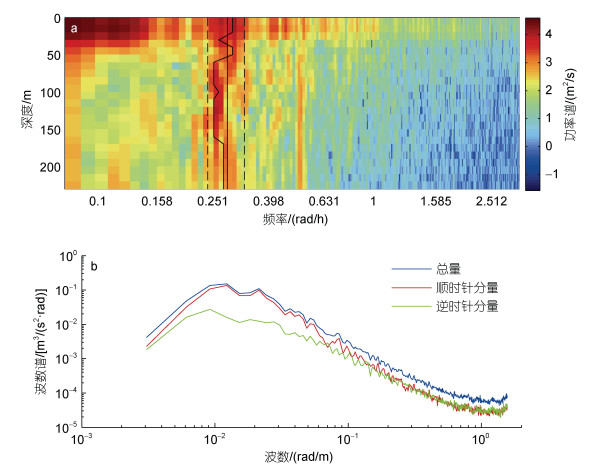 |
| 图 13 ADCP观测水平流速的功率谱(a)以及基于系缆式剖面仪观测的300~1 350 m处WKB修正近惯性流速的旋转波数谱(b) Fig. 13 Power spectra of the ADCP measured horizontal velocity (a), and the rotary wavenumber spectra of the WKB-scaled near-inertial velocity within 300~1 350 m obtained from moored profiler measurements (b) 注: a中的功率谱是取对数log10后的结果, 黑色细实线表示局地惯性频率f0, 黑色虚线分别表示0.85f0 (左)和1.15f0 (右), 粗实线表示近惯性频率峰值 |
计算300~1 350 m处WKB近似的近惯性流速的(旋转)垂向波数谱, 结果如图 13b所示, 在波数小于0.06 rad/m, 即波长大于100 m时, 其主要由随深度顺时针旋转的分量主导, 即近惯性能量以下传为主导, 这与前文中的谱分析结果一致。最终, 估算得到下传的近惯性能量通量Fzdown为1.2×10-3 W/m2, 是上传能量通量Fzup的4倍。考虑到1 350 m以深的近惯性内波远弱于300~1 350 m的内波(图 10, 12), 这里得到的Fzdown可以近似看作是300和1 350 m之间的能量通量差异。同时, 300~1 350 m垂向平均的耗散率为2.3×10-3 W/m2。因此, 下传的近惯性能量Fzdown为湍流混合提供了52%的能量, 证实了近惯性能量对于维持深海跨等密度面湍流混合确实起着重要作用。此外, 在这期间的平均风生近惯性能量为1.7×10-3 W/m2, 这意味着其71%下传至深海。我们同样估算了2004年6~7月的能量收支, 结果发现仅有18%的风生近惯性能量下传, 与Alford等(2012)在东北太平洋得到的结果(12%~33%)一致。进一步比较8~9月和6~7月两个时间段的平均地转涡度分别为-0.15f0和0.16f0, 这一结果也显示了负地转涡度对于近惯性能量向深海穿透的促进作用(Kunze, 1985)。
为了检验以上能量通量估算的准确性, 我们又对2005年1月4~14日地转涡度也是负值时的垂向近惯性能量通量进行了计算。为了便于比较, 这里也采用了由MMP观测得到的15 h采样间隔的去混叠的近惯性流速。结果表明, 此时的近惯性频率fobs比局地惯性频率f0小8%, 下传能量通量Fzdown是3.6×10-3 W/m2, 约为上传能量通量Fzup的4倍。这一结果与Jing等(2014)基于对同期的2 h采样间隔的流速进行二维频率-波数谱分析得到的下传能量通量3.5×10-3 W/m2一致。可见, 我们利用去混叠的近惯性流速计算的能量通量结果是可信的。此外, 这期间的平均风生近惯性能量是4.8×10-3 W/m2, 而平均垂向积分的耗散率为5.5×10-3 W/m2。因此, 风输入的近惯性能量有75%下传, 为深海湍流混合提供了65%的能量。通过比较可以看到, 尽管2004年8月11日至9月4日的风生近惯性能量较弱, 但其能量下传效率及其对深海跨等密度面湍流混合的贡献与2005年1月4~14日相当。
3 结论本文基于黑潮延伸体区的K7潜标观测资料, 利用细尺度参数化方法分析了跨等密度面湍流混合的次季节变化, 发现了一系列现象如下:
K7处300~1 350 m的湍流混合存在明显的次季节变化, 表现在2004年8月份的平均耗散率是2.7×10-9 m2/s3, 是同年9月份的3倍。湍流混合的这一次季节变化与风生近惯性内波的剪切方差密切相关。
在2004年6~9月有6个台风经过研究海区, 其中有4个在K7处输入了大量的近惯性能量。在8月中旬, K7处的风生近惯性能量最强达到35 J/m3, 此时虽然台风鲇鱼过境, 但由于其距离观测站位较远且风力较弱, 而对K7处的近惯性能量无明显影响, 因此这里的风生近惯性能量增强是一局地现象, 由局地风导致。伴随着风输入海洋中的近惯性能量增强, K7处的地转涡度也在8月中旬由正变负, 相应地, 一个强近惯性内波波包下传至1 300 m。能量收支分析显示, 在8月11日至9月4日期间, K7处的平均风生近惯性能量为1.7×10-3 W/m2, 其中约有71%下传, 为300~1 350 m的跨等密度面耗散提供了52%的能量。相比之下, 在2004年6~7月, 地转涡度为正时, 仅有18%的风生近惯性能量下传。因此, 8月份的负地转涡度也促进了近惯性能量的下传, 从而使得跨等密度面湍流混合增强。
总之, 与台风过境时在海洋混合层中激发出较强的近惯性内波进而促进海洋混合的情况不同, 本文研究结果表明, 在正常风或弱风环境下, 在负的背景涡度中, 也会存在较强的近惯性能量及湍流混合。Martínez-Marrero等(2019)在大西洋中也观测到这一现象。已有理论研究指出, 在水平方向上, 近惯性内波从正涡度区向负涡度区辐射(Lee et al, 1998), 而在垂直方向上, 负背景涡度也能促进近惯性内波下传(Kunze, 1985)。因此可以推测以上现象可能广泛存在于开阔海洋中。
另外, 对于西北太平洋风生近惯性能量向下传播的穿透深度, 已有一些研究通过比较风生近惯性能量和湍流混合的季节变化, 间接估算得到的结果是600~1 800 m (如Jing et al, 2010, 2011; 闫晓梅等, 2014; Li et al, 2014)。而在本文中, 我们通过直接分析黑潮延伸体区的近惯性流速, 发现局地风引起的强近惯性内波能够下传1 300 m, 为风生近惯性内波在调制深海湍流混合次季节变化中所起的重要作用提供了更直观的证据。然而, 除了垂向传播, 风生近惯性内波也能水平传播, 但后者无法从单个锚定站位观测中确定。因此, 为了获取近惯性内波的所有特性, 更深入地理解其对深海跨等密度面湍流混合的影响, 也为了验证我们的以上猜测, 提高关于海洋对正常风和弱风的近惯性响应的认识, 今后仍需基于更多的现场观测以及高分辨率数值模式进行分析研究。
闫晓梅, 李颖, 徐永生. 2014. 西北太平洋跨等密度面湍流混合的时空变化分析. 海洋与湖沼, 45(6): 1148-1157 |
祝从文, 刘伯奇, 左志燕, 等. 2019. 东亚夏季风次季节变化研究进展. 应用气象学报, 30(4): 401-415 |
ALFORD M H, 2001. Internal swell generation: The spatial distribution of energy flux from the wind to mixed layer near-inertial motions. Journal of Physical Oceanography, 31(8): 2359-2368 DOI:10.1175/1520-0485(2001)031<2359:ISGTSD>2.0.CO;2 |
ALFORD M H, 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophysical Research Letters, 30(8): 1424 |
ALFORD M H, CRONIN M F, KLYMAK J M, 2012. Annual cycle and depth penetration of wind-generated near-inertial internal waves at Ocean Station Papa in the northeast Pacific. Journal of Physical Oceanography, 42(6): 889-909 DOI:10.1175/JPO-D-11-092.1 |
ALFORD M H, Mackinnon J A, SIMMONS H L et al, 2016. Near-inertial internal gravity waves in the ocean. Annual Review of Marine Science, 8: 95-123 DOI:10.1146/annurev-marine-010814-015746 |
CHELTON D B, SCHLAX M G, SAMELSON R M, 2011. Global observations of nonlinear mesoscale eddies. Progress in Oceanography, 91(2): 167-216 DOI:10.1016/j.pocean.2011.01.002 |
CHEN G X, XUE H J, WANG D X et al, 2013. Observed near-inertial kinetic energy in the northwestern South China Sea. Journal of Geophysical Research: Oceans, 118(10): 4965-4977 DOI:10.1002/jgrc.20371 |
D'ASARO E A, 1985. The energy flux from the wind to near-inertial motions in the surface mixed layer. Journal of Physical Oceanography, 15(8): 1043-1059 DOI:10.1175/1520-0485(1985)015<1043:TEFFTW>2.0.CO;2 |
FURUICHI N, HIBIYA T, NIWA Y, 2008. Model-predicted distribution of wind-induced internal wave energy in the world's oceans. Journal of Geophysical Research: Oceans, 113(C9): C09034 |
GARGETT A E, 1990. Do we really know how to scale the turbulent kinetic energy dissipation rate ε due to breaking of oceanic internal waves?. Journal of Geophysical Research: Oceans, 95(C9): 15971-15974 DOI:10.1029/JC095iC09p15971 |
GREGG M C, KUNZE E, 1991. Shear and strain in Santa Monica Basin. Journal of Geophysical Research: Oceans, 96(C9): 16709-16719 DOI:10.1029/91JC01385 |
GREGG M C, SANFORD T B, WINKEL D P, 2003. Reduced mixing from the breaking of internal waves in equatorial waters. Nature, 422(6931): 513-515 DOI:10.1038/nature01507 |
HU S J, LIU L L, GUAN C et al, 2020. Dynamic features of near-inertial oscillations in the Northwestern Pacific derived from mooring observations from 2015 to 2018. Journal of Oceanology and Limnology, 38(4): 1092-1107 DOI:10.1007/s00343-020-9332-1 |
INOUE R, WATANABE M, OSAFUNE S, 2017. Wind-induced mixing in the North Pacific. Journal of Physical Oceanography, 47(7): 1587-1603 DOI:10.1175/JPO-D-16-0218.1 |
JAIMES B, SHAY L K, 2010. Near-inertial wave wake of Hurricanes Katrina and Rita over mesoscale oceanic eddies. Journal of Physical Oceanography, 40(6): 1320-1337 DOI:10.1175/2010JPO4309.1 |
JIANG J, LU Y Y, PERRIE W, 2005. Estimating the energy flux from the wind to ocean inertial motions: The sensitivity to surface wind fields. Geophysical Research Letters, 32(15): L15610 DOI:10.1029/2005GL023289 |
JING Z, CHANG P, DIMARCO S F et al, 2015. Role of near-inertial internal waves in subthermocline diapycnal mixing in the Northern Gulf of Mexico. Journal of Physical Oceanography, 45: 3137-3154 DOI:10.1175/JPO-D-14-0227.1 |
JING Z, WU L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress. Geophysical Research Letters, 37(23): L23604 |
JING Z, WU L X, 2013. Low-frequency modulation of turbulent diapycnal mixing by anticyclonic eddies inferred from the HOT time series. Journal of Physical Oceanography, 43(4): 824-835 DOI:10.1175/JPO-D-11-0150.1 |
JING Z, WU L X, 2014. Intensified diapycnal mixing in the midlatitude western boundary currents. Scientific Reports, 4: 7412 |
JING Z, WU L X, LI L et al, 2011. Turbulent diapycnal mixing in the subtropical northwestern Pacific: Spatial-seasonal variations and role of eddies. Journal of Geophysical Research: Oceans, 116(C10): C10028 DOI:10.1029/2011JC007142 |
JING Z, WU L X, MA X H et al, 2016. Overlooked role of mesoscale winds in powering ocean diapycnal mixing. Scientific Reports, 6(1): 37180 DOI:10.1038/srep37180 |
KUNZE E, 1985. Near-inertial wave propagation in geostrophic shear. Journal of Physical Oceanography, 15(5): 544-565 DOI:10.1175/1520-0485(1985)015<0544:NIWPIG>2.0.CO;2 |
KUNZE E, FIRING E, HUMMON J M et al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553-1576 DOI:10.1175/JPO2926.1 |
KUNZE E, KENNELLY M A, SANFORD T B, 1992. The depth dependence of shear finestructure off point arena and near pioneer seamount. Journal of Physical Oceanography, 22(1): 29-41 DOI:10.1175/1520-0485-22.1.29 |
LEAMAN K D, 1976. Observations on the vertical polarization and energy flux of near-inertial waves. Journal of Physical Oceanography, 6(6): 894-908 DOI:10.1175/1520-0485(1976)006<0894:OOTVPA>2.0.CO;2 |
LEE D K, NIILER P P, 1998. The inertial chimney: The near-inertial energy drainage from the ocean surface to the deep layer. Journal of Geophysical Research: Oceans, 103(C4): 7579-7591 DOI:10.1029/97JC03200 |
LI Y, XU Y S, 2014. Penetration depth of diapycnal mixing generated by wind stress and flow over topography in the northwestern Pacific. Journal of Geophysical Research: Oceans, 119(8): 5501-5514 DOI:10.1002/2013JC009681 |
MARTINEZ-MARRERO A, BARCELó-LLULL B, PALLAS-SANZ E et al, 2019. Near-inertial wave trapping near the base of an anticyclonic mesoscale eddy under normal atmospheric conditions. Journal of Geophysical Research: Oceans, 124(11): 8455-8467 DOI:10.1029/2019JC015168 |
MUNK W, WUNSCH C, 1998. Abyssal recipes Ⅱ: Energetics of tidal and wind mixing. Deep Sea Research I, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
NAGAI T, ROSALES QUINTANA G M, DURán GOMEZ G S et al, 2021. Elevated turbulent and double-diffusive nutrient flux in the Kuroshio over the Izu Ridge and in the Kuroshio Extension. Journal of Oceanography, 77(1): 55-74 DOI:10.1007/s10872-020-00582-2 |
OSBORN T R, 1980. Estimates of the local rate of vertical diffusion from dissipation measurements. Journal of Physical Oceanography, 10(1): 83-89 DOI:10.1175/1520-0485(1980)010<0083:EOTLRO>2.0.CO;2 |
POLLARD R T, MILLARD R C, 1970. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Research, 17: 813-821 |
POLZIN K L, TOOLE J M, SCHMITT R W, 1995. Finescale parameterizations of turbulent dissipation. Journal of Physical Oceanography, 25(3): 306-328 DOI:10.1175/1520-0485(1995)025<0306:FPOTD>2.0.CO;2 |
RAINVILLE L, JAYNE S R, CRONIN M F, 2014. Variations of the north Pacific Subtropical Mode water from direct observations. J ournal of Climate, 27(8): 2842-2860 DOI:10.1175/JCLI-D-13-00227.1 |
RAY R D, MITCHUM G T, 1997. Surface manifestation of internal tides in the deep ocean: Observations from altimetry and island gauges. Progress in Oceanography, 40(1/4): 135-162 |
ROSSBY H T, SANFORD T B, 1976. A study of velocity profiles through the main thermocline. Journal of Physical Oceanography, 6(5): 766-774 DOI:10.1175/1520-0485(1976)006<0766:ASOVPT>2.0.CO;2 |
SUN H, YANG Q X, ZHAO W et al, 2016. Temporal variability of diapycnal mixing in the northern South China Sea. Journal of Geophysical Research: Oceans, 121(12): 8840-8848 DOI:10.1002/2016JC012044 |
WATANABE M, HIBIYA T, 2002. Global estimates of the wind-induced energy flux to inertial motions in the surface mixed layer. Geophysical Research Letters, 29(8): 64-1 |
WHALEN C B, TALLEY L D, MACKINNON J A, 2012. Spatial and temporal variability of global ocean mixing inferred from Argo profiles. Geophysical Research Letters, 39(18): L18612 |
WHITT D B, NICHOLSON S A, CARRANZA M M, 2019. Global impacts of subseasonal (< 60 day) wind variability on ocean surface stress, buoyancy flux, and mixed layer depth. Journal of Geophysical Research: Oceans, 124(12): 8798-8831 DOI:10.1029/2019JC015166 |
WUNSCH C, FERRARI R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annual Review of Fluid Mechanics, 36: 281-314 DOI:10.1146/annurev.fluid.36.050802.122121 |
ZHAI X M, GREATBATCH R J, EDEN C et al, 2009. On the loss of wind-induced near-inertial energy to turbulent mixing in the upper ocean. Journal of Physical Oceanography, 39(11): 3040-3045 DOI:10.1175/2009JPO4259.1 |
 2022, Vol. 53
2022, Vol. 53


