
中国海洋湖沼学会主办。
文章信息
- 宋利明, 任士雨, 洪依然, 张天蛟, 隋恒寿, 李彬, 张敏. 2022.
- SONG Li-Ming, REN Shi-Yu, HONG Yi-Ran, ZHANG Tian-Jiao, SUI Heng-Shou, LI Bin, ZHANG Min. 2022.
- 大西洋热带海域长鳍金枪鱼渔场预报模型的比较
- COMPARISON ON FISHING GROUND FORECAST MODELS OF THUNNUS ALALUNGA IN THE TROPICAL WATERS OF ATLANTIC OCEAN
- 海洋与湖沼, 53(2): 496-504
- Oceanologia et Limnologia Sinica, 53(2): 496-504.
- http://dx.doi.org/10.11693/hyhz20211000253
文章历史
-
收稿日期:2021-10-23
收修改稿日期:2021-12-20
2. 国家远洋渔业工程技术研究中心 上海 201306;
3. 中水集团远洋股份有限公司 北京 100032
2. National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China;
3. CNFC Overseas Fisheries Co, Ltd, Beijing 100032, China
长鳍金枪鱼(Thunnus alalunga)广泛分布于热带、亚热带及温带海域, 为高度洄游性鱼类, 是我国远洋延绳钓渔业重要的捕捞对象之一。近年来, 国内外学者研究了长鳍金枪鱼分布与海洋环境之间的关系(Chen et al, 2005; Domokos et al, 2007; Zainuddin et al, 2008; Briand et al, 2011; 林显鹏等, 2011; 杨嘉樑等, 2014; Goñi et al, 2015; Lehodey et al, 2015; Williams et al, 2015; 储宇航等, 2016; 郭刚刚等, 2016; 宋利明等, 2017a), 宋利明等(2017b)研究得出温度是影响库克群岛海域长鳍金枪鱼分布的主要环境因子; 闫敏等(2015)认为海表面温度和叶绿素a浓度与长鳍金枪鱼渔获率分布有关; 张嘉容等(2020)认为温度对长鳍金枪鱼分布的影响最大, 叶绿素a浓度的影响最小。但大部分模型仅分析海洋表层环境与长鳍金枪鱼分布的关系, 缺乏使用海洋立体环境因子的分析研究。
目前长鳍金枪鱼渔场预测大多使用较为传统的单一预报模型, 如一元非线性回归模型(范江涛, 2011)、栖息地指数模型(任中华等, 2014)和神经网络模型(毛江美等, 2016)等。随着渔业生产对渔场预报精度要求的提高, 深度学习开始在长鳍金枪鱼渔场预测中得到应用, 如袁红春等(2019a, 2020)。Stacking集成学习是一种多模型的集成方法, 能够得到比单模型更准确的结果(罗智青等, 2019; 侯娟等, 2020)。但海洋立体环境因子间的共线性会影响如逻辑斯蒂回归(logistic regression, LR)模型的预测精度(Raykov et al, 2010), 且环境因子过多容易导致K最近邻(k nearest neighbor, KNN)、梯度提升决策树(gradient boosting decision tree, GBDT)、随机森林(random forest, RF)和支持向量机(support vector machine, SVM)等模型的复杂性, 造成过拟合问题, 降低模型可解释性(Jou et al, 2014; Assegie et al, 2021)。目前大部分机器学习模型均未针对海洋立体环境因子间的共线性进行分析及因子筛选。
本研究根据2016~2019年中国船队在大西洋公海作业的延绳钓渔业数据, 结合不同深度的海洋环境数据进行共线性分析与因子筛选, 建立KNN、LR、决策与分类树(classfication and regression tree, CART)、GBDT、RF、SVM和Stacking集成(stacking ensemble learning, STK)模型; 各模型取75%站位的数据作为训练数据, 25%站位的数据为测试数据, 采用预报准确率(accuracy, ACC)与接受者操作特征(receiver operating characteristic, ROC)曲线下面积(area under curve, AUC)进行性能评价, 以提高大西洋热带海域长鳍金枪鱼渔场预报的准确性。
1 材料与方法 1.1 数据来源本研究选取的渔业数据来源于中水集团远洋股份有限公司, 时间为2016~2019年, 区域为19°16′S~ 16°21′N; 46°27′W~2°09′E范围内的大西洋中部热带海域, 数据信息包括延绳钓捕捞渔船(共13艘)船名、作业时间(年-月-日)、作业地点(经纬度)、不同鱼种的产量、渔获尾数及下钩数等。将每天长鳍金枪鱼的渔获尾数划分到1°×1°的网格内, 并算出CPUE (尾/千钩)。
海洋环境因子主要包括表层因子和0~500 m深度因子共29个。其中, 表层因子包括: 叶绿素a浓度(chl_a)、混合层深度(mixed layer depth, MLD)、海表面风速(wind speed, WS)、涡动能(eddy kinetic energy, EKE); 0~500 m深度因子包括: 0、50、100、150、200、250、300、400、500 m水深处的温度(采用T0、T50、T100、T150、T200、T250、T300、T400、T500表示); 0、50、100、150、200、250、300、350、400、450、500 m水深处的溶解氧(采用D0、D50、D100、D150、D200、D250、D300、D350、D400、D450、D500表示); 100、200、300、400、500 m水深处的盐度(采用S100、S200、S300、S400、S500表示)。以上因子数据除WS来源于美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)的数据库(https://oceanwatch.pifsc.noaa.gov/)外, 其他数据均来源于哥白尼海洋环境监测服务中心(copernicus marine environment monitoring service, CMEMS)网站(http://marine.copernicus.eu)。环境因子数据的初始时间分辨率为d, 初始空间分辨率为0.25°×0.25°。本文将环境因子和渔业数据进行了匹配, 最终的空间分辨率统一为1°×1°, 以d为单位。以上数据预处理过程通过MATLAB软件完成。
1.2 数据处理 1.2.1 长鳍金枪鱼CPUE的计算方法CPUE作为评价渔场的指标(沈智宾等, 2015)。将每天的长鳍金枪鱼的渔获尾数划分到1°×1°的网格内, 根据每天的船位数据等得到每天每网格内的总钓钩数, 算出每天每个网格内的长鳍金枪鱼CPUE (尾/千钩), 计算各网格内CPUE的公式为
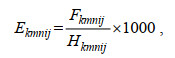 (1)
(1)式(1)中: Ekmnij, Fkmnij和Hkmnij分别表示在第k年、第m月、第n天、第i经度、第j纬度的网格内的CPUE、尾数和下钩数量。
1.2.2 海洋环境因子的共线性分析由于建立模型所用的叶绿素a浓度、混合层深度、海表面风速、涡动能以及0~500 m水层的温度、溶解氧、盐度等海洋环境因子的量级单位不同, 数值范围差别较大, 为防止对模型产生数值影响且为了提高模型运行的准确度, 对所有环境变量进行归一化处理(张天蛟, 2016), 公式为
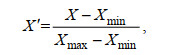 (2)
(2)式(2)中: X'、X、Xmax、Xmin分别为归一化后的值、实际值、最大值、最小值。
针对29个海洋环境因子之间存在的多重共线性, 本文采用方差膨胀因子(variance expansion factor, VIF)(Akinwande et al, 2015)进行分析。
对于方程:
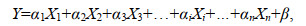 (3)
(3)式(3)中, y为因变量, x为自变量, α1、α2、α3、…、αn为回归系数, β为常数项。则第i个自变量的VIF计算公式为:
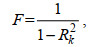 (4)
(4)式(4)中, F表示方差膨胀因子VIF的取值; Rk为线性方程中的决定系数。当VIF值较大时, 表示环境变量之间存在多重共线性, 即VIF值越大, 表示环境变量之间多重共线性越严重, 一般认为F < 10, 即表示各环境变量之间没有多重共线性。选取F < 10的海洋环境因子用于建立大西洋热带海域长鳍金枪鱼的渔场预报模型。
1.2.3 海洋环境因子相对重要性分析海洋环境因子相对重要性的计算方法为: 利用SPSS软件计算长鳍金枪鱼CPUE与筛选后各环境因子的Pearson相关系数; 根据Pearson相关系数绝对值判断其相对重要性。
1.3 模型建立渔场分类时, 若CPUE等于0, 为“非渔场”; CPUE大于0, 则为“渔场”, 其中零值比列为40.11%。从数据集中随机选取75%站点的数据作为训练数据, 25%站点的数据为测试数据; 并使用训练数据分别建立KNN、LR、SVM、CART、RF、GBDT和STK7种模型。系列模型的基本原理和参数选择方法如表 1。
| 模型名称 | 参考文献 | 基本原理 | 参数选择 |
| K最近邻模型(k nearest neighbor, KNN) | (Hwang et al, 1998; 王超学等, 2012; 张莹, 2015; Zhang et al, 2018; 吴昊等, 2019) | 为分类模型, 主要是针对测试数据, 找到与该测试数据距离最近的k个训练数据, 即对该训练数据进行分类 | 取邻近点的个数K=7 |
| 逻辑斯蒂回归(logistic regression, LR) | (Dahlem et al, 1989; Zhang et al, 2018) |
在线性回归模型的基础上使用sigmoid函数, 将线性模型的结果压缩到[0, 1]之间, 使其拥有概率意义 | 惩罚系数C=1; 最大的迭代次数100; 当目标函数(样本集最大似然函数)导数的第j个分量小于0.000 1时, 迭代停止 |
| 支持向量机(support vector machine, SVM) | (Suykens et al, 2000; 邵元海等, 2020) | SVM的中心思想是通过二分类方法找到使数据集到分隔超平面的几何间隔最远的点集合面, SVM通过引入核函数, 实现从非线性学习到线性学习的过渡 | 惩罚系数为1 |
| 决策树算法(classfication and regression tree, CART) | (Kristensen et al, 1998; 谢金梅等, 2008; 田欣, 2017) | 主要通过计算Gini指数不纯度, 再根据最小的Gini指标作为分裂属性, 最终使测试样本数据集形成二分类递归的分割树杈 | 复杂度为0.01, 最大深度为30 |
| 随机森林算法(random forest, RF) | (Ou et al, 2002; 陈雪忠等, 2013; 吕红燕等, 2019) | 对于原始测试样本随机抽取训练子集, 生成分类树, 再随机抽取q个特征作为分裂属性, 至每棵决策树完整形成随机森林模型 | 最小样本数量为1, 节点最小样本数量为1 |
| 梯度提升决策树(gradient boosting decision Tree, GBDT) | (Friedman, 2003; 田欣, 2017) | 是一种对决策树进行Boosting集成的学习算法, 由集中选取相对简易的决策树来提高模型的预测性能 | 树的个数为100, 树的深度为6, 学习率为0.1 |
| Stacking集成学习(stacking ensemble learning, STK) | (Džeroski et al, 2004; 张春霞等, 2011; 袁培森等, 2019) | 通过集合训练多个分类器来得到较单个分类器 更强、更优化的分层模型集成框架 |
初级学习器classifiers=[RF, GBDT, KNN]; 次级学习器meta_classifier=LR; 交叉验证折数R=5 |
Stacking算法框架如图 1所示, 第一层由3个基学习器组成, 并输入原始训练集, 即第一步将与各个海洋环境因子匹配好的大西洋热带海域长鳍金枪鱼CPUE原始数据集S, 基于非共线性海洋环境因子的筛选, 划分为75%的训练数据D和25%测试数据T; 第二步从7个模型中选择预测效果较好的3个模型作为初级学习器, 选取结构简单的LR作为次级学习器; 第三步将75%的训练样本随机划分为k个数量相同的训练集子集D1, D2, …, Dk, 取Ti作为测试子集, Dk–1{D1, D2, …, Dk}(Di ∉Dk–1)作为KNN、RF和GBDT的训练子集, 接着将各个模型的预测结果统一为LR模型的训练集D′, 各个单模型对测试集T的预测结果合并为LR模型的测试集T′, 最终输出预测结果。
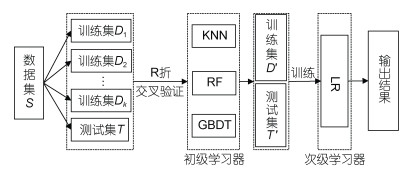 |
| 图 1 Stacking集成学习方法 Fig. 1 Method of stacking ensemble learning 注: KNN: k nearest neighbor, K最近邻模型; RF: random forest, 随机森林算法; GBDT: gradient boosting decision tree, 梯度提升决策树; LR: logistic regression, 逻辑斯蒂回归 |
将25%测试数据代入各模型得出预测结果, 对模型性能进行评价。本文采用AUC和ACC作为模型性能评价指标。其中AUC取值范围为0~1, 值越大说明该模型的预测性能越好, 反之预测性能越差(张天蛟, 2016); 同理, 所得ACC值越大, 说明该模型整体预测效果越好, 反之预测效果越差, 所以本文按照两者结果, 对比并选取预测准确度较高且性能稳定的模型。
将25%的测试数据代入预测能力最佳的模型, 计算得出“渔场”和“非渔场”并使用ArcGIS软件画出实际“渔场”和“非渔场”与模型预测得到的“渔场”和“非渔场”叠图, 定性评价最佳模型的预测能力。
1.5 中心渔场的确定本研究把25%的测试站点的环境数据代入预测能力最佳的模型, 计算得出“渔场”位置, 利用ArcGIS软件的核密度分析工具计算并画出“渔场”位置密度分布图, 把密度大于最大密度的60% (8个/km2)以上的范围定义为中心渔场。
2 结果 2.1 长鳍金枪鱼渔场分布通过ArcGIS软件画出长鳍金枪鱼CPUE分布图(图 2), 得出长鳍金枪鱼渔场主要分布在15°N~15°S, 15°~45°W的大西洋中部热带海域, 其高CPUE渔区集中分布在4°~10°N, 30°~45°W海域和5°~10°S, 18°~30°W的海域。
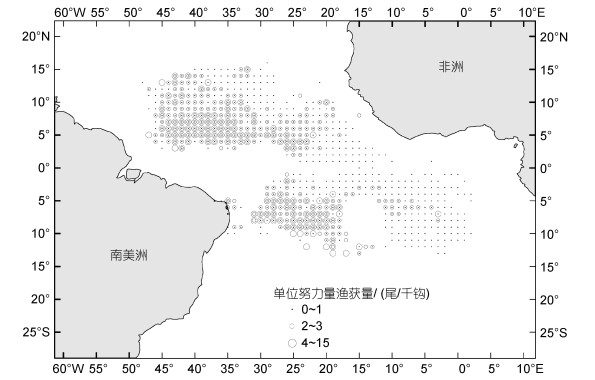 |
| 图 2 2016~2019年大西洋热带海域13艘渔船长鳍金枪鱼CPUE分布 Fig. 2 CPUE distribution of Thunnus alalunga from 13 fishing vessels in the tropical waters of Atlantic Ocean in 2016~2019 |
按照各环境因子的|F| < 10, 筛选得出20个用于渔场预测的环境因子, 分别是chl a、MLD、WS、EKE、T0、T50、T100、T150、T250、T400、D0、D50、D100、D150、D200、D500、S100、S200、S300和S500 (表 2)。相关系数分析结果表明, 100 m水层温度(T100)与CPUE的相关系数最高, 达到0.399; 100、150、500 m水层的溶解氧、100 m水层的盐度与CPUE的相关系数较高, 分别达到0.372、0.334、0.322和0.322; 相关系数较小的是MLD和叶绿素a浓度, 分别为0.21和−0.148; 海表面温度(T0)和海表面风速(WS)的相关系数分别为0.140和0.069; 而涡动能(EKE)的相关系数最低, 为−0.036, 影响程度最小(表 2)。
| 变量 | 容差 | VIF | 相关系数R |
| chl_a | 0.433 | 2.310 | −0.148 |
| EKE | 0.810 | 1.235 | −0.036 |
| MLD | 0.494 | 2.022 | 0.210 |
| WS | 0.726 | 1.377 | 0.069 |
| S100 | 0.265 | 3.769 | 0.322 |
| S200 | 0.174 | 5.758 | 0.067 |
| S300 | 0.177 | 5.656 | −0.105 |
| S500 | 0.223 | 4.483 | −0.113 |
| T0 | 0.160 | 6.251 | 0.140 |
| T50 | 0.240 | 4.173 | 0.228 |
| T100 | 0.152 | 6.561 | 0.399 |
| T150 | 0.234 | 4.266 | 0.313 |
| T250 | 0.131 | 7.612 | −0.037 |
| T400 | 0.223 | 4.481 | −0.079 |
| D0 | 0.112 | 8.964 | 0.046 |
| D50 | 0.179 | 5.593 | 0.062 |
| D100 | 0.229 | 4.365 | 0.372 |
| D150 | 0.178 | 5.617 | 0.334 |
| D200 | 0.184 | 5.425 | 0.230 |
| D500 | 0.388 | 2.574 | 0.322 |
各个模型总体的ACC和AUC如表 3所示, 单个模型预测结果中RF的准确度最高, 为75.57%, KNN和GBDT的准确度并列为第二(73.92%), 因此选取RF、KNN和GBDT用于STK模型; CART最低, 为66.85%。STK模型的ACC最高, 达到75.92%, AUC也达到了0.742。综合上述结果, 表明STK模型预测性能良好。
| 模型 | ACC/% | AUC |
| LR | 71.93 | 0.692 |
| RF | 75.57 | 0.737 |
| GBDT | 73.92 | 0.715 |
| KNN | 73.92 | 0.709 |
| CART | 66.85 | 0.656 |
| SVM | 71.62 | 0.684 |
| STK | 75.92 | 0.742 |
| 注: ACC: accuracy, 预报准确率; AUC: area under curve, 曲线下面积 | ||
对于STK模型, 将测试数据中得到的实际渔场与预测渔场进行叠加, 得出渔场主要分布在2°~14°N, 32°~45°W和2°~10°S, 18°~28°W的海域, 极少分布在5°~10°W附近, 且预测的0°~18°W海域的渔场的误判率很高(图 3); 将测试数据中的实际非渔场与预测非渔场进行叠加, 实际非渔场主要分布在5°~14°N, 30°~45°W和2°S~7°N, 12°~30°W的海域, 极少分布在2°~12°S, 2°~10°W海域附近, 且预测的2°~8°S, 20°~30°W海域的实际非渔场的误判率较高(图 4)。各模型对渔场和非渔场的判别准确率比较结果见表 4。说明Stacking集成模型的预测性能良好。
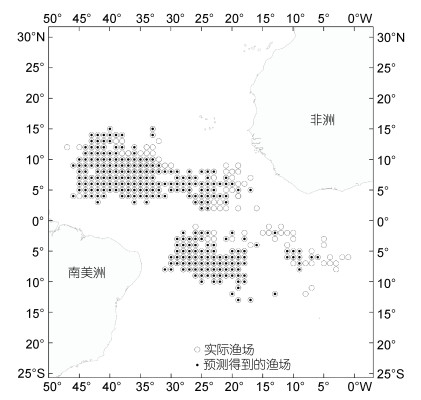 |
| 图 3 实际渔场与预报得到的渔场对比图 Fig. 3 Comparison of actual fishing ground and predicted fishing ground |
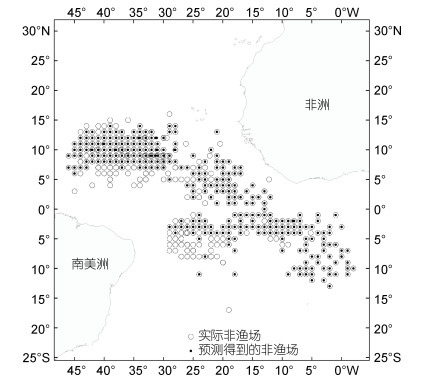 |
| 图 4 实际非渔场与预报得到的非渔场对比图 Fig. 4 Comparison of actual non-fishing ground and predicted non-fishing ground |
| 模型 | 渔场 | 非渔场 |
| KNN | 80.52 | 61.21 |
| LR | 84.08 | 54.31 |
| SVM | 84.78 | 51.05 |
| CART | 71.60 | 57.76 |
| RF | 82.96 | 63.79 |
| GBDT | 83.81 | 58.14 |
| STK | 85.09 | 62.75 |
2016~2019年25%的测试数据中实际渔场密度分布如图 5a所示, 其中心渔场集中分布在4°~10°N, 33°~43°W海域, 以及5°~8°S, 27°~29°W和7°~9°S, 22°~24°W的海域。STK模型预测渔场密度分布如图 5b所示, 从整体来看预测的中心渔场比实际中心渔场略大, 但基本吻合。
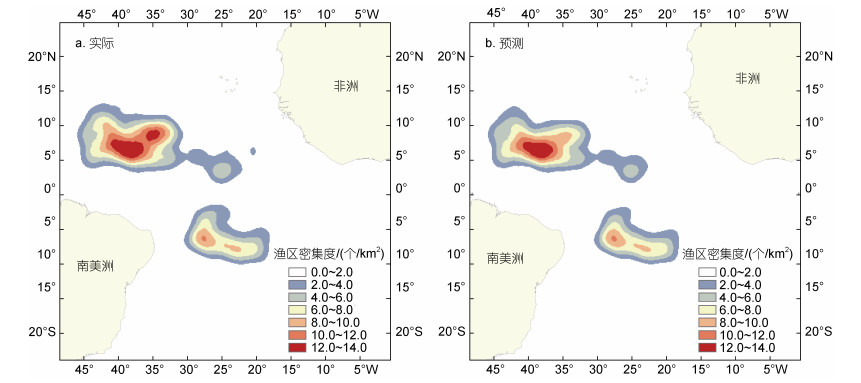 |
| 图 5 25%的测试数据中渔区密度分布图 Fig. 5 Distribution of fishing ground density in the 25% test data |
STK模型的渔场预报性能比6种单一模型(KNN、LR、CART、SVM、RF、GBDT)对大西洋热带海域长鳍金枪鱼渔场预报的性能要好, 为最佳模型。CART的渔场预报性能最差。这是因为STK是一种堆叠集成方法, 能够将KNN、RF和GBDT预测结果再次进行次级训练, 克服单一模型的局限性, 能综合三种模型的优势, 而CART容易过拟合, 导致泛化能力不强, 且某些自变量的占比过高时, 容易导致预测能力降低。RF对长鳍金枪鱼渔场的预报性能与STK模型相近, 这可能是因为RF在构建模型时通过自助采样选取训练样本, 增强其泛化和抗噪能力, 在一定程度上降低了不良数据对模型预测能力的影响(方匡南等, 2011)。GBDT与RF都是由多个分类树通过不同算法构建的模型, 但GBDT的预测性能明显低于RF, 这是因为GBDT训练样本选取的方法与RF不同, 其在模型构建过程中使用同一个训练样本, 导致模型泛化能力降低。LR、KNN、SVM的预测性能都比较低, 这几个模型不能有效克服构建模型所使用的样本数据质量不高的问题(如各类别的样本数据不平衡、数据缺失等)。
3.2 环境变量共线性分析由于海洋环境非常复杂, 环境因子相互影响, 可能导致环境变量之间存在多重共线性, 会对预测结果产生偏差。Dormann et al (2013)认为当环境变量之间的相关系数大于0.7时, 说明存在共线性的可能性较大。多重共线性是影响SVM和LR预测精度和运行速率的主要原因之一(惠守博等, 2006; 张玲, 2010), 虽然CART、RF和GBDT在模型训练的过程中会自动消除多重共线性对预测精度的影响, 但是共线性使得环境变量的大部分信息相互叠加, 导致数据大量冗余, 模型的运行效率降低以及误判解释变量的贡献率。故消除环境变量之间的多重共线性, 在一定程度上提高了模型的预测精度、稳定性和可靠性。
VIF方法虽然可以消除共线性, 但也有可能导致原本生态学意义重要的因子被删除, 本研究从29个潜在的影响因子中删除了9个具有共线性的因子(T200、T300、T500、D250、D300、D350、D400、D450、S400)。这些被删除的因子均为200 m以深的因子, 由于长鳍金枪鱼偏好觅食的水层为160~240 m水层, 且在该水层主要受饵料分布及水温的影响(杨嘉樑等, 2014), 因此本研究未删除对长鳍金枪鱼具有生态学重要意义的因子。
3.3 环境因子的相对重要性及中心渔场研究认为温度直接或间接影响鱼类分布、集群和洄游(陈雪忠等, 2013), 其垂直水温是影响长鳍金枪鱼渔场分布主要原因之一(郭刚刚等, 2016)。研究表明, 100 m水层的温度、溶解氧和盐度与长鳍金枪鱼CPUE关系较为密切, 可能的原因是该水层是水温急剧下降的温跃层, 温度和盐度等环境因子适宜长鳍金枪鱼生存, 并且具有丰富的饵料生物资源, 较高的溶解氧含量(张嘉容等, 2020)。张嘉容等(2020)研究分析得到南太平洋中对长鳍金枪鱼CPUE具有显著影响的环境因子是120 m水层的温度和盐度, 这与本研究结果基本一致。叶绿素a浓度和WS对长鳍金枪鱼渔场分布的影响较小, 这是由于海面风速能够改变叶绿素a的空间位置和含量(Pickett et al, 2006; Jufaili et al, 2019), 而较高的叶绿素a浓度会吸引更多浮游生物在附近繁殖(杨胜龙等, 2012), 但长鳍金枪鱼并不会直接捕食浮游生物。EKE对长鳍金枪鱼渔场分布的影响最小, 这可能是因为EKE是通过影响环流、海洋温度以及叶绿素a的垂直和水平分布(Tussadiah et al, 2018)间接影响长鳍金枪鱼渔场的分布。2016~2019年25%的测试数据中预测得到的中心渔场比实际中心渔场范围略大, 可能是由于渔业生产作业不能均匀、完全覆盖整个区域, 而预测是根据海洋环境数据进行平滑计算得出的, 预测得到的中心渔场范围可靠。另外, 准确预测中心渔场能够使渔船缩短搜索渔场的时间、节省燃油, 增加长鳍金枪鱼的渔获量, 提高经济效益。
4 展望本研究根据29种海洋环境因子, 建立6种模型并筛选最佳的三个预测模型构成STK模型, 提高了大西洋热带海域长鳍金枪鱼渔场预报的精度, 但长鳍金枪鱼渔场预报的精度还与数据的空间分辨率、渔捞日志记录的数据的准确度、饵料资源分布、洋流、流速等其他环境变量有关, 还会受到气候的年代际, 如北大西洋涛动等大尺度海洋事件的影响, 本研究中CPUE为0的比例较高, 还需要进一步收集数据开展研究。另外, 本研究结果适用于大西洋热带海域长鳍金枪鱼渔场的预报, 对于大西洋温带水域的长鳍金枪鱼渔场的预报还需要进一步收集数据开展相关研究。
致谢 本研究得到了中水集团远洋股份有限公司宗文峰、叶少华和邓荣成先生的大力支持, 谨致谢意。
王超学, 潘正茂, 马春森, 等, 2012. 改进型加权KNN算法的不平衡数据集分类. 计算机工程, 38(20): 160-163, 168 |
毛江美, 陈新军, 余景, 2016. 基于神经网络的南太平洋长鳍金枪鱼渔场预报. 海洋学报, 38(10): 34-43 DOI:10.3969/j.issn.0253-4193.2016.10.004 |
方匡南, 吴见彬, 朱建平, 等, 2011. 随机森林方法研究综述. 统计与信息论坛, 26(3): 32-38 DOI:10.3969/j.issn.1007-3116.2011.03.006 |
田欣, 2017. 决策树算法的研究综述. 现代营销, (1): 36 DOI:10.3969/j.issn.1009-2994.2017.01.024 |
吕红燕, 冯倩, 2019. 随机森林算法研究综述. 河北省科学院学报, 36(3): 37-41 |
任中华, 陈新军, 方学燕, 2014. 基于栖息地指数的东太平洋长鳍金枪鱼渔场分析. 海洋渔业, 36(5): 385-395 DOI:10.3969/j.issn.1004-2490.2014.05.001 |
闫敏, 张衡, 樊伟, 等, 2015. 南太平洋长鳍金枪鱼渔场CPUE时空分布及其与关键海洋环境因子的关系. 生态学杂志, 34(11): 3191-3197 |
杨胜龙, 张禹, 樊伟, 等, 2012. 热带印度洋大眼金枪鱼渔场时空分布与温跃层关系. 中国水产科学, 19(4): 679-689 |
杨嘉樑, 黄洪亮, 宋利明, 等, 2014. 基于分位数回归的库克群岛海域长鳍金枪鱼栖息环境综合指数. 中国水产科学, 21(4): 832-851 |
吴昊, 秦立春, 罗柳容, 2019. 基于提升度的KNN分类子的分类原则改良模型. 广西师范大学学报(自然科学版), 37(2): 75-81 |
沈智宾, 陈新军, 汪金涛, 2015. 基于海表温度和海面高度的东太平洋大眼金枪鱼渔场预测. 海洋科学, 39(10): 45-51 DOI:10.11759/hykx20140621002 |
宋利明, 周建坤, 沈智宾, 等, 2017a. 基于支持向量机的库克群岛海域长鳍金枪鱼栖息环境综合指数. 海洋通报, 36(2): 195-208 |
宋利明, 谢凯, 赵海龙, 等, 2017b. 库克群岛海域海洋环境因子对长鳍金枪鱼渔获率的影响. 海洋通报, 36(1): 96-106 |
张玲, 2010. 多重共线性的检验及对预测目标影响程度的定量分析. 通化师范学院学报, 31(4): 19-20, 38 DOI:10.3969/j.issn.1008-7974.2010.04.007 |
张莹, 2015. 基于自然最近邻居的分类算法研究[D]. 重庆: 重庆大学.
|
张天蛟, 2016. 产漂流性卵小型鱼类的生态位建模及分析[D]. 北京: 中国农业大学.
|
张春霞, 张讲社, 2011. 选择性集成学习算法综述. 计算机学报, 34(8): 1399-1410 |
张嘉容, 杨晓明, 戴小杰, 等, 2020. 南太平洋长鳍金枪鱼延绳钓渔获率与环境因子的关系研究. 南方水产科学, 16(1): 69-77 |
陈雪忠, 樊伟, 崔雪森, 等, 2013. 基于随机森林的印度洋长鳍金枪鱼渔场预报. 海洋学报, 35(1): 158-164 DOI:10.3969/j.issn.0253-4193.2013.01.018 |
邵元海, 刘黎明, 黄凌伟, 等, 2020. 支持向量机的关键问题和展望. 中国科学: 数学, 50(9): 1233-1248 |
范江涛, 2011. 南太平洋长鳍金枪鱼延绳钓渔业渔情预报研究[D]. 上海: 上海海洋大学: 21-22.
|
林显鹏, 郭爱, 张洪亮, 等, 2011. 所罗门群岛海域长鳍金枪鱼的垂直分布与环境因子的关系. 浙江海洋学院学报(自然科学版), 30(4): 303-306 DOI:10.3969/j.issn.1008-830X.2011.04.005 |
罗智青, 莫汉培, 王汝辉, 等, 2019. 基于Stacking模型融合的失压故障识别算法. 能源与环保, 41(2): 41-45 |
侯娟, 周为峰, 樊伟, 等, 2020. 基于集成学习的南太平洋长鳍金枪鱼渔场预报模型研究. 南方水产科学, 16(5): 42-50 |
袁红春, 陈冠奇, 张天蛟, 等, 2020. 基于全卷积网络的南太平洋长鳍金枪鱼渔场预报模型. 江苏农业学报, 36(2): 423-429 DOI:10.3969/j.issn.1000-4440.2020.02.024 |
袁红春, 陈骢昊, 2019a. 基于融合深度学习模型的长鳍金枪鱼渔情预测研究. 渔业现代化, 46(5): 74-81 |
袁红春, 胡光亮, 陈冠奇, 等, 2019b. 基于粒子群可拓的南太平洋长鳍金枪鱼产量预测方法研究. 渔业现代化, 46(6): 96-103 |
袁培森, 杨承林, 宋玉红, 等, 2019. 基于Stacking集成学习的水稻表型组学实体分类研究. 农业机械学报, 50(11): 144-152 |
郭刚刚, 张胜茂, 樊伟, 等, 2016. 南太平洋长鳍金枪鱼垂直活动水层空间分析. 南方水产科学, 12(5): 123-130 |
惠守博, 王文杰, 2006. 支持向量机分类算法中多元变量共线性问题的改进. 计算机工程与设计, 27(8): 1385-1388 |
储宇航, 戴小杰, 田思泉, 等, 2016. 南太平洋延绳钓长鳍金枪鱼生物学组成及其与栖息环境关系. 海洋渔业, 38(2): 130-139 |
谢金梅, 王艳妮, 2008. 决策树算法综述. 软件导刊, 7(11): 83-85 |
AKINWANDE M O, DIKKO H G, SAMSON A, 2015. Variance inflation factor: as a condition for the inclusion of suppressor variable(s) in regression analysis. Open Journal of Statistics, 5(7): 754-767 |
ASSEGIE T A, SUSHMA S J, BHAVYA B G, et al, 2021. Correlation analysis for determining effective data in machine learning: detection of heart failure. SN Computer Science, 2(3): 213 |
BRIAND K, MOLONY B, LEHODEY P, 2011. A study on the variability of albacore (Thunnus alalunga) longline catch rates in the southwest Pacific Ocean. Fisheries Oceanography, 20(6): 517-529 |
CHEN I C, LEE P F, TZEND W N, 2005. Distribution of albacore (Thunnus alalunga) in the Indian Ocean and its relation to environmental factors. Fisheries Oceanography, 14(1): 71-80 |
DAHLEM A M, HASSAN A S, SWANSON S P, et al, 1989. A model system for studying the bioavailability of intestinally administered microcystin‐LR, a hepatotoxic peptide from the cyanobacterium Microcystis aeruginosa. Pharmacology & Toxicology, 64(2): 177-181 |
DOMOKOS R, SEKI M P, POLOVINA J J, et al, 2007. Oceanographic investigation of the American Samoa albacore (Thunnus alalunga) habitat and longline fishing grounds. Fisheries Oceanography, 16(6): 555-572 |
DORMANN C F, ELITH J, BACHER S, et al, 2013. Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography, 36(1): 27-46 |
DŽEROSKI S, ŽENKO B, 2004. Is combining classifiers with stacking better than selecting the best one?. Machine Learning, 54(3): 255-273 |
FRIEDMAN J H, 2003. Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4): 367-378 |
GOÑI N, DIDOUAN C, ARRIZABALAGA H, et al, 2015. Effect of oceanographic parameters on daily albacore catches in the Northeast Atlantic. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 113: 73-80 |
HWANG W J, WEN K W, 1998. Fast KNN classification algorithm based on partial distance search. Electronics Letters, 34(21): 2062-2063 |
JOU Y J, HUANG C C L, CHO H J, 2014. A VIF-based optimization model to alleviate collinearity problems in multiple linear regression. Computational Statistics, 29(6): 1515-1541 |
JUFAILI S A, PIONTKOVSKI S A, 2019. Seasonal and interannual variations of Yellowfin tuna catches along the Omani Shelf. International Journal of Oceans and Oceanography, 13(2): 427-454 |
KRISTENSEN P, JUDGE M E, THIM L, et al, 1998. Hypothalamic CART is a new anorectic peptide regulated by leptin. Nature, 393(6680): 72-76 |
LEHODEY P, SENINA I, NICOL S, et al, 2015. Modelling the impact of climate change on South Pacific albacore tuna. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 113: 246-259 |
OU J J, JIN X D, MA I, et al, 2002. CMOS RF modeling for GHz communication IC's [C] // Proceedings of 1998 Symposium on VLSI Technology Digest of Technical Papers. Honolulu, HI, USA: IEEE: 94-95.
|
PICKETT M H, SCHWING F B, 2006. Evaluating upwelling estimates off the west coasts of North and South America. Fisheries Oceanography, 15(3): 256-269 |
RAYKOV T, PENEV S, 2010. Testing multivariate mean collinearity via latent variable modelling. British Journal of Mathematical and Statistical Psychology, 63(3): 481-490 |
SUYKENS J A K, LUKAS L, VANDEWALLE J, 2000. Sparse approximation using least squares support vector machines [C] // Proceedings of 2000 IEEE International Symposium on Circuits and Systems. Geneva, Switzerland: IEEE: 757-760.
|
TUSSADIAH A, PRANOWO W S, SYAMSUDDIN M L, et al, 2018. Characteristic of eddies kinetic energy associated with yellowfin tuna in Southern Java Indian Ocean. IOP Conference Series: Earth and Environmental Science, 176(1): 012004 |
WILLIAMS A J, ALLAIN V, NICOL S J, et al, 2015. Vertical behavior and diet of albacore tuna (Thunnus alalunga) vary with latitude in the South Pacific Ocean. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 113: 154-169 |
ZAINUDDIN M, SAITOH K, SAITOH S I, 2008. Albacore (Thunnus alalunga) fishing ground in relation to oceanographic conditions in the western North Pacific Ocean using remotely sensed satellite data. Fisheries Oceanography, 17(2): 61-73 |
ZHANG S C, LI X L, ZONG M, et al, 2018. Efficient KNN classification with different numbers of nearest neighbors. IEEE Transactions on Neural Networks and Learning Systems, 29(5): 1774-1785 |
 2022, Vol. 53
2022, Vol. 53

