中国海洋湖沼学会主办。
文章信息
- 李博, 杨昊, 欧素英, 蔡华阳, 刘锋, 杨清书. 2022.
- LI Bo, YANG Hao, OU Su-Ying, CAI Hua-Yang, LIU Feng, YANG Qing-Shu. 2022.
- 珠江磨刀门河口潮波振幅梯度与上下游动力边界的关系异变研究
- THE VARIATION OF THE RELATIONSHIP BETWEEN TIDAL AMPLITUDE GRADIENT AND UPSTREAM AND DOWNSTREAM DYNAMIC BOUNDARY CONDITIONS IN MODAOMEN ESTUARY, ZHUJIANG (PEARL) RIVER
- 海洋与湖沼, 53(3): 513-527
- Oceanologia et Limnologia Sinica, 53(3): 513-527.
- http://dx.doi.org/10.11693/hyhz20211200334
文章历史
-
收稿日期:2021-12-22
收修改稿日期:2022-02-18
2. 河口水利技术国家地方联合工程实验室 广东广州 510275;
3. 广东省海岸与岛礁工程技术研究中心 广东广州 510275;
4. 南方海洋科学与工程广东省实验室(珠海) 广东珠海 519000
2. State and Local Joint Engineering Laboratory of Estuarine Hydraulic Technology, Guangzhou 510275, China;
3. Guangdong Provincial Engineering Research Center of Coasts, Islands and Reefs, Guangzhou 510275, China;
4. Southern Laboratory of Ocean Science and Engineering (Zhuhai), Zhuhai 519000, China
河口是陆海径潮动力耦合的独特区域, 既有上游径流汇入, 又有外海潮波上溯, 还受人类活动叠加效应的影响, 导致其动力结构复杂多变。河口动力的典型特征包括径潮相互作用、斜压效应、波流耦合等, 其中, 径潮相互作用对洪水下泄、盐淡水混合、最大浑浊带形成、营养盐和污染物输移等物理、化学和生物过程均有直接影响。潮波振幅梯度, 即潮波振幅沿程的平均变化率, 综合反映了径流、潮汐和底床摩擦等多因子影响在河口空间上的差异, 是探讨河口复杂径潮动力结构的有效切入点。因此, 揭示潮波振幅梯度与上下游动力边界(即上游径流和外海潮汐)的耦合过程及机制是河口动力学研究的基础科学前沿问题, 可为河口海岸区域自然灾害(如咸潮上溯、洪涝、赤潮等)的防治和水资源的高效开发利用等提供重要科学依据(Schuttelaars et al, 2013; Cao et al, 2020; 杨昊等, 2020)。
国内外针对河口径潮相互作用的研究由来已久。研究表明, 当潮波受到径流和地形的调制作用时呈现出明显的非线性变化(Hoitink et al, 2017; Ji et al, 2019), 河口潮波衰减主要通过流量和底床的摩擦效应实现(Godin, 1985; Savenije, 1992; Horrevoets et al, 2004)。当流量增大时, 全日分潮和半日分潮的振幅以不同幅度衰减, 而河道底床下切, 水深增大可导致底床摩擦效应减弱, 引起沿程潮波振幅不同程度的增加(Cai et al, 2012)。对河口地形进行概化并考虑下泄径流影响, 采用一维潮波传播解析模型可通过潮波振幅梯度和余水位梯度等参数揭示潮波传播的时空变化特征及其动力学机制(Cai et al, 2016)。当河口动力以径流作用为主时, 传统调和分析(Pawlowicz et al, 2002)的水位预报误差明显增大。针对流量影响下河口潮波传播的非定常和非线性问题, 对水位序列采用连续小波变换(Guo et al, 2015; Moftakhari et al, 2016)、经验模态分解(Pan et al, 2018a)、经验正交函数(Pan et al, 2019)、非平稳潮汐调和分析(Matte et al, 2013, 2014; Pan et al, 2018b)等处理方法探讨流量对潮波传播的影响过程及机制均取得较好效果。
近年来, 流量对潮波传播的衰减及其阈值效应研究得到广泛关注。研究表明, 在长江河口感潮河段, 流量与潮波振幅梯度之间存在阈值效应, 即流量小于临界阈值时, 随着流量增大潮波衰减效应增强, 但当潮波振幅梯度达到极小值后, 随着流量增大衰减效应反而减弱(Cai et al, 2019; 张先毅等, 2019)。在珠江磨刀门河口也观察到类似现象, 即在甘竹-马口河段潮波振幅梯度随流量变化有先减小后上升的特点, 在人类活动干预较弱的自然演变阶段, 潮波振幅梯度在流量为5 000~10 000 m3/s时达到极小值, 而在人类活动强烈影响后的恢复调整阶段, 该流量阈值上升至15 000~20 000 m3/s, 且其对应的潮波振幅梯度极小值增大(Yang et al, 2020; 张先毅等, 2020), 反映因采砂导致的河槽容积增大对潮波振幅梯度阈值的增大效应。综上所述, 对于河口径潮相互作用及潮波振幅梯度与流量动力边界关系的研究已有较多成果, 但是对于定量辨识流量驱动下潮汐调和分析结果的阶段性演变以及潮波振幅梯度与下游动力边界关系的研究等相关科学问题还尚待深入。
位于我国粤港澳大湾区国家战略核心经济圈的珠江三角洲是全球受到人类活动影响程度最大的区域之一。高强度的人类活动(如水库建设、口门围垦、无序采砂、航道疏浚等)导致来水来沙和地形地貌发生明显变化, 进而显著改变珠江河网的径潮动力格局。水库建设使河流挟沙量锐减, 三角洲河道下切加剧; 地形变化导致西江、北江的水沙分配格局发生变化, 河网中上部地区余水位梯度变缓(Liu et al, 2019); 口门围垦、口门整治叠加海平面上升的影响则导致磨刀门河口的形态向窄深化趋势演变(Tan et al, 2019)。以上变化导致珠江主要出海口, 即磨刀门河口的潮流界和潮区界显著向上游移动, 咸潮上溯灾害风险增大, 对粤港澳大湾区城市的居民生活、工农业生产用水的水质安全形成严峻挑战。因此, 本文针对强人类活动驱动下的径潮动力异变问题, 采用数据驱动模型探究流量驱动下珠江磨刀门河口潮波传播特征的异变过程, 并分析潮波调和常数的阶段性演变, 揭示潮波振幅梯度对上下游动力边界的响应过程及机制, 研究成果可为受到高强度人类活动影响的河口三角洲的治理和保护等提供科学依据。
1 研究区域概况珠江河网(图 1)流域面积达4.5×105 km2, 具有三江(东江、西江、北江)汇流, 八口(自东向西依次为虎门、蕉门、洪奇门、横门、磨刀门、鸡啼门、虎跳门、崖门)入海的特点, 河网纵横交错导致径潮动力相互作用过程复杂。珠江每年约有2 823×108 m3淡水流量及72.4×106 t悬沙量流入南海(Liu et al, 2018), 平均流量约为8 952 m3/s, 口门附近潮差为1.0~1.7 m。磨刀门河口为西江入海口, 是八大口门中输水输沙量最大的河口, 该河口属典型的河控型河口。据三角洲顶端马口水文站1959~2016年月均流量资料, 其多年平均流量为7 078 m3/s, 月均流量最大值为29 000 m3/s (6月), 最小值为1 210 m3/s (1月), 洪枯季差异明显(杨昊等, 2020)。潮汐以不规则半日潮为主, 日不等现象显著, 灯笼山站平均涨落潮历时分别为5.37 h和7.25 h, 口门处三灶站潮型系数为1.30。
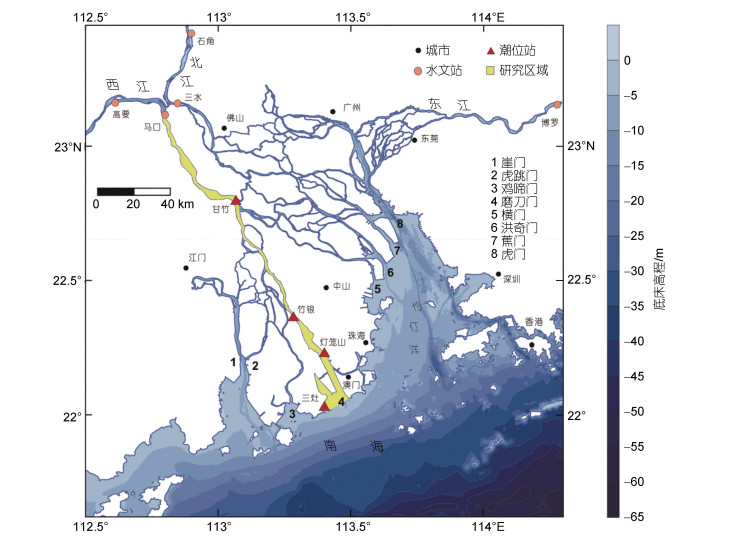 |
| 图 1 研究区域及所用潮位站或水文站位置 Fig. 1 The study area and the deployment of the tidal gauging stations and the hydrological station |
随着经济社会高速发展, 强人类活动已成为河口三角洲系统演变的第三驱动力(陈吉余等, 2008)。口门围垦、联围筑闸、河道采砂及上游流域水库建设等高强度人类活动极大影响磨刀门河口的河道形态和径潮动力, 其“动力-沉积-地貌”体系发生显著变化(吴超羽, 2018)。20世纪80年代前, 磨刀门地区主要人类活动为大规模滩涂围垦, 至1997年已有16.5 km2的浅滩被围填成陆地(Tan et al, 2019)。围垦、疏浚、口门整治等一系列工程措施使河口口门区水域面积减小, 入海水道水深增大, 至20世纪90年代初入海口门向海延伸约13 km (何用等, 2018)。其次, 20世纪50~70年代中期, 大规模的联围筑闸导致三角洲腹部水位壅高, 中上游水面比降变缓, 流速减小, 水流挟沙能力降低, 河床产生淤积(刘锋等, 2011)。20世纪80年代中期开始, 由于用沙需求激增, 在珠江河网区出现大规模河道采砂活动。磨刀门采砂活动主要集中在珠海大桥以北河段, 1991~2000年共挖沙420×104 m3 (韩志远等, 2010)。截至2006年, 西江流域大坝总库容达5.38×1010 m3, 占其入海淡水流量的24.7% (Liu et al, 2018)。大坝建成后流域内大部分沉积物被截留在上游地区, 西江干支流输沙量均呈下降趋势, 下游泥沙供给量锐减(Wang et al, 2011)。在上述强人类活动的综合影响下, 珠江磨刀门河口沿程河床大幅下切, 河槽容积增大, 导致近年来潮汐动力显著增强, 咸潮上溯加剧(韩志远等, 2010; 张先毅等, 2020)。
2 数据与方法 2.1 数据及其处理方法本文所用数据取自《广东省水文年鉴》第八卷和广东省水文局, 潮位原始数据高程为冻结基面, 已统一转换至珠江基面。数据包括磨刀门河口沿程4个潮位站(三灶、灯笼山、竹银、甘竹站)逐日高、低潮位数据和相应时段马口水文站日均流量及逐日高、低潮位数据, 并对潮位和流量数据进行分段三次Hermite插值处理后获得的逐时数据。站点具体信息见表 1。
| 站点 | 经度 | 纬度 | 时间跨度 | 时间长度/a |
| 马口(MK) | 112°48′E | 23°07′N | 1966~2016年 | 51 |
| 甘竹(GZ) | 113°04′E | 22°48′N | 1966~2016年 | 51 |
| 竹银(ZY) | 113°17′E | 22°22′N | 1966~2016年 | 51 |
| 灯笼山(DLS) | 113°24′E | 22°14′N | 1966~2016年 | 51 |
| 三灶(SZ) | 113°24′E | 22°02′N | 1966~2016年 | 51 |
本文采用径潮耦合的数据驱动模型(river-tidal harmonic analysis, R_TIDE)对逐时潮位数据进行调和分析(欧素英等, 2017), 模型可输出重构的逐时水位、特定分潮的振幅和迟角等。在径流动力占主导的河口, 潮波上溯受到径流季节性周期变化的调制影响, 传统的潮汐调和分析模型对河口区潮波特征的分析和预报误差较大, 不能满足径潮信号分离的要求。为有效辨识潮波在流量影响下的传播特征, 基于Matte等(2013, 2014)提出的非平稳调和分析(nonstationary tidal harmonic analysis, NS_TIDE)思路, 假设河口任意位置潮波振幅和迟角主要受上游流量和地形变化的非线性调制影响, 在此基础上进一步假定分析时段内河口地形边界不变, 将信号分成由流量Q引起的水位变化和径流调制影响下的潮水位变化, 通过信号分离定量分析感潮河段径潮动力相互作用。
无径流调制时, 对于月球和太阳引起的周期性潮汐现象可看作是许多假想天体引起的简单的潮汐简谐波动的总和(Pawlowicz et al, 2002), 即潮位曲线可近似看作是由许多振幅、周期、相位不同的分潮组成。潮位可表达成以下多个余弦函数的叠加形式:
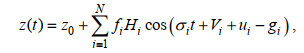 (1)
(1)其中, z(t)为站点的实测潮位; t为时间; z0为平均海面高度; N为分潮个数; fi为分潮振幅的订正因子, 为时间的函数, 常取一年的中值; Hi为分潮平均振幅; σi为分潮角频率; Vi为分潮初相角; ui为天文相角的交角订正角, gi为由于海底摩擦、海水惯性引起的迟角。其中Hi和gi合称为分潮调和常数。
Kukulka等(2003)基于一维圣维南方程组推导得出河口三角洲内任意位置x的潮波振幅变化:
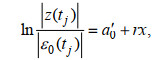 (2)
(2)其中, j=1, 2, 3, …, m, m为逐时序列的数据个数; r为衰减系数; ε0(tj)为河口口门位置x=0处的潮波振幅; a'为常数。衰减系数r为潮波传播速度、水深、流量和河道摩擦系数的函数(Jay et al, 1997)。若摩擦系数采用曼宁公式, 且摩擦系数与潮波传播速度均为水深的函数, 则衰减系数r可简写为水深h(tj)和流量Q(tj)的函数:
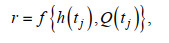 (3)
(3)或:
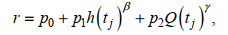 (4)
(4)其中, h(tj)和Q(tj)表示随时间变化的水深和流量; p0、p1、p2、β、γ均为待定参数。式(3)未考虑外海非潮动力边界比如风暴等因素的影响, 这是与Matte等(2013, 2014)提出的非定常调和分析模型的不同之处。假定研究时间段河道底床高程不随时间变化, 则式(4)中水深项可归到常数项, 衰减系数r可简写为
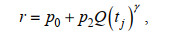 (5)
(5)即河口潮汐非线性变化仅受流量驱动影响。结合式(1)、(2)、(5)可得流量影响下任意位置x的潮水位变化:
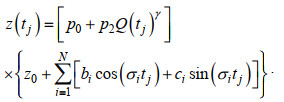 (6)
(6)式(6)的待定系数bi、ci、γ可通过粒子群优化算法(Kennedy et al, 1995)或求解带约束的非线性多变量方程组来确定该参数的最优值。由于流量对不同分潮的影响程度存在差异(Guo et al, 2015), 半日分潮的衰减效应大于全日分潮, 将流量对每一个分潮族的调制影响均采用不同的待定系数, 则式(6)可表示为:
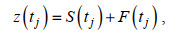 (7)
(7)其中,
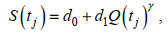 (8)
(8)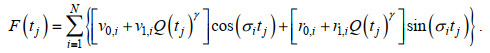 (9)
(9)式(7)即为流量驱动下的R_TIDE模型, S(tj)为底床高程或水深变化、海平面、流量等引起的平均水面变化, 称为余水位项; F(tj)代表不同流量条件下径潮耦合引起的水位变化, 称为径潮耦合项。d0、d1、v0、v1、r0、r1为模型的待定参数, 通过求解带约束的非线性多变量方程组来确定。同时, 由于磨刀门河口径流动力占优势导致径潮动力非线性因素作用较强, 洪水流量时导致三角洲上段为径流控制, 无潮汐波动。因此, 在R_TIDE模型中引入临界流量QC, 当连续2 d潮差小于某个值(如0.001 m)时所对应的最小流量即为临界流量, 当流量大于QC时, 表示该站点及其以上河段不存在潮汐信号。
假设河口三角洲任意位置采用时间间隔为Δt的观测潮位y(tj)(j=1, 2, 3, …, m)序列, 根据实测资料序列长度mΔt、分潮频率差和Rayleigh准则判据Δσ =max[(mΔt)-1, σi-σj], 选择待提取的分潮, 将参数tj、σj、Q(tj)代入式(9), 要求模型计算结果y(tj)和实测水位z(tj)的误差平方和达到最小, 即:
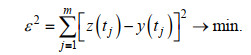 (10)
(10)选择对应资料长度的全日分潮、半日分潮等分潮族, 对实测潮位进行回归拟合, 回归模型效果以均方根误差ERMS和相关指数R2表示, 即:
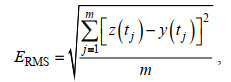 (11)
(11)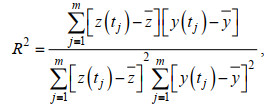 (12)
(12)式(12)中, 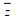
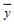
三角洲水道径潮动力相互作用的阶段性特征可通过余水位梯度(S)和潮波振幅梯度(δ)来表述。基于R_TIDE模型计算出来的余水位(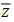
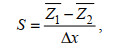 (13)
(13)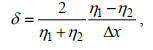 (14)
(14)式中,
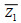
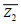
前期研究表明, 基于灯笼山-马口河段月均余水位梯度(或潮波振幅梯度绝对值)与流量的双累积曲线变化趋势, 可知曲线斜率在1990年与2000年发生明显改变(张先毅等, 2020)。根据上述结果, 可将磨刀门河口径潮动力格局的演变分为三个阶段: 1990年前为自然演变和人类活动共同作用的阶段, 但此阶段人类活动尚未对河口径潮动力格局产生明显影响, 河口处在动态平衡期, 以自然演变为主, 称为“平衡期”(简称P1); 2000年后, 河道中下游采砂活动基本已停止, 滩涂围垦面积锐减, 河口在人类活动影响下已发生径潮动力格局转换, 为强人类活动干预后河口的自适应调整阶段, 称为“调整期”(简称P2); 1991~2000年为人类活动影响最强烈的时期, 河口从自然演变为主的平衡态向强人类活动干预后的平衡态转变, 为两个平衡态的过渡阶段, 称为“过渡期”。
3.2 R_TIDE数据驱动模型率定效果围绕珠江磨刀门河口径潮动力异变问题, 采用流量驱动的R_TIDE数据驱动模型对径潮信号进行分离。表 2为磨刀门河口两个阶段沿程站点的临界流量QC、模型主要率定参数及相关的模型评价指标(ERMS和R2)结果。C1~C9为不同分潮族所使用的参数, 其中C1代表长周期气象分潮, 其周期约为15 d, 反映一个大小潮周期变化; C2、C3分别代表全日和半日分潮族, 为主导该区域潮汐动力的分潮族; C4~C9分别代表短周期波动, 由分潮浅水变形效应(如M4、MS4、M6、M8)产生, 反映地形、底床摩擦等边界条件的影响。由表 2可知, 越往下游ERMS值越大, 表明模型对潮流优势区域水位的重构效果略低于上游区域, 但是其R2均大于0.79, 模型结果合理。对于马口站, 由于其为流量驱动边界, 除受洪峰影响外还受边界效应影响, 因此其ERMS相对较大。调整期阶段的ERMS比平衡期普遍增大, R2减小, 表明强人类活动对地形的改造导致水面线为适应地形变化, 水位对流量的响应敏感度有所降低, 由此一定程度上影响了模型的准确性。
| 参数 | 参数意义(选用分潮) | P1阶段取值 | P2阶段取值 | |||||||||
| 三灶 | 灯笼山 | 竹银 | 甘竹 | 马口 | 三灶 | 灯笼山 | 竹银 | 甘竹 | 马口 | |||
| R2 | 见2.2 | 0.83 | 0.79 | 0.87 | 0.99 | 0.98 | 0.80 | 0.79 | 0.81 | 0.95 | 0.96 | |
| ERMS/m | 见2.2 | 0.17 | 0.14 | 0.14 | 0.16 | 0.17 | 0.17 | 0.15 | 0.15 | 0.17 | 0.22 | |
| QC/(×104m3/s) | 见2.2 | 4.01 | 4.01 | 4.01 | 1.89 | 1.13 | 5.27 | 5.27 | 5.27 | 2.90 | 2.21 | |
| γ | 见2.2 | 0.20 | 0.34 | 0.87 | 1.10 | 1.07 | 1.99 | 1.12 | 1.32 | 1.36 | 1.35 | |
| C1 | Msf (D1/14) | 0.02 | 0.03 | 0.01 | 0.27 | 1.18 | 0.98 | 1.69 | 0.96 | 2.00 | 0.79 | |
| C2 | O1、K1 (D1) | 1.99 | 0.18 | 0.43 | 1.00 | 0.04 | 1.85 | 0.53 | 0.37 | 1.03 | 0.72 | |
| C3 | M2、S2 (D2) | 1.70 | 1.05 | 0.95 | 0.93 | 0.82 | 1.13 | 1.16 | 1.19 | 1.25 | 1.09 | |
| C4 | M3、2MK3 (D3) | 0.76 | 1.67 | 1.44 | 1.73 | 1.11 | 1.04 | 0.65 | 0.39 | 0.75 | 0.94 | |
| C5 | M4、MS4、S4 (D4) | 0.08 | 0.01 | 0.02 | 1.90 | 1.11 | 0.03 | 0.02 | 0.02 | 1.99 | 1.88 | |
| C6 | 2MK5、2SK5 (D5) | 0.76 | 0.69 | 0.58 | 1.09 | 1.10 | 0.78 | 0.31 | 0.41 | 0.52 | 1.01 | |
| C7 | M6、2MS6 (D6) | 0.81 | 0.84 | 0.38 | 1.05 | 1.10 | 0.91 | 0.85 | 0.89 | 0.73 | 0.94 | |
| C8 | 3MK7 (D7) | 0.79 | 1.04 | 1.00 | 1.07 | 1.10 | 0.93 | 0.96 | 1.04 | 1.05 | 1.06 | |
| C9 | M8 (D8) | 0.80 | 1.06 | 1.01 | 1.07 | 1.10 | 0.93 | 0.96 | 1.05 | 1.07 | 1.07 | |
| 注: Msf表示以半个月为周期的长周期分潮 | ||||||||||||
图 2为R_TIDE模型在平衡期和调整期重构得到的不同站点日均水位与实测值的对比结果, 其中黑色虚线表示实测值与重构值完全一致。当流量大于临界流量QC时潮波基本消失, 率定过程中流量大于QC时间段所对应的潮波信号为虚假信号, 结果分析部分已剔除这部分信息。由图 2可知, 马口站下游站点模型拟合的效果较好(ERMS介于0.14~0.22 m, R2介于0.79~0.99)。但由于夏季洪峰出现次数多且持续时间长, 对径潮信号分离产生较大影响, 模型误差较大, 因此当流量接近临界流量QC时, 马口站重构水位比实测值偏大。
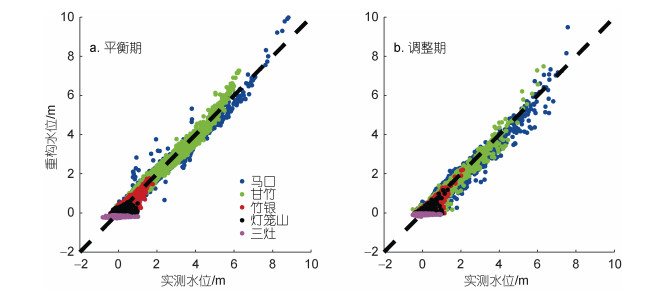 |
| 图 2 R_TIDE数据驱动模型率定结果 Fig. 2 Calibration of the adopted R_TIDE data-driven model |
由表 2可见, 调整期的QC和γ均大于平衡期, 主要原因为调整期阶段潮汐动力增强, 潮区界向上游移动。流量指数γ反映地形边界条件变化, 其值增大表明河床下切, 过水断面增大。其中三灶站变化最大, 反映入海水道水深剧增, 而上游各站点水深均有不同程度增大。竹银、灯笼山站主要受采砂影响, 而马口、甘竹站点除受采砂影响外, 还受上游流域水库调蓄等影响, 导致马口水文站的分流、分沙比发生变化, 进而显著改变底床形态。竹银及其下游站点为潮流优势河段, QC均一致, 而甘竹、马口则受强烈径流影响, 流量越大, 潮区界越往下游移动, 因此, QC逐渐减小。
3.3 M2分潮振幅及其梯度的阶段性变化特征由于磨刀门水位及其梯度发生阶段性异变, 导致潮波振幅及其梯度亦发生显著变化。磨刀门河口潮汐动力主要由M2分潮主导, 因此选用其作为代表性分潮进行分析。M2分潮振幅及其梯度的季节及年均变化如表 3所示。潮波向上游传播过程中振幅沿程衰减, 洪季振幅小于枯季(三灶站除外), 表明径流对潮波传播存在明显的衰减作用, 尤其是在磨刀门河口上游。平衡期灯笼山站振幅的洪枯季差异仅为0.03 m, 甘竹站则为0.07 m, 调整期潮波振幅有明显增大(三灶站除外), 且上游马口站振幅的洪枯季差异增大(约为0.02 m), 其下游的甘竹、竹银站则减小, 灯笼山、三灶站振幅的洪枯季差异基本不变。
| 阶段 | 站点 | 潮波振幅η/m | 河段 | 潮波振幅梯度δ/(×10-6 m-1) | ||||||||
| 春 | 夏 | 秋 | 冬 | 年均 | 春 | 夏 | 秋 | 冬 | 年均 | |||
| P1 | SZ | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 | SZ-MK | -10.74 | -12.36 | -10.86 | -8.81 | -10.70 |
| P2 | 0.42 | 0.43 | 0.42 | 0.42 | 0.42 | -5.99 | -8.30 | -5.47 | -4.56 | -6.08 | ||
| d | -0.01 | -0.01 | -0.01 | 0 | -0.01 | 4.75 | 4.06 | 5.39 | 4.26 | 4.61 | ||
| P1 | DLS | 0.31 | 0.28 | 0.31 | 0.33 | 0.31 | SZ-DLS | -21.59 | -28.16 | -20.78 | -17.20 | -21.95 |
| P2 | 0.37 | 0.33 | 0.37 | 0.37 | 0.36 | -9.78 | -17.14 | -8.58 | -6.40 | -10.49 | ||
| d | 0.06 | 0.05 | 0.06 | 0.06 | 0.05 | 11.81 | 11.03 | 12.20 | 10.80 | 11.46 | ||
| P1 | ZY | 0.23 | 0.19 | 0.23 | 0.26 | 0.23 | DLS-ZY | -16.26 | -22.03 | -15.55 | -12.45 | -16.59 |
| P2 | 0.32 | 0.28 | 0.33 | 0.34 | 0.32 | -6.34 | -8.59 | -6.01 | -5.52 | -6.62 | ||
| d | 0.10 | 0.10 | 0.10 | 0.09 | 0.09 | 9.93 | 13.44 | 9.54 | 6.93 | 9.97 | ||
| P1 | GZ | 0.12 | 0.07 | 0.12 | 0.17 | 0.12 | ZY-GZ | -13.00 | -19.32 | -11.97 | -7.98 | -13.08 |
| P2 | 0.21 | 0.16 | 0.22 | 0.24 | 0.21 | -7.83 | -11.41 | -7.27 | -6.45 | -8.25 | ||
| d | 0.09 | 0.09 | 0.10 | 0.07 | 0.09 | 5.17 | 7.90 | 4.70 | 1.53 | 4.83 | ||
| P1 | MK | 0.07 | 0.03 | 0.06 | 0.10 | 0.07 | GZ-MK | -16.44 | -22.82 | -16.21 | -9.72 | -16.32 |
| P2 | 0.18 | 0.12 | 0.19 | 0.22 | 0.18 | -4.44 | -9.11 | -3.36 | -1.89 | -4.71 | ||
| d | 0.11 | 0.09 | 0.13 | 0.12 | 0.11 | 12.00 | 13.71 | 12.85 | 7.84 | 11.61 | ||
| 注: d表示P2阶段减去P1阶段 | ||||||||||||
为探究潮波传播过程的时空不均匀性, 对比分析强人类活动前后各站点日均M2分潮振幅及相邻站点间日均M2分潮潮波振幅梯度的阶段性演变, 绘制时间过程线如图 3所示, 图中黑色实线表示阶段性演变为0。图 3a为强人类活动前后各站点日均M2分潮振幅变化值的年内分布, 其中日均M2分潮振幅变化值定义为调整期的M2分潮振幅的日平均值减去平衡期所对应的值, 记为Δη (以下日均M2分潮潮波振幅梯度变化值的定义类似, 记为Δδ)。由图 3a可见, 站点距离口门越远其值越大, 其中三灶站振幅年均减小0.01 m, 而马口站则变化0.11 m。季节变化也有类似规律(马口站夏季和甘竹站冬季除外), 表明振幅变化量的季节性差异有向上游累积的效应。日均潮波振幅梯度的时空变化如图 3b所示。潮波振幅梯度最小值出现在夏季, 最大值出现在冬季。三灶-甘竹河段的潮波振幅梯度在调整期阶段的洪枯季差异减小(各河段洪枯季差异的阶段性变化分别为7.14×10-7、4.86×10-6、5.11×10-6 m-1), 且越往上游减小量越大, 表明强人类活动对潮波振幅梯度的增大效应在甘竹以下河段都有累积效应, 但在甘竹-马口河段, 洪枯季差异虽减小但幅度小于竹银-甘竹河段(洪枯季差异的阶段性变化为4.24×10-6 m-1), 表明强人类活动干预后甘竹-马口河段潮波振幅梯度对流量响应减弱。从潮波振幅梯度变化量来看, 三灶-灯笼山河段在秋季变化最大, 灯笼山-甘竹河段则为夏季变化最大, 甘竹-马口河段则是夏季。上述结果表明三灶-灯笼山河段水动力主要受海平面变化控制(秋季三灶余水位最大); 而甘竹-马口河段受径流控制为主, 由于该区域在调整期明显受水库调蓄影响(即洪季蓄水、枯季放水), 虽然潮波振幅梯度夏季阶段性变化最大, 冬季最小, 但是其洪枯季差异减小, 是流量季节性差异减小的直接反映。
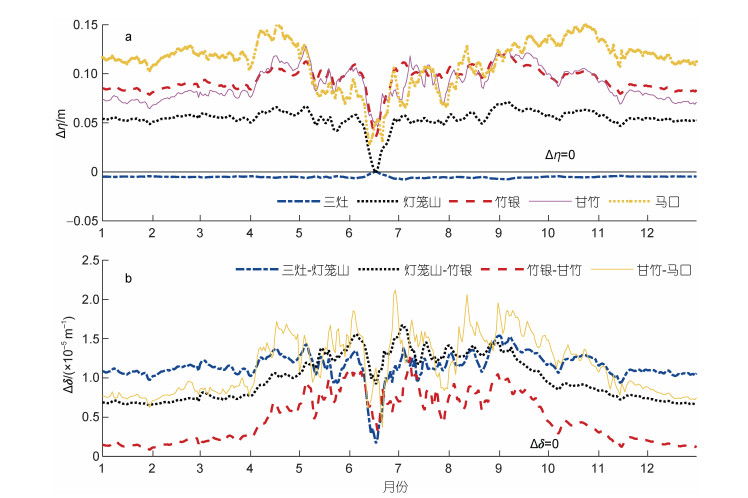 |
| 图 3 强人类活动前后磨刀门河口日均M2分潮潮波振幅及其梯度的阶段性差异 Fig. 3 Stepwise alteration in tidal amplitude and gradient under intensive human activities in the Modaomen estuary 注: Δη表示日均M2分潮振幅变化值; Δδ表示日均M2分潮潮波振幅梯度变化值 |
图 4为三灶-马口河段M2分潮日均潮波振幅梯度与马口站日均流量的关系曲线(图 4a)及其季节变化(图 4b~4e)。平衡期阶段三灶-马口河段潮波振幅梯度极小值(记为δM)为-1.41×10-5 m-1, 对应流量阈值为10 500 m3/s, 而在调整期阶段则分别变为-1.38×10-5 m-1和19 500 m3/s (其中流量阈值定义为当潮波振幅梯度达到极小值所对应的流量值, 记为QM)。日均尺度下, 阈值效应在调整期的冬季基本消失。从季节变化来看, 平衡期的秋季潮波振幅梯度极小值最小, 调整期则为夏季最小, 冬季最大, 大流量下潮波衰减效应更明显。调整期阶段潮波振幅梯度极小值(约为-1.38× 10-5 m-1)和对应流量阈值(约为19 500 m3/s)均大于平衡期。
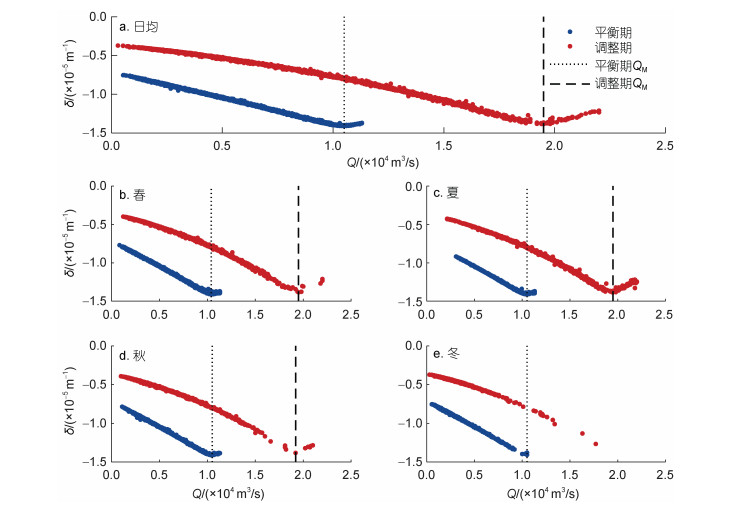 |
| 图 4 三灶-马口河段M2分潮日均潮波振幅梯度(δ)与马口站日均流量(Q)的阈值关系(a)及其季节变化(b~e) Fig. 4 Relationship between the daily averaged M2 tidal amplitude gradient over SZ-MK reach (δ) and the river discharge (Q) observed at the MK hydrological station to illustrate the threshold effect (a) and its seasonal alteration (b~e) 注: QM表示流量阈值, 定义为当潮波振幅梯度达到极小值所对应的流量值 |
潮波振幅梯度是径潮动力相互作用的直接结果, 因此类似流量阈值效应, 外海潮汐动力变化(即周期约为15 d的大小潮)亦会导致潮波振幅梯度产生振幅阈值效应(记为ηM)。图 5为磨刀门河口三灶-马口河段日均M2分潮潮波振幅梯度与三灶站日均M2分潮振幅的关系曲线。由图 5可见, 日均潮波振幅梯度极小值在调整期略有增大, 约为2.49×10-7 m-1, 对应的振幅阈值基本不变(约增大0.14 cm)。图 5b~5e为日均M2分潮潮波振幅梯度与三灶站日均M2分潮振幅阈值关系的季节变化。与图 4类似, 除调整期的冬季振幅阈值效应消失外(图 5e), 其余季节均存在较明显的振幅阈值效应, 其中夏季振幅梯度极小值最小, 其次为春、秋两季, 最大为冬季。而平衡期阶段秋季的振幅阈值最小, 冬季最大。调整期冬季阈值效应消失的主要原因是下泄流量较小, 即便经过流域水库调蓄, 调整期口门振幅依旧未能达到使衰减效应达到最大的临界值(约0.43 m)。达到振幅阈值前, 由于大潮流速振幅较大导致其底床摩擦较大, 衰减效应增强, 潮波振幅梯度减小。而达到振幅阈值后, 流速振幅增大导致的潮能耗散不足以平衡地形辐聚增强(大潮时水深增大)导致的潮能增加, 因此, 潮波振幅梯度略微增大。
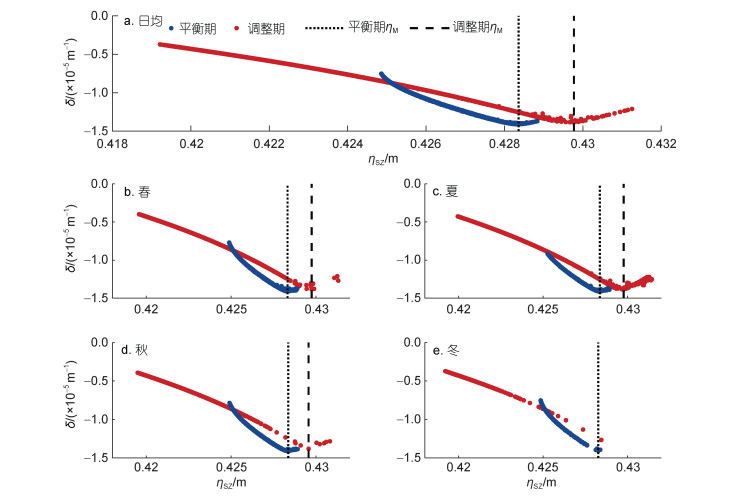 |
| 图 5 三灶-马口河段M2分潮日均潮波振幅梯度(δ)与三灶站日均M2分潮振幅(ηSZ)的阈值关系(a)及其季节变化(b~e) Fig. 5 Relationship between the daily averaged M2 tidal amplitude gradient (δ) in SZ-MK sector and the M2 tidal amplitude (ηSZ) observed at the SZ tidal gauging station to illustrate the threshold effect (a) and its seasonal alteration (b~e) 注: ηM表示振幅阈值 |
图 6为相邻站点间沿程潮波振幅梯度随口门三灶站振幅的变化曲线。结果表明, 振幅阈值效应仅存在于径流动力占优势的河段, 主要存在于甘竹-马口河段(仅调整期的冬季消失), 另外, 在竹银-甘竹河段(春、夏季和平衡期的秋季)及灯笼山-竹银河段(调整期的夏季)也有类似现象, 而在三灶-灯笼山河段, 该现象则不存在。对于甘竹-马口河段, 平衡期阶段, 其秋季潮波振幅梯度极小值最小, 为-3.55×10-5 m-1, 冬季值最大, 为-3.52×10-5 m-1。虽然冬季余水位减小、底床摩擦增大, 但由于流量减小, 对潮能的耗散作用亦减弱, 潮波振幅梯度反而增大, 表明在年内变化中甘竹-马口河段主要受径流影响。而在调整期阶段, 冬季振幅阈值效应消失, 这是由于冬季衰减效应减小, 尚未达到阈值(约为-3.23×10-5 m-1); 其余季节均存在阈值效应, 表明要在更大的外海潮汐动力驱动下才能使该河段发生阈值效应, 这与强人类活动驱动下各站点(三灶站除外)振幅均有不同程度的抬升有关, 即两个站点间振幅差值需要达到临界值, 潮波振幅梯度极小值才会出现。
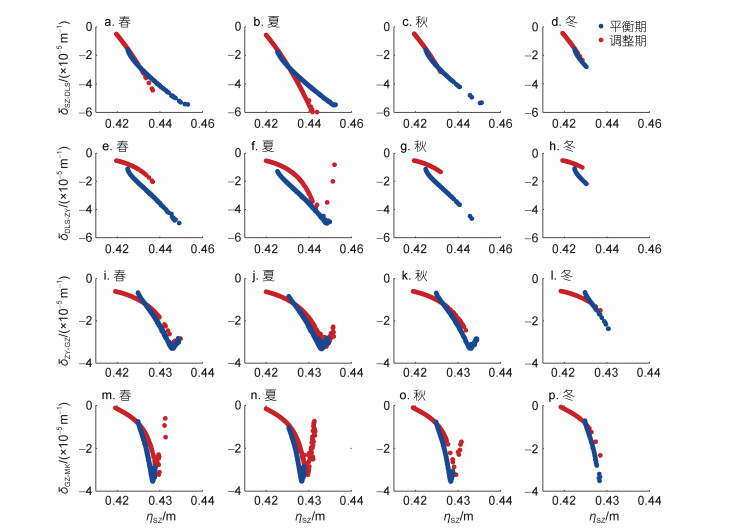 |
| 图 6 相邻站点间河段M2分潮日均潮波振幅梯度(δ)与三灶站日均振幅(ηSZ)关系曲线的季节变化 Fig. 6 Seasonal alteration in the relationship between the daily averaged M2 tidal amplitude gradient of the sub-sector along neighboring tidal gauging stations and tidal amplitude observed in SZ tidal gauging station 注: a~d: 三灶-灯笼山(δSZ-DLS); e~h: 灯笼山-竹银(δDLS-ZY); i~l: 竹银-甘竹(δZY-GZ); m~p: 甘竹-马口(δGZ-MK) |
对于下游河段(竹银以下), 该区域主要受口门围垦、河道整治工程等地形边界影响, 对径流非线性作用的响应不明显, 潮波振幅梯度随口门振幅的变化基本呈线性关系, 而灯笼山-竹银河段出现阈值效应(平衡期的夏季)主要是由于夏季衰减效应已达到调整期阶段的阈值(约为-3.92×10-5 m-1), 而平衡期振幅梯度极值更小, 潮波衰减尚未达到该临界值。竹银-甘竹河段阈值效应出现的原因与甘竹-马口河段类似。
表 4为三灶-马口河段及相邻站点间河段的潮波振幅梯度阈值及其对应的振幅阈值。沿程潮波振幅梯度极小值变化规律与该河段M2分潮潮波振幅梯度的空间变化规律相似, 竹银-甘竹河段衰减效应减弱, 到甘竹-马口河段衰减效应又增大, 表明甘竹站以上河段受强烈径流调制, 潮波衰减效应增强。在上游河段振幅沿程减小, 若要达到潮波振幅梯度阈值已不需要更大的口门振幅, 因此, 对应振幅阈值沿程略有减小。
| 河段 | 阶段 | 季节 | δM/ (×10-5 m-1) | ηM/m |
| 三灶-马口 | 平衡期 | 春 | -1.41 | 0.43 |
| 夏 | -1.41 | 0.43 | ||
| 秋 | -1.41 | 0.43 | ||
| 冬 | -1.40 | 0.43 | ||
| 调整期 | 春 | -1.38 | 0.43 | |
| 夏 | -1.39 | 0.43 | ||
| 秋 | -1.38 | 0.43 | ||
| 冬 | — | — | ||
| 灯笼山-竹银 | 平衡期 | 春 | — | — |
| 夏 | — | — | ||
| 秋 | — | — | ||
| 冬 | — | — | ||
| 调整期 | 春 | — | — | |
| 夏 | -3.92 | 0.44 | ||
| 秋 | — | — | ||
| 冬 | — | — | ||
| 竹银-甘竹 | 平衡期 | 春 | -3.31 | 0.43 |
| 夏 | -3.33 | 0.43 | ||
| 秋 | -3.31 | 0.43 | ||
| 冬 | — | — | ||
| 调整期 | 春 | -3.07 | 0.43 | |
| 夏 | -3.22 | 0.43 | ||
| 秋 | — | — | ||
| 冬 | — | — | ||
| 甘竹-马口 | 平衡期 | 春 | -3.55 | 0.43 |
| 夏 | -3.54 | 0.43 | ||
| 秋 | -3.55 | 0.43 | ||
| 冬 | -3.51 | 0.43 | ||
| 调整期 | 春 | -3.23 | 0.43 | |
| 夏 | -3.23 | 0.43 | ||
| 秋 | -3.23 | 0.43 | ||
| 冬 | — | — | ||
| 注: “—”表示无阈值效应 | ||||
上述结果表明, 磨刀门河口流量-余水位及其梯度关系在调整期阶段发生显著变化, 同流量下沿程各站点余水位及其梯度明显下降(张蔚等, 2008; Yang et al, 2020)。然而三角洲顶端的马口水文站年均流量仅减小816 m3/s (约为11%), 下游口门处三灶站M2分潮振幅年均值仅变化0.01 m, 表明上下游动力边界的阶段性变化不是导致潮波振幅梯度与上下游关系异变的主要原因, 地形异变及其导致的底床摩擦效应变化才是导致径潮动力格局转换的主导因素。
余水位梯度作为表征径潮动力的重要参数, 其形成演变是探究地形异变对潮波传播影响机制的重要依据和有效切入点, 其解析表达式可由一维动量守恒方程得到(Savenije et al, 2005)
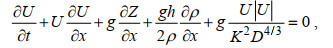 (15)
(15)式中, x为距离口门处的距离; ρ为水体密度; U为断面平均流速; Z为自由水面高程; D为水深; g为重力加速度; K为曼宁摩擦系数的倒数。忽略密度效应和对流加速度项并假定流速具有周期性, 式(15)在一个潮周期内积分可得式(16)(Cai et al, 2014)。
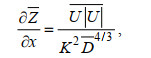 (16)
(16)式(16)为余水位梯度的解析表达式, 其中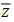
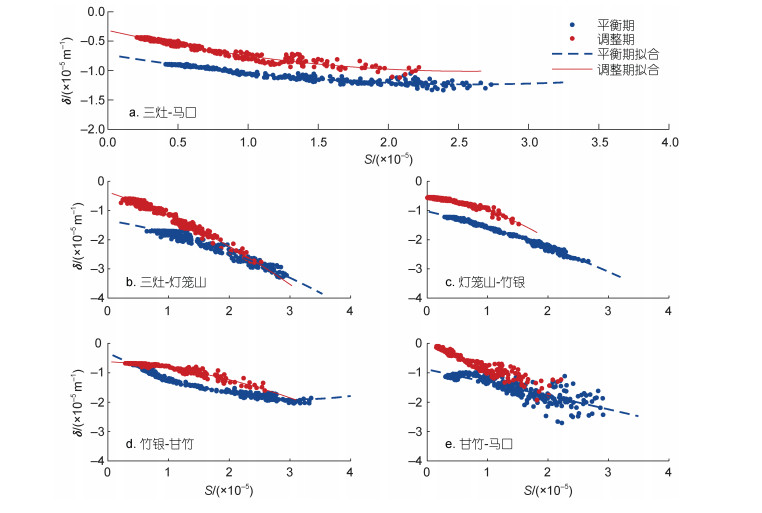 |
| 图 7 相邻站点间河段M2分潮日均潮波振幅梯度(δ)与日均余水位梯度(S)的变化 Fig. 7 Stepwise alteration in the relationship between the daily averaged M2 tidal amplitude gradient (δ) in SZ-MK sector and the corresponding residual water level gradient (S) observed in each sub-sector |
余水位梯度的阶段性变化是水面线适应地形变化的直接反映。在人类活动干预前, 河床缓慢抬升, 底坡降变化不大。1962~1977年为缓慢淤积状态, 磨刀门河口竹洲头-大排沙河段、大排沙-灯笼山河段平均水深分别减小0.49, 0.28 m; 1977~1999年, 水道受到明显冲刷, 河道深泓下切深度为0.59~1.70 m不等, 平均水深增加1.13 m (刘锋等, 2011); 磨刀门河口沿程平均宽深比从1960年的6.25减小到1999年的4.73 (河道趋向窄深化趋势发展), 同期河槽容积增大34.15×106 m3 (Liu et al, 2019)。表 5统计了三灶-竹银河段1964、1977、1999、2016年各水深区间的容积和面积。按水深分成0~2、2~5、5~10和 > 10 m四个区间, 分别计算各区间的河槽容积和面积。1964~1977年, 各水深段容积和面积均显著减小, 反映以围垦为主导的淤积作用。1977~1999年, 口门围垦和采砂共存, 前者导致口门大部分水域被围填成陆地, 0~2 m水深区间容积和面积均锐减, 然而水深5 m以下容积和面积显著增大, 表明河床大幅下切, 两岸侵蚀效应增强, 河道被冲刷, 容积和面积增加量分别为每年3.78×106 m3和0.90×106 m2。1999~2016年, 强人类活动逐渐减弱, 但潮波传播过程已发生异变, 加上上游水库建设导致泥沙减少, 导致河道水沙分配格局发生变化, 潮汐动力显著增强, 冲刷效应进一步加剧, 5 m以下水深容积持续增大, 增加量为每年1.06×106 m3, 面积仅增大2.93×106 m2。当冲淤态势由淤积转变为冲刷时, 河道容积增大, 底床摩擦减小, 潮波振幅梯度增大。
| 水深区间/m | 容积/(×106 m3) | 面积/(×106 m2) | |||||||
| 1964年 | 1977年 | 1999年 | 2016年 | 1964年 | 1977年 | 1999年 | 2016年 | ||
| 0~2 | 533.35 | 370.06 | 173.80 | 166.41 | 110.73 | 100.44 | 23.49 | 18.04 | |
| 2~5 | 263.13 | 136.56 | 155.28 | 161.83 | 113.68 | 80.91 | 25.80 | 22.60 | |
| 5~10 | 32.60 | 13.87 | 88.23 | 104.85 | 33.14 | 10.86 | 29.13 | 30.30 | |
| >10 | 0.94 | 0.63 | 9.41 | 16.20 | 0.75 | 0.56 | 2.10 | 3.86 | |
本文基于珠江磨刀门河口沿程4个潮位站的高、低潮数据及相应时段马口水文站高、低潮数据和流量数据, 采用基于流量驱动的R_TIDE数据驱动模型对河口潮波传播的异变过程进行分析, 根据余水位及其梯度、M2分潮振幅及其梯度的阶段性变化重点探讨潮波振幅梯度与上下游动力边界的关系异变过程及机制, 主要结论如下:
(1) 与平衡期相比, 在强人类活动影响后的调整期阶段, 各站点日均M2分潮振幅及其梯度增大, 其中振幅在秋季变化最大(灯笼山-马口分别为0.06、0.10、0.10、0.13 m), 冬季最小(马口除外, 灯笼山、竹银、甘竹分别为0.05、0.08、0.07 m), 年内差异不大; 潮波振幅梯度变化则较为复杂, 三灶-甘竹河段沿程减小, 甘竹-马口河段阶段性变化增大。
(2) 日均M2分潮潮波振幅梯度与下游动力边界之间存在阈值效应, 主要出现在甘竹-马口河段。强人类活动驱动下潮波振幅梯度阈值增大(三灶-马口河段增量约为2.50×10-7 m-1), 振幅阈值基本不变(仅增大约0.14 cm)。由于底床有效摩擦减小导致沿程潮能耗散减弱, 因此当口门振幅相同时, 调整期的潮波振幅梯度大于平衡期, 随着振幅增大, 底床摩擦效应越明显, 导致调整期潮波衰减速度减缓, 当两个阶段的口门振幅均达到振幅阈值时(此处假定振幅阈值相同), 则调整期对应的潮波振幅梯度大于平衡期。
(3) 对于潮波振幅梯度与大小潮的关系异变分析需综合考虑地形、摩擦、流量等多因素影响。由于上下游动力边界的阶段性变化不足以导致上述关系的异变, 因此地形及其引起的底床摩擦变化则是径潮动力异变的根本原因。从1964~2016年, 10 m以下水深的容积增大15.26×106 m3, 0~2 m水深容积则减小366.94×106 m3, 反映河道窄深化的演变趋势。由于地形的异变, 在口门振幅增大过程中, 达到振幅阈值前, 由于底床摩擦增大, 小潮时的潮波振幅梯度大于大潮, 而达到振幅阈值后, 此时以地形辐聚为主导影响因子导致潮波振幅梯度增大。
刘锋, 田向平, 韩志远, 等, 2011. 近四十年西江磨刀门水道河床演变分析. 泥沙研究, (1): 45-50 |
杨昊, 欧素英, 傅林曦, 等, 2020. 珠江磨刀门河口日均水位变化及影响因子辨识. 水利学报, 51(7): 869-881 |
吴超羽, 2018. 珠江三角洲千年尺度演变的动态平衡及其唯象判据探讨. 海洋学报, 40(7): 22-37 DOI:10.3969/j.issn.0253-4193.2018.07.002 |
何用, 卢陈, 杨留柱, 等, 2018. 珠江河口口门区滩槽演变及对泄洪的影响研究. 水利学报, 49(1): 72-80 |
张先毅, 杨昊, 黄竞争, 等, 2020. 强人类活动驱动下珠江磨刀门河口径潮动力的季节性异变特征. 海洋与湖沼, 51(5): 1043-1054 |
张先毅, 黄竞争, 杨昊, 等, 2019. 长江河口潮波传播机制及阈值效应分析. 海洋与湖沼, 50(4): 788-798 |
张蔚, 严以新, 诸裕良, 等, 2008. 人工采沙及航道整治对珠江三角洲水流动力条件的影响. 水利学报, 39(9): 1098-1104 DOI:10.3321/j.issn:0559-9350.2008.09.011 |
陈吉余, 程和琴, 戴志军, 2008. 河口过程中第三驱动力的作用和响应——以长江河口为例. 自然科学进展, 18(9): 994-1000 DOI:10.3321/j.issn:1002-008X.2008.09.005 |
欧素英, 杨清书, 杨昊, 等, 2017. 河口三角洲径流和潮汐相互作用模型及应用. 热带海洋学报, 36(5): 1-8 |
韩志远, 田向平, 欧素英, 2010. 人类活动对磨刀门水道河床地形和潮汐动力的影响. 地理科学, 30(4): 582-587 |
BUSCHMAN F A, HOITINK A J F, VAN DER VEGT M, et al, 2009. Subtidal water level variation controlled by river flow and tides. Water Resources Research, 45(10): W10420 |
CAI H Y, SAVENIJE H H G, GAREL E, et al, 2019. Seasonal behaviour of tidal damping and residual water level slope in the Yangtze River estuary: identifying the critical position and river discharge for maximum tidal damping. Hydrology and Earth System Sciences, 23(6): 2779-2794 DOI:10.5194/hess-23-2779-2019 |
CAI H Y, SAVENIJE H H G, JIANG C J, et al, 2016. Analytical approach for determining the mean water level profile in an estuary with substantial fresh water discharge. Hydrology and Earth System Sciences, 20(3): 1177-1195 DOI:10.5194/hess-20-1177-2016 |
CAI H, SAVENIJE H H G, TOFFOLON M, 2014. Linking the river to the estuary: influence of river discharge on tidal damping. Hydrology and Earth System Sciences, 18(1): 287-304 DOI:10.5194/hess-18-287-2014 |
CAI H Y, SAVENIJE H H G, YANG Q S, et al, 2012. Influence of River Discharge and dredging on tidal wave propagation: Modaomen Estuary Case. Journal of Hydraulic Engineering, 138(10): 885-896 DOI:10.1061/(ASCE)HY.1943-7900.0000594 |
CAO Y, ZHANG W, ZHU Y L, et al, 2020. Impact of trends in river discharge and ocean tides on water level dynamics in the Pearl River Delta. Coastal Engineering, 157: 103634 DOI:10.1016/j.coastaleng.2020.103634 |
GODIN G, 1985. Modification of river tides by the discharge. Journal of Waterway, Port, Coastal, and Ocean Engineering, 111(2): 257-274 DOI:10.1061/(ASCE)0733-950X(1985)111:2(257) |
GUO L C, VAN DER WEGEN M, JAY D A, et al, 2015. River-tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. Journal of Geophysical Research: Oceans, 120(5): 3499-3521 DOI:10.1002/2014JC010491 |
HOITINK A J F, WANG Z B, VERMEULEN B, et al, 2017. Tidal controls on river delta morphology. Nature Geoscience, 10(9): 637-645 DOI:10.1038/ngeo3000 |
HORREVOETS A C, SAVENIJE H H G, SCHUURMAN J N, et al, 2004. The influence of river discharge on tidal damping in alluvial estuaries. Journal of Hydrology, 294(4): 213-228 DOI:10.1016/j.jhydrol.2004.02.012 |
JAY D A, FLINCHEM E P, 1997. Interaction of Fluctuating River Flow with a Barotropic Tide: a demonstration of wavelet tidal analysis methods. Journal of Geophysical Research: Oceans, 102(C3): 5705-5720 DOI:10.1029/96JC00496 |
JI X M, ZHANG W, 2019. Tidal influence on the discharge distribution over the Pearl river Delta, China. Regional Studies in Marine Science, 31: 100791 DOI:10.1016/j.rsma.2019.100791 |
KENNEDY J, EBERHART R, 1995. Particle swarm optimization [C] //Proceedings of ICNN'95 - International Conference on Neural Networks. Perth, WA, Australia: IEEE: 1942-1948.
|
KUKULKA T, JAY D A, 2003. Impacts of Columbia River discharge on salmonid habitat: 1. A nonstationary fluvial tide model. Journal of Geophysical Research: Oceans, 108(C9): 3293 DOI:10.1029/2002JC001382 |
LIU F, HU S, GUO X J, et al, 2018. Recent changes in the sediment regime of the Pearl River (South China): causes and implications for the Pearl River Delta. Hydrological Processes, 32(12): 1771-1785 DOI:10.1002/hyp.11513 |
LIU F, XIE R Y, LUO X X, et al, 2019. Stepwise adjustment of deltaic channels in response to human interventions and its hydrological implications for sustainable water managements in the Pearl River Delta, China. Journal of Hydrology, 573: 194-206 DOI:10.1016/j.jhydrol.2019.03.063 |
MATTE P, JAY D A, ZARON E D, 2013. Adaptation of classical tidal harmonic analysis to Nonstationary Tides, with Application to River Tides. Journal of Atmospheric and Oceanic Technology, 30(3): 569-589 DOI:10.1175/JTECH-D-12-00016.1 |
MATTE P, SECRETAN Y, MORIN J, 2014. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: an application of nonstationary tidal harmonic analysis. Journal of Geophysical Research: Oceans, 119(9): 5724-5744 DOI:10.1002/2014JC009791 |
MOFTAKHARI H R, JAY D A, TALKE S A, 2016. Estimating river discharge using multiple‐tide gauges distributed along a channel. Journal of Geophysical Research: Oceans, 121(4): 2078-2097 DOI:10.1002/2015JC010983 |
PAN H D, GUO Z, WANG Y Y, et al, 2018a. Application of the EMD Method to River Tides. Journal of Atmospheric and Oceanic Technology, 35(4): 809-819 DOI:10.1175/JTECH-D-17-0185.1 |
PAN H D, LV X Q, 2019. Reconstruction of spatially continuous water levels in the Columbia River Estuary: the method of Empirical Orthogonal Function revisited. Estuarine, Coastal and Shelf Science, 222: 81-90 DOI:10.1016/j.ecss.2019.04.011 |
PAN H D, LV X Q, WANG Y Y, et al, 2018b. Exploration of tidal-fluvial interaction in the Columbia River estuary using S_TIDE. Journal of Geophysical Research: Oceans, 123(9): 6598-6619 DOI:10.1029/2018JC014146 |
PAWLOWICZ R, BEARDSLEY B, LENTZ S, 2002. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Computers & Geosciences, 28(8): 929-937 |
SASSI M G, HOITINK A J F, 2013. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river. Journal of Geophysical Research: Oceans, 118(9): 4139-4151 DOI:10.1002/jgrc.20297 |
SAVENIJE H H G, 1992. Lagrangian solution of St. Venant's equations for alluvial estuary. Journal of Hydraulic Engineering, 118(8): 1153-1163 DOI:10.1061/(ASCE)0733-9429(1992)118:8(1153) |
SAVENIJE H H G, VELING E J M, 2005. Relation between tidal damping and wave celerity in estuaries. Journal of Geophysical Research, 110(C4): C04007 |
SCHUTTELAARS H M, DE JONGE V N, CHERNETSKY A, 2013. Improving the predictive power when modelling physical effects of human interventions in estuarine systems. Ocean & Coastal Management, 79: 70-82 |
TAN C, HUANG B S, LIU F, et al, 2019. Recent morphological changes of the mouth bar in the Modaomen Estuary of the Pearl River Delta: causes and environmental implications. Ocean & Coastal Management, 181: 104896 |
WANG H J, SAITO Y, ZHANG Y, et al, 2011. Recent changes of sediment flux to the western Pacific Ocean from major rivers in East and Southeast Asia. Earth-Science Reviews, 108(1/2): 80-100 |
YANG H, ZHANG X Y, CAI H Y, et al, 2020. Seasonal changes in river-tide dynamics in a highly human-modified estuary: Modaomen Estuary case study. Marine Geology, 427: 106273 DOI:10.1016/j.margeo.2020.106273 |
 2022, Vol. 53
2022, Vol. 53


